Exploring Time-Resolved Fluorescence Data: A Software Solution for Model Generation and Analysis
Abstract
1. Introduction
2. Materials and Methods
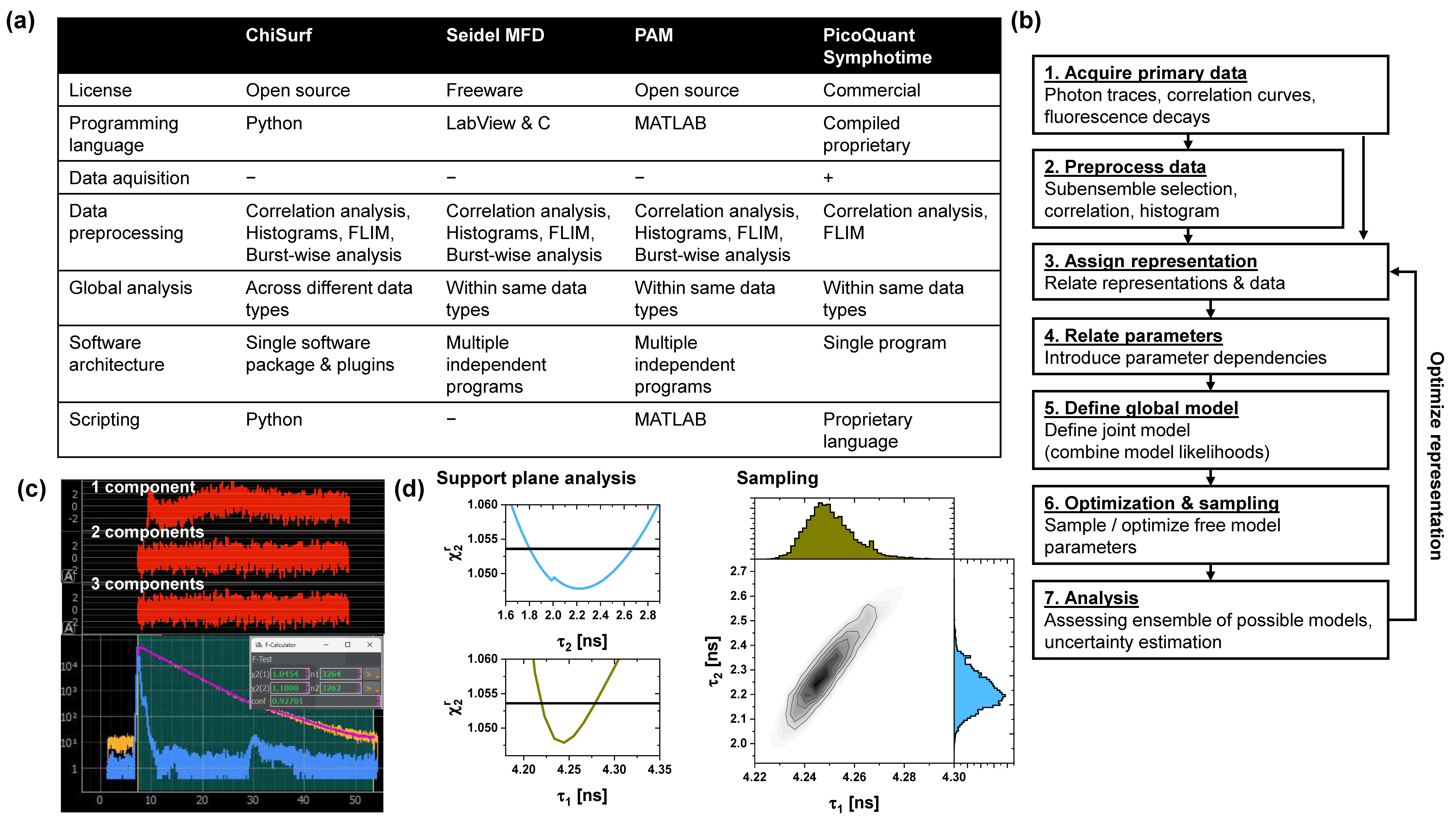
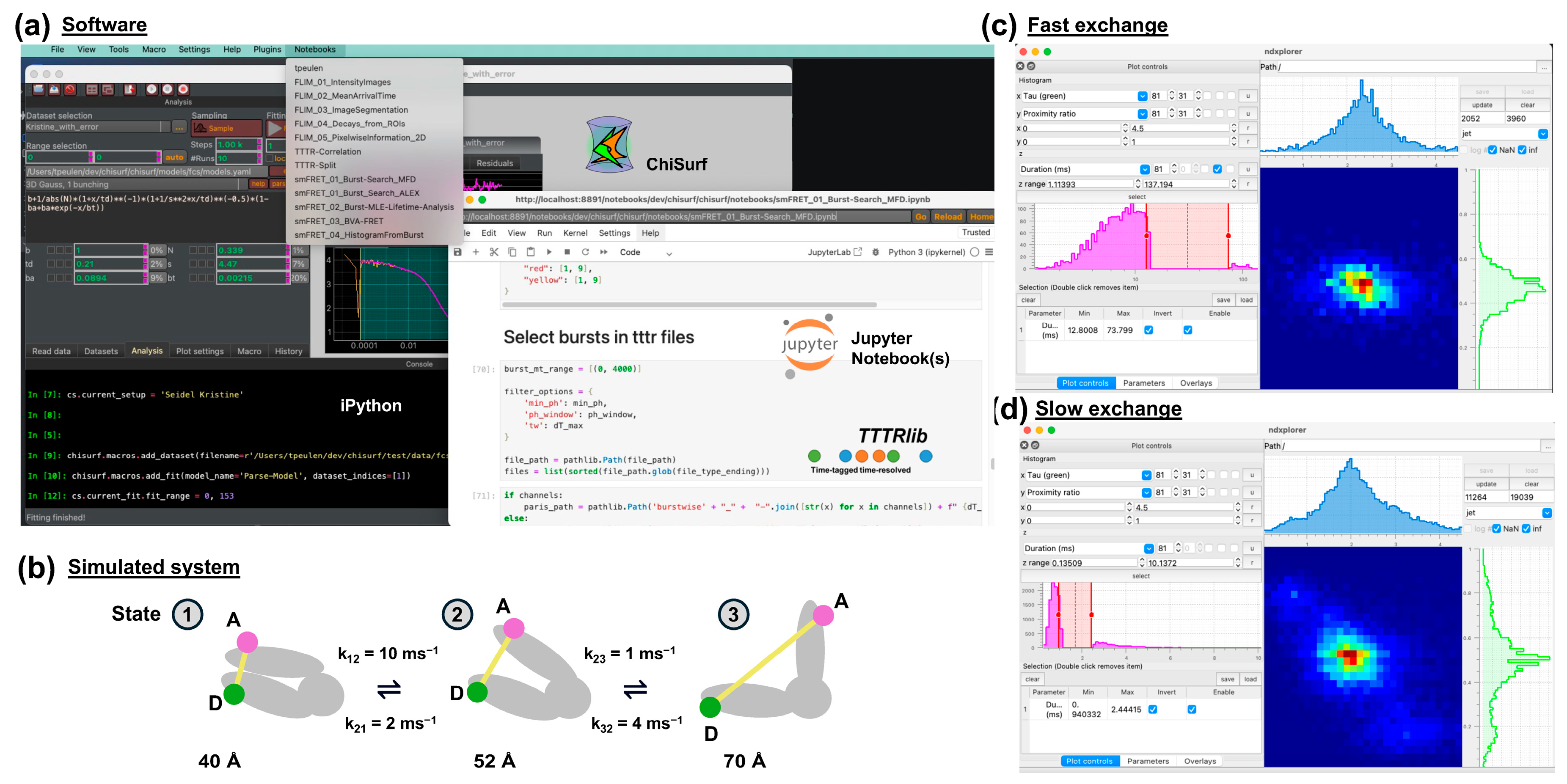
2.1. Software
2.2. Nomenclature
2.3. Förster Theory
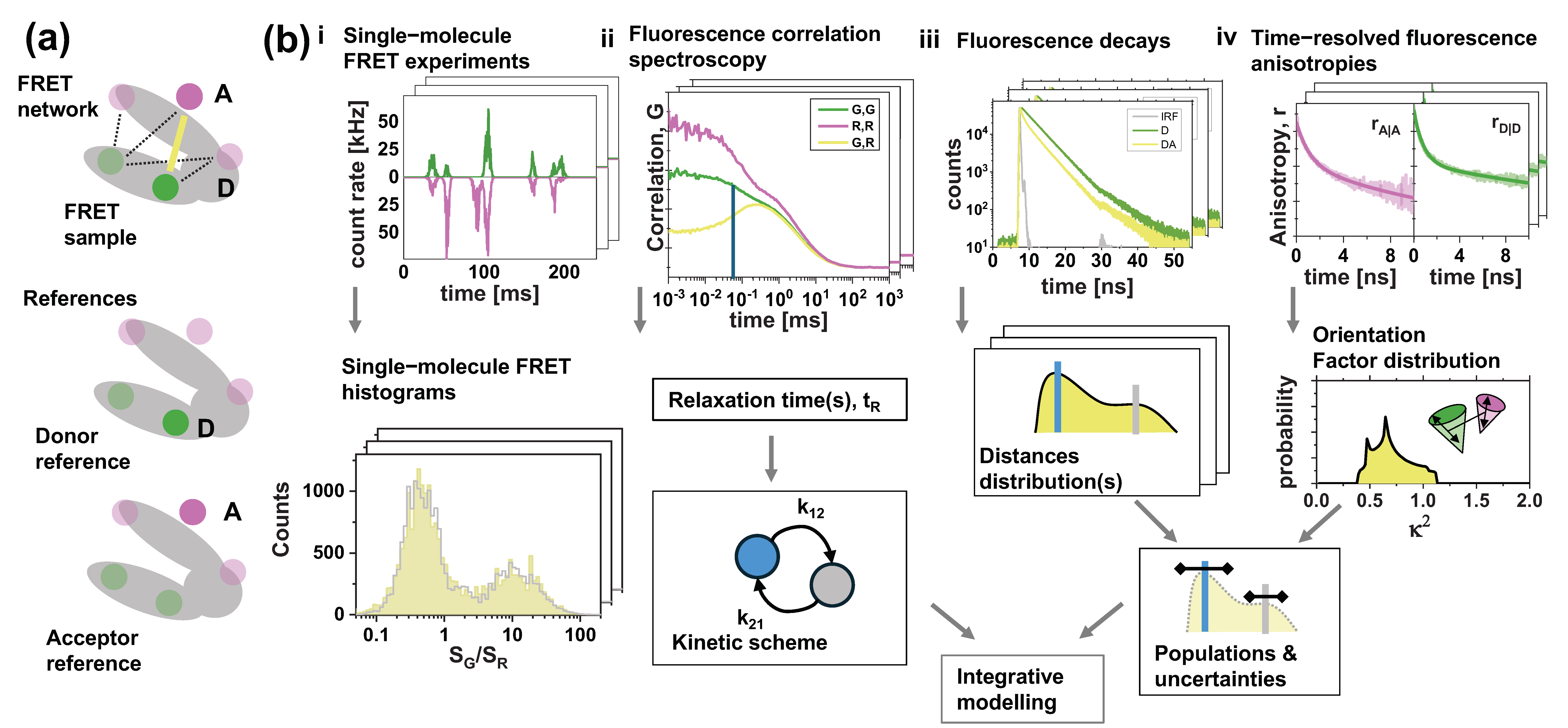
2.4. Time-Resolved Experiments
Time-Resolved Anisotropy
2.5. Burst Analysis
2.6. Single-Molecule Histograms
2.7. Fluorescence Correlation Spectroscopy
2.8. Orientation Factor Distributions
2.9. Simulation of Synthetic Data
2.10. FLIM Experiments
2.10.1. Sample Preparation
2.10.2. PIE Measurement
2.11. Global Analysis and Error Estimation
3. Results and Discussion
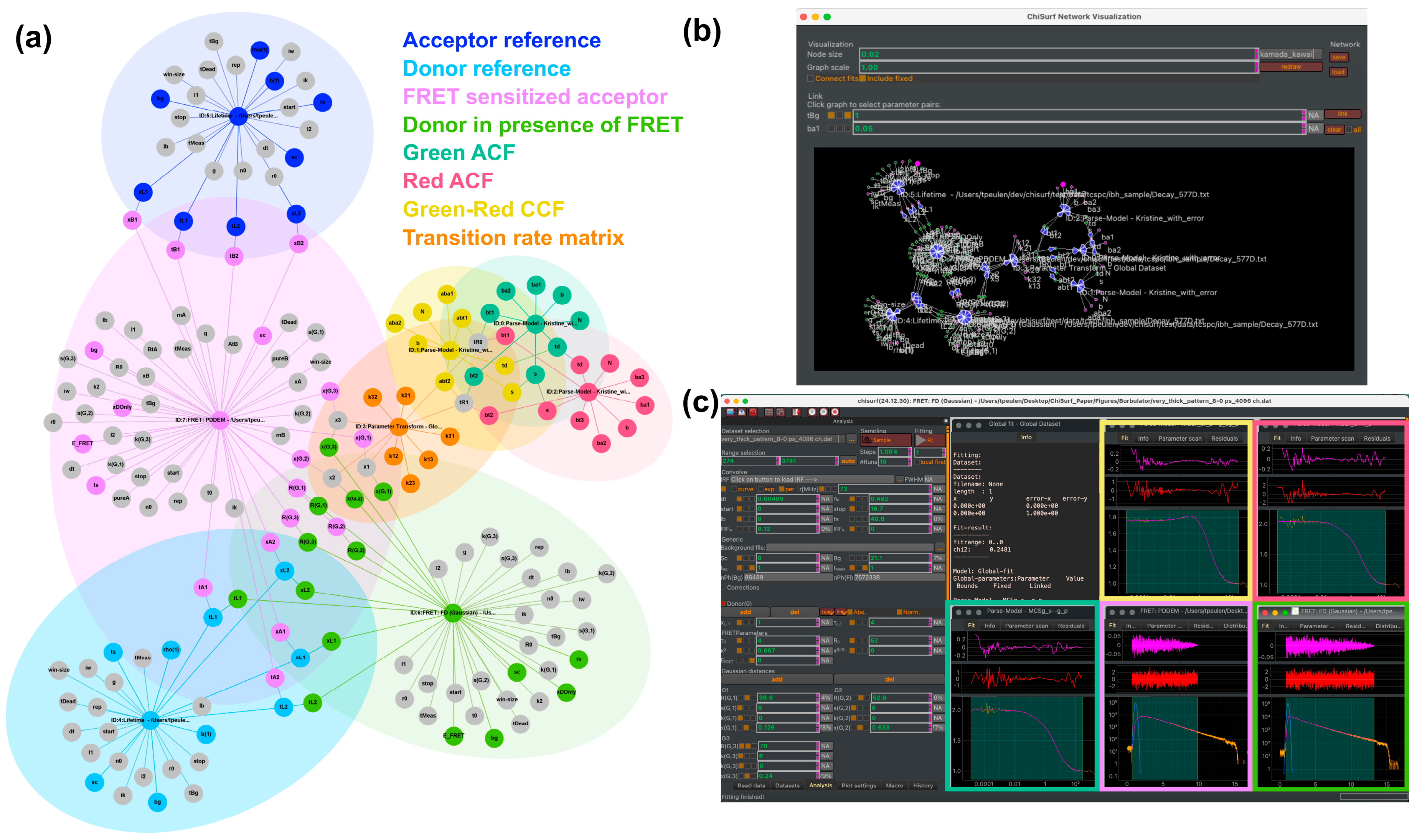
3.1. Software Overview
3.2. Global Analysis
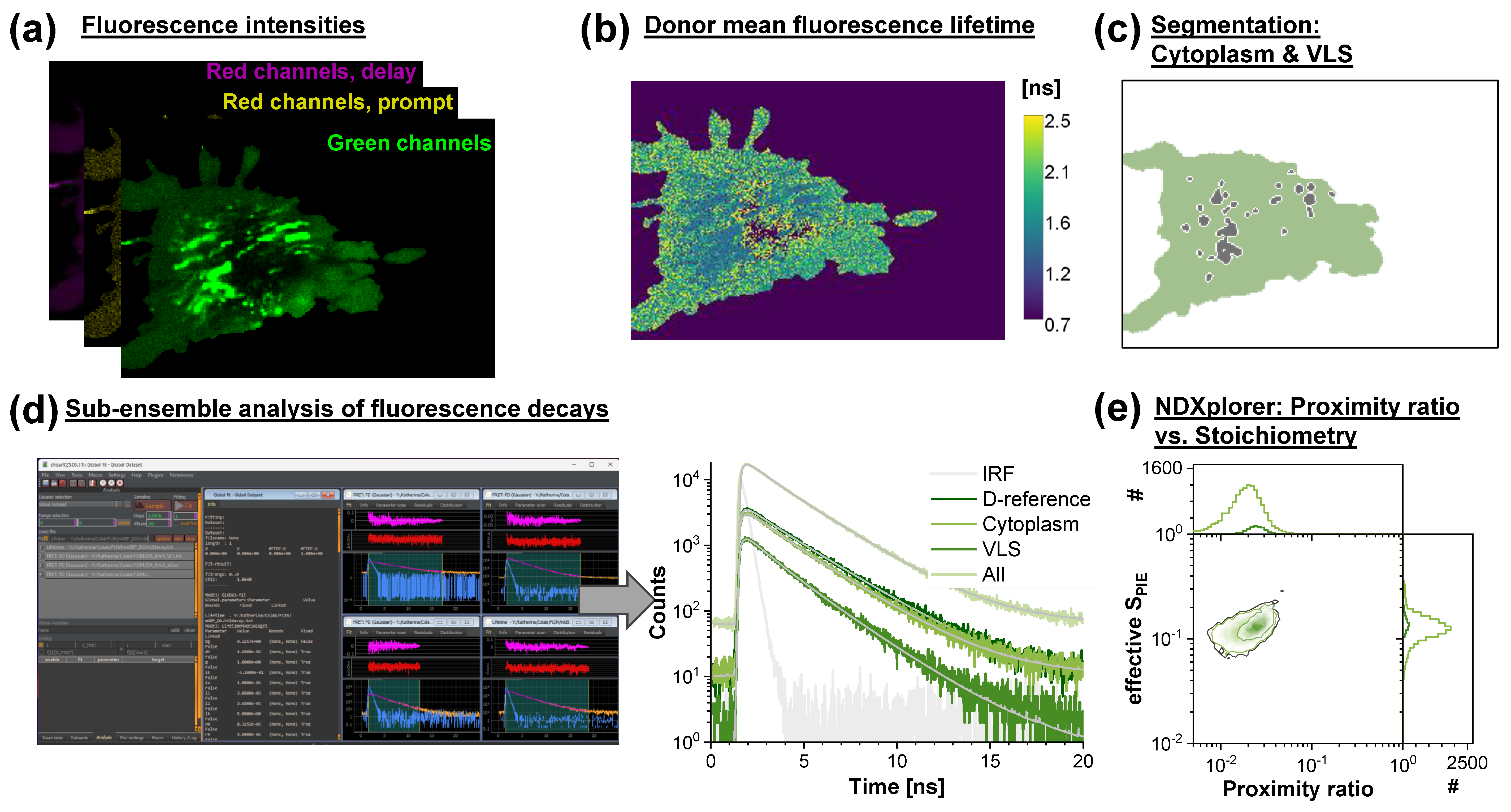
3.3. Fluorescence Lifetime Imaging
3.4. Installation and Practical Considerations
4. Outlook
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lerner, E.; Barth, A.; Hendrix, J.; Ambrose, B.; Birkedal, V.; Blanchard, S.C.; Börner, R.; Sung Chung, H.; Cordes, T.; Craggs, T.D.; et al. FRET-Based Dynamic Structural Biology: Challenges, Perspectives and an Appeal for Open-Science Practices. Elife 2021, 10, e60416. [Google Scholar] [CrossRef] [PubMed]
- Peulen, T.O.; Hengstenberg, C.S.; Biehl, R.; Dimura, M.; Lorenz, C.; Valeri, A.; Folz, J.; Hanke, C.A.; Ince, S.; Vöpel, T.; et al. Integrative Dynamic Structural Biology Unveils Conformers Essential for the Oligomerization of a Large GTPase. Elife 2023, 12, e79565. [Google Scholar] [CrossRef]
- Hanke, C.A.; Westbrook, J.D.; Webb, B.M.; Peulen, T.O.; Lawson, C.L.; Šali, A.; Berman, H.M.; Seidel, C.A.M.; Vallat, B.K. Making Fluorescence-Based Integrative Structures and Associated Kinetic Information Accessible. Nat. Methods 2024, 21, 1972. [Google Scholar] [CrossRef]
- Dittrich, J.; Popara, M.; Kubiak, J.; Dimura, M.; Schepers, B.; Verma, N.; Schmitz, B.; Dollinger, P.; Kovacic, F.; Jaeger, K.-E.; et al. Resolution of Maximum Entropy Method-Derived Posterior Conformational Ensembles of a Flexible System Probed by FRET and Molecular Dynamics Simulations. J. Chem. Theory Comput. 2023, 19, 2389–2409. [Google Scholar] [CrossRef] [PubMed]
- Russel, D.; Lasker, K.; Webb, B.; Velázquez-Muriel, J.; Tjioe, E.; Schneidman-Duhovny, D.; Peterson, B.; Sali, A. Putting the Pieces Together: Integrative Modeling Platform Software for Structure Determination of Macromolecular Assemblies. PLoS Biol. 2012, 10, e1001244. [Google Scholar] [CrossRef]
- Vöpel, T.; Hengstenberg, C.S.; Peulen, T.-O.; Ajaj, Y.; Seidel, C.A.M.; Herrmann, C.; Klare, J.P. Triphosphate Induced Dimerization of Human Guanylate Binding Protein 1 Involves Association of the C-Terminal Helices: A Joint Double Electron-Electron Resonance and FRET Study. Biochemistry 2014, 53, 4590–4600. [Google Scholar] [CrossRef] [PubMed]
- Sanabria, H.; Rodnin, D.; Hemmen, K.; Peulen, T.-O.; Felekyan, S.; Fleissner, M.R.; Dimura, M.; Koberling, F.; Kühnemuth, R.; Hubbell, W.; et al. Resolving Dynamics and Function of Transient States in Single Enzyme Molecules. Nat. Commun. 2020, 11, 1231. [Google Scholar] [CrossRef]
- Morales-Inostroza, L.; Folz, J.; Kühnemuth, R.; Felekyan, S.; Wieser, F.-F.; Seidel, C.A.M.; Götzinger, S.; Sandoghdar, V. An Optofluidic Antenna for Enhancing the Sensitivity of Single-Emitter Measurements. Nat. Commun. 2024, 15, 2545. [Google Scholar] [CrossRef]
- Imam, N.; Choudhury, S.; Hemmen, K.; Heinze, K.G.; Schindelin, H. Deciphering the Conformational Dynamics of Gephyrin-Mediated Collybistin Activation. Biophys. Rep. 2022, 2, 100079. [Google Scholar] [CrossRef]
- Hamilton, G.L.; Saikia, N.; Basak, S.; Welcome, F.S.; Wu, F.; Kubiak, J.; Zhang, C.; Hao, Y.; Seidel, C.A.M.; Ding, F.; et al. Fuzzy Supertertiary Interactions within PSD-95 Enable Ligand Binding. Elife 2022, 11, e77242. [Google Scholar] [CrossRef]
- Imam, N.; Choudhury, S.; Heinze, K.G.; Schindelin, H. Differential Modulation of Collybistin Conformational Dynamics by the Closely Related GTPases Cdc42 and TC10. Front. Synaptic Neurosci. 2022, 14, 959875. [Google Scholar] [CrossRef] [PubMed]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. Emcee: The MCMC Hammer. Publ. Astro. Soc. Pac. 2013, 125, 306–312. [Google Scholar] [CrossRef]
- Opanasyuk, O.; Barth, A.; Peulen, T.-O.; Felekyan, S.; Kalinin, S.; Sanabria, H.; Seidel, C.A.M. Unraveling Multi-State Molecular Dynamics in Single-Molecule FRET Experiments. II. Quantitative Analysis of Multi-State Kinetic Networks. J. Chem. Phys. 2022, 157, 031501. [Google Scholar] [CrossRef] [PubMed]
- Tsytlonok, M.; Sanabria, H.; Wang, Y.; Felekyan, S.; Hemmen, K.; Phillips, A.H.; Yun, M.-K.; Waddell, M.B.; Park, C.-G.; Vaithiyalingam, S.; et al. Dynamic Anticipation by Cdk2/Cyclin A-Bound P27 Mediates Signal Integration in Cell Cycle Regulation. Nat. Commun. 2019, 10, 1676. [Google Scholar] [CrossRef] [PubMed]
- Tsytlonok, M.; Hemmen, K.; Hamilton, G.; Kolimi, N.; Felekyan, S.; Seidel, C.A.M.; Tompa, P.; Sanabria, H. Specific Conformational Dynamics and Expansion Underpin a Multi-Step Mechanism for Specific Binding of P27 with Cdk2/Cyclin A. J. Mol. Biol. 2020, 432, 2998–3017. [Google Scholar] [CrossRef]
- Hemmen, K.; Choudhury, S.; Friedrich, M.; Balkenhol, J.; Knote, F.; Lohse, M.J.; Heinze, K.G. Dual-Color Fluorescence Cross-Correlation Spectroscopy to Study Protein-Protein Interaction and Protein Dynamics in Live Cells. Available online: https://app.jove.com/t/62954/dual-color-fluorescence-cross-correlation-spectroscopy-to-study (accessed on 10 September 2024).
- Agam, G.; Gebhardt, C.; Popara, M.; Mächtel, R.; Folz, J.; Ambrose, B.; Chamachi, N.; Chung, S.Y.; Craggs, T.D.; de Boer, M.; et al. Reliability and Accuracy of Single-Molecule FRET Studies for Characterization of Structural Dynamics and Distances in Proteins. Nat. Methods 2023, 20, 523–535. [Google Scholar] [CrossRef]
- Hellenkamp, B.; Wortmann, P.; Kandzia, F.; Zacharias, M.; Hugel, T. Multidomain Structure and Correlated Dynamics Determined by Self-Consistent FRET Networks. Nat. Methods 2017, 14, 174–180. [Google Scholar] [CrossRef]
- Dimura, M.; Peulen, T.-O.; Sanabria, H.; Rodnin, D.; Hemmen, K.; Hanke, C.A.; Seidel, C.A.M.; Gohlke, H. Automated and Optimally FRET-Assisted Structural Modeling. Nat. Commun. 2020, 11, 5394. [Google Scholar] [CrossRef]
- Chen, J.; Zaer, S.; Drori, P.; Zamel, J.; Joron, K.; Kalisman, N.; Lerner, E.; Dokholyan, N.V. The Structural Heterogeneity of α-Synuclein Is Governed by Several Distinct Subpopulations with Interconversion Times Slower than Milliseconds. Structure 2021, 29, 1048–1064.E6. [Google Scholar] [CrossRef]
- Peulen, T.O.; Opanasyuk, O.; Seidel, C.A.M. Combining Graphical and Analytical Methods with Molecular Simulations to Analyze Time-Resolved FRET Measurements of Labeled Macromolecules Accurately. J. Phys. Chem. B 2017, 121, 8211–8241. [Google Scholar] [CrossRef]
- Hellenkamp, B.; Schmid, S.; Doroshenko, O.; Opanasyuk, O.; Kühnemuth, R.; Rezaei Adariani, S.; Ambrose, B.; Aznauryan, M.; Barth, A.; Birkedal, V.; et al. Precision and Accuracy of Single-Molecule FRET Measurements-a Multi-Laboratory Benchmark Study. Nat. Methods 2018, 15, 669–676. [Google Scholar] [CrossRef]
- Gopich, I.V.; Szabo, A. FRET Efficiency Distributions of Multistate Single Molecules. J. Phys. Chem. B 2010, 114, 15221–15226. [Google Scholar] [CrossRef] [PubMed]
- Kalinin, S.; Felekyan, S.; Antonik, M.; Seidel, C.A.M. Probability Distribution Analysis of Single-Molecule Fluorescence Anisotropy and Resonance Energy Transfer. J. Phys. Chem. B 2007, 111, 10253–10262. [Google Scholar] [CrossRef]
- Kim, S.A.; Heinze, K.G.; Schwille, P. Fluorescence Correlation Spectroscopy in Living Cells. Nat. Methods 2007, 4, 963–973. [Google Scholar] [CrossRef] [PubMed]
- Gregor, I.; Enderlein, J. Time-Resolved Methods in Biophysics. 3. Fluorescence Lifetime Correlation Spectroscopy. Photochem. Photobiol. Sci. 2007, 6, 13–18. [Google Scholar] [CrossRef]
- Felekyan, S.; Sanabria, H.; Kalinin, S.; Kühnemuth, R.; Seidel, C.A.M. Analyzing Förster Resonance Energy Transfer with Fluctuation Algorithms. Methods Enzymol. 2013, 519, 39–85. [Google Scholar] [CrossRef] [PubMed]
- Dimura, M.; Peulen, T.O.; Hanke, C.A.; Prakash, A.; Gohlke, H.; Seidel, C.A. Quantitative FRET Studies and Integrative Modeling Unravel the Structure and Dynamics of Biomolecular Systems. Curr. Opin. Struct. Biol. 2016, 40, 163–185. [Google Scholar] [CrossRef]
- Sindbert, S.; Kalinin, S.; Nguyen, H.; Kienzler, A.; Clima, L.; Bannwarth, W.; Appel, B.; Müller, S.; Seidel, C.A.M. Accurate Distance Determination of Nucleic Acids via Förster Resonance Energy Transfer: Implications of Dye Linker Length and Rigidity. J. Am. Chem. Soc. 2011, 133, 2463–2480. [Google Scholar] [CrossRef]
- Kravets, E.; Degrandi, D.; Ma, Q.; Peulen, T.-O.; Klümpers, V.; Felekyan, S.; Kühnemuth, R.; Weidtkamp-Peters, S.; Seidel, C.A.; Pfeffer, K. Guanylate Binding Proteins Directly Attack Toxoplasma gondii via Supramolecular Complexes. Elife 2016, 5, e11479. [Google Scholar] [CrossRef]
- Somssich, M.; Ma, Q.; Weidtkamp-Peters, S.; Stahl, Y.; Felekyan, S.; Bleckmann, A.; Seidel, C.A.M.; Simon, R. Real-Time Dynamics of Peptide Ligand-Dependent Receptor Complex Formation in Planta. Sci. Signal. 2015, 8, ra76. [Google Scholar] [CrossRef]
- Jares-Erijman, E.A.; Jovin, T.M. Imaging Molecular Interactions in Living Cells by FRET Microscopy. Curr. Opin. Chem. Biol. 2006, 10, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Schrimpf, W.; Barth, A.; Hendrix, J.; Lamb, D.C. PAM: A Framework for Integrated Analysis of Imaging, Single-Molecule, and Ensemble Fluorescence Data. Biophys. J. 2018, 114, 1518–1528. [Google Scholar] [CrossRef] [PubMed]
- Gao, D.; Barber, P.R.; Chacko, J.V.; Kader Sagar, M.A.; Rueden, C.T.; Grislis, A.R.; Hiner, M.C.; Eliceiri, K.W. FLIMJ: An Open-Source ImageJ Toolkit for Fluorescence Lifetime Image Data Analysis. PLoS ONE 2020, 15, e0238327. [Google Scholar] [CrossRef]
- Globals Software. Available online: https://www.lfd.uci.edu/globals/ (accessed on 31 December 2024).
- Hancock, M.; Peulen, T.-O.; Webb, B.; Poon, B.; Fraser, J.S.; Adams, P.; Sali, A. Integration of Software Tools for Integrative Modeling of Biomolecular Systems. J. Struct. Biol. 2022, 214, 107841. [Google Scholar] [CrossRef]
- Barth, A.; Opanasyuk, O.; Peulen, T.-O.; Felekyan, S.; Kalinin, S.; Sanabria, H.; Seidel, C.A.M. Unraveling Multi-State Molecular Dynamics in Single-Molecule FRET Experiments. I. Theory of FRET-Lines. J. Chem. Phys. 2022, 156, 141501. [Google Scholar] [CrossRef]
- Kalinin, S.; Peulen, T.; Sindbert, S.; Rothwell, P.J.; Berger, S.; Restle, T.; Goody, R.S.; Gohlke, H.; Seidel, C.A.M. A Toolkit and Benchmark Study for FRET-Restrained High-Precision Structural Modeling. Nat. Methods 2012, 9, 1218–1225. [Google Scholar] [CrossRef] [PubMed]
- Antonik, M.; Felekyan, S.; Gaiduk, A.; Seidel, C.A.M. Separating Structural Heterogeneities from Stochastic Variations in Fluorescence Resonance Energy Transfer Distributions via Photon Distribution Analysis. J. Phys. Chem. B 2006, 110, 6970–6978. [Google Scholar] [CrossRef]
- Greife, A.; Felekyan, S.; Ma, Q.; Gertzen, C.G.W.; Spomer, L.; Dimura, M.; Peulen, T.O.; Wöhler, C.; Häussinger, D.; Gohlke, H.; et al. Structural Assemblies of the Di- and Oligomeric G-Protein Coupled Receptor TGR5 in Live Cells: An MFIS-FRET and Integrative Modelling Study. Sci. Rep. 2016, 6, 36792. [Google Scholar] [CrossRef]
- Agam, G.; Barth, A.; Lamb, D.C. Folding Pathway of a Discontinuous Two-Domain Protein. Nat. Commun. 2024, 15, 690. [Google Scholar] [CrossRef]
- Medina, E.; R Latham, D.; Sanabria, H. Unraveling Protein’s Structural Dynamics: From Configurational Dynamics to Ensemble Switching Guides Functional Mesoscale Assemblies. Curr. Opin. Struct. Biol. 2021, 66, 129–138. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Sikor, M.; Kalinin, S.; Mokranjac, D.; Seidel, C.A.M.; Lamb, D.C. Combining MFD and PIE for Accurate Single-Pair Forster Resonance Energy Transfer Measurements. Chemphyschem 2012, 13, 1060–1078. [Google Scholar] [CrossRef] [PubMed]
- Clegg, R.M. Fluorescence Resonance Energy Transfer and Nucleic Acids. Methods Enzymol. 1992, 211, 353–388. [Google Scholar] [CrossRef]
- Sisamakis, E.; Valeri, A.; Kalinin, S.; Rothwell, P.J.; Seidel, C.A.M. Accurate Single-Molecule FRET Studies Using Multiparameter Fluorescence Detection. Methods Enzymol. 2010, 475, 455–514. [Google Scholar] [CrossRef]
- Widengren, J.; Schweinberger, E.; Berger, S.; Seidel, C.A.M. Two New Concepts to Measure Fluorescence Resonance Energy Transfer via Fluorescence Correlation Spectroscopy: Theory and Experimental Realizations. J. Phys. Chem. A 2001, 105, 6851–6866. [Google Scholar] [CrossRef]
- Rothwell, P.J.; Berger, S.; Kensch, O.; Felekyan, S.; Antonik, M.; Wohrl, B.M.; Restle, T.; Goody, R.S.; Seidel, C.A.M. Multiparameter Single-Molecule Fluorescence Spectroscopy Reveals Heterogeneity of HIV-1 Reverse Transcriptase: Primer/Template Complexes. Proc. Natl. Acad. Sci. USA 2003, 100, 1655–1660. [Google Scholar] [CrossRef]
- Förster, T. Experimentelle Und Theoretische Untersuchung Des Zwischenmolekularen Übergangs von Elektronenanregungsenergie. Z. Für Naturforschung 1949, 4, 321–327. [Google Scholar] [CrossRef]
- Jovin, T.M.; Jares-Erijman, E.A. Goodbye to Foerster Constant RO: FRET Imaging By Kf/kt. Biophys. J. 2010, 98, 579a. [Google Scholar] [CrossRef]
- Hummer, G.; Szabo, A. Dynamics of the Orientational Factor in Fluorescence Resonance Energy Transfer. J. Phys. Chem. B 2017, 121, 3331–3339. [Google Scholar] [CrossRef]
- Kalinin, S.; Molotkovsky, J.G.; Johansson, L.B.-Å. Distance Measurements Using Partial Donor−Donor Energy Migration within Pairs of Fluorescent Groups in Lipid Bilayers. J. Phys. Chem. B 2003, 107, 3318–3324. [Google Scholar] [CrossRef]
- van der Meer, W.B.; van der Meer, D.M.; Vogel, S.S. Optimizing the Orientation Factor Kappa-Squared for More Accurate FRET Measurements. In FRET—Förster Resonance Energy Transfer: From Theory to Applications; Medintz, I., Hildebrandt, N., Eds.; Wiley-VCH Verlag: Weinheim, Germany, 2014. [Google Scholar]
- Striker, G.; Subramaniam, V.; Seidel, C.A.M.; Volkmer, A. Photochromicity and Fluorescence Lifetimes of Green Fluorescent Protein. J. Phys. Chem. B 1999, 103, 8612–8617. [Google Scholar] [CrossRef]
- Koshioka, M.; Sasaki, K.; Masuhara, H. Time-Dependent Fluorescence Depolarization Analysis in Three-Dimensional Microspectroscopy. Appl. Spectrosc. 1995, 49, 224–228. [Google Scholar] [CrossRef]
- Erdelyi, M.; Simon, J.; Barnard, E.A.; Kaminski, C.F. Analyzing Receptor Assemblies in the Cell Membrane Using Fluorescence Anisotropy Imaging with TIRF Microscopy. PLoS ONE 2014, 9, e100526. [Google Scholar] [CrossRef] [PubMed]
- Gohlke, C.; Murchie, A.I.H.; Lilley, D.M.J.; Clegg, R.M. Kinking of DNA and RNA Helices by Bulged Nucleotides Observed by Fluorescence Resonance Energy-Transfer. Proc. Natl. Acad. Sci. USA 1994, 91, 11660–11664. [Google Scholar] [CrossRef]
- Tramier, M.; Coppey-Moisan, M. Fluorescence Anisotropy Imaging Microscopy for Homo-FRET in Living Cells. Methods Cell Biol. 2008, 85, 395–414. [Google Scholar] [CrossRef]
- Bader, A.N.; Hoetzl, S.; Hofman, E.G.; Voortman, J.; Henegouwen, P.M.P.V.E.; van Meer, G.; Gerritsen, H.C. Homo-FRET Imaging as a Tool to Quantify Protein and Lipid Clustering. Chemphyschem 2011, 12, 475–483. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.A.; Sarkar, P.; Veetil, J.V.; Koushik, S.V.; Vogel, S.S. Fluorescence Polarization and Fluctuation Analysis Monitors Subunit Proximity, Stoichiometry, and Protein Complex Hydrodynamics. PLoS ONE 2012, 7, e38209. [Google Scholar] [CrossRef]
- Isaksson, M.; Hägglöf, P.; Håkansson, P.; Ny, T.; Johansson, L.B.-A. Extended Förster Theory for Determining Intraprotein Distances: 2. an Accurate Analysis of Fluorescence Depolarisation Experiments. Phys. Chem. Chem. Phys. 2007, 9, 3914–3922. [Google Scholar] [CrossRef]
- Fries, J.R.; Brand, L.; Eggeling, C.; Köllner, M.; Seidel, C.A.M. Quantitative Identification of Different Single Molecules by Selective Time-Resolved Confocal Fluorescence Spectroscopy. J. Phys. Chem. A 1998, 102, 6601–6613. [Google Scholar] [CrossRef]
- Maus, M.; Cotlet, M.; Hofkens, J.; Gensch, T.; De Schryver, F.C.; Schaffer, J.; Seidel, C.A.M. An Experimental Comparison of the Maximum Likelihood Estimation and Nonlinear Least-Squares Fluorescence Lifetime Analysis of Single Molecules. Anal. Chem. 2001, 73, 2078–2086. [Google Scholar] [CrossRef]
- Schaffer, J.; Volkmer, A.; Eggeling, C.; Subramaniam, V.; Striker, G.; Seidel, C.A.M. Identification of Single Molecules in Aqueous Solution by Time-Resolved Fluorescence Anisotropy. J. Phys. Chem. A 1999, 103, 331–336. [Google Scholar] [CrossRef]
- Brünger, A.T.; Strop, P.; Vrljic, M.; Chu, S.; Weninger, K.R. Three-Dimensional Molecular Modeling with Single Molecule FRET. J. Struct. Biol. 2011, 173, 497–505. [Google Scholar] [CrossRef] [PubMed]
- McCann, J.J.; Choi, U.B.; Zheng, L.; Weninger, K.; Bowen, M.E. Optimizing Methods to Recover Absolute FRET Efficiency from Immobilized Single Molecules. Biophys. J. 2010, 99, 961–970. [Google Scholar] [CrossRef] [PubMed]
- Gopich, I.; Szabo, A. Theory of Photon Statistics in Single-Molecule Forster Resonance Energy Transfer. J. Chem. Phys. 2005, 122, 14707. [Google Scholar] [CrossRef]
- Nir, E.; Michalet, X.; Hamadani, K.M.; Laurence, T.A.; Neuhauser, D.; Kovchegov, Y.; Weiss, S. Shot-Noise Limited Single-Molecule FRET Histograms: Comparison between Theory and Experiments. J. Phys. Chem. B 2006, 110, 22103–22124. [Google Scholar] [CrossRef]
- Kalinin, S.; Felekyan, S.; Valeri, A.; Seidel, C.A.M. Characterizing Multiple Molecular States in Single-Molecule Multiparameter Fluorescence Detection by Probability Distribution Analysis. J. Phys. Chem. B 2008, 112, 8361–8374. [Google Scholar] [CrossRef] [PubMed]
- Tomov, T.E.; Tsukanov, R.; Masoud, R.; Liber, M.; Plavner, N.; Nir, E. Disentangling Subpopulations in Single-Molecule FRET and ALEX Experiments with Photon Distribution Analysis. Biophys. J. 2012, 102, 1163–1173. [Google Scholar] [CrossRef]
- Gopich, I.V.; Szabo, A. Single-Macromolecule Fluorescence Resonance Energy Transfer and Free-Energy Profiles. J. Phys. Chem. B 2003, 107, 5058–5063. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, H. Photon-by-Photon Determination of Emission Bursts from Diffusing Single Chromophores. Abstr. Pap. Am. Chem. Soc. 2006, 231, 21930–21937. [Google Scholar] [CrossRef]
- Nettels, D.; Gopich, I.V.; Hoffmann, A.; Schuler, B. Ultrafast Dynamics of Protein Collapse from Single-Molecule Photon Statistics. Proc. Natl. Acad. Sci. USA 2007, 104, 2655–2660. [Google Scholar] [CrossRef]
- Peulen, T.-O.; Hemmen, K.; Greife, A.; Webb, B.M.; Felekyan, S.; Sali, A.; Seidel, C.A.M.; Sanabria, H.; Heinze, K.G. Tttrlib: Modular Software for Integrating Fluorescence Spectroscopy, Imaging, and Molecular Modeling. Bioinformatics 2025, 41, btaf025. [Google Scholar] [CrossRef]
- Kalinin, S.; Sisamakis, E.; Magennis, S.W.; Felekyan, S.; Seidel, C.A.M. On the Origin of Broadening of Single-Molecule FRET Efficiency Distributions beyond Shot Noise Limits. J. Phys. Chem. B 2010, 114, 6197–6206. [Google Scholar] [CrossRef] [PubMed]
- Elson, E.L. 40 Years of FCS: How It All Began. In Fluorescence Fluctuation Spectroscopy; Tetin, S.Y., Ed.; Methods in Enzymology; Elsevier Academic Press Inc.: San Diego, CA, USA, 2013; Volume 518, pp. 1–10. ISBN 9780123884220. [Google Scholar]
- Elson, E.L.; Magde, D. Fluorescence Correlation Spectroscopy. I. Conceptual Basis and Theory. Biopolym. Orig. Res. 1974, 13, 1–27. [Google Scholar] [CrossRef]
- Magde, D.; Elson, E.; Webb, W.W. Thermodynamic Fluctuations in a Reacting System—Measurement by Fluorescence Correlation Spectroscopy. Phys. Rev. Lett. 1972, 29, 705–708. [Google Scholar] [CrossRef]
- Slaughter, B.D.; Allen, M.W.; Unruh, J.R.; Bieber Urbauer, R.J.; Johnson, C.K. Single-Molecule Resonance Energy Transfer and Fluorescence Correlation Spectroscopy of Calmodulin in Solution. J. Phys. Chem. B 2004, 108, 10388–10397. [Google Scholar] [CrossRef]
- Torres, T.; Levitus, M. Measuring Conformational Dynamics: A New FCS-FRET Approach. J. Phys. Chem. B 2007, 111, 7392–7400. [Google Scholar] [CrossRef]
- Johnson, C.K. Calmodulin, Conformational States, and Calcium Signaling. A Single-Molecule Perspective. Biochemistry 2006, 45, 14233–14246. [Google Scholar] [CrossRef]
- Price, E.S.; Aleksiejew, M.; Johnson, C.K. FRET-FCS Detection of Intralobe Dynamics in Calmodulin. J. Phys. Chem. B 2011, 115, 9320–9326. [Google Scholar] [CrossRef]
- Price, E.S.; DeVore, M.S.; Johnson, C.K. Detecting Intramolecular Dynamics and Multiple Förster Resonance Energy Transfer States by Fluorescence Correlation Spectroscopy. J. Phys. Chem. B 2010, 114, 5895–5902. [Google Scholar] [CrossRef]
- Slaughter, B.D.; Unruh, J.R.; Allen, M.W.; Bieber Urbauer, R.J.; Johnson, C.K. Conformational Substates of Calmodulin Revealed by Single-Pair Fluorescence Resonance Energy Transfer: Influence of Solution Conditions and Oxidative Modification. Biochemistry 2005, 44, 3694–3707. [Google Scholar] [CrossRef]
- Gurunathan, K.; Levitus, M. FRET Fluctuation Spectroscopy of Diffusing Biopolymers: Contributions of Conformational Dynamics and Translational Diffusion. J. Phys. Chem. B 2010, 114, 980–986. [Google Scholar] [CrossRef]
- Levitus, M. Relaxation Kinetics by Fluorescence Correlation Spectroscopy: Determination of Kinetic Parameters in the Presence of Fluorescent Impurities. J. Phys. Chem. Lett. 2010, 1, 1346–1350. [Google Scholar] [CrossRef] [PubMed]
- Al-Soufi, W.; Reija, B.; Novo, M.; Felekyan, S.; Kühnemuth, R.; Seidel, C.A.M. Fluorescence Correlation Spectroscopy, a Tool to Investigate Supramolecular Dynamics: Inclusion Complexes of Pyronines with Cyclodextrin. J. Am. Chem. Soc. 2005, 127, 8775–8784. [Google Scholar] [CrossRef]
- Kim, S.A.; Heinze, K.G.; Bacia, K.; Waxham, M.N.; Schwille, P. Two-Photon Cross-Correlation Analysis of Intracellular Reactions with Variable Stoichiometry. Biophys. J. 2005, 88, 4319–4336. [Google Scholar] [CrossRef]
- Eggeling, C.; Berger, S.; Brand, L.; Fries, J.R.; Schaffer, J.; Volkmer, A.; Seidel, C.A.M. Data Registration and Selective Single-Molecule Analysis Using Multi-Parameter Fluorescence Detection. J. Biotechnol. 2001, 86, 163–180. [Google Scholar] [CrossRef] [PubMed]
- Böhmer, M.; Wahl, M.; Rahn, H.-J.; Erdmann, R.; Enderlein, J. Time-Resolved Fluorescence Correlation Spectroscopy. Chem. Phys. Lett. 2002, 353, 439–445. [Google Scholar] [CrossRef]
- Felekyan, S.; Kalinin, S.; Sanabria, H.; Valeri, A.; Seidel, C.A.M. Filtered FCS: Species Auto- and Cross-Correlation Functions Highlight Binding and Dynamics in Biomolecules. Chemphyschem 2012, 13, 1036–1053. [Google Scholar] [CrossRef] [PubMed]
- Dale, R.E.; Eisinger, J.; Blumberg, W.E. Orientational Freedom of Molecular Probes—Orientation Factor in Intra-Molecular Energy-Transfer. Biophys. J. 1979, 26, 161–193. [Google Scholar] [CrossRef]
- Johansson, L.B.-A.; Edman, P.; Westlund, P.O. Energy Migration and Rotational Motion within Bichromophoric Molecules. II. A Derivation of the Fluorescence Anisotropy. J. Chem. Phys. 1996, 105, 10896–10904. [Google Scholar] [CrossRef]
- Dolghih, E.; Ortiz, W.; Kim, S.; Krueger, B.P.; Krause, J.L.; Roitberg, A.E. Theoretical Studies of Short Polyproline Systems: Recalibration of a Molecular Ruler. J. Phys. Chem. A 2009, 113, 4639–4646. [Google Scholar] [CrossRef]
- Dolghih, E.; Roitberg, A.E.; Krause, J.L. Fluorescence Resonance Energy Transfer in Dye-Labeled DNA. J. Photochem. Photobiol. A Chem. 2007, 190, 321–327. [Google Scholar] [CrossRef]
- VanBeek, D.B.; Zwier, M.C.; Shorb, J.M.; Krueger, B.P. Fretting about FRET: Correlation between Kappa and R. Abstr. Pap. Am. Chem. Soc. 2007, 233, 4168–4178. [Google Scholar] [CrossRef] [PubMed]
- Steffens, N.; Beuter-Gunia, C.; Kravets, E.; Reich, A.; Legewie, L.; Pfeffer, K.; Degrandi, D. Essential Role of MGBP7 for Survival of Toxoplasma gondii Infection. MBio 2020, 11, e02993-19. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peulen, T.-O. Exploring Time-Resolved Fluorescence Data: A Software Solution for Model Generation and Analysis. Spectrosc. J. 2025, 3, 16. https://doi.org/10.3390/spectroscj3020016
Peulen T-O. Exploring Time-Resolved Fluorescence Data: A Software Solution for Model Generation and Analysis. Spectroscopy Journal. 2025; 3(2):16. https://doi.org/10.3390/spectroscj3020016
Chicago/Turabian StylePeulen, Thomas-Otavio. 2025. "Exploring Time-Resolved Fluorescence Data: A Software Solution for Model Generation and Analysis" Spectroscopy Journal 3, no. 2: 16. https://doi.org/10.3390/spectroscj3020016
APA StylePeulen, T.-O. (2025). Exploring Time-Resolved Fluorescence Data: A Software Solution for Model Generation and Analysis. Spectroscopy Journal, 3(2), 16. https://doi.org/10.3390/spectroscj3020016






