Dynamic FTIR Spectroscopy for Assessing the Changing Biomolecular Composition of Bacterial Cells During Growth
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation and Bacterial Growth
2.2. FTIR Spectroscopy Measurements
2.3. Spectral Data Analysis
2.4. Statistical Analysis
3. Results and Discussion
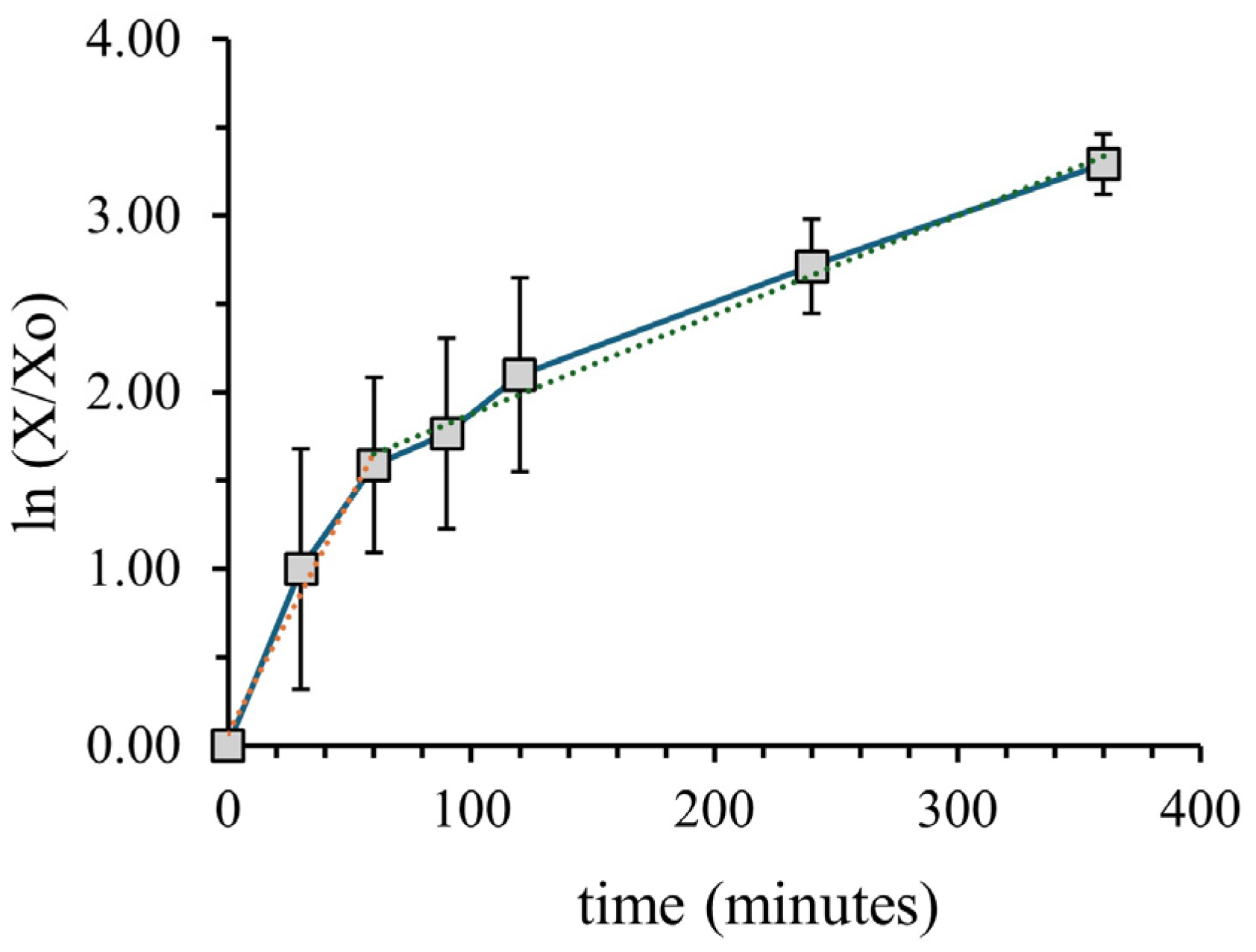
3.1. Growth Phases over the Course of the Experiment
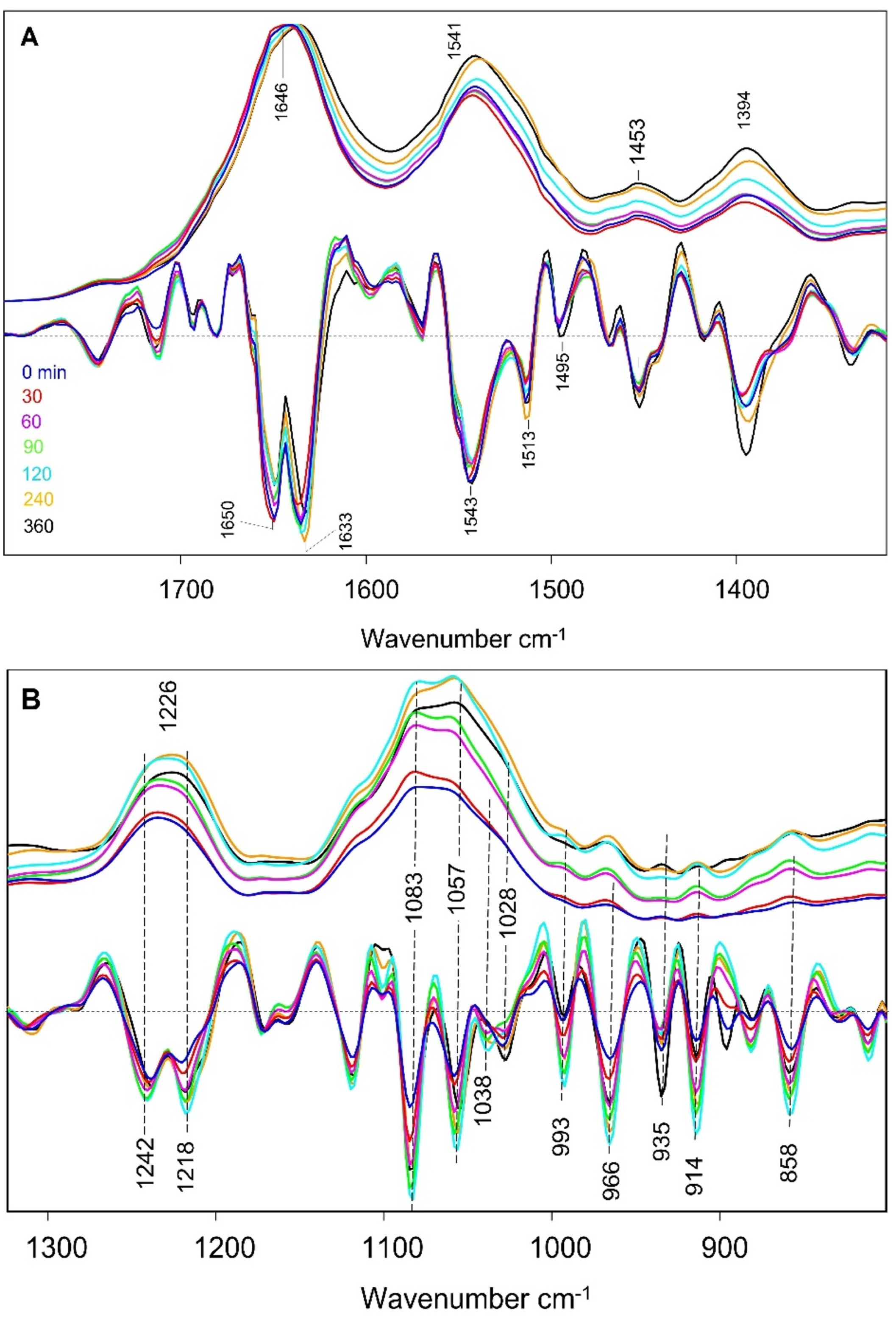
3.2. ATR-FTIR Absorption Spectra
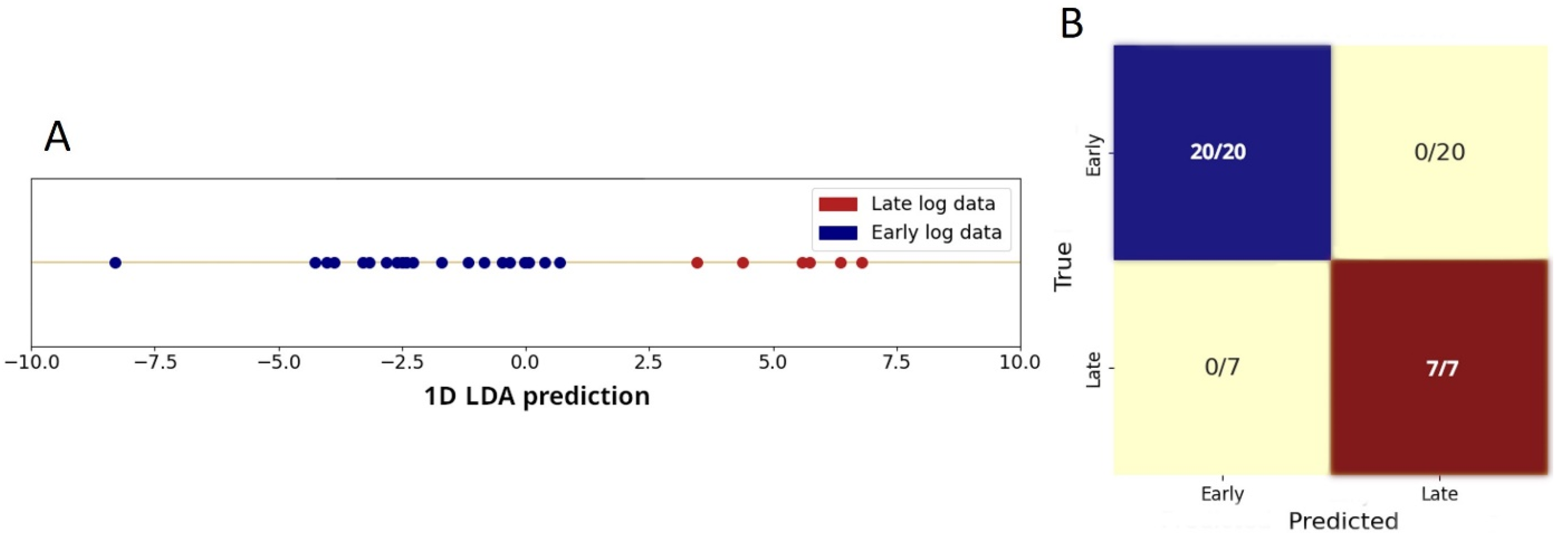
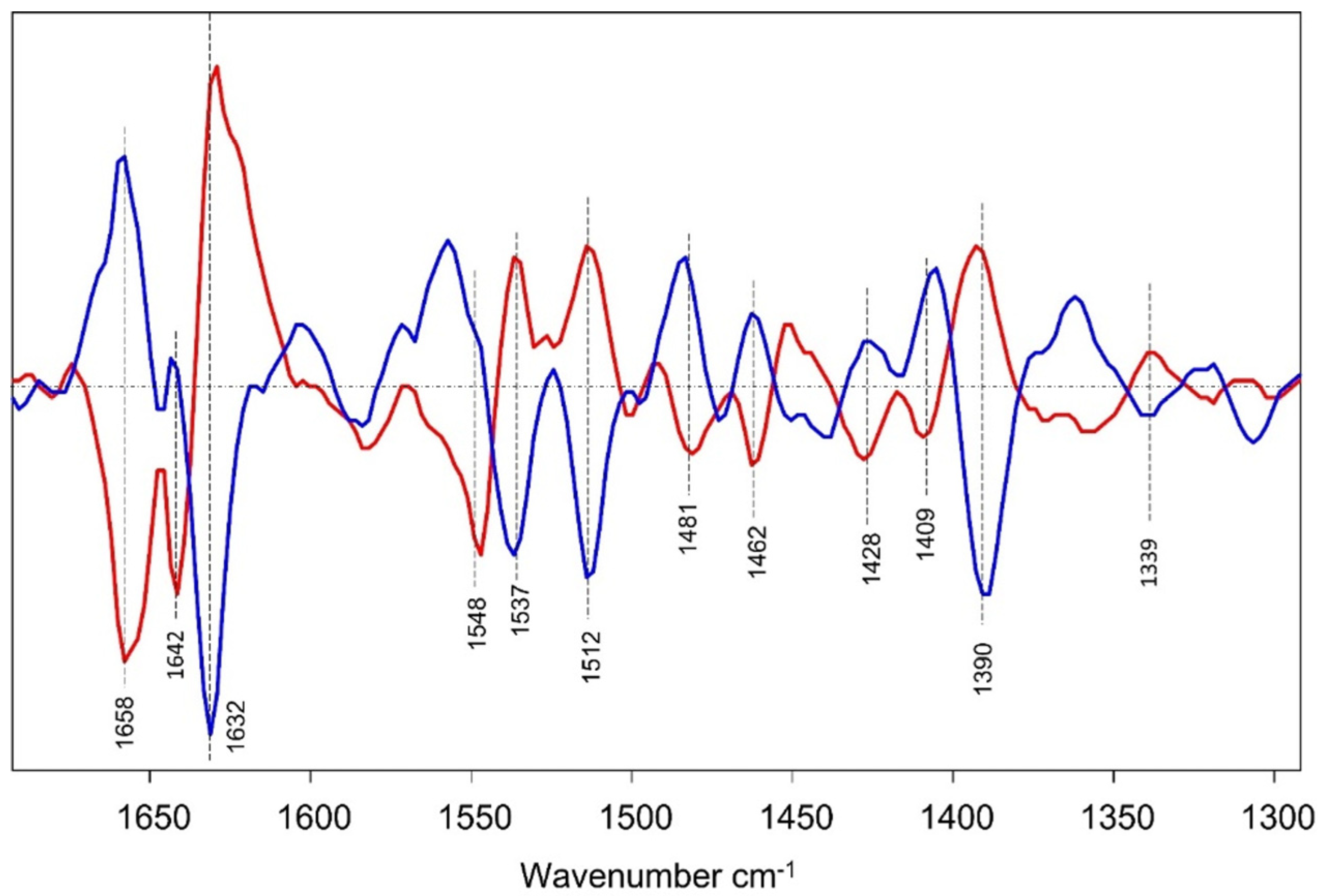
3.3. Spectral Alterations on Going from the Early to Late Log Phase
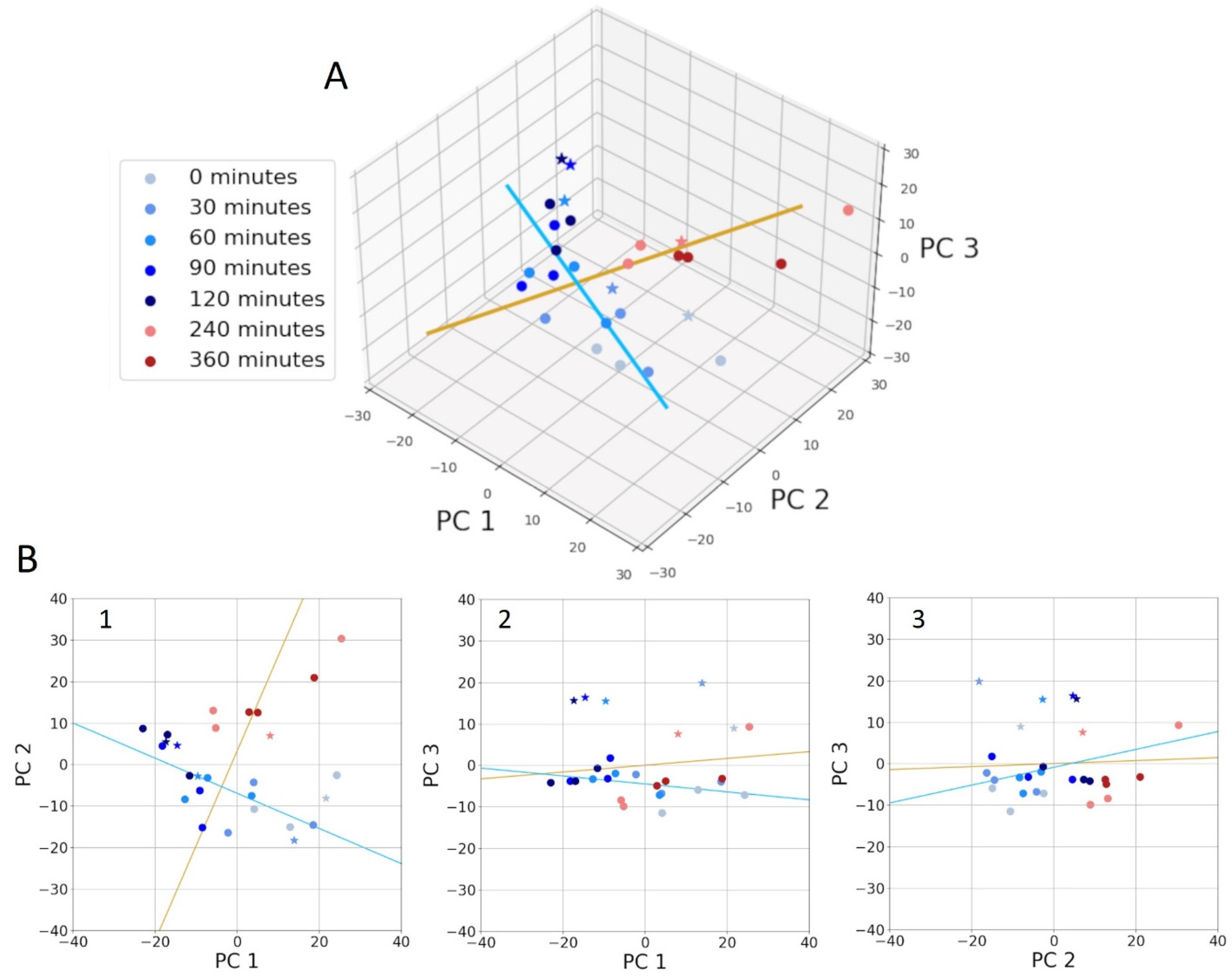
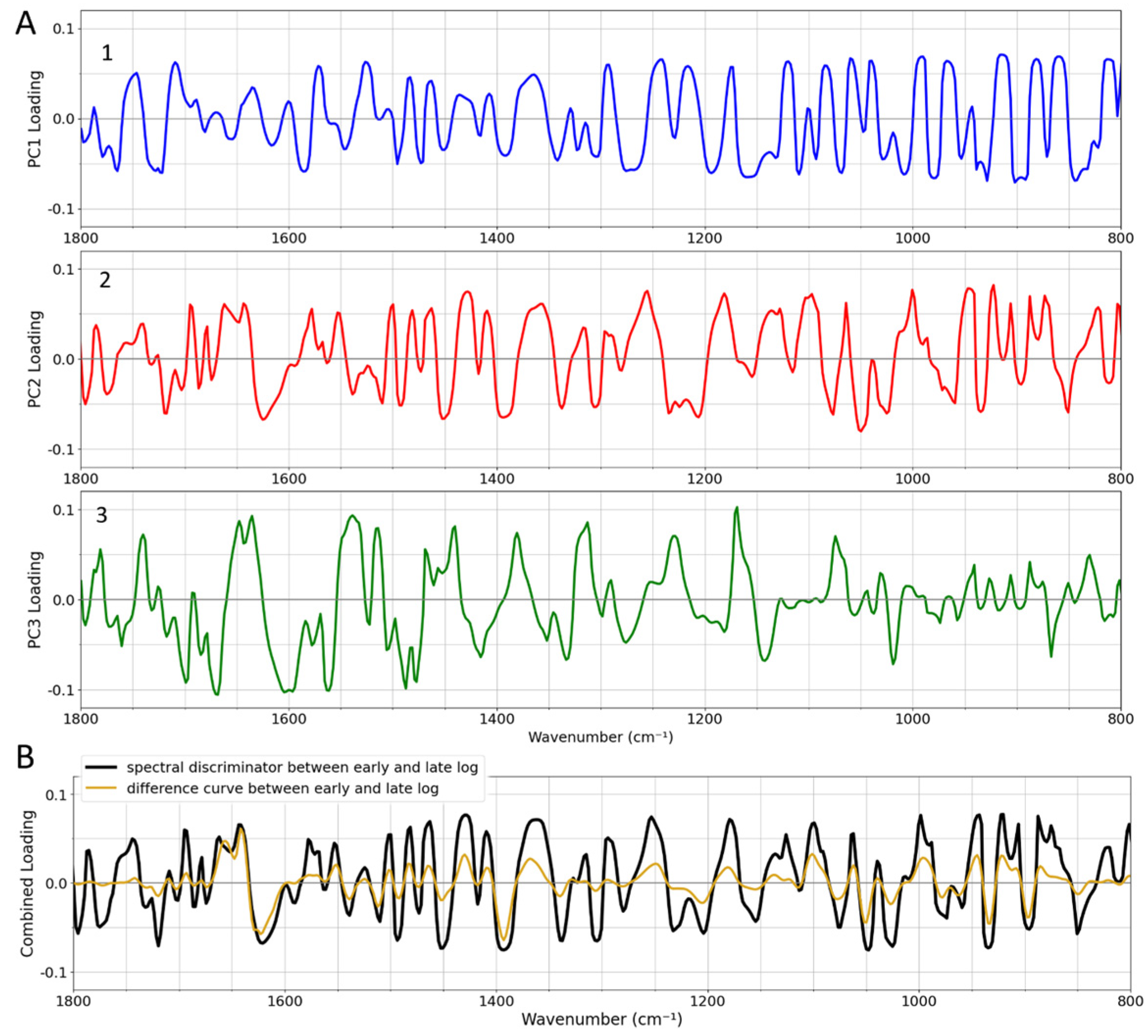
Statistical Analysis to Discriminate Spectra of Cells During Log-Phase Growth
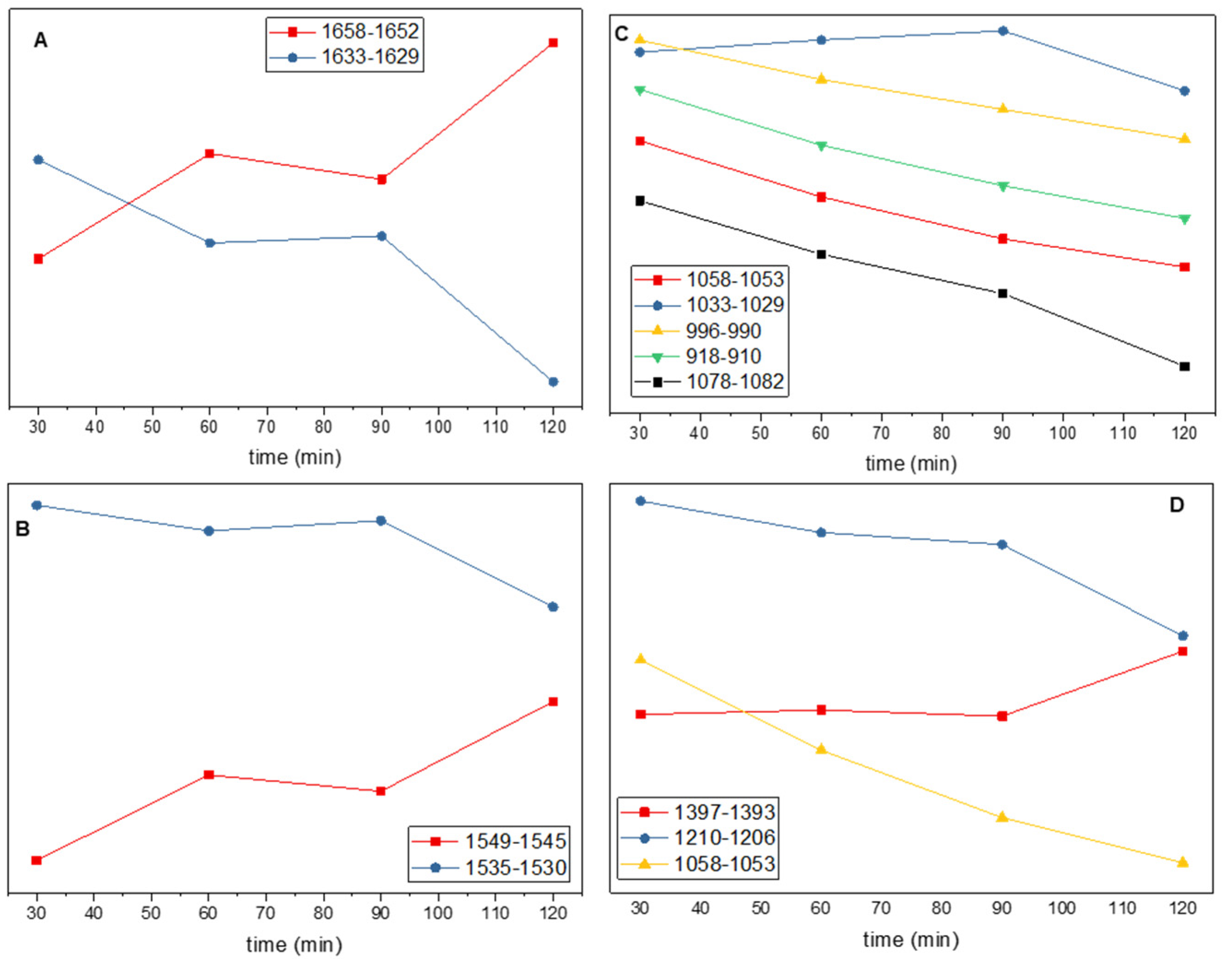
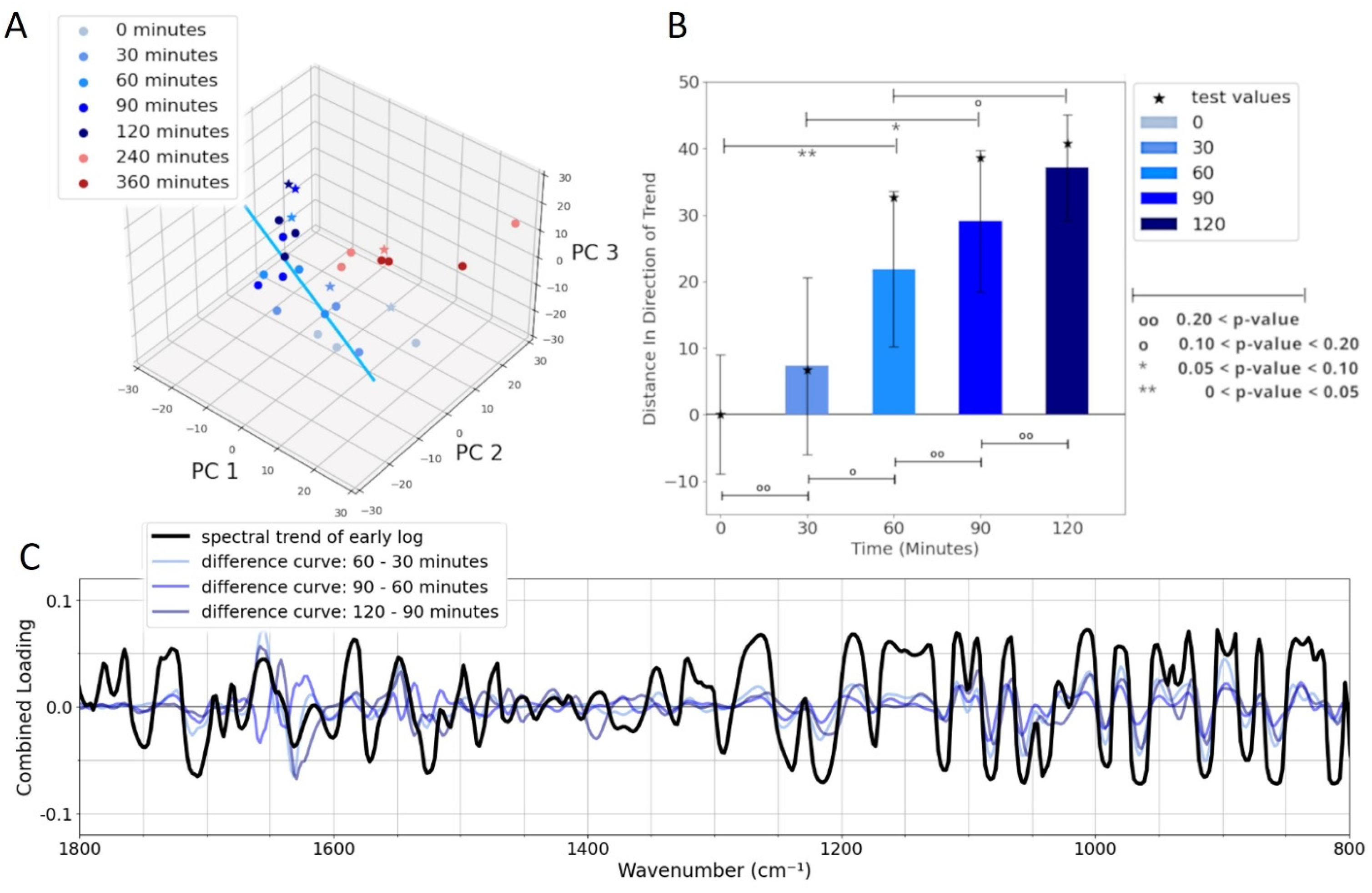
3.4. Alterations of the Spectra for Cells During the Early Log Phase of Growth
3.5. Statistical Analysis of Spectra for Cells During Early Log-Phase Growth
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ATR | Attenuated total reflectance |
| FTIR | Fourier-transform infrared |
| LB broth | Luria–Bertani broth |
| LDA | Linear Discriminant Analysis |
| LOOCV | Leave-one-out cross-validation |
| PCA | Principal Component Analysis |
| SA6538 | Staphylococcus aureus ATCC 6538 |
| SVD | Singular Value Decomposition |
References
- AlMasoud, N.; Muhamadali, H.; Chisanga, M.; AlRabiah, H.; Lima, C.A.; Goodacre, R. Discrimination of bacteria using whole organism fingerprinting: The utility of modern physicochemical techniques for bacterial typing. Analyst 2021, 146, 770–788. [Google Scholar] [CrossRef] [PubMed]
- Novais, Â.; Freitas, A.R.; Rodrigues, C.; Peixe, L. Fourier transform infrared spectroscopy: Unlocking fundamentals and prospects for bacterial strain typing. Eur. J. Clin. Microbiol. Infect. Dis. 2019, 38, 427–448. [Google Scholar] [CrossRef] [PubMed]
- Kassem, A.; Abbas, L.; Coutinho, O.; Opara, S.; Najaf, H.; Kasperek, D.; Pokhrel, K.; Li, X.; Tiquia-Arashiro, S. Applications of Fourier Transform-Infrared spectroscopy in microbial cell biology and environmental microbiology: Advances, challenges, and future perspectives. Front. Microbiol. 2023, 14, 1304081. [Google Scholar]
- Veettil, T.C.P.; Kochan, K.; Williams, G.C.; Bourke, K.; Kostoulias, X.; Peleg, A.Y.; Lyras, D.; De Bank, P.A.; Perez-Guaita, D.; Wood, B.R. A Multimodal Spectroscopic Approach Combining Mid-infrared and Near-infrared for Discriminating Gram-positive and Gram-negative Bacteria. Anal. Chem. 2024, 96, 18392–18400. [Google Scholar]
- Novais, Â.; Gonçalves, A.B.; Ribeiro, T.G.; Freitas, A.R.; Méndez, G.; Mancera, L.; Read, A.; Alves, V.; López-Cerero, L.; Rodríguez-Baño, J.; et al. Development and validation of a quick, automated, and reproducible ATR FT-IR spectroscopy machine-learning model for Klebsiella pneumoniae typing. J. Clin. Microbiol. 2024, 62, e01211-23. [Google Scholar] [CrossRef]
- Bertrand, R.L. Lag Phase Is a Dynamic, Organized, Adaptive, and Evolvable Period That Prepares Bacteria for Cell Division. J. Bacteriol. 2019, 201, 10–1128. [Google Scholar] [CrossRef]
- Rolfe, M.D.; Rice, C.J.; Lucchini, S.; Pin, C.; Thompson, A.; Cameron, A.D.S.; Alston, M.; Stringer, M.F.; Betts, R.P.; Baranyi, J.; et al. Lag Phase Is a Distinct Growth Phase That Prepares Bacteria for Exponential Growth and Involves Transient Metal Accumulation. J. Bacteriol. 2012, 194, 686–701. [Google Scholar] [CrossRef]
- Widdel, F. Theory and measurement of bacterial growth. Dalam Grund. Mikrobiol. 2007, 4, 1–11. [Google Scholar]
- Swinnen, I.A.M.; Bernaerts, K.; Dens, E.J.J.; Geeraerd, A.H.; Van Impe, J.F. Predictive modelling of the microbial lag phase: A review. Int. J. Food Microbiol. 2004, 94, 137–159. [Google Scholar] [CrossRef]
- Eymann, C.; Dreisbach, A.; Albrecht, D.; Bernhardt, J.; Becher, D.; Gentner, S.; Tam, L.T.; Büttner, K.; Buurman, G.; Scharf, C.; et al. A comprehensive proteome map of growing Bacillus subtilis cells. Proteomics 2004, 4, 2849–2876. [Google Scholar] [CrossRef]
- Kumar, V.; Ahluwalia, V.; Saran, S.; Kumar, J.; Patel, A.K.; Singhania, R.R. Recent developments on solid-state fermentation for production of microbial secondary metabolites: Challenges and solutions. Bioresour. Technol. 2021, 323, 124566. [Google Scholar] [CrossRef] [PubMed]
- Siegele, D.A.; Kolter, R. Life after log. J. Bacteriol. 1992, 174, 345–348. [Google Scholar] [CrossRef] [PubMed]
- Overton, T.W. Recombinant protein production in bacterial hosts. Drug Discov. Today 2014, 19, 590–601. [Google Scholar] [CrossRef] [PubMed]
- San-Miguel, T.; Pérez-Bermúdez, P.; Gavidia, I. Production of soluble eukaryotic recombinant proteins in E. coli is favoured in early log-phase cultures induced at low temperature. Springerplus 2013, 2, 89. [Google Scholar] [CrossRef]
- Mitsakakis, K.; Kaman, W.E.; Elshout, G.; Specht, M.; Hays, J.P. Challenges in identifying antibiotic resistance targets for point-of-care diagnostics in general practice. Future Microbiol. 2018, 13, 1157–1164. [Google Scholar] [CrossRef]
- Centers_for_Disease_Control. COVID-19: U.S. Impact on Antimicrobial Resistance, Special Report 2022; CDC: Atlanta, GA, USA, 2022. [Google Scholar]
- Haaber, J.; Cohn, M.T.; Frees, D.; Andersen, T.J.; Ingmer, H. Planktonic aggregates of Staphylococcus aureus protect against common antibiotics. PLoS ONE 2012, 7, e41075. [Google Scholar] [CrossRef]
- Zhang, M.; Michie, K.L.; Cornforth, D.M.; Dolan, S.K.; Wang, Y.; Whiteley, M. Impact of Growth Rate on the Protein-mRNA Ratio in Pseudomonas aeruginosa. mBio 2023, 14, e0306722. [Google Scholar] [CrossRef]
- Chaffin, D.O.; Taylor, D.; Skerrett, S.J.; Rubens, C.E. Changes in the Staphylococcus aureus transcriptome during early adaptation to the lung. PLoS ONE 2012, 7, e41329. [Google Scholar] [CrossRef]
- Kochan, K.; Lai, E.; Richardson, Z.; Nethercott, C.; Peleg, A.Y.; Heraud, P.; Wood, B.R. Vibrational Spectroscopy as a Sensitive Probe for the Chemistry of Intra-Phase Bacterial Growth. Sensors 2020, 20, 3452. [Google Scholar] [CrossRef]
- Sezonov, G.; Joseleau-Petit, D.; D’Ari, R. Escherichia coli physiology in Luria-Bertani broth. J. Bacteriol. 2007, 189, 8746–8749. [Google Scholar] [CrossRef]
- Jones, E.W.; Derrick, J.; Nisbet, R.M.; Ludington, W.B.; Sivak, D.A. First-passage-time statistics of growing microbial populations carry an imprint of initial conditions. Sci. Rep. 2023, 13, 21340. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, J.; Flemming, H.C. FTIR-spectroscopy in microbial and material analysis. Int. Biodeterior. Biodegrad. 1998, 41, 1–11. [Google Scholar] [CrossRef]
- Barth, A. Infrared spectroscopy of proteins. Biochim. Biophys. Acta BBA Bioenerg. 2007, 1767, 1073–1101. [Google Scholar] [CrossRef] [PubMed]
- Movasaghi, Z.; Rehman, S.; Rehman, D.I.U. Fourier Transform Infrared (FTIR) Spectroscopy of Biological Tissues. Appl. Spectrosc. Rev. 2008, 43, 134–179. [Google Scholar] [CrossRef]
- Kochan, K.; Bedolla, D.E.; Perez-Guaita, D.; Adegoke, J.A.; Veettil, T.C.P.; Martin, M.; Roy, S.; Pebotuwa, S.; Heraud, P.; Wood, B.R. Infrared Spectroscopy of Blood. Appl. Spectrosc. 2021, 75, 611–646. [Google Scholar] [CrossRef]
- Yang, H.; Shi, H.; Feng, B.; Wang, L.; Chen, L.; Alvarez-Ordóñez, A.; Zhang, L.; Shen, H.; Zhu, J.; Yang, S.; et al. Protocol for bacterial typing using Fourier transform infrared spectroscopy. STAR Protoc. 2023, 4, 102223. [Google Scholar] [CrossRef]
- Zhang, F.; Tang, X.; Tong, A.; Wang, B.; Wang, J. An Automatic Baseline Correction Method Based on the Penalized Least Squares Method. Sensors 2020, 20, 2015. [Google Scholar] [CrossRef]
- Grunert, T.; Wenning, M.; Barbagelata, M.S.; Fricker, M.; Sordelli, D.O.; Buzzola, F.R.; Ehling-Schulz, M. Rapid and Reliable Identification of Capsular Serotypes by Means of Artificial Neural Network-Assisted Fourier Transform Infrared Spectroscopy. J. Clin. Microbiol. 2013, 51, 2261–2266. [Google Scholar] [CrossRef]
- Kochan, K.; Nethercott, C.; Taghavimoghaddam, J.; Richardson, Z.; Lai, E.; Crawford, S.A.; Peleg, A.Y.; Wood, B.R.; Heraud, P. Rapid Approach for Detection of Antibiotic Resistance in Bacteria Using Vibrational Spectroscopy. Anal. Chem. 2020, 92, 8235–8243. [Google Scholar] [CrossRef]
- Lee, L.C.; Liong, C.-Y.; Jemain, A.A. A contemporary review on Data Preprocessing (DP) practice strategy in ATR-FTIR spectrum. Chemom. Intell. Lab. Syst. 2017, 163, 64–75. [Google Scholar] [CrossRef]
- Grdadolnik, J. ATR-FTIR Spectroscopy: Its Aadvantages and Limitations. Acta Chim. Slov. 2002, 49, 631–642. [Google Scholar]
- Wiercigroch, E.; Szafraniec, E.; Czamara, K.; Pacia, M.Z.; Majzner, K.; Kochan, K.; Kaczor, A.; Baranska, M.; Malek, K. Raman and infrared spectroscopy of carbohydrates: A review. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2017, 185, 317–335. [Google Scholar] [CrossRef] [PubMed]
- Cai, S.; Singh, B.R. A distinct utility of the amide III infrared band for secondary structure estimation of aqueous protein solutions using partial least squares methods. Biochemistry 2004, 43, 2541–2549. [Google Scholar] [CrossRef] [PubMed]
- Jenul, C.; Horswill, A.R. Regulation of Staphylococcus aureus Virulence. Microbiol. Spectr. 2019, 19, 1128. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hastings, G.; Nelson, M.; Taylor, C.; Marchesani, A.; Hudson, W.; Jiang, Y.; Gilbert, E. Dynamic FTIR Spectroscopy for Assessing the Changing Biomolecular Composition of Bacterial Cells During Growth. Spectrosc. J. 2025, 3, 15. https://doi.org/10.3390/spectroscj3020015
Hastings G, Nelson M, Taylor C, Marchesani A, Hudson W, Jiang Y, Gilbert E. Dynamic FTIR Spectroscopy for Assessing the Changing Biomolecular Composition of Bacterial Cells During Growth. Spectroscopy Journal. 2025; 3(2):15. https://doi.org/10.3390/spectroscj3020015
Chicago/Turabian StyleHastings, Gary, Michael Nelson, Caroline Taylor, Alex Marchesani, Wilbur Hudson, Yi Jiang, and Eric Gilbert. 2025. "Dynamic FTIR Spectroscopy for Assessing the Changing Biomolecular Composition of Bacterial Cells During Growth" Spectroscopy Journal 3, no. 2: 15. https://doi.org/10.3390/spectroscj3020015
APA StyleHastings, G., Nelson, M., Taylor, C., Marchesani, A., Hudson, W., Jiang, Y., & Gilbert, E. (2025). Dynamic FTIR Spectroscopy for Assessing the Changing Biomolecular Composition of Bacterial Cells During Growth. Spectroscopy Journal, 3(2), 15. https://doi.org/10.3390/spectroscj3020015





