Schlesinger Nailed It! Assessing a Key Primary Pharmacodynamic Property of Phages for Phage Therapy: Virion Encounter Rates with Motionless Bacterial Targets
Abstract
:1. Introduction
2. Some Background
3. In Silico Exploration
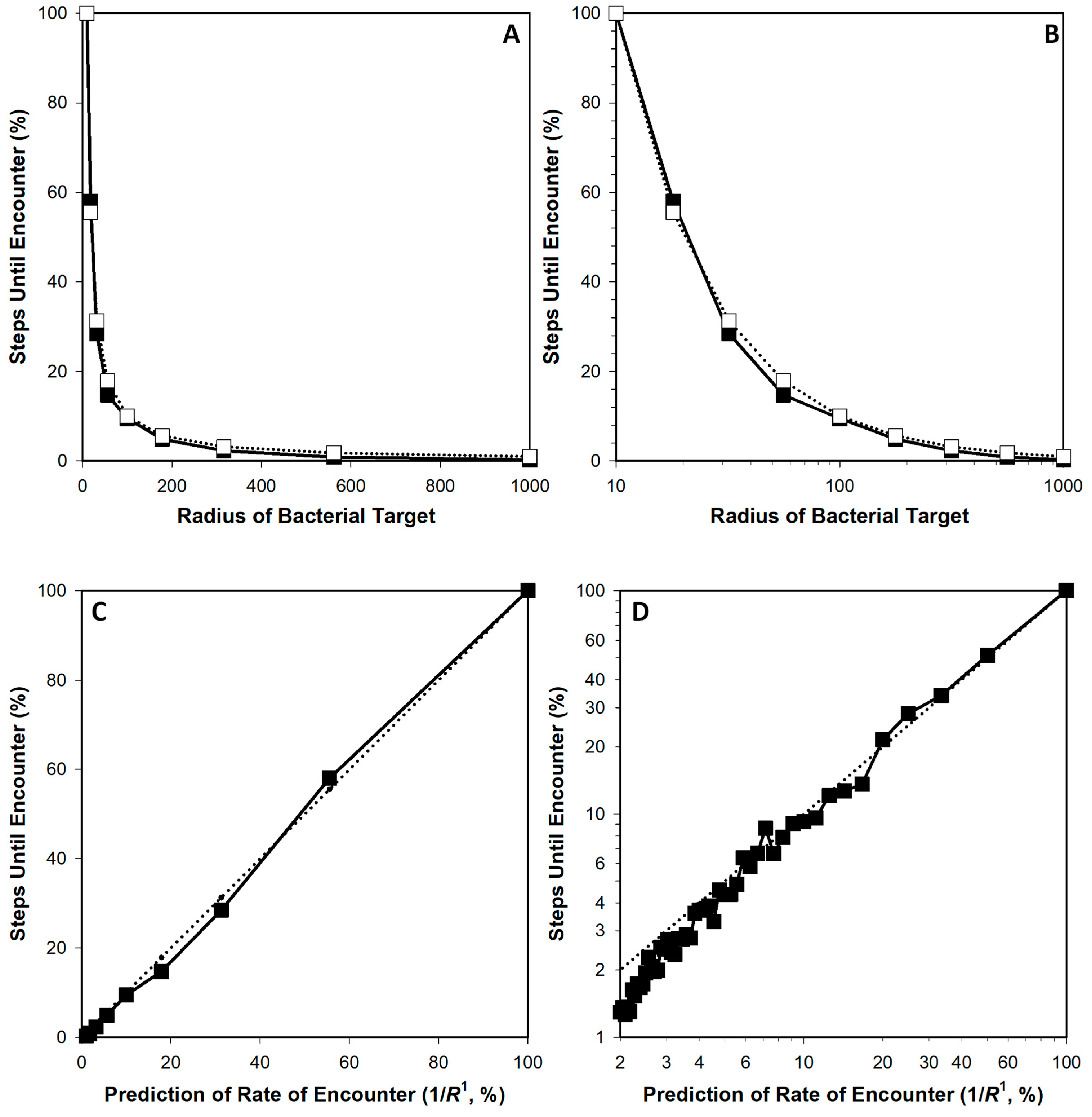
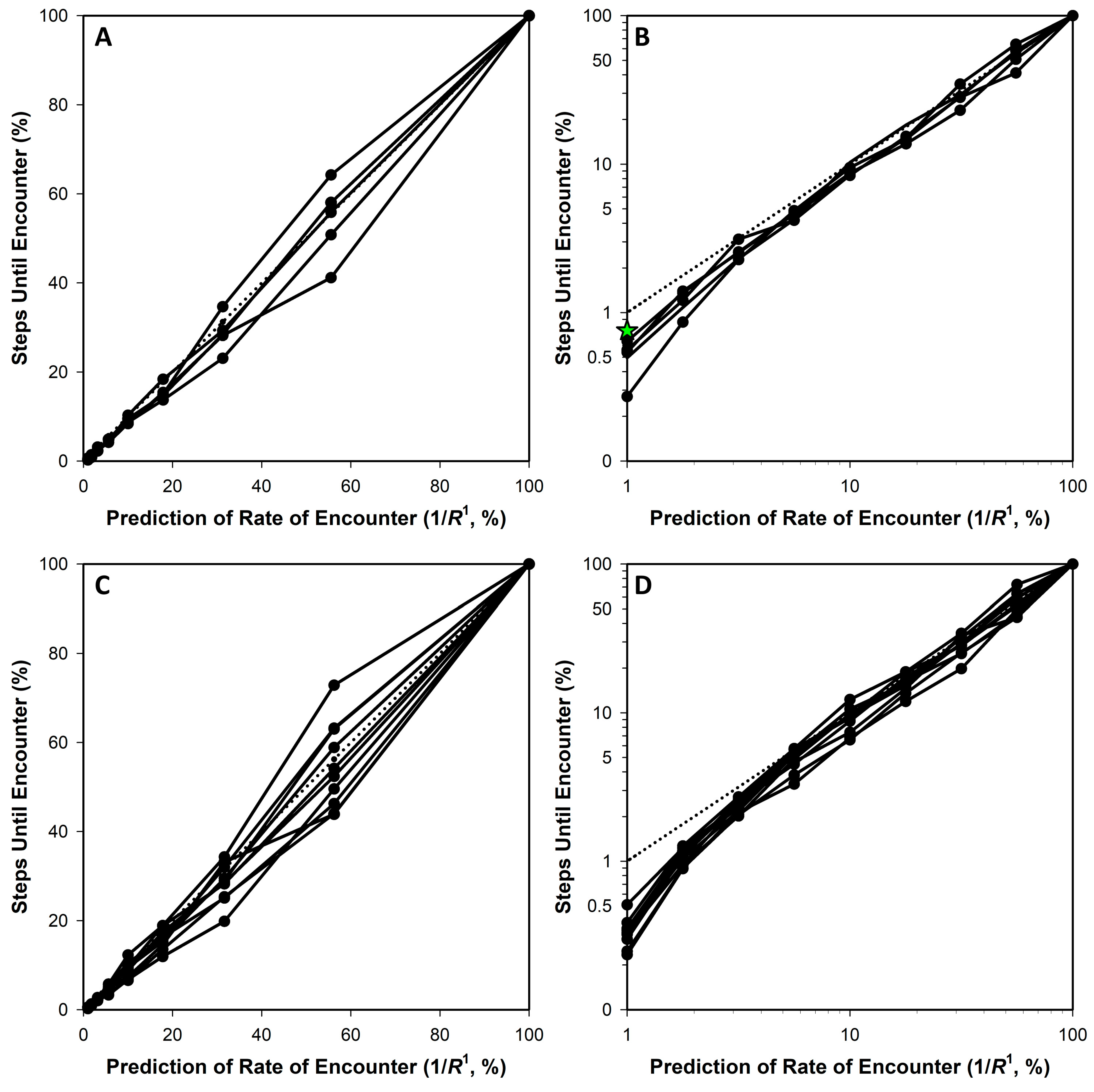
3.1. Simulation Approach
3.2. Comparing R1 and R2
4. Evidence for R1 vs. R2 from the Literature
4.1. Experimental Evidence?
4.1.1. Comparing Adsorption Rates to Theory
4.1.2. Comparing Adsorption Rates to Cell Size
4.2. Adsorption to Rods and Spherical Clusters of Bacteria
4.3. Unit Analysis
5. Discussion
6. Materials and Methods
7. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Górski, A.; Międzybrodzki, R.; Borysowski, J. Phage Therapy: A Practical Approach; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Petrovic Fabijan, A.; Iredell, J.; Danis-Wlodarczyk, K.; Kebriaei, R.; Abedon, S.T. Translating phage therapy into the clinic: Recent accomplishments but continuing challenges. PLoS Biol. 2023, 21, e3002119. [Google Scholar] [CrossRef] [PubMed]
- Strathdee, S.A.; Hatfull, G.F.; Mutalik, V.K.; Schooley, R.T. Phage therapy: From biological mechanisms to future directions. Cell 2023, 186, 17–31. [Google Scholar] [CrossRef]
- Dąbrowska, K.; Abedon, S.T. Pharmacologically aware phage therapy: Pharmacodynamic and pharmacokinetic obstacles to phage antibacterial action in animal and human bodies. Microbiol. Mol. Biol. Rev. 2019, 83, e00012-19. [Google Scholar] [CrossRef] [PubMed]
- Dąbrowska, K. Phage therapy: What factors shape phage pharmacokinetics and bioavailability? Systematic and critical review. Med. Res. Rev. 2019, 39, 2000–2025. [Google Scholar] [CrossRef]
- Pirnay, J.P.; Ferry, T.; Resch, G. Recent progress toward the implementation of phage therapy in Western medicine. FEMS Microbiol. Rev. 2022, 46, fuab040. [Google Scholar] [CrossRef] [PubMed]
- Abedon, S.T. Further considerations on how to improve phage therapy experimentation, practice, and reporting: Pharmacodynamics perspectives. Phage 2022, 3, 95–97. [Google Scholar] [CrossRef]
- Bull, J.J.; Regoes, R.R. Pharmacodynamics of non-replicating viruses, bacteriocins and lysins. Proc. Biol. Sci. 2006, 273, 2703–2712. [Google Scholar] [CrossRef]
- Adams, M.H. Bacteriophages; InterScience: New York, NY, USA, 1959. [Google Scholar]
- Stent, G.S. Molecular Biology of Bacterial Viruses; WH Freeman and Co.: San Francisco, CA, USA, 1963. [Google Scholar]
- Storms, Z.J.; Arsenault, E.; Sauvageau, D.; Cooper, D.G. Bacteriophage adsorption efficiency and its effect on amplification. Bioprocess Biosyst. Eng. 2010, 33, 823–831. [Google Scholar] [CrossRef]
- Abedon, S.T. Bacteriophage adsorption: Likelihood of virion encounter with bacteria and other factors affecting rates. Antibiotics 2023, 12, 723. [Google Scholar] [CrossRef]
- Schlesinger, M. Ueber die Bindung des Bakteriophagen an homologe Bakterien. II. Quantitative, Untersuchungen über die Bindungsgeschwindigkeit und die Sättigung. Berechnung der Teilchengröße des Bakteriophagen aus deren Ergebnissen. [Adsorption of bacteriophages to homologous bacteria. II Quantitative investigations of adsorption velocity and saturation. Estimation of particle size of the bacteriophage]. Z. Hygenie Immunitiitsforsch. 1932, 114, 149–160. [Google Scholar]
- Schlesinger, M. Adsorption of bacteriophages to homologous bacteria. II Quantitative investigations of adsorption velocity and saturation: Estimation of particle size of the bacteriophage [translation]. In Bacterial Viruses; Stent, G.S., Ed.; Little, Brown and Co.: Boston, MA, USA, 1960; pp. 26–36. [Google Scholar]
- Hadas, H.; Einav, M.; Fishov, I.; Zaritsky, A. Bacteriophage T4 development depends on the physiology of its host Escherichia coli. Microbiology 1997, 143, 179–185. [Google Scholar] [CrossRef] [PubMed]
- Eriksen, R.S.; Mitarai, N.; Sneppen, K. On phage adsorption to bacterial chains. Biophys. J. 2020, 119, 1896–1904. [Google Scholar] [CrossRef] [PubMed]
- Darch, S.E.; Kragh, K.N.; Abbott, E.A.; Bjarnsholt, T.; Bull, J.J.; Whiteley, M. Phage inhibit pathogen dissemination by targeting bacterial migrants in a chronic infection model. MBio 2017, 8, e00240-17. [Google Scholar] [CrossRef] [PubMed]
- Smoluchowski, M.V. Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen [Attempt at a mathematical theory of the coagulation kinetics of colloidal solutions]. Z. Phys. Chem 1917, 92, 129–168. [Google Scholar]
- Delbrück, M. Adsorption of bacteriophage under various physiological conditions of the host. J. Gen. Physiol. 1940, 23, 631–642. [Google Scholar] [CrossRef]
- Berg, H.C.; Purcell, E.M. Physics of chemoreception. Biophys. J. 1977, 20, 193–219. [Google Scholar] [CrossRef]
- Dunaway, K.; Siddique, I. LibreTextsTM Chemistry, 6.1.4: Collision Frequency. 2023. Available online: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Kinetics/06%3A_Modeling_Reaction_Kinetics/6.01%3A_Collision_Theory/6.1.04%3A_Collision_Frequency (accessed on 14 August 2023).
- Meyer, C.J.; Deglon, D.A. Particle collision modeling—A review. Miner. Eng. 2011, 24, 719–730. [Google Scholar] [CrossRef]
- Eriksen, R.S.; Svenningsen, S.L.; Sneppen, K.; Mitarai, N. A growing microcolony can survive and support persistent propagation of virulent phages. Proc. Natl. Acad. Sci. USA 2018, 115, 337–342. [Google Scholar] [CrossRef]
- Wang, I.-N.; Dykhuizen, D.E.; Slobodkin, L.B. The evolution of phage lysis timing. Evol. Ecol. 1996, 10, 545–558. [Google Scholar] [CrossRef]
- Stent, G.S.; Wollman, E.L. On the two step nature of bacteriophage adsorption. Biochim. Biophys. Acta 1952, 8, 260–269. [Google Scholar] [CrossRef]
- Witkin, E.M. Inherited differences in sensitivity to radiation in Escherichia coli. Proc. Natl. Acad. Sci. USA 1946, 32, 59–68. [Google Scholar] [CrossRef] [PubMed]
- Hyman, P.; Abedon, S.T. Practical methods for determining phage growth parameters. Meth. Mol. Biol. 2009, 501, 175–202. [Google Scholar]
- Kropinski, A.M. Practical advice on the one-step growth curve. Meth. Mol. Biol. 2018, 1681, 41–47. [Google Scholar]
- Zaritsky, A.; Woldringh, C.L.; Mirelman, D. Constant peptidoglycan density in the sacculus of Escherichia coli B/r growing at different rates. FEBS Lett. 1979, 98, 29–32. [Google Scholar] [CrossRef] [PubMed]
- Bull, J.J.; Vimr, E.R.; Molineux, I.J. A tale of tails: Sialidase is key to success in a model of phage therapy against K1-capsulated Escherichia coli. Virology 2010, 398, 79–86. [Google Scholar] [CrossRef]
- Nzakizwanayo, J.; Hanin, A.; Alves, D.R.; McCutcheon, B.; Dedi, C.; Salvage, J.; Knox, K.; Stewart, B.; Metcalfe, A.; Clark, J.; et al. Bacteriophage can prevent encrustation and blockage of urinary catheters by Proteus mirabilis. Antimicrob. Agents Chemother. 2016, 60, 1530–1536. [Google Scholar] [CrossRef]
- Bjarnsholt, T. The role of bacterial biofilms in chronic infections. APMIS 2013, 121, 1–58. [Google Scholar] [CrossRef]
- Scali, C.; Kunimoto, B. An update on chronic wounds and the role of biofilms. J. Cutan. Med. Surg. 2013, 17, 371–376. [Google Scholar] [CrossRef]
- Cooper, R.A.; Bjarnsholt, T.; Alhede, M. Biofilms in wounds: A review of present knowledge. J. Wound Care 2014, 23, 570–580. [Google Scholar] [CrossRef]
- Del Pozo, J.L. Biofilm-related disease. Expert Rev. Anti. Infect. Ther. 2018, 16, 51–65. [Google Scholar] [CrossRef]
- Vestby, L.K.; Gronseth, T.; Simm, R.; Nesse, L.L. Bacterial biofilm and its role in the pathogenesis of disease. Antibiotics 2020, 9, 59. [Google Scholar] [CrossRef] [PubMed]



| m (x = 1/R1) | b (x = 1/R1) | r (x = 1/R1) | m (x = 1/R2) | b (x = 1/R2) | r (x = 1/R2) | |
|---|---|---|---|---|---|---|
| 1 | 1.0184 | −1.2667 | 0.9990 | 0.9861 | 8.4143 | 0.9604 |
| 2 | 0.9946 | −1.1662 | 0.9992 | 0.9738 | 8.1196 | 0.9698 |
| 3 | 0.9973 | −0.7747 | 0.9993 | 0.9729 | 8.5935 | 0.9664 |
| 4 | 0.9909 | −3.3821 | 0.9933 | 0.9901 | 5.5440 | 0.9839 |
| 5 | 1.0311 | −0.3799 | 0.9976 | 0.9880 | 9.5944 | 0.9477 |
| 6 | 0.9706 | −1.6504 | 0.9948 | 0.9657 | 7.1596 | 0.9812 |
| 7 | 1.0590 | 0.8696 | 0.9896 | 0.9943 | 11.4469 | 0.9211 |
| 8 | 0.9735 | −2.7446 | 0.9933 | 0.9735 | 6.0116 | 0.9848 |
| 9 | 1.0163 | −0.9341 | 0.9992 | 0.9847 | 8.7232 | 0.9596 |
| 10 | 1.0296 | −0.7564 | 0.9974 | 0.9909 | 9.1348 | 0.9515 |
| Means: | 1.0081 | −1.2186 | 0.9963 | 0.9820 | 8.2742 | 0.9626 |
| SDs: | 0.0278 | 1.1905 | 0.0034 | 0.0097 | 1.7228 | 0.0196 |
| p-values † | 0.0168 | 0.0000 | 0.0004 | NA | NA | NA |
| m (x = 1/R1) | b (x = 1/R1) | r (x = 1/R1) | m (x = 1/R2) | b (x = 1/R2) | r (x = 1/R2) | |
|---|---|---|---|---|---|---|
| 1 | 1.0606 | −6.1192 | 0.9763 | 0.8391 | 24.1075 | 0.9706 |
| 2 | 0.8794 | −4.5956 | 0.9751 | 0.6966 | 20.4377 | 0.9707 |
| 3 | 1.0769 | −4.4772 | 0.9790 | 0.8454 | 26.4352 | 0.9658 |
| 4 | 0.9266 | −4.2082 | 0.9842 | 0.7338 | 22.1728 | 0.9796 |
| 5 | 0.9220 | −5.9269 | 0.9785 | 0.7317 | 20.2775 | 0.9758 |
| 6 | 1.0330 | −2.6378 | 0.9819 | 0.8133 | 26.9357 | 0.9715 |
| 7 | 1.0117 | −3.7888 | 0.9852 | 0.7935 | 25.2762 | 0.9711 |
| 8 | 0.9541 | −5.0865 | 0.9845 | 0.7559 | 22.0701 | 0.9802 |
| 9 | 1.0255 | −7.0626 | 0.9852 | 0.8121 | 22.1242 | 0.9805 |
| 10 | 1.0546 | −3.7976 | 0.9813 | 0.8272 | 26.4984 | 0.9673 |
| Means: | 0.9944 | −4.7700 | 0.9811 | 0.7849 | 23.6335 | 0.9733 |
| SDs: | 0.0685 | 1.3081 | 0.0037 | 0.0517 | 2.5433 | 0.0054 |
| p-values † | 0.0000 | 0.0000 | 0.0017 | NA | NA | NA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abedon, S.T. Schlesinger Nailed It! Assessing a Key Primary Pharmacodynamic Property of Phages for Phage Therapy: Virion Encounter Rates with Motionless Bacterial Targets. Drugs Drug Candidates 2023, 2, 673-688. https://doi.org/10.3390/ddc2030034
Abedon ST. Schlesinger Nailed It! Assessing a Key Primary Pharmacodynamic Property of Phages for Phage Therapy: Virion Encounter Rates with Motionless Bacterial Targets. Drugs and Drug Candidates. 2023; 2(3):673-688. https://doi.org/10.3390/ddc2030034
Chicago/Turabian StyleAbedon, Stephen T. 2023. "Schlesinger Nailed It! Assessing a Key Primary Pharmacodynamic Property of Phages for Phage Therapy: Virion Encounter Rates with Motionless Bacterial Targets" Drugs and Drug Candidates 2, no. 3: 673-688. https://doi.org/10.3390/ddc2030034
APA StyleAbedon, S. T. (2023). Schlesinger Nailed It! Assessing a Key Primary Pharmacodynamic Property of Phages for Phage Therapy: Virion Encounter Rates with Motionless Bacterial Targets. Drugs and Drug Candidates, 2(3), 673-688. https://doi.org/10.3390/ddc2030034







