Machine Learning Classification of 3D Intracellular Trafficking Using Custom and Imaris-Derived Motion Features
Abstract
1. Introduction
2. Materials and Methods
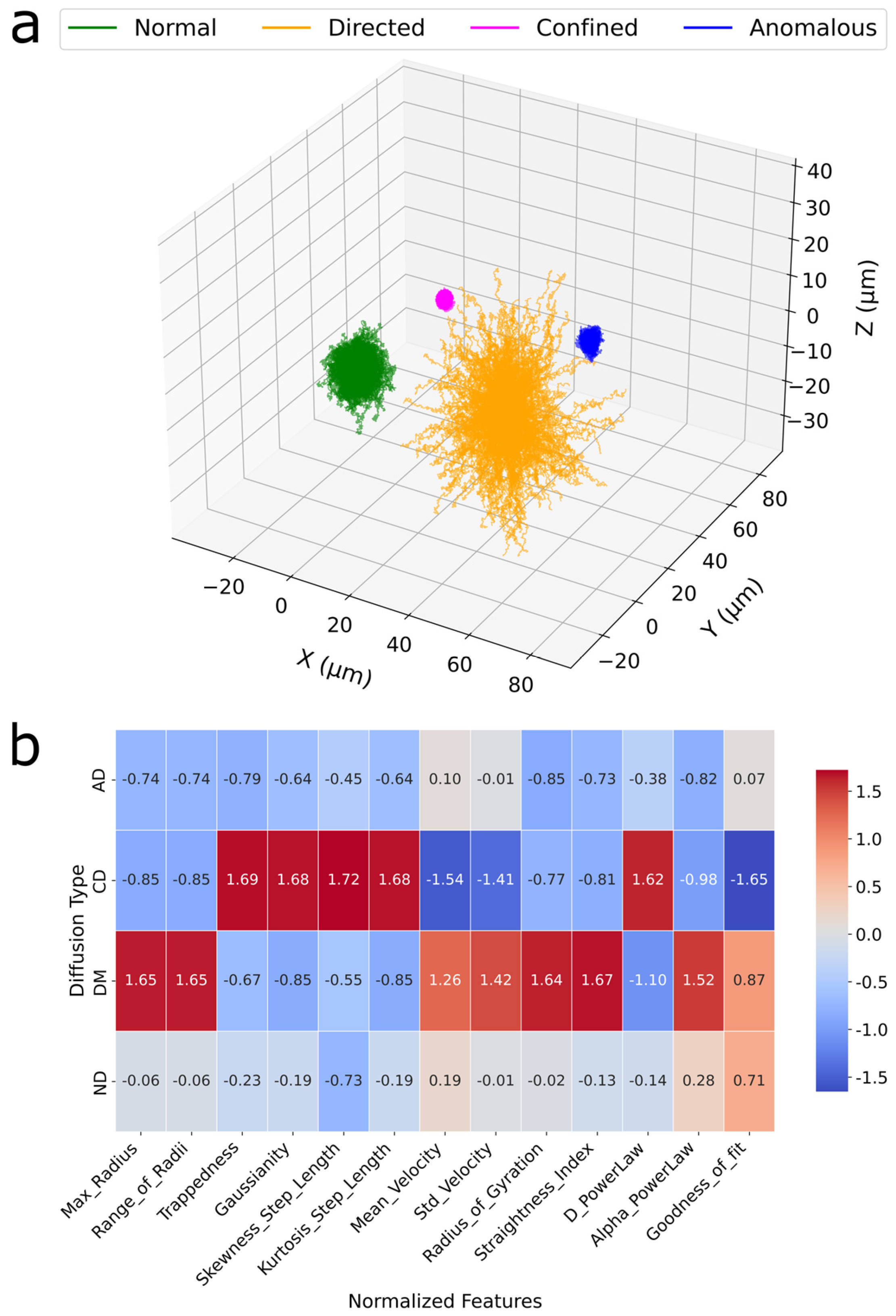
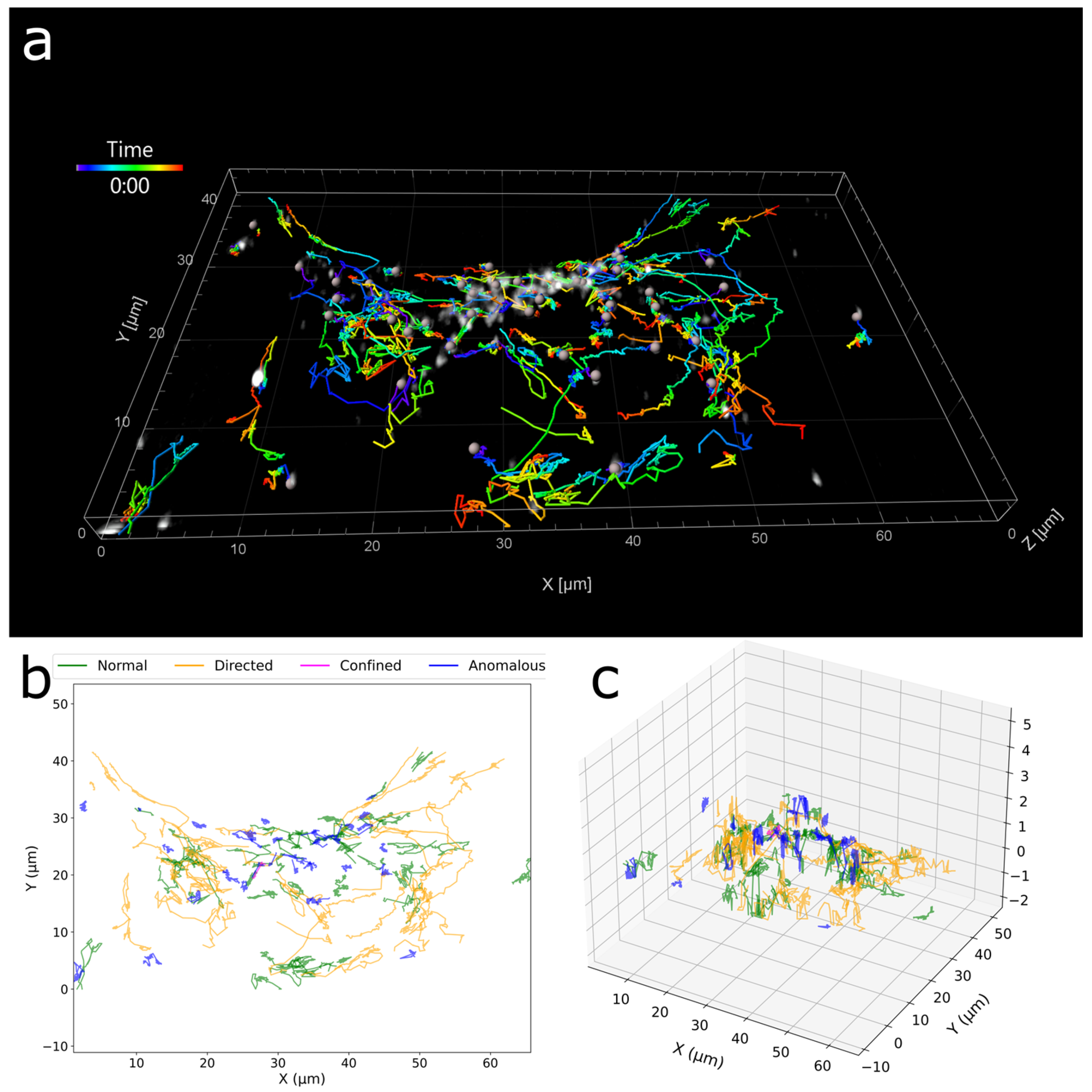
3. Results
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kusumi, A.; Tsunoyama, T.A.; Hirosawa, K.M.; Kasai, R.S.; Fujiwara, T.K. Tracking single molecules at work in living cells. Nat. Chem. Biol. 2014, 10, 524–532. [Google Scholar] [CrossRef] [PubMed]
- Lelek, M.; Gyparaki, M.T.; Beliu, G.; Schueder, F.; Griffié, J.; Manley, S.; Jungmann, R.; Sauer, M.; Lakadamyali, M.; Zimmer, C. Single-molecule localization microscopy. Nat. Rev. Methods Primers 2021, 1, 39. [Google Scholar] [CrossRef] [PubMed]
- Guthrie, D.A.; Klein Herenbrink, C.; Lycas, M.D.; Ku, T.; Bonifazi, A.; DeVree, B.T.; Mathiasen, S.; Javitch, J.A.; Grimm, J.B.; Lavis, L.; et al. Novel Fluorescent Ligands Enable Single-Molecule Localization Microscopy of the Dopamine Transporter. ACS Chem. Neurosci. 2020, 11, 3288–3300. [Google Scholar] [CrossRef] [PubMed]
- Grimm, J.B.; English, B.P.; Choi, H.; Muthusamy, A.K.; Mehl, B.P.; Dong, P.; Brown, T.A.; Lippincott-Schwartz, J.; Liu, Z.; Lionnet, T.; et al. Bright photoactivatable fluorophores for single-molecule imaging. Nat. Methods 2016, 13, 985–988. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Chen, Y.I.; Chen, L.H.; Yeh, H.C. Recent Advances in Single-Molecule Tracking and Imaging Techniques. Annu. Rev. Anal. Chem. (Palo Alto Calif) 2023, 16, 253–284. [Google Scholar] [CrossRef]
- Yanagawa, M.; Hiroshima, M.; Togashi, Y.; Abe, M.; Yamashita, T.; Shichida, Y.; Murata, M.; Ueda, M.; Sako, Y. Single-molecule diffusion-based estimation of ligand effects on G protein–coupled receptors. Sci. Signal. 2018, 11, eaao1917. [Google Scholar] [CrossRef]
- Dupuis, J.P.; Groc, L. Surface trafficking of neurotransmitter receptors: From cultured neurons to intact brain preparations. Neuropharmacology 2020, 169, 107642. [Google Scholar] [CrossRef]
- Sungkaworn, T.; Jobin, M.-L.; Burnecki, K.; Weron, A.; Lohse, M.J.; Calebiro, D. Single-molecule imaging reveals receptor–G protein interactions at cell surface hot spots. Nature 2017, 550, 543–547. [Google Scholar] [CrossRef]
- Möller, J.; Isbilir, A.; Sungkaworn, T.; Osberg, B.; Karathanasis, C.; Sunkara, V.; Grushevskyi, E.O.; Bock, A.; Annibale, P.; Heilemann, M.; et al. Single-molecule analysis reveals agonist-specific dimer formation of µ-opioid receptors. Nat. Chem. Biol. 2020, 16, 946–954. [Google Scholar] [CrossRef]
- Halls, M.L.; Yeatman, H.R.; Nowell, C.J.; Thompson, G.L.; Gondin, A.B.; Civciristov, S.; Bunnett, N.W.; Lambert, N.A.; Poole, D.P.; Canals, M. Plasma membrane localization of the μ-opioid receptor controls spatiotemporal signaling. Sci. Signal. 2016, 9, ra16. [Google Scholar] [CrossRef]
- Kovtun, O.; Torres, R.; Ferguson, R.S.; Josephs, T.; Rosenthal, S.J. Single Quantum Dot Tracking Unravels Agonist Effects on the Dopamine Receptor Dynamics. Biochemistry 2021, 60, 1031–1043. [Google Scholar] [CrossRef] [PubMed]
- Kovtun, O.; Torres, R.; Bellocchio, L.G.; Rosenthal, S.J. Membrane Nanoscopic Organization of D2L Dopamine Receptor Probed by Quantum Dot Tracking. Membranes 2021, 11, 578. [Google Scholar] [CrossRef] [PubMed]
- Calebiro, D.; Nikolaev, V.O.; Persani, L.; Lohse, M.J. Signaling by internalized G-protein-coupled receptors. Trends Pharmacol. Sci. 2010, 31, 221–228. [Google Scholar] [CrossRef] [PubMed]
- Calebiro, D.; Koszegi, Z. The subcellular dynamics of GPCR signaling. Mol. Cell. Endocrinol. 2019, 483, 24–30. [Google Scholar] [CrossRef]
- Eichel, K.; Jullié, D.; Barsi-Rhyne, B.; Latorraca, N.R.; Masureel, M.; Sibarita, J.-B.; Dror, R.O.; von Zastrow, M. Catalytic activation of β-arrestin by GPCRs. Nature 2018, 557, 381–386. [Google Scholar] [CrossRef]
- von Zastrow, M.; Sorkin, A. Mechanisms for Regulating and Organizing Receptor Signaling by Endocytosis. Annu. Rev. Biochem. 2021, 90, 709–737. [Google Scholar] [CrossRef]
- Kowalek, P.; Loch-Olszewska, H.; Szwabiński, J. Classification of diffusion modes in single-particle tracking data: Feature-based versus deep-learning approach. Phys. Rev. E 2019, 100, 032410. [Google Scholar] [CrossRef]
- Pinholt Henrik, D.; Bohr Søren, S.R.; Iversen Josephine, F.; Boomsma, W.; Hatzakis Nikos, S. Single-particle diffusional fingerprinting: A machine-learning framework for quantitative analysis of heterogeneous diffusion. Proc. Natl. Acad. Sci. USA 2021, 118, e2104624118. [Google Scholar] [CrossRef]
- Vega, A.R.; Freeman, S.A.; Grinstein, S.; Jaqaman, K. Multistep Track Segmentation and Motion Classification for Transient Mobility Analysis. Biophys. J. 2018, 114, 1018–1025. [Google Scholar] [CrossRef]
- Kovtun, O.; Tomlinson, I.D.; Ferguson, R.S.; Rosenthal, S.J. Quantum dots reveal heterogeneous membrane diffusivity and dynamic surface density polarization of dopamine transporter. PLoS ONE 2019, 14, e0225339. [Google Scholar] [CrossRef]
- Wagner, T.; Kroll, A.; Haramagatti, C.R.; Lipinski, H.-G.; Wiemann, M. Classification and Segmentation of Nanoparticle Diffusion Trajectories in Cellular Micro Environments. PLoS ONE 2017, 12, e0170165. [Google Scholar] [CrossRef] [PubMed]
- Kowalek, P.; Loch-Olszewska, H.; Łaszczuk, Ł.; Opała, J.; Szwabiński, J. Boosting the performance of anomalous diffusion classifiers with the proper choice of features. J. Phys. A Math. Theor. 2022, 55, 244005. [Google Scholar] [CrossRef]
- Chen, B.-C.; Legant, W.R.; Wang, K.; Shao, L.; Milkie, D.E.; Davidson, M.W.; Janetopoulos, C.; Wu, X.S.; Hammer, J.A.; Liu, Z.; et al. Lattice light-sheet microscopy: Imaging molecules to embryos at high spatiotemporal resolution. Science 2014, 346, 1257998. [Google Scholar] [CrossRef]
- Rosenberg, J.; Cao, G.; Borja-Prieto, F.; Huang, J. Lattice Light-Sheet Microscopy Multi-dimensional Analyses (LaMDA) of T-Cell Receptor Dynamics Predict T-Cell Signaling States. Cell Syst. 2020, 10, 433–444.e435. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-L.; Perillo, E.P.; Liu, C.; Yu, P.; Chou, C.-K.; Hung, M.-C.; Dunn, A.K.; Yeh, H.-C. Segmentation of 3D Trajectories Acquired by TSUNAMI Microscope: An Application to EGFR Trafficking. Biophys. J. 2016, 111, 2214–2227. [Google Scholar] [CrossRef]
- Hatzakis, N.; Kaestel-Hansen, J.; de Sautu, M.; Saminathan, A.; Scanavachi, G.; Correia, R.; Nielsen, A.J.; Bleshoey, S.; Boomsma, W.; Kirchhausen, T. Deep Learning Assisted Single Particle Tracking for Automated Correlation Between Diffusion and Function. Available online: https://doi.org/10.21203/rs.3.rs-3716053/v1 (accessed on 15 November 2024).
- Michalet, X.; Berglund, A.J. Optimal diffusion coefficient estimation in single-particle tracking. Phys. Rev. E 2012, 85, 061916. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Qian, H.; Sheetz, M.P.; Elson, E.L. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys. J. 1991, 60, 910–921. [Google Scholar] [CrossRef]
- Ernst, D.; Köhler, J.; Weiss, M. Probing the type of anomalous diffusion with single-particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 7686–7691. [Google Scholar] [CrossRef]
- Tinevez, J.-Y.; Perry, N.; Schindelin, J.; Hoopes, G.M.; Reynolds, G.D.; Laplantine, E.; Bednarek, S.Y.; Shorte, S.L.; Eliceiri, K.W. TrackMate: An open and extensible platform for single-particle tracking. Methods 2017, 115, 80–90. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Saxton, M.J. A Biological Interpretation of Transient Anomalous Subdiffusion. I. Qualitative Model. Biophys. J. 2007, 92, 1178–1191. [Google Scholar] [CrossRef] [PubMed]
- Saxton, M.J.; Jacobson, K. Single-Particle Tracking: Applications to Membrane Dynamics. Annu. Rev. Biophys. Biomol. Struct. 1997, 26, 373–399. [Google Scholar] [CrossRef]
- ZEISS Lattice Lightsheet 7 Dataset. Available online: https://www.zeiss.com/microscopy/en/resources/insights-hub/life-sciences/vesicle-trafficking.html (accessed on 19 June 2024).
- Jaqaman, K.; Loerke, D.; Mettlen, M.; Kuwata, H.; Grinstein, S.; Schmid, S.L.; Danuser, G. Robust single-particle tracking in live-cell time-lapse sequences. Nat. Methods 2008, 5, 695–702. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Gil, G.; Volpe, G.; Garcia-March, M.A.; Aghion, E.; Argun, A.; Hong, C.B.; Bland, T.; Bo, S.; Conejero, J.A.; Firbas, N.; et al. Objective comparison of methods to decode anomalous diffusion. Nat. Commun. 2021, 12, 6253. [Google Scholar] [CrossRef] [PubMed]
- Patel, N.M.; Ripoll, L.; Peach, C.J.; Ma, N.; Blythe, E.E.; Vaidehi, N.; Bunnett, N.W.; von Zastrow, M.; Sivaramakrishnan, S. Myosin VI drives arrestin-independent internalization and signaling of GPCRs. Nat. Commun. 2024, 15, 10636. [Google Scholar] [CrossRef]
- Lee, J.; Jeong, M.; Ko, B.C. Graph convolution neural network-based data association for online multi-object tracking. IEEE Access 2021, 9, 114535–114546. [Google Scholar] [CrossRef]
- Pineda, J.; Midtvedt, B.; Bachimanchi, H.; Noé, S.; Midtvedt, D.; Volpe, G.; Manzo, C. Geometric deep learning reveals the spatiotemporal features of microscopic motion. Nat. Mach. Intell. 2023, 5, 71–82. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Spilger, R.; Imle, A.; Lee, J.-Y.; Mueller, B.; Fackler, O.T.; Bartenschlager, R.; Rohr, K. A recurrent neural network for particle tracking in microscopy images using future information, track hypotheses, and multiple detections. IEEE Trans. Image Process. 2020, 29, 3681–3694. [Google Scholar] [CrossRef]



| Precision | Recall | F1 Score | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Δt = 1 | 1/10Δt | 1/30Δt | Imaris | Δt = 1 | 1/10Δt | 1/30Δt | Imaris | Δt = 1 | 1/10Δt | 1/30Δt | Imaris | |
| Anomalous | 0.98 | 0.98 | 0.99 | 0.94 | 0.99 | 0.99 | 0.97 | 0.98 | 0.98 | 0.98 | 0.98 | 0.96 |
| Confined | 1.00 | 0.99 | 0.97 | 0.93 | 0.98 | 0.97 | 0.99 | 0.94 | 0.99 | 0.98 | 0.98 | 0.93 |
| Directed | 0.90 | 0.96 | 0.92 | 0.93 | 0.89 | 0.89 | 0.89 | 0.89 | 0.89 | 0.92 | 0.91 | 0.91 |
| Normal | 0.88 | 0.88 | 0.89 | 0.89 | 0.90 | 0.95 | 0.92 | 0.88 | 0.89 | 0.92 | 0.90 | 0.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovtun, O. Machine Learning Classification of 3D Intracellular Trafficking Using Custom and Imaris-Derived Motion Features. Receptors 2025, 4, 6. https://doi.org/10.3390/receptors4010006
Kovtun O. Machine Learning Classification of 3D Intracellular Trafficking Using Custom and Imaris-Derived Motion Features. Receptors. 2025; 4(1):6. https://doi.org/10.3390/receptors4010006
Chicago/Turabian StyleKovtun, Oleg. 2025. "Machine Learning Classification of 3D Intracellular Trafficking Using Custom and Imaris-Derived Motion Features" Receptors 4, no. 1: 6. https://doi.org/10.3390/receptors4010006
APA StyleKovtun, O. (2025). Machine Learning Classification of 3D Intracellular Trafficking Using Custom and Imaris-Derived Motion Features. Receptors, 4(1), 6. https://doi.org/10.3390/receptors4010006






