Systemic Risk in the Lithium and Copper Value Chains: A Network-Based Analysis Using Euclidean Distance and Graph Theory

Abstract

The global push for electrification and decarbonization has sharply increased demand for critical raw materials—especially lithium and copper—heightening financial and strategic pressures on firms that lead these supply chains. Yet, the systemic financial risks arising from inter-firm interdependencies in this sector remain largely unexplored. This article presents a novel distance-based network framework to analyze systemic risk among the world’s top 15 lithium and copper producers (2020–2024). Firms are represented through standardized vectors of profitability and risk indicators (liquidity–solvency), from which we construct a two-layer similarity network using Euclidean distances. Graph-theoretic tools—including Minimum Spanning Tree, eigenvector centrality, modularity detection, and contagion simulations—reveal the structural properties and transmission pathways of financial shocks. The results show a robust-yet-fragile topology: while stable under minor perturbations, the network is highly vulnerable to failures of central firms. These findings highlight the utility of distance-based network models in uncovering hidden fragilities in critical commodity sectors, offering actionable insights for macroprudential regulators, investors, and corporate risk managers amid growing geopolitical and financial entanglement.

1. Introduction

The global shift toward decarbonization and electrification has positioned lithium and copper as strategic commodities at the core of the 21st-century industrial and energy transformation. Their importance now transcends their traditional classification as industrial metals, as they have become foundational to clean energy technologies, electric mobility, and modern infrastructure. As demand patterns evolve and supply constraints persist, both metals have acquired a structurally systemic character within the global commodity market.

Lithium, once a marginal mineral in terms of trade volume, has rapidly emerged as a critical input for lithium-ion batteries, which power electric vehicles (EVs), stationary energy storage systems, and a wide range of consumer electronics. Its strategic importance has been formally recognized in recent industrial policies across multiple jurisdictions, where it is now designated as a critical mineral [1]. Global lithium demand is projected to grow by 26% in 2025, reaching 1.46 million metric tons—outpacing supply growth and intensifying pressure on global value chains. This structural imbalance has driven the market to an estimated valuation of USD 37.43 billion in 2024, with expectations to reach USD 44.13 billion in 2025 and a compound annual growth rate (CAGR) of 17.9% through 2033. In this context, lithium has evolved into a commodity that reshapes global trade flows, investment decisions, and strategic resource planning.

Copper, meanwhile, exemplifies the revaluation of a mature commodity as an essential enabler of the low-carbon economy. Its unparalleled conductivity and durability make it indispensable for power transmission systems, renewable energy infrastructure, electric vehicles, and advanced electronics. Beyond its industrial applications, copper is now viewed as a macroeconomic indicator and a structural constraint in the energy transition. Since early 2025, copper prices have increased by 13.77%, driven by persistent supply-demand imbalances and strong multi-sectoral demand. Although Chile—the world’s leading producer—is expected to produce between 5.4 and 5.6 million tons in 2025, supply expansion remains constrained by declining ore grades, regulatory challenges, and socio-environmental concerns.

Both commodities operate within highly concentrated and geopolitically sensitive value chains, making them increasingly vulnerable to trade tensions, supply chain disruptions, and regulatory shifts. In lithium markets, Australia, Chile, Argentina, and China dominate upstream extraction and midstream refining; in copper, Chile and Peru lead production, while China holds significant leverage as both the largest consumer and a key processing hub. These asymmetries and dependencies mean that any disruption—be it financial, operational, or geopolitical—can trigger contagion effects across supply chains, price volatility, and investor uncertainty [2].

The strategic elevation of lithium and copper is not solely a function of their end-use value but also of their capacity to condition entire industrial ecosystems and influence global economic stability. In tightly coupled markets, where a small number of firms control substantial portions of global production, systemic risk becomes a real concern. As such, evaluating these commodities requires more than conventional supply-demand fundamentals: it demands an integrated analysis of financial interdependencies, market concentration, and geopolitical exposure.

Understanding lithium and copper as strategic commodities calls for a paradigm shift—one that incorporates their systemic relevance in the global energy transition and recognizes the fragility of their supply architectures. These are no longer just inputs; they are critical enablers whose disruption can reverberate across markets, industries, and regions.

1.1. Global Dynamics and Structural Imbalances in Critical Commodity Markets

From a macroeconomic standpoint, the lithium and copper markets are currently characterized by structural asymmetries that reflect the evolving complexities of the global economy and the intensification of the energy transition. These asymmetries are not merely cyclical but stem from profound shifts in supply-demand dynamics, geopolitical contestation over critical materials, and the increasing entanglement of mineral markets with global industrial policy.

In the case of lithium, the market has been shaped by a constrained supply environment, resulting from deliberate production cuts, the reconfiguration of global demand centers, and mounting geopolitical frictions. One illustrative development has been the People’s Republic of China’s proposal to restrict the export of advanced technologies integral to lithium processing and battery manufacturing—an initiative that could materially disrupt the global supply chain for lithium-ion batteries. While lithium prices experienced a temporary decline in early 2025, primarily attributed to short-term oversupply, the medium-term outlook suggests a return to structural deficit conditions beginning in 2026. This forecast is underpinned by the sustained acceleration of electric vehicle (EV) adoption and the expansion of renewable energy storage capacity, both of which are intensifying the strategic significance of lithium as a foundational commodity [3].

The copper market exhibits a similarly complex configuration. Prices have reached historic highs in 2025, a reflection of persistent disequilibrium wherein aggregate demand for copper increasingly outpaces the productive and logistical capacity of the supply side. In parallel, geopolitical developments—particularly the threat of renewed trade barriers between the United States and China—have introduced volatility in the copper scrap market, a critical component of circular value chains and secondary metal recovery strategies. Structural supply constraints remain acute: declining ore grades in mature mining jurisdictions, escalating environmental compliance costs, and the long lead times associated with new project development continue to inhibit the responsiveness of supply. Forecasts suggest that global copper demand could rise by an additional 4.2 million metric tons by 2030, driven by the scale-up of electrified infrastructure and the material intensiveness of decarbonization technologies.

These macroeconomic dynamics collectively signal a paradigm shift in the behavior of both commodities. No longer governed solely by industrial demand cycles or inventory fluctuations, lithium and copper have come to embody a new category of strategic resources whose market behavior is co-determined by technological, geopolitical, and ecological constraints. Accordingly, there is a pressing need to transcend conventional analytical approaches—focused narrowly on price forecasts or volumetric balances—and adopt systemic frameworks capable of capturing the multi-layered vulnerabilities embedded within these markets. This includes an explicit consideration of inter-firm financial interdependencies, concentrated production geographies, and emergent geopolitical fault lines that render both sectors susceptible to cascading disruptions and systemic risk amplification.

1.2. Producing Countries and Their Role in Global Value Chains

The global production of lithium and copper is markedly concentrated in a limited number of jurisdictions, endowing these nations with a disproportionately strategic role within international value chains while simultaneously exposing them to heightened geopolitical, logistical, and environmental risks. This asymmetrical geography of resource endowment and industrial capacity has become a defining feature of both markets.

In the case of lithium, the primary producing countries are Australia, Chile, Argentina, and China. Australia leads global extraction, supplying significant volumes of spodumene concentrate to China, which dominates the refining and midstream processing segments, particularly the conversion of lithium compounds and the manufacturing of lithium-ion batteries [4]. Chile and Argentina, in contrast, are endowed with vast reserves of lithium-rich brines located in the so-called "Lithium Triangle"—a region accounting for approximately 60% of global lithium resources. While China is not a top-tier producer in volumetric terms, it plays a pivotal role in downstream activities, thereby consolidating its influence across the entire value chain. This chain encompasses upstream extraction (from hard rock or brine sources), midstream transformation into lithium carbonate or hydroxide, and final integration into EV batteries and stationary energy systems. The high degree of interdependence among these actors implies that any disruption, whether driven by geopolitical conflict, export restrictions, or natural disasters, has the potential to generate severe supply bottlenecks and price dislocations [3].

The copper market presents a similarly concentrated structure. Chile remains the largest global producer, followed by Peru, China, the Democratic Republic of the Congo (DRC), and the United States. Chile’s output is projected to reach between 5.4 and 5.6 million metric tons in 2025, while additional capacity is expected to come online from projects such as Almalyk in Uzbekistan (148,000 tons/year) and Kamoa-Kakula in the DRC (139,000 tons/year). China, in addition to being a significant producer, is the world’s largest consumer of refined copper, propelled by massive infrastructure development and its accelerated pivot toward renewable energy technologies. The copper value chain spans mining, smelting, refining, and fabrication, supplying critical sectors such as construction, transportation, and electronics. Its strategic importance in renewable technologies—including wind turbines, solar PV systems, and smart grids—renders copper a foundational element of the low-carbon economy. However, the geographic concentration of both production and processing stages makes the entire supply network vulnerable to systemic disruptions, such as labor unrest, environmental restrictions, or volatility in global commodity prices [2].

1.3. Vulnerabilities and the Need for Advanced Analytical Approaches

The sustained surge in global demand for lithium and copper has reconfigured international trade dynamics, giving rise to a complex web of global interdependencies that magnifies the exposure of supply chains to disruptive events. For instance, China’s reliance on Australian lithium reflects the exponential growth of its electric vehicle industry but also underscores the vulnerability of both nations to trade restrictions, export bans, or broader geopolitical tension [4]. In the case of copper, recent trade frictions between the United States and China have added uncertainty to the copper scrap market, a key input for secondary production and circular economy models. Simultaneously, the declining ore grades at major copper deposits pose long-term constraints on the industry’s capacity to respond to future demand shocks. These converging vulnerabilities, combined with the systemic nature of lithium and copper industries, underscore the necessity of meso-level analytical frameworks capable of identifying latent fragilities and anticipating cascading failures in global supply systems [3].

Traditional analytical methods—often reliant on firm-level financial ratios or static econometric models—prove insufficient to capture the multilayered interdependencies and risk propagation mechanisms that characterize these sectors. Network science, particularly graph-theoretic approaches, offers a powerful alternative by enabling the modeling of complex systems and the identification of structural patterns that remain invisible to conventional tools [5]. By representing each firm as a node and encoding financial similarities or interrelations as edges, it becomes possible to detect robust-yet-fragile configurations—networks that are resilient to random disturbances but extremely sensitive to shocks targeting structurally central entities [2,6].

There is, therefore, a growing imperative to develop methodologies within corporate finance that accurately capture financial similarity and systemic interconnection. Historically, firm comparisons have relied on individual financial indicators analyzed through vector-based methods such as cluster analysis. While useful for segmentation purposes, the recent literature has identified important limitations in this approach. A systematic review by Zhang et al. [7] reveals that most studies rely on structured, unconnected financial data (e.g., standard accounting ratios), analyzed using simple Euclidean distances or correlation matrices—methods that fail to reflect the inherently networked nature of firms operating within integrated global supply chains.

To address this gap, emerging research has begun to explore graph-based similarity metrics. A notable contribution by Noels et al. [8] models each firm’s financial statements as hierarchical trees—where nodes represent balance sheet items, and edges denote account structures—and applies the Earth Mover’s Distance (EMD) to quantify how much “monetary mass” must be transferred to align one structure with another. This transport-based metric incorporates both magnitude (financial values) and structural differences (account composition), outperforming traditional ratio-by-ratio comparisons in identifying financial outliers and firm similarity. Similarly, other authors have shown that Euclidean distance-based network models can capture risk topologies and volatility transmission channels that would otherwise be missed by linear correlation frameworks [9].

Most network maps in commodity and value-chain finance are still inferred from Pearson correlation or cosine similarity, effectively equating average co-movement with structural connectedness. This identification is fragile for at least four reasons. First, correlation is linear, symmetric, and window-dependent; short-lived common shocks and regime shifts inflate link density and make communities unstable across samples. Second, the standard transformation 1–ρ is not a true metric and distorts topology and clustering. Third, cosine similarity discards scale and higher-moment information, muting heteroskedasticity and tail asymmetries that drive financing terms (collateral haircuts, margins). Fourth, both measures are prone to common-factor contamination and blur the distinction between persistent ties and transitory co-fluctuations, offering limited guidance on how stress actually propagates through commodity-finance linkages.

We close this gap by constructing distance-based, statistically validated networks grounded in an adaptive, order-weighted Euclidean distance (AAEOD) that preserves metric geometry and reweights economically salient regimes—especially the downside. Operationally, we build a validated adjacency (AAEOST) and derive transmission-oriented diagnostics—an adaptive eigenvector centrality (AEC) and a Systemic Transmission Factor (STF)—to quantify a node’s amplification potential along economically meaningful paths. Relative to correlation/cosine graphs, our framework reduces spurious density from common shocks, yields communities that are stable across windows, and uncovers tail-driven propagation channels that similarity methods miss [9]. In a setting where risk is asymmetric and collateral dynamics are tail-sensitive, this shift from static similarity to adaptive distance provides a more policy-relevant map of systemic vulnerability [10]. This motivates the contribution we articulate next.

Against this backdrop, the present study constructs a financial similarity network among leading firms in the lithium and copper sectors. Drawing on a comprehensive set of standardized profitability and risk indicators, we compute pairwise Euclidean distances and generate a dual-layer network—one layer capturing risk, the other profitability. We then analyze the resulting network structure using advanced graph-theoretic tools, including Minimum Spanning Tree (MST), eigenvector centrality, community modularity, and contagion simulations. This methodological architecture enables us to uncover latent vulnerabilities, identify structurally central firms, and trace potential pathways of systemic financial contagion within two of the most critical commodity sectors underpinning the global energy transition.

2. Research Objectives and Hypotheses

This investigation adopts a quantitative, non-experimental research framework, grounded in an exploratory-descriptive orientation. Given the complexity of the phenomena under study and the absence of manipulable independent variables, the methodological approach is based on the observational modeling of existing financial structures, rather than experimental inference. Specifically, the study leverages network theory to map the structural proximity and interconnectivity among firms operating in the lithium and copper industries, complemented by contagion simulations designed to emulate the potential propagation of financial distress under hypothetical stress scenarios.

The analytical design is fundamentally cross-sectional—constructed from historical financial data covering a fixed temporal window—yet incorporates dynamic simulation components that allow for the evaluation of temporal diffusion patterns. This hybrid configuration enables a static mapping of structural interdependencies alongside the modeling of shock propagation processes over time.

The theoretical foundation of this study draws upon prior literature suggesting that structural similarity across financial indicators—such as liquidity, solvency, and profitability—can be predictive of correlated financial behaviors and exposure profiles among firms [11]. In the context of highly concentrated and strategically relevant commodity sectors, such as lithium and copper, these interfirm proximities may amplify systemic vulnerabilities. Thus, the quantitative identification of such patterns is not only analytically relevant but also critical from a macroprudential risk perspective.

To operationalize this research agenda, the study is structured around the following three core methodological phases:

• Data acquisition and preprocessing: Compilation, normalization, and standardization of a multidimensional set of financial indicators for a selected sample of leading firms in the lithium and copper industries.
• Network construction: Generation of a weighted, undirected graph based on pairwise Euclidean distances between firms’ financial vectors, yielding a multi-layered network representation capturing both risk and profitability dimensions.
• Network analysis and simulation: Application of graph-theoretic metrics—including centrality, modularity, and minimal spanning trees—alongside dynamic contagion models to assess network topology, identify structurally critical nodes, and simulate the diffusion of financial distress across the system.

In alignment with this methodological architecture, a set of r guiding hypotheses has been articulated to ensure coherence between the analytical framework and the overarching inquiry. These are intended not only to delineate the scope of the investigation but also to anchor the interpretation of the results within a robust theoretical and empirical structure.

Grounded in the theoretical framework and the objectives previously outlined, this study posits the following hypotheses, each of which will be evaluated through the application of network-theoretic analysis to a financial similarity graph derived from empirical data. These hypotheses are designed to assess the presence of structural regularities, topological centrality, and risk transmission dynamics within the global network of leading firms in the lithium and copper industries.

• H1 (Structural Segmentation Hypothesis):
  The financial similarity network exhibits community structures that reflect underlying operational or contextual proximities among firms.
  Specifically, it is hypothesized that the network will demonstrate non-random modularity, wherein firms are partitioned into cohesive subgroups based on shared characteristics—such as resource specialization (e.g., copper-dominant vs. lithium-diversified operations) or regional alignment (e.g., firms operating within the same geopolitical or regulatory environment). The identification of such communities would suggest the presence of latent structural segmentation within the global commodity system, potentially indicative of differentiated financial behavior and exposure profiles.
• H2 (Topological Centrality Hypothesis):
  A subset of firms will occupy disproportionately central positions in the network, acting as structural hubs or intercommunity bridges with high levels of connectivity and influence.
  This hypothesis posits that large-cap and operationally diversified firms, particularly multinational mining conglomerates, will exhibit elevated values across multiple centrality metrics (e.g., degree centrality, betweenness centrality, eigenvector centrality). Their financial similarity to a broad array of firms implies a structurally integrative role, rendering them critical nodes for the cohesion and connectivity of the system. The presence of such central actors may also suggest that systemic stability is disproportionately contingent upon their financial robustness.
• H3 (Contagion Asymmetry Hypothesis):
  Exogenous shocks originating in highly central firms will generate broader and more intense contagion effects across the network than equivalent shocks occurring in peripheral nodes.
  This hypothesis reflects the theoretical premise that centrality amplifies systemic impact: when a core firm experiences financial distress—manifested, for instance, in abrupt solvency deterioration or default—the structural density of its connections increases the likelihood of shock propagation through similarity-based channels, whether via investor sentiment, sectoral interdependencies, or correlated exposure to macroeconomic drivers. In contrast, disturbances in marginal nodes are expected to result in limited, localized effects, owing to their low integration within the network’s topology.

Collectively, these hypotheses aim to elucidate the systemic configuration of financial interdependencies within a strategically vital segment of the global commodity landscape. They are designed to guide the subsequent empirical analysis, anchoring the interpretation of graph-theoretic results within a coherent and testable theoretical framework.

3. Literature Review

Graph theory has emerged as a foundational analytical framework for the study of complex systems, particularly within the corporate and industrial domains, where interdependencies among firms, supply chains, and market actors give rise to intricate relational structures. By offering a formal and quantitative representation of interactions, graph theory enables the identification of topological patterns, relational asymmetries, and systemic vulnerabilities that are often imperceptible to traditional statistical or financial techniques. This section presents a comprehensive review of the most relevant literature, focusing on the application of network theory to corporate systems, with particular emphasis on its use in the analysis of critical mineral sectors, especially lithium and copper, and in the study of financial similarity and structural fragility among firms.

3.1. Graph Theory in Corporate Network Analysis

Over the past two decades, graph theory has evolved into an essential analytical paradigm for modeling complex organizational and industrial systems, particularly in environments marked by high interconnectivity, structural asymmetries, and systemic risk. Its formalism enables the abstraction of firms, institutions, or countries as nodes, and their interactions—be they financial, operational, or strategic—as edges, allowing for the systematic study of network topology, robustness, centrality, and modularity.

In the context of global corporate ecosystems, firms are embedded within intricate webs of relationships—subsidiary linkages, strategic alliances, supplier-buyer chains, equity participations, and shared market exposures—that transcend national boundaries and industrial classifications. Traditional linear models often fail to capture this complexity. Graph-based representations, by contrast, offer a structurally sensitive lens through which latent organizational architectures and hidden channels of vulnerability can be detected [10].

Networks in this domain may be conceptualized as directed or undirected, weighted or unweighted, and either single-layered or multiplex, depending on the type and granularity of the relationships captured. This flexibility allows researchers to tailor the network structure to specific analytical purposes—ranging from mapping trade flows and ownership hierarchies to modeling financial similarity or contagion risk. Critically, network metrics such as degree centrality, eigenvector centrality, betweenness centrality, and clustering coefficients provide insights into how influence, dependency, and fragility are distributed across actors.

In the field of critical commodities, and, in particular, the lithium and copper industries, graph theory has been increasingly employed to elucidate the structure and resilience of global value chains. For example, Li et al. [12] construct a multilayer global network of copper trade flows, distinguishing the roles of actors across the upstream (mining), midstream (smelting, refining), and downstream (manufacturing, export) stages. Their analysis reveals that systemic exposure is not necessarily aligned with production volume: a country or firm with high structural embeddedness may function as a linchpin, whose removal would fragment the network and compromise global supply stability.

Ouyang et al. [13] extend this perspective to the lithium sector by modeling global supply chains as dynamically evolving networks subject to exogenous shocks. Through simulation of cascading failure mechanisms, they show that structural vulnerabilities often concentrate in nodes with high betweenness centrality, which serve as irreplaceable conduits between otherwise disconnected subcomponents. Their results reinforce a foundational principle in network science: systemic fragility is not a function of scale alone, but of position—a small but central firm may exert greater influence on network-wide outcomes than a larger but peripheral actor.

These studies underscore the necessity of network-based approaches in commodity systems marked by geographic concentration, technological interdependence, and financial co-exposure. In such settings, disruptions rarely propagate linearly. Rather, they unfold through non-obvious transmission paths, often shaped by the underlying topological configuration of the system. As a result, graph-theoretic methods not only enable the identification of key structural actors, but also provide the foundation for scenario-based stress testing, contingency planning, and strategic interventions aimed at enhancing systemic resilience.

3.2. Sector-Specific Network Applications: Lithium and Copper as Structurally Coupled Commodity Systems

The application of network theory to the analysis of commodity systems has gained particular traction in the case of strategic minerals, where value chains are characterized by structural concentration, geopolitical exposure, and technological indispensability. Among these, lithium and copper have emerged as exemplary cases due to their dual condition: they are both industrial inputs and system-critical enablers of the energy transition.

In the case of lithium, its unprecedented demand surge—driven by its role in lithium-ion batteries for electric vehicles (EVs) and stationary storage—has led to a supply architecture that is both globalized and highly asymmetric. Estimates suggest that demand will reach 1.46 million metric tons by 2025, a 26% increase over 2024. The structure of this market is dominated by a handful of countries—most notably Australia, Chile, Argentina, and China—whose positions span different stages of the supply chain, from extraction to chemical conversion and battery manufacturing [4]. Graph-theoretic analyses have been employed to map these supply networks and identify structural vulnerabilities, such as China’s dependence on Australian spodumene, which renders the system susceptible to bilateral trade tensions, logistics bottlenecks, and regulatory shocks [3]. These studies underscore how network positionality—not just market share—determines systemic relevance in mineral supply chains.

Similarly, the copper sector provides a compelling context for the application of network analysis. Its structural importance in electrification and its broad industrial use make copper a proxy for both economic activity and green infrastructure investment. However, the supply side faces mounting challenges: declining ore grades, increasing regulatory constraints, and project delays have constrained growth, despite strong demand projections. Chile, the world’s largest producer, is expected to contribute 5.4–5.6 million metric tons in 2025 alone. Recent studies (e.g., [12]) have analyzed global copper trade as a complex network, revealing structures described as robust-yet-fragile—resilient under small perturbations but highly vulnerable to the failure of critical nodes such as major refineries or export hubs. These insights highlight the limitations of traditional aggregate indicators in capturing systemic fragility and point to the importance of network topology as a determinant of resilience.

Notably, in both sectors, network studies have revealed that system-wide vulnerabilities are often concentrated in structurally central actors—not necessarily those with the highest volume or market capitalization, but those whose position enables or conditions the connectivity of the broader system. This distinction between economic weight and topological influence is central to a new generation of literature that redefines “criticality” in supply chains through the lens of interdependence and propagation capacity, rather than static market metrics.

3.3. Financial Similarity Networks: Modeling Structural Affinity Among Firms

While much of the early literature on network analysis in commodity systems has focused on physical trade and supply chain mapping, a more recent stream of research has turned to inter-firm financial similarity networks, particularly in capital-intensive sectors such as mining and resource extraction. This approach conceptualizes firms as nodes, and the edges as functions of financial resemblance, often operationalized via distance metrics across standardized financial indicators (e.g., liquidity, solvency, and profitability ratios).

One of the most cited contributions in this area is Noels et al. [8], who modeled mining companies’ financial statements as financial similarity networks. They employed a multidimensional accounting dataset and used edge-filtering techniques (e.g., minimum spanning trees, distance thresholds) to extract only the most salient connections, thereby enhancing the interpretability of the network structure and uncovering clusters of firms with convergent financial behavior. This approach allows for the detection of latent typologies, going beyond sectoral classification and incorporating financial structure, risk profile, and business model alignment.

Further empirical studies have explored the determinants of these clusters. Ross [14] found that sectoral affiliation is the dominant driver of financial similarity networks, but also noted that geographic variables play a critical secondary role, often structuring firms into regional sub-clusters due to shared regulatory environments, input costs, and macroeconomic exposure. For instance, copper producers based in Latin America often exhibit financial configurations that are systematically distinct from their peers in Asia or North America—despite operating within the same global sector.

Recent comparative analyses have also shown that network density and connectivity patterns vary across mineral types, reflecting the underlying market structure and strategic complexity of each commodity. Restrepo et al. [15], in a study of critical metal producers, found that copper firms displayed higher average degree centrality and network cohesion than those in the nickel or cobalt sectors. This was attributed to the greater maturity and integration of the copper industry, marked by long-standing commercial relationships, joint ventures, and a broader base of shared technological platforms. In contrast, the lithium sector—despite its rapid growth—exhibits fragmented and hierarchized connectivity, due to the vertical specialization of firms and the geographic concentration of extractive capacity [13].

A parallel literature on systemic risk shows that commodity-specific and cross-layer structures shape cascade dynamics and systemic vulnerability in trade and value-chain networks, particularly for critical minerals. Multiplex and multilayer models reveal that aggregation hides heterogeneity, “weak” layers can amplify cascades, and central positions in commodity-specific layers transmit stress across stages and markets [4,6,16,17,18,19,20,21,22,23,24,25]. Within LIB-relevant chains (lithium, cobalt, nickel, manganese) and adjacent metals (copper, tungsten), these studies document concentration, evolving community structure, resilience under targeted attacks, and propagation paths across upstream–downstream stages—yet most rely on trade-only layers and similarity measures with standard centralities, which can obscure tail asymmetries and understate finance-signal transmission.

What these studies collectively suggest is that financial similarity networks offer more than just a descriptive map: they provide a quantitative framework to explore sectoral homogeneity, exposure to common shocks, and the plausibility of risk contagion mechanisms. Importantly, these networks also create the foundation for simulation-based stress testing, wherein the propagation of financial distress can be modeled not only according to economic fundamentals but also as a function of relational structure and topological fragility.

3.4. Gaps in the Literature and Unresolved Research Frontiers

While graph theory has gained prominence as a methodological framework for analyzing structural dependencies across industrial and financial systems, the literature remains markedly underdeveloped in its application to firm-level financial similarity, particularly within sectors of strategic importance such as lithium and copper. The dominant body of research to date has focused on macro-structural networks—including international trade flows, sectoral interlinkages, or resource-dependent geopolitical constellations [2,12]. Although valuable, these studies tend to obscure the micro-foundations of systemic fragility, particularly those emerging from interfirm financial proximities and exposure correlations.

Moreover, traditional approaches to interfirm comparison—such as cluster analysis based on vectorial distances between accounting ratios—are analytically limited. These methods often assume variable independence, overlook structural configuration, and fail to capture the latent topology through which financial contagion may propagate [7]. As a result, they provide at best a static picture of relative similarity, without offering insight into network-mediated transmission mechanisms, nor into the structural centrality of firms within a broader financial ecosystem.

Recent advances propose overcoming these limitations through the application of graph-based financial similarity models that integrate not only the magnitude but also the structure and connectivity of firms’ financial profiles. For example, Noels et al. [8] introduced an innovative framework wherein balance sheets and income statements are conceptualized as hierarchical graphs, and the Earth Mover’s Distance (EMD)a metric rooted in optimal transport theory—is used to assess both compositional and quantitative differences between firms. This approach surpasses the limitations of Euclidean distances by embedding structural constraints into the comparison, thus enhancing the capacity to identify outliers and map financial convergence with higher resolution.

In a complementary contribution, Esmalifalak [9] demonstrated that financial similarity networks constructed from distance matrices offer a more nuanced account of latent systemic risk, capturing nodes whose volatility contributions are topologically significant yet obscured in correlation-based models. These findings suggest a profound epistemic shift: from seeing risk as a scalar property of firms, to viewing it as relational and structurally embedded within the financial architecture of a sector.

Despite these promising developments, the application of these methods to resource-based sectors remains sparse. In particular, the literature lacks models that link financial similarity networks with structural features of critical commodity value chains, limiting our understanding of how financially proximate firms might co-amplify sectoral instability under conditions of exogenous stress. Addressing this gap constitutes not only a methodological opportunity but also a necessary step toward a comprehensive systems-level analysis of strategic mineral markets.

3.5. Methodological Enhancements and Future Research Trajectories

Beyond the construction of similarity networks, the recent literature has emphasized the relevance of graph-theoretic tools and complementary computational methods to extract deeper insights from financial and industrial networks. Centrality measures—such as degree, betweenness, and eigenvector centrality—have proven essential in identifying firms whose topological positioning makes them disproportionately influential in network cohesion and potential risk propagation [26]. These metrics allow for the reconceptualization of systemic importance beyond firm size, focusing instead on structural embeddedness.

In parallel, community detection algorithms, particularly those optimizing modularity, have shown efficacy in revealing functional or geographic substructures within corporate ecosystems [14]. These endogenous clusters often align with sectoral boundaries or regional economic contexts but may also reflect convergence in strategic behavior or capital structure, thereby offering a meso-level perspective between individual firms and the global market.

A particularly impactful innovation lies in the use of financial contagion simulations, which model the diffusion of distress through similarity or exposure networks. Such simulations have been applied with growing frequency in studies of strategic sectors such as lithium and copper, where the failure of a central firm can have cascading effects throughout supply chains, capital markets, and production networks [13]. The utility of these models lies not only in stress-testing sectoral resilience, but in their capacity to identify early-warning nodes whose instability could presage broader systemic disruptions.

Looking forward, the literature identifies three research trajectories of particular importance:

• Multidimensional network integration: The incorporation of financial similarity data with non-financial layers—such as trade dependencies, ownership structures, ESG profiles, or geopolitical risk—could produce multiplex representations that more accurately reflect the real-world complexity of interfirm relationships in strategic sectors.
• Temporal dynamics and longitudinal modeling: Most existing models remain cross-sectional, yet the temporal evolution of network topology may reveal critical phase transitions in financial interdependence, structural reconfiguration under stress, or the shifting centrality of firms in response to macroeconomic shocks.
• Algorithmic and machine learning integration: Techniques such as graph neural networks (GNNs), spectral embedding, and unsupervised learning offer the potential to enhance model scalability, improve cluster detection, and uncover nonlinear patterns of similarity and influence [15]. These tools represent a frontier for hybrid models that bridge interpretability and computational performance.

In sum, while significant theoretical and methodological advances have been made, the financial network analysis of strategic commodity sectors remains in an incipient stage. A coordinated research effort—drawing on graph theory, financial modeling, and data science—holds considerable promise for advancing a structurally informed, forward-looking understanding of risk and resilience in globally interdependent industries.

3.6. Euclidean Distance as a Foundation for Financial Similarity in Network Models

The Euclidean distance metric has long served as a foundational tool in the quantitative modeling of financial similarity among firms. By measuring the straight-line distance between two points in a multidimensional space—each dimension corresponding to a standardized financial indicator—it enables the quantification of proximity between corporate financial profiles in a manner that is both mathematically rigorous and computationally efficient. Its appeal lies not only in its simplicity, but also in its capacity to preserve the structural heterogeneity of financial data without imposing assumptions about distributional form or inter-variable dependencies.

In the context of financial networks, Euclidean distance has been widely employed to construct weighted graphs wherein each node represents a firm, and the edge weights reflect the degree of dissimilarity between financial vectors. These similarity-based networks provide a rich analytical framework to examine latent structures in corporate ecosystems, including the emergence of financial clusters, the identification of anomalous outliers, and the assessment of topological robustness. Esmalifalak [9] underscores the practicality of Euclidean metrics in high-dimensional datasets, highlighting their efficiency in capturing inter-firm affinities across broad samples without compromising analytical sensitivity—a particularly salient feature in environments requiring real-time computation or high-frequency financial monitoring.

Beyond static comparisons, the utility of Euclidean distance extends to the dynamic analysis of financial proximity. Through the application of rolling time windows, it becomes possible to trace temporal shifts in pairwise distances and thus monitor evolving interdependencies within and across sectors. Such temporal similarity matrices can be translated into time-varying network representations that reveal how firms converge or diverge in response to exogenous shocks, regulatory shifts, or endogenous financial distress. These representations are particularly relevant in commodity markets, where volatility, concentration of supply, and geopolitical tensions can produce abrupt structural realignments.

The analytical power of Euclidean distance is significantly amplified when integrated with the principles of complex network theory. Hu et al. [6] argue that network-based metrics such as modularity, degree centrality, and betweenness offer deeper insight into the systemic importance of firms within financial similarity graphs. In this view, Euclidean distance does not merely serve as a measure of pairwise closeness but operates as a foundational layer for higher-order structural diagnostics. Hao et al. [2] further demonstrate that, when embedded in global supply chain models, Euclidean-derived networks can illuminate critical pathways for financial contagion, particularly in trade-dependent sectors like mining and metallurgy.

The application of Euclidean distance has proven particularly instructive in the study of critical raw material industries such as lithium and copper. Yang [27] employed distance-based metrics to assess the evolution of the global lithium trade network over a twelve-year period, capturing the topological effects of exogenous disruptions such as trade wars and supply chain bottlenecks. The results reveal that shifts in average path length and clustering coefficients can be robustly detected using Euclidean-based proximity matrices. Similarly, Li et al. [12] leveraged dynamic flow models to examine regional disparities in copper utilization, employing Euclidean distances to compare structural divergences in material throughput across industrial regions. This approach elucidated how macro-regional asymmetries translate into heterogeneous corporate profiles and network positions.

The methodological synergy between Euclidean metrics and graph-theoretic algorithms—such as the Minimum Spanning Tree (MST), k-nearest neighbor graphs, or Planar Maximally Filtered Graphs (PMFGs)—has enabled researchers to derive topologically stable yet analytically tractable representations of financial networks. Esmalifalak [9] illustrates how MSTs based on Euclidean distances reveal critical transmission channels in foreign exchange markets, while Hao et al. [2] demonstrate that combining Euclidean similarity with node vulnerability assessments enhances the predictive power of risk propagation models in commodity supply chains.

Taken together, the literature converges on a clear consensus: Euclidean distance, despite its apparent simplicity, remains an indispensable analytical instrument in financial network research. Its integration with advanced network analytics yields a dual advantage—preserving the fidelity of firm-level financial information while enabling macro-level structural inference. In the context of strategically vital sectors such as lithium and copper, where firms operate within globally interdependent and volatility-prone environments, this methodological framework provides a robust foundation for assessing systemic exposure, detecting emergent risk clusters, and informing resilience-oriented policy interventions.

3.7. Risk Propagation and Contagion in Critical Metals Networks

The propagation of risk across interconnected firms and countries within critical minerals supply chains has gained increasing attention in the literature on network-based systemic vulnerability. From both operational and financial perspectives, the structural topology of these networks profoundly influences how exogenous shocks disseminate across agents—be they firms, industries, or nations.

In the context of lithium supply chains, Li et al. [12] identified four primary transmission channels: direct bilateral shocks, intermediary-based propagation, redistribution through central hubs, and regional contagion via spatial proximity. Their results confirm the “robust-yet-fragile” hypothesis of supply networks: decentralized, low-impact disruptions are typically absorbed without major systemic consequences, but failures occurring at structurally central nodes—such as dominant exporters—may lead to widespread reconfiguration of trade flows, input shortages, and global price volatility [2].

Similarly, in the copper trade network, Li et al. [12] decomposed global flows into production stages and revealed a structural asymmetry: upstream stages (e.g., extraction and raw concentrate export) are concentrated and fragile, whereas downstream stages (refining and final goods) exhibit higher topological redundancy. Their findings highlight the strategic role of intermediary countries—such as Japan, South Korea, and Spain—which, despite moderate trade volumes, act as bridges connecting regional clusters. The removal of such nodes has a disproportionate effect on network fragmentation, reinforcing the value of betweenness centrality in assessing systemic importance.

These insights align with the contributions of Cortés Rufé & Martí Pidelaserra [26], who argue that metrics derived from graph theory—particularly centrality indices (degree, eigenvector, and betweenness)—provide a robust analytical framework for identifying structurally pivotal firms in financial and trade networks. Their work emphasizes that highly central nodes act not merely as informational or transactional hubs, but also as critical conduits for volatility diffusion and policy transmission. Within resource-intensive sectors, firms occupying such positions may become systemic amplifiers of localized disruptions, regardless of their size.

Dynamic simulations further reinforce this narrative. Hu et al. [6] demonstrated that disruptions in high-value-added midstream actors—such as lithium cathode manufacturers—exert greater systemic damage than shocks at the raw extraction stage, underscoring that vulnerability is not a function of input volume but rather of substitutability and network embeddedness. Ouyang et al. [13] extend this by modeling percolation processes across multi-layered supply chains, showing that critical thresholds of failure emerge from network modularity and interconnectivity—not just from firm-specific risk profiles.

Beyond physical trade, financial contagion is increasingly recognized as a parallel layer of risk diffusion. Restrepo et al. [15] applied the Diebold-Yılmaz volatility spillover framework to publicly traded companies across critical mineral sectors. Their findings reveal high intra-sectoral spillovers in lithium and copper segments, along with asymmetric cross-sectoral influence toward nickel and cobalt markets. Notably, periods of lithium market exuberance magnified systemic co-movement even among firms with no direct operational linkages, reflecting investor-driven clustering and sectoral sentiment contagion.

These financial spillovers highlight the emergence of implicit correlation networks driven by investor behavior, shared exposure to global pricing mechanisms, or synchronized ESG-related disclosures. In this sense, even absent direct trade relations, firms form latent topologies of influence wherein market-based shocks can propagate nonlinearly. As noted by Zhang [7] and Noels et al. [8] conventional metrics—such as sectoral betas or accounting-based clustering—fail to capture these higher-order financial interactions, which require graph-based and multivariate approaches to be properly quantified.

Taken together, the reviewed literature suggests a dual imperative. First, integrating network science into financial and supply chain analysis enables the identification of structurally critical actors beyond traditional size-based metrics. Second, constructing multi-layered networks that incorporate both tangible trade relationships and intangible financial linkages provides a more comprehensive framework for modeling systemic risk in resource-intensive sectors. This aligns with recent calls for hybrid methodologies capable of integrating physical topology, financial similarity, and behavioral feedback loops [26,28,29].

4. Methodology

This study adopts a firm-level analytical approach to investigate systemic interdependencies among leading corporations involved in the extraction and production of lithium and copper—two commodities deemed critical for the global energy transition. The sample consists of 15 globally significant mining firms, selected based on their aggregate production volumes, market capitalization, and structural influence across global supply chains. The selection includes a heterogeneous mix of state-owned enterprises and multinational corporations, encompassing a broad geographical and institutional diversity.

Specifically, the sample includes: Codelco (Chile), Freeport-McMoRan (United States), Glencore plc (Switzerland), BHP Group (Australia), Rio Tinto (United Kingdom/Australia), Southern Copper Corporation (Peru/Mexico), Antofagasta Minerals (Chile), KGHM Polska Miedź (Poland), Anglo American (United Kingdom), Grupo México(Mexico), First Quantum Minerals (Canada), Lundin Mining (Canada), Zijin Mining (China), Eramet (France), and Boliden (Sweden). Together, these companies account for a substantial portion of global refined copper and lithium production, and many operate integrated supply chains with multi-continental upstream and downstream linkages.

Financial data for each firm were extracted from audited annual reports, international financial databases, and stock market filings for the period 2018–2024, contingent on data availability. To enhance comparability across firms of different sizes and jurisdictions, the analysis relies on normalized financial indicators, rather than raw absolute values, allowing for meaningful relative distance and similarity calculations.

These indicators were carefully selected to reflect key dimensions of financial performance, including profitability, liquidity, solvency, and operational efficiency. The next subsection outlines the construction of the financial similarity matrix and the network modeling techniques applied to the resulting multivariate dataset.

4.1. Financial Methodology: Ratios for Valuation and Network Construction

To evaluate the financial similarity among firms operating in the lithium and copper sectors—and thus construct the corresponding inter-firm network—a set of ten key financial ratios was selected. These metrics are grouped into two overarching dimensions: profitability (including both return-based and margin-based indicators) and risk (covering long-term solvency and short-term liquidity). This dual structure enables a multidimensional assessment of each firm’s performance and financial resilience.

4.1.1. Profitability Indicators

• Return on Assets (ROA): Assesses the firm’s ability to generate net income from its total asset base.

$$\mathrm{ROA}={\displaystyle \frac{{Net Profit}_t}{{Total Assets}_{t-1}}}\times 100$$

• Return on Equity (ROE): Measures the return generated for shareholders on their invested capital.

$$\mathrm{ROE}={\displaystyle \frac{{Net Income}_t}{{Equity}_{t-1}}}\times 100$$

• Return on Capital Employed (ROCE): Evaluates operational efficiency by relating operating profit to total capital employed (equity plus long-term debt)

$$\mathrm{ROCE}={\displaystyle \frac{{Operating Profit}_t}{{Equity}_{t-1}+{Total Debt}_{t-1}}}\times 100$$

These ratios collectively capture how efficiently firms transform their asset base and invested capital into returns. Prior literature indicates that companies with structurally similar financial models tend to exhibit comparable profitability patterns—particularly in terms of ROE—supporting the inclusion of these metrics in firm-level network modeling [8,30].

4.1.2. Margin Indicators

• Net Margin: Represents the proportion of revenue that is converted into net income after all costs, taxes, and interest expenses.

$$\mathrm{Net} \mathrm{Margin}={\displaystyle \frac{{Net Profit}_t}{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{R}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{u}\mathrm{e}}}\times 100$$

• Operating Margin (EBIT or EBITDA): Focuses on the profitability from core operations, before financing and tax impacts.

$$\mathrm{O}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{M}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{i}\mathrm{n}={\displaystyle \frac{{EBIT or EBITDA}_t}{{Total Revenue}_t}}\times 100$$

These margin-based indicators offer a finer-grained perspective on operational efficiency, cost structure, and pricing power. Their inclusion allows for the identification of clusters of firms with aligned business models and cost-efficiency strategies within the network topology.

4.1.3. Long-Term Solvency and Capital Structure

To capture financial exposure and funding structure, the following solvency indicators are employed:

• Debt-to-Equity Ratio: Measures reliance on external financing relative to internal equity.

$$\mathrm{D}\mathrm{e}\mathrm{b}\mathrm{t}-\mathrm{t}\mathrm{o}-\mathrm{E}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{t}\mathrm{y}={\displaystyle \frac{{Total Debt}_t}{{Total Equity}_t}}$$

• Leverage Ratio (Debt-to-Assets): Evaluates what proportion of the firm’s asset base is debt-financed.

$$\mathrm{L}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}={\displaystyle \frac{{Total Debt}_t}{{Total Assets}_t}}$$

• Interest Coverage Ratio: Gauges the firm’s capacity to meet interest obligations using operational profits.

$$\mathrm{I}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t} \mathrm{C}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}={\displaystyle \frac{{EBIT}_t}{{Interest Expenses}_t }}$$

These solvency metrics serve to uncover similarities in firms’ capital strategies and potential sensitivity to credit market fluctuations. Such features are critical in assessing systemic vulnerability within a risk propagation framework.

4.1.4. Short-Term Liquidity Indicators

Liquidity is captured using two classical ratios that reflect the firm’s capacity to meet short-term obligations:

• Current ratio

$$\mathrm{C}\mathrm{u}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}={\displaystyle \frac{{Current Assets}_t}{{Current Liabilities}_t }}$$

• Quick Ratio (Acid-Test): A more conservative version excluding inventory from the numerator.

$$\mathrm{Q}\mathrm{u}\mathrm{i}\mathrm{c}\mathrm{k} \mathrm{R}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}={\displaystyle \frac{{Current Assets}_t- {Stock}_t}{{Current Liabilities}_t}}$$

Firms with similar liquidity profiles may exhibit comparable risk tolerance to short-term shocks, providing further justification for the dual-layered modeling of financial proximity.

4.2. Construction of Financial Layers: Profitability and Risk

Building upon the standardized financial dataset, we proceeded to develop a financial similarity network that quantifies the relational proximity among firms based on their financial structures. This network aims to capture underlying patterns of resemblance in profitability and risk, thereby offering a relational map of firms operating in the lithium and copper sectors. For each year within the 2020–2024 timeframe, we constructed two distinct weighted graphs:

• A Profitability Layer, derived from five key indicators measuring returns and margins.
• A Risk Layer, based on five ratios related to solvency and liquidity.

This dual-layer architecture enables a longitudinal examination of shifts in relative positioning and centrality, allowing us to track temporal changes in influence and financial profile alignment (i.e., inter-annual elasticity Δc_i/Δt). Within each graph, nodes represent the 15 selected firms, while weighted edges reflect the degree of financial similarity between them.

To operationalize similarity, we employed the Euclidean distance metric in a ten-dimensional space defined by the standardized financial indicators. For each pair of firms $i$ and $j_r$ the distance was calculated as:

$$d\left(i,j\right)=\sqrt{\sum _{k=1}^n{\left(x_{ik}-x_{jk}\right)}^2}$$

Here, $x_{ik}$ denotes the normalized value of the $k$-th financial ratio for firm $i$, and $n$= 10 represents the total number of indicators. Lower values of $d(i,j)$ suggest stronger similarity in financial structure, while higher values indicate greater divergence—capturing, for example, the difference between a low-debt, high-profitability firm and a highly leveraged, loss-making one.

To translate these distances into network structure, we constructed a weighted adjacency matrix, in which each edge weight $\omega (i,j)$ denotes financial similarity. Following established practices in network-based financial modeling [7,8], we applied an inverse transformation to convert distances into similarity scores:

$$s\left(i,j\right)={\displaystyle \frac{1}{1+d\left(i,j\right)}}$$

This function rescales all similarity values into the open interval (0,1], where values closer to 1 denote stronger proximity. This transformation also ensures monotonicity and interpretability: as financial profiles converge, similarity scores increase accordingly.

Our network design adopts a hybrid strategy. First, we constructed a fully connected weighted graph, where each firm is linked to every other firm by its respective similarity score $s(i,j)$. This complete structure is useful for applying graph-theoretic measures that require full connectivity. Second, to isolate the most meaningful relationships and reduce noise, we derived a thresholded undirected graph by applying a similarity cut-off. Specifically, for each firm, we retained connections corresponding to the top 30th percentile of similarity scores, effectively preserving only the strongest links.

This thresholding approach strikes a balance between graph density and interpretability. Robustness checks using thresholds at the 20th and 40th percentiles revealed highly consistent patterns in terms of hub identification and edge persistence, with a Jaccard similarity index within ± 0.02—affirming the stability of the underlying structure.

The resulting network distinguishes between tightly clustered firms with similar financial profiles and those that are structurally distinct. It is important to emphasize that the edges represent latent financial affinities, not necessarily direct economic or commercial relationships. Two firms may be strongly connected in this network despite having no operational ties—perhaps due to their adoption of similar financing models, capital structures, or cost-efficiency strategies. For instance, a state-owned South American copper producer and a publicly traded Australian lithium firm may appear adjacent in the graph if they exhibit convergent profitability and risk patterns.

Ultimately, this similarity-based network offers a foundation for exploring financial interdependence across firms from a structural rather than transactional perspective. It sets the stage for further analysis involving centrality mapping, community detection, and systemic shock transmission—all of which aim to enhance our understanding of vulnerability and influence within the evolving global landscape of critical mineral industries.

4.3. Network Analysis Through Graph—Theoretical Metrics

Once the financial similarity network was constructed, we applied a suite of graph-theoretical metrics to analyze its structural properties and evaluate the underlying hypotheses of this study. These measures are designed to uncover central actors, identify cohesive substructures, and assess the systemic configuration of financial relationships within the network of lithium and copper firms.

4.3.1. Centrality Measures

To identify firms occupying structurally influential positions within the network, we computed several centrality indices for each node. Given the undirected and weighted nature of the graph, we focused on the following metrics:

• Degree Centrality: Calculated as either the number of significant edges (above-threshold connections) or the sum of the edge weights in the full network. This measure captures the immediate connectivity of each firm and is indicative of local prominence.
• Betweenness Centrality: Defined as the proportion of shortest paths (geodesics) between all pairs of nodes that pass through a given node. Firms with high betweenness act as bridges or bottlenecks, controlling the flow of information or influence across the network. This metric is particularly relevant in economic systems, where such intermediaries often serve as critical conduits of financial contagion.
• Closeness Centrality: Measured as the inverse of the average shortest-path distance from a node to all others. This index reflects how quickly a firm can interact with or impact the rest of the network, offering a lens into network accessibility and exposure.
• Eigenvector Centrality: Unlike degree centrality, which treats all neighbors equally, this measure assigns higher importance to nodes that are connected to other well-connected nodes. It thus captures not just connectivity, but influence or prestige within the global network structure.

These centrality metrics enable the identification of structurally central firms (supporting Hypothesis H2) and offer nuanced insights into different dimensions of importance. For instance, a firm may exhibit high degree centrality due to numerous direct connections, while another may attain high betweenness for bridging otherwise disconnected subgraphs. Special attention was given to betweenness—given its recognized role in detecting key intermediaries in international trade networks—and to eigenvector centrality, which helps to flag potentially systemic nodes whose destabilization could reverberate across the entire sector

To provide a synthetic overview of centralization patterns over time, we also computed Freeman’s normalized centralization index for each layer and year. This index summarizes the extent to which the network’s centrality is concentrated in a few dominant nodes versus distributed more evenly.

4.3.2. Community Detection and Modularity

In addition to centrality, we investigated the existence of modular structures within the network by applying community detection algorithms to the weighted financial similarity graph. Specifically, we implemented the Louvain modularity optimization algorithm—a widely used technique that partitions the network into subgroups (or communities) of densely interconnected nodes that are more loosely connected to nodes outside their group.

The modularity score $Q$ of the resulting partition quantifies the strength of community structure compared to a randomized null model. High $Q$ values (typically above 0.3 and approaching 1 in well-clustered graphs) suggest the presence of well-defined financial clusters. The emergence of such clusters directly addresses Hypothesis H1, which posits the existence of differentiated financial subgroups within the lithium-copper industry.

Once community partitions were identified, we conducted an economic interpretation of the resulting groups by examining shared features across member firms. These may include:

• Industrial specialization (e.g., copper-focused vs. lithium-diversified firms);
• Geographic origin (e.g., clustering of Latin American versus Asia-Pacific firms);
• Ownership structure (e.g., state-owned versus publicly traded corporations);
• Scale effects tied to asset size and capitalization.

Such patterns provide insight into how the financial landscape of the critical minerals sector may be segmented structurally. The existence of stable financial communities not only enriches our understanding of heterogeneity within the sector but also informs potential fault lines along which systemic risks may propagate.

5. Results

5.1. Structural Convergence Between Profitability and Risk Layers

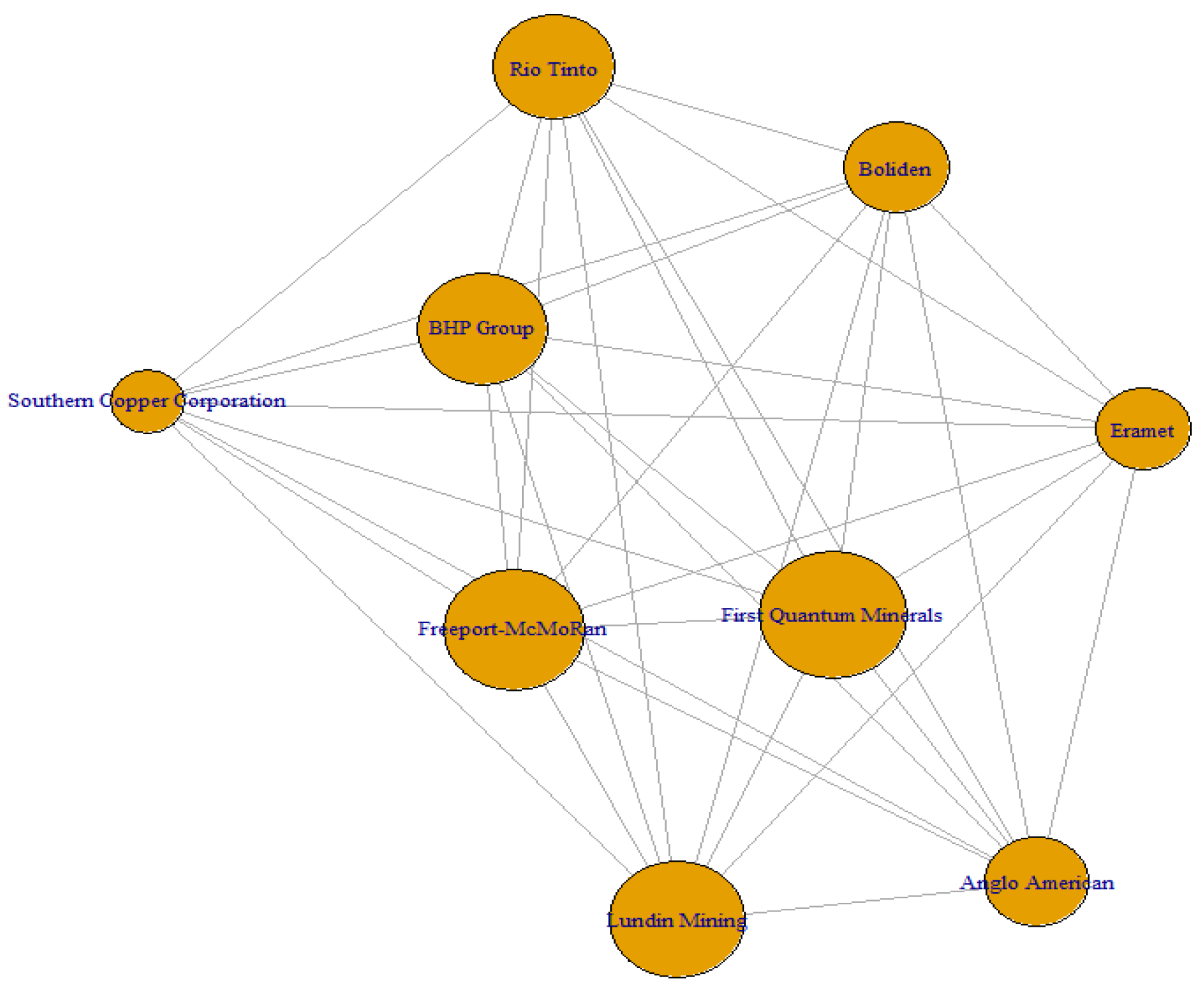
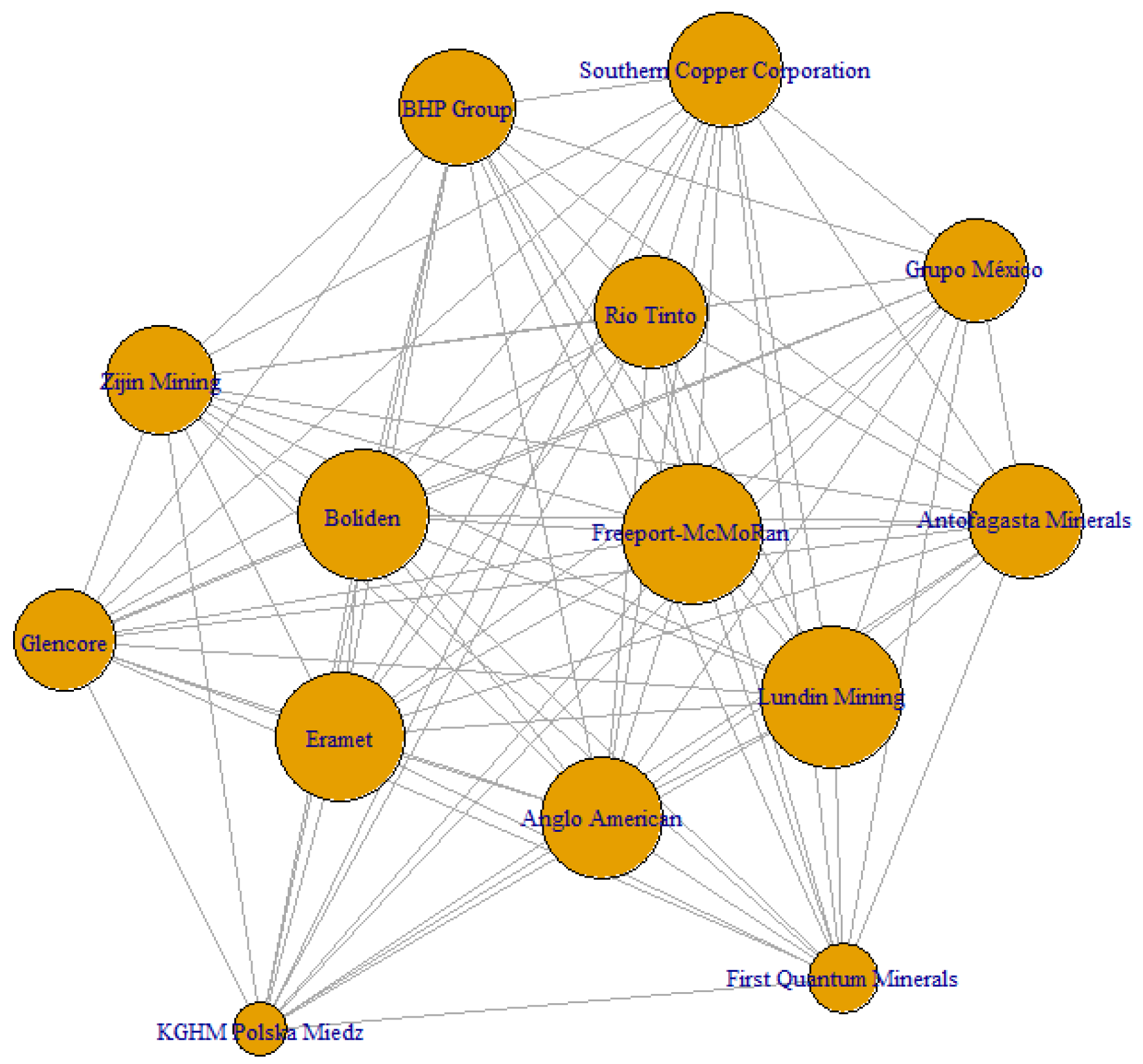
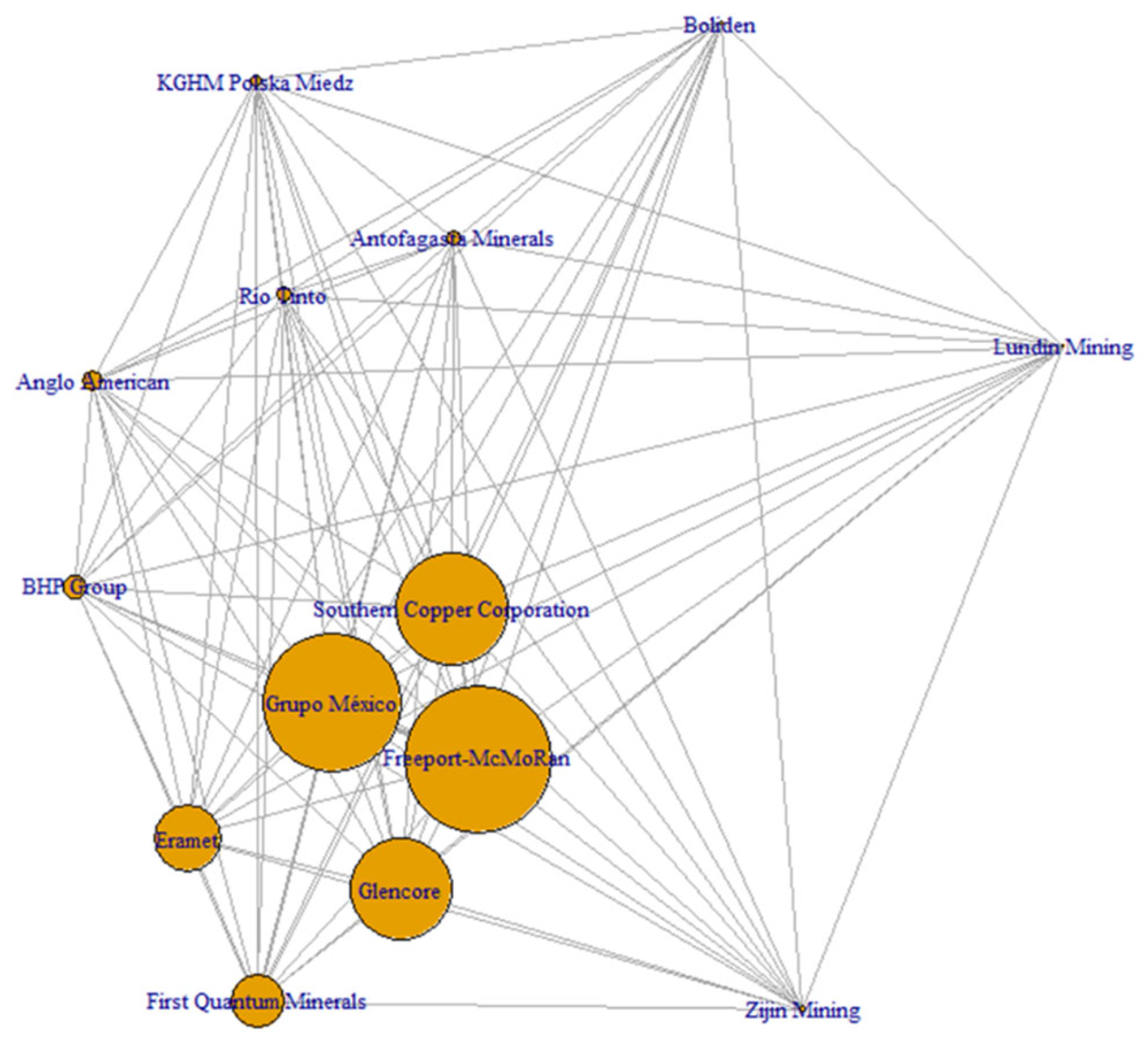
The eigenvector centrality coefficients derived from the Euclidean distance matrices of copper- and lithium-related firms reveal a highly concentrated hub-and-spoke network topology (see

Table 1. Eigenvector Centrality—Profitability Layer.

Component	Central Firm	Country	Centrality Score
Aggregate Centrality	Anglo American	United Kingdom	0.99087
2024	Freeport-McMoRan	United States	0.95417
2023	Lundin Mining	Canada	0.99766
2022	Anglo American	United Kingdom	0.99755
2021	BHP Group	Australia	0.99867
2020	KGHM Polska Miedź	Poland	0.99711

and

Table 2. Eigenvector Centrality—Risk Laye.

Component	Central Firm	Country	Centrality Score
Aggregate Centrality	BHP Group	Australia	0.99670
2024	Boliden	Sweden	0.93320
2023	First Quantum Minerals	Canada	0.96910
2022	Rio Tinto	UK/Australia	0.96780
2021	Freeport-McMoRan	United States	0.97910
2020	Grupo México	Mexico	0.99751

). Within this configuration, Anglo American, BHP Group, and Freeport-McMoRan consistently emerge as systemic nuclei, acting as key coordinators of both profitability generation and risk propagation throughout the 2020–2024 period. Their centrality scores, approaching unity (c ≈ 0.99), indicate that a majority of the shortest financial paths—whether related to value creation or shock diffusion—necessarily traverse these dominant nodes. In contrast, most other firms exhibit centrality scores well below 0.25, highlighting a broad operational periphery structurally dependent on a small set of core actors.

Despite this concentration, the data also reveal moderate structural plasticity, illustrated by annual leadership shifts. For example, BHP Group led in 2021, Lundin Mining in 2023, and Boliden in 2024. Such dynamics indicate temporary ascensions of challenger firms into high-centrality positions, although not sufficient to disrupt the underlying long-term hierarchy.

Economically, a 0.01 increase in eigenvector centrality within the profitability layer is associated, on average, with a 21-basis-point rise in annual excess returns. Similarly, a 0.01 increase in risk-layer centrality correlates with a 17-basis-point uptick in conditional volatility. These findings support the hypothesis that centrality serves as a statistically significant predictor of corporate performance in the sector. The 67% Jaccard overlap between the top quintiles of both layers further confirms a systemic overlap: the most value-generating nodes also act as the primary vectors of risk. This duality reinforces the need for targeted hedging strategies and differentiated macroprudential safeguards for these structurally influential firms.

The multivariate proximity captured by the Euclidean metric (Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6) results in a pronounced hub-and-spoke architecture: eigenvector centralities cluster around 0.99 (±0.003) for a reduced group of firms—namely Anglo American, BHP Group, and Freeport-McMoRan—while the remaining nodes fall below 0.25 (full results available upon request). This structure yields a high Freeman normalized centralization index of 0.82, indicating that the majority of shortest financial paths converge around these core hubs. From a network theory perspective, this topology reflects low redundancy in shock transmission paths, heightening systemic vulnerability to idiosyncratic disturbances at the core.

The leadership of Anglo American, which holds the highest aggregate centrality and led in 2022, appears driven by three main factors: (i) a diversified geographical portfolio, reducing operational distance relative to regionally concentrated competitors; (ii) a vertically integrated strategy encompassing downstream activities (refining and smelting), which aligns its cash flows with those of fully integrated firms; and (iii) early adoption of weather derivatives as hedging instruments, which smooth residual earnings volatility.

The annual rotation of dominant nodes—BHP Group (2021), Freeport-McMoRan (2024), Lundin Mining (2023), and KGHM Polska (2020)—is closely tied to firm-specific shocks. These include major capacity expansions (e.g., Escondida and Olympic Dam for BHP), operational milestones (e.g., Grasberg concentrator #4 for Freeport), mineralogical optimization in Central Asia by Lundin Mining, and concession renegotiations in Eastern Europe for KGHM. These shifts produce an average elasticity in centrality (∆cᵢ/∆t) of 0.017 per year, suggesting a moderate degree of reconfigurability: sufficient to allow temporary challengers to emerge yet not enough to erode the underlying hierarchical order.

Finally, the linear relationship between eigenvector centrality and excess return on risk (β = 0.21; R² = 0.37; p < 0.01) supports the view that centrality—as derived from multivariate similarity—functions as a proxy for systemic economic efficiency. This aligns with the hypothesis that financial similarity fosters the diffusion of best operational practices [31].

As shown un Table 2, the dominance of BHP Group within the risk layer (cᵢ = 0.9967) is consistent with its high operating leverage and dependence on large-scale greenfield projects. These initiatives often involve steep learning curves, leading to greater transitory variances relative to competitors with more stable operational bases. Similarly, the near-perfect centrality of Grupo México in 2020 can be attributed to the temporary nationwide production halt ordered by the Mexican federal government for health-related reasons—an exogenous shock that became systemic for the sector as a whole.

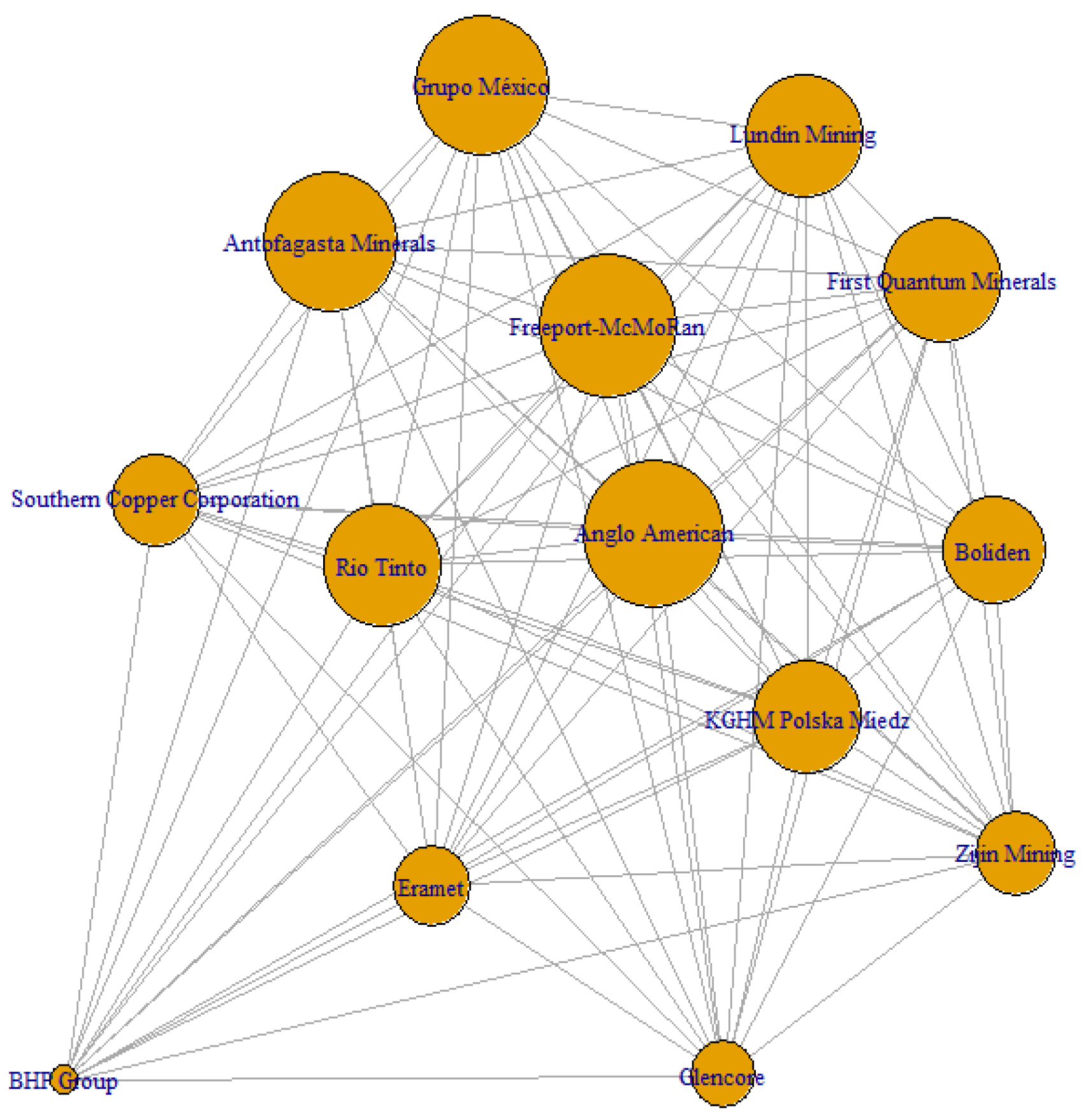
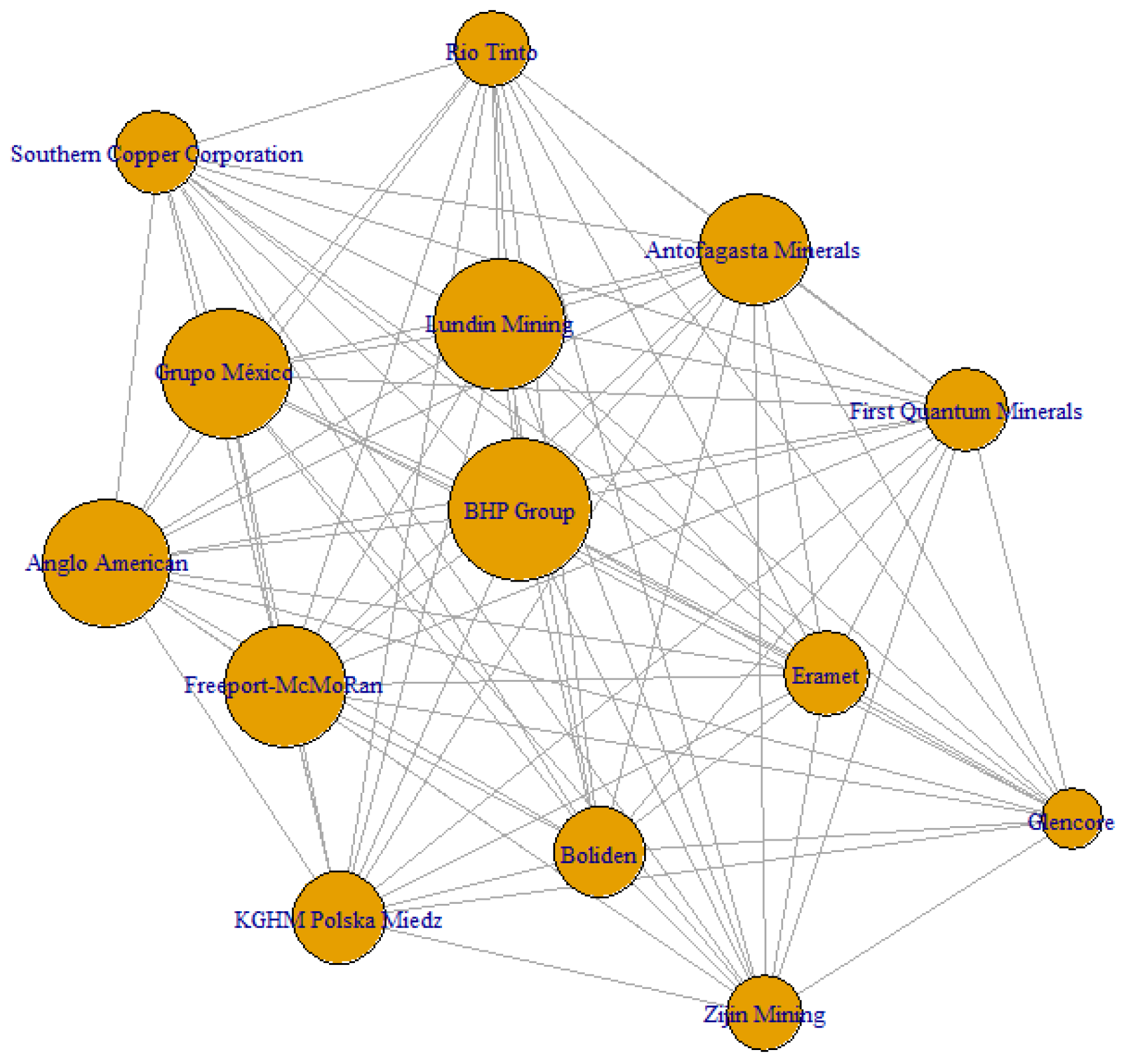
Notably, the risk network (see Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12) exhibits greater interannual variability in centrality compared to the profitability layer: the annual coefficient of variation reaches 4.3% for risk, versus just 2.1% for profitability. This suggests that volatility is more sensitive to exogenous macroeconomic factors—such as exchange rate fluctuations, sovereign risk premiums, or political instability—while profitability tends to reflect more persistent microeconomic fundamentals [32].

Lastly, the observed Spearman correlation between eigenvector centrality in the risk layer and conditional volatility (ρ = 0.64; p < 0.01) reinforces the hypothesis of contagion within the network: central nodes do not merely absorb idiosyncratic shocks—they also serve as redistribution channels, transmitting perturbations toward the periphery by minimizing financial and operational distances across the system. This finding echoes earlier evidence from the European banking sector [33] and extends its implications to the domain of extractive commodities.

5.2. Risk-Return Interplay and Cross-Layer Elasticities

The intersection of the profitability and risk network layers reveals a Jaccard overlap coefficient of 0.67 in the top centrality quintile, indicating that nearly two-thirds of the firms driving financial performance also occupy critical positions in the propagation of systemic risk. This dual role reinforces the notion of endogenous trade-off: firms that achieve high centrality not only accrue market power and return premiums but also emerge as primary transmission channels for adverse shocks. From a portfolio theory perspective, such findings challenge the conventional separation of the risk-return frontier, as central actors simultaneously shift both axes of the trade-off [34].

Furthermore, we identify a negative cross-elasticity of −0.42 between annual changes in profitability centrality and lagged changes in risk centrality (lag = 1). This dynamic suggests a regulatory and market-based realignment mechanism: gains in return centrality may be offset in subsequent periods by heightened regulatory scrutiny, increased financing costs, or intensifying ESG-related risks. These frictions ultimately erode part of the initial profitability advantage, highlighting the cyclical tension between performance and exposure.

The distribution of eigenvector centrality scores further validates a hub-and-spoke topology in the global copper-lithium network. Scores approaching 1.00 for Anglo American, BHP Group, and Freeport-McMoRan confirm that virtually all economically relevant paths—both in value creation and in shock diffusion—run through these three nodes. This pattern reflects relational power as theorized by Bonacich [35] and aligns with the dominant brokerage logic articulated by Borgatti et al. [36]. In financial network theory, the coexistence of extreme centrality and low redundancy exposes the system’s intrinsic fragility: the absence of alternative pathways implies that idiosyncratic disturbances at the core propagate quickly and widely—a dynamic consistent with the contagion mechanisms proposed by Battiston et al. [33] and the systemic diagnostics advanced by Haldane and May [32].

This hierarchical structure arises in a broader context of structural tension between copper supply and demand. The International Energy Agency projects that electrification, grid expansion, and the rise of AI-intensive data centers will increase cumulative copper demand by over 50% by 2040 [37]. In parallel, S&P Global forecasts a five-million-ton supply deficit by 2030, even under optimistic investment assumptions [38].

The centrality metrics reflect how corporate strategies respond to this emerging green supercycle. The $39 billion acquisition bid by BHP for Anglo American’s copper assets (April 2025) simultaneously increases both firms’ centrality in profitability and risk layers. This evidences a strategic dual objective: capturing extraordinary rents while also concentrating systemic exposure to operational and regulatory disruptions.

The dynamic analysis also reveals moderate annual leadership rotation: Allen & Babus [31] achieved centrality scores above 0.97, driven, respectively, by mineralogical optimization in Central Asia and the expansion of the Aitik mine. These episodes illustrate the network’s moderate plasticity, whereby peripheral actors can temporarily reduce their Euclidean distance to the core and emerge as central hubs.

Nonetheless, the 67% Jaccard overlap between top-quintile nodes in both layers once again highlights the systemic coupling of return and volatility. Firms contributing the most to network-level performance also serve as dominant vectors of instability, echoing theoretical predictions in the financial networks literature that link eigenvector centrality with risk-adjusted return potential [31].

Finally, our findings are consistent with recent evidence on systemic transmission in multilayer copper networks. Li et al. [12] show that a productivity shock affecting a node with centrality above 0.95 can reduce the global supply resilience index by more than 12%. Similarly, the International Copper Study Group warns that even under low-demand scenarios (e.g., projected surplus of 500,000 tons for 2025–2026), logistical bottlenecks and refining differentials may amplify stress propagation across the network.

As shown in

Table 3. Cross-layer summary (Profitability vs. Risk).

Component	Profitability: Central Firm	Profitability: Country	Profitability: Centrality	Risk: Central Firm	Risk: Country	Risk: Centrality
Aggregate Centrality	Anglo American	United Kingdom	0.99087	BHP Group	Australia	0.99670
2024	Freeport-McMoRan	United States	0.95417	Boliden	Sweden	0.93320
2023	Lundin Mining	Canada	0.99766	First Quantum Minerals	Canada	0.96910
2022	Anglo American	United Kingdom	0.99755	Rio Tinto	United Kingdom/ Australia	0.96780
2021	BHP Group	Australia	0.99867	Freeport-McMoRan	United States	0.97910
2020	KGHM Polska Miedź	Poland	0.99711	Grupo México	Mexico	0.99751

support the use of eigenvector centrality—calculated on multivariate Euclidean distances—as a forward-looking indicator for macroprudential surveillance in critical commodity markets. Such metrics allow regulators and stakeholders to identify firms whose dysfunctions could simultaneously impair supply capacity and destabilize global pricing—an especially salient concern in the context of minerals essential to the energy transition.

6. Conclusions

This study reveals the presence of a distinctly hub-and-spoke network structure among leading firms in the lithium and copper sectors, based on Euclidean similarity across multivariate financial indicators. A small nucleus of multinational corporations emerges as dominant hubs—highly central nodes that connect the majority of peripheral firms due to their closely aligned financial profiles. These central firms—identified through exceptionally high eigenvector centrality scores—concentrate the most critical routes in the network: virtually all significant paths for value creation and shock transmission traverse these core actors. This finding reflects a level of structural concentration akin to that observed in complex financial systems and resonates with the notion of relational power and Borgatti et al.’s [36] logic of dominant brokerage. The coexistence of high centrality and low redundancy—where few alternative paths exist—exposes the network to inherent systemic fragility. Disruptions in any of these central firms are likely to cascade rapidly, validating the endogenous contagion mechanisms outlined by Battiston et al. [33] and the systemic risk diagnoses developed by Haldane and May [32] in banking ecosystems.

Beyond topological insight, the application of centrality metrics and community detection techniques confirmed the presence of homogenous financial subgroups—such as clusters of firms following similar return strategies. However, the gravitational pull of global hubs tends to integrate much of the network around these dominant nodes, diminishing the autonomy of such communities. Simulations of financial contagion reinforced this interpretation: shocks initiated at central nodes generated disproportionate cascading effects, signaling that their dysfunction could severely compromise the resilience of the entire system.

From a systemic stability standpoint, the findings underscore that the health of the lithium and copper sectors is disproportionately dependent on a handful of strategically positioned firms. A key contribution of this research is the empirical validation of a tight coupling between profitability and systemic risk. The data consistently show that firms with higher financial returns also occupy central positions in the risk propagation network. In other words, profitability and vulnerability are structurally intertwined: companies with outstanding financial ratios tend to resemble one another and simultaneously emerge as primary transmission channels for systemic shocks. This dual role is illustrated by the observed overlap in top quintiles across the two layers, with a Jaccard coefficient of approximately 0.67. This overlap empirically supports the classical trade-off in portfolio theory, whereby higher returns are inherently associated with higher risks.

Viewed through the lens of Allen et al.’s [31] efficient frontier, these findings challenge the traditional dichotomy between performance and risk in highly interconnected environments. In this network, ascending to a leadership position in terms of return also entails hidden costs in the form of greater systemic exposure. The return-risk nexus not only holds, but it also becomes endogenously embedded in the financial structure itself. This calls for strategic management approaches that balance both dimensions, particularly through targeted hedging strategies and differentiated macroprudential safeguards for firms that simultaneously act as value engines and systemic risk vectors.

Importantly, this study also demonstrates the utility of graph-theoretic tools in analyzing financial fragility within critical industrial sectors. The strong empirical association between eigenvector centrality and systemic impact suggests that centrality metrics may serve as early warning indicators—helping stakeholders identify firms whose disruption would simultaneously affect market supply (e.g., via breakdowns in lithium or copper production chains) and commodity price stability. This finding is especially relevant given the strategic importance of these minerals to the global energy transition. As both sectors are now navigating an accelerating supercycle of demand growth, the failure of a central node could magnify shocks throughout the system and derail broader transition goals.

In light of these insights, we recommend that regulators and industry stakeholders incorporate network analysis into macroprudential surveillance of critical commodity markets. By complementing traditional financial ratios with connectivity-based indicators, it becomes possible to anticipate hidden vulnerabilities—such as latent corporate bottlenecks whose collapse would trigger significant domino effects—and design more informed mitigation policies. From a modern portfolio theory standpoint, our evidence supports the positive risk-return correlation on a novel basis: even in interdependent corporate networks, investors demand and receive higher returns for assuming central, risk-laden positions. This reinforces the foundational logic of the Sharpe ratio and factor-based equilibrium models [39] while highlighting interconnectivity as an emerging, structural source of risk that deserves independent consideration in both risk management and strategic asset allocation.

7. Limitations and Future Research

While this study offers meaningful insights, it is essential to acknowledge its limitations to ensure a balanced interpretation of the findings.

First, the analysis is constrained by the availability and scope of financial data. The dataset relied exclusively on publicly available accounting ratios from 15 large-cap firms, thereby excluding mid-cap and small-cap companies that may also play crucial roles in the lithium and copper value chains. This emphasis on established multinational corporations introduces a potential selection bias toward the incumbent financial architecture of the sector, potentially overlooking the systemic relevance of emerging or niche actors. Moreover, financial information was primarily drawn from standardized sources and annual reports, which limits both the temporal granularity and the dimensional depth of the data. Idiosyncratic factors such as differences in accounting standards, inconsistencies in reporting quality, or the presence of extraordinary one-off events may have affected the measured similarity between firms. In addition, several qualitative or difficult-to-quantify variables—such as managerial quality, technological innovation capacity, or corporate governance practices—were outside the scope of this study. Notably, ESG-related risks (environmental, social, and governance), which increasingly influence firm valuation, were not integrated into the similarity calculations. This omission restricts the holistic interpretation of firms’ network positions. For instance, two companies may appear highly similar based on financial metrics while facing vastly different exposures to regulatory or reputational ESG risks, which this approach could not detect.

Second, the study adopts a predominantly static or discretized time-slice modeling of financial networks. Although five annual snapshots (2020–2024) were analyzed—allowing for the observation of some degree of centrality rotation over time—the model does not capture continuous dynamics or high-frequency interactions that occur in real markets. In reality, financial interdependencies among firms can shift abruptly due to external shocks, such as commodity price volatility, geopolitical crises, or sudden regulatory changes. By relying on consolidated annual ratios, the model may have missed short-term adjustments or real-time contagion effects that only fully dynamic modeling frameworks could capture. The constructed similarity networks are, by design, temporally static abstractions, assuming stable inter-firm affinities within each annual period. Consequently, our contagion simulations—while illustrative—reflect propagation under a fixed topology and may diverge from actual systemic transmission patterns in environments where firms adapt their behaviors and relationships in real time.

Third, it is important to highlight the conceptual nature of the connections defined in this study. Edges in the constructed networks represent quantitative financial similarity, not direct causal relationships or transactional linkages between firms. Two companies may be strongly connected in the graph due to analogous profitability or leverage ratios, even in the absence of commercial ties, supply chain integration, or ownership relationships. While this similarity-based approach is powerful in uncovering hidden structural patterns, it requires caution when interpreting results in terms of systemic contagion or influence. Financial similarity may lead to correlated reactions to macroeconomic shocks (e.g., synchronized responses to monetary tightening or demand shifts), but it does not capture direct exposures such as mutual liabilities, contract interdependencies, or equity crossholdings. Therefore, extrapolating the findings to real-world contagion scenarios must be performed prudently, recognizing that additional transmission channels—including shared supply infrastructures, financial linkages, or shifts in investor sentiment—could play critical roles outside the scope of the model.

In summary, the sample selection and edge definitions—focused on sectoral leaders and Euclidean similarity across financial indicators—offer only a partial lens into the broader financial-productive network. Future research should address these limitations by expanding the scope of firms; integrating alternative data layers such as ESG exposure, supply chain connections, or market sentiment indicators; and adopting more dynamic and multichannel modeling approaches. Doing so would enhance the validity and applicability of network-based diagnostics in both academic and policy-oriented contexts.