An Algebraic Proof of the Nishimura Theorem

Abstract

An algebraic proof of the Nishimura theorem on one-generated Heyting algebras is presented.

1. Introduction

In [1], Nishimura introduced the following formulas:

$$\begin{array}{cc}\hfill & p_{\infty }\left(x\right)=x\to x,p_0\left(x\right)=x\wedge \neg x,p_1\left(x\right)=x,p_2\left(x\right)=\neg x,\hfill \\ \hfill & p_{2n+3}\left(x\right)=p_{2n+1}\left(x\right)\vee p_{2n+2}\left(x\right),p_{2n+4}\left(x\right)=p_{2n+3}\left(x\right)\to p_{2n+1}\left(x\right)\hfill \end{array}$$

and he proved Theorem 1, which describes all (up to equivalence in intuitionistic propositional calculus ($\mathsf{IPC}$)) formulas for one variable.

Theorem 1 

(Theorems I, II [1]). The following holds:

(a) 

For any distinct $n,m\in [0,\infty ]$, the formulas $p_n\left(x\right)$ and $p_m\left(x\right)$ are not equivalent in $\mathsf{IPC}$;

(b) 

Any formula for one variable is equivalent in $\mathsf{IPC}$ to the formula $p_n\left(x\right)$ for some $n\in [0,\infty ]$.

Almost all known proofs of this theorem (see, e.g., Chapter 6, pp. 108–120, [2]) are syntactic and tedious. The only semantic proof (that we know of) was given in [3] and based on the techniques developed in [4].

In algebraic terms, the Nishimura theorem states the following.

Theorem 2. 

The following holds:

(a) 

For any distinct $n,m\in [0,\infty ]$, $\mathit{H}\mathit{A}⊭p_n\left(x\right)\approx p_m\left(x\right)$;

(b) 

For any term $s\left(x\right)$, there is $n\in [0,\infty ]$ such that $\mathit{H}\mathit{A}\models s\left(x\right)\approx p_n\left(x\right)$.

In this paper, we give an algebraic proof of the Nishimura theorem based on the well-known properties of Heyting algebras for a slightly different sequence of formulas (treated as terms) for one variable, as introduced in [5]:

$$\begin{array}{cc}\hfill & x^{\infty }=x\to x,x^0=x\wedge \neg x,x^1=\neg x,x^2=x,\hfill \\ \hfill & x^{2n+3}=x^{2n+1}\to x^{2n},x^{2n+4}=x^{2n+1}\vee x^{2n+2}.\hfill \end{array}$$

Specifically, we prove the following theorem.

Theorem 3. 

The following holds:

(a) 

For any distinct $n,m\in [0,\infty ]$, $\mathit{H}\mathit{A}⊭x^n\approx x^m$;

(b) 

For any term $s\left(x\right)$, there is $n\in [0,\infty ]$ such that $\mathit{H}\mathit{A}\models s\left(x\right)\approx x^n$.

In Section 2, we give the necessary definitions and recall some facts about Heyting algebras, and in Section 3, Section 4, Section 5 and Section 6, we prove Theorem 3 in the following way:

(1)

In Section 3, we show that for each $n\ge 2$, there exists a one-generated Heyting algebra of cardinality n, and for each $n\ge 2$, we construct such an algebra.

(2)

In Section 4, we show that any one-generated finite Heyting algebra of cardinality n is isomorphic to ${\mathbf{Z}}_n$ (Theorem 6).

(3)

In Section 5, we show that for any term $s\left(x\right)$ on one variable with $\mathit{H}\mathit{A}⊭s\left(x\right)\approx \mathbf{1}$, the relation $s\left(x\right)=\mathbf{1}$ defines a finite algebra (Theorem 7).

(4)

In Section 6, we show that for each $n\ge 2$, the relation $x^n=\mathbf{1}$ defines ${\mathbf{Z}}_n$ (Theorem 8).

Let us recall that for any two terms $t\left(x\right)$ and $s\left(x\right)$, the relations $t\left(x\right)=\mathbf{1}$ and $s\left(x\right)=\mathbf{1}$ define isomorphic algebras if and only if $\mathit{H}\mathit{A}\models t\left(x\right)\approx s\left(x\right)$. Thus, (1) and (4) clearly entail Theorem 3(a), and (2), (3), and (4) entail Theorem 3(b). Indeed, if $s\left(x\right)$ is such that $\mathit{H}\mathit{A}\models s\left(x\right)\approx \mathbf{1}$, then $\mathit{H}\mathit{A}\models s\left(x\right)\approx x^{\infty }$. If $\mathit{H}\mathit{A}⊭s\left(x\right)\approx \mathbf{1}$, by (3), the relation $s\left(x\right)=\mathbf{1}$ defines a finite algebra $\mathbf{A}$; by (2), $\mathbf{A}\cong {\mathbf{Z}}_n$ for some $n\ge 2$; and by (4), the relation $x^n=\mathbf{1}$ defines ${\mathbf{Z}}_n$, and hence, $\mathit{H}\mathit{A}\models s\left(x\right)\approx x^n$.

Let us observe that (3) and (4) show that (as noted in [5]) the properties of one-generated Heyting algebras are similar to those of cyclic groups: for every $n>0$, each cyclic group of cardinality n is isomorphic to ${\mathbf{Z}}_n$ and is defined by the relation $nx\approx 0$.

In addition, in Section 6, we prove (Corollary 9) that every infinite one-generated Heyting algebra is free in the variety of all Heyting algebras and, consequently, in any variety or quasi-variety of Heyting algebra that contains it, which be viewed as an algebraic counterpart of Rieger’s theorem [6].

2. Preliminaries

We consider Heyting algebra in the signature $\{\wedge ,\vee ,\to ,\mathbf{0}\}$. Let us recall that every Heyting algebra has a top element denoted by $\mathbf{1}$, and we use $\neg a$ as a shortcut for $a\to \mathbf{0}$, and $a\leftrightarrow b$ as a shortcut for $(a\to b)\wedge (b\to a)$. The class of all Heyting algebras is a variety denoted by $\mathit{H}\mathit{A}$.

If a is an element of Heyting algebra $\mathbf{A}$, we use $\left[a\right)$ to denote the set $\{b\in \mathbf{A}|a\le b\}$, which is a principal filter generated by a, and $\left(a\right]$ to denote the set $\{b\in \mathbf{A}|b\le a\}$, which is a principal ideal generated by a.

Two equations $t_1\approx s_1$ and $t_2\approx s_2$ are equivalent if both quasi-equations $t_1\approx s_1\Rightarrow t_2\approx s_2$ and $t_2\approx s_2\Rightarrow t_1\approx s_1$ hold in $\mathit{H}\mathit{A}$. Note that any equation $t\approx s$ is equivalent to equation $(t\leftrightarrow s)\approx \mathbf{1}$.

2.1. Some Properties of One-Generated Heyting Algebras

First, let us recall the following properties of Heyting algebras.

Element a of Heyting algebra is regular if $\neg \neg a=a$, dense if $\neg a=\mathbf{0}$, and ordinary if it is neither regular nor dense. If $a,b$ are elements of Heyting algebra, we denote by $a\ll b$ that a is covered by b, that is, $a\le b$, and there are no elements strongly between them. Element a is an atom of algebra $\mathbf{A}$ if it covers the bottom element of $\mathbf{A}$, and it is a coatom if it is covered by the top element.

Let us recall (see, e.g., Lemmas 2.1 and 2.2, [7]) that the following hold.

Proposition 1. 

Let $\mathbf{A}$ be a Heyting algebra. Then, the following holds:

(a) 

If $\left[a\right)$ is a principal filter generated by element a, then every coset $b/\left[a\right)$ contains the largest element $a\to b$ and the smallest element $a\wedge b$;

(b) 

If $\mathsf{D}$ is a filter of all dense elements of $\mathbf{A}$, then $\mathbf{A}/\mathsf{D}$ is a Boolean algebra. Hence, if $\mathbf{A}$ is n-generated, then the cardinality of $\mathbf{A}/\mathsf{D}$ is at most $2^{2^n}$;

(c) 

For any element $a\in \mathbf{A}$, the quotient algebra $\mathbf{A}/\left[a\right)$ as a lattice is isomorphic to ideal $\left(a\right]$, and hence,

$$\begin{array}{c}\hfill |\mathbf{A}/[a\left)\right|=\left|\right(a\left]\right|;\end{array}$$

(1)

(d) 

If $\mathbf{A}$ is generated by elements $g_1,\dots ,g_n$, then element $(g_1\vee \neg g_1)\wedge \cdots \wedge (g_n\vee \neg g_n)$ is the smallest dense element.

Immediately, from Proposition 1(b), we have the following.

Corollary 1. 

If D is a filter of Heyting algebra A containing all dense elements of A, then A/D is a Boolean algebra.

Proposition 2. 

Every nontrivial Heyting algebra generated by a regular element is isomorphic to one of the algebras Z₂, Z₄, or Z₅, whose Hasse diagrams are depicted in Figure 1.

Proof. 

Suppose that nontrivial algebra $\mathbf{A}$ is generated by a regular element g. Then, it is not hard to verify that the set $\{\mathbf{0},g,\neg g,g\vee \neg g,\mathbf{1}\}$ is closed under fundamental operations. Hence, every Heyting algebra generated by a regular element is a homomorphic image of algebra ${\mathbf{Z}}_5$; that is, it is isomorphic to ${\mathbf{Z}}_5,{\mathbf{Z}}_4$, or ${\mathbf{Z}}_2$. □

Proposition 3. 

Every nontrivial Heyting algebra generated by a dense element is isomorphic to one of the algebras ${\mathbf{Z}}_2$ or ${\mathbf{Z}}_3$, Hasse diagrams of which are depicted in Figure 1.

Proof. 

Suppose that nontrivial algebra $\mathbf{A}$ is generated by a dense element g. Then, it is not hard to verify that the set $\{\mathbf{0},g,\mathbf{1}\}$ is closed under fundamental operations. Hence, every nontrivial Heyting algebra generated by a dense element is a homomorphic image of algebra ${\mathbf{Z}}_3$; that is, it is isomorphic to ${\mathbf{Z}}_2$ or ${\mathbf{Z}}_3$. □

Let us observe that the algebras ${\mathbf{Z}}_i,i\in [2,5]$, do not contain any ordinary elements. This means that algebras generated by an ordinary element cannot be generated by a single regular or dense element.

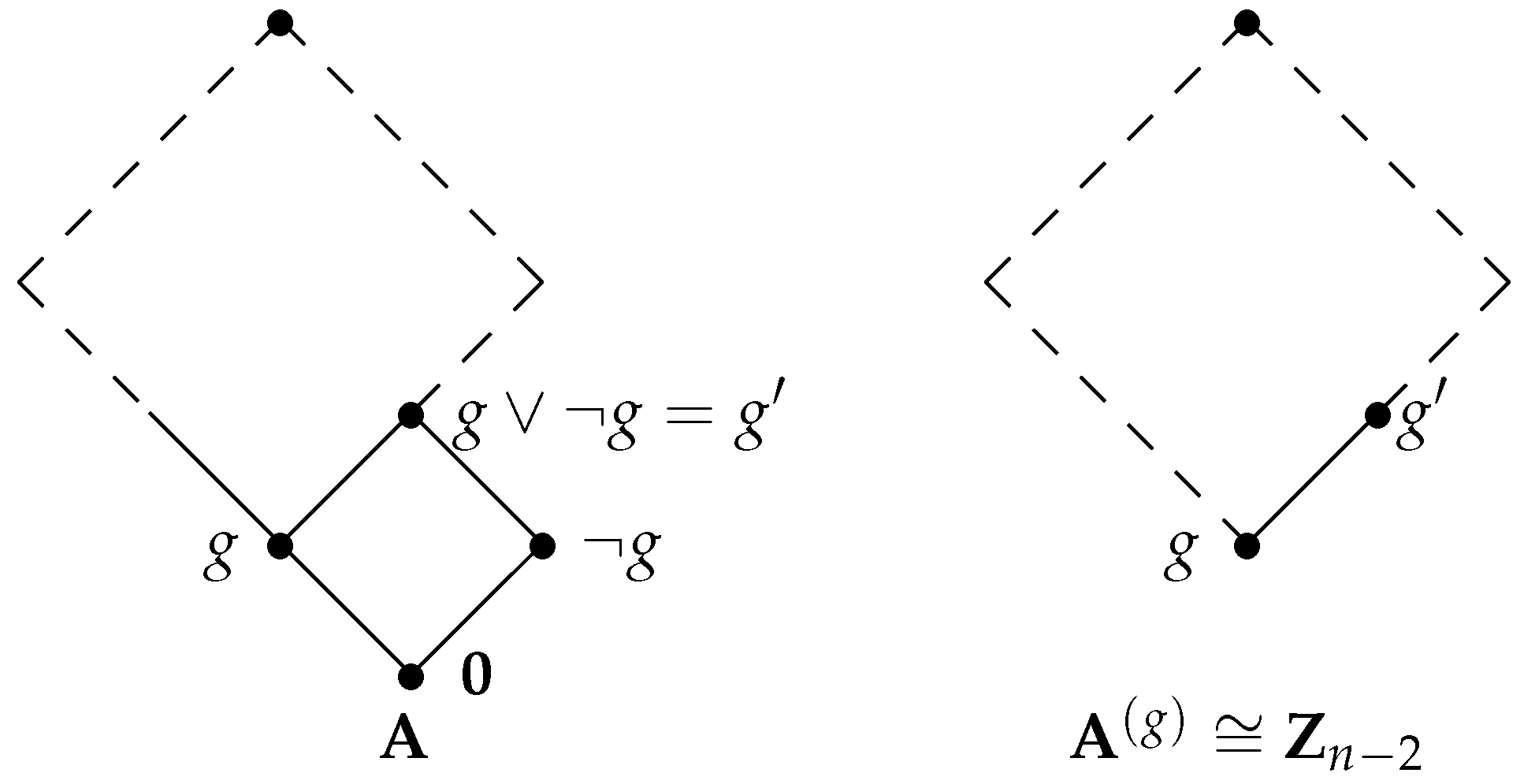
Proposition 4. 

Let $\mathbf{A}$ be a Heyting algebra generated by an ordinary element g. Then, the following holds:

(a) 

$\mathbf{A}$ has precisely two atoms: g and $\neg g$;

(b) 

Element $g\vee \neg g$ covers elements g and $\neg g$;

(c) 

$\mathbf{A}$ contains more than five elements.

Proof. 

Let $d=g\vee \neg g$. It is clear that d is a dense element, and from Proposition 1(d), d is the smallest dense element in $\mathbf{A}$. Let $\mathsf{D}\subseteq \mathbf{A}$ be a filter of all dense elements of $\mathbf{A}$. Let us consider the quotient algebra $\mathbf{A}/\mathsf{D}$. By Proposition 1(b), $\mathbf{A}/\mathsf{D}$ is a Boolean algebra. As g generates $\mathbf{A}$, coset $g/\mathsf{D}$ generates $\mathbf{A}/\mathsf{D}$; hence, the cardinality of $\mathbf{A}/\mathsf{D}$ is at most 4. Observe that $g\to \neg g=\neg g\notin \mathsf{D}$. Thus, $g/\mathsf{D}\ne \neg g/\mathsf{D}$, and therefore, $\mathbf{A}/\mathsf{D}$ contains more than two elements; that is, it contains exactly four elements: $\mathbf{0}/\mathsf{D},g/\mathsf{D},\neg g/\mathsf{D}$, and $\mathbf{1}/\mathsf{D}$.

Let us show that $\mathbf{0}/\mathsf{D}=\left\{\mathbf{0}\right\}$ and $\neg g/\mathsf{D}=\{\neg g\}$.

Indeed, $\mathbf{0}/\mathsf{D}=\left\{\mathbf{0}\right\}$ because $\mathbf{0}\wedge d=\mathbf{0}$ and $d\to \mathbf{0}=\mathbf{0}$; hence, by Proposition 1(a), $\mathbf{0}$ is the smallest and the largest element of $\mathbf{0}/\mathsf{D}$ and thus is the only element of $\mathbf{0}/\mathsf{D}$.

Similarly, $\neg g/\mathsf{D}=\{\neg g\}$ because $\neg g\wedge d=\neg g$ and $d\to \neg g=\neg g$; hence, by Proposition 1(a), $\neg g$ is the smallest and the largest element of $\neg g/\mathsf{D}$.

Observe that $g\wedge d=g$; hence, g is the smallest element of $g/\mathsf{D}$. Thus, (a) and (b) hold.

To prove (c), recall that $\mathbf{A}/\mathsf{D}=\{\mathbf{0}/\mathsf{D},g/\mathsf{D},\neg g/\mathsf{D},\mathsf{D}\}$, and we already proved that $|\mathbf{0}/\mathsf{D}|=|\neg g/\mathsf{G}|=1$. Because g is an ordinary element, $\neg \neg g\ne g$, and therefore, $|g/\mathsf{D}|>1$. Finally, $g\vee \neg g\ne \mathbf{1}$, because otherwise, $\mathbf{A}$ would be a Boolean algebra and would not contain any ordinary elements; hence, $\left|\mathsf{D}\right|>1$. Thus, $\left|\mathsf{A}\right|>5$. □

Corollary 2. 

If $\mathbf{A}$ is a Heyting algebra generated by element $g>0$, then g is an atom.

Proof. 

If g is a regular or a dense element, the statement follows from Propositions 2 and 3. If g is an ordinary element, the statement follows from Proposition 1(a). □

2.2. Some Properties of Finitely Presented Heyting Algebras

Let us recall that by (Chapter 5 §11 Theorem 4, [8]), for any term $t(x_1,\dots ,x_n)$, the relation $t=\mathbf{1}$ (as a defining relation) defines a Heyting algebra.

Definition 1. 

Let $t(x_1,\dots ,x_n)$ be a term. A Heyting algebra $\mathbf{A}$ is said to be defined by relation   $t(x_1,\dots ,x_n)=\mathbf{1}$   in generators   $g_1,\dots ,g_n\in \mathbf{A}$ if the following are true:

1. 

Elements $g_1,\dots ,g_n$ generate $\mathbf{A}$;

2. 

$t(g_1,\dots ,g_n)=\mathbf{1}$;

3. 

If $s(x_1,\dots ,x_n)$ is a term with $s(g_1,\dots ,g_n)=\mathbf{1}$, then the quasi-equation $t(x_1,\dots ,x_n)\approx \mathbf{1}\Rightarrow s(x_1,\dots ,x_n)\approx \mathbf{1}$ holds in $\mathit{H}\mathit{A}$.

Corollary 3. 

Let $\mathbf{A}$ be an algebra defined by the relation $t(x_1,\dots ,x_n)=\mathbf{1}$ in generators $g_1,\dots ,g_n$. Then, the terms $t(x_1,\dots ,x_n)$ and $s(x_1,\dots ,x_n)$ are equivalent if and only if the relation $s(x_1,\dots ,x_n)$$=\mathbf{1}$ also defines $\mathbf{A}$ in generators $g_1,\dots ,g_n$.

Because we are concerned with one-generated algebras and the generating set is apparent, we will often omit the reference to generators.

The following theorem gives one of the most commonly used properties of finitely presented algebras, that is algebras defined by relation.

Theorem 4 

(Chapter 5 §11 Theorem 1, [8]). Let $t(x_1,\dots ,x_n)$ be a term and $\mathbf{A}$ be a Heyting algebra defined by the relation $t(x_1,\dots ,x_n)=\mathbf{1}$ in generators $g_1,\dots ,g_n\in \mathbf{A}$. Then,

1. 

Elements $g_1,\dots ,g_n$ generate $\mathbf{A}$;

2. 

$t(g_1,\dots ,g_n)=\mathbf{1}$;

3. 

For every Heyting algebra $\mathbf{B}$ and elements $b_1,\dots ,b_n\in \mathbf{B}$ such that $t(b_1,\dots ,b_n)=\mathbf{1}$, there is a homomorphism $h:\mathbf{A}⟶\mathbf{B}$ with $f\left(g_i\right)=b_i,i\in [1,n]$.

Let us recall (Chapter V §11 Theorem 4, [8]) that since $\mathit{H}\mathit{A}$ is a variety, any relation defines some algebra. In particular, the following holds.

Corollary 4. 

Let $t(x_1,\dots ,t_n)$ be a term, and suppose that there is no infinite Heyting algebra $\mathbf{A}$ generated by elements $g_1,\dots ,g_n\in \mathbf{A}$ with $t(g_1,\dots ,g_n)=\mathbf{1}$. Then, algebra $\mathbf{B}$ of maximal cardinality from the class

$$\begin{array}{c}\hfill \{\mathbf{A}\in \mathit{H}\mathit{A}|\mathbf{A}\mathit{is}\mathit{generated}\mathit{by}\mathit{elements}{g}_1,\dots ,g_n,\mathit{with}t(g_1,\dots ,g_n)=\mathbf{1}\}\end{array}$$

being defined by the relation $t(x_1,\dots ,x_n)=\mathbf{1}$.

Corollary 5 

(Theorem 8, [9]). Every finitely presented Heyting algebra is a subdirect product of finite algebras.

Proof. 

Let $\mathbf{A}$ be a finitely presented algebra given by the relation $t(x_1,\dots ,t_n)=\mathbf{1}$ in generators $g_1,\dots ,g_n$. We prove that for every distinct-from-the-top element $a\in \mathbf{A}$, there is a finite homomorphic image of $\mathbf{A}$ such that the natural homomorphism sends a in the distinct-from-the-top element.

Indeed, let $a\in \mathbf{A}$ be a distinct-from-the-top element. Then, there is a term $s(x_1,\dots ,x_n)$ with $s(g_1,\dots ,g_n)=a$. Thus,

$$\begin{array}{c}\hfill t(g_1,\dots ,g_n)\to s(g_1,\dots ,g_n)\ne \mathbf{1},\end{array}$$

and hence, $\mathit{H}\mathit{A}⊭(t\to s)\approx \mathbf{1}$. Because $\mathit{H}\mathit{A}$ is generated by finite algebras, there is a finite algebra $\mathbf{B}$ and elements $b_1,\dots ,b_n$ such that $t(b_1,\dots ,b_n)=\mathbf{1}$ and $s(b_1,\dots ,b_n)\ne \mathbf{1}$. By Theorem 4, the subalgebra of $\mathbf{B}$ generated by elements $b_1,\dots ,b_n$ is a homomorphic image of $\mathbf{A}$. It should be clear that this homomorphism does not send a into the top element. □

3. Sequence of One-Generated Algebras

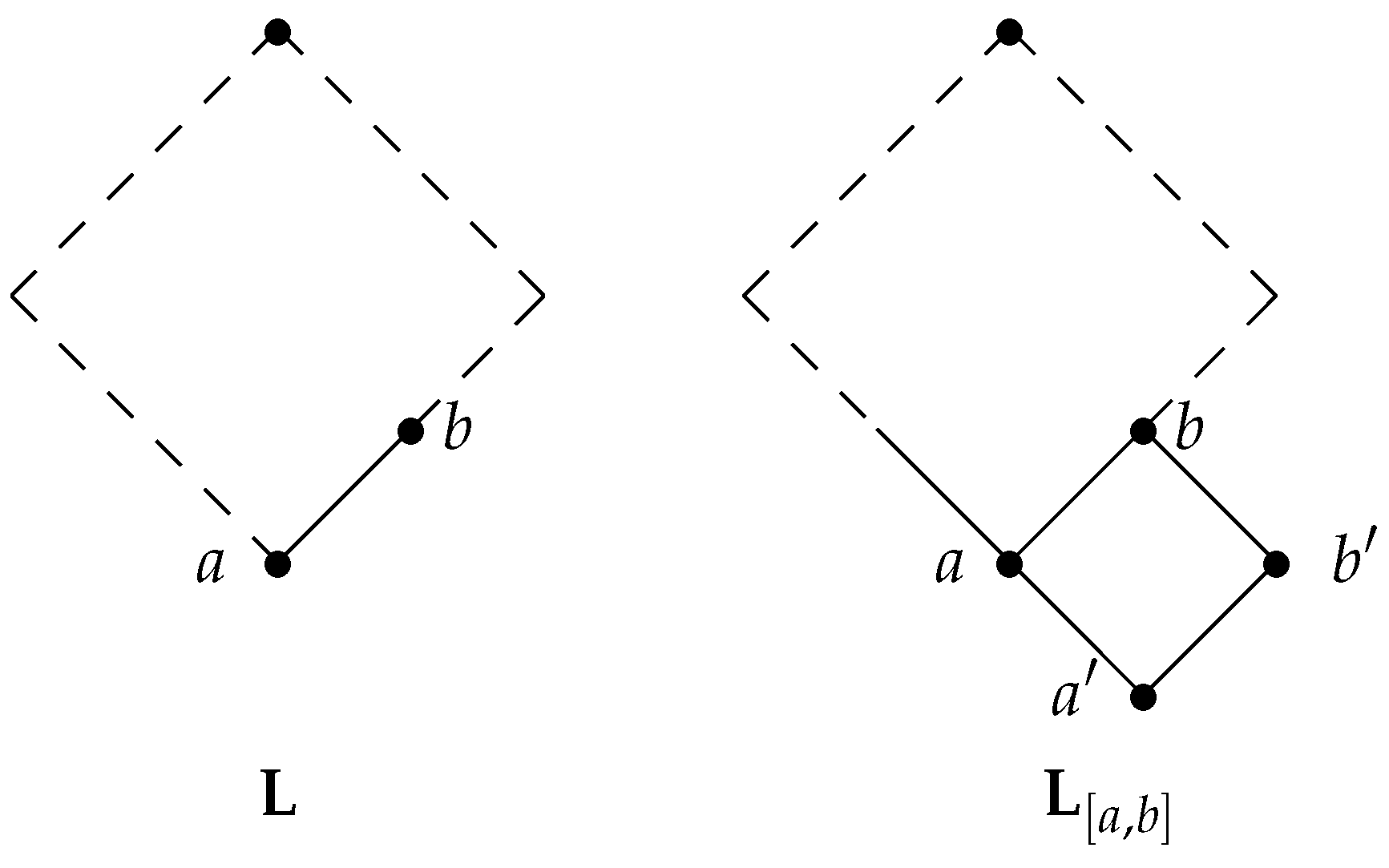
In this section, for each $n>1$, we construct one-generated Heyting algebra of cardinality n, and in the following section, using this construction, we show that such an algebra is unique up to isomorphism.

Suppose $\mathbf{L}=(L,\le )$ is a distributive lattice with its smallest element a and an atom b. We denote by ${\mathbf{L}}_{[a,b]}$ a lattice obtained from $\mathbf{L}$ by endowing it with two new elements, $a^{\prime }$ and $b^{\prime }$ (Figure 2), and letting

$$a^{\prime }\ll a,a^{\prime }\ll b^{\prime },b^{\prime }\ll b.$$

It should be clear that ${\mathbf{L}}_{[a,b]}$ is a lattice; if $\mathbf{L}$ is a bounded lattice, so is ${\mathbf{L}}_{[a,b]}$, and ${\mathbf{L}}_{[a,b]}$ has as many coatoms as $\mathbf{L}$. Moreover, if $\mathbf{A}$ is a Heyting algebra, ${\mathbf{A}}_{[0,b]}$ is a Heyting algebra as well (this is not hard to prove; for a more general case, see [10]), and the following holds.

Proposition 5. 

Let $\mathbf{A}$ be a Heyting algebra. Suppose that a is the smallest element in $\mathbf{A}$, b is an atom of $\mathbf{A}$, and $\mathbf{A}$ is generated by elements $\left\{b\right\}\cup G$, where $G\subseteq \mathbf{A}$. Then, elements $\left\{a\right\}\cup G$ generate algebra ${\mathbf{A}}_{[a,b]}$.

Proof. 

Indeed, as a is one of the generators,

$$a^{\prime }=\mathbf{0}=a\wedge \neg a,b^{\prime }=\neg a,b=a\vee \neg a.$$

Let $c\in {\mathbf{A}}_{[a,b]}$ and $c>a$. Then, there is a term $t(x_0,\dots ,x_m)$ such that $c=t(b,g_1,\dots ,g_m)$, where $g_i\in G,i\in [1,m]$. Let $t^{\prime }$ be a term obtained from t by replacing every $\mathbf{0}$ with a. Then, $c=t^{\prime }(a\vee \neg a,g_1,\dots ,g_m)$. □

Corollary 6. 

If a is the smallest element of Heyting algebra $\mathbf{A}$ generated by its atom b, then algebra ${\mathbf{A}}_{[\mathbf{0},b]}$ is generated by element a.

By Corollary 2, every one-generated Heyting algebra is generated by its atom; hence, we can always endow it with two new elements and obtain a one-generated algebra of higher cardinality in a process we call expansion. Thus, as expansion increases cardinality by 2, starting with ${\mathbf{Z}}_2$ and ${\mathbf{Z}}_3$, we can construct a one-generated Heyting algebra of any given cardinality n, which is denoted by ${\mathbf{Z}}_n$. Hence, the following holds.

Theorem 5. 

For each $n>1$, there is a one-generated Heyting algebra of cardinality n.

Example 1. 

Because algebras ${\mathbf{Z}}_2$ and ${\mathbf{Z}}_3$ are generated by their atoms, by adding two new elements for any $n>1$, we can construct a one-generated Heyting algebra of cardinality n; see Figure 3, where the added elements are denoted by ⋆, the old generator is denoted by ⊛, and the new generator (which at the same time is the old bottom element) is denoted by $\odot •$; all elements above $\odot •$ belong to the initial algebra.

Later, we will need the following properties of algebras ${\mathbf{Z}}_n$.

Proposition 6. 

From the construction of the sequence ${\mathbf{Z}}_n,n=2,3,4,\dots$ and properties of expansion, the following hold:

(a) 

Since algebra ${\mathbf{Z}}_3$ has a single coatom, each algebra ${\mathbf{Z}}_{2k+1},k>0$ has a single coatom as well; that is, all algebras with odd subscripts are subdirectly irreducible.

(b) 

Since algebra ${\mathbf{Z}}_4$ has two coatoms, each algebra ${\mathbf{Z}}_{2k+2},k>0$ has two coatoms as well, and hence, it is not subdirectly irreducible. Moreover, for each $k>1$, if $a,b$ are coatoms of ${\mathbf{Z}}_{2k+2}$, then $\left|\right(a\left]\right|=2k$ and $\left|\right(b\left]\right|=2k-1$ (or $\left|\right(a\left]\right|=2k-1$ and $\left|\right(b\left]\right|=2k$).

Now, let us show that every finite one-generated algebra is isomorphic to ${\mathbf{Z}}_n$ for some $n>1$.

4. Proof of Uniqueness

The goal of this section is to prove the following theorem.

Theorem 6. 

Suppose that $\mathbf{A}$ is a finite one-generated Heyting algebra of cardinality $n,n>1$. Then, $\mathbf{A}\cong {\mathbf{Z}}_n$.

Proof. 

Let $\mathbf{A}$ be a one-generated algebra of cardinality $n,n>1$.

From Proposition 4(c), we know that the cardinality of any Heyting algebra generated by an ordinary element is greater than 5. Thus, all one-generated Heyting algebras of cardinality 5 at most are generated by a regular or a dense element. From Propositions 2 and 3, we know that all of these algebras are isomorphic to one of the algebras ${\mathbf{Z}}_n,n\in [1,5]$.

By induction on $n,n\ge 4$, we prove that any one-generated algebra of cardinality n is isomorphic to ${\mathbf{Z}}_n$.

Basis. We already established that if $\left|\mathbf{A}\right|\in [3,4]$, then $\mathbf{A}$ is isomorphic to ${\mathbf{Z}}_3$ or ${\mathbf{Z}}_4$.

Assumption. Suppose that the statement holds for all $m<n$.

Steps. As $n>5$, $\mathbf{A}$ is generated by an ordinary element g. Then, from Proposition 1(a) and (b), the bottom part of the Hasse diagram is as shown in Figure 4.

Let us consider elements $\{a\in \mathbf{A}|g\le a\}$ and observe that this set is closed under $\wedge ,\vee$ and →, and hence, it forms a Heyting algebra denoted by ${\mathbf{A}}^{\left(g\right)}$ (note that ${\mathbf{A}}^{\left(g\right)}$ is not a subalgebra of $\mathbf{A}$). By (Corollary 9, [11]), ${\mathbf{A}}^{\left(g\right)}$ is generated by element $g\vee \neg g$ and contains $n-2$ elements. Thus, we can apply the induction assumption to ${\mathbf{A}}^{\left(g\right)}$ and conclude that ${\mathbf{A}}^{\left(g\right)}\cong {\mathbf{Z}}_{n-2}$. The observation that $\mathbf{A}={\mathbf{A}}_{[g,g^{\prime }]}^{\left(g\right)}$ completes the proof. □

Corollary 7. 

Let $t\left(x\right)$ and $s\left(x\right)$ be terms. Then, $\mathit{H}\mathit{A}\models t\approx s$ if and only if for every $i>1$, $t\left(g_i\right)=s\left(g_i\right)$, where $g_i$ is a generator of algebra ${\mathbf{Z}}_i$.

Proof. 

If $\mathit{H}\mathit{A}\models t\left(x\right)\approx s\left(x\right)$, the statement is trivial. Suppose that $\mathit{H}\mathit{A}⊭t\left(x\right)\approx s\left(x\right)$.

As the variety $\mathit{H}\mathit{A}$ is generated by finite algebras, there is an element $\mathsf{a}$ of a finite algebra $\mathbf{A}$ with $t\left(a\right)\ne s\left(a\right)$. By Theorem 6, a subalgebra of $\mathbf{A}$ generated by element a is isomorphic to algebra ${\mathbf{Z}}_n$ for some $n>1$. □

5. One-Generated Finitely Presented Algebras

In this section, we show that for any term $t\left(x\right)$ with $\mathit{H}\mathit{A}⊭t\left(x\right)\approx \mathbf{1}$, the algebra defined by relation $t\left(x\right)=\mathbf{1}$ is finite. Throughout this section, for any $n>1$, $g_n$ denotes a generator of algebra ${\mathbf{Z}}_n$ (for $n\le 5$, see Figure 1).

Proposition 7. 

Let $t\left(x\right)$ be a term. Then, the following statements are equivalent:

(a) 

$\mathit{H}\mathit{A}\models t\left(x\right)\approx \mathbf{1}$;

(b) 

For each $n>1$ there is $m\ge n$ such that $t\left(g_m\right)=\mathbf{1}$;

(c) 

For each $n>1$, $t\left(g_n\right)=\mathbf{1}$.

Proof. 

(a) ⟹ (b) is trivial.

(b) ⟹ (c). First, by induction on n, we prove that for any $n>0$, if $t\left(g_{2n+2}\right)=\mathbf{1}$, then, for every $m\le 2n$, we have $t\left(g_m\right)=\mathbf{1}$.

Basis. For $n=1$, it should be clear that if $t\left(g_4\right)=\mathbf{1}$, then $t\left(g_2\right)=\mathbf{1}$, because ${\mathbf{Z}}_2\cong {\mathbf{Z}}_4/\left[g_4\right)$ and the natural homomorphism sends $g_4$ to $g_2$.

Assumption. Assume that if $t\left(g_{2n}\right)=\mathbf{1}$, then for every $m\le 2n-2$, $t\left(g_m\right)=\mathbf{1}$.

Steps. Let $t_{(}{g}_{2n+2})=\mathbf{1}$. By Corollary 6(b), algebra ${\mathbf{Z}}_{2n+2}$ has two coatoms, a and b, with $\left|\right[a\left)\right|=2n$ and $\left|\right[b\left)\right|=2n-1$. Then, by (1), $|{\mathbf{Z}}_{2n+2}/\left[a\right)|=2k$ and $|C_{2n+2}/\left[b\right)|=2k-1$, and consequently, by Theorem 6, ${\mathbf{Z}}_{2n+2}/\left[a\right)\cong {\mathbf{Z}}_{2n}$ and ${\mathbf{Z}}_{2n+2}/\left[b\right)\cong {\mathbf{Z}}_{2n-1}$. Let us observe that the natural homomorphisms send $g_{2n+2}$ to $g_{2n}$ and $g_{2n-1}$; thus, $t\left(g_{2n}\right)=\mathbf{1}$ and $t\left(g_{2n-1}\right)=\mathbf{1}$. As $t\left(g_{2n}\right)=\mathbf{1}$, we can apply the induction assumption and conclude that $t\left(g_m\right)=\mathbf{1}$ for all $m\le 2n-2$. Thus, for all $m\le 2n$, we have $t\left(g_m\right)=\mathbf{1}$.

Next, we observe that if $t\left(g_{2n+3}\right)=\mathbf{1}$, then $t\left(g_{2n+2}\right)=\mathbf{1}$ for ${\mathbf{Z}}_{2n+2}\cong {\mathbf{Z}}_{2n+3}/\left[a\right)$, where $a\in {\mathbf{Z}}_{2n+3}$ is a coatom, and the natural homomorphism sends $g_{2n+3}$ to $g_{2n+2}$. Therefore, again, for all $m\le 2n$, we have $t\left(g_m\right)=\mathbf{1}$.

What we have proved is that for all $n>4$, if $t\left(g_n\right)=\mathbf{1}$, then $t\left(g_m\right)=\mathbf{1}$ for all $m\le n-3$, and now it is not hard to see that (b) entails (c).

(c) ⟹ (a) follows from Corollary 7. □

Now, we can prove the main statement of this section.

Theorem 7. 

Suppose that $t\left(x\right)$ is a term with $\mathit{H}\mathit{A}⊭t\left(x\right)\approx \mathbf{1}$ and $\mathbf{A}$ is an algebra defined by the relation $t\left(x\right)=\mathbf{1}$ in generator g. Then, $\mathbf{A}$ is a finite algebra.

Proof. 

For contradiction, suppose that $\mathbf{A}$ is an infinite algebra defined by the relation $t\left(x\right)\approx \mathbf{1}$ in generator g and $\mathit{H}\mathit{A}⊭t\approx \mathbf{1}$. Then, by definition of the defining relation, $t\left(g\right)=\mathbf{1}$.

By Corollary 5, every finitely presented Heyting algebra is a subdirect product of finite algebras. Hence, $\mathbf{A}$ is a subdirect product of some finite algebras ${\mathbf{A}}_i,i\in I$, which are homomorphic images of $\mathbf{A}$. Because $\mathbf{A}$ is one-generated, so is every factor ${\mathbf{A}}_i,i\in I$; let us say ${\mathbf{A}}_i$ is generated by $g_i\in {\mathbf{A}}_i,i\in I$. Thus, $\mathbf{A}$ is isomorphic to a subalgebra of the Cartesian product ${\prod }_{i\in I}{\mathbf{A}}_i$ generated by element $g^{\prime }$ such that every i-th projection of it is a $g_i$.

Observe that if algebra $\mathbf{A}$ is generated by element g, subalgebra of algebra $\mathbf{A}\times \mathbf{A}$ generated by element $(g,g)$ is isomorphic to $\mathbf{A}$. Hence, without losing generality, we can assume that for any distinct $i,j\in I$, algebras ${\mathbf{A}}_i$ and ${\mathbf{A}}_j$ are not isomorphic, and therefore, by Theorem 6, $|{\mathbf{A}}_i|\ne |{\mathbf{A}}_j|$. Thus, as, by definition, algebra $\mathbf{A}$ is infinite, it has subdirect factors of cardinality greater than any given n; that is, condition (b) from Proposition 7 holds true, and consequently, condition (a) of Proposition 7 holds true, and we have arrived at the contradiction. □

6. Algebras Finitely Presented by $x^n=\mathbf{1}$

The aim of this section is to show that for every $n>1$ relation, $x^n=\mathbf{1}$ defines algebra isomorphic to ${\mathbf{Z}}_n$.

Let $t\left(x\right)$ be a term. We define a transformation $S\left(t\right(x\left)\right)$ in the following way: $S\left(t\right(x\left)\right)$ is the term obtained from $t\left(x\right)$ by performing the following:

1.

Replacing all occurrences of $\mathbf{0}$ by y;

2.

Substituting $y\vee (y\to \mathbf{0})$ for x;

3.

Renaming y back to x.

Let us point out that the order of the steps is very important. It is not hard to see that for any term $t\left(x\right)$, any algebra ${\mathbf{Z}}_n$, and generator $g_n$, $S\left(t\right)\left(g\right)=t^{\prime }\left(g\right)$, where $t^{\prime }$ is a term from the proof of Proposition 5.

Example 2. 

$t\left(x\right)$	$S\left(t\right(x\left)\right)$
x	x$\vee \neg$x
¬x	(x $\vee \neg$ x) → x = $\neg \neg$ x
$\neg \neg$x	((x $\vee \neg$ x) → x) → x = $\neg \neg$ x → x
x$\vee \neg$x	(x $\vee \neg$ x) ∨ ((x $\vee \neg$ x) → x) = ¬ x $\vee \neg \neg$ x

Proposition 8. 

For any terms $t\left(x\right),s\left(x\right)$,

(a) 

$S(t\wedge s)=S\left(t\right)\wedge S\left(s\right)$;

(b) 

$S(t\vee s)=S\left(t\right)\vee S\left(s\right)$;

(c) 

$S(t\to s)=S\left(t\right)\to S\left(s\right)$.

Proof. 

(a)–(c) follow at once from the definition of S. Let us also observe that from (c), we have $S(t\to \mathbf{0})=S\left(t\right)\to S\left(\mathbf{0}\right)=S\left(t\right)\to x$. □

Proposition 9. 

For any natural n, $\mathit{H}\mathit{A}\models S\left(x^n\right)\approx x^{n+2}$.

Proof. 

We prove the statement by induction on n.

Basis. If $n=0$, then the following are true:

$$\begin{array}{cc}\hfill & S\left(x^0\right)=S\left(\mathbf{0}\right)=x=x^2;\hfill \\ \hfill & S\left(x^1\right)=S(x\to \mathbf{0})=(x\vee \neg x)\to x=\neg \neg x;\hfill \\ \hfill & S\left(x^2\right)=S\left(x\right)=x\vee \neg x=x^4.\hfill \end{array}$$

Assumption. Suppose that for all $m<n$, $S\left(x^m\right)=x^{m+2}$.

Steps. Assume that $n=2k$ and $k>1$. Then, by definition, $x^n=x^{2k}=x^{2k-3}\vee x^{2k-2}$, and consequently, by Proposition 8(b) and the assumption of induction,

$$\begin{array}{c}\hfill S(x^{2k-3}\vee x^{2k-2})=S\left(x^{2k-3}\right)\vee S\left(x^{2k-2}\right)=x^{2k-1}\vee x^{2k}=x^{2k+2}.\end{array}$$

Now, assume that $n=2k+1$ and $k>1$. Then, by definition, $x^n=x^{2k+1}=x^{2k-1}\to x^{2k-2}$, and consequently, by Proposition 8(c) and the assumption of induction,

$$\begin{array}{c}\hfill S(x^{2k-1}\to x^{2k-2})=S\left(x^{2k-1}\right)\to S\left(x^{2k-2}\right)=x^{2k+1}\to x^{2k}=x^{2k+3}.\end{array}$$

□

Proposition 10. 

For each $n>1$, all elements of ${\mathbf{Z}}_n$ are $g_n^i,i\in [0,n]$, with $g_n^n=\mathbf{1}$, and if $n\in \{2k,2k+1\}$, then $g_n^{2k-1}=g_n^{2k-2}$.

Proof. 

We prove the statement by induction on n.

Basis.

$$\begin{array}{c}\hfill \begin{array}{ccccc}n\hfill & \hfill & & \hfill & \\ 2:\hfill & g_2^0=g_2^1=\neg g_2=\mathbf{0},\hfill & g_2^2=g_2=\mathbf{1};\hfill & \hfill & \\ 3:\hfill & g_3^0=g_3^1=\mathbf{0},\hfill & g_3^2=g_3\hfill & g_r^3=\neg \neg g_3=\mathbf{1};\hfill & \\ 4:\hfill & g_4^0=\mathbf{0},\hfill & g_4^1=\neg g_4=g_4^{\prime },\hfill & g_4^2=g_4^3=\neg \neg g^4=g^4,\hfill & g_4^4=\mathbf{1}.\hfill \end{array}\end{array}$$

Assumption. Assume that the statement holds for all $m<n$.

Steps. Let $n>4$. Then, algebra ${\mathbf{Z}}_n$ can be obtained via the expansion of algebra ${\mathbf{Z}}_{n-2}$. Two newly added elements, $a^{\prime }$ and $b^{\prime }$ (see Figure 2), are $a^{\prime }=\mathbf{0}=a^0$ and $b^{\prime }=\neg a=a^1$. Let us recall that during expansion, the bottom element becomes a generator of the expanded algebra, that is, $a=g_n=g_n^2$, and by Proposition 9 and the induction assumption, the statement holds true. □

Theorem 8. 

For any $n>1$, the relation $x^n=\mathbf{1}$ defines algebra ${\mathbf{Z}}_n$.

Proof. 

We will prove that for a given $n>1$ relation, $x^n=\mathbf{1}$ defines the one-generated algebra of cardinality n, and then, by Theorem 6, we can conclude that this algebra is isomorphic to ${\mathbf{Z}}_n$.

Suppose that $\mathbf{A}$ is an algebra defined by the relation $x^n=\mathbf{1}$. By Proposition 10, $g_m^n\ne \mathbf{1}$ for any $m>n$; hence, by Theorem 7, $\mathbf{A}$ is finite, and therefore, by Theorem 6, $\mathbf{A}\cong {\mathbf{Z}}_m$ for some m. Now, we only need to show that $n=m$.

Indeed, by Proposition 10, in algebra ${\mathbf{Z}}_n$, we have $g_n^n=\mathbf{1}$; that is, ${\mathbf{Z}}_n$ is a homomorphic image of $\mathbf{A}$, and hence, $n\le m$. On the other hand, for all $m>n$, by Proposition 10, $g_m^n<\mathbf{1}$; therefore, ${\mathbf{Z}}_m$ is not defined by $x^n=\mathbf{1}$. Thus, $n=m$ and $\mathbf{A}\cong {\mathbf{Z}}_n$. □

Corollary 8. 

For any natural number n, the relation $x^n=\mathbf{1}$ defines a finite Heyting algebra.

Proof. 

For $n>1$, the statement follows from Theorem 8. If $n=0$, then $x^0=x\wedge \neg x$, and therefore, the relation $x^0=\mathbf{1}$ defines the trivial algebra. If $n=1$, then $x^1=\neg x$, and the relation $x^1=\mathbf{1}$ defines the two-element Heyting algebra. □

Corollary 9. 

Every infinite one-generated Heyting algebra is free and, thus, isomorphic to ${\mathbf{F}}_{\mathit{H}\mathit{A}}\left(1\right)$.

Proof. 

Suppose that $\mathbf{A}$ is an infinite Heyting algebra generated by element $g\in \mathbf{A}$. To prove that g is a free generator, we will show that for any term $t\left(x\right)$, $t\left(g\right)=\mathbf{1}$ if and only if $\mathit{H}\mathit{A}\models t\left(x\right)\approx \mathbf{1}$.

If $\mathit{H}\mathit{A}\models t\left(x\right)\approx \mathbf{1}$, clearly, $t\left(g\right)=\mathbf{1}$.

Now, let us assume that $t\left(g\right)=\mathbf{1}$ and show that $\mathit{H}\mathit{A}\models t\left(x\right)\approx \mathbf{1}$.

For contradiction, assume that $\mathit{H}\mathit{A}⊭t\left(x\right)\approx \mathbf{1}$. Then, by Theorem 3(2), there is $n\in [0,\infty ]$ such that $\mathit{H}\mathit{A}\models t\left(x\right)\approx x^n$. Since $x^{\infty }=(x\to x)$ and $\mathit{H}\mathit{A}⊭t\left(x\right)\approx \mathbf{1}$, we have $\mathit{H}\mathit{A}\models t\left(x\right)\approx x^n$ for some $n\ne \infty$. Thus, the relations $t\left(x\right)=\mathbf{1}$ and $x^n=\mathbf{1}$ define isomorphic algebras; that is, by Theorem 8, the relation $t\left(x\right)=\mathbf{1}$ defines algebra isomorphic to ${\mathbf{Z}}_n$. By assumption, $t\left(g\right)=\mathbf{1}$, and hence, by Theorem 4, there is a homomorphism $\phi :{\mathbf{Z}}_n⟶\mathbf{A}$ with $\phi \left(g_n\right)=g$. Because element g generates the entire algebra $\mathbf{A}$, $\phi$ is a homomorphism of ${\mathbf{Z}}_n$ onto $\mathbf{A}$, which is impossible, because ${\mathbf{Z}}_n$ is a finite algebra, while $\mathbf{A}$ is infinite. □

Thus, we have proved that for any natural number $n>1$ there is a unique up to isomorphism one-generated Heyting algebra of cardinality n, and the infinite one-generated Heyting algebra is free in $\mathit{H}\mathit{A}$.