Abstract
In this paper we explain the different meanings of the word “logic” and the circumstances in which it makes sense to use its singular or plural form. We discuss the multiplicity of logical systems and the possibility of developing a unifying theory about them, not itself a logical system. We undertake some comparisons with other sciences, such as biology, physics, mathematics, and linguistics. We conclude by delineating the origin, scope, and future of the journal Logics.
1. Classical Logic(s) vs. Non-Classical Logic(s)
One natural reason to put an “s” at the end of the substantive “logic” is to understand “logic” as shorthand for “logic systems” (or “systems of logic” or “logical systems”). There are plenty of different logic systems. For many years, one system was dominant: syllogistic logic, due to Aristotle (384–322 BC)1, often considered the father of logic. This system was developed, improved, and extended in different ways by various scholars [1,2,3,4,5,6,7]2. Then in modern logic, which started in the mid-19th century with the work of George Boole (1815–1864) [8,9,10], who wanted not to reject syllogistic but to provide a mathematical account of it, thousands of logic systems have been developed. The result is that we are currently facing a proliferation of logics. This booming effect is due to formalization, symbolization, and mathematization.
These three phenomena are interrelated and have given rise to corresponding terminologies, which are alternatively used: formal logic, symbolic logic, and mathematical logic. The expression “formal logic” was promoted by Immanuel Kant (1724–1804); it is an ambiguous expression, having five different meanings [11]. The expression “symbolic logic” was introduced by John Venn (1834–1923) [12], and it was used by Lewis Carroll (1832–1898) [13,14]3. Later, it became a symbol for modern logic, with The Association for Symbolic Logic and The Journal of Symbolic Logic, which ironically are using this word in a quite opposite meaning [15]. It is not clear who introduced the expression “mathematical logic”, but it has an ambiguous double meaning: it can be interpreted as the study of the logic of mathematics (mathematical reasoning) or the mathematics of logic (a mathematical study of reasoning in general, not only mathematical reasoning).
Note that these three expressions are singular. One of the reasons to not use the simple word logic was to emphasize the difference with Aristotelian or neo-Aristotelian “traditional logic”. Louis Couturat (1868–1914) proposed the terminology “logistics” [16]. The “s” in English is not related to the word being plural but to English phonetics, such as the word “phonetics” itself. In French, the term is singular: “la logistique”, like “la phonétique”. Today, both “logistics” in English and “logistique” in French are used to discuss organizational matters, in which logic is, at best, on the backstage.
A typical, not to say symptomatic, example of the proliferation of logic systems is the development of many-valued logics, a natural, easy, straightforward generalization of the mathematics of classical two-valued logic. However, there is a dark philosophical side of that “many”: does it make sense to say than there is a third truth value besides “truth” and “falsity”? This was criticized by two famous citizens of the 20th century logical world: W.V.O. Quine (1908–2000) [17] and Roman Suszko (1919–1979) [18].
Sometimes, the universe of logic systems is presented in a dichotomic way: classical logic vs. non-classical logics, that is, one system of logic facing a multiplicity of opposed systems. However, we can also present this dichotomy as fully plural, classical logics vs. non-classical, logics, or as fully singular, classical logic vs. non-classical logic. Let us examine the different meanings of the different locations of the plural letter “s”.
We can say classical logics vs. non-classical logics because there is not only one system of classical logic, but many: propositional logic, first-order logic, second-order logic, etc.; and their variations are not necessarily equivalent, for example, classical propositional logic, conceived as a consequence relation (with no cardinality restriction on the theories, i.e., sets of formulas), is not compact, in contrast to classical propositional logic conceived as a set of tautologies (with no cardinality restriction on the set of atomic formulas) [19]. Compactness is a fundamental feature of a logic, according to which if a proposition is a consequence of a theory, it is a consequence of a finite subtheory of this theory [20].
It is also possible to say classical logic vs. non-classical logic, considering “classical logic” as a singular expression referring to the different classical systems and “non-classical logic” as referring to the whole set of non-classical logic systems, considered not only as a collection of systems but also as a field of study. One may say, “I am studying non-classical logic”, meaning “I am studying the different non-classical systems of logic: their properties, motivations, applications, and their relations (between each other and also with classical logic)”.
The opposition between classical logic(s) and non-classical logic(s) has been challenged in different ways at the philosophical and mathematical levels. At the philosophical level, the adjective “classical” is quite ambiguous, as is the opposite adjective “non-classical” facing it. Classical propositional logic is not classical in the sense of something related to the classics of Greek antiquity (Figure 1) nor in the sense of classical music or classical physics [21,22]4. The term rather means “orthodox”. Francisco Miró Quesada (1918–2019) [23] preferred the dichotomy orthodox/heterodox, Susan Haack used the dichotomy deviation/extension [24], Lloyd Humberstone introduced the notion of “contra-classical logic” [25], and there is also “anti-classical logic” [26]. There are many different ways to describe and understand the universe of logic systems.

Figure 1.
Classical negation is not classic.
Anyway, non-classical logic is something more heterogeneous than classical logic; there are many different “families” of non-classical logics, such as modal logic, many-valued logic, relevant logic, and paraconsistent logic, but it would be strange to talk about the “family” of non-classical systems of logic because all they have in common is not being part of the family of classical systems of logic. Funnily enough, the “non” in “non-classical logics” is a classical negation, leading to a fuzzy reality, not to say chaos or absurdity [27].
At the mathematical level, it is possible to offer a three-valued semantics to classical propositional two-valued logic and a two-valued semantics to a three-valued logic, such as Lukasiewicz’s three-valued logic L3 [28,29,30]. Furthermore, considering that there is a translation of classical logic within intuitionistic logic, which is, from another perspective, a subsystem of classical logic, the relationship of opposition between the two is not clear [31]. Moreover, according to sequent proof theory developed by Gerhard Gentzen (1909–1945) [32], the logical rules of both classical and intuitionistic logics are the same, the difference according to this approach being structural. Another surprising result is that classical logic can be translated into one of its halves [33], which is a typical example of the so-called Béziau’s translation paradox [34].
2. From the Universe of Logic Systems to Universal Logic
A general theory of logic systems has been developed, particularly to better understand strange phenomena and paradoxes mentioned in the previous section. Its given name is “universal logic” (1993) [35,36,37], but this theory goes back to the work of Paul Hertz (1881–1940) and Alfred Tarski (1901–1983) in the 1920s [38,39]. Universal logic is not itself a system of logic; it is a general study of the various systems of logic, considered as logical structures, in the same way that universal algebra is a general study of algebras considered as algebraic structures [40]. Universal logic promotes unity in diversity not by reducing everything to one system but by developing concepts in a general framework to have a better understanding of the universe of logic systems.
Some of these concepts are generalizations of concepts used in particular classical or non-classical logic systems, such as the pivotal notion for an abstract version of the completeness theorem, the notion of maximal non-trivial theory; a theory is maximal non-trivial if any proposition is a consequence of any strict extension of it [41]. Some are used for giving new definitions and understandings of notions, such as substitution, characterized by Łoś and Suszko as endomorphism, leading to the notion of structural consequence relation [42]. Furthermore, some have been introduced especially from the perspective of a general theory of logics, such as fibring, a key notion in the theory of the combination of logics [43].
Universal logic is in the line of “conceptual mathematics” [44]. As such, it offers a new philosophical perspective and understanding of logic, for example, breaking the dichotomy syntax/semantics; however, it does not reduce to philosophy of logic because it is not only a reflection of what exists but also the transformation and evolution of the (science) of logic.
A series of events was launched in 2005 in Montreux, Switzerland, called UNILOG: Word Congress and School on Universal Logic (Figure 2) [45].

Figure 2.
The first UNILOG.
Since the first edition, there has been a contest during the event. The first three contests were related to fundamental problems regarding relationships between logic systems:
- 1st UNILOG, Montreux, 2005, How to define identity between logics?
- 2nd UNILOG, Xi’an, 2007, How to translate one logic into another one?
- 3rd UNILOG, Lisbon, 2010, How to combine logics?
In the sixth edition (Vichy, 2018), the universal logic contest took the shape of a World Logic Prizes Contest, in which winners of contests from different countries competed, universality being then about the unification of logic research worldwide [46,47]. In this same spirit, the Logica Universalis Association (LUA) launched on 14 January 2019 the first World Logic Day [48], which was recognized the same year unanimously by the general UNESCO assembly [49] and which since 2020 has been part of the calendar of international days of UNESCO (Figure 3).

Figure 3.
The fifth edition of World Logic Day.
The 2nd World Logic Prizes Contest was organized at the 7th edition of UNILOG in Crete, and the third one will take place at the 8th UNILOG in Cusco, Peru, in 2025. This contest has been developed not only in the spirit of the unification of logic(s) but also in the spirit of the unification of science(s) [50,51].
Universal logic can be considered as synonymous to metalogic, a word successively and independently promoted in different ways by Arthur Schopenhauer (1788–1860), Nicolai Vasiliev (1880–1940), and Mordchaj Wajsberg (1902–194?) [52]. Universal logic uses as tools the four main metalogic theories that have been developed in modern logic, in order of appearance: set theory, proof theory, recursion theory, and model theory. It also uses various mathematical theories, such as topology, universal algebra, category theory, and graph theory.
We can talk about different metalogics: the metalogic of classical logic, the metalogic of intuitionistic logic, the metalogic of modal logic, etc. However, if we consider that all these metalogics are developed in a common unifying framework, it is better to singularize the name: “metalogic”. The expression universal logic is less ambiguous because the plural “universal logics” does not really make sense, in the same way that “universal algebras” is rather meaningless and is not used. Moreover, the etymological meaning of the word “universal”, which comes from Latin through French, is “turned into one”.
The idea of universal logic, like the idea of universal algebra promoted by Garrett Birkhoff (1911–1996), is to undertake unification not through axioms but through concepts. And, like universal algebra, it does not reject plurality but embraces it as a whole [53].
3. The Singular Science of Logic
Logic as a field is the study of the various systems of logic; their applications, interpretations, and meanings; and the historical and philosophical aspects of the theory of reasoning, including the art of thinking, argumentation, fallacies, and paradoxes.
Systems of logic are supposed to describe and/or prescribe natural and artificial reasoning. The substantive “logic” is used in three different ways:
- (1)
- reasoning;
- (2)
- a system describing reasoning, that is, “a logic”;
- (3)
- the science studying reasoning through the development of logical systems and tools to study them (for details, see [54,55]).
There is no sense placing an “s” on “logic” as the science of reasoning, in the same way that we do not place an “s” on “biology”. If there is an “s” on “physics”, it is for a phonetic, linguistic reason, related to English language; in French, it is “la physique”; in German, it is also a singular female word, “die Physik”. No doubt that there are different theories in physics, but it is good to have one single singular name for all these theories, thus forming a science. Physical reality has various aspects; a theory embracing everything, a single system, does not yet exist. Maybe there will never be such a system [56]; nevertheless, reality is one, and its very nature, if any, does not depend on us [57]5.
In the case of logic, the situation is a bit different because reasoning is a human activity that may vary over time and space, and we both practice it and theorize it. The magnitude of this variation is unclear, as is the sense in which we can transform, change, and mold this reality.
Logic, as the science of reasoning, varies like other sciences, but this fact is not a reason to put an “s” on it. In the case of reasoning, one may argue that there are different types of reasoning, not (only) in the sense of different aspects of reasoning, similarly to different aspects of physical reality, but (also) similarly to the variety of languages. One may be tempted to move in this direction, given that logic is deeply tied to language, the Greek word logos meaning both reasoning and language (and also science and relation; see Figure 4).
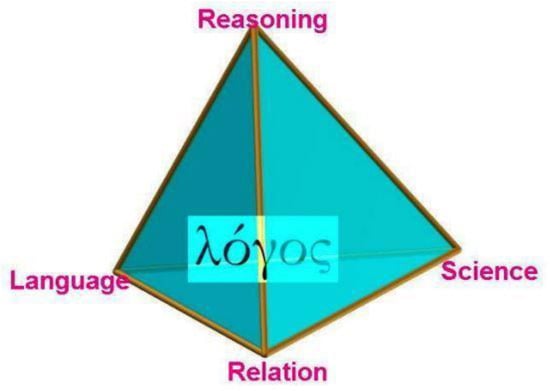
Figure 4.
The four aspects of logos.
Human beings speak many different languages, and these languages are lively phenomena, changing all the time, emerging, growing, and dying… However, all these human languages have something in common despite some striking differences, and this similarity allows translations from Chinese to Arabic, Arabic to Puppy-Guarana, and Puppy-Guarana to Esperanto. The science of all these languages is called in English “linguistics”, with again an “s” for phonetic reasons. In French, there is a singular name for this science, “la linguistique”, a name which was amplified by Ferdinand de Saussure (1857–1923) with his Cours de Linguistique Générale (1916) [58]. The singular is used to denote a unified science that studies the multiple languages and the multiple aspects of these languages.
Saussure is considered the father of structuralism, which was developed in mathematics by Bourbaki, a singular name for a non-empty set of mathematicians (about the development of structuralism, see the interesting book by Gilles-Gaston Granger (1920–2016) entitled Pensée formelle et science de l’homme [59]). Again, in English, there is an “s” at the end of “mathematics” for the same reason as with “physics” and “linguistics” but this time in French too! In French, in contrast to “la physique” and “la linguistique”, people say “les mathématiques”, a real plural, with the “s” not being a phonetic ornament. The reason for this “s”, if any, is not clear. The General Nicolas Bourbaki (1934–1968) felt it was too much, and in a famous paper entitled “L’Architecture des mathématiques” with subtitle “La mathématique ou les mathématiques” [60], he argued for the singularity of mathematics, unifying it with the notion of structure but considering that there were three “mother structures” (Figure 5) [61].

Figure 5.
Mathematics as a singular science based on a multiplicity of structures.
In German, the word for mathematics is singular and female: “die Mathematik”. However, Heidegger introduced a male counterpart, “der Mathematik”, to denote the very “object” that it is dealing with [62], in the same sense that we say that biology deal with life, a singular word to denote the essence of all living creatures. In the case of the science of logic, the object of study is reasoning, which is also sometimes called “logic” (the English substantive “reasoning”, derived from Latin, won over “logic”, derived from Greek).
As for languages, there are variations of reasoning but also something in common to all reasonings. To use the singular word “reasoning” does not necessarily mean that there is only one (correct) way of reasoning, but like for “language”, it is a way to provide a unifying perspective.
There are many different cats, but all of them have something in common, and the same is true with human beings. This common thing is reasoning, which distinguishes them from other animals. In Ancient Greek, human beings were called “logical animals”, which later became famous in the Latinized form “rational animals” [63].
As in mathematics, we can gather the study of different theories and systems describing reasoning into a unifying theory based on the notion of structure. Structuralism is directly related to one of the four original meanings of logos, “relation”, which is found in words such as “analogy” or “rational numbers”. Something is understood, makes sense, or exists not by itself alone but in relation to other things; that fact is the basis of structuralism.
A phenomenon also typical of human beings and that can be considered a byproduct of rationality is a laugh. Laughter has many aspects, but the plural is rarely used. However, there are different expressions describing/qualifying the different ways of laughing. On the other hand, in English, the word “smile” is radically different from the word “laugh”, in contrast to what happens in French, in which the word “rire” for laughter appears as a subproduct of “sourire” [64]. When we have two radically different common names in a given language, it is generally because their meanings strongly differ due to the fact that they denote fairly distinct realities. There may be some variations from one language to another, indicating that people using different languages do not think in the same way and do not have the same appraisal of reality.
Science, in contrast to ordinary thought and language, tends toward unification, through a thinking, a language, an understanding that is universal. This phenomenon is true for all sciences but especially for those using the symbolic language of mathematics [65], which is today the case of logic, and those in which reasoning is the key, which is the case of logic by its very nature.
4. Birth of the Journal Logics
I proposed in July 2021 to MDPI to create a journal called Logics [66]. It is a short, simple, and direct title. I had in mind a journal both dealing with all kinds of logic systems and the different perspectives that we can have on logic. Having founded a journal on universal logic emphasizing unity among the diversity of logic systems, a journal entitled Logica Universalis [67], I thought it would also be interesting to have a journal emphasizing diversity but still preserving unity—a journal addressing all logics, in opposition to a journal devoted to a specific family of logic systems, such as a journal devoted to many-valued logics, fuzzy logics, or non-monotonic logics.
This project and the corresponding title spontaneously came to my mind in particular because I have been a member of the editorial board of another MDPI plural journal entitled Philosophies since its creation in 2016. Among MDPI journals, some end with an “s”, and some end without an “s”, e.g., Knowledge. One of the MDPI journals with an “s” is Languages. This journal focuses more on the study of some specific linguistic phenomena than on the development of a general abstract theory of language, but considering any language or linguistic phenomenon. This is the perspective I had analogously in mind for Logics. The “s” is not for phonetics, as for “linguistics”, but for plurality, as for “languages”.
MDPI proposed having me launch this journal Logics, forming an editorial board, etc. [68]. I did not have the time to do so right away; meanwhile, someone else proposed to MDPI launching a journal on Logical Systems, MPDI decided to simply call this journal Logics, as I had suggested, and Valentin Goranko was appointed Editor-in-Chief. I think the idea is quite the same, I wish good luck to Valentin Goranko for the success of this new journal, and I will be glad to help as a member of the editorial board.
Funding
This research was funded by the Brazilian Research Council (CNPq).
Conflicts of Interest
The author declares no conflict of interest.
Notes
| 1 | We are indicating the dates of birth and death of the main personalities whom we are discussing to fix the ideas and to provide a more precise historical account, as well as to emphasize that a science like logic has been developed until now by human beings who were born and died (some are still alive) and not by robots. |
| 2 | There were other proposals, such as Indian logic (see, e.g., [1,2]), Talmudic logic [3], Stoic logic [4], etc., but their influence was not as important as that of Aristotelian logic, and they were not developed in as systematic a way. The systematization of Aristotelian syllogistic logic has many aspects, such as the theory of the square opposition (see, e.g., [5]), the introduction of singular terms [6], and all kinds of variations, such Abelard’s logic [7]. |
| 3 | Carroll is famous for his novel Alice’s Adventures in Wonderland (1865), but he was also a logician [14]. |
| 4 | I organized two workshops discussing the names for logic systems, in particular the expression “classical logic”, in Helsinki in 2015 at the 15th CLMPS [21] and in Vichy in 2018 at the 6th UNILOG [22]. |
| 5 | I wrote a master’s thesis in philosophy at the Sorbonne in 1987 on the question of objective reality according to modern physics [57], comparing the views of Heisenberg, Bohr, and Bohm, under the supervision of the famous physicist Bernard d’Espagnat (1921–2015), who received the Templeton prize in 2009. |
References
- Schumann, A. On the Origin of Indian Logic from the Viewpoint of the Pāli Canon. Log. Univers. 2019, 13, 347–393. [Google Scholar] [CrossRef]
- Matilal, B.K. Indian Approach to Logic; Centre for Policy Studies: London, UK, 1985; Available online: https://cpsindia.org/dl/science/logic-c2.pdf (accessed on 19 May 2023).
- Schumann, A. On the Origin of Logical Determinism in Babylonia. Log. Univers. 2021, 15, 331–357. [Google Scholar] [CrossRef]
- Gourinat, J.-B. La Dialectique des Stoïciens; Vrin: Paris, France, 2000. [Google Scholar]
- Beziau, J.-Y.; Jacquette, D. Around and Beyond the Square of Opposition; Birkhäuser: Basel, Switzerland, 2012. [Google Scholar]
- Ashworth, J.E. Medieval Theories of Singular Terms. In Stanford Encyclopedia of Philosophy; Stanford University: Stanford, CA, USA, 2003; Available online: https://plato.stanford.edu/entries/singular-terms-medieval/#SinTerLog (accessed on 23 September 2019).
- Lenzen, W. Abaelards Logik; Brill: Leiden, The Netherlands, 2021. [Google Scholar]
- Boole, G. The Mathematical Analysis of Logic, Being an Essay towards a Calculus of Deductive Reasoning; Macmillan: London, UK, 1847. [Google Scholar]
- Boole, G. The Calculus of Logic. Camb. Dublin Math. J. 1848, 3, 183–198. [Google Scholar]
- Boole, G. An Investigation of the Laws of Thought on Which Are Founded the Mathematical Theories of Logic and Probabilities; Macmillan: London, UK, 1854. [Google Scholar]
- Beziau, J.-Y. What is “formal logic”? In Proceedings of the XXII World Congress of Philosophy, Seoul 2018; Hyun-Lee, M., Ed.; Korean Philosophical Association: Seoul, Republic of South Korea, 2008; Volume 13, pp. 9–22. [Google Scholar]
- Venn, J. Symbolic Logic; Macmillan: London, UK, 1881. [Google Scholar]
- Carroll, L. Symbolic Logic; Macmillan: London, UK, 1896. [Google Scholar]
- Abeles, F. Lewis Carroll: Logic. The Internet Encyclopedia of Philosophy. Available online: https://iep.utm.edu/lewis-carroll-logic/ (accessed on 1 March 2023).
- Beziau, J.-Y. La puissance du symbole. In La Pointure du Symbole; Beziau, J.-Y., Ed.; Petra: Paris, France, 2014; pp. 9–34. [Google Scholar]
- Schlaudt, O.; Schmid, A.-F. (Eds.) Louis Couturat: The History of Modern Symbolic Logic and Other French Manuscripts; Birkäuser: Cham, Switzerland, 2021. [Google Scholar]
- Quine, W.V. The Philosophy of Logic; Harvard University Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Suszko, R. The Fregean axiom and Polish mathematical logic in the 1920s. Stud. Log. 1977, 36, 87–90. [Google Scholar] [CrossRef]
- Beziau, J.-Y. What is classical propositional logic? Log. Investig. 2001, 8, 266–277. [Google Scholar]
- Paseau, A.C.; Leek, R. The Compactness Theorem. The Internet Encyclopedia of Philosophy. Available online: https://iep.utm.edu/compactness (accessed on 18 May 2023).
- Naming Logic(s). In Proceedings of the Workshop at the 15th Congress on Logic, Methodology, and Philosophy of Science, Helsinki, Finland, 3–8 August 2015; Available online: https://clmps2015.sched.com/event/31PW (accessed on 1 April 2023).
- Naming Logics, II. In Proceedings of the Workshop at the 6th World School and Congress on Universal Logic, Vichy, France, 16–26 June 2018; Available online: https://uni-log.org/wk6-NAM.html (accessed on 1 April 2023).
- Miró Quesada, F. Heterodox logics and the problem of the unity of logic; Unpublished, Campinas, 1976. Translation into Spanish: Las lógicas heterodoxas y el problema de la unidad de la lógica. In Lógica. Aspectos Formales y Filosóficos; Rosales Papa, D., Ed.; PUCP: Lima, Peru, 1978; pp. 13–44. [Google Scholar]
- Haack, S. Philosophy of Logics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Humberstone, L. Contra-classical logics. Australas. J. Philos. 2000, 78, 438–474. [Google Scholar] [CrossRef]
- Beziau, J.-Y.; Buchsbaum, A. Let us be Antilogical: Anti-Classical Logic as a Logic. In Soyons Logiques/Let Us Be Logical; Moktefi, A., Moretti, A., Schang, F., Eds.; College Publications: London, UK, 2016; pp. 1–10. [Google Scholar]
- Beziau, J.-Y. Cats that are not cats. In Natural Arguments—A Tribute to John Woods; Gabbay, D., Magnani, L., Park, W., Pitarinen, A.V., Eds.; College Publications: London, UK, 2019; pp. 49–71. [Google Scholar]
- Beziau, J.-Y. A sequent calculus for Lukasiewicz’s three-valued logic based on Suszko’s bivalent semantics. Bull. Sect. Log. 1999, 28, 89–97. [Google Scholar]
- Beziau, J.-Y. History of truth-values. In Handbook of the History of Logic, Vol. 11—Logic: A History of Its Central Concepts; Gabbay, D.M., Woods, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 233–305. [Google Scholar]
- da Costa, N.C.A.; Beziau, J.-Y.; Bueno, O.A.S. Malinowski and Suszko on many-valued logics: On the reduction of many-valuedness to two-valuedness. Mod. Log. 1996, 6, 272–299. [Google Scholar]
- D’Ottaviano, I.M.L.; Feitosa, H.A. Conservative translations. Ann. Pure App. Log. 2001, 108, 205–227. [Google Scholar]
- Gentzen, G. Untersuchungen über das logische Schließen. I. Math. Z. 1935, 39, 176–210. [Google Scholar] [CrossRef]
- Beziau, J.-Y. Classical negation can be expressed by one of its halves. Log. J. IGPL 1999, 7, 145–151. [Google Scholar] [CrossRef]
- Humberstone, L. Béziau’s translation paradox. Theoria 2005, 71, 138–381. [Google Scholar] [CrossRef]
- Beziau, J.-Y. Universal logic. In Proceedings of the Logica’94—Proceedings of the 8th International Symposium, Liblice, Czech Republic, 10–12 June 1994; Childers, T., Majer, O., Eds.; Czech Academy of Science: Prague, Czech Republic, 1994; pp. 73–93. [Google Scholar]
- Beziau, J.-Y. Recherches sur la Logique Universelle. Ph.D. Thesis, University Paris 7 Denis Diderot, Paris, France, 1995. [Google Scholar]
- Beziau, J.-Y. 13 Questions about universal logic. Bull. Sect. Log. 2006, 35, 133–150. [Google Scholar]
- Beziau, J.-Y. From consequence operator to universal logic: A survey of general abstract logic. In Logica Universalis: Towards a General Theory of Logic; Beziau, J.-Y., Ed.; Birkhäuser: Basel, Switzerland, 2005; pp. 3–17. [Google Scholar]
- Beziau, J.-Y. (Ed.) Universal Logic, an Anthology—From Paul Hertz to Paul Gabbay; Birkhäuser: Basel, Switzerland, 2010. [Google Scholar]
- Birkhoff, G. Universal algebra. In Selected Papers on Algebra and Topology by Garret Birkhoff; Rota, G.-C., Oliveira, J.S., Eds.; Birkhäuser: Basel, Switzerland, 1987; pp. 111–115. [Google Scholar]
- Beziau, J.-Y. La véritable portée du théorème de Lindenbaum-Asser. Log. Anal. 1999, 167–168, 341–359. [Google Scholar]
- Łoś, J.; Suszko, R. Remarks on sentential logics. Indigationes MathemaIicae 1958, 10, I77–I183. [Google Scholar] [CrossRef]
- Gabbay, D.M. Fibring Logics; Clarendon: Oxford, UK, 1998. [Google Scholar]
- Lawvere, F.W.; Schanuel, S. Conceptual Mathematics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Word Congress and School on Universal Logic. Available online: http://uni-log.org/ (accessed on 11 March 2023).
- Beziau, J.-Y. Logic Prizes et Cætera. Log. Univers. 2018, 12, 271–296. [Google Scholar] [CrossRef]
- Beziau, J.-Y. Universal Logic: Evolution of a Project. Log. Univers. 2018, 12, 1–8. [Google Scholar] [CrossRef]
- Beziau, J.-Y. 1st World Logic Day: 14 January 2019. Log. Univers. 2019, 13, 1–20. [Google Scholar] [CrossRef]
- Fontenele Reis, M.E. Inclusion of the World Logic Day in the UNESCO Calendar of International Days. Available online: http://www.logica-universalis.org/wld3-brazilian-unesco-ambassador (accessed on 10 February 2023).
- Beziau, J.-Y. The 2nd World Logic Prizes Contest, 7th UNILOG, Crete 2022. Log. Univers. 2022, 16, 1–9. [Google Scholar] [CrossRef]
- Andréka, H.; Gyenis, Z.; Németi, I.; Sain, I. Universal Algebraic Logic—Dedicated to the Unity of Science; Birkhäuser: Cham, Switzerland, 2010. [Google Scholar]
- Beziau, J.-Y. Metalogic, Schopenhauer and Universal Logic. In Language, Logic, and Mathematics in Schopenhauer; Lemanski, J., Ed.; Birkhäuser: Basel, Switzerland, 2020; pp. 207–257. [Google Scholar]
- Beziau, J.-Y. What is a logic?—Towards axiomatic emptiness. Log. Investig. 2010, 16, 272–279. [Google Scholar]
- Beziau, J.-Y. Logic is not logic. Abstracta 2010, 6, 73–102. [Google Scholar]
- Beziau, J.-Y. Is Logic Exceptional? In Logic in Question—Talks from the Annual Sorbonne Logic Workshop (2011–2019); Beziau, J.-Y., Desclés, J.-P., Mokteki, A., Pascu, A., Eds.; Birkhäuser: Cham, Switzerland, 2022; pp. 261–279. [Google Scholar]
- Beziau, J.-Y. Is there an axiom for everything? In Wider den Reduktionismus—Ausgewählte Beiträge zum Kurt Gödel Preis 2019; Passon, O., Benzmüller, C., Eds.; Springer Spektrum: Heidelberg, Germany, 2021; pp. 103–117. [Google Scholar]
- Beziau, J.-Y. L’holomouvement chez David Bohm. Master’s Thesis, University Paris 1 Panthéon-Sorbonne, Paris, France, 1987. [Google Scholar]
- de Saussure, F. Cours de Linguistique Générale; Payot: Lausanne, Switzerland, 1916. [Google Scholar]
- Granger, G.-G. Pensée Formelle et Science de l’homme; Aubier: Paris, France, 1960. [Google Scholar]
- Bourbaki, N. L’architecture des mathématiques—La mathématique ou les mathématiques. In Les Grands Courants de la Pensée Mathématique; le Lionnais, F., Ed.; Cahiers du Sud: Marseilles, France, 1948; pp. 35–47. [Google Scholar] [CrossRef]
- Bourbaki, N. Eléments de Mathématique; Hermann: Paris, France, 1939. [Google Scholar]
- Heidegger, M. Die Frage nach dem Ding, Zu Kants Lehre von den Transzendentalen Grundsätzen; Niemeyer: Tübingen, Germany, 1962. [Google Scholar]
- Beziau, J.-Y. Being aware of rational animals. In Representation and Reality: Humans, Animals and Machines; Dodig-Crnkovic, G., Giovagnoli, R., Eds.; Springer: Cham, Switzerland, 2017; pp. 319–331. [Google Scholar]
- Beziau, J.-Y. Risoto et Rosita au Pays du Rire—A Comic Trip for the Few Happy Francophones. Trágica 2019, 12, 125–149. [Google Scholar]
- Serfati, M. La Révolution Symbolique. La Constitution de l’écriture Symbolique Mathématique; Pétra: Paris, France, 2005. [Google Scholar]
- Beziau, J.-Y. (The Federal University of Rio de Janeiro, Rio de Janeiro, Brazil). Personal email communication to D.Liao MDPI, 2021.
- Logica Universalis. Available online: https://www.springer.com/journal/11787/ (accessed on 9 May 2023).
- Li, J. (MDPI, Basel, Switzerland). Personal email communication to J.-Y.Beziau, 2021.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).