On Periodic Generalized Poisson INGARCH Models †
Abstract
:1. Introduction
2. Notations, Definitions and Main Assumptions
3. Periodically Stationary Conditions
3.1. Periodically Stationary in the Mean
3.2. Periodically Stationary in the Second Order
4. Existence of Higher Moments and Their Calculations
5. Autocovariance Structure
6. Parameter Estimation
6.1. Yule-Walker Estimation
6.2. Conditional Maximum Likelihood Estimation
7. Application
7.1. Simulation Study
- Model 1:
- Model 2: with and
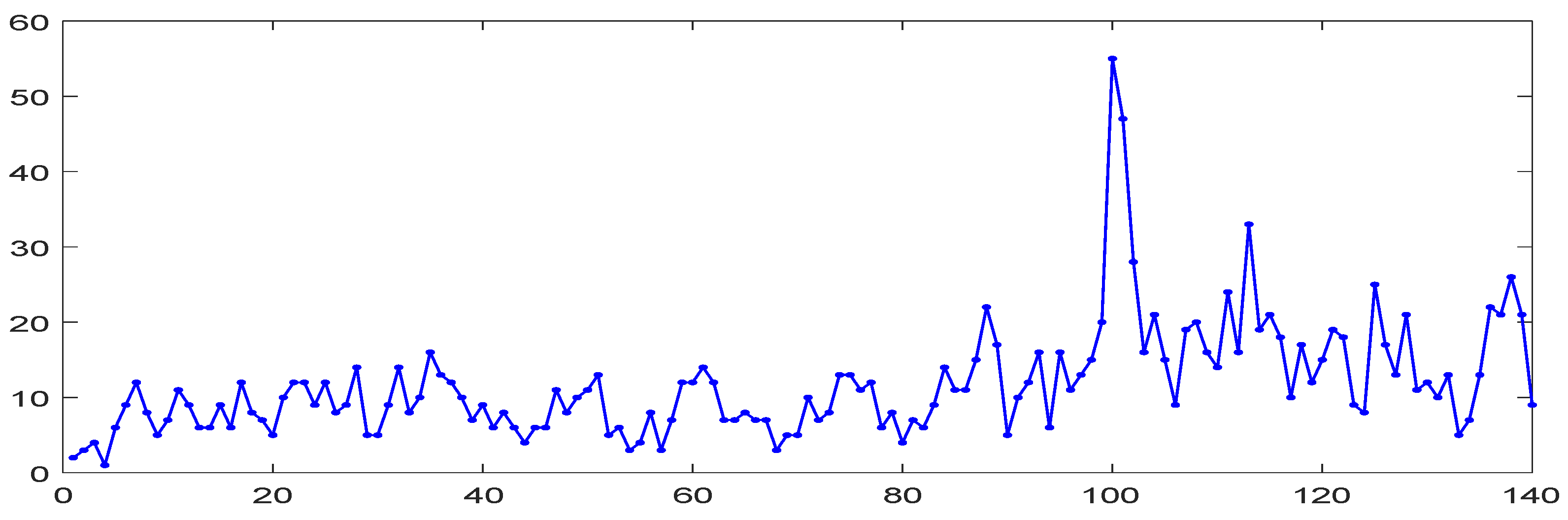
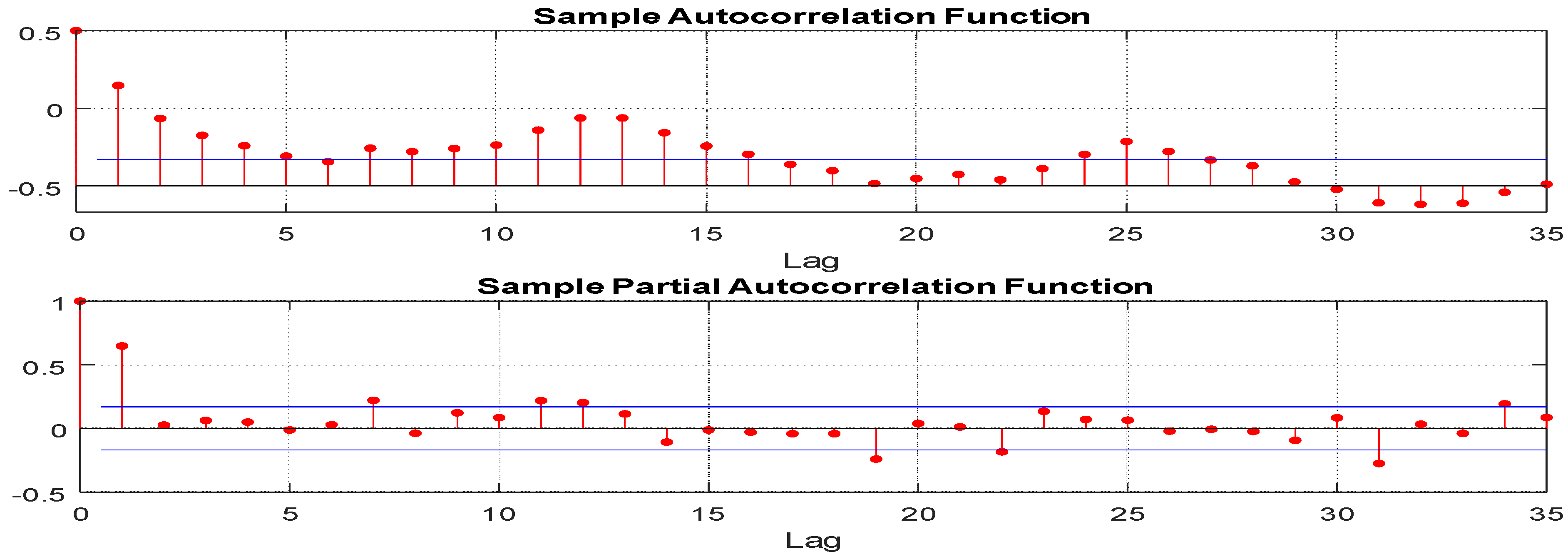
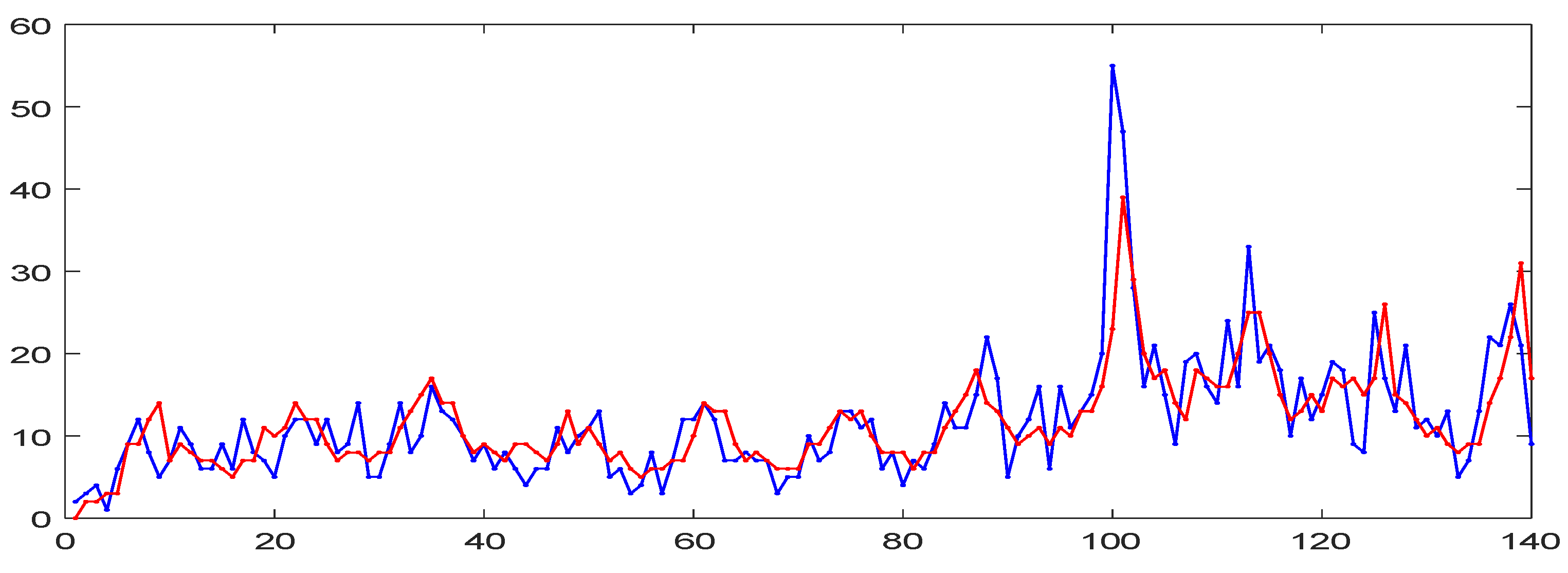
7.2. Empirical Application
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ferland, R.; Latour, A.; Oraichi, D. Integer-valued GARCH process. J. Time Ser. Anal. 2006, 27, 923–942. [Google Scholar] [CrossRef]
- Zhu, F.; Wang, D.; Li, F.; Li, H. Empirical likelihood inference for an integer-valued ARCH(p) model. J. Jilin Univ. Inf. Sci. Ed. 2008, 46, 1042–1048. [Google Scholar]
- Zhu, F.; Li, Q. Moment and Bayesian estimation of parameters in the INGARCH(1, 1) model. J. Jilin Univ. Inf. Sci. Ed. 2009, 47, 899–902. [Google Scholar]
- Fokianos, K.; Rahbek, A.; Tjostheim, D. Poisson autoregression. J. Am. Stat. Assoc. 2009, 104, 1430–1439. [Google Scholar] [CrossRef]
- Fokianos, K.; Fried, R. Interventions in INGARCH processes. J. Time Ser. Anal. 2010, 31, 210–225. [Google Scholar] [CrossRef]
- Doukhan, P.; Leucht, A.; Neumann, M.H. Mixing properties of non-stationary INGARCH(1, 1) processes. arXiv 2020, arXiv:2011.05854. [Google Scholar] [CrossRef]
- Zhu, F. A negative binomial integer-valued GARCH model. J. Time Ser. Anal. 2011, 32, 54–67. [Google Scholar] [CrossRef]
- Zhu, F. Zero-inflated Poisson and negative binomial integer-valued GARCH models. J. Stat. Plan. Inference 2012, 142, 826–839. [Google Scholar] [CrossRef]
- Zhu, F. Modeling overdispersed or underdispersed count data with generalized Poisson integer-valued GARCH models. J. Math. Anal. Appl. 2012, 389, 58–71. [Google Scholar] [CrossRef]
- Zhu, F. Modeling time series of counts with COM-Poisson INGARCH models. Math. Comput. Model. 2012, 56, 191–203. [Google Scholar] [CrossRef]
- McKenzie, E. Autoregressive moving-average processes with negative binomial and geometric marginal distributions. Adv. Appl. Probab. 1986, 18, 679–705. [Google Scholar] [CrossRef]
- McKenzie, E. Some ARMA models for dependent sequences of Poisson counts. Adv. Appl. Probab. 1988, 20, 822–835. [Google Scholar] [CrossRef]
- Al-Osh, M.A.; Alzaid, A.A. First-order integer-valued autoregressive process. J. Time Ser. Anal. 1987, 8, 261–275. [Google Scholar] [CrossRef]
- Weiß, C.H. An Introduction to Discrete-Valued Time Series; Wiley: Chichester, UK, 2018. [Google Scholar]
- Bentarzi, M.; Bentarzi, W. Periodic integer-valued GARCH(1, 1) model. Commun. Stat.-Simul. Comput. 2017, 46, 1167–1188. [Google Scholar] [CrossRef]
- Consul, P.C.; Jain, G.C. A generalization of the Poisson distribution. Technometrics 1973, 15, 791–799. [Google Scholar] [CrossRef]
- Consul, P.C. Generalized Poisson Distributions: Properties and Applications; Marcel Dekker: New York, NY, USA, 1989. [Google Scholar]
- Efron, B. Double exponential families and their use in generalized linear regression. J. Am. Stat. Assoc. 1986, 81, 709–721. [Google Scholar] [CrossRef]
- Gladyshev, E.G. Periodically and almost periodically correlated random processes with continuous time parameter. Theory Probab. Appl. 1963, 8, 173–177. [Google Scholar] [CrossRef]
- White, H. Maximum likelihood estimation of misspecified models. Econometrica 1982, 50, 1–25. [Google Scholar] [CrossRef]
- Weiß, C.; Scherer, L.; Aleksandrov, B.; Feld, M. Checking Model Adequacy for Count Time Series by Using Pearson Residuals. J. Time Ser. Econ. 2019, 12, 20180018. [Google Scholar] [CrossRef]
- Ouzzani, F.; Bentarzi, M. On mixture periodic Integer-Valued ARCH models. Commun. Stat.-Simul. Comput. 2021, 50, 3931–3957. [Google Scholar] [CrossRef]

| T.V | 1 | 2 | 3 | 4 | 0.15 | 0.25 | 0.35 | 0.45 | 0.1 | 0.2 | 0.3 | 0.4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | EST | ||||||||||||
| 500 | YW | 0.9386 (1.2392) | 1.9950 (0.9161) | 2.8670 (4.5134) | 3.6495 (9.0003) | 0.1492 (0.0492) | 0.2515 (0.1287) | 0.3638 (0.2464) | 0.4511 (0.2064) | 0.1078 (0.1579) | 0.2022 (0.3129) | 0.3787 (1.3028) | 0.4629 (1.7544) |
| CML | 0.9805 (0.7456) | 1.8702 (0.8981) | 2.7615 (1.1957) | 3.8261 (1.7268) | 0.1500 (0.0554) | 0.2522 (0.0918) | 0.3430 (0.1105) | 0.4472 (0.1165) | 0.1035 (0.0983) | 0.2378 (0.2649) | 0.3797 (0.3522) | 0.4361 (0.3433) | |
| 700 | YW | 0.9579 (1.0524) | 1.9606 (0.7801) | 2.8153 (2.0798) | 3.8214 (3.4814) | 0.1505 (0.0396) | 0.2460 (0.1062) | 0.3510 (0.1486) | 0.4533 (0.1570) | 0.1045 (0.1299) | 0.2182 (0.2700) | 0.3539 (0.6145) | 0.4374 (0.6807) |
| CML | 0.9426 (0.7026) | 1.9057 (0.6798) | 2.7839 (1.0909) | 3.8258 (1.5770) | 0.1483 (0.0470) | 0.2476 (0.0794) | 0.3491 (0.0916) | 0.4474 (0.1001) | 0.1079 (0.0929) | 0.2331 (0.2244) | 0.3644 (0.3245) | 0.4355 (0.3116) | |
| 1000 | YW | 1.0051 (0.7147) | 1.9646 (0.6156) | 2.8776 (1.7303) | 3.8663 (2.3715) | 0.1496 (0.0328) | 0.2524 (0.0893) | 0.3517 (0.1270) | 0.4566 (0.1312) | 0.0999 (0.0814) | 0.2095 (0.2199) | 0.3370 (0.4960) | 0.4208 (0.4699) |
| CML | 0.9934 (0.6302) | 1.9529 (0.6350) | 2.8595 (0.9824) | 3.9241 (1.3433) | 0.1482 (0.0378) | 0.2448 (0.0667) | 0.3518 (0.0779) | 0.4456 (0.0820) | 0.1025 (0.0792) | 0.2198 (0.2067) | 0.3408 (0.2881) | 0.4174 (0.2690) | |
| 1500 | YW | 0.9722 (0.6019) | 1.9837 (0.4943) | 2.9172 (1.1180) | 3.9079 (1.8497) | 0.1510 (0.0269) | 0.2485 (0.0708) | 0.3534 (0.0921) | 0.4565 (0.1039) | 0.1022 (0.0746) | 0.2069 (0.1730) | 0.3226 (0.3428) | 0.4104 (0.3708) |
| CML | 0.9990 (0.5715) | 1.9540 (0.5209) | 2.9386 (0.8077) | 3.9310 (1.1122) | 0.1487 (0.0312) | 0.2496 (0.0555) | 0.3493 (0.0639) | 0.4502 (0.0684) | 0.1016 (0.0730) | 0.2153 (0.1699) | 0.3175 (0.2455) | 0.4142 (0.2226) | |
| 2000 | YW | 0.9857 (0.5091) | 2.0112 (0.4264) | 2.9796 (0.9822) | 3.8969 (1.6045) | 0.1504 (0.0220) | 0.2519 (0.0636) | 0.3487 (0.0796) | 0.4549 (0.0931) | 0.1010 (0.0635) | 0.1941 (0.1501) | 0.3071 (0.2977) | 0.4165 (0.3226) |
| CML | 0.9869 (0.5238) | 2.0044 (0.4492) | 2.9828 (0.6768) | 3.9127 (1.0164) | 0.1493 (0.0263) | 0.2466 (0.0475) | 0.3471 (0.0568) | 0.4506 (0.0610) | 0.1016 (0.0666) | 0.2013 (0.1488) | 0.3076 (0.2037) | 0.4166 (0.2046) | |
| 3000 | YW | 0.9790 (0.4409) | 1.9745 (0.3425) | 3.0055 (0.7515) | 3.9237 (1.3427) | 0.1494 (0.0183) | 0.2507 (0.0503) | 0.3483 (0.0652) | 0.4523 (0.0684) | 0.1494 (0.0183) | 0.2507 (0.0503) | 0.3483 (0.0652) | 0.4523 (0.0684) |
| CML | 0.9982 (0.3823) | 2.0016 (0.2994) | 2.9789 (0.5914) | 4.0134 (0.8065) | 0.1505 (0.0146) | 0.2501 (0.0437) | 0.3521 (0.0540) | 0.4498 (0.0479) | 0.1030 (0.0552) | 0.1988 (0.1021) | 0.3082 (0.1769) | 0.3972 (0.2064) |
| T.V | 3 | 0.1 | 0.35 | 2 | 4 | 0.15 | 0.4 | 3 |
| N | ||||||||
| 500 | 2.6617 (1.9797) | 0.0957 (0.0493) | 0.3914 (0.2164) | 0.1811 (0.0595) | 3.8397 (2.4274) | 0.1554 (0.1013) | 0.4175 (0.3471) | 0.2858 (0.0520) |
| 700 | 2.7718 (1.8795) | 0.0993 (0.0422) | 0.3744 (0.2006) | 0.1878 (0.0477) | 3.9208 (2.1885) | 0.1509 (0.0893) | 0.4105 (0.3125) | 0.2924 (0.0414) |
| 1000 | 2.7184 (1.6915) | 0.1013 (0.0351) | 0.3801 (0.1819) | 0.1896 (0.0400) | 4.0460 (1.8685) | 0.1514 (0.0728) | 0.3915 (0.2636) | 0.2942 (0.0348) |
| 1500 | 2.9046 (1.3452) | 0.0995 (0.0285) | 0.3593 (0.1424) | 0.1941 (0.0312) | 3.9332 (1.7243) | 0.1506 (0.0598) | 0.4076 (0.2434) | 0.2963 (0.0283) |
| 2000 | 2.8613 (1.2117) | 0.1001 (0.0245) | 0.3639 (0.1281) | 0.1970 (0.0266) | 4.0189 (1.5046) | 0.1505 (0.0526) | 0.3965 (0.2123) | 0.2968 (0.0240) |
| 3000 | 2.9384 (0.9882) | 0.1007 (0.0206) | 0.3560 (0.1031) | 0.1972 (0.0227) | 4.0844 (1.2677) | 0.1507 (0.0422) | 0.3881 (0.1733) | 0.2987 (0.0195) |
| T.V | 5 | 0.2 | 0.45 | 4 | 2 | 0.25 | 0.5 | 5 |
| N | ||||||||
| 500 | 4.4673 (3.4020) | 0.2092 (0.1139) | 0.5052 (0.4420) | 0.3894 (0.0466) | 2.7288 (2.9745) | 0.2457 (0.0937) | 0.4339 (0.3079) | 0.4900 (0.0410) |
| 700 | 4.3711 (3.3367) | 0.2071 (0.0940) | 0.5197 (0.4320) | 0.3884 (0.0403) | 2.6811 (2.7833) | 0.2473 (0.0824) | 0.4395 (0.2840) | 0.4952 (0.0325) |
| 1000 | 4.6191 (3.0316) | 0.2053 (0.0773) | 0.4917 (0.3875) | 0.3943 (0.0314) | 2.5714 (2.6295) | 0.2453 (0.0683) | 0.4483 (0.2639) | 0.4949 (0.0282) |
| 1500 | 4.6576 (2.7919) | 0.2024 (0.0644) | 0.4900 (0.3537) | 0.3949 (0.0256) | 2.3840 (2.3175) | 0.2531 (0.0564) | 0.4608 (0.2303) | 0.4975 (0.0225) |
| 2000 | 4.8544 (2.5130) | 0.2060 (0.0559) | 0.4629 (0.3188) | 0.3987 (0.0213) | 2.2584 (2.1164) | 0.2491 (0.0483) | 0.4763 (0.2121) | 0.4982 (0.0186) |
| 3000 | 4.9205 (2.1632) | 0.2004 (0.0460) | 0.4502 (0.2731) | 0.3979 (0.0179) | 2.1389 (1.8643) | 0.2512 (0.0406) | 0.4851 (0.1840) | 0.4978 (0.0157) |
| Sample Size | Minimum | Maximum | Median | Mean | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| 140 | 1 | 55 | 10 |
| s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4373 | 2882 | 961 | 2222 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aries, N. On Periodic Generalized Poisson INGARCH Models. Comput. Sci. Math. Forum 2023, 7, 53. https://doi.org/10.3390/IOCMA2023-14526
Aries N. On Periodic Generalized Poisson INGARCH Models. Computer Sciences & Mathematics Forum. 2023; 7(1):53. https://doi.org/10.3390/IOCMA2023-14526
Chicago/Turabian StyleAries, Nawel. 2023. "On Periodic Generalized Poisson INGARCH Models" Computer Sciences & Mathematics Forum 7, no. 1: 53. https://doi.org/10.3390/IOCMA2023-14526
APA StyleAries, N. (2023). On Periodic Generalized Poisson INGARCH Models. Computer Sciences & Mathematics Forum, 7(1), 53. https://doi.org/10.3390/IOCMA2023-14526





