The Asymptotics of Moments for the Remaining Time of Heavy-Tail Distributions ^†

Abstract

Recent mathematical models of reliability computer systems and telecommunication networks are based on distributions with heavy tails. This paper falls into the category of exploring the classical models with heavy tails: Gnedenko–Weibull, Burr, Benktander distributions. The moment’s asymptotics for residual time have been derived especially for there heavy-tailed distributions. A simulation study is presented to give a practice characterization of the distributions with heavy tails.

1. Motivation and Background

Definition 1. 

One defines a cumulative distribution function (DF) F to be (right-) heavy-tailed if and only if

$$\underset{x\to +\infty }{lim}{e}^{\lambda x}\overline{F}\left(x\right)=\infty$$

for the tail: $\overline{F}=1-F$ and for all $\lambda >0$.

Thus, one can say that the tail of a distribution (tending to zero) is heavy-tailed if it fails to be bounded by a decreasing exponential function.

Definition 2. 

A cumulative distribution function F is called light-tailed if and only if it fails to be heavy-tailed.

The slow decrease in the tail of a distribution leads to the fact that a random variable can take on very large values with a positive probability. Therefore, such distributions are used to model phenomena that are subject to strong fluctuations. Thus, the sample predominately contains relatively small values, but also has a sufficient number of very large values as illustrated by the plot in Figure 1 for 200 realisations of independent, identically distributed random variables for heavy- (Gnedenko–Weibull DF with less then one shape parameter) and light-tailed (exponential) DF.

Innovated mathematical models of computer systems and telecommunication networks have presented well-characterized heavy-tailed distributions. For example, the superposition of ON/OFF processes with a heavy-tailed distribution was presented in [1]. Such processes converge to a self-similar (fractal) process with self-similarity Hurst exponent $H=\left(3-\alpha \right)/2$, where $0<\alpha <2$ is the tail index (or coefficient of heavy-tailedness).

It is well known that there is a correspondence between the generated traffic and actual Ethernet traffic. Empirical self-similar processes of Ethernet traffic remain unchanged at varying time scales unlike Poisson processes, which flatten out as time scales change.

Let X be a non-negative random variable with a cumulative distribution function F. Consider the random variable $X_t=(X-t\left|X>t\right.)$, which in survival analysis called the residual life time with distribution function $F_t$ or distribution of the excess over a threshold t. The function

$${\overline{F}}_t\left(x\right)=1-F_t\left(x\right)=P(X-t>x\left|X>t\right)$$

is known as the distribution tail. The mathematical expectation of a random variable $X_t$ is the mean residual life (MRL) or mean excess function (ME). The ME term is used in risk management, actuarial science and other extreme value problems. This function is defined as

$$\mu \left(t\right)=E(X-t\left|X>t\right.)=\underset{t}{\overset{+\infty }{\int }}\overline{F}\left(x\right)dx/\overline{F}\left(t\right)$$

(1)

and the residual variance (excess variance) is defined by

$${\sigma }^2\left(t\right)=E\left(X_t^2\right)-{\mu }^2\left(t\right)=\frac{2}{\overline{F}\left(t\right)}\underset{t}{\overset{+\infty }{\int }}\overline{F}\left(x\right)·\mu \left(x\right)dx-{\mu }^2\left(t\right).$$

(2)

The physical application of the MRL to the reliability of the "well–pump" system has been reported in [2].

On the other hand, the accuracy of the simulation obtained depends on the accuracy of the approximation of the distributions with a heavy tail. In model selection it is advisable to study the residual lifetime in terms of its moments for relatively small t. A more precise asymptotic expansion of moments is required. We have obtained new asymptotic expansion terms of the mean excess function (mean residual) and residual variance asymptotic expansion for known distributions.

The paper is organized as follows. In Section 2, we consider the problem of asymptotics of the residual lifetime distribution (mean excess function) for classical models (Tables 1.25, 1.2.6 in [3]). We derive some refinements of asymptotic expansions from (Table 3.4.7 in [3], p. 161). Asymptotic expansions of the residual variance are also obtained.

2. Residual Moments for Heavy Tails

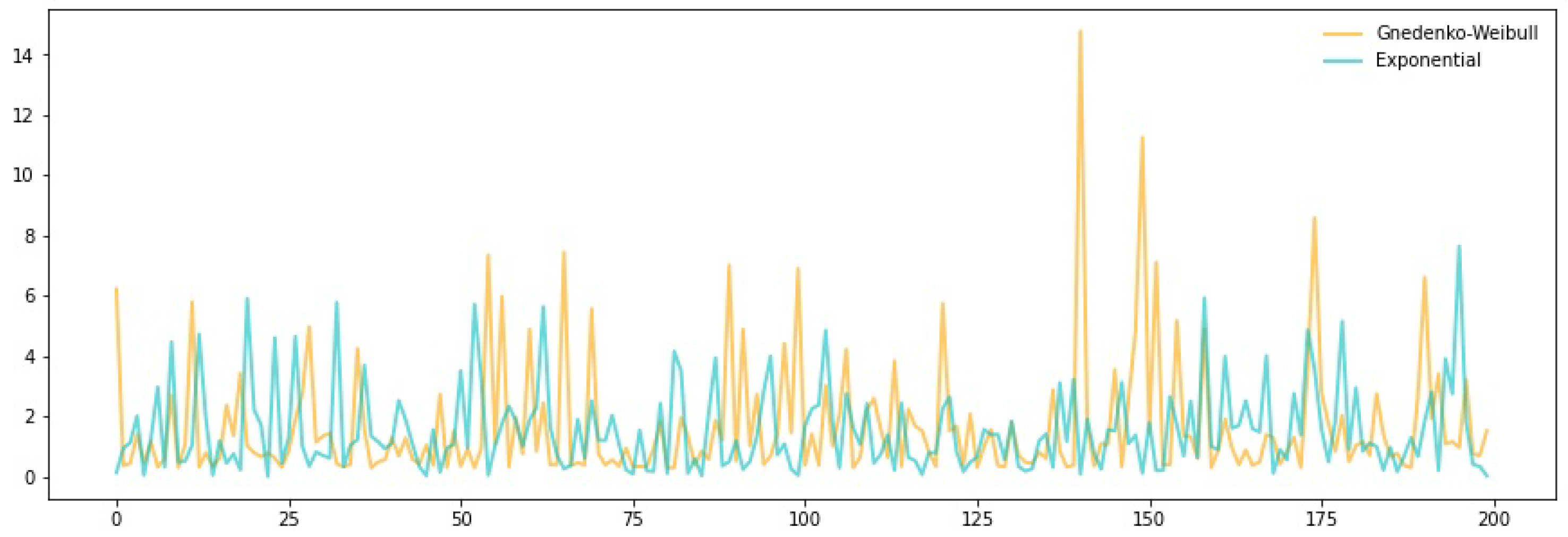
2.1. Gnedenko–Weibull Distribution

The tail two-parameter Gnedenko–Weibull distribution

$$\overline{F}(t;\alpha ,\beta )=e^{-{\left(\alpha t\right)}^{\beta }},t\ge 0$$

is heavy tailed if $0<\alpha ,0<\beta <1$.

Let T be a random variable with a two-parameter Gnedenko–Weibull distribution, then $\forall \alpha >0,\forall \beta >0$ holds

$$\mu \left(t\right)=\frac{t}{\beta {\left(\alpha t\right)}^{\beta }}\left(1+\frac{1-\beta }{\beta {\left(\alpha t\right)}^{\beta }}+\frac{(1-\beta )(1-2\beta )}{{\beta }^2{\left(\alpha t\right)}^{2\beta }}+O\left(\frac{1}{t^{3\beta }}\right)\right),\mathrm{as}t\to \infty ,$$

(3)

$${\sigma }^2\left(t\right)=\frac{1}{{\beta }^2{\alpha }^{2\beta }{t}^{2(\beta -1)}}\left(1+\frac{4(1-\beta )}{\beta {\left(\alpha t\right)}^{\beta }}+\frac{(1-\beta )(11-17\beta )}{{\beta }^2{\left(\alpha t\right)}^{2\beta }}+O\left(\frac{1}{t^{3\beta }}\right)\right),\mathrm{as}t\to \infty .$$

(4)

The proof of the asymptotic expressions for the MRL and residual variance is considered in [4].

2.2. Benktander Type I Distribution

The Benktander type I distribution is close to a log normal distribution. These distributions are used to model heavy-tailed losses in actuarial science. Theoretically predicted sizes by Benktander type I distributions are consistent with statistical size distributions in economics and actuarial sciences. The Benktander type I distribution function tail is given by

$$1-F\left(x\right)=\left(1+2\frac{\beta }{\alpha }lnx\right)e^{-\beta {\left(lnx\right)}^2-\left(\alpha +1\right)lnx},\alpha >0,\beta >0,x>0.$$

It then follows that

$$\underset{t}{\overset{\infty }{\int }}\left(1-F\left(x\right)\right)dx=\underset{t}{\overset{\infty }{\int }}\left(1+2\frac{\beta }{\alpha }lnx\right)e^{-\beta {\left(lnx\right)}^2-\left(\alpha +1\right)lnx}dx=$$

$$=\underset{lnt}{\overset{\infty }{\int }}\left(1+2\frac{\beta }{\alpha }z\right)e^{-\beta {\left(z\right)}^2-\left(\alpha +1\right)z}{e}^{z}dz=\underset{lnt}{\overset{\infty }{\int }}\left(1+2\frac{\beta }{\alpha }z\right)e^{-\beta z^2-\alpha z}dz=$$

$$=\underset{lnt}{\overset{\infty }{\int }}\left(1+2\frac{\beta }{\alpha }z\right)e^{-\beta \left(z^2+\frac{\alpha }{\beta }z\right)}dz.$$

Let $\gamma =\frac{\beta }{\alpha }$. The mean excess function is directly calculated as:

$$\underset{lnt}{\overset{\infty }{\int }}\left(1+2\gamma z\right)e^{-\beta \left(z^2+\gamma z\right)}dz=\underset{lnt}{\overset{\infty }{\int }}\left(1+2\gamma z\right)e^{-\frac{\beta }{\gamma }\left(\gamma z^2+z\right)}dz=$$

$$=\underset{lnt}{\overset{\infty }{\int }}{e}^{-\frac{\beta }{\gamma }\left(\gamma z^2+z\right)}d\left(\gamma z^2+z\right)=-\frac{\gamma }{\beta }\underset{lnt}{\overset{\infty }{\int }}{e}^{-\frac{\beta }{\gamma }\left(\gamma z^2+z\right)}d\left(-\frac{\beta }{\gamma }\right)\left(\gamma z^2+z\right)=$$

$$={\left.-\frac{\gamma }{\beta }{e}^{-\frac{\beta }{\gamma }\left(\gamma z^2+z\right)}\right|}_{lnt}^{\infty }=\frac{\gamma }{\beta }{e}^{-\frac{\beta }{\gamma }\left(\gamma {\left(lnt\right)}^2+lnt\right)}=\frac{1}{\alpha }{e}^{-\alpha \left(\frac{\beta }{\alpha }{\left(lnt\right)}^2+lnt\right)};$$

$$\mu \left(t\right)=\frac{\underset{t}{\overset{+\infty }{\int }}\left(1-F\left(x\right)\right)dx}{1-F\left(t\right)}=\frac{\frac{1}{\alpha }{e}^{-\alpha \left(\frac{\beta }{\alpha }{\left(lnt\right)}^2+lnt\right)}}{\left(1+2\frac{\beta }{\alpha }lnt\right)e^{-\beta {\left(lnt\right)}^2-\left(\alpha +1\right)lnt}}=$$

$$=\frac{e^{-\beta {\left(lnt\right)}^2}{t}^{-\alpha }}{\left(\alpha +2\beta lnt\right)e^{-\beta {\left(lnt\right)}^2}{t}^{-\alpha -1}}=\frac{t}{\alpha +2\beta lnt}.$$

Thus, the Benktander type I distribution has the following exact equality for the mean exceedance:

$$\mu \left(t\right)=\frac{t}{\alpha +2\beta lnt}.$$

(5)

Note that (5) is contained in the Table 3.4.7 in [3], p.161, without proof. The proof is given for completeness.

From the above results and the presentation of the integral

$$\underset{x}{\overset{\infty }{\int }}{e}^{-z^2}dz=e^{-x^2}\left(\frac{1}{2x}+\frac{1}{4x^3}+O\left(\frac{1}{x^5}\right)\right),\mathrm{as}x\to \infty ,$$

it follows

$$\underset{t}{\overset{+\infty }{\int }}(1-F(x\left)\right)·\mu \left(x\right)dx=\frac{1}{\alpha }\underset{t}{\overset{+\infty }{\int }}{e}^{-\beta {\left(lnx\right)}^2-\left(\alpha +1\right)lnx}xdx=$$

$$=\frac{1}{\alpha }\underset{lnt}{\overset{\infty }{\int }}{e}^{-\beta {\left(z\right)}^2-\left(\alpha +1\right)z}{e}^{2z}dz=\frac{1}{\alpha }\underset{lnt}{\overset{\infty }{\int }}{e}^{-\beta {\left(z\right)}^2-\alpha z+z}dz=$$

$$=\frac{e^{\frac{{\left(\alpha -1\right)}^2}{4\beta }}}{\alpha }\underset{lnt}{\overset{\infty }{\int }}{e}^{-\beta {\left(z+\frac{\alpha -1}{2\beta }\right)}^2}d\left(z+\frac{\alpha -1}{2\beta }\right)=\frac{e^{\frac{{\left(\alpha -1\right)}^2}{4\beta }}}{\alpha \sqrt{\beta }}\underset{\sqrt{\beta }\left(lnt+\frac{\alpha -1}{2\beta }\right)}{\overset{\infty }{\int }}{e}^{-u^2}du=$$

$$=\frac{e^{\frac{{\left(\alpha -1\right)}^2}{4\beta }}}{\alpha \sqrt{\beta }}{e}^{-\beta {\left(lnt+\frac{\alpha -1}{2\beta }\right)}^2}\left[\frac{1}{2\sqrt{\beta }\left(lnt+\frac{\alpha -1}{2\beta }\right)}+\frac{1}{4{\left(\sqrt{\beta }\left(lnt+\frac{\alpha -1}{2\beta }\right)\right)}^3}+\cdots \right].$$

The residual variance, according to (2) and the above asymptotics, is derives by the equation

$${\sigma }^2\left(t\right)=\frac{2\alpha }{\alpha +2\beta lnt}·e^{\beta {\left(lnt\right)}^2+\left(\alpha +1\right)lnt}·\frac{e^{\frac{{\left(\alpha -1\right)}^2}{4\beta }}}{\alpha \sqrt{\beta }}{e}^{-\beta {\left(lnt+\frac{\alpha -1}{2\beta }\right)}^2}\times$$

$$\times \left[\frac{1}{2\sqrt{\beta }\left(lnt+\frac{\alpha -1}{2\beta }\right)}+\frac{1}{4{\left(\sqrt{\beta }\left(lnt+\frac{\alpha -1}{2\beta }\right)\right)}^3}+O\left(\frac{1}{{\left(lnt\right)}^5}\right)\right]-\frac{t^2}{{\left(\alpha +2\beta lnt\right)}^2}=$$

$$=\frac{2t^2}{\alpha +2\beta lnt}·\left[\frac{1}{\left(2\beta lnt+\alpha -1\right)}+\frac{1}{4\beta {\left(lnt+\frac{\alpha -1}{2\beta }\right)}^3}+O\left(\frac{1}{{\left(lnt\right)}^5}\right)\right]-\frac{t^2}{{\left(\alpha +2\beta lnt\right)}^2}=$$

$$=\frac{t^2}{\alpha +2\beta lnt}\left[\frac{2}{\left(2\beta lnt+\alpha -1\right)}-\frac{1}{\left(2\beta lnt+\alpha \right)}+\frac{4{\beta }^2}{{\left(2\beta lnt+\alpha -1\right)}^3}+O\left(\frac{1}{{\left(lnt\right)}^5}\right)\right]=$$

$$=\frac{t^2}{{\left(\alpha +2\beta lnt\right)}^2}\left[\frac{2\beta lnt+\alpha +1}{\left(2\beta lnt+\alpha -1\right)\left(2\beta lnt+\alpha \right)}+O\left(\frac{1}{{\left(lnt\right)}^3}\right)\right]=$$

$$=\frac{t^2}{{\left(\alpha +2\beta lnt\right)}^2}\left[1+\frac{2}{2\beta lnt+\alpha -1}+O\left(\frac{1}{{\left(lnt\right)}^3}\right)\right]\mathrm{as}t\to \infty .$$

Hence,

$${\sigma }^2\left(t\right)=\frac{t^2}{{\left(\alpha +2\beta lnt\right)}^2}\left[1+\frac{2}{2\beta lnt+\alpha -1}+O\left(\frac{1}{{\left(lnt\right)}^3}\right)\right], \mathrm{as}t\to \infty .$$

(6)

By binomial expansion, one can derive the residual standard deviation

$$\sigma \left(t\right)=\frac{t}{\alpha +2\beta lnt}\left[1+\frac{1}{2\beta lnt+\alpha -1}-\frac{1}{4}·\frac{1}{{\left(2\beta lnt+\alpha -1\right)}^2}+o\left(\frac{1}{{\left(lnt\right)}^2}\right)\right],$$

(7)

$$\mathrm{as}t\to \infty .$$

2.3. Benktander Type II Distribution

This distribution is similar to the Gnedenko–Weibull distribution. The formula Benktander type II average residual resource looks like the asymptotics of the average residual resource of the Weibull distribution. However, it is an exact equality, yet for the residual variance there is only an asymptotic expansion. Consider the Benktander type II distribution with distribution tail

$$1-F\left(t\right)=e^{\frac{\alpha }{\beta }}{t}^{\beta -1}{e}^{-\frac{\alpha }{\beta }{t}^{\beta }}\alpha >0,0<\beta <1.$$

(8)

It is immediately follows from (1), see Table 3.4.7 in [3]

$$\mu \left(t\right)=\frac{1}{\alpha }{t}^{1-\beta },\alpha >0,0<\beta <1.$$

(9)

Using the presentation in (9) of $\mu \left(t\right)$ the following formula is derived

$$\underset{t}{\overset{+\infty }{\int }}(1-F(x\left)\right)·\mu \left(x\right)dx=\frac{e^{\frac{\alpha }{\beta }}}{\alpha }\underset{t}{\overset{+\infty }{\int }}{e}^{-\frac{\alpha }{\beta }{x}^{\beta }}dx.$$

Substituting $z=\frac{\alpha }{\beta }{x}^{\beta }$ into the integral above we obtain

$$\underset{t}{\overset{+\infty }{\int }}{e}^{-\frac{\alpha }{\beta }{x}^{\beta }}dx=\frac{{\beta }^{\frac{1}{\beta }-1}}{{\alpha }^{\frac{1}{\beta }}}\underset{\frac{\alpha }{\beta }{t}^{\beta }}{\overset{+\infty }{\int }}{e}^{-z}{z}^{\frac{1}{\beta }-1}dz=\frac{{\beta }^{\frac{1}{\beta }-1}}{{\alpha }^{\frac{1}{\beta }}}\mathsf{\Gamma }\left(\frac{1}{\beta },\frac{\alpha }{\beta }{t}^{\beta }\right),$$

(10)

where $\mathsf{\Gamma }\left(a,x\right)$ is an incomplete gamma function:

$$\mathsf{\Gamma }\left(a,x\right)=\frac{1}{\mathsf{\Gamma }\left(a\right)}\underset{x}{\overset{+\infty }{\int }}{e}^{-t}{t}^{a-1}dt.$$

The presentation in (2) and formula (10) give

$${\sigma }^2\left(t\right)=\frac{2}{e^{\frac{\alpha }{\beta }}{t}^{\beta -1}{e}^{-\frac{\alpha }{\beta }{t}^{\beta }}}\frac{e^{\frac{\alpha }{\beta }}}{\alpha }\frac{{\beta }^{\frac{1}{\beta }-1}}{{\alpha }^{\frac{1}{\beta }}}\mathsf{\Gamma }\left(\frac{1}{\beta },\frac{\alpha }{\beta }{t}^{\beta }\right)-\frac{t^{2-2\beta }}{{\alpha }^2}.$$

Thus, for the residual variance an exact equality is obtained using an incomplete gamma function:

$${\sigma }^2\left(t\right)=\frac{2t^{1-\beta }}{e^{-\frac{\alpha }{\beta }{t}^{\beta }}}\frac{{\beta }^{\frac{1}{\beta }-1}}{{\alpha }^{\frac{1}{\beta }+1}}\mathsf{\Gamma }\left(\frac{1}{\beta },\frac{\alpha }{\beta }{t}^{\beta }\right)-\frac{t^{2-2\beta }}{{\alpha }^2}.$$

(11)

Formula 8.357 from [5] immediately leads to the expansion of the incomplete gamma function in (10)

$$\mathsf{\Gamma }\left(\frac{1}{\beta },\frac{\alpha }{\beta }{t}^{\beta }\right)=$$

$$={\left(\frac{\alpha }{\beta }\right)}^{\frac{1}{\beta }-1}{t}^{1-\beta }{e}^{-\frac{\alpha }{\beta }{t}^{\beta }}\left(1-\frac{\beta \left(1-\frac{1}{\beta }\right)}{\alpha }{t}^{-\beta }+\frac{{\beta }^2\left(1-\frac{1}{\beta }\right)\left(2-\frac{1}{\beta }\right)}{{\alpha }^2}{t}^{-2\beta }+O\left(t^{-3\beta }\right)\right),$$

$$\mathrm{as}t\to \infty .$$

By inserting asymptotics from the above into (11), it follows that

$${\sigma }^2\left(t\right)=$$

$$=2\frac{t^{2-2\beta }}{\alpha }\left(1-\frac{\left(\beta -1\right)}{\alpha }{t}^{-\beta }+\frac{\left(\beta -1\right)\left(2\beta -1\right)}{{\alpha }^2}{t}^{-2\beta }+O\left(t^{-3\beta }\right)\right)-\frac{t^{2-2\beta }}{{\alpha }^2}=$$

$$=\frac{t^{2-2\beta }}{{\alpha }^2}\left(1-2\frac{\left(\beta -1\right)}{\alpha }{t}^{-\beta }+2\frac{\left(\beta -1\right)\left(2\beta -1\right)}{{\alpha }^2}{t}^{-2\beta }+O\left(t^{-3\beta }\right)\right),\mathrm{as}t\to \infty .$$

Finally, the following asymptotic result is found for the residual variance of a Benktander type II distribution

$${\sigma }^2\left(t\right)=\frac{t^{2-2\beta }}{{\alpha }^2}\left(1-2\frac{\left(\beta -1\right)}{\alpha }{t}^{-\beta }+2\frac{\left(\beta -1\right)\left(2\beta -1\right)}{{\alpha }^2}{t}^{-2\beta }+O\left(t^{-3\beta }\right)\right),\mathrm{as}t\to \infty ,$$

(12)

and residual standard deviation

$$\sigma \left(t\right)=\frac{t^{1-\beta }}{\alpha }\left(1-\frac{\left(\beta -1\right)}{\alpha }\frac{1}{t^{\beta }}+\frac{\left(\beta -1\right)\left(2\beta -1\right)}{{\alpha }^2}\frac{1}{t^{2\beta }}+O\left(\frac{1}{t^{3\beta }}\right)\right),\mathrm{as}t\to \infty .$$

(13)

2.4. Burr Distribution

The Burr distribution or Burr Type XII distribution (see [6]) is popular as a fit model for a set of insurance data. The following representations are obtained for the Burr distribution moments:

$$\mu \left(t\right)=\frac{t}{ck-1}\left[1+\frac{ck}{ck-1+c}·\frac{1}{t^c}+\frac{ck\left(1-c\right)}{\left(ck-1+c\right)\left(ck-1+2c\right)}·\frac{1}{t^{2c}}+o\left(\frac{1}{t^{2c}}\right)\right];$$

$${\sigma }^2\left(t\right)=\frac{ck}{{\left(ck-1\right)}^2}·t^2·\left[\frac{1}{ck-2}+\frac{2c\left(k+1\right)}{\left(ck-1+c\right)\left(ck-2+c\right)}·\frac{1}{t^c}+o\left(\frac{1}{t^c}\right)\right],\mathrm{as}t\to \infty .$$

3. Conclusions

We illustrated the behaviour of the empirical composite samples for some simulated datasets of heavy-tailed distributions in Section 1. The explicit accurate innovated asymptotic expansions were found for the MRL (ME) and residual variance for well-known models from Table 3.4.7 in [3], p. 161. By applying the Balkema de Haan [7] criterion, one may find that these distributions belong (or not) to the attraction exponential distribution.