The J-Band of J-Aggregates as the Egorov Nano-Resonance ^†

Abstract

The well-known narrow and intense optical absorption J-band was discovered experimentally by Jelley and independently Scheibe in 1936. In 1938, Franck and Teller, associating the appearance of the J-band with the formation of molecular J-aggregates, gave a theoretical explanation for the J-band based on the Frenkel exciton model. This explanation has been developed in detail over a long period of time by many authors, including the author of this paper. The main shortcoming of all those explanations is the inability to explain the shape of the dye monomer bands from which J-aggregates are formed. In this mini-review, the author gives an explanation of the J-band as the so-called Egorov nano-resonance discovered in a new theory, quantum–classical mechanics, which includes an explanation of the shape of monomer bands.

1. Introduction

The well-known optical absorption J-band arises as a result of the formation of J-aggregates of polymethine dyes in their aqueous solutions. Compared to dye monomers, this band is narrow, high-intensity, and redshifted. The narrowness and high intensity of the J-band are used in many applications, in particular in the development of modern dye lasers. The J-band was discovered experimentally by Jelley and independently by Scheibe in 1936 [1,2]. In 1938, Franck and Teller [3] gave a theoretical explanation of the J-band based on the Frenkel exciton model. In 1984, based on the same exciton model, Knapp explained the shape of the J-band [4]. Subsequently, within the framework of the Frenkel exciton model, the shape of the J-band was studied by a large number of theorists, including the author of this paper [5]. The author’s reviews [6,7] discuss the fundamental shortcomings of the exciton model of the J band. In particular, a significant drawback of this model is its inability to explain the optical bands of dye monomers from which J-aggregates are formed [6,7,8]. The author gives an alternative explanation of the nature of the J-band in the framework of a new fundamental physical theory—the quantum–classical mechanics of elementary electron transfers in condensed matter—which also explains the nature of the band shapes of the dye monomers that form J-aggregates [8]. This theory is the simplest case of quantum–classical mechanics, where one can take the Green’s function of the free electron motion (propagator) as the electronic Green’s function and also neglect local phonons and take into account only non-local phonons. Quantum–classical mechanics is a significantly modified quantum mechanics, in which the initial and final states of the “electron + nuclear environment” system and its “quantum” transitions are quantum in the adiabatic approximation, and the transient chaotic electron–nuclear(–vibrational) state is classical due to chaos [8]. This chaos is called dozy chaos. The new explanation of the nature and shape of the J-band is based on the so-called Egorov nano-resonance discovered in quantum–classical mechanics of elementary electron transfers [8]. Egorov nano-resonance is an electron–nuclear–reorganization resonance during quantum–classical transitions in the optical chromophore under the condition of weak dozy chaos in the electron–nuclear(–vibrational) transient state.

2. Result for the Shape of the Optical Absorption Band from Quantum–Classical Mechanics of Elementary Electron Transfers and Egorov Nano-Resonance

When using the Einstein model ${\omega }_{\kappa }=\mathrm{constant}\equiv \omega$, the result for the optical absorption $K=K(\Omega )$ (where $\Omega$ is the frequency of light) is given by the following equations [9,10,11]:

$$K=K_0\exp W,$$

(1)

$$\begin{gathered} W=\frac{1}{2}\ln \left(\frac{\omega \tau \sinh {\beta }_T}{4\pi \cosh t}\right)-\frac{2}{\omega \tau }\left(\coth {\beta }_T-\frac{\cosh t}{\sinh {\beta }_T}\right) \\ +\left({\beta }_T-t\right)\frac{1}{\omega \tau \Theta }-\frac{\sinh {\beta }_T}{4\omega \tau {\Theta }^2\cosh t}, \end{gathered}$$

(2)

$$1<<\frac{1}{\omega \tau \Theta }\le \frac{2\cosh t}{\omega \tau \sinh {\beta }_T},$$

(3)

where ${\beta }_T\equiv \hslash \omega /2k_{\mathrm{B}}T$, and $T$ is the absolute temperature,

$$t=\frac{\omega {\tau }_{\mathrm{e}}}{\theta }\left[\frac{AC+BD}{A^2+B^2}+\frac{2\Theta \left(\Theta -1\right)}{{\left(\Theta -1\right)}^2+{\left(\Theta /{\theta }_0\right)}^2}+\frac{{\theta }_0^2}{{\theta }_0^2+1}\right],$$

(4)

$$\left|{\theta }_0\right|>>\frac{E}{2J_1},$$

(5)

$$\theta \equiv \frac{{\tau }_{\mathrm{e}}}{\tau }=\frac{L E}{\hslash \sqrt{2J_1/m}}, \Theta \equiv \frac{{\tau }^{\prime }}{\tau }=\frac{E}{\Delta }, {\theta }_0\equiv \frac{{\tau }_0}{\tau }=\frac{E}{\gamma },$$

(6)

$${\tau }_{\mathrm{e}}=\frac{L}{\sqrt{2J_1/m}}, \tau =\frac{\hslash }{E}, {\tau }^{\prime }=\frac{\hslash }{\Delta }, {\tau }_0=\frac{\hslash }{\gamma }.$$

(7)

Here, we use the notation

$$A=\cos \left(\frac{\theta }{{\theta }_0}\right)+\Lambda +{\left(\frac{1}{{\theta }_0}\right)}^2\mathrm{N},$$

(8)

$$B=\sin \left(\frac{\theta }{{\theta }_0}\right)+\frac{1}{{\theta }_0}\mathrm{M},$$

(9)

$$C=\theta \left[\cos \left(\frac{\theta }{{\theta }_0}\right)-\frac{1-{\xi }^2}{2{\theta }_0}\sin \left(\frac{\theta }{{\theta }_0}\right)\right]+\mathrm{M},$$

(10)

$$D=\theta \left[\sin \left(\frac{\theta }{{\theta }_0}\right)+\frac{1-{\xi }^2}{2{\theta }_0}\cos \left(\frac{\theta }{{\theta }_0}\right)\right]-\frac{2}{{\theta }_0}\mathrm{N},$$

(11)

and

$$\xi \equiv {\left(1-\frac{E}{J_1}\right)}^{1/2}\hspace{1em}(J_1>E \mathrm{by} \mathrm{definition}),$$

(12)

and where we finally have

$$\Lambda =-{\left(\Theta -1\right)}^2\mathrm{E}+\left[\frac{\left(\Theta -1\right)\theta }{\rho }+\Theta \left(\Theta -2\right)\right]{\mathrm{E}}^{\frac{1-\rho }{1-\xi }},$$

(13)

$$\mathrm{M}=2\Theta \left(\Theta -1\right)\mathrm{E}-\left[\frac{\left(2\Theta -1\right)\theta }{\rho }+2\Theta \left(\Theta -1\right)\right]{\mathrm{E}}^{\frac{1-\rho }{1-\xi }},$$

(14)

$$\mathrm{N}=\Theta \left[\Theta \mathrm{E}-\left(\frac{\theta }{\rho }+\Theta \right){\mathrm{E}}^{\frac{1-\rho }{1-\xi }}\right],$$

(15)

$$\mathrm{E}\equiv \exp \left(\frac{2\theta }{1+\xi }\right),\hspace{1em}\rho \equiv \sqrt{{\xi }^{ 2}+\frac{1-{\xi }^{ 2}}{\Theta }}.$$

(16)

The factor $K_0$ becomes

$$K_0=K_0^e{K}_0^p,$$

(17)

where

$$K_0^e=\frac{2{\tau }^3{J}_1}{m}\frac{\left(A^2+B^2\right){\rho }^3{\Theta }^4\xi }{{\theta }^2{\left[{\left(\Theta -1\right)}^2+{\left(\frac{\Theta }{{\theta }_0}\right)}^2\right]}^2\left[1+{\left(\frac{1}{{\theta }_0}\right)}^2\right]}\cdot \eta ,$$

(18)

and

$$\eta \equiv \exp \left(-\frac{4\theta }{1-{\xi }^2}\right),$$

(19)

and

$$K_0^p=\frac{1}{\omega \tau }{\left[1+\frac{\sinh \left({\beta }_T-2t\right)}{\sinh {\beta }_T}\right]}^2+\frac{\cosh \left({\beta }_T-2t\right)}{\sinh {\beta }_T}.$$

(20)

In Equations (6) and (7), $\Delta$ is thermal energy, which is included in the energy conservation law:

$$\hslash \Omega =J_1-J_2+\Delta ,$$

(21)

where $J_1$ and $J_2$ are the binding energies of the electron at the donor and acceptor (1 and 2); $E$ is the nuclear reorganization energy; $\gamma$ is the dozy chaos energy [6,7]; L is the donor–acceptor distance or the length of the polymethine chain—the main optical chromophore of polymethine dyes [6,7,9,10,11,12,13]; and $m$ is the effective mass of the electron. The time scales given by Equation (7) are discussed in [6,7,9,11,12], where

$${\tau }_{\mathrm{e}}=\frac{L}{\sqrt{2J_1/m}}$$

(22)

and

$$\tau =\frac{\hslash }{E}$$

(23)

are included in the Egorov nano-resonance as follows:

$${\left(2{\tau }_e\right)}^{-1}={\tau }^{-1}.$$

(24)

The extinction coefficient $\epsilon$, measured in the experiment, is related to the optical absorption $K$ by the equation [14]:

$$\epsilon =\frac{4{\pi }^2{q}^2{N}_{\mathrm{A}}\Omega }{3\hslash c{n}_{\mathrm{ref}}}K,$$

(25)

where $q$ is the electron charge transferred in a quantum–classical transition and $N_{\mathrm{A}}$ is the Avogadro constant.

3. Adaptation of Quantum–Classical Mechanics of Elementary Electron Transfers to Quantum–Classical Transitions in Extended Polymethine Chromophores

The possibility of applying of quantum–classical mechanics of elementary electron transfers to quantum–classical transitions in polymethine dyes is based on the sufficiently long length of the polymethine chain—the main optical chromophore of polymethine dyes—and on the alternation of the electronic charge on carbon atoms along the chain (see Figure 1), which alternatively redistributes upon optical excitation. This fact of the redistribution can be described as the sum of many acts of short elementary transfers of an electron charge, interacting with the nuclear environment, along a sequence of methine groups that quickly follow each other [12,13]. The short-distance electron-charge transfers within a polymethite chain make it possible to almost completely neglect the tunneling effects and take the tunneling factor $\eta$ close to unity [6,7,10,11,12,13] (see above, Section 2, Equations (18) and (19), $\eta \le 1$). This picture also assumes taking into account the interaction of transferred charges only with vibrations of the nuclei of the medium and neglecting the interaction of charges with intramolecular vibrations, which is justified for sufficiently long polymethine chains $L$ when the number of effective vibrational modes of the nuclei of the environment significantly exceeds the number of effective intramolecular modes. Therefore, due to the dominant role of nonlocal phonons, the Egorov nano-resonance (22)–(24) is already observed for polymethine dye monomers (see below, Figure 2a), and not only for J-aggregates (see below, Section 4); see discussion above in Section 1.

Experimentally, the Egorov nano-resonance is observed by changing the shape and intensity of optical absorption bands with a change in chain length L (Figure 2a).

Figure 2b shows the fitting of the theoretical shape of the optical band (1)–(21), (25) to the well-known experimental data of Brooker et al. [18]. The Egorov nano-resonance corresponds to a band with n = 3 or chain length L = 1.4 nm.

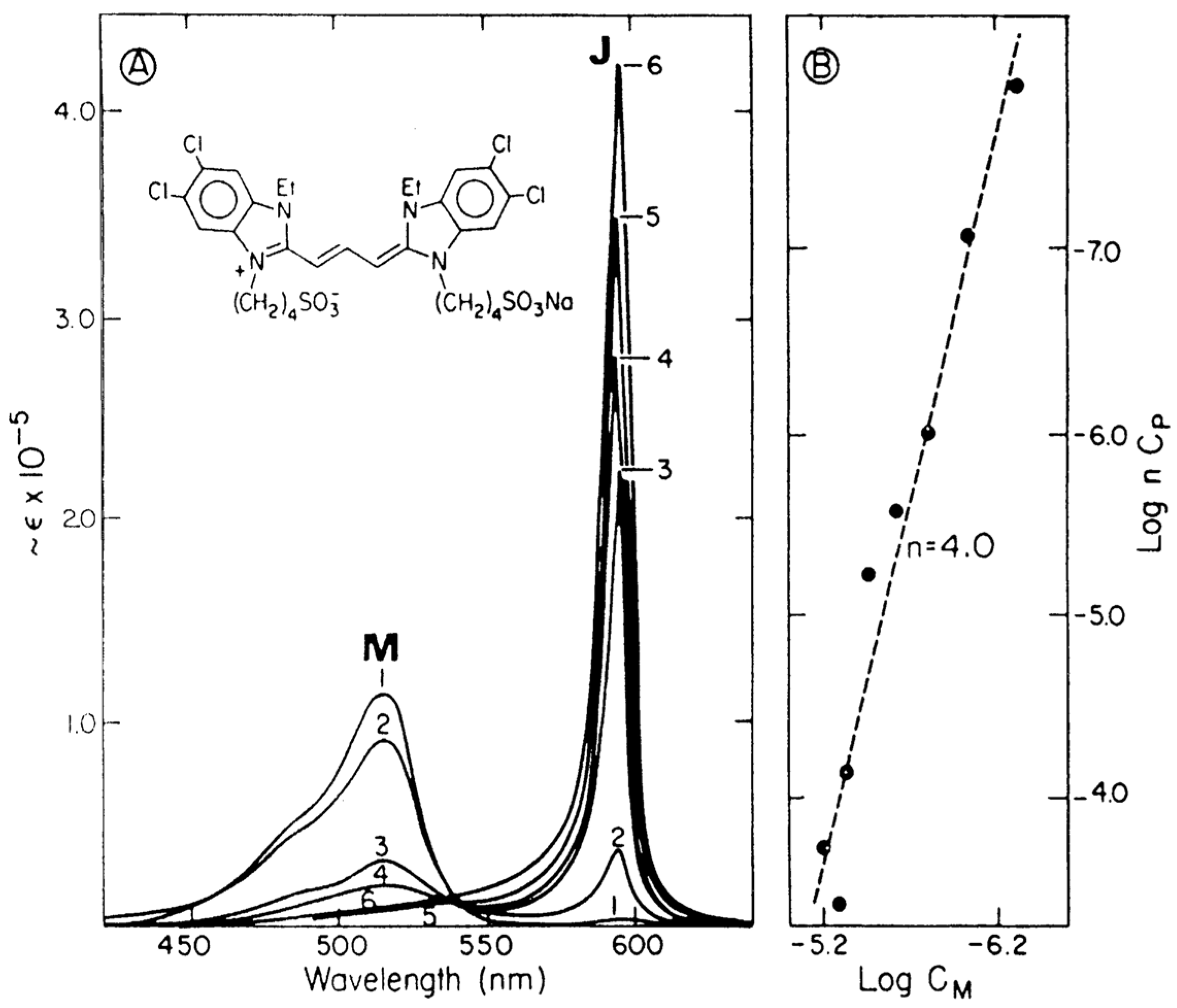
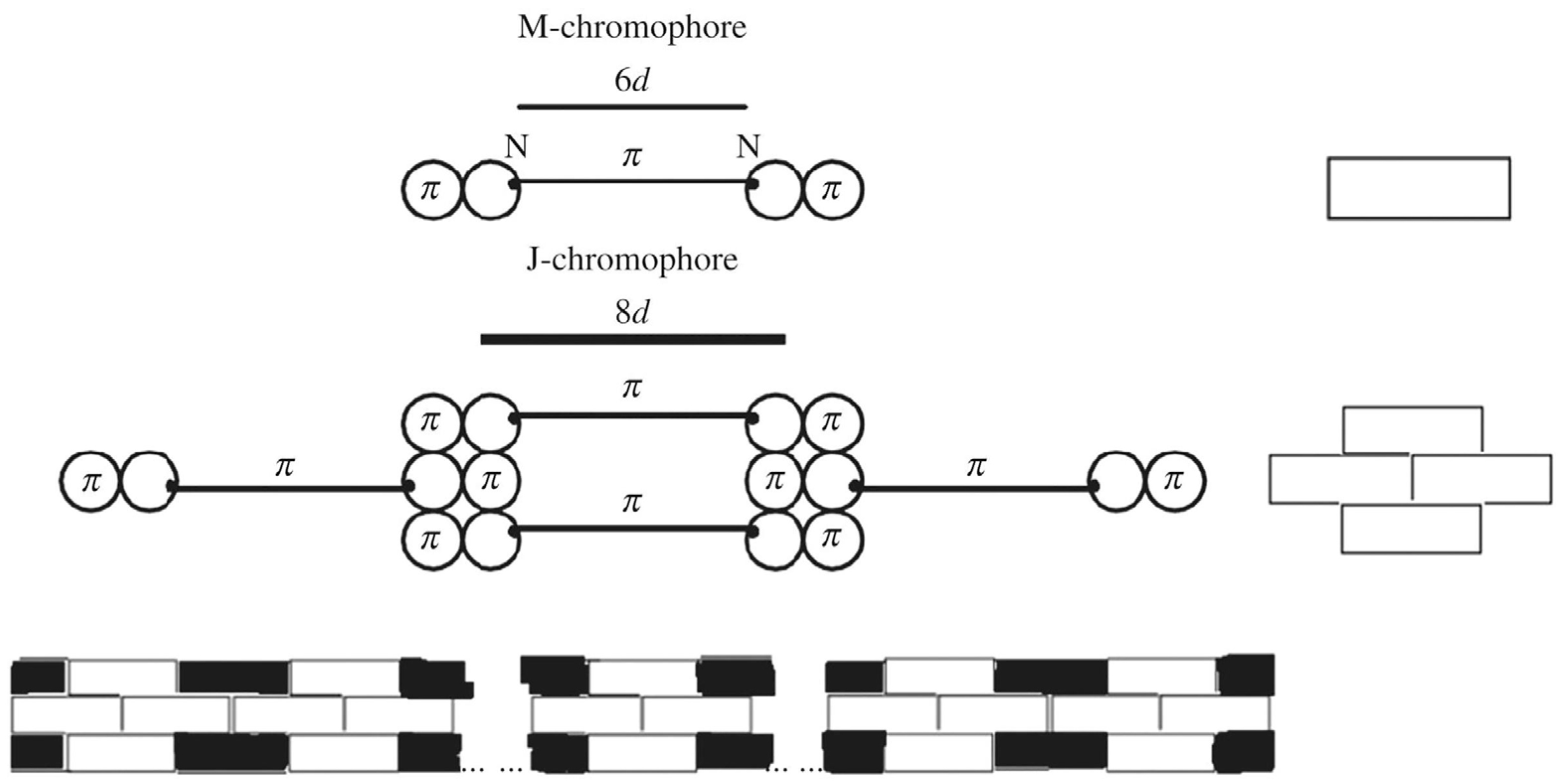
4. Explanation of the J-Band of J-Aggregates by Egorov Nano-Resonance

Figure 3 (top) shows the well-known experimental data of Herz [17,20], obtained by increasing the concentration of the polymethine dye, benzimidazolocarbocyanine, in an aqueous solution, which leads to the formation of J-aggregates in it.

From the law of mass action, Herz showed that the optical chromophore of the J-aggregate consists of four dye monomer molecules. Following Hans Kuhn (see [21] and references therein), Herz [20] suggested that the J-aggregate forms a brickwork-like structure from the dye monomers.

Figure 4 shows the scheme for the formation of an optical J-chromophore from four dye monomers and the scheme for the formation of the entire J-aggregate, which has the form of a long thin rod [6,7,10,11,12,13] with a brickwork-like structure.

Figure 3 (bottom) shows the result of fitting the theoretical band shape (1)–(21), (25) to Hertz’s experimental data [17,20] (Figure 3 (top)).

In Egorov nano-resonance, the movement of the nuclear reorganization of the medium surrounding an extended electronic transition promotes this transition and leads to a resonance-like change in the optical band shape for polymethine dye monomers, shown in Figure 2. The Egorov nano-resonance corresponds to the chain length L for n = 3 (L = 1.4 nm). In the case of optical chromophores of J-aggregates, the stacking of the $\pi$-electron structure of the quasi-one-dimensional polymethine chain of one molecule with the $\pi$-electron structures of planar benzene rings of two neighboring molecules (see Figure 4), due to such a transition from one-dimensional to two-dimensional geometry and the formation of an optical J-chromophore of four molecules, leads to a significant increase in the interaction of the electronic transition for the nano-resonance chain (Figure 2, n = 3) with the nuclear environment and, accordingly, to a significant increase in the Egorov nano-resonance.

5. Conclusions

In ordinary molecular physics of small molecules, one can use standard quantum mechanics in the framework of the Born–Oppenheimer adiabatic approximation [22] and the Franck–Condon principle [23,24,25,26] since the shape of the optical spectra depends only on the characteristics of the initial and final states of the molecular transition and very weakly depends on the dynamics of the transient state, which, according to the new theory—quantum–classical mechanics [8,9]—is chaotic. In photochemistry and nanophotonics, where the spatial extension of a molecular transition can be large, that is, of the order of a nanometer or more, it becomes necessary to take into account the regular nature of the dynamics of the transient state, which occurs against the background of transient or dozy chaos [8]. One of the most striking results of quantum–classical mechanics is the Egorov nano-resonance between the electron motion and the nuclear reorganization motion [6,7,8,27,28,29], which currently explains the nature of the well-known narrow and intense J-band of J-aggregates of polymethine dyes that arises in aqueous solutions of their monomers (Figure 3 and Figure 4), as well as a resonance-like transformation of the optical band shape of a dye monomer with the varying length of its polymethine chain (Figure 2).