A Branch and Bound Algorithm for Counting Independent Sets on Grid Graphs ^†

Abstract

A relevant problem in combinatorial mathematics is the problem of counting independent sets of a graph G, denoted by $i\left(G\right)$. This problem has many applications in combinatorics, physics, chemistry and computer science. For example, in statistical physics, the computation of $i\left(G\right)$ has been useful in studying the behavior of the particles of a gas on a space modeled by a grid structure. Regarding hard counting problems, the computation of $i\left(G\right)$ for a graph G has been key to determining the frontier between efficient counting and intractable counting procedures. In this article, a novel algorithm for counting independent sets on grid-like structures is presented. We propose a novel algorithm for the computation of $i\left(G_{m,n}\right)$ for a grid graph with m rows and n columns based on the ‘Branch and Bound’ design technique. The splitting rule in our proposal is based on the well-known vertex reduction rule. The vertex in any subgraph from $G_{m,n}$, which is to be selected for the reduction rule, must have four internal incident faces. The ramification process is used to build a computation tree. Our proposal consists of decomposing the initial grid graph until outerplanar graphs are obtained as the ‘basic subgrids’ associated with the leave nodes of the computation tree. The resulting time-complexity of our proposal is inferior to the time-complexity of other classic methods, such as the transfer matrix method.

1. Introduction

Although counting problems have a long tradition in combinatorics, the complexity theory results are not as numerous as the decision problems at present. For example, there are few graph counting problems that can be solved in polynomial time at present. Counting problems have emerged as an important line of research in the area of combinatorial mathematics and complexity theory as counting algorithms have been used as a tool for solving practical problems in mathematics, physics, chemistry and engineering. Counting independent sets on a graph is recognized as an intractable problem, although efficient algorithms have been designed to solve this problem over specific graph topologies.

Computing the number of independent sets on mesh structures, as is the case for a grid graph $G_{m,n}$ (a grid with m rows and n columns), has different applications. For example, in the "hard square model" used in statistical physics and to obtain the hard quadratic entropy constant [1], diverse researchers have considered the problem of counting independent sets on grid graphs. Among those researchers, Calkin [2] and Euler [3] have introduced a matrix method for counting independent sets, called the transfer matrix method. This last method has been adapted as a counting method to attack statistical physic problems. For example, in physics, a model based on a grid graph is used (the hard square model) to model, in a statistical way, the behavior of the particles of a gas, as well as to count q-particle Widow–Rowlinson configurations by considering, for instance, $q>2$ [4,5].

On the other hand, a graph invariant is any function on a graph that does not depend on the labelling of its vertices. A topological index is a numerical value that is correlated with the chemical constitution or physical properties of a molecular graph.

Since the pioneering works from Merrifield and Simmons [6], the correlation between the number of independent sets of a molecular graph G (denoted by $i\left(G\right)$) and the boiling point of the chemical compound, represented by that molecular graph, has been recognized. Since that previous initial study, much researching has been carried out in the area of computational chemistry on the calculation of $i\left(G\right)$ for different topologies of molecular graphs.

The branch and bound paradigm has been widely used to attack problems with an intrinsic combinatorial exponential character. This method allows for us to branch the original problem into similar subproblems with lower input parameters than the original problem. This branching process is continued by the formation of a computation tree whose leaves have associated instances derived from the original problem, allowing for such instances to be solved efficiently.

In this article, we present a branch and bound algorithm in order to compute the Merrifield–Simmons topological index of a grid $G_{m,n}$. Our proposal provides an exact algorithm that can be applied to any type of grid, whether regular, irregular, or with non-squares internal faces. The complexity function of the time for our proposal in the calculation of $i\left(G_{m,n}\right)$ has a much smaller growth than the growth in the complexity function for the classical method of the transfer matrix.

2. Preliminares

Let $G=(V,E)$ be an undirected simple graph with a set of vertices V and a set of edges E. The edge connecting the vertices u and v is denoted by $uv$, or we can also use the notation $\{u,v\}$ to denote the edge $uv$.

We denote $N\left(x\right)=\{y\in V:\{x,y\}\in E\}$ as the neighborhood of $x\in V$. Meanwhile, $N\left[x\right]=N\left(x\right)\cup \left\{x\right\}$ is the closed neighborhood of x. Let $\left|A\right|$ be the cardinality of the set A. Furthermore, we denote the degree of a vertex x as $\delta \left(x\right)=\left|N\right(x\left)\right|$. Meanwhile, the degree of the graph G is $\Delta \left(G\right)=max\left\{\delta \right(x):x\in V\}$.

Given a subset of vertices $S\subseteq V$ of a graph G, S is called an independent set of G if, for any $u,v\in S$, it holds that $\{u,v\}\notin E\left(G\right)$. In order to denote all the independent sets of G, the notation $I\left(G\right)$ is used. We will use the notation $I_v\left(G\right)$ to denote those independent sets from G, where the vertex v appears. Meanwhile, $I_{-v}\left(G\right)$ denotes those independent sets from G where the vertex v does not appear.

On the other hand, if we want to express the number of independent sets in G, the notation $i\left(G\right)$ is used. In this case, $i\left(G\right)=\left|I\right(G\left)\right|$. However, when an independent set $S\in I\left(G\right)$ is not a subset of any other independent set of G, then S is a maximal independent set. Meanwhile, S will be a maximum independent set (MIS of G) if S has the maximum length among all the elements of $I\left(G\right)$.

It is known that the computation of $i\left(G\right)$, for any graph G where $\Delta \left(G\right)\ge 3$, is a #P-complete problem [4,7,8]. The computation of $i\left(G\right)$ remains #P-complete, even if it is restricted to three regular graphs [7]. However, for a few graph topologies G, there are efficient procedures to compute $i\left(G\right)$ [9,10,11,12].

Planar graphs play an important role in both the graph theory and the graph-drawing area. When a graph G can be drawn as an embedding in the plane, then G is called a planar graph. The internal regions delimited by the vertices and edges are called the internal faces of the graph. Meanwhile, the unbounded face is called the outer face or the external face of the graph. When a planar graph can be drawn with all of its vertices incident to the outer face, then the graph G is called outerplanar. Given an embedding of a planar graph G, we differentiate external vertices to all vertex of G incident to the outer face; otherwise, it is an internal vertex of G.

Let $F\left(G\right)=\{f_1,\dots ,f_k\}$ be the set of non-intersected internal faces (or just faces) of the planar graph G. Note that the outer face of the graph is not considered in $F\left(G\right)$. Two different faces of G are adjacent when they have common edges; otherwise, we say that both faces are independent. Thus, two independent faces can have common vertices, but no common edges.

A special planar graph is the called grid graph. Let $G=(V,E)$ be a grid graph of size $mxn$; then, the vertex set is $V=\left\{\right(i,j):1\le i\le m,1\le j\le n\}$, and the edge set is $E=\left\{\right((j,i),(j+1,i)\left)\right|1\le j<m,1\le i\le n\}\cup \{\left(\right(j,i),(j,i+1\left)\right)|1\le j<m,1\le i<n\}$. In our case, we consider that the grid graph has m rows and n columns; then, it is denoted as $G_{m,n}$, letting $k=m\ast n$ be the number of internal faces (tiling) in $G_{m,n}$.

There is some research on embedded structures in a grid graph, e.g., spanning trees, Hamiltonian cycles, independent sets, acyclic orientations, and k-coloring [2,3,13,14]. Applications of the counting objects on grids also include, for instance, tiling and efficient coding schemes in data storage [15].

One of the main methods of counting independent sets on grid graphs is the transfer matrix method [2,3]. However, this method has an exponential complexity time over dimensions m and n of the grid.

3. A Branch and Bound Algorithm

There are two common rules for counting combinatorial objects on graphs. Those rules allow for us to decompose the graph based on a vertex or an edge.

• Vertex reduction rule: let $v\in V\left(G\right)$,

  $$i\left(G\right)=i(G-v)+i(G-(N\left[v\right]\left)\right)$$
• Edge division rule: let $e=\{x,y\}\in E\left(G\right)$,

  $$i\left(G\right)=i(G-e)-i(G-(N\left[x\right]\cup N\left[y\right]\left)\right)$$

The other decomposition rule for counting independent sets of a graph is to consider each connected component of the graph in an independent way. For example, if $G_i,i=1,\dots ,k$ are the connected components of G, then $i\left(G\right)={\prod }_{i=1}^{k}i\left(G_i\right)$, and the total time complexity for computing $i\left(G\right)$ will be $T\left(i\left(G\right)\right)=max\{T\left(i\left(G_i\right)\right)$: $G_i$ is a connected component of $G\}$.

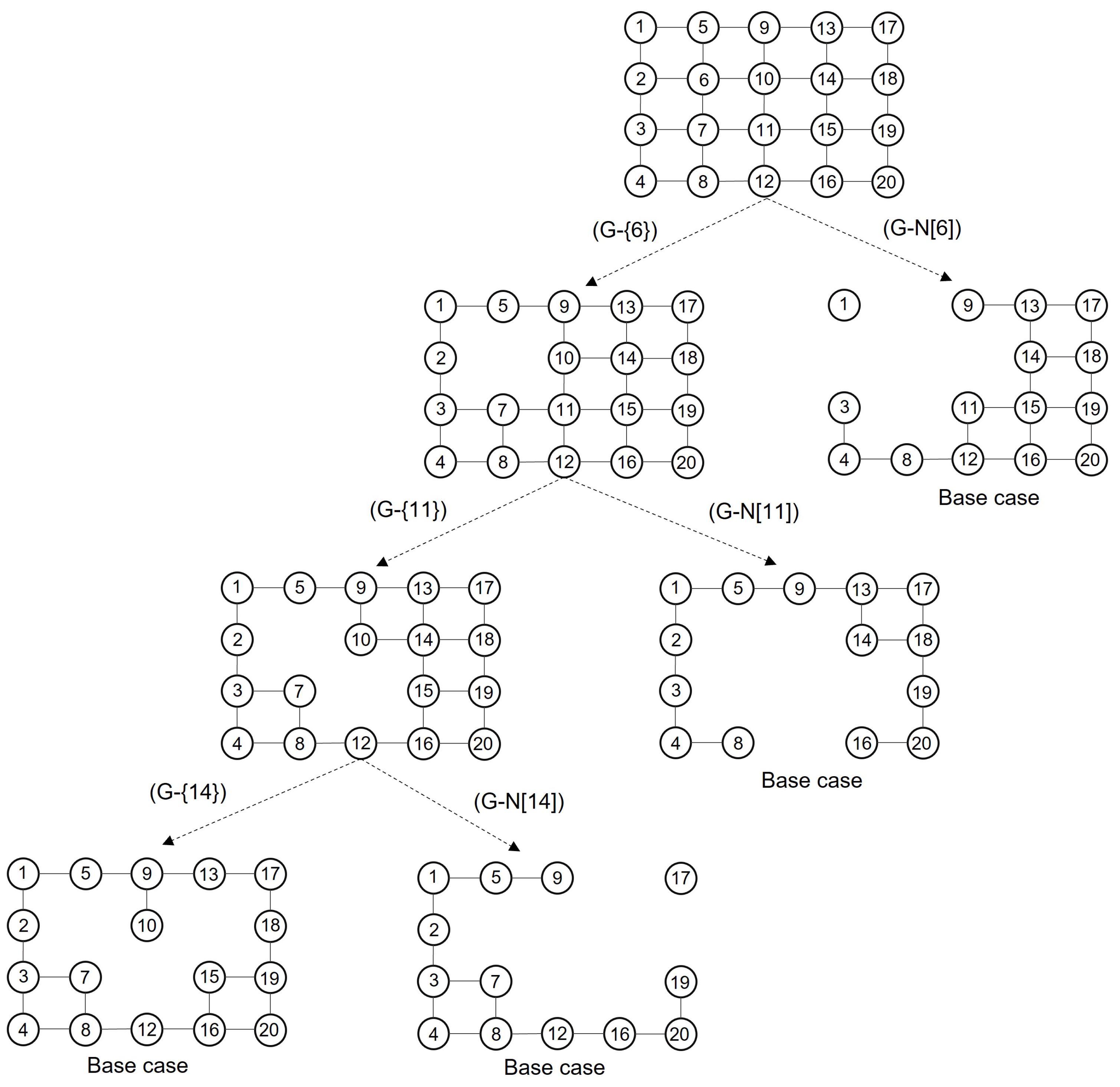
We designed a typical branch and bound algorithm in order to count the number of independent sets from a grid graph that we denote as the BB algorithm. BB builds a computation tree. In the ramification processes of the computation tree, BB considers two main points: the criterion to choose a vertex v when applying the vertex division rule, and a halting criterion to stop the branching on any node of the computation tree. The selected vertex v from any subgraph to apply the vertex division rule holds:

• $N\left[v\right]$ is at least incident to five internal faces from the current graph.
• One of the internal faces incident to v has a maximum size with respect to the other internal faces in the subgraph, or it is incident to at least one face with vertices in the outerface.

The application of the division rule on the vertex v builds two new child nodes $v_1$ and $v_2$ from the current node in the computation tree. The subgraph associated with $v_1$ is formed as $G_1=G-\left\{v\right\}$, and the subgraph associated with $v_2$ is formed as $G_2=G-N\left[v\right]$.

At this stage, we have a similar problem for each subgraph $G_i,i=1,2$ to the problem we had with the original grid G. If we solve the problem in a recurrent way and $r_i$ is its solution, then the complete solution for $r=i\left(G\right)$ is $r=r_1+r_2$. The above procedure determines a enumerative tree whose leaves correspond to the basic subgraph instances.

This process of ramification iterates until obtained as subgraph associated with each child-node-based instance $G_p$. The main characteristic of the topology of any base instance $G_p$ is that no vertex $u\in V\left(G_p\right)$ exists that is incident to four internal faces and, in this case, we achieved a child node for the enumerative tree. In Figure 1, an example of the computation tree formed by the algorithm BB can be seen for an initial input grid $G_{4,5}$.

We have shown that, for the basic prime graph $G_p$, $i\left(G_p\right)$ can be computed in linear time regarding its number of edges, since we can consider those basic prime graphs as outerplanar graphs [16,17]. Let us define $H\left(E_G\right)=\{G_p:G_p$ is the graph associated to a leaf node of the previous enumerative tree. }. After $E_G$ has been built, $i\left(G\right)={\Sigma }_{G_p\in H\left(E_G\right)}i\left(G_p\right)$. As the computation for each $i\left(G_p\right)$ can be carried out in linear time, then the complexity time for $i\left(G\right)$ depends on the time complexity of the number of nodes of the enumerative tree.

Let $k=n·m$ be the number of internal tiling faces existing on the initial grid $G_{m,n}$. Then, the complexity time of the branch and bound procedure depends on the recurrence $i\left(G\right)=i(G-\{u\left\}\right)+i(G-N[u\left]\right)$. This splitting rule has different cases according of the number of internal faces incident to the vertices in $N\left[u\right]$. In the best case, $N\left[u\right]$ can be incident to eight tiling faces and, in this case, the decomposition rule expressed by the number of rectangles that are decomposed is given by the recurrence: $T\left(k\right)=T(k-8)+T(k-3)$.

However, in the worst case, if G does not correspond to a basic case, then $N\left[u\right]$ should be incident to at least five internal tilings. In this case, the splitting rule expressed by the number of rectangles that are decomposed is given by the recurrence:

$$T\left(k\right)=T(k-5)+T(k-3)$$

(1)

We seek a solution to the form $x^k=T\left(k\right)$. Substituting this into the previous recurrence relation (1) leads to the characteristic polynomial: $P\left(x\right)=x^5-x^2-1$, whose five roots $r_i,i=1,\dots ,5$ give rise to solutions of the form $T\left(k\right)=r_i^k$.

As we are interested in the asymptotic behavior of the recurrence $T\left(k\right)$, we only consider the real root $r_1$, such that $|r_1|\ge |r_i|,i=2,\dots ,5$. In this case, the maximum real root is $r_1\approx 1.194$, and then we obtain a worst-case upper bound of $O(r_1^k·poly\left(k\right))$, where $poly\left(k\right)$ is a polynomial function that corresponds to the time-processing of the basic case graphs. Thus, the complexity time of our proposal has an upper bound of $O(1.{1939}^k·poly\left(k\right))=O(1.{1939}^{m·n}·poly\left(k\right))$.

Our proposal works without any problem on irregular grids or on variants of grids such as the aztec diamonds graphs [18], since it looks for vertices incident to more than three internal faces. On the other hand, although our proposal continues to have an exponential time-complexity, it does not have the explosive combinatorial character that the classic transfer matrix method has for the computation of $i\left(G_{m,n}\right)$.

4. Conclusions

We introduced a branch and bound algorithm for the computation of $i\left(G_{m,n}\right)$, for a grid graph with m rows and n columns. We applied the well-known vertex reduction rule as the splitting rule. The vertex v in any subgraph from $G_{m,n}$, which is to be selected for the reduction rule, must hold that $N\left[v\right]$ is incident to at least five internal faces. Our proposal consists of decomposing the initial grid graph until only outerplanar subgraphs are obtained as basic cases.

The resulting time-complexity of our proposal for computing the number of independent sets for grid graphs is dramatically inferior to the time-complexity that the classic transfer matrix method required to compute the same value.