The Impact of a Non-Uniform Magnetic Field on Mixed Convection in a Lid-Driven Cavity Filled with Fe₃O₄/Water Nanofluid ^†

Abstract

Research on Fe₃O₄/water nano liquid in a lid-driven chamber under mixed convection conditions has been carried out with a focus on the impact of a non-uniform magnetic field on the heat exchange process. The governing equations were resolved using the finite-volume-method-based in-house solver. Several parameters were considered in the analysis, including the magnetic number and the Reynolds number. According to the primary findings, the existence of a magnetic field (MF) generates a region of recirculation near the magnetic source, resulting in improved local heat exchange. Moreover, the effectiveness of the magnetic field is greater at lower Richardson numbers, and the buoyancy force diminishes the influence of the magnetic source.

1. Introduction

Ferrofluids are a type of nanofluid that contain magnetizable nanoparticles. When a magnetic field (MF) is applied to a ferrofluid system, it results in ferrohydrodynamic (FHD) effects, which has attracted a lot of attention from researchers. Various studies have explored this area extensively. For instance, Ghorbani et al. [1] investigated the impact of MF on the heat exchange of ferrofluid flow through a tube. They found that the magnetic field alters the flow pattern, resulting in increased heat transmission. Siddiqui and Turkyilmazoglu [2] studied the flow of a ferrofluid in a porous chamber. They observed that the application of a MF on the surface can alter the heat exchange rate based on a variety of criteria. Sheikholeslami et al. [3] focused on the effect of non-uniform magnetic fields on a convection problem in a circular enclosure. They presented the effect of a magnetic source on heat exchange and highlighted several parameters in the thermal and dynamic domains.

2. Physical Model

The problem is affected by an MF that is made by a permanent electric current (I) flowing through a conductive wire. The magnetic field around the problem is not uniform (a, c). In this study, the “a” and “c” coordinates are fixed at (L/2, 0). Figure 1 shows the shapes of the different MFs that were used.

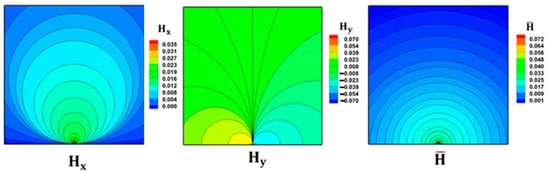
Figure 1. MF contours.

The MF components could be expressed as:

$$H_x\left(x,y\right)=\frac{I}{2\pi }\frac{y-c}{{\left(x-a\right)}^2{+\left(y-c\right)}^2}$$

(1)

$$H_y\left(x,y\right)=-\frac{I}{2\pi }\frac{x-a}{{\left(x-a\right)}^2{+\left(y-c\right)}^2}$$

(2)

$$H\left(x,y\right)=\sqrt{H_x^2+H_y^2}=\frac{I}{2\pi }\frac{1}{\sqrt{{\left(x-a\right)}^2{+\left(y-c\right)}^2}}$$

(3)

The patterns of the MFs used are shown in Figure 1

3. Problem Geometry

Figure 2 demonstrates the current concern, which is represented by a square cavity with a length (L). The bottom plate of the cavity is partially heated, whereas the other plates are adiabatic. The top wall is movable in the x direction, and the design is influenced by the nearby magnetic source.

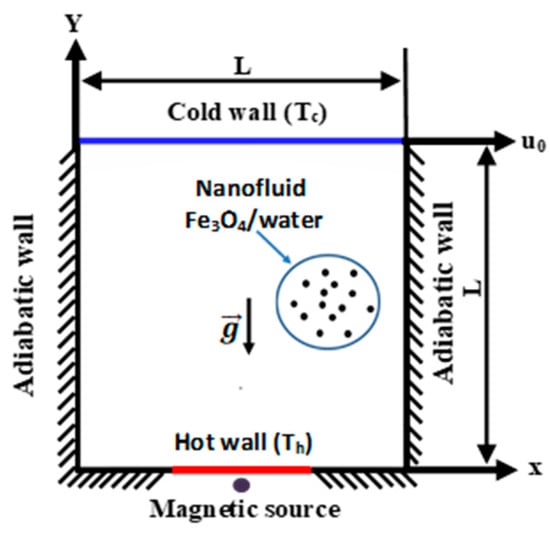
Figure 2. Problem geometry.

4. Results

Figure 3 shows the creation of a circulation region caused by the magnetic source at various Richardson numbers. However, as the buoyant force starts to dominate the flow, the circulation region starts to vanish, and the primary vortex’s strength diminishes. This indicates that the heat exchange declines as the Richardson number rises.

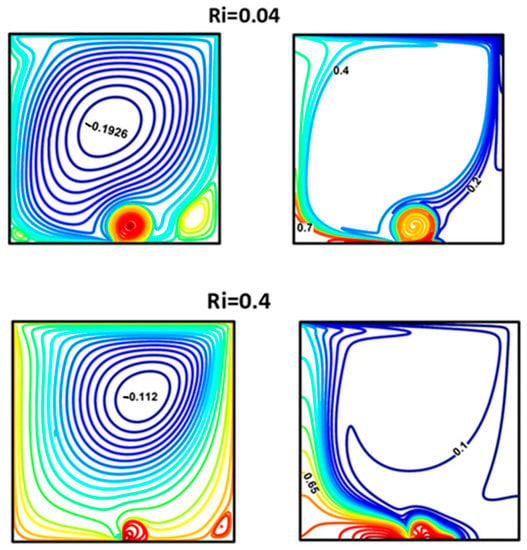
Figure 3. Streamlines and isotherms at ϕ = 0.05 and Mn = 100.

In addition, according to Table 1, the average Nusselt is higher for a lower Richardson number due to the generated vortex which initiates the diffusion phenomena.

Table 1. Average Nusselt number.

	Ri = 0.4		Ri = 0.04
	Mn = 25	Mn = 50	Mn = 25	Mn = 50
Average Nusselt number	15.3111	18.403	52.7946	67.643

Ri: Richardson number, Mn: magnetic number, and ϕ: solid volume fraction

5. Conclusions

The outcomes of the data analysis can be summed up as follows:

✓

The magnetic field is more beneficial at lower Richardson values.

✓

The buoyancy force is dominant, which reduces the effectiveness of the MF.

✓

The average Nusselt number is higher at a lower Richardson number.