Abstract
In this paper, we study the laminar, incompressible, and steady flow of a biomagnetic fluid, such as blood, containing gold nanoparticles through a shrinking sheet in the presence of a magnetic dipole. This model is consistent with both the principles of magnetohydrodynamics (MHD) and ferro-hydrodynamics (FHD). An effective numerical method that is based on an iterative process, tridiagonal matrix manipulation, and a common finite difference method with central differencing is used to generate the numerical solution of obtained ordinary differential equations (ODEs). The major numerical results show that the fluid velocity decreases as the ferromagnetic number increases whereas the skin friction coefficient shows the opposite behavior. As the ferromagnetic number increases, the rate of heat transfer with ferromagnetic interaction parameter is likewise observed and shown to be decreasing.
1. Introduction
The study of biomagnetic fluid has grown rapidly because it aims to uncover and develop remedies for several human body-related illnesses and disorders, such as producing artificial organs, making nanorobots for surgery, and creating cutting-edge imaging and signal processing methods for cancer, tumors, and other terminal illnesses. The field of medical imaging-based diagnostics (MRI, CT scan, ultrasound, etc.), targeted drug delivery, or hyperthermia therapies are only a few examples of how these study areas can directly affect the actual world [1,2,3]. Based on the principles of Ferrohydrodynamics, Haik et al. [4] first proposed a biomagnetic fluid dynamics (BFD) model, the biomagnetic fluid is a Newtonian, electrically non-conducting magnetic fluid, according to this model. They stated that under the effect of high gradient magnetic fields, the fluid magnetization significantly affects the flow. This BFD model was further extended by Tzirtzilakis et al. [5] by combining both principles of FHD and MHD. Murtaza et al. [6] investigated both electrical conductivity and magnetization affected the BFD flow over a stretching sheet. In order to increase the qualities of nanoparticles, Choi et al. [7] invented a new fluid in 1995 called nanofluid that mixes them with a base fluid such as blood, water, or oil. A nanofluid is a base fluid that has nanoparticles spread throughout it. The significance of magnetic dipole on heat characteristics of blood flow with CoFe2O4 particles towards an extended cylinder was investigated by Ferdows et al. [8] using MHD and FHD principles.
To the best of the authors’ knowledge, none of the aforementioned research has yet examined the effect of a strong magnetic field on blood flow with gold nanoparticles toward a shrinking sheet. The governing boundary layer equations were resolved using a well-known finite difference technique.
2. Mathematical Flow Equations with Flow Geometry
The two-dimensional boundary layer flow, heat, and mass transfer of a steady, viscous, laminar, incompressible, and electrically conductive bio-magnetic fluid flow (namely, blood) that contains gold nanoparticles in the presence of a magnetic dipole towards a shrinking sheet is considered here. This shrinking sheet is kept at a constant temperature and concentration , at , where the -axis is taken in the direction of the flow and the -axis is normal to it. It is assumed that the free stream velocity is and the plate is shrunk with the velocity , where b and c are positive constants. It is also assumed that the constant mass flux velocity is with for suction and for injection. The ambient temperature is denoted by and the concentration of nanoparticles by , respectively. In addition, a constant transverse magnetic field is applied to the flow, with the assumption that it is applied in the positive y-direction. As seen in Figure 1, the magnetic dipole is situated far below the sheet, creating a magnetic field strong enough to saturate the biomagnetic fluid.
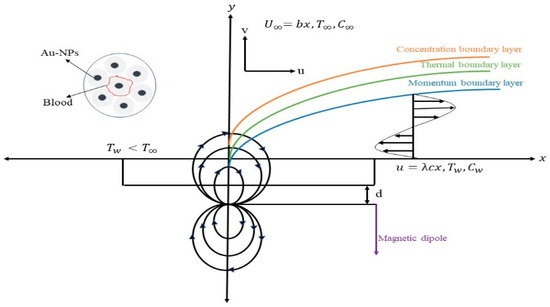
Figure 1.
Schematic diagram of flow problem.
Under these considerations, we extend the work of [9,10], and the governing boundary equations are:
The equations are subjected to the boundary conditions [9]:
where and are the velocity components along the and direction, respectively. The meaning of the symbols is found in [2,5,6,9]. The magnetic field of intensity is given by [5,6]: Fluid magnetization with temperature is given by: , where k is a
pyromagnetic coefficient constant. Thermophysical corelation of nanofluid is
given by [2]:
The following transformations are introduced [9]:
Therefore, the reduced form of the above equations are:
The transformed boundary conditions are:
Here,
3. Results and Discussion
An effective numerical finite difference technique is used to solve ODEs numerically as proposed by [2,6]. According to the authors’ knowledge, this technique is based on (1) the common finite difference method with central differencing, (2) a tridiagonal matrix manipulation, and (3) an iterative procedure. A comparison between the present study and earlier studies was also calculated to show the accuracy of the applied code, and it is presented in Table 1. This encourages us to continue the work. Table 2 shows the thermo-physical values of blood and gold.

Table 1.
Comparison values of for different values of when .

Table 2.
Thermophysical values of blood and gold nanoparticles [8,13].
In Figure 2, the effect of ferromagnetic interaction parameters on velocity, temperature, and concentration profiles is depicted. In Figure 2, indicates pure blood and indicates Au (gold)-pure blood. In Figure 2a, it is observed that the increasing values of ferromagnetic interaction parameter magnetic fluid velocity decreases. This happens due to the correlation between the ferromagnetic number and the Kelvin force. Figure 2b. signifies the impact of the ferromagnetic interaction parameter on the temperature profile. It is observed that the temperature profile is decreased with increasing values of . This is due to the fact that the applied magnetic field caused by the magnetic dipole generates the Kelvin, also known as the resistive force. The interaction of blood velocity and the applied magnetic field is responsible for this. In Figure 2c, the influence of ferromagnetic interaction parameter on the concentration profile graph is as the values of ferromagnetic interaction parameter increase, and the concentration boundary layer thickness is increasing in both cases for pure blood and gold pure blood.
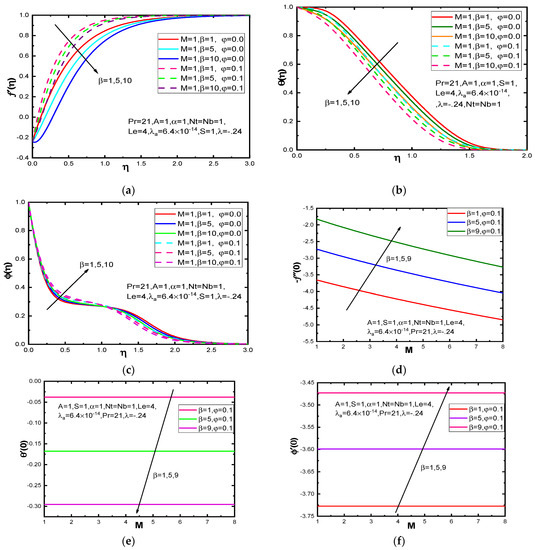
Figure 2.
Variations of ferromagnetic interaction parameter on (a) velocity; (b) temperature profiles. (c) concentration profile; (d) skin friction coefficient; (e) rate of heat transfer; (f) local Sherwood Number.
Finally, Figure 2d–f depict the variation of skin friction coefficient , local Nusselt Number , and local Sherwood Number for different values of ferromagnetic parameter against magnetic parameter . From the figures, it is seen that and are both increases with the increasing values of , whereas the reverse trend is observed in .
4. Conclusions
Based on numerical results, our findings can be summarized as follows:
- (i)
- For enlarging values of ferromagnetic number, fluid velocity and temperature decreases, but the reverse phenomena is observed in the concentration profile.
- (ii)
- A significant improvement is observed for blood temperature and velocity profile when gold nanoparticles are mixed with blood compared to that of conventional regular fluid.
- (iii)
- Local Sherwood Number as well as skin friction coefficient are enhanced with augmenting values of ferromagnetic number, while major reduction is observed for the rate of heat transfer.
Author Contributions
Conceptualization, L.B. and M.F.; Data curation, G.M. and L.B.; Formal analysis, L.B. and G.M.; Investigation, G.M., M.F. and E.E.T.; Methodology, E.E.T. and M.F.; Project administration, M.F.; Resources, M.F., L.B. and G.M.; Software, E.E.T.; Supervision, M.F. and E.E.T.; Validation, G.M. and L.B.; Writing original draft, L.B. and G.M.; Writing reviewing and editing, M.F. and E.E.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funding by Comilla University, Bangladesh. Grant No. 485/2013/1312(03).
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haik, Y.; Pai, V.C.; Chen, C.J. Development of magnetic device for cell separation. J. Magn. Magn. Mater. 1999, 194, 254–261. [Google Scholar] [CrossRef]
- Alam, J.; Murtaza, M.G.; Tzirtzilakis, E.E.; Ferdows, M. Application of biomagnetic fluid dynamics modeling for simulation of flow with magnetic particles and variable fluid properties over a stretching cylinder. Math. Comput. Simul. 2022, 199, 438–462. [Google Scholar] [CrossRef]
- Misra, J.C.; Sinha, A.; Shit, G.C. Flow of a biomagnetic viscoelastic fluid: Application to estimation of blood flow in arteries during electromagnetic hyperthermia, a therapeutic procedure for cancer treatment. Appl. Math. Mech. (Eng. Ed.) 2010, 31, 1405–1420. [Google Scholar] [CrossRef]
- Haik, Y.; Chen, C.J.; Pai, V.M. Development of bio-magnetic fluid dynamics. In Proceedings of the IX International Sysmposium on Transport Properties in Thermal Fluid Engineering, Singapore, 25–28 June 1996; Winoto, S.H., Chew, Y.T., Wijeysundera, N.E., Eds.; pp. 121–126. [Google Scholar]
- Tzirtzilakis, E.E. Mathematical model for blood flow in magnetic field. Phys. Fluids 2005, 17, 077103. [Google Scholar] [CrossRef]
- Murtaza, M.G.; Tzirtzilakis, E.E.; Ferdows, M. Effect of electrical conductivity and magnetization on the biomagnetic fluid flow over a stretching sheet. Z. Fur Angew. Math. Und Phys. 2017, 68, 93. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Ferdows, M.; Alam, J.; Murtaza, G.; Tzirtzilakis, E.E.; Sun, S. Biomagnetic Flow with CoFe2O4 Magnetic Particles through an Unsteady Stretching/Shrinking Cylinder. Magnetochemistry 2022, 8, 27. [Google Scholar] [CrossRef]
- Mansur, S.; Ishak, A.; Pop, I. The magnetohydrodynamic stagnation point flow of a nanofluid over stretching/shrinking sheet with suction. PLoS ONE 2015, 10, e0117733. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, W.; Shankar, B.; Nandeppanavar, M.M. MHD stagnation point flow and heat transfer due to nanofluid towards a stretching sheet. Int. J. Heat Mass Transf. 2013, 56, 1–9. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Gupta, A.S. Heat transfer in stagnation-point flow towards a stretching sheet. Heat Mass Transf. 2002, 38, 517–521. [Google Scholar] [CrossRef]
- Hayat, T.; Javed, T.; Abbas, Z. MHD flow of a micropolar fluid near a stagnation-point towards a non-linear stretching surface. Nonlinear Anal. Real World Appl. 2009, 10, 1514–1526. [Google Scholar] [CrossRef]
- Alam, J.; Murtaza, G.; Tzirtzilakis, E.E.; Ferdows, M. Biomagnetic fluid flow and heat transfer study of blood with gold nanoparticles over a stretching sheet in the presence of magnetic dipole. Fluids 2021, 6, 113. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).