Abstract
In this study, we have dealt with a scheduling problem that has not been studied enough: the parallel-flow shop-scheduling problem. Its difficulty lies in the fact that it consists of two sub-problems: the assignment of jobs to workshops and the scheduling of these jobs once assigned. Due to the complexity of the research problem, we propose a hybridization of two well-known optimization algorithms, a bio-inspired meta-heuristic algorithm (Particle Swarm Optimization—PSO) and a local search algorithm (tabu search, TS), with the aim of minimizing the maximum execution time of all jobs within constraints. The purpose of this hybridization is to combine the strengths of the two methods in order to obtain more efficient results than those achieved by classic methods. The concept of the proposed method is to start by generating a set of near-optimal solutions by the PSO meta-heuristic algorithm. Then, the TS algorithm refines and improves these solutions in order to attain the optimal solution.
1. Introduction
The scheduling problem is a classical optimization problem that consists of assigning tasks to resources in an optimal way, according to their availability, dependencies, and deadlines. Although solving this problem brings many benefits such as increased productivity, reduced costs, and better customer satisfaction, the scheduling challenges cover many areas such as production, transport, health, and project management. In particular, effective scheduling in project management is essential to completing jobs on time and on budget.
In this study, we aim to minimize the total time required to execute a set of jobs in a parallel-flow shop (PFS), which is a manufacturing environment with multiple production lines running in parallel to complete a set of jobs, and wherein each line is composed of a set of machines in series. Unlike exact methods, approximate methods have proven to be effective in solving this problem. This study aims to provide a better understanding of the PFS problem and to propose a hybridization of two approximate optimization methods to deal with this problem.
To test the performance of the proposed method (PSO–TS) in a parallel-flow shop, we apply it to six different scales, and the results obtained are compared with those found previously by a PSO method [1].
2. Parallel-Flow Shop-Scheduling Problem
A parallel-flow shop is a type of manufacturing shop in which several identical line flow shops are arranged in parallel. Each line of this workshop consists of a sequence of machines. The job is first assigned to a line and once a job is assigned, it must be scheduled on the machines of the assigned line.
The PFSP seeks to minimize the makespan, which is the sum of the processing times of all jobs. While adhering to the scheduling constraints, this issue consists of two subproblems—job assignment and job sequence—and has not been well studied due to the many variables involved:
- Each job can only be assigned to a single line, and each line can process only one job at a time;
- Each machine can process only one job at a time and once a job is being processed on a machine, it must finish processing before the next job can begin processing on the same machine;
- The order in which jobs are processed on each machine must match the order in which they were assigned to the production line.
The complexity of the parallel-flow workshop problem depends on the number of line-flow workshops and the number of machines in each line flow workshop. Although it is known to be NP-hard, no known algorithm can solve it optimally in polynomial time. However, there are heuristic and metaheuristic algorithms that have been developed to find near-optimal solutions to the problem, such as combining Tabu search and Johnson’s method [2], quantum algorithm [3], constructive heuristic [4], etc.,
The mathematical model for the PFSP can be formulated as follows:
Let n be the number of jobs to be processed in a parallel flow shop system, and l be the number of identical production lines, each containing m machines.
Sets and indices:
- Set of jobs: J = 1, 2, …, n
- Set of machines: M = 1, 2, …, m
- Set of lines: L = 1,2, …, l
Parameter:
- Let be processing time of job j on machine m
Variables:
- Let be the start time of job j on line l
- Let be the completion time of job j on machine m.
The decision variables for this problem are binary variables which take value 1 if job j is assigned to line l, and 0 otherwise. which take the value 1 if job j is assigned to machine m, and 0 otherwise
The scheduling constraints are as follows:
where j′, j are jobs assigned to line l and j′ is immediately after j
(1) Each job can only be assigned to one line. (2) Each line can process only one job at a time. (3) Each machine can process only one job at a time. (4) Each machine can process only one job at a time and once a job is being processed on a machine, it must finish processing before the next job can begin processing on the same machine. (5) The order in which jobs are processed on each machine must match the order in which they were assigned to the production line. (6) Start time of the first job on the first machine equals 0. (6′) The start time of job j′ on the first machine equals the completion time of job j on the first machine. (6″) Start time of jobs beyond the first machine. (7) Completion times of jobs on each machine.
3. Methods
Before selecting a method to deal with the problem, it is necessary to analyze its complexity. The PFSSP is considered a combinational problem that falls under the NP-hard category. As a solution, we recommend applying a hybridization method including the particle swarm method and tabu search.
3.1. Particle Swarm Optimization
Particle swarm optimization (PSO) is a well-known, nature-inspired method that mimics the behavior of a swarm of particles. This computational method is used to find the optimal solution in a large and complex search space. Kennedy and Eberhart first proposed it in 1995 and it has since been widely applied in various fields.
Recently, there have been multiple advances in the development of this algorithm: multi-objective PSO (MOPSO) [5], parallel PSO (PPSO) [6], adaptive swarm size [7], hybridization PSO—studies combining PSO with other optimization methods for better results, such as PSO with genetic algorithms (GA) [8] and PSO with simulated annealing (SA) [9]. This has inspired us to develop a hybridization of PSO with the tabu search method.
The classic version employs a group of particles that move through the search space, adjusting their positions and velocities based on their own experience and the best experience of their neighbors. Each particle has its own fitness value, and they share information among themselves to improve their positions and velocities. This iterative process is repeated until the algorithm converges to an optimal or close-to-optimal solution.
3.2. Tabu Search
Tabu search (TS) is a heuristic optimization method proposed by Fred Glover in 1986 to solve combinatorial optimization problems, and has since been used in various fields.
Tabu search uses a short-term memory of recently explored solutions and leverages this memory to direct searches of promising regions of the search space. The basic idea is to restrict the steps leading to the solution that have already been visited, thus avoiding getting stuck in local optima.
This heuristic method has undergone many changes since its inception. For example, using adaptive memory [10] allows the algorithm to dynamically adjust memory parameters as the search progresses. Another important development is hybridization [11], which combines tabu search with other optimization methods to improve efficiency.
3.3. Proposed Hybridization Method
Hybridization is a combination of the strengths of different algorithms such as global search and local search methods, in order to overcome the limitations of individual algorithms, such as premature convergence or blocking of local optima.
The PSO–TS hybridization seems efficient in the sense that the PSO algorithm is good in the global exploration of the space of solutions and TS is good in the local exploitation of promising regions, which explores the neighborhood of solutions to find the optimal one. Both complement each other and can offer quality solutions combining exploration and exploitation in the search for the optimum.
The steps of the proposed method are details as follows:
- Initialization: random generation of the initial population of particles by the PSO method.
- Fitness evaluation: evaluate the fitness of each particle.
An update at each iteration of the velocity and the position of the particles is carried out according to the fitness found.
- 3.
- The algorithm process is terminated once the maximum number of iterations is reached.
- 4.
- Tabu search—the taboo search starting solution is the best overall fitness found by the particle swarm.
- 5.
- The tabu search is carried out on the best particles selected previously, then for the neighbors of these particles. The neighbors are then evaluated and the best one is selected.
- 6.
- The tabu list is updated after each iteration.
- 7.
- Termination—the process is terminated once the maximum number of iterations is reached.
4. Computational Experiment
The proposed algorithm is tested to minimize the makespan function in a flow shop workshop composed of three identical parallel lines with six different instances of jobs and machines ((20*50), (20*10), (50*05), (50*10), (100*05), (100*10)).
The algorithm is programmed by (MATLAB R2018b) a computer of the following performance specifications: Intel(R) Core (TM) i5-7200U CPU, 2.50GHz, 2.71 GHz, 4.00 Go memory. Table 1 represents the results of the conducted experiment, as well as the previously found results for PSO alone, for the same instances.

Table 1.
The results of the experiment for the six instances.
As seen in Figure 1, the resulting curves show that PSO–TS hybridization excels over PSO. Additionally, as seen in Figure 2, the computation time that the PSO–TS algorithm takes to be executed is higher than that of the PSO.
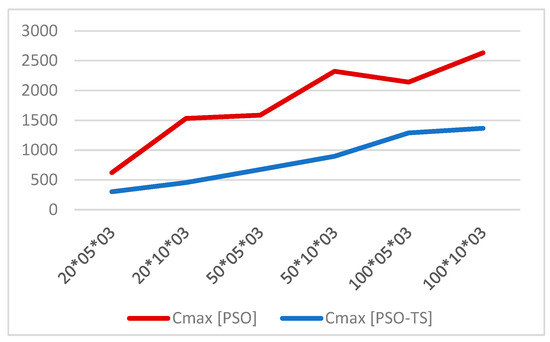
Figure 1.
Optimal values of PSO and PSO–TS algorithms for six different scales. The abscise axis represents the instances and the ordinate axis represents the optimum values for PSO and PSO–TS.
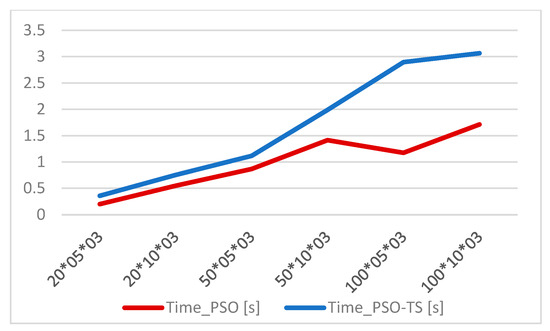
Figure 2.
Computation time values of PSO and PSO–TS algorithms. The abscise axis represents the instances and the ordinate axis represents the computation time values.
We note that the proposed PSO–TS method is more efficient regarding the makespan value for different sizes of instances. Still, it takes longer to be executed compared to PSO alone.
5. Conclusions
This study used a hybrid method (PSO–TS) for a parallel-flow shop scheduling problem in order to minimize the makespan function. To evaluate the performance of the proposed method, we conducted a computational experiment and compared the results obtained with those obtained by the PSO method alone. In terms of makespan values, hybridization (PSO–TS) is better than PSO alone. Still, in terms of computational time, PSO alone is better than (PSO–TS), which encourages us to improve our method so that the computational time will be as optimal as the makespan values.
Author Contributions
Formalization, M.M.; methodology, M.M.; programming, M.M.; validation, M.M. and Y.B.; result's analysis, Y.B.; resources, M.M.; writing—original draft preparation, M.M.; writing—review and editing, M.M.; Y.B. and H.S.; visualization, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mansouri, M.; Bahmani, Y.; Smadi, H. Preprint Monocriterion Optimization in Parallel Flow. In Proceedings of the 12th International Confernece on Information Systems and Advenced Technologies (ICISAT’2022), Online, 26–27 August 2022. [Google Scholar]
- Taylor, P.; Cao, D.; Chen, M. Parallel flowshop scheduling using Tabu search. Int. J. Prod. 2010, 41, 3059–3073. [Google Scholar] [CrossRef]
- Jiang, Y.; Wan, S. Parallel Flow Shop Scheduling Problem Using Quantum Algorithm. In Proceedings of the Applied Informatics and Communication: International Conference, ICAIC 2011, Xi’an, China, 20–21 August 2011; pp. 269–274. [Google Scholar]
- Ribas, I.; Companys, R.; Tort-Martorell, X. Efficient heuristics for the parallel blocking flow shop scheduling problem. Expert Syst. Appl. 2017, 74, 41–54. [Google Scholar] [CrossRef]
- Coello, C.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1051–1056. [Google Scholar] [CrossRef]
- Lalwani, S.; Sharma, H.; Satapathy, S.C.; Deep, K.; Bansal, J.C. A Survey on Parallel Particle Swarm Optimization Algorithms. Arab. J. Sci. Eng. 2019, 44, 2899–2923. [Google Scholar] [CrossRef]
- Chen, D.B.; Zhao, C.X. Particle swarm optimization with adaptive population size and its application. Appl. Soft Comput. J. 2009, 9, 39–48. [Google Scholar] [CrossRef]
- Dziwinski, P.; Bartczuk, L. A New Hybrid Particle Swarm Optimization and Genetic Algorithm Method Controlled by Fuzzy Logic. IEEE Trans. Fuzzy Syst. 2020, 28, 1140–1154. [Google Scholar] [CrossRef]
- Yin, Z.; Qin, R.; Liu, Y. A New Solving Method Based on Simulated Annealing Particle Swarm Optimization for the Forward Kinematic Problem of the Stewart–Gough Platform. Appl. Sci. 2022, 12, 7657. [Google Scholar] [CrossRef]
- Glover, F.; Laguna, M. Tabu Search; Springer US: New York, NY, USA, 1997. [Google Scholar] [CrossRef]
- Bennell, J.A.; Dowsland, K.A. Hybridising tabu search with optimisation techniques for irregular stock cutting. Manag. Sci. 2001, 47, 1160–1172. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).