Abstract
Machine learning applications usually become a subject of data unavailability, complexity, and drift, resulting from massive and rapid changes in data volume, velocity, and variety (3V). Recent advances in deep learning have brought many improvements to the field, providing generative modeling, nonlinear abstractions, and adaptive learning to address these challenges. In fact, deep learning aims to learn from representations that provide a consistent abstraction of the original feature space, which makes it more meaningful and less complex. However, data complexity related to different distortions, such as higher levels of noise, remains difficult to overcome. In this context, recurrent expansion (RE) algorithms have recently been developed to explore deeper representations than ordinary deep networks, providing further improvement in feature mapping. Unlike traditional deep learning, which extracts meaningful representations through inputs abstraction, RE enables entire deep networks to be merged into another one consecutively, allowing the exploration of inputs, maps, and estimated targets (IMTs) as primary sources of learning; three sources of information that provide additional knowledge about their interactions in a deep network. In addition, RE makes it possible to study IMTs of several networks and learn significant features, improving its accuracy with each round. In this context, this paper presents a general overview of RE, its main learning rules, advantages, disadvantages, and its future opportunities, while reviewing the state-of the art and providing some illustrative examples.
1. Introduction
Machine learning models generally aim to build prediction models using a set of training samples to be able to generalize them on the coming unseen samples related to the same phenomena [1]. Basically, a well-trained machine learning model should have resilience and adaptability against rapidly varying 3V of big data [2]. As a result, the current growth in 3V of big data has led to the emergence of deep learning philosophies in a variety of applications [3]. To better understand the difference between machine learning and deep learning models, we present a simple mathematical description. If we consider a machine learning model as a function, , that approximates a set of training samples, , by estimating their targets, , then Equation (1) will look very much like a definition of machine learning. Thus, traditional machine learning in this case does not consider the effect of feature representations on the training process, while only focusing on hyperparameter optimization as the main problem of approximation and generalization. Indeed, deep learning emphasizes the improvement of feature representations by introducing well-defined intermediate feature mapping, considering the 3V issues of big data. Mathematically, if we assume that a well-structured feature map is defined as , the mathematical representations of the deep network can be demonstrated as in Equation (2).
in this case can be any type of deep learning network feature maps, including, but not limited to, autoencoder (AE) hidden layers of all types [4], recurrent neural network (RNN) hidden layers and their variants [5], convolutional neural network (CNN) feature maps [6], and deep belief network (DBN) hidden layers [7].
In fact, deep learning has exhibited a massive evolution targeting the current rapid change in the 3V of big data by introducing a sophisticated complex nonlinear feature mapping process, adaptive learning features, and generative modeling targeting all problems of complexity, dynamism, and the availability of data.
Despite these massive improvements in deep learning, the continuous massive growth and rapid change in the 3V of big data has always made it difficult to demand new, up-to-date features to make learning systems more adaptive and resilient. The main research gaps in this case are related to the complexity and the dynamism resulting from this massive growth of the 3V of big data.
Accordingly, as an insight to solve these challenges, a recent algorithm called recurrent expansion with multiple repeats (REMR) is introduced in the literature. The REMR algorithm aims to introduce deeper space then deep learning investigating and experimenting new, more meaningful feature representations leading to better performance.
As a main contribution of this paper with respect to the previous research gap analysis and since there is now a literature review introducing this new tool, this paper is introduced to provide a clear state-of-the-art of this new method, its learning rules, while going through various illustrative examples, and finally to illustrate future opportunities.
This paper is organized as follows. Section 2 presents the REMR algorithm and its main learning rules through some explanations, illustrations of flowcharts, and some important pseudo-codes, while comparing representations of the general REMR Equation to previous Equations (1) and (2). Second, some examples are presented in Section 3 based on previous work, and clarified to highlight the advantages and limitations of REMR algorithms. Section 4 concludes this paper by discussing some future opportunities.
2. REMR Background
REMR is a representation learning algorithm built on a philosophy that aims to explore and profit from pre-trained deep learning models and their behaviors towards unseen sample predictions when building new models. REMR has previously been used to solve learning problems related to the imbalanced classification of complex and dynamic data, with missing values [8], as well as for time series predictions in the near future [9,10]. REMR has proven its ability to improve both deep learning and small-scale machine learning algorithms.
Accordingly, REMR algorithms are designed to fully merge deep learning networks into others consecutively in different rounds to build more complex architecture and experiencing new, more meaningful feature representations. Accordingly, and unlike deep learning algorithms, which use inputs, , as the main source of information, REMR exploits three main sources, namely, inputs, , maps, , and estimated targets, , previously called IMTs as the main training features. Moreover, REMR actually uses IMTs of several trained deep networks, studies their behaviors, and builds a new robust and more accurate model. Mathematically, following the previous illustrations in Equations (1) and (2), REMR can be expressed similarly to in Equation (3). is the maximum number of training rounds.
IMTs, which are referred to as , are generally expected to be massive, especially under multiple layers of deep learning nonlinear mappings; therefore, well-defined data processing, , as detailed in Equation (4), is required before feeding the next deep network.
Considering the previous representation of Equation (3) and compared with Equations (1) and (2), the REMR appears to be more complex than any other deep network witnessed so far in reference to deeper nonlinear abstractions.
The flowchart depicted in Figure 1 clearly illustrates REMR learning rules. This flowchart shows the positions of IMTs and demonstrates the process of collecting, processing, and feeding back IMTs to upcoming deep learning networks.
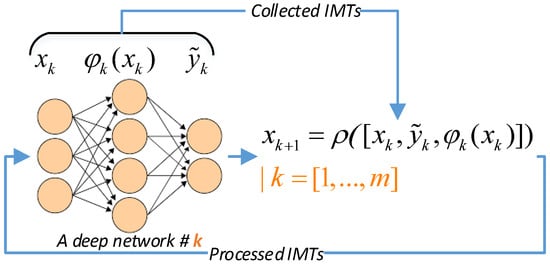
Figure 1.
IMT flows in REMR algorithms.
REMR does not really include an approximation process by hyperparameter optimization, which is usually performed via gradient descent algorithms; this is more like the submerging of deep networks [11]. Therefore, the traditional equations of the loss function will not be useful in evaluating its convergence behavior at every round. In this context, REMR uses a special metric developed on the basis of the behavior of the expected loss function at each round. The REMR philosophy expects that with each round, and assuming that the performance of the learning process improves, the loss function should exhibit better, smoother, and faster loss behavior of each deep network at each subsequent round. These improved loss function characteristics could result in less area under the loss curve (AULC). Therefore, the AULC parameter addressed in Equation (5) is elected as the key metric for evaluating the convergence of the learning process in REMR. and represent the maximum number of iterations in each round and the loss function, respectively.
To better understand the REMR algorithm and its main steps, its pseudo-codes are introduced in Algorithm 1.
| Algorithm 1 REMR Algorithm |
| Inputs: Outputs: % Start training process For % Train the deep network and collect IMTs ; % Evaluate the AULC ; % Reinitialize parameters ; End (For) |
3. Some Illustrative Examples
This section presents two main examples obtained from previous applications of REMR. The first comes from a classification problem [8]; the second is related to a regression problem [12]. These sections are not dedicated to displaying numerical evaluations because some of these results have already been revealed in previous studies [8,9,10]. Accordingly, the main objective of this section is to illustrate the advantages of REMR from the point of view of data representations by showing some important data visualizations.
3.1. Classification Problem
The classification problem addressed in this case is closely related to imbalanced complex and dynamic data suffering from higher cardinality level under missing values. These data were the subject of REMR training using the LSTM network as the main element of recurrent expansion. Information on LSTM hyperparameters has been published elsewhere [8]. Figure 2 shows some important results at this stage. The REMR was unwound for 20 rounds. The results in Figure 2a show clear convergences in AULC behavior, as expected during the training process. This confirms the first REMR learning hypothesis, explained in Section 2. Figure 2b,c display processed IMTs of the first and last rounds, respectively. The purpose of this second illustration is to show the effect of REMR mappings on representations. REMR in this case not only shows feature separation ability, but also shows agglomeration and outlier correction ability.
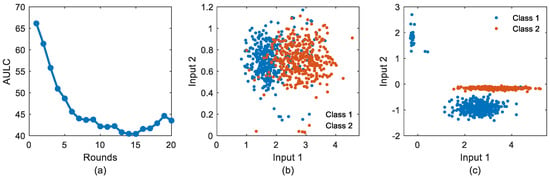
Figure 2.
REMR performance for a complex classification problem: (a) behavior of the AULC function; (b) data scatter at round 1; (c) data scatter at round 20 (i.e., final round).
3.2. Regression Problems
The regression problem adopted in this study is related to an approximation of a linear deterioration functions based on a set of nonlinear and complex features detailed elsewhere [12]. Similarly, LSTM was also involved in this experiment, while the hyperparameters were tuned similarly to the LSTM network introduced in [12] for 30 rounds. Figure 3 presents the results obtained on the REMR performance. The AULC function of Figure 3a still indicates great convergence of the REMR algorithm. This also confirms the ability of REMR to fit both regression and classification even if the loss functions are of different types. Figure 3b,c show examples of deterioration trajectory curve fitting using REMR at the first and last rounds, respectively. A 99% confidence interval was used to provide insight into prediction uncertainties. The results show that the REMR algorithm attempts to approach desired responses at each round. This reflects the benefits of learning from different IMTs produced from different deep networks to teach the model to behave appropriately. We believe that the reason for this large approximation is closely related to new sources of information (i.e., mainly estimated targets) providing additional knowledge to the system. Moreover, learning consecutively from different IMTs will be helpful in understanding the effects of changing inputs, maps, and targets on the approximation process, leading to better results each time based on better understanding of these behaviors.
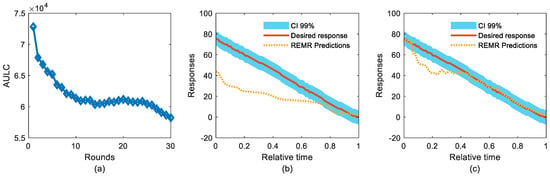
Figure 3.
REMR performance for a complex regression problem: (a) behavior of AULC function; (b) REMR predictions at round 1; (c) REMR predictions at round 30 (i.e., final round).
3.3. Advantages of REMR
In summary, from previous studies performed so far using the REMR algorithm [8,9,10], REMR shows its ability to improve the learning performance of deep networks through the following aspects:
- Improve feature representations through understanding the different IMTs of different deep networks;
- Providing a new source of information, such as estimated targets, helps introduce additional knowledge into the system through a kind of transductive transfer learning;
- The REMR pseudocode in Algorithm 1 shows that building an REMR algorithm does not require much intervention and is simple to design with only a few hyperparameters (i.e., , , and );
- REMR not only shows the ability to improve feature representations, but also the correction of outliers.
3.4. Disadvantages of REMR
It is undeniable that REMR was able to achieve excellent prediction results from both classification and regression; thus, it also experiences some burdens during model reconstructions, including the following:
- When building an REMR model by merging complex deep networks, it means that the computational complexity will be increased and will require more computational power than ordinary deep learning. This means that this architecture is computationally expensive;
- Convergence of the AULC function strongly depends on IMT initialization. This means that stacking in the inappropriate IMTs will cause the AULC function to diverge, which could lead to a worse outcome at each round;
- Thus far, IMT initialization has been evaluated on the basis of trial and error, which means that it takes a lot of intervention when rebuilding the model at this stage.
3.5. Future Opportunities of REMR
As a result of the aforementioned advantages of REMR algorithms, future research opportunities of REMR algorithms revolve around the following:
- Target IMT initialization problems by performing experiments on IMT selection and optimization in a few primary rounds. This will be useful in deciding whether to choose this model or not without consuming a lot of computing resources throughout the training rounds;
- Explore available REMR architecture inspired by ensemble learning and parallel architectures to help deliver even better initial IMTs.
4. Conclusions
This paper reviews REMR algorithms through important cutting-edge work. It shows the main learning rules with respect to some illustrative flowcharts and pseudo-codes. Moreover, it illustrates the performance of REMR by illustrating some important points for both classification and regression. It also has significant pros, cons, and future opportunities to focus on. The most important conclusion, in this case, is that REMR behaves appropriately as expected if, and only if, the IMTs are better initialized initially. This means that future opportunities will revolve around it to better improve its performance and application.
Author Contributions
Conceptualization, T.B.; methodology, T.B.; software, T.B.; validation, T.B. and M.B.; formal analysis, T.B.; investigation, T.B.; resources, T.B.; data curation, T.B.; writing—original draft preparation, T.B.; writing—review and editing, T.B. and M.B.; visualization, T.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, T.; Korfiatis, N.; Zicari, R.V. On the inequality of the 3V’s of big data Architectural Paradigms: A case for heterogeneity. arXiv 2013, arXiv:1311.0805. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Bank, D.; Koenigstein, N.; Giryes, R. Autoencoders. arXiv 2020, arXiv:2003.05991v2. [Google Scholar]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Networks Learn. Syst. 2022, 33, 6999–7019. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G. Deep belief networks. Scholarpedia 2009, 4, 5947. [Google Scholar] [CrossRef]
- Berghout, T.; Benbouzid, M.; Ferrag, M.A. Deep Learning with Recurrent Expansion for Electricity Theft Detection in Smart Grids. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022. [Google Scholar]
- Berghout, T.; Benbouzid, M.; Amirat, Y. Improving Small-scale Machine Learning with Recurrent Expansion for Fuel Cells Time Series Prognosis. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022. [Google Scholar]
- Berghout, T.; Benbouzid, M.; Bentrcia, T.; Amirat, Y.; Mouss, L. Exposing Deep Representations to a Recurrent Expansion with Multiple Repeats for Fuel Cells Time Series Prognosis. Entropy 2022, 24, 1009. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Zhang, Y.; Zhang, H. Recent Advances in Stochastic Gradient Descent in Deep Learning. Mathematics 2023, 11, 682. [Google Scholar] [CrossRef]
- Berghout, T.; Mouss, M.-D.; Mouss, L.; Benbouzid, M. ProgNet: A Transferable Deep Network for Aircraft Engine Damage Propagation Prognosis under Real Flight Conditions. Aerospace 2022, 10, 10. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).