Analyzing All the Instances of a Chaotic Map to Generate Random Numbers ^†

Abstract

All possible configurations of a chaotic map without fixed points, called “nfp1”, in its implementation in fixed-point arithmetic are analyzed. As the multiplication on the computer does not follow the associative property, we analyze the number of forms in which the multiplications can be performed in this chaotic map. As chaos enhanced the small perturbations produced in the multiplications, it is possible to built different pseudorandom number generators using the same chaotic map.

1. Introduction

The multiplication inside a computer does not follow the associative property, that is, for the three different numbers a, b, and c, $a\left(bc\right)\ne \left(ab\right)c\ne \left(ac\right)b$. This fact is produced because of using fixed-point arithmetic; the multiplication of two numbers, $i.f$, with i bits in the integer part and f bits in the factional part, produces a number $(2i+1).2f$. This resulted number must be returned to the same used representation, then the result is shifted f bits to the right. Moreover, to avoid the increasing size of the bits in the integer part, the number of bits in this part is chosen large enough to keep all the results of the multiplications within i bits. Fixed-point arithmetic is mostly used in the hardware implementation of chaotic circuits because of its simplicity [1,2,3].

The dynamics of a chaotic system are highly sensitive to small changes in its initial conditions. In this work, a map without fixed points to generate pseudorandom numbers by changing the order in the multiplications is studied, which also produces small changes that are increased by the chaos. In [4], the authors study the sensitivity of a chaotic system more as a problem. In this work, the sensitivity of a chaotic map is taken as an advantage to generate more maps by changing the order in the multiplications of the map terms.

Random numbers are very important in simulations [5], video games, in Monte Carlo methods, in cryptography [6], and in evolutionary algorithms [7] as the genetic algorithms, because these kind of algorithms can be considered a guided (intelligent) random search.

In the next Section 2, the chaotic map used and the generation of random sequences are described. In Section 3, the process to generate new sequences by changing the order of the multiplication is described. In this section, it is also shown that generated sequences are uncorrelated and random. Finally, in Section 4, the conclusion of this work is given.

2. Chaotic Map

The map nfp1 in [8] is used in this work. This map is defined as

$$\begin{array}{cc}\hfill x(i+1)& =a\left[y^2\left(i\right)-1\right]x\left(i\right)+c,\hfill \\ \hfill y(i+1)& =x\left(i\right)+y\left(i\right),\hfill \end{array}$$

(1)

with parameters values $a=1.78$ and $c=0.001$. These parameters values are the suggested in [8].

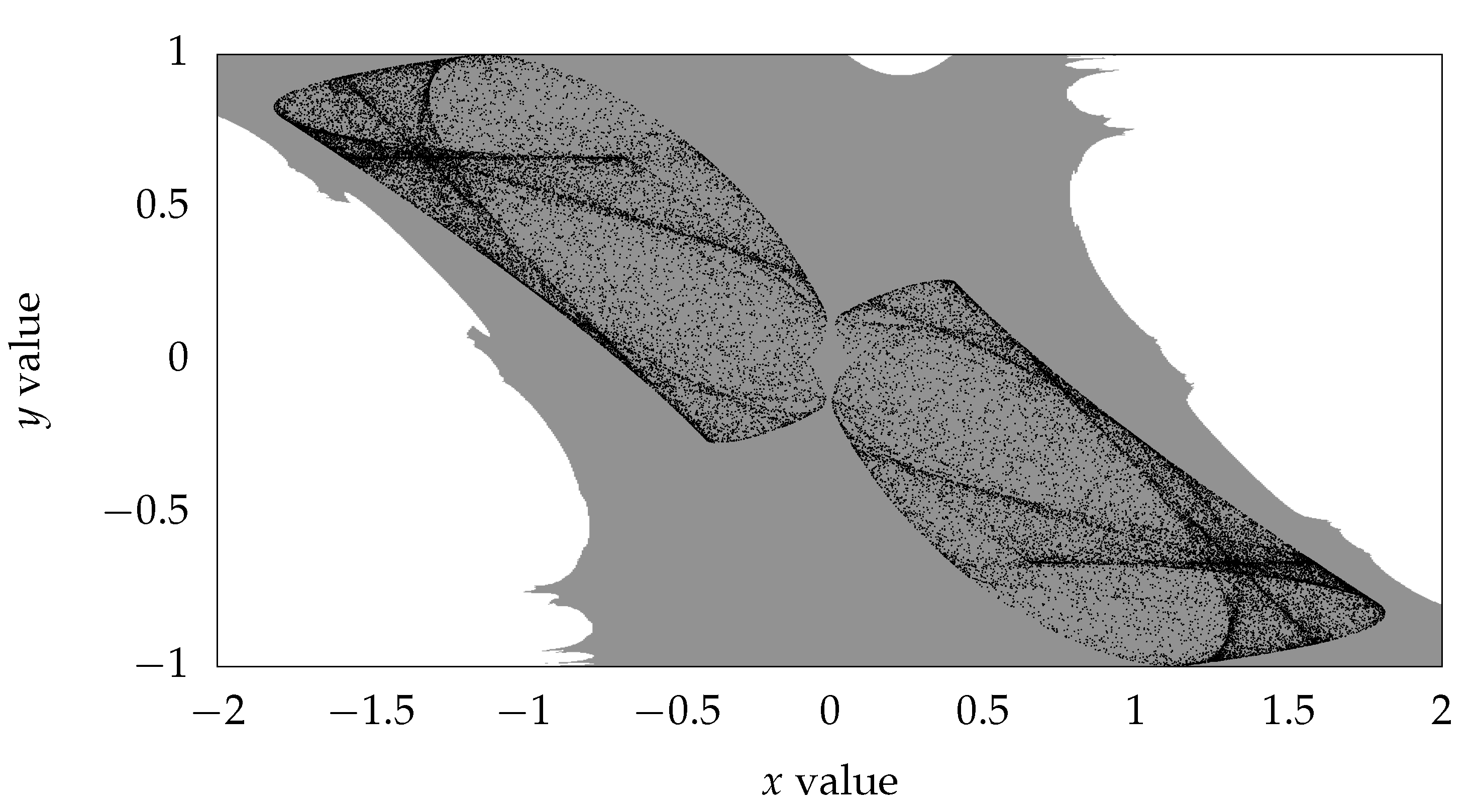
The domain of attraction for Equation (1) is shown in Figure 1. The gray zone in Figure 1 represents where the initial values take the shown values on the x and y axes, and the maps converge to the behavior shown as the black points. The white zone in Figure 1 represents where, with the shown initial values, the map’s dynamic behavior is destroyed. Thus, from this figure, it is possible to choose the initial values for $x\left(0\right)$ and $y\left(0\right)$ within the interval $[-0.5,0.5]$. Moreover, from Figure 1, it possible to see that the range of values for $x(i+1)$ is the interval $[-2,2]$ and $[-1,1]$ for $y(i+1)$, then 2 bits in the integer part are necessary for the calculations. For the fractional part, we decided to use 61 bits, plus the sign bit, then numbers of 64 bits are used. Then, the initial values can be expressed as the interval $[-0.5+u,-0.5+v]$, where $u,v\in [0,1)$, and $1=2^{61}$ with the used representation. Thus, the possible values for the initial values are ${\left(2^{61}\right)}^2=2^{122}$. These values can also be seen as the different possible values for the seed of the pseudorandom number generator (PRNG). A PRNG gives the same output sequence if the same seed is used. A PRNG is a deterministic process that generates a sequence of binary numbers that looks random.

An output binary sequence of 16 bits can be generated by concatenating two iterations of

$$b[i+1]=x[i+1]\mathrm{mod}256,$$

(2)

that is, the last 8 bits of the value of x variable are consider random. The value of the y variable cannot be used because it can be obtained easily from the previous values. In Equation (2) brackets are used due the sequences now being discrete binary values. This same technique was applied in [9] using a 2D map.

3. Analysis of the Map

The Equation (1), for the calculation of the $x(i+1)$ term can be expressed as

$$x(i+1)=a{y}^2\left(i\right)x\left(i\right)-ax\left(i\right)+c,$$

(3)

where the first term in the right part can be also expressed as the calculation of three terms: $\left(ay\right)\left(y\right)\left(x\right)$ or as $\left(a\right)\left(y^2\right)\left(x\right)$. Each one of these two triplets of terms can be multiplied in three forms as $\left(t_1{t}_2\right)t_3$, $t_1\left(t_2{t}_3\right)$, or $\left(t_1{t}_3\right)t_2$; therefore, with the map in Equation (1), $3\times 3=9$ different forms of multiplying the terms to obtain $x(i+1)$ in Equation (3) are possible. This can be seen as, if three more bits are added to the possible initial values, then now $(2^3+1)\times 2^{122}=2^{125}+2^{122}$ different initial values could be possible.

As a test of this idea, eight sequences are generated, four sequences with the values shown in

Table 1. Initial values and codes for the first four generated sequences.

Seq. Name	$\mathit{x}\left(0\right)$	$\mathit{y}\left(0\right)$	Code
$s_1$	$-0.5$	$-0.5$	00
$s_2$	$-0.5$	$-0.5+2^{-61}$	00
$s_3$	$-0.5$	$-0.5$	01
$s_4$	$-0.5$	$-0.5$	02

, and another four sequences with the codes 10, 10, 11, and 12 named as sequences $s_5$, $s_6$, $s_7$, and $s_8$. The first number in the code selects between the terms $\left(ay\right)\left(y\right)\left(x\right)$ or $\left(a\right)\left(y^2\right)\left(x\right)$. The second number in the code selects among the three possible forms of multiplying the three previous terms: 0 for $\left(t_1{t}_2\right)t_3$, 1 for $t_1\left(t_2{t}_3\right)$, and 2 for $\left(t_1{t}_3\right)t_2$.

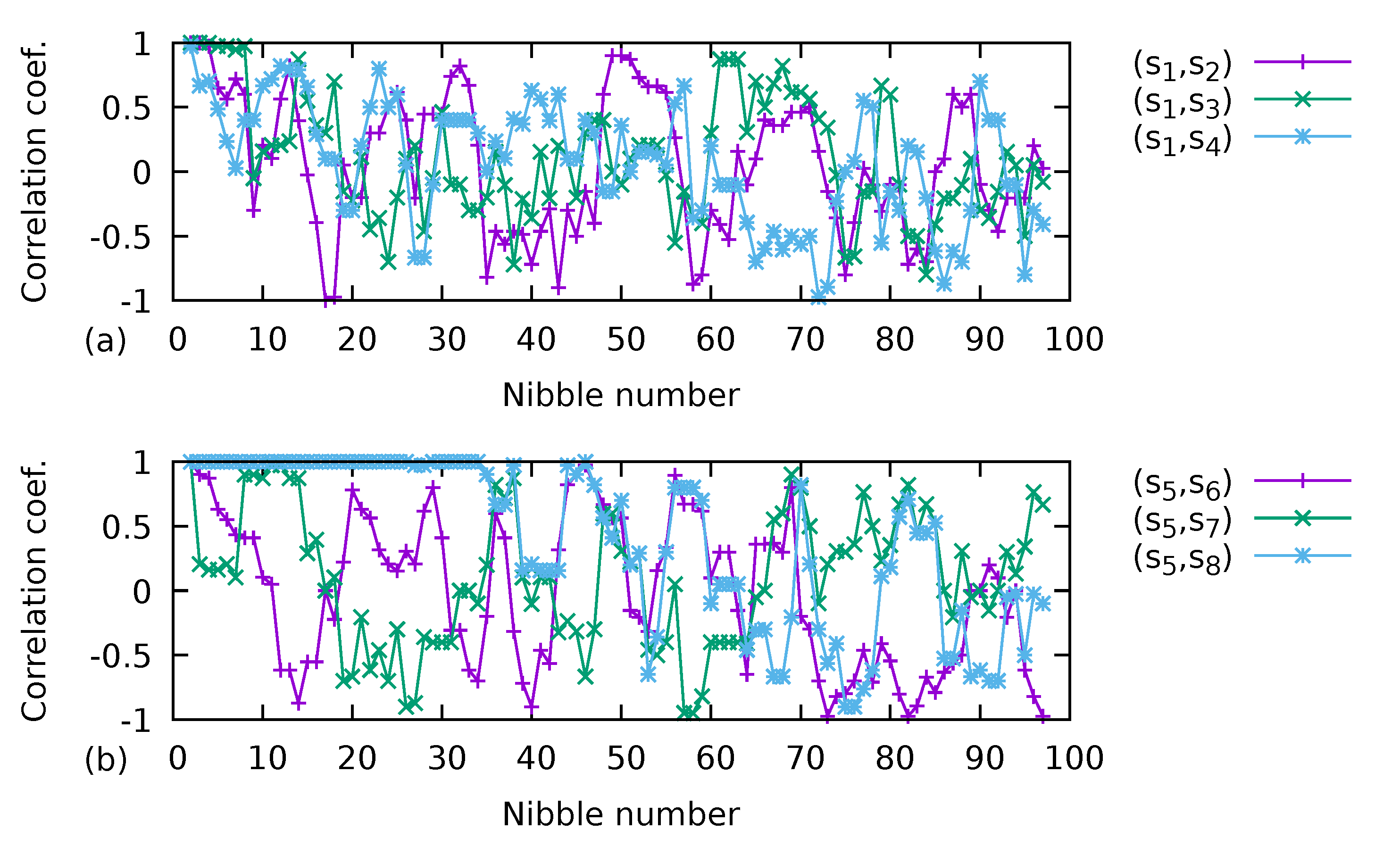
The correlations between the pair of sequences $(s_1,s_2)$, $(s_1,s_3)$, and $(s_1,s_4)$ are show in the graph of Figure 2a; the correlations between the sequences $(s_5,s_6)$, $(s_5,s_7)$, and $(s_5,s_8)$ are show in the graph of Figure 2b. The correlation is calculated with the overlapped pairs of five samples of the sequences. The values of the each of the four nibbles ranging from the most significant to the least significant at the output of the PRNG are used as the samples values.

From Figure 2, it is possible to see that sequences are uncorrelated if the initial values are change in a single bit (as sequences $s_2$ and $s_6$ are generated) or by changing the order of the multiplication around the nibble 10, or 40 bits, except for the correlation of sequences $(s_5,s_8)$. This last case, in which the sequence $s_8$ is calculated with the code 12, is when the term $\left(a\right)\left(y^2\right)\left(x\right)$ is calculated as $\left(ax\right)y^2$. 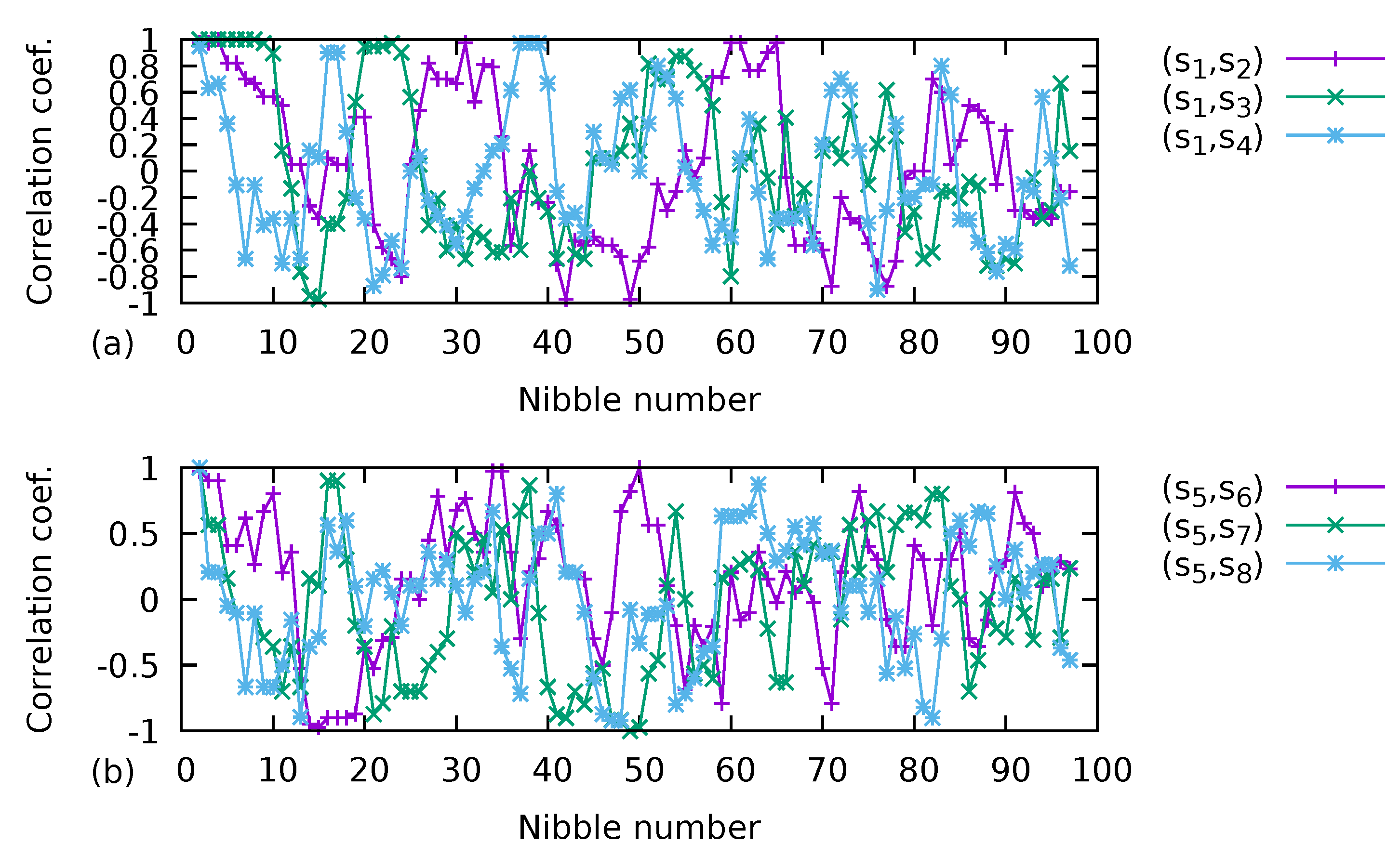If the value of the constant a in Equation (1) is changed from 1.78 to 1.7777777, or as 0x38e38e38e38e38e3 in hexadecimal, the correlations change, as shown in Figure 3.

From Figure 3, the first 40 bits of each sequence must be discharged to consider them as uncorrelated sequences when the order in the multiplications in the map is changed.

To demonstrate that the generated sequences are random, three tests of TestU01 suite, Rabbit, Alphabit, and BlockAlphabit are applied on 100 sequences of ${10}^6$ bits. These tests were designed for bits stored in a file (or a physical device). Rabbit and Alphabit apply 40 and 17 different statistical tests, respectively. BlockAlphabit applies the Alphabit battery of tests repeatedly to a binary file after reordering the bits by blocks of different sizes (with sizes of 2, 4, 8, 16, and 32 bits) [10]. Applying the TestU01 to the eight generated sequences from $s_1$ to $s_8$ gives the results shown in

Table 2. Results of applying the TestU01 to the generated sequences.

	Test Name	Seqs. ${\mathit{s}}_1$, ${\mathit{s}}_2$, ${\mathit{s}}_3$, ${\mathit{s}}_4$, ${\mathit{s}}_5$, ${\mathit{s}}_6$, ${\mathit{s}}_8$	Seqs. ${\mathit{s}}_7$
1	Rabbit	All 40 tests passed	17/40
2	Alphabit	All 17 tests passed	1/17
3	Block Alphabit	All 6 repetitions of Alphabit tests passed	8/102

. All the sequences passed the tests, except the sequence $s_7$. This sequence is generated as the multiplication of the terms $a\left(y^{2}x\right)$. It looks as though multiplication by the constant a does not give enough variability to generate a random sequence by obtaining the last 8 bits of each iteration on the map calculation.

As a configuration does not give random sequences, the number of possible initial values is $2^3\times 2^{122}=2^{125}$.

Discussing the number of bits used in the number representation, the number of bits in the integer part is clear: they are necessary to perform the calculations of Equation (1). The number of bits for the fractional part is not so clear: they must be necessary to maintain the map behavior shown in Figure 1 and to keep a random behavior in the eight less significant bits. The used representation of 64 bits is more precise than real numbers (doubles in C programming language) that have around 52 bits of precision. Lesser bits in the fractional part could keep the map behavior but, at the same time, stop the random behavior of the less significant bits.

4. Conclusions

A map without a fixed point was used to generate random numbers by changing the association in the multiplication of a term with three variables. Fixed-point arithmetic was used with numbers with 2 bits for the integer part and 61 bits for the fractional part. The value of a constant used by the map was changed slightly (from 1.78 to 1.7777777) to generate uncorrelated sequences. One of the configuration multiplies the constant values by the other terms; this configuration does not generate random sequences. With the used numbers, $2^{122}$ values can be used as the seed for the random number generator. With the different association in the multiplication, three bits can be added to the seed values, given a total of $2^{125}$ possible values for the seed. An efficient design in hardware can be proposed in a future work, as well as the search for more applications for the studied configuration.