Further Remarks on Irrational Systems and Their Applications †
Abstract
1. Introduction
2. Preliminaries
Origins and Connection with Fractional Calculus
- The network should contain only linear lumped elements. For instance, viscous dampers, springs, capacitors, or inductors.
- All initial conditions should be equal to zero.
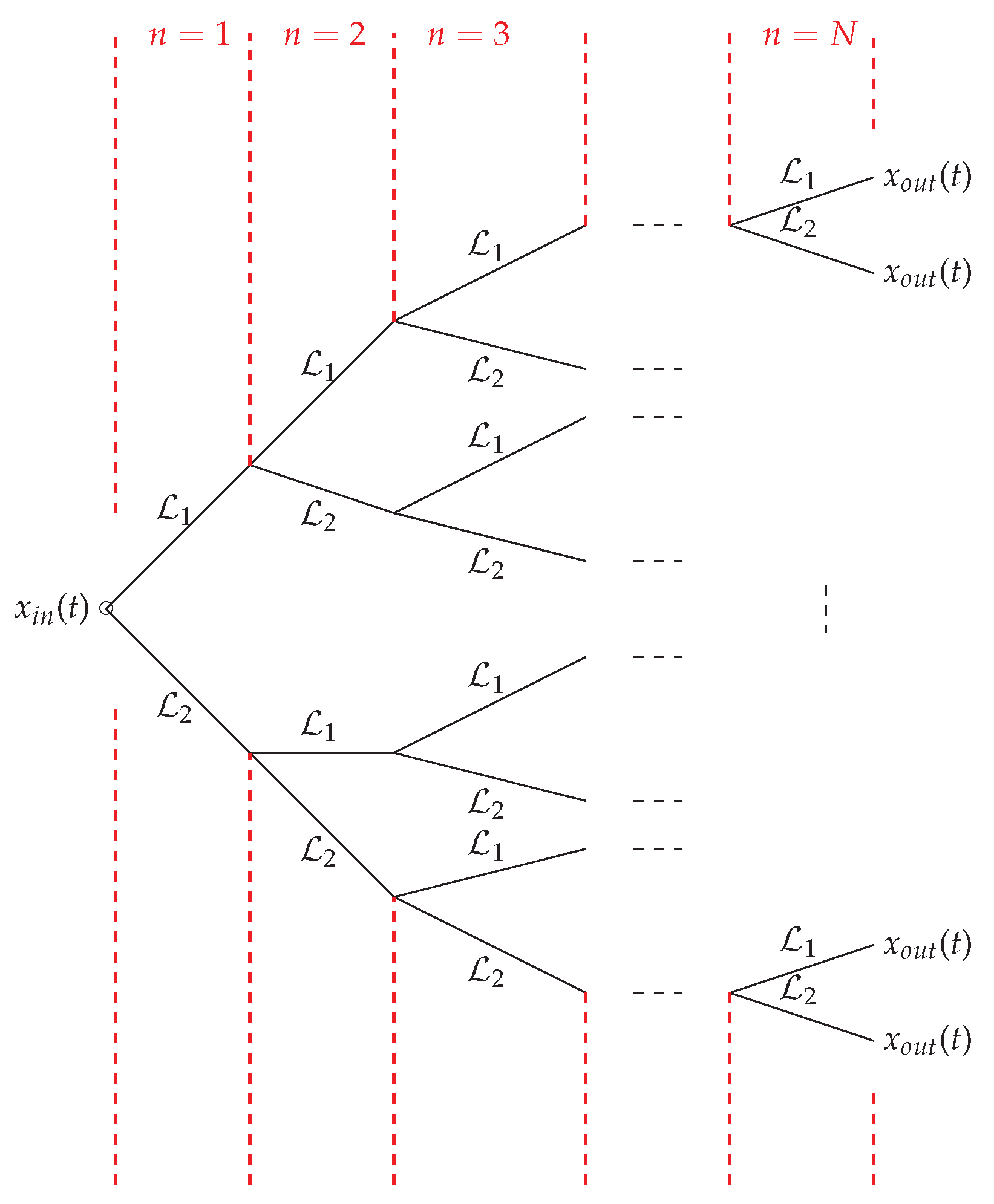
- Elements in the network should have equal impedance value. For example, the tree-like network shown in Figure 1 contains only two linear operators and , which have the same value throughout all the layers of the network.
- The network is one-dimensional and infinite.
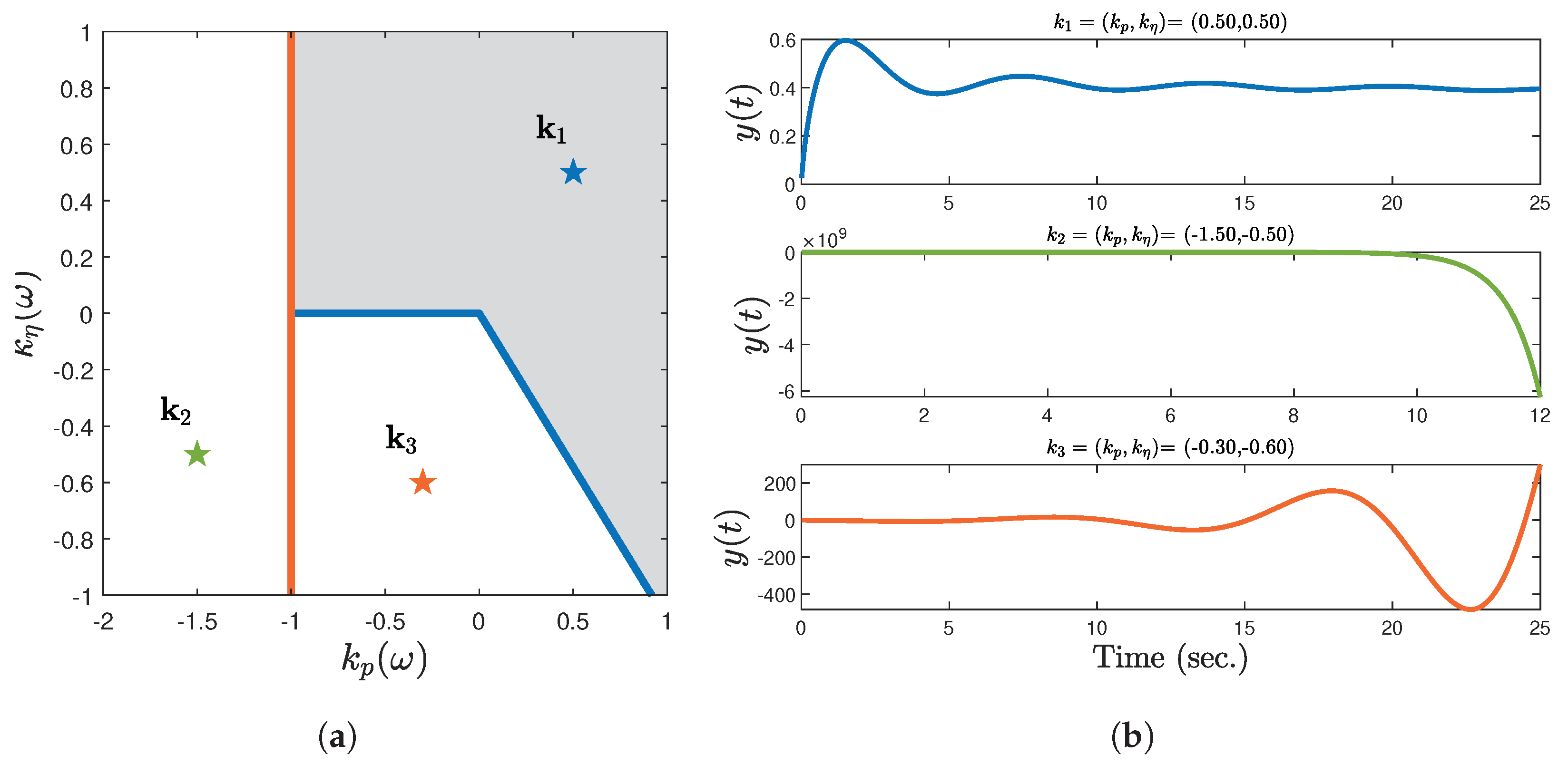
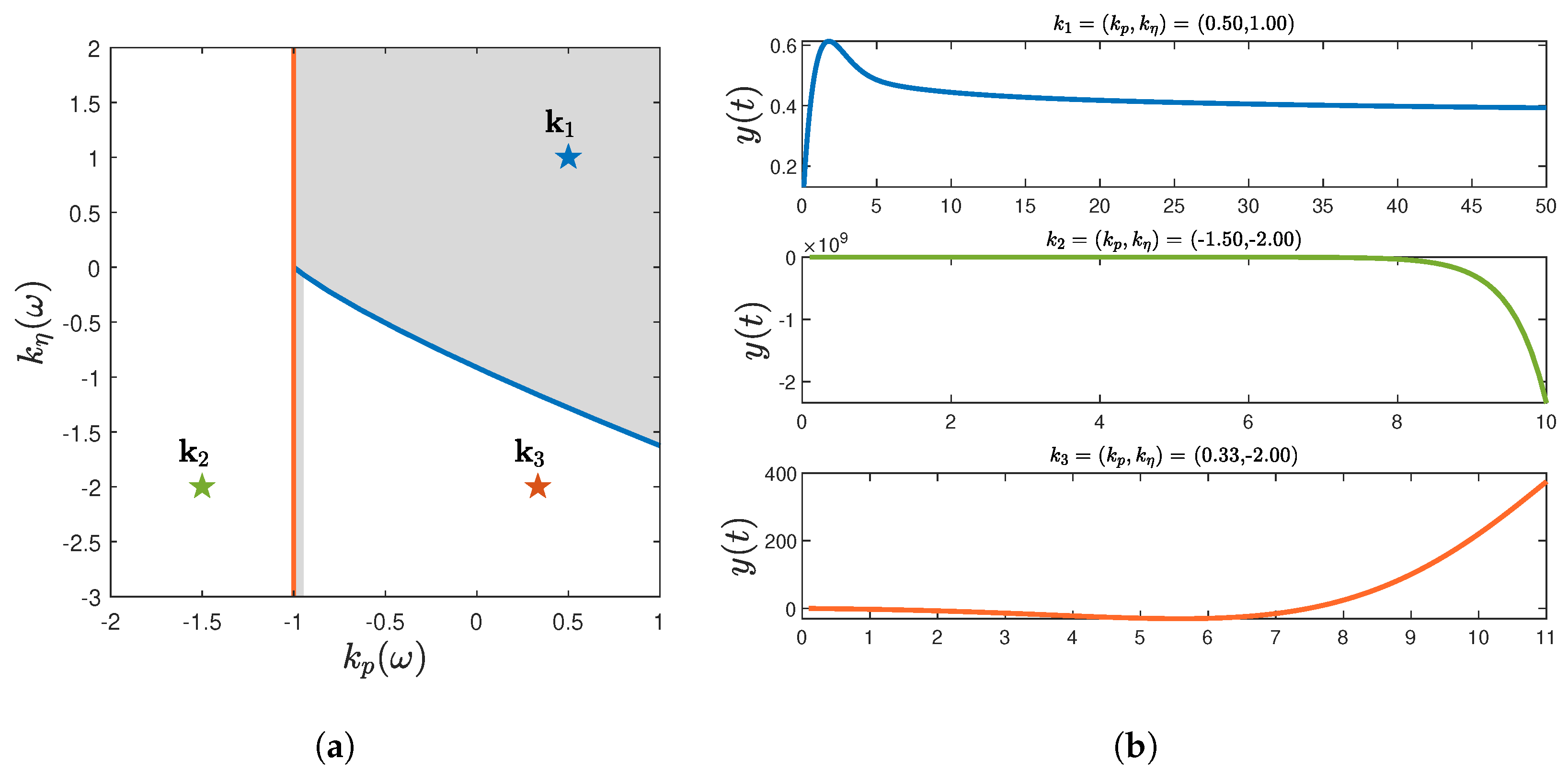
3. Stability Analysis
4. Control Design
PD Control
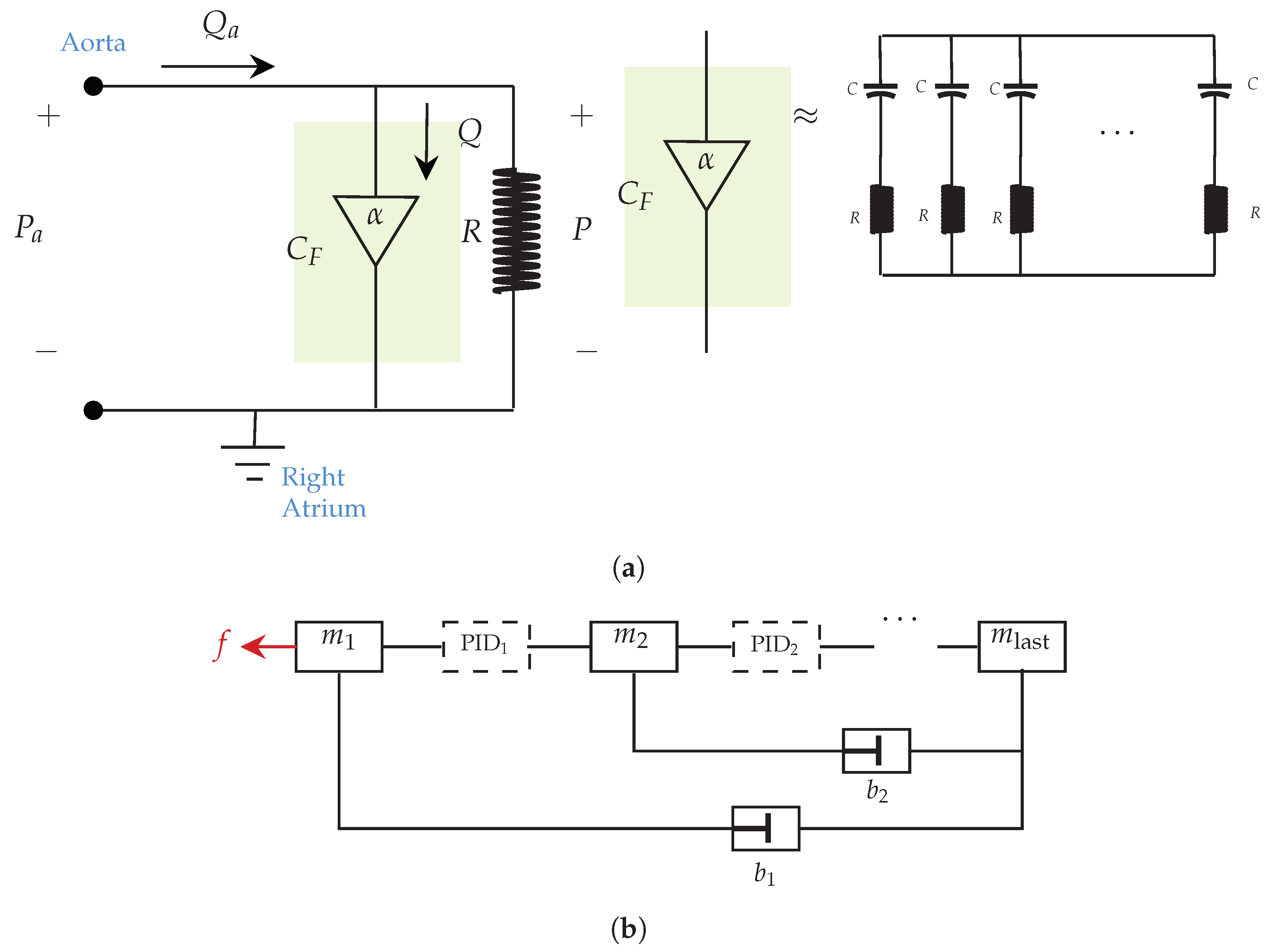
5. Applications
5.1. Control of IS
5.2. Bessel
5.3. First Order IS
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IS | Irrational system |
| PD | Proportional derivative |
| PI | Proportional integral |
| BP | Branch point |
| PID | Proportional integral derivative |
Appendix A. Example 1

Appendix B. Example 2

References
- Guel-Cortez, A.J. Modeling and Control of Fractional-Order Systems. The Linear Systems Case. Ph.D. Thesis, CIEP-UASLP, San Luis, Mexico, 2018. [Google Scholar]
- Sen, M.; Hollkamp, J.P.; Semperlotti, F.; Goodwine, B. Implicit and fractional-derivative operators in infinite networks of integer-order components. Chaos Solitons Fractals 2018, 114, 186–192. [Google Scholar] [CrossRef]
- Guel-Cortez, A.J.; Sen, M.; Goodwine, B. Closed form time response of an infinite tree of mechanical components described by an irrational transfer function. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 5828–5833. [Google Scholar]
- Guel-Cortez, A.J.; Kim, E. A Fractional-Order Model of the Cardiac Function. In Proceedings of the 13th Chaotic Modeling and Simulation International Conference, Florence, Italy, 9–12 June 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 273–285. [Google Scholar]
- Leyden, K.; Sen, M.; Goodwine, B. Large and infinite mass–spring–damper networks. J. Dyn. Syst. Meas. Control 2019, 141, 061005. [Google Scholar] [CrossRef]
- Ni, X.; Goodwine, B. Frequency Response and Transfer Functions of Large Self-similar Networks. arXiv 2020, arXiv:2010.11015. [Google Scholar] [CrossRef]
- Mayes, J.; Sen, M. Approximation of potential-driven flow dynamics in large-scale self-similar tree networks. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 2810–2824. [Google Scholar] [CrossRef]
- Merrikh-Bayat, F.; Karimi-Ghartemani, M. On the essential instabilities caused by fractional-order transfer functions. Math. Probl. Eng. 2008, 2008, 419046. [Google Scholar] [CrossRef]
- Guel-Cortez, A.J.; Sen, M.; Goodwine, B. Fractional- PDμ Controllers for Irrational Systems. In Proceedings of the 2019 International Conference on Control, Decision and Information Technologies, Paris, France, 23–26 April 2019. [Google Scholar]
- Guel-Cortez, A.J.; Méndez-Barrios, C.F.; Kim, E.j.; Sen, M. Fractional-order controllers for irrational systems. IET Control Theory Appl. 2021, 15, 965–977. [Google Scholar] [CrossRef]
- Cohen, H. Complex Analysis with Applications in Science and Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Harvey, C. Conformal mapping on Riemann Surfaces; Dover Publications, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Needham, T. Complex Visual Analysis; Oxford University Press, Inc.: New York, NY, USA, 1997. [Google Scholar]
- Capoccia, M. Development and characterization of the arterial W indkessel and its role during left ventricular assist device assistance. Artif. Organs 2015, 39, E138–E153. [Google Scholar] [CrossRef] [PubMed]
- Piovesan, D.; Pierobon, A.; DiZio, P.; Lackner, J.R. Measuring multi-joint stiffness during single movements: Numerical validation of a novel time-frequency approach. PLoS ONE 2012, 7, e33086. [Google Scholar] [CrossRef][Green Version]
- Ni, X.; Goodwine, B. Frequency Response of Transmission Lines with Unevenly Distributed Properties with Application to Railway Safety Monitoring. arXiv 2020, arXiv:2012.09247. [Google Scholar]
- Leyden, K.; Goodwine, B. Using fractional-order differential equations for health monitoring of a system of cooperating robots. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 366–371. [Google Scholar]
- Leyden, K.; Sen, M.; Goodwine, B. Models from an implicit operator describing a large mass-spring-damper network. IFAC-PapersOnLine 2018, 51, 831–836. [Google Scholar] [CrossRef]
- Shukla, A.; Prajapati, J. On a generalization of Mittag-Leffler function and its properties. J. Math. Anal. Appl. 2007, 336, 797–811. [Google Scholar] [CrossRef]
- Sabatier, J.; Farges, C.; Tartaglione, V. Some alternative solutions to fractional models for modelling power law type long memory behaviors. Mathematics 2020, 8, 196. [Google Scholar] [CrossRef]
- Sabatier, J. Some Proposals for a Renewal in the Field of Fractional behavior Analysis and Modelling. In Proceedings of the International Conference on Fractional Differentiation and its Applications (ICFDA’21); Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–25. [Google Scholar]
- Ramos-Avila, D.; Rodrıguez, C.; Hernández-Carrillo, J.; Guel-Cortez, A.; Sen, M.; Méndez-Barrios, C.; González-Galván, E.; Goodwine, B. Experiments with PD-controlled robots in ring formation. In Proceedings of the XXI Congreso Mexicano de Robótica–COMRob, Ciudad de Manzanillo, Colima, Mexico, 13–15 November 2019. [Google Scholar]
- Gryazina, E.N. The D-decomposition theory. Autom. Remote Control 2004, 65, 1872–1884. [Google Scholar] [CrossRef]
- Hernández-Díez, J.E.; Méndez-Barrios, C.F.; Mondié, S.; Niculescu, S.I.; González-Galván, E.J. Proportional-delayed controllers design for LTI-systems: A geometric approach. Int. J. Control 2018, 91, 907–925. [Google Scholar] [CrossRef]
- Barrios, C.F.M. Low-Order Controllers for Time-Delay Systems: An Analytical Approach. Ph.D. Thesis, Université Paris Sud-Paris XI, Bures-sur-Yvette, France, 2011. [Google Scholar]
- Abate, J.; Whitt, W. A unified framework for numerically inverting Laplace transforms. INFORMS J. Comput. 2006, 18, 408–421. [Google Scholar] [CrossRef]
- Moslehi, L.; Ansari, A. Some remarks on inverse Laplace transforms involving conjugate branch points with applications. UPB Sci. Bull. Ser. A-Appl. Math. Phys. 2016, 78, 107–118. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guel-Cortez, A.-J.; Méndez-Barrios, C.-F.; Torres-García, D.; Félix, L. Further Remarks on Irrational Systems and Their Applications. Comput. Sci. Math. Forum 2022, 4, 5. https://doi.org/10.3390/cmsf2022004005
Guel-Cortez A-J, Méndez-Barrios C-F, Torres-García D, Félix L. Further Remarks on Irrational Systems and Their Applications. Computer Sciences & Mathematics Forum. 2022; 4(1):5. https://doi.org/10.3390/cmsf2022004005
Chicago/Turabian StyleGuel-Cortez, Adrián-Josué, César-Fernando Méndez-Barrios, Diego Torres-García, and Liliana Félix. 2022. "Further Remarks on Irrational Systems and Their Applications" Computer Sciences & Mathematics Forum 4, no. 1: 5. https://doi.org/10.3390/cmsf2022004005
APA StyleGuel-Cortez, A.-J., Méndez-Barrios, C.-F., Torres-García, D., & Félix, L. (2022). Further Remarks on Irrational Systems and Their Applications. Computer Sciences & Mathematics Forum, 4(1), 5. https://doi.org/10.3390/cmsf2022004005





