A Novel Strategy for Tall Building Optimization via the Combination of AGA and Machine Learning Methods ^†

Abstract

The optimum design of tall buildings, which have a proportionately huge quantity of structural elements and a variety of design code constraints, is a very computationally expensive process. In this paper, a novel strategy, with a combination of evolutionary algorithms and machine learning methods, is developed for achieving the optimal design of tall buildings. The most time-consuming part is the analysis of tall buildings and the control of design code constraints requiring long and frequent analyses. The main idea is to use machine learning methods for this purpose. In this study, a practical methodology for obtaining the optimal design of tall building structures, regarding the constraints imposed by typical building codes, is introduced. The optimization process will be performed by a novel evolutionary algorithm, named asymmetric genetic algorithm (AGA), and in each iteration that requires checking the constraints for a large number of different structural states, machine learning methods, including MLP, GMDH and ANFIS-PSO are facilitators. More specifically, MLP (R² = 0.988) has performed better than GMDH (R² = 0.961) and ANFIS-PSO (R² = 0.953). By coupling ETABS and MATLAB software, various combinations of sections for structural elements are assigned and analyzed automatically, thus creating a database for training neural networks. The applicability of the suggested procedure is described through the determination of the optimal seismic design for a 40-story framed tube building. Results designate that the present method not only supports the precision of the methodology but also remarkably diminishes the computational time and memory needed in comparison with the existing classical methods. More importantly, the optimization process time is also significantly decreased.

1. Introduction

In recent years, the demand for the optimal candidate of tall building structures has grown significantly due to financial issues. On the other hand, the dependable design of such structures brings many difficulties for an engineer because of the significant number of structural members and also the strict design constraints imposed by codes. This makes the conventional design provided by engineers not necessarily economical. This highlights the significance of optimization tools in the design process of these structures to save on construction costs [1,2,3,4]. Many of the studies in the field of tubular structures deal with the modeling of a tall building as a huge cantilever box beam [5,6,7]. The recent advances in high-performance computers made possible the precise analysis of the whole frame of the high-rise building during the optimization process. Chan et al. [8] introduced an iterative procedure based on drift, strength, and fabrication constraints. The effects of various parameters on the tube action of a reinforced concrete 55-story hotel building were investigated by Shin et al. [9]. Some researchers proposed techniques for the minimization of the weight of high-rise buildings subject to wind loads [10,11]. Aldwaik and Adeli [12] conducted a review of the optimization of high-rise buildings with either tubular or other structural systems.

The above-mentioned studies mostly consider fixed patterns of loads; however, another line of thought deals exclusively with the seismic loads which lead to more cumbersome behavior in the structure. In this respect, the design codes prescribe additional strict limitations on the design of structures subject to seismic loads. During the past decades, many researchers focused on the seismic assessment of the structures [13,14]. More specifically, many studies incorporated seismic considerations into optimization problems [15,16,17]. Moghaddam and Hajirasouliha [18] introduced an optimization technique to reach the uniform deformation of members in two-dimensional (2D) tall shear buildings subject to seismic excitation. Furthermore, Ganjavi et al. [19] investigated the best distribution of seismic lateral loads to achieve uniform damage distribution in 2D shear buildings considering the soil–structure interaction (SSI). Recently, many researchers employed optimization methods to reach the desired seismic performance objectives at various seismic hazard levels in 2D low-rise and mid-rise steel frames [20,21] and also in 2D reinforced concrete frames [22]. Recently, with the aid of gradient-based optimization algorithms, Sarcheshmehpour et al. proposed practical methodologies for optimal seismic design of steel-framed tube tall buildings based on conventional building codes [23], as well as life cycle costs [24].

Notwithstanding ample research on the optimization problems of tall buildings, using soft computing methods in optimal seismic design of tall buildings is scarce in the literature. In the current research, a practical methodology with logical computational demand to achieve the most beneficial possible design within the constructional aspects, by the combination of machine learning methods and evolutionary algorithms, was proposed. First, the optimization problem considering all constraints is described. Then, by establishing the connection between MATLAB and ETABS software, a huge database, which was used for training ANNs, is created. The methods of MLP, GMDH, and ANFIS-PSO were investigated and the best one was selected for evaluating the constraints in the optimization process, which was based on the AGA algorithm. Finally, the result for a sample 40-story building was presented. The structural analysis procedure for creating the database is convoyed based on the Iranian National Building Code (INBC), which is almost identical to the ANSI/AISC 360-10 LRFD design guide [25].

2. Formulation of the Optimization Problem

In this section, the general formulation for seismic design optimization of high-rise buildings is presented. The structural design is performed according to the conventional load and resistance factor design (LRFD) approach:

Design for serviceability: Based on the Iranian Code of Practice for Seismic Resistant Design of Buildings (Standard No. 2800), the inter-story drift ratio (${\Delta }_i$) of different stories of the buildings more than five stories high, the following constraint shall be satisfied under design seismic forces:

$$C_d{\Delta }_i\le 0.02,$$

(1)

In which $C_d$ indicates the amplification factor accounting for the expected inelastic response.

• Design for Strength
  According to the building code, the demand–capacity ratio defined in Equation (2) shall be equal to or less than one for all load combinations, i.e.,

  $$\frac{R_u}{\varphi R_n}\le 1,$$

  (2)

  where $R_u$ represents the required strength under all LRFD load combinations and $\varphi R_n$ indicates the design strength of each structural element.
• Strong-column/weak-beam (SC/WB): For the design of Special Moment Frames (SMFs), the moment ratio shall satisfy the following constraint at each beam-to-column connection:

  $$\frac{\sum M_{pb}^{*}}{\sum M_{pc}^{*}}<1,$$

  (3)

  where $\sum M_{pb}^{*}$ represents the total flexural strength of all beams attached to the connection and $\sum M_{pc}^{*}$ indicates the total flexural strength of the columns with a reduction for the axial force.
• Practical limitations: from a practical perspective, the dimensions of columns in each story shall not be less than those in the upper stories. This constraint can be formulated as:

  $$d_{j,i}^{Col}\ge d_{j+1,i}^{Col}, b_{j,i}^{Col}\ge b_{j+1,i}^{Col} , j=1,2,\cdots , NS-1; i=1,2,\cdots , NC,$$

  (4)

In Equation (4), $d_{j,i}^{Col}$ and $b_{j,i}^{Col}$ represent the depth and the width of the section of the $i$th column in the $j$th story, respectively. Furthermore,$NC$ denotes the number of columns in each story and $NS$ is the total number of stories.

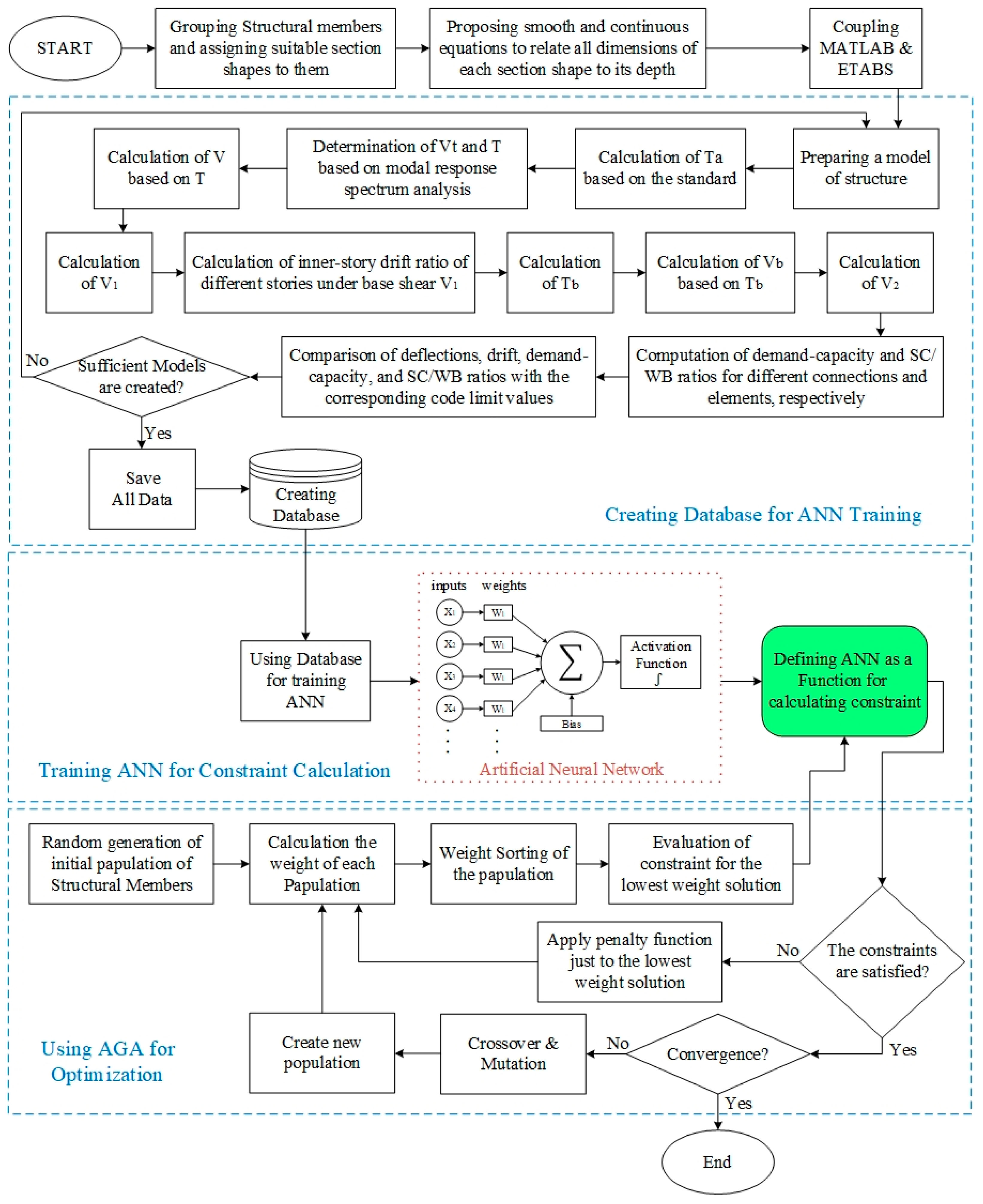
In the current design optimization problem, the total weight of all beams and columns in the 3D steel tall building indicates the objective function and all the above-mentioned inequalities behave as the optimization constraints. In addition, the section properties of the structural elements are considered as the design variables. The resulting nonlinear constrained optimization problem is attacked by two basic approaches, in the current study. The first one is the metaheuristic optimization method, named AGA. The second one is using machine learning techniques for determining nonlinear inequality constraints instead of time-consuming analytical approaches. For the sake of convenience, the proposed procedure of the optimal seismic design is illustrated in Figure 1. A full description of the parameters available in Figure 1 can be found in [23].

3. Structural Model

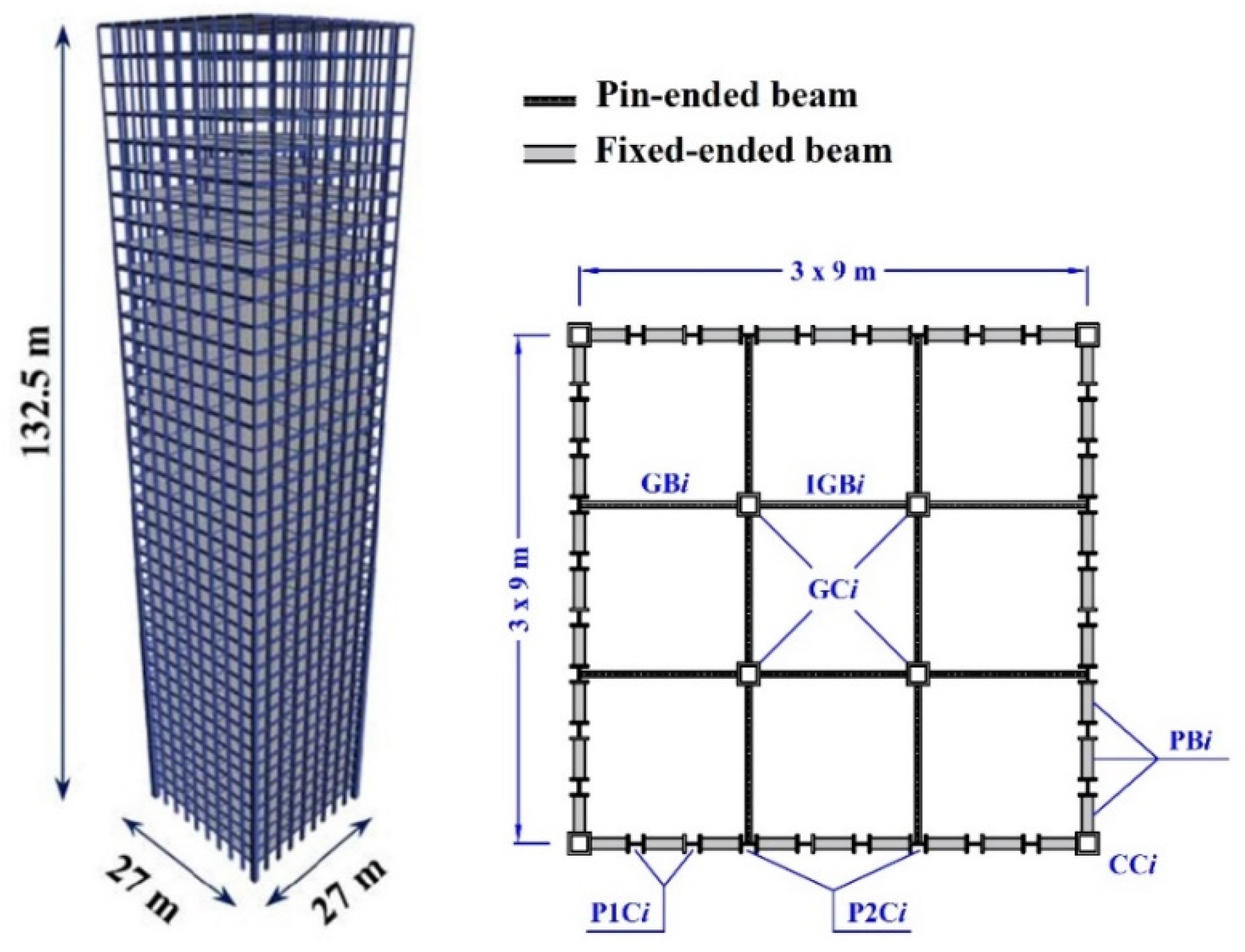
In this study, a 40-story framed tube building is considered as the case study to demonstrate the applicability of the proposed strategy. The 3D view and the typical floor plan of this building are shown in Figure 2. As seen, in both directions, the plan consists of nine bays, each with a length of 3 m. The gravitational columns (GC) and the corner columns (CC) of the perimeter tube have box sections. The sections of the rest of the columns (P1C and P2C) are I-shaped sections. As shown in Figure 2, there are two types of non-corner perimeter columns: P1C columns which are only connected to the perimeter beams from both sides, and P2C columns which are also connected to the pin-ended gravitational beams (GB). The spandrel beams (PB) are fixed-ended and have a length of 3 m. Moreover, both types of gravitational beams (GB and IGB) are pin-ended with a length of 9 m. As seen in Figure 2, IGB beams connect the gravitational columns together and GB beams connect the gravitational columns to the perimeter tube.

The case study is a residential building in which the first four stories are considered as parking lots. The gravitational beams (GB or IGB) are divided into two groups based on their position in either residential floors or parking lots. For practical design purposes, all spandrel beams and all columns are grouped every four stories. This leads to a considerable reduction in the number of design variables. It is worth mentioning that the index i in Figure 2 represents the group number of each structural section.

The building is considered to be located in Tehran with a very high level of seismicity. Furthermore, the soil beneath the building is consistent with Soil Type 2 of Iranian seismic code (in a depth of 30 m, the average shear wave velocity is between 375 m/s and 750 m/s). A fixed base is assumed at the ground level and all supports are fixed in the structural model.

By coupling ETABS [26] and MATLAB software, 7800 combinations of sections for structural elements are assigned and analyzed automatically, thus creating a database for training neural networks.

Section Decision Variables

In this research, the sections properties indicating the decision variables are considered to be continuous. The number of design variables reduces appreciably by relating all dimensions of the section to its depth through rational equations. In this study, linear equations relating the dimensions of the sections to their depths are determined according to Euro-standard sections. For more details refer to [23,24].

The above-mentioned relations for I-shape sections pertinent to the non-corner columns of the perimeter tube and beams are presented in Equations (5) and (6), respectively.

$$\begin{array}{c}{b}_f=d,\\ t_f=0.055d+0.35\\ t_w=0.015d+0.6\end{array}$$

(5)

$$\begin{array}{c}{b}_f=0.35d+3.3,\\ t_f=0.026d+0.33\\ t_w=0.016d+0.25\end{array}$$

(6)

In Equations (5) and (6), $d$ is the section depth, $b_f$ denotes the flange width, $t_f$ is the flange thickness, and $t_w$ represents the web thickness.

As mentioned before, all the corner and gravitational columns have box shape sections. The equation relating the thickness (t) of the box section to its depth (d) is given as:

$$t=0.06d$$

(7)

4. Machine Learning Techniques for Constraint Evaluation

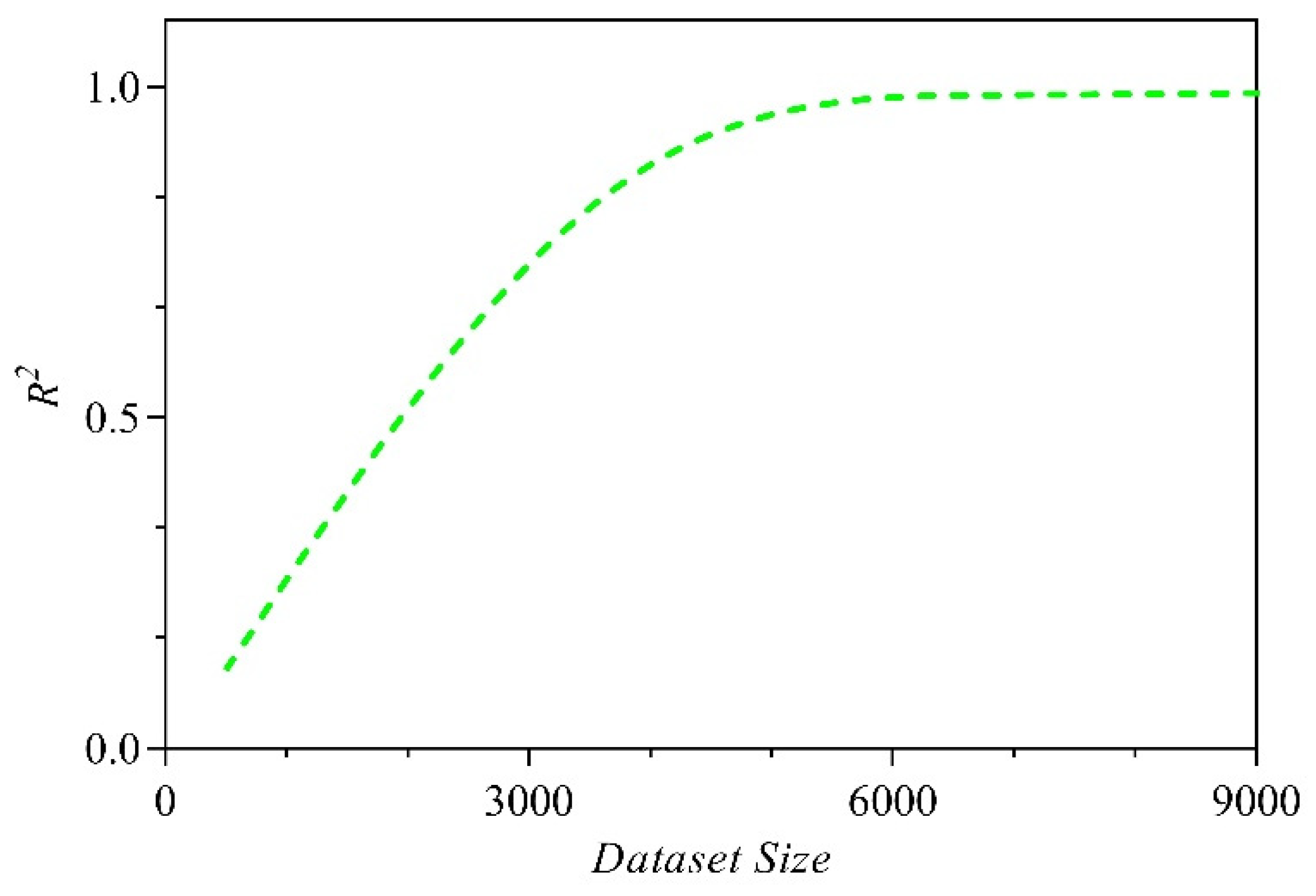
Recently, machine learning has become very popular in engineering applications [27,28]. In this study, three non-linear machine learning models, namely multiplayer perceptron (MLP) [29], group method of data handling (GMDH) [30], and combining adaptive-network-based fuzzy inference system and particle swarm optimization (ANFIS–PSO) [31] were employed to estimate structural constraints. These methods are examined and the best one is selected in the optimization process as the function of constraint evaluation. For training ANNs, 7800 models were created. For instance, the effect of dataset size for estimation of one of the constraints, design ratio of CC1, by MLP method, is shown in Figure 3. As shown in this figure, the number of 6000 is sufficient for the dataset size. Therefore, creating the 7800 model is appropriate. By trying several different models for neural networks, their final structures are presented in

Table 1. The parameters of Machine Learning methods.

ML Methods	Parametrs
MLP	Number of Layers:	1	Training Percentage:	65%
	Number of neurons:	20	Testing Percentage:	30%
	Structure:	54-20-1 ANN	Validation Percentage:	5%
GMDH	Maximum number of neurons in a layer:			30
	Maximum number of layers:	6	Training percentage:	50%
	Selection pressure:	0.2	Testing percentage:	50%
ANFIS-PSO	Number of the iterations:	5000	Cognitive acceleration:	1
	Number of particles:	65	Social acceleration:	1.5
	Initial inertia weight:	0.8	Training percentage:	70%
	Final inertia weight:	0.2	Testing percentage:	50%

.

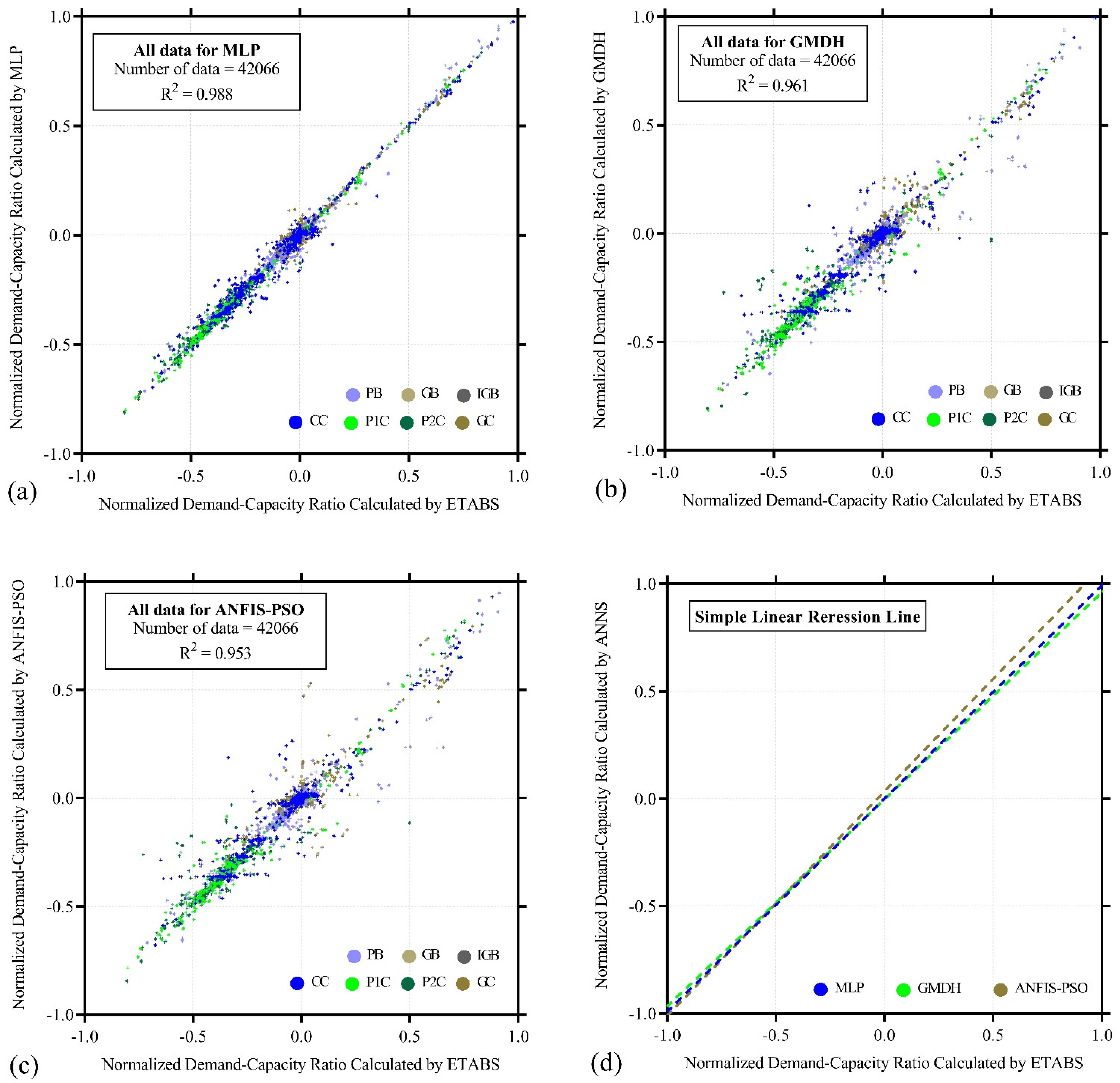
In Figure 4, the performances of the three selected ML tools are compared. It can be seen that MLP is more accurate than GMDH and ANFIS-PSO in calculating the constraints and catching the structural response. The output provided by MLP is shown to be much less scattered than the others, and the linear interpolation of all the pairs of results is well aligned with the (perfect fit) bisector of the quadrant. Therefore, for the optimization process, the MLP method is selected.

5. Results

In this part, the details of the optimal designs and the seismic behavior of the 40-story framed tube are presented. For the optimization process, the algorithms of AGA, which are depicted in [2], are used. The AGA algorithm has some differences from the GA, the most important of which are in the constraints evaluation strategy. In AGA, initial population members are sorted by goal function, and, despite GA, just the constraints of the best member are evaluated. If the best member satisfies the constraints, AGA does not evaluate other members’ constraints. If not, the penalty function is applied to the best one, and then the population is sorted again, and the new best solution is evaluated by the constraints again. This procedure proceeds to achieve the lowest weight member that is satisfied by whole constraints. After reaching this goal, AGA goes to the next level, as is shown in the related part in Figure 1. As a result, evaluation of constraints is not carried out for whole members of the population in AGA. See [2] for more information. The hyperparameters of AGA were selected by trying different values of the number of generations, the population size, the crossover probability, and the mutation probability, and the amounts of them are 200, 50, 60, and 5, respectively.

The optimization of the 40-story building consists of 54 decision variables. The sections’ depths of the optimal designs associated with the 40-story building with both systems are given in

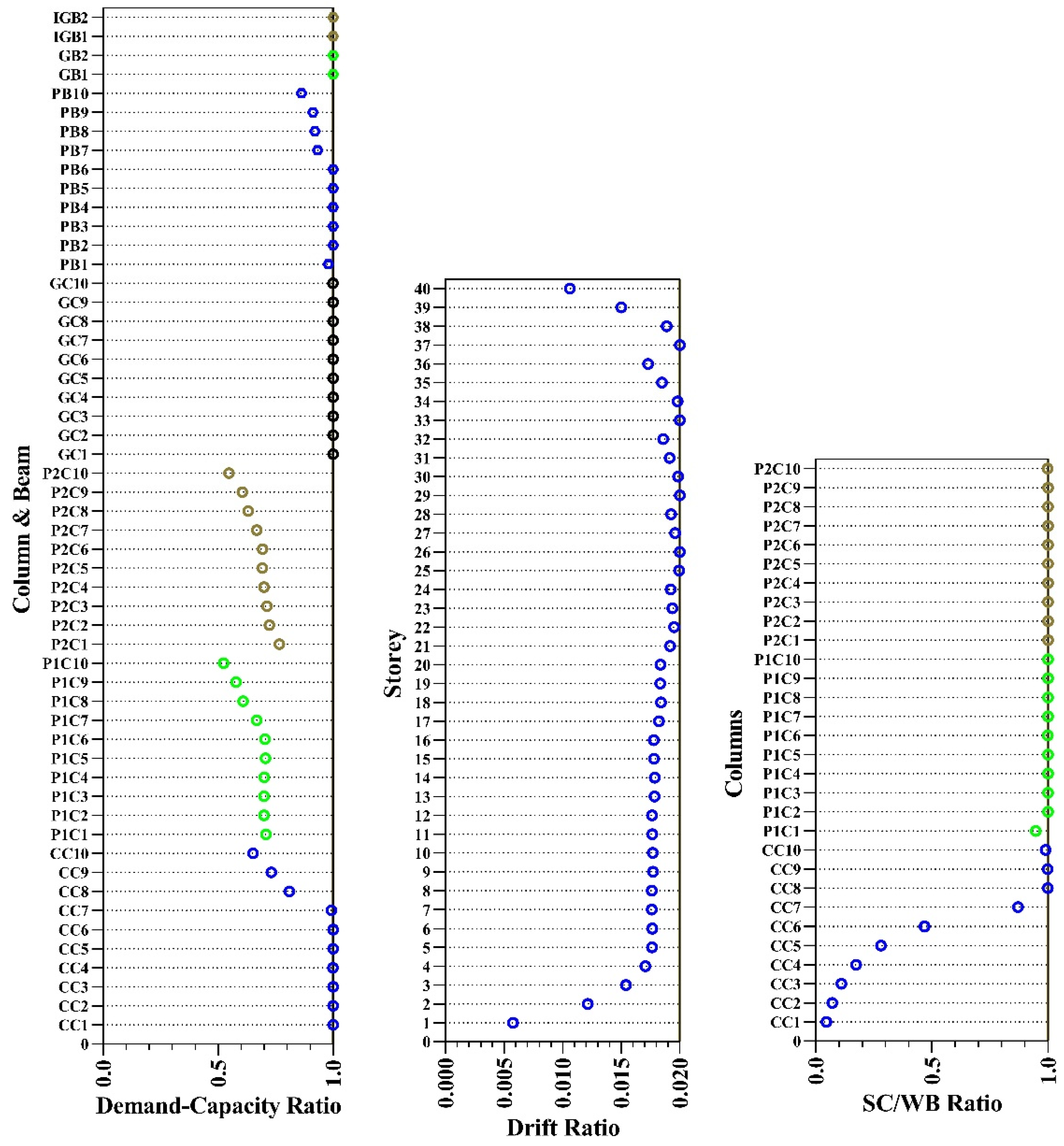
Table 2. The depth of columns sections in the optimal design of the building in (mm).

Element Name	Group Number
	1	2	3	4	5	6	7	8	9	10
CC	1210	1118	983	853	724	598	475	401	340	273
P1C	593	593	581	569	553	533	511	480	433	357
P2C	605	599	583	566	544	517	493	468	428	358
GC	994	829	779	728	674	616	550	476	391	281
PB	577	635	637	631	615	585	563	539	495	423
GB	598	552	…	…	…	…	…	…	…	…
IGB	590	554	…	…	…	…	…	…	…	…

. The inter-story drift ratios of different stories, SC/WB ratios, and demand–capacity ratios relevant to the optimal design of the 40-story building, as well as the corresponding code limits, are depicted in Figure 5.

6. Conclusions

In the current work, the optimal seismic design of high-rise buildings, which is a large-scale optimization problem, a time-consuming process requiring huge computational demands, was investigated. These problems are cast into the context of optimization with the combination of evolutionary algorithms and machine learning methods. AGA, as a novel evolutionary algorithm, was employed for the optimization process. The algorithm converged to optimal design, whose specifications were presented, with an initial population of 50 after 200 iterations. For constraint evaluation, three machine learning methods including MLP, GMDH, and ANFIS-PSO were investigated and the best one, MLP, with a coefficient of determination of 0.988, was selected. Therefore, the strategy mentioned in this paper can be used to achieve the minimum weight of the tall buildings along with meeting all practical and design code constraints. This strategy donates a methodical procedure for the reasonable comparison of different tall building designs.