Two-Scale Deep Learning Model for Polysilicon MEMS Sensors †
Abstract
:1. Introduction
2. Model of the Polysilicon MEMS and Intrinsic Uncertainties
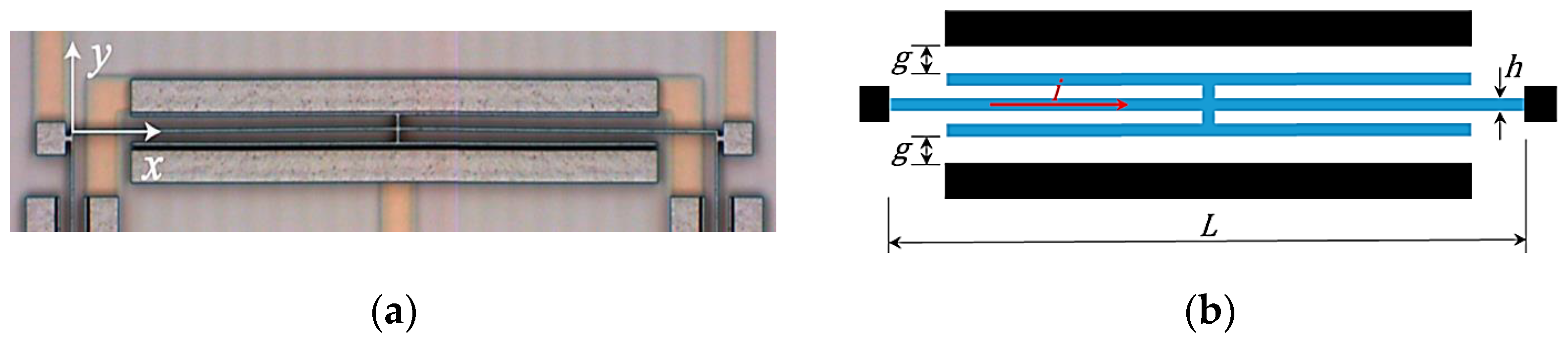
2.1. Oscillation Amplitude of the Lorentz Force MEMS Magnetometer
2.2. Sources of Uncertainty in Polysilicon MEMS
3. Methodology
3.1. Representation of the Resonant Structure
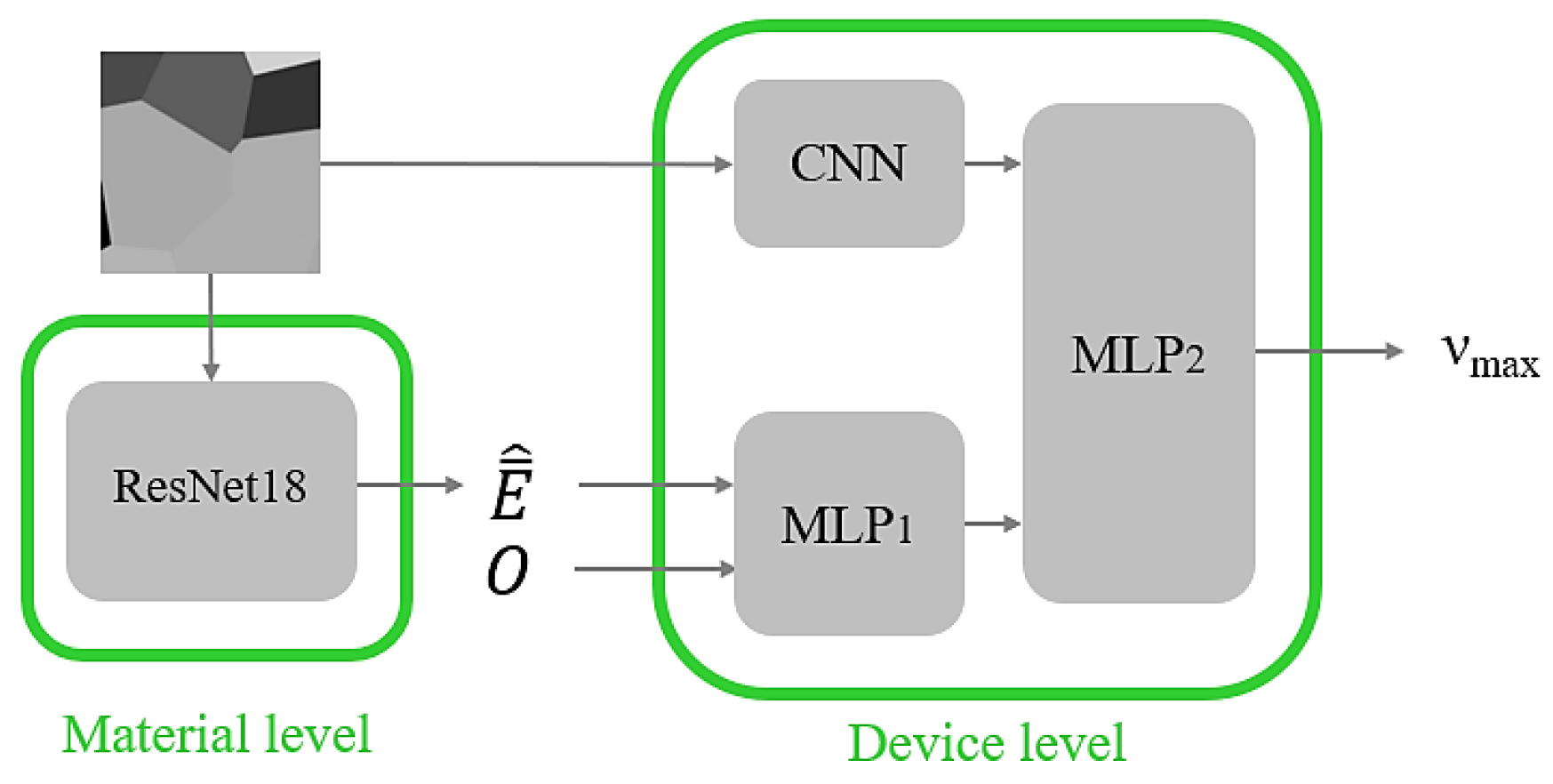
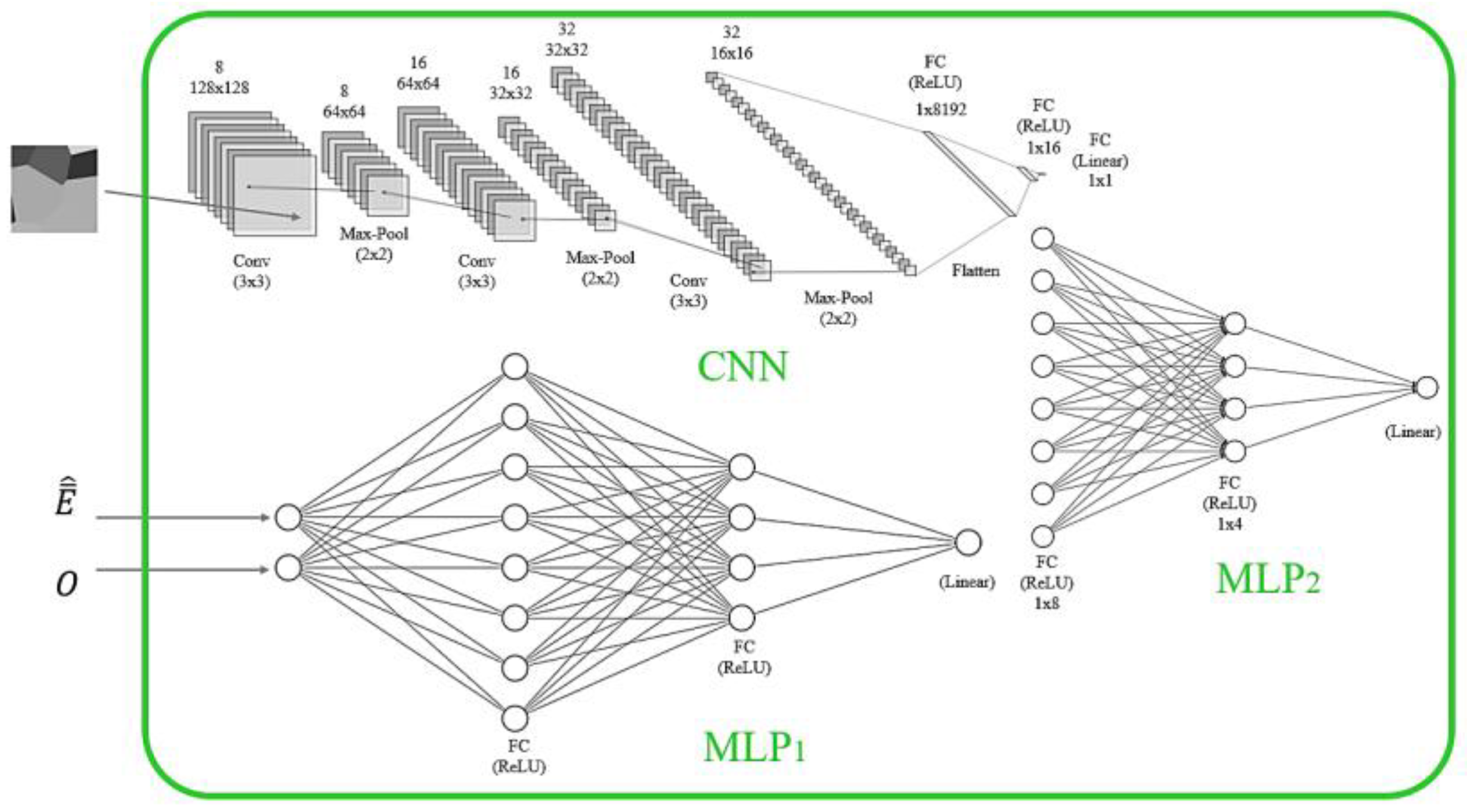
3.2. The Neural Network-Based Model
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Owens, J.D.; Houston, M.; Luebke, D.; Green, S.; Stone, J.E.; Phillips, J.C. GPU Computing. Proc. IEEE 2008, 96, 879–899. [Google Scholar] [CrossRef]
- Nickolls, J.; Dally, W.J. The GPU Computing Era. IEEE Micro 2010, 30, 56–69. [Google Scholar] [CrossRef]
- Schmidt, J.; Marques, M.R.G.; Botti, S.; Marques, M.A.L. Recent advances and applications of machine learning in solid-state materials science. NPJ Comput. Mater. 2019, 5, 83. [Google Scholar] [CrossRef]
- Himanen, L.; Geurts, A.; Foster, A.S.; Rinke, P. Data-Driven Materials Science: Status, Challenges, and Perspectives. Adv. Sci. 2019, 6, 1900808. [Google Scholar] [CrossRef] [PubMed]
- Bock, F.E.; Aydin, R.C.; Cyron, C.J.; Huber, N.; Kalidindi, S.R.; Klusemann, B. A Review of the Application of Machine Learning and Data Mining Approaches in Continuum Materials Mechanics. Front. Mater. 2019, 6, 110. [Google Scholar] [CrossRef] [Green Version]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach, 1st ed.; Pearson Education Limited: Kuala Lumpur, Malaysia, 2016. [Google Scholar]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psych. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, L. Deep Learning: Methods and Applications. FNT Signal Processing 2014, 7, 197–387. [Google Scholar] [CrossRef] [Green Version]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
- Cang, R.; Ren, M.Y. Deep Network-Based Feature Extraction and Reconstruction of Complex Material Microstructures. In Proceedings of the 42nd Design Automation Conference, Charlotte, NC, USA, 21–24 August 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Lubbers, N.; Lookman, T.; Barros, K. Inferring low-dimensional microstructure representations using convolutional neural networks. Phys. Rev. E 2017, 96, 052111. [Google Scholar] [CrossRef] [Green Version]
- Napoletano, P.; Piccoli, F.; Schettini, R. Anomaly Detection in Nanofibrous Materials by CNN-Based Self-Similarity. Sensors 2018, 18, 209. [Google Scholar] [CrossRef] [Green Version]
- Hwang, H.; Oh, J.; Lee, K.-H.; Cha, J.-H.; Choi, E.; Yoon, Y.; Hwang, J.-H. Synergistic approach to quantifying information on a crack-based network in loess/water material composites using deep learning and network science. Comp. Mat. Sci. 2019, 166, 240–250. [Google Scholar] [CrossRef]
- Yang, Z.; Yabansu, Y.C.; Al-Bahrani, R.; Liao, W.; Choudhary, A.N.; Kalidindi, S.R.; Agrawal, A. Deep learning approaches for mining structure-property linkages in high contrast composites from simulation datasets. Comp. Mat. Sci. 2018, 151, 278–287. [Google Scholar] [CrossRef]
- Cecen, A.; Dai, H.; Yabansu, Y.C.; Kalidindi, S.R.; Song, L. Material structure-property linkages using three-dimensional convolutional neural networks. Acta Materialia. 2018, 146, 76–84. [Google Scholar] [CrossRef]
- Cang, R.; Li, H.; Yao, H.; Jiao, Y.; Ren, Y. Improving direct physical properties prediction of heterogeneous materials from imaging data via convolutional neural network and a morphology-aware generative model. Comp. Mat. Sci. 2018, 150, 212–221. [Google Scholar] [CrossRef] [Green Version]
- Frankel, A.L.; Jones, R.E.; Alleman, C.; Templeton, J.A. Predicting the mechanical response of oligocrystals with deep learning. Comp. Mat. Sci. 2019, 169, 109099. [Google Scholar] [CrossRef] [Green Version]
- Abueidda, D.W.; Almasri, M.; Ammourah, R.; Ravaioli, U.; Jasiuk, I.M.; Sobh, N.A. Prediction and optimization of mechanical properties of composites using convolutional neural networks. Comp. Struct. 2019, 227, 111264. [Google Scholar] [CrossRef] [Green Version]
- Bagherinia, M.; Bruggi, M.; Corigliano, A.; Mariani, S.; Lasalandra, E. Geometry optimization of a Lorentz force, resonating MEMS magnetometer. Micro. Rel. 2014, 54, 1192–1199. [Google Scholar] [CrossRef]
- Bagherinia, M.; Mariani, S. Stochastic Effects on the Dynamics of the Resonant Structure of a Lorentz Force MEMS Magnetometer. Actuators 2019, 8, 36. [Google Scholar] [CrossRef] [Green Version]
- Mariani, S.; Martini, R.; Ghisi, A.; Corigliano, A.; Beghi, M. Overall elastic properties of polysilicon films: A statistical investigation of the effects of polycrystal morphology. Int. J. Mult. Comp. Eng. 2011, 9, 327–346. [Google Scholar] [CrossRef]
- Mirzazadeh, R.; Mariani, S. Uncertainty Quantification of Microstructure-Governed Properties of Polysilicon MEMS. Micromachines 2017, 8, 248. [Google Scholar] [CrossRef] [Green Version]
- Mariani, S.; Ghisi, A.; Mirzazadeh, R.; Azam, S.E. On-Chip Testing: A Miniaturized Lab to Assess Sub-Micron Uncertainties in Polysilicon MEMS. Micro Nanosyst. 2018, 10, 84–93. [Google Scholar] [CrossRef]
- Mirzazadeh, R.; Eftekhar Azam, S.; Mariani, S. Mechanical Characterization of Polysilicon MEMS: A Hybrid TMCMC/POD-Kriging Approach. Sensors 2018, 18, 1243. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghisi, A.; Mariani, S. Effect of Imperfections Due to Material Heterogeneity on the Offset of Polysilicon MEMS Structures. Sensors 2019, 19, 3256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dassi, L.; Merola, M.; Riva, E.; Santalucia, A.; Venturelli, A.; Ghisi, A.; Mariani, S. A Stochastic Model to Describe the Scattering in the Response of Polysilicon MEMS. Eng. Proc. 2021, 2, 95. [Google Scholar] [CrossRef]
- Herrera-May, A.; Soler-Balcazar, J.; Vázquez-Leal, H.; Martínez-Castillo, J.; Vigueras-Zuñiga, M.; Aguilera-Cortés, L. Recent Advances of MEMS Resonators for Lorentz Force Based Magnetic Field Sensors: Design, Applications and Challenges. Sensors 2016, 16, 1359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lenz, J.; Edelstein, S. Magnetic sensors and their applications. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Hartzell, A.; Silva, M.; Shea, H. MEMs Reliability, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Hemker, K.J.; Sharpe, W.N., Jr. Microscale Characterization of Mechanical Properties. Annu. Rev. Mater. Res. 2007, 37, 93–126. [Google Scholar] [CrossRef]
- Uhl, T.; Martowicz, A.; Codreanu, I.; Klepka, A. Analysis of uncertainties in MEMS and their influence on dynamic properties. Arch. Mech. 2009, 61, 349–370. [Google Scholar]
- Hopcroft, M.A.; Nix, W.D.; Kenny, T.W. What is the Young’s Modulus of Silicon? J. Micro. Syst. 2010, 19, 229–238. [Google Scholar] [CrossRef] [Green Version]
- Quesada-Molina, J.P.; Rosafalco, L.; Mariani, S. Mechanical Characterization of Polysilicon MEMS Devices: A Stochastic, Deep Learning-based Approach. In Proceedings of the 2020 21st International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Cracow, Poland, 5–8 July 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef] [Green Version]


| SVE Size | μ [GPa] | σ [GPa] |
|---|---|---|
| 2m × 2m | 150.1 | 5.5 |
| 5m × 5m | 149.3 | 2.4 |
| Size | SVEs | |||
|---|---|---|---|---|
| Training | 2m × 2m | 1898 | 0.028 | 0.004 |
| 5m × 5m | 800 | 0.01 | 0.002 | |
| Validation | 2m × 2m | 400 | 0.028 | 0.004 |
| 5m × 5m | 200 | 0.01 | 0.002 | |
| Test | 2m × 2m | 198 | 0.028 | 0.004 |
| 5m × 5m | 99 | 0.01 | 0.002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quesada-Molina, J.P.; Mariani, S. Two-Scale Deep Learning Model for Polysilicon MEMS Sensors. Comput. Sci. Math. Forum 2022, 2, 12. https://doi.org/10.3390/IOCA2021-10888
Quesada-Molina JP, Mariani S. Two-Scale Deep Learning Model for Polysilicon MEMS Sensors. Computer Sciences & Mathematics Forum. 2022; 2(1):12. https://doi.org/10.3390/IOCA2021-10888
Chicago/Turabian StyleQuesada-Molina, José Pablo, and Stefano Mariani. 2022. "Two-Scale Deep Learning Model for Polysilicon MEMS Sensors" Computer Sciences & Mathematics Forum 2, no. 1: 12. https://doi.org/10.3390/IOCA2021-10888
APA StyleQuesada-Molina, J. P., & Mariani, S. (2022). Two-Scale Deep Learning Model for Polysilicon MEMS Sensors. Computer Sciences & Mathematics Forum, 2(1), 12. https://doi.org/10.3390/IOCA2021-10888







