Abstract
This study presents a coalition-based parallel metaheuristic algorithm for solving the Permutation Flow Shop Scheduling Problem (PFSP). This novel approach incorporates five different single-solution-based metaheuristic algorithms (SSBMA) (Simulated Annealing Algorithm, Random Search Algorithm, Great Deluge Algorithm, Threshold Accepting Algorithm and Greedy Search Algorithm) and a population-based algorithm (Weighted Superposition Attraction–Repulsion Algorithm) (WSAR). While SSBMAs are responsible for exploring the search space, WSAR serves as a controller that handles the coalition process. SSBMAs perform their searches simultaneously through the MATLAB parallel programming tool. The proposed approach is tested on PFSP against the state-of-the-art algorithms in the literature. Moreover, the algorithm is also tested against its constituents (SSBMAS and WSAR) and its serial version. Non-parametric statistical tests are organized to compare the performances of the proposed approach statistically with the state-of-the-art algorithms, its constituents and its serial version. The statistical results prove the effectiveness of the proposed approach.
1. Introduction
Optimization constitutes finding the solution that gives the best result in the solution space of a problem. In other words, it is used to achieve the best solutions under the given conditions. Today, different optimization algorithms are used to solve many optimization problems [1,2,3,4]. These algorithms can be classified into two groups: exact algorithms and approximate algorithms. Exact algorithms search the entire search space and try every possible alternative solution. Even if they provide the optimal solution, they need a long runtime, especially as the size of the problem grows. On the other hand, approximate algorithms perform their solution space searches through some logical operators. Although they do not guarantee an optimal solution, they provide near-optimal solutions in reasonable time. Through this superiority, most researchers prefer approximate algorithms in optimization problem solving.
Approximate algorithms are classified into two groups: heuristic and metaheuristic algorithms. While a heuristic algorithm’s structure is problem specific, a metaheuristic algorithm’s structure is generic, allowing it to be applied to any optimization problem. Metaheuristic algorithms are more flexible than heuristic algorithms in that they can handle any problem. They can also provide better solutions to optimization problems than heuristic algorithms. Metaheuristic algorithms, on the other hand, may have drawbacks such as an early convergence and poor speed, and a metaheuristic algorithm may be superior to other metaheuristic algorithms.
The No Free Lunch Theorem [5] must also be mentioned at this point in order to underline the logic for integrating diverse search techniques within the framework of creating successful optimization methods. According to this theorem, no optimization method beats all remaining solution processes for all optimization problems, and there is no statistical difference between the performances of different metaheuristics when all optimization problems are solved [6]. This is a result that implies that the computing cost of finding a solution for optimization problems is the same for any solution technique. This theorem can be a base point to combine various metaheuristic algorithms to tackle optimization problems more effectively. It will take substantial time to combine the various metaheuristic algorithms and run them sequentially [7]. Most of the metaheuristic algorithms are designed to run sequentially, and the parallel execution of metaheuristic algorithms can increase solution quality while shortening the run time [8,9].
This research is the outcome of an attempt to combine several metaheuristics in order to reveal a high level of synergy and, as a result, deliver a sufficient performance while solving optimization problems.
This paper provides a new framework for addressing the Permutation Flow Shop Scheduling Problem (PFSP) based on a combination of diverse metaheuristics in a parallel computing environment. To implement the multiple metaheuristic algorithms in parallel, a new optimization system combining different single-solution-based metaheuristic algorithms (SSBMA) (Simulated Annealing Algorithm (SA), Random Search Algorithm (RS), Great Deluge Algorithm (GD), Threshold Accepting Algorithm (TA) and Greedy Search Algorithm (GS)) and a controller (Weighted Superposition Attraction algorithm) is designed.
The remainder of the paper is organized as follows: In Section 2, parallel computing is explained and, in Section 3, the proposed optimization approach (p-WSAR) is introduced. In Section 4, PFSP is presented and experimental results are reported. Finally, concluding remarks are presented in Section 5.
2. Parallel Computing
Parallel computing is a type of computing architecture in which many processors execute or process an application or computation simultaneously. Parallel computing helps us carry out large computations by dividing the workload among multiple processors, all working at the same time. Most supercomputers use parallel computing principles to work. Parallel computing is also known as parallel processing. For this to happen, we need to properly empower resources to execute concurrently. Parallel computing can reduce the solution time, increase energy efficiency in our application, and allow us to tackle bigger problems. It is a computational technique developed to solve complex problems faster and more efficiently [10,11].
3. p-WSAR Algorithm
The p-WSAR algorithm is introduced in this section. p-WSAR is comprised of five SSBMAs, namely, Random Search (RS) [12], Threshold Accepting (TA) [13], Great Deluge [14], Simulated Annealing (SA) [15], Greedy Search (GS) [16] and a controller WSAR [17]. p-WSAR mainly has three stages, namely, the search stage, information-sharing stage and reproduction stage. In the search stage, all of the SSBMAs explore the solution space in parallel. After exploring the solution space, they share their findings with other SSBMAs through the WSAR algorithm superposition principle. One can see the details of the superposition principle in the following study, [17]. Then, all SSBMAs move through their next positions. In the last stage, SSBMAs’ parameters are reproduced. This iterative process lasts until the termination criteria are met. Notations of the p-WSAR algorithm are given below.
The main stages of the WSAR algorithm and flow chart of the algorithm are depicted in Figure 1 and Figure 2, respectively.

Figure 1.
Main steps of p-WSAR.
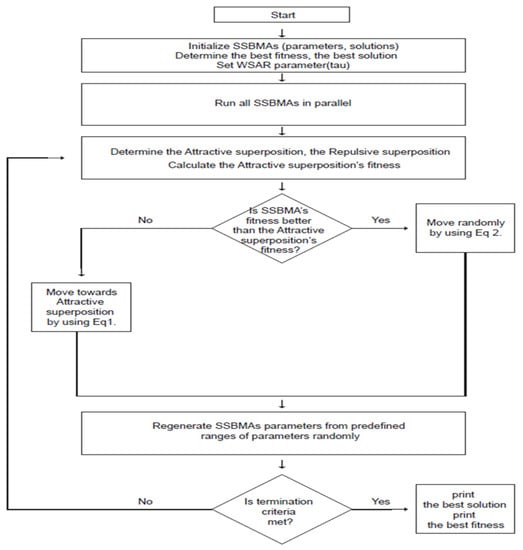
Figure 2.
Flow chart of the p-WSAR algorithm.
4. Permutation Flow Shop Scheduling Problem and Experimental Results
In this section, PFSP is first introduced, and then the experimental results are given.
4.1. Permutation Flow Shop Scheduling Problem (PFSP)
The PFSP has a set of m machines and a group of n jobs. Every job is made up of m operations that must be accomplished on several machines. For each of the n jobs, the machine ordering for the process sequence is the same. Each machine may only conduct one operation at a time, and all jobs are completed sequentially according to a permutation schedule. It is assumed that no machine problems would occur during the manufacturing stage, and thus all of the machines will be ready to process activities. Operation pre-emption is also disallowed. The goal is to design a schedule that reduces the total job completion time (makespan) while adhering to the preceding assumptions.
A permutation-type n-dimensional real-number vector can be utilized in the PFSP to determine the job process sequence. After identifying the job order, the makespan can be calculated using the “completion time matrix approach”, which Onwubolu and Davendra proposed [18].
4.2. Experimental Results
The p-WSAR’s performance in PFSP was evaluated using the Taillard [19] benchmark instances, which are divided into 12 groups of problems. Five of these problems were selected to test p-WSAR’s performance against some state-of-the-art algorithms and WSAR. These problems’ size (PS: (J × M) and well-known solutions (WKS) are given in Table 1. The best, the worst and the average performances of 30 runs of each algorithm were recorded. In all of the instances, p-WSAR was able to find better solutions than other algorithms.

Table 1.
Comparison of p-WSAR with some state-of-the-art algorithms and WSAR.
In addition, the performance of p-WSAR was statistically compared with the other algorithms through non-parametric statistical tests by using average values. Table 2 indicates that (based on the Friedman test results) p-WSAR surpasses the other algorithms. Furthermore, according to the Wilcoxon signed-rank test, the difference between p-WSAR and HPSO is found to be negligible as the p > 0.1. In addition, p-WSAR performed slightly better than TLBO, NPSO, and WSAR, as p < 0.1.

Table 2.
Non-parametric test results on Taillard Instances.
Another computational study was conducted to test the performance of p-WSAR with its constituents (SSBMAs) in terms of solution quality. The results are presented in Table 3 and Table 4. According to the computational results, p-WSAR’ performance is far beyond that of its constituents (SSBMAs). Additionally, in respect of the non-parametric statistical tests, p-WSAR is able to produce more effective results than its constituents. Additionally, there is statistically significant difference between the performance of the p-WSAR and its constituents since p-value is < 0.1.

Table 3.
Comparison of p-WSAR with SSBMAs.

Table 4.
Non-parametric test results on Taillard Instances p-WSAR vs. SSBMAs.
5. Conclusions
In this research, multiple metaheuristic algorithms are combined to build a coalition for tackling PFSP. The suggested methodology uses WSAR as the controller to run multiple single solution-based metaheuristic algorithms (SSBMAs) in parallel. The suggested method is put to the test on some of the Taillard instances. According to the results, the proposed approach is capable of finding the best solutions. Furthermore, the proposed approach surpasses its constituents. The proposed approach is supported by the computational results. Applying the proposed approach to the other type of problems is planned for a future study.
Author Contributions
Conceptualization, A.B. and M.E.S.; methodology, A.B. and M.E.S.; software, M.E.S.; validation, A.B., M.E.S.; formal analysis, A.B.; investigation, A.B. and M.E.S.; resources, A.B.; data curation, A.B.; writing—original draft preparation, A.B. and M.E.S.; writing—review and editing, A.B. and M.E.S.; visualization, A.B. and M.E.S.; supervision, A.B.; project administration, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Precup, R.-E.; David, R.-C.; Roman, R.-C.; Petriu, E.M.; Szedlak-Stinean, A.-I. Slime Mould Algorithm-Based Tuning of Cost-Effective Fuzzy Controllers for Servo Systems. Int. J. Comput. Intell. Syst. 2021, 14, 1042–1052. [Google Scholar] [CrossRef]
- Ang, K.M.; Lim, W.H.; Isa, N.A.M.; Tiang, S.S.; Wong, C.H. A constrained multi-swarm particle swarm op-timization without velocity for constrained optimization problems. Exp. Syst. Appl. 2020, 140, 112882. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Dudaklı, N.; Subulan, K.; Taşan, A.S. An integrated fleet planning model with empty vehicle repositioning for an intermodal transportation system. Oper. Res. 2021, 1–36. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Malek, R. Collaboration of metaheuristic algorithms through a multi-agent system. In Proceedings of the International Conference on Industrial Applications of Holonic and Multi-Agent Systems, Linz, Austria, 31 August 2009–2 September 2009. [Google Scholar]
- Baykasoğlu, A.; Hamzadayi, A.; Akpınar, S. Single Seekers Society (SSS): Bringing together heuristic optimization algorithms for solving complex problems. Knowl.-Based Syst. 2019, 165, 53–76. [Google Scholar] [CrossRef]
- Parallel Metaheuristics. In Parallel Metaheuristics; Wiley: Hoboken, NJ, USA, 2005.
- Alba, E.; Troya, J.M. Improving flexibility and efficiency by adding parallelism to genetic algorithms. Stat. Comput. 2002, 12, 91–114. [Google Scholar] [CrossRef]
- Almasi, G.S.; Gottlieb, A. Highly Parallel Computing Benjamin; Cummings: Redwood City, CA, USA, 1994. [Google Scholar]
- Kohli, R.; Krishnamurti, R. Optimal product design using conjoint analysis: Computational complexity and al-gorithms. Eur. J. Operat. Res. 1989, 40, 186–195. [Google Scholar] [CrossRef]
- Rogers, D. Random Search and Insect Population Models. J. Anim. Ecol. 1972, 41, 369. [Google Scholar] [CrossRef]
- Dueck, G.; Scheuer, T. Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing. J. Comput. Phys. 1990, 90, 161–175. [Google Scholar] [CrossRef]
- Dueck, G. New Optimization Heuristics: The Great Deluge Algorithm and the Record-to-Record Travel. J. Comput. Phys. 1993, 104, 86–92. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Feo, T.A.; Resende, M.G.C. Greedy Randomized Adaptive Search Procedures. J. Glob. Optim. 1995, 6, 109–133. [Google Scholar] [CrossRef] [Green Version]
- Baykasoğlu, A. Optimising cutting conditions for minimising cutting time in multi-pass milling via weighted superposition attraction-repulsion (WSAR) algorithm. Int. J. Prod. Res. 2020, 59, 4633–4648. [Google Scholar] [CrossRef]
- Onwubolu, G.; Davendra, D. Scheduling flow shops using differential evolution algorithm. Eur. J. Oper. Res. 2006, 171, 674–692. [Google Scholar] [CrossRef]
- Taillard, E. Some efficient heuristic methods for the flow shop sequencing problem. Eur. J. Oper. Res. 1990, 47, 65–74. [Google Scholar] [CrossRef]
- Baykasoglu, A.; Hamzadayi, A.; Köse, S.Y. Testing the performance of teaching–learning based optimization (TLBO) algorithm on combinatorial problems: Flow shop and job shop scheduling cases. Inf. Sci. 2014, 276, 204–218. [Google Scholar] [CrossRef]
- Lin, S.-Y.; Horng, S.-J.; Kao, T.-W.; Huang, D.-K.; Fahn, C.-S.; Lai, J.-L.; Chen, R.-J.; Kuo, I.-H. An efficient bi-objective personnel assignment algorithm based on a hybrid particle swarm optimization model. Expert Syst. Appl. 2010, 37, 7825–7830. [Google Scholar] [CrossRef]
- Lian, Z.; Gu, X.; Jiao, B. A novel particle swarm optimization algorithm for permutation flow-shop scheduling to minimize makespan. Chaos Solitons Fractals 2008, 35, 851–861. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).