Modeling South African Stock Prices with Mixture Distributions ^†

Abstract

This study investigates the behavior of South African stock prices during divestment periods using mixture distributions. Divestment often triggers significant market reactions, necessitating a deeper understanding of stock return distributions in such events. Given the complexities of emerging markets like South Africa, this research models stock price behavior to assess associated risks. A mixture distribution approach is employed to capture the return dynamics of stocks listed on the Johannesburg Stock Exchange (JSE) between 2015 and 2024. Gaussian Mixture Models (GMMs), Lognormal Mixture, and Student’s t mixture models are applied to financial, technology, and energy stocks affected by divestment. Statistical tests including AIC and BIC assess the model performance. Mixture distributions outperform single-distribution models, effectively capturing heavy tails, volatility clustering, and asymmetry in stock returns. The GMM and Student’s t mixture models provide the best fit, revealing increased volatility and extreme negative returns following divestment events. Mixture distributions offer a robust framework for modeling South African stock prices during divestment periods. These models enhance the understanding of market dynamics, supporting better financial modeling and risk management in emerging markets.

1. Introduction

Stock price modeling is a fundamental area of financial econometrics, with significant implications for risk management, portfolio optimization, and financial decision-making. Traditional modeling approaches often assume that stock returns follow a normal distribution. However, empirical studies have demonstrated that stock return distributions exhibit skewness, kurtosis, and heavy tails, making standard models inadequate for capturing the true underlying behavior of stock prices [1]. In response, mixture probability distributions have been increasingly employed to model financial returns more accurately. This study aims to model the divestment of South African stock prices using mixture distributions to enhance the understanding of stock price behavior in the South African financial market.

South Africa, as an emerging market, has experienced various economic and political events that have influenced stock market dynamics. The concept of divestment, particularly in response to sociopolitical and environmental factors, has been a crucial aspect of the South African financial landscape. Understanding the impact of divestment on stock prices requires sophisticated modeling techniques capable of capturing heterogeneous market behaviors. Mixture distributions provide a flexible approach by modeling stock returns as a combination of multiple probability distributions, allowing for a better fit to empirical data.

Mixture distributions have gained prominence in financial modeling due to their ability to capture the complex characteristics of asset returns. Early studies, such as those by Kon [2], showed that financial returns often deviate from normality, making mixture models a suitable alternative. These models assume that stock returns arise from different market regimes, such as periods of high volatility and low volatility, each represented by distinct probability distributions.

Various mixture models have been applied in financial research, including the normal mixture models [3], finite mixture models [4], and Markov switching models [5]. These models allow for a more precise representation of asset return distributions, capturing characteristics such as volatility clustering and fat tails. Studies focusing on emerging markets, such as those by Bekaert and Harvey [6], emphasize the importance of considering regime-switching behaviors and heterogeneous market participants in stock price modeling.

In the South African context, research has highlighted the impact of sociopolitical and macroeconomic factors on stock market behavior [7]. Divestment decisions by institutional investors, driven by factors such as governance concerns, environmental policies, and political risks, have contributed to market fluctuations. However, few studies have explicitly modeled the effect of divestment on stock price behavior using mixture distributions.

Recent advancements in financial econometrics have integrated machine learning techniques with mixture models to enhance predictive accuracy [8]. These approaches offer promising avenues for improving stock return modeling in the South African market, particularly in the context of divestment strategies.

This study aims to fill the gap in the existing literature by applying mixture distributions to model divested South African stock prices. By leveraging the flexibility of mixture models, the study seeks to provide deeper insights into stock price behavior amid divestment events. The findings will contribute to the broader field of financial econometrics and offer practical implications for investors, policymakers, and financial analysts navigating the South African stock market.

2. Materials and Methods

2.1. Data and Data Sources

Daily stock price data for Naspers, Sasol, and Standard Bank were sourced from Yahoo Finance, covering the period from 1 January 2015 to 30 June 2024. Naspers, Sasol, and Standard Bank represent diverse sectors, namely media and technology, energy and chemicals, and financial services, respectively. Each of these companies has unique volatility drivers. Naspers has shown significant price swings due to its stake in Tencent and China’s regulatory shifts, experiencing rapid growth tempered by geopolitical impacts on tech stocks. Sasol’s performance is closely tied to global oil and commodity prices, and after a downturn during the 2020 pandemic, its stock has rebounded with rising energy prices and debt reduction efforts. Standard Bank, being one of South Africa’s largest banks, is influenced by macroeconomic conditions and has shown resilience through economic recoveries, benefiting from its exposure across Africa. Analyzing historical returns, volatility, and correlations among these stocks could further clarify their individual and comparative performance. The adjusted closing prices were used to compute daily returns, defined as follows:

$$r_t=ln\left({\displaystyle \frac{P_t}{P_{t-1}}}\right),$$

(1)

where:

• $r_t$ is the log return at time t,
• $P_t$ is the current price at time period t, and
• $P_{t-1}$ is the price at the previous time period $t-1$.

2.2. Normality and Stationarity Tests

2.2.1. Jarque–Bera Test for Normality

The Jarque–Bera test [9] checks whether stock returns follow a normal distribution. It is given by:

$$JB={\displaystyle \frac{n}{6}}\left(S^2+{\displaystyle \frac{{(K-3)}^2}{4}}\right),$$

(2)

where S is the skewness, K is the kurtosis, and n is the sample size.

2.2.2. Phillips–Perron Test for Stationarity

The Phillips–Perron test [10] assesses the presence of a unit root in stock returns, ensuring stationarity. The test statistic modifies the standard Augmented Dickey–Fuller (ADF) test by allowing for heteroscedasticity and autocorrelation.

2.3. Mixture Models

Mixture models assume that stock returns follow a distribution composed of multiple underlying distributions.

2.3.1. Gaussian Mixture Model (GMM)

The Gaussian Mixture Model (GMM) [11] is defined as

$$f\left(r\right)=\sum _{i=1}^k{\pi }_i{\displaystyle \frac{1}{\sqrt{2\pi {\sigma }_i^2}}}exp\left(-{\displaystyle \frac{{(r-{\mu }_i)}^2}{2{\sigma }_i^2}}\right),$$

(3)

where ${\pi }_i$ are the mixture weights, and ${\mu }_i$ and ${\sigma }_i^2$ are the mean and variance of each component.

2.3.2. Log-Normal Mixture Distribution

Stock returns may also follow a mixture of log-normal distributions [11]:

$$f\left(r\right)=\sum _{i=1}^k{\pi }_i{\displaystyle \frac{1}{r{\sigma }_i\sqrt{2\pi }}}exp\left(-{\displaystyle \frac{{(lnr-{\mu }_i)}^2}{2{\sigma }_i^2}}\right).$$

(4)

2.3.3. Student’s t Mixture Distribution

Given the heavy-tailed nature of financial returns, a mixture of Student’s t distributions [11] is also considered:

$$f\left(r\right)=\sum _{i=1}^k{\pi }_i{\displaystyle \frac{\mathrm{\Gamma }\left(\frac{{\nu }_i+1}{2}\right)}{\mathrm{\Gamma }\left(\frac{{\nu }_i}{2}\right)\sqrt{\pi {\nu }_i{\sigma }_i^2}}}{\left(1+{\displaystyle \frac{{(r-{\mu }_i)}^2}{{\nu }_i{\sigma }_i^2}}\right)}^{-{\displaystyle \frac{{\nu }_i+1}{2}}},$$

(5)

where ${\nu }_i$ represents the degrees of freedom.

2.4. Model Selection Criteria

To select the best-fitting mixture model, the Akaike Information Criterion [12] (AIC) and Bayesian Information Criterion [13] (BIC) are used:

$$AIC=-2lnL+2k,$$

(6)

$$BIC=-2lnL+klnn,$$

(7)

where L is the likelihood function, k is the number of parameters, and n is the sample size.

3. Results

3.1. Data and Data Manipulation

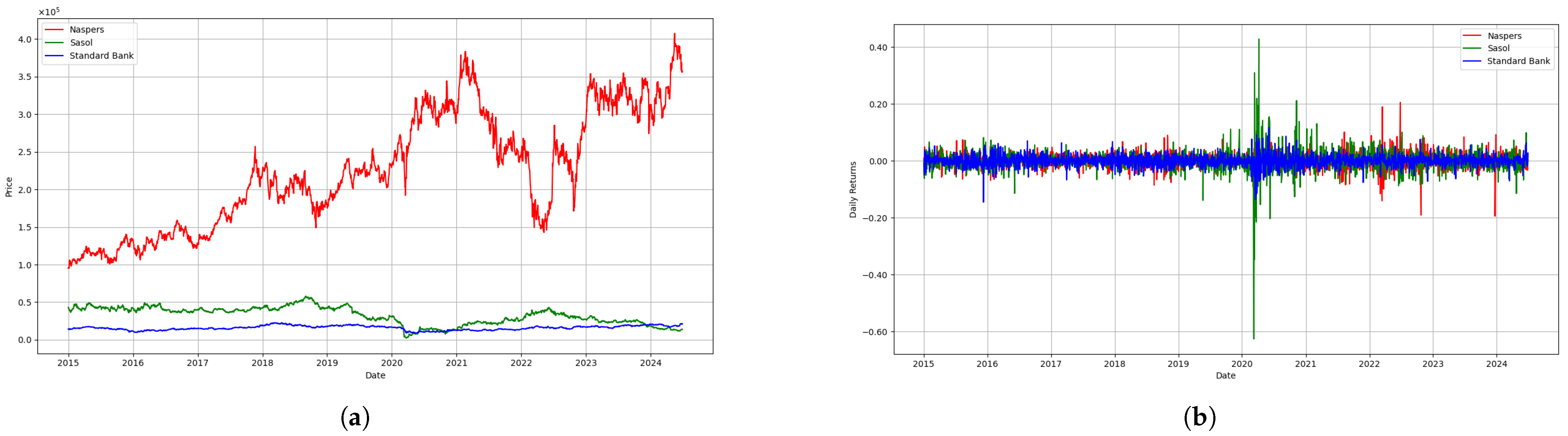
The log prices and log returns plots are shown in Figure 1 (a) and (b), respectively. Sasol is the most volatile, followed by Naspers, with Standard Bank exhibiting the most stability. The 2020 period shows heightened volatility across all three stocks, with Sasol being the most impacted, likely due to its exposure to oil prices.

3.2. Descriptive Analysis

The descriptive statistics show different features for the daily log returns of Standard Bank, Sasol, and Naspers. With a standard deviation of 0.0354 and the greatest difference between the lowest and maximum returns, Sasol has the most volatility, indicating its susceptibility to external factors such as changes in oil prices. It also has the highest kurtosis of 46.0789 and the highest positive skewness of 1.0105, suggesting hefty tails and frequent extreme positive returns. Naspers indicates sporadic extreme values with high kurtosis of 8.6464 representing a moderate volatility and mild positive skew. Of the three equities, Standard Bank is the most stable due to its moderate kurtosis of 4.3994 which reveal symmetric returns with a tiny negative skew, and lowest volatility.

The Jarque–Bera test was employed to assess whether the daily log returns of the selected stocks followed a normal distribution. The results are summarized in

Table 1. Summary statistics for daily log returns.

Stocks	Min	Max	$\overline{\mathit{r}}$	$\mathit{Sd}$	$\mathit{Sk}$	K	$\mathit{JBpv}$	$\mathit{PPpv}$
Naspers	−0.1770	0.2279	0.0009	0.0246	0.3422	8.6464	0.0000	0.0619
Sasol	−0.4656	0.5348	0.0003	0.0354	1.0105	46.0789	0.0000	0.5176
Standard Bank	−0.1354	0.1241	0.0006	0.0202	−0.0606	4.3994	0.0000	0.4706

$\overline{r}$ is the mean of the log returns, $Sd$ is standard deviation, $Sk$ is the skewness, K is the kurtosis, $JBpv$ is the p-value Jarque–Bera statistic and $PPpv$ is the p-value Phillips–Perron statistic.

. For all three stocks, the Jarque–Bera test yielded p-values below 0.05, indicating that the returns of Naspers, Sasol, and Standard Bank significantly deviate from normality. This non-normality is a common feature in financial return series, which often display skewness and excess kurtosis. The Phillips–Perron test was conducted to check the stationarity of the stock price series, which is essential for ensuring valid econometric models. The Phillips–Perron test results indicate that the price series for Naspers, Sasol, and Standard Bank are non-stationary with p-values of 0.0619, 0.5175, and 0.4706, respectively. The test suggests that all of the stock price series are non-stationary, which implies that stock prices follow a stochastic trend. However, the log return series for Naspers, Sasol, and Standard Bank are stationary with p-values of zeros.

Table 2. AIC and BIC for different mixture models across stock prices.

Model Selection	Naspers (NPN.JO)	Sasol (SOL.JO)	Standard Bank (SBK.JO)
GMM_AIC	−11,306.100	−10,484.647	−12,199.244
GMM_BIC	−11,282.967	−10,461.516	−12,176.113
Lognormal Mixture_AIC	−11,303.267	−10,487.805	−12,197.783
Lognormal Mixture_BIC	−11,280.136	−10,464.673	−12,174.652
Student’s t Mixture_AIC	−11,309.544	−10,487.364	−12,199.336
Student’s t Mixture_BIC	−11,286.413	−10,464.233	−12,176.205

shows the model selection criteria for GMM, Lognormal and Student’s t Mixures. The student’s t mixture model for Naspers and Standard Bank returns have the lowest AIC and BIC respectively. While, the Lognormal mixture models was the lowest for Sasol returns. This suggest that student’s t mixture model is appropriate for capturing the heavy tails observed from the returns of Naspers and Standard Bank.

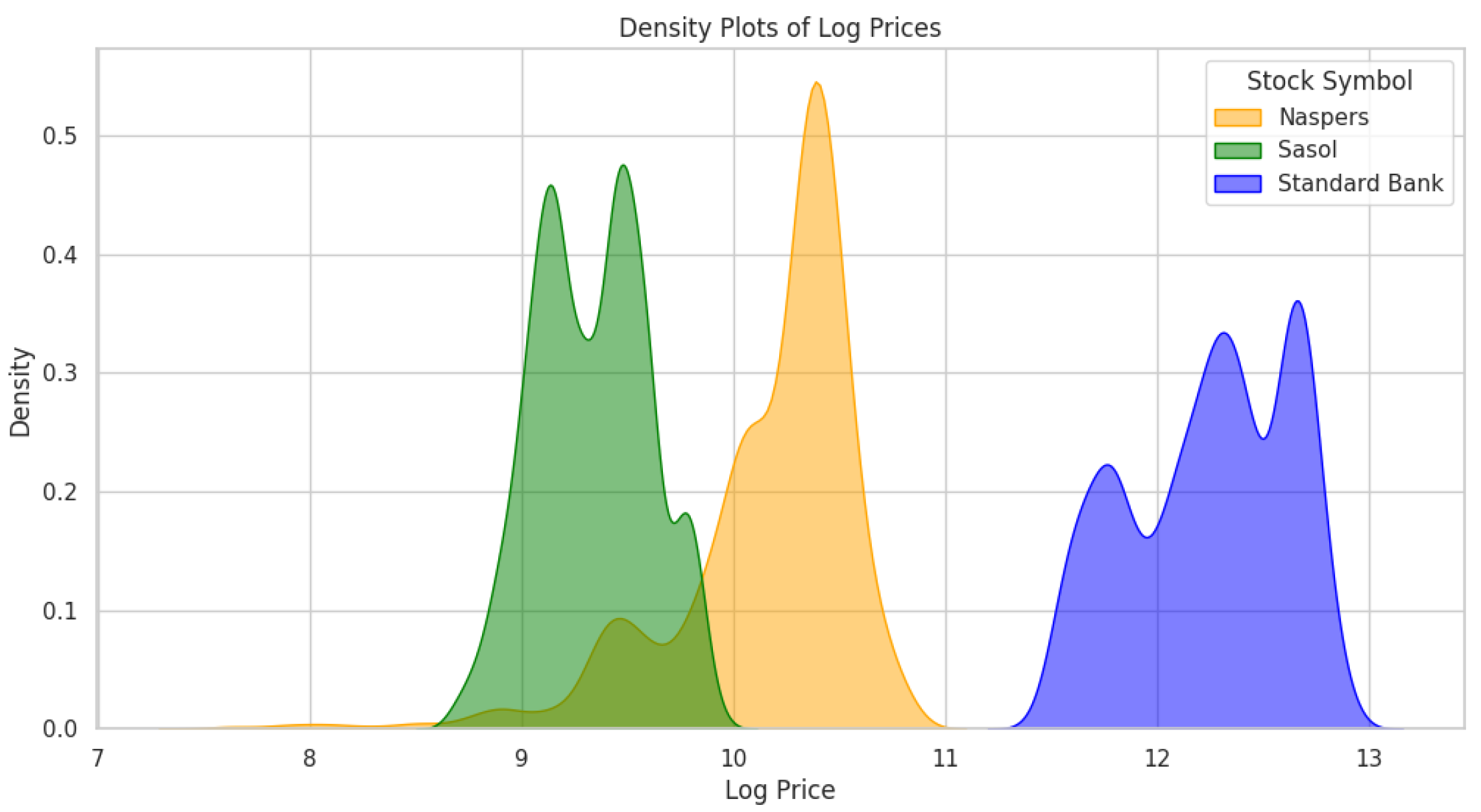
The density plot of log prices for Naspers, Sasol, and Standard Bank shown in Figure 2 reveals distinct distribution patterns for each stock. Naspers has the highest log-adjusted prices, while Standard Bank has the lowest adjusted log prices. The three stocks are multi-modal, indicating variability in price ranges that may reflect differing responses to market conditions, economic cycles, or sector-specific influences. This multimodality behavior are also shown in

Table 3. Parameter estimates and weights for each model and stock.

Component	Stock	Location ($\mathit{\mu }$)	Scale ($\mathit{\sigma }$)	Weight ($\mathit{\pi }$)
GMM Comp 1	NPN.JO	0.002162	0.001319	0.344980
GMM Comp 2	NPN.JO	0.000178	0.000225	0.655020
Lognormal Comp 1	NPN.JO	0.000789	0.000221	0.643316
Lognormal Comp 2	NPN.JO	0.000152	0.001286	0.356684
Student’s t Comp 1	NPN.JO	0.002162	0.001319	0.344980
Student’s t Comp 2	NPN.JO	0.000178	0.000225	0.655020
GMM Comp 1	SOL.JO	0.008176	0.008521	0.102493
GMM Comp 2	SOL.JO	−0.000627	0.000415	0.897507
Lognormal Comp 1	SOL.JO	0.001369	0.009111	0.099048
Lognormal Comp 2	SOL.JO	−0.000545	0.000419	0.900952
Student’s t Comp 1	SOL.JO	0.008176	0.008521	0.102493
Student’s t Comp 2	SOL.JO	−0.000627	0.000415	0.897507
GMM Comp 1	SBK.JO	−0.005325	0.000399	0.461598
GMM Comp 2	SBK.JO	0.005656	0.000362	0.538402
Lognormal Comp 1	SBK.JO	−0.000429	0.000874	0.353180
Lognormal Comp 2	SBK.JO	0.000826	0.000156	0.646820
Student’s t Comp 1	SBK.JO	−0.005325	0.000399	0.461598
Student’s t Comp 2	SBK.JO	0.005656	0.000362	0.538402

suggesting that each stock has experienced price-level shifts over time, possibly due to volatility, external market events, or investor sentiment. Each of the models in Table 3 denoted as GMM, Lognormal mixture, Student’s t mixture provides two components per stock. GMM’s and Student’s t mixuture first component for Naspers has a higher mean of 0.002162 and volatility of 0.001319, but it occurs less frequently denoted by a weight of 0.34498. While the second component of GMM for Naspers has lower mean and volatility which dominates the return distribution. Similar behaviour is observed for Standard Bank returns. Overall, the GMM identifies distinct market regimes when there is calm and volatile movements, which gives a clear indication of losses and gains. The Lognormal mixtures captured asymmetric behavior it seem to be useful when returns are skewed, especially for Sasol returns. While, the Student’s t mixtures offer robustness to fat tails, better capturing extreme returns noted from Naspers and Standard Bank. This distribution highlights the complexity of stock price behavior and the potential influence of temporal factors on each company’s valuation.

3.3. Fitting Mixture Probability Distributions

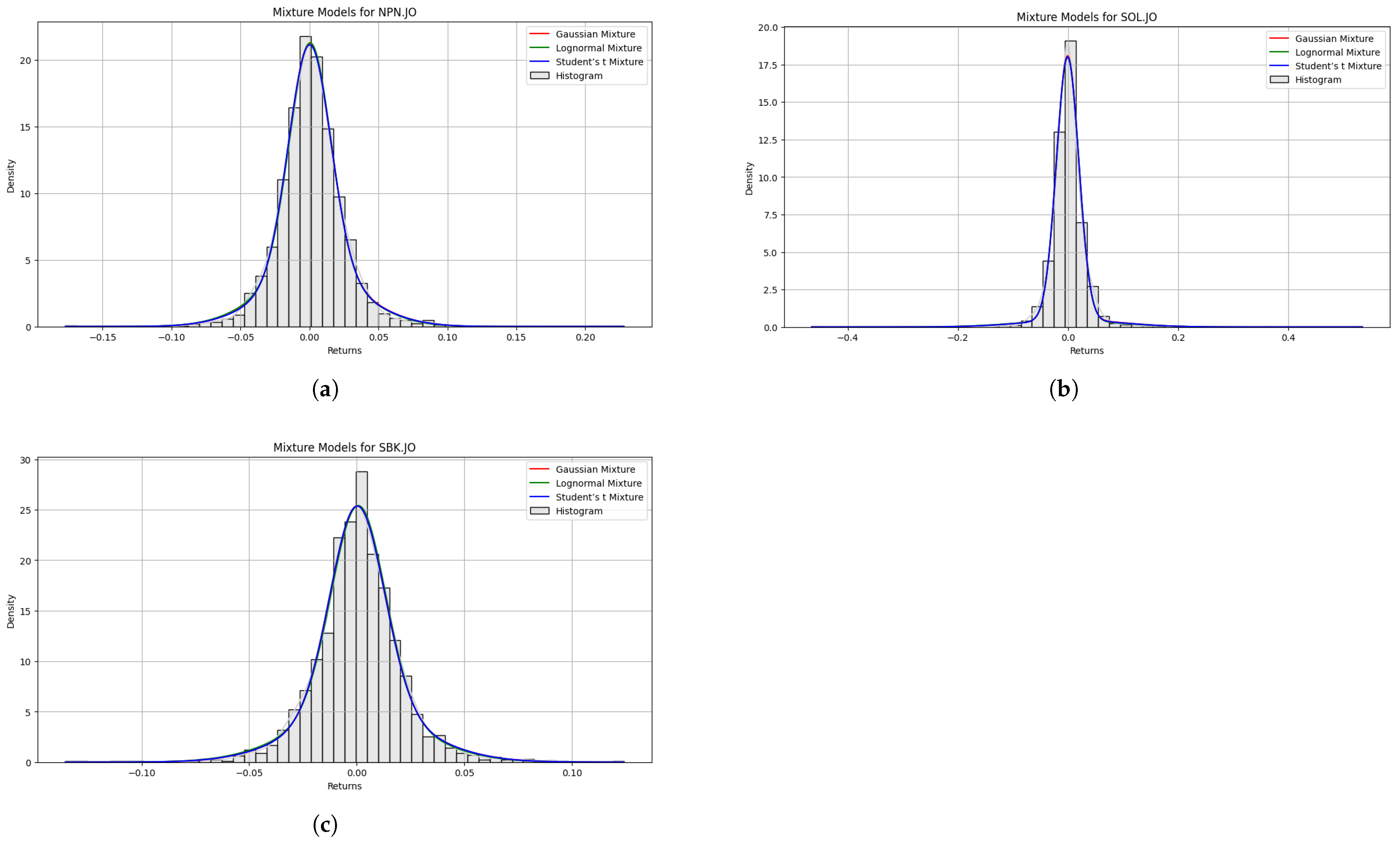
The density plots shown in Figure 3 gives a visual representation of how well each mixture model fits the stock returns. Models like the GMM and Student’s t mixture will be useful for stocks with multiple regimes or extreme returns, while models like Lognormal Mixture and Skewed Normal Mixture will perform better for stocks with skewed distributions.

Goodness of Fit Tests

The Student’s t mixture model has the smallest AIC/BIC values compared to the other models for the three stocks. This suggests that the Student’s t mixture model fits the data well as its AIC/BIC values are substantially lower than those of the GMM and Lognormal Mixture. Based on the GOF results, the GMM and Lognormal mixture are also good models; however, Student’s t mixture is the best model.

4. Discussion

The findings of this study underscore the effectiveness of mixture distributions in modeling South African stock prices during divestment periods. Traditional single-distribution models often fail to capture the complex behaviors of stock returns, particularly in emerging markets such as South Africa, where market conditions can be highly volatile [1,14,15]. The application of Gaussian Mixture Models (GMMs), Lognormal Mixture and Student’s t mixture allowed a more precise characterization of return distributions, capturing key stylized facts such as heavy tails, skewness, and volatility clustering [4,16].

The results indicate that the Student’s t mixture model provided the best fit across the three analyzed stocks—Naspers, Sasol, and Standard Bank—based on AIC and BIC values. This suggests that the heavy-tailed nature of stock returns, particularly during divestment-induced market disruptions, is best modeled using Student’s t distributions [17,18]. This aligns with previous research highlighting the importance of accounting for extreme negative returns and tail dependencies in financial modeling [19].

Sector-specific differences in stock price behavior were also evident. Sasol exhibited the highest volatility and kurtosis, reflecting its sensitivity to external macroeconomic factors such as global oil prices [20]. Naspers showed sporadic extreme values, likely influenced by regulatory changes in the technology sector [21], while Standard Bank exhibited relative stability, consistent with financial sector resilience [22]. These findings emphasize the need for tailored risk management approaches depending on industry-specific characteristics.

The multimodal nature of stock return distributions observed in the density plots further supports the utility of mixture models in capturing multiple market regimes. The identified components within the mixture models suggest the presence of distinct market conditions, such as high-volatility and low-volatility regimes [23]. This is particularly relevant for policymakers and institutional investors seeking to develop robust risk mitigation strategies during periods of financial uncertainty.

Overall, the study confirms that mixture models offer superior flexibility in modeling financial returns, especially in emerging markets where stock price behaviors are influenced by a combination of local and global factors [24]. The implications of these findings extend to risk assessment, portfolio optimization, and policy decisions, highlighting the importance of adopting advanced statistical techniques for financial modeling in volatile market environments.

5. Conclusions

This study examined the behavior of South African stock prices during divestment periods using mixture distribution models. The results demonstrate that mixture distributions outperform single-distribution models in capturing the key statistical properties of stock returns, such as fat tails, volatility clustering, and multimodal distributions.

Among the tested models, the Student’s t mixture model provided the best overall fit, effectively capturing extreme negative returns and high volatility associated with divestment events. This highlights the significance of using heavy-tailed distributions in financial modeling, particularly in emerging markets where price movements can be abrupt and unpredictable.

The study also revealed significant sectoral differences in stock price behaviors, emphasizing the need for industry-specific risk management strategies. Sasol exhibited the highest volatility and kurtosis, Naspers demonstrated sporadic extreme values, and Standard Bank remained relatively stable. These insights provide valuable guidance for investors, portfolio managers, and policymakers navigating divestment-related financial risks.

The findings contribute to the broader field of financial econometrics by reinforcing the applicability of mixture models in capturing heterogeneous stock market behaviors. Future research could explore the integration of machine learning techniques with mixture models to enhance predictive accuracy and further improve risk management strategies.

In conclusion, mixture distributions offer a robust framework for modeling South African stock prices during divestment periods. By leveraging these models, investors and financial analysts can gain deeper insights into market dynamics, supporting more informed decision-making in the context of an evolving financial landscape.