1. Introduction
Metastasis is the primary cause of cancer-related mortality and accounts for over 90% of cancer-related deaths [
1]. Metastatic cancer is challenging to treat because it can be diffusely localized in various organs and is often resistant to cytotoxic agents. Understanding the processes driving cancer metastasis, such as dissemination from the primary tumor and invasion, may lead to improved treatment and prognosis of cancer patients.
As a tumor grows and expands, it applies pressure onto the surrounding tissue. However, factors beyond physical expansion, such as altered tissue mechanics or increased interstitial fluid pressure, can also contribute to this effect. In addition, tumors actively remodel their surrounding tissue, including the extracellular matrix (ECM). The ECM is a network of glycoproteins, including collagen, providing mechanical support as well as signaling cues to cells [
2]. The composition, structural organization, and stiffness of the ECM are altered in tumors, with increased stromal stiffness being associated with more aggressive cancers [
3,
4]. Within the tumor microenvironment (TME), multiple cell types, including tumor cells and fibroblasts, act in concert to stiffen the ECM. The remodeling of fibrilar collagens in the ECM through enhanced deposition, degradation, and cross-linking is an important aspect of ECM stiffening. Collagen cross-linking by fibroblasts and tumor cells can help tumor progression by promoting focal adhesion formation and increasing integrin binding [
5]. Secretion of lysyl oxidases (LOX) and lysyl hydroxilase 2 (LH2), which contributes to cross-linking is increased in cancers. Targeting LOX has been suggested as a therapeutic avenue for cancer patients [
6].
Confinement of tumors growing inside a tissue combined with ECM stiffening and application of traction forces drives mechanical stress and pressure buildup in tumors, which, in turn, can activate mechanosensitive pathways [
7]. A stiffer matrix can be pro-tumorigenic, it can activate tumor-promoting fibroblasts, it can trigger chemoresistance, and it has been associated with increased cancer risk in fibrotic organs [
8,
9,
10,
11]. While a stiff ECM may be thought of as a barrier for cell migration, ECM stiffness also induces promigratory morphological changes in tumor cells, epithelial–mesenchymal transition (EMT), invasion, metastasis, and resistance to chemotherapy [
12,
13,
14,
15]. Indeed, cancer spheroids showed enhanced migration in a stiff ECM as they exert higher integrin-mediated traction forces [
16]. ECM fibers create migration tracks that promote cancer cell invasion [
17,
18], and radially aligned collagen fibers at the tumor–stroma interface facilitate local invasion [
19]. A stiffer ECM was also shown to promote breast cancer progression by promoting the appearance of cancer-associated fibroblasts (CAFs) [
20].
Rho/Rho-associated protein kinase (ROCK) signaling drives cell contractility and application of force on collagen matrices [
21]. Simultaneously, mechanical forces generated by the cellular cytoskeleton are required for active cell movement [
22]. Vice versa, elevated ECM stiffness activates FAK/RhoA/ROCK and PI3K/AKT signaling pathways via integrins [
23]. The stiffness of the ECM has a major influence on the traction forces, as increased substrate stiffness triggers higher cell traction forces [
24]. This positive feedback loop of ECM stiffness activating ROCK and ROCK activation increasing tissue stiffness is believed to be a key process in promoting the invasiveness of cancer.
Taken together, solid tumors generate pressure in tissue and alter local tissue mechanics by remodeling the ECM. Such tissue stiffening, in turn, activates tumor growth, invasion, and metastasis. Preventing or reversing tissue stiffening in tumors may have the potential to reduce cancer progression [
25]. Yet, the connection between tumor pressure, ECM stiffness, ECM remodeling, and tumor cell migration is unresolved. Recent technological advances permit the measurement of traction forces even in complex 3D environments [
26,
27]. Here, we use an innovative 3D traction force technique [
28], applying soft elastic hydrogel micro-spheres to measure mechanical stress and pressure in and around ECM-embedded spheroids derived from tumor cells versus those derived from fibroblasts. This stress analysis is combined with correlative quantitative measurements of ECM remodeling and cell migration. Our results connect strains and pressures within spheroids, as well as their reach into the surrounding ECM, to the stiffness of the ECM and to cell migration, offering new insights into the mechanobiology of tumors.
2. Materials and Methods
2.1. Microparticle Synthesis
Microparticle synthesis and functionalization were performed similarly to what was previously described in detail [
28]. In short, deformable acrylamide-co-acrylic-acid microparticles were synthesized using Shirasu porous glass membranes (SPG Technology, Miyazaki, Japan). These tubular membranes with tunable pore size enabled us to produce spherical particles in large quantities and of uniform size in a range of 5–50
m. A solution of 150 mM NaOH, 0.3% (
v/
v) tetramethylethelenediamine (TEMED; Thermo Fisher Scientific, Waltham, MA, USA, 17919) and 150 mM 3-(N-Morpholino)propanesulfonic acid (MOPS) sodium salt (Sigma-Aldrich, Waltham, MA, USA, M9381) was supplemented with acrylamide (AAm), acrylic acid (AAc) and cross-linker N,N’-methylenebisacrylamide (BIS) (all Sigma-Aldrich, A9099, 147230, 146072, respectively) with a final pH of 7.4. The total mass concentration of acrylic components was
mg/mL. The relative concentration of acrylamide was set to 10%. A cross-linker concentration
of 1.5% was used. The Young’s modulus of the particles was subsequently characterized using atomic force microscopy. The Young’s modulus was
Pa.
2.2. Microparticle Functionalization
First, particles were washed in activation buffer (100 mM MES (Sigma-Aldrich, M5057) and 200 mM NaCl) and subsequently incubated for 15 min in reaction buffer of 0.1% tween20 (Sigma-Aldrich, P7949), 4% (w/v) EDC (Sigma-Aldrich, E7750) and 2% (w/v) NHS (Thermo Fisher Scientific, 22500). Microparticles were washed and incubated for 1 h with 5 g/mL of BSA in PBS for SV80 experiments and 5 g/mL E-cadherin-FC in PBS for 4T1 experiments at pH 8. Subsequently, Alexa647-Cadaverine (Thermo Fisher Scientific, A30679) was added for 30 min. Unreacted NHS groups were blocked using 300 mM Tris and 100 mM ethanolamine (Sigma-Aldrich, 398136) (pH 9). Finally, particles were washed thrice in PBS with 0.1% tween20 and stored for use in PBS (pH 7.4) with 5 mM sodium azide.
2.3. Cell Culture
Cell lines SV80 and 4T1 (obtained from the ATCC) were cultured in high-glucose Dulbecco’s Modified Eagle’s Medium (DMEM, Gibco, Thermo Fisher Scientific, Waltham, MA, USA, 11504496) containing L-Glutamine and Sodium Pyruvate, supplemented with 10% fetal calf serum (Thermo Fisher Scientific) and 25 g/mL penicillin/streptomycin in a humidified incubator at 37 °C with 5% CO2.
2.4. Rheology
To test the glutaraldehyde (GTA) efficiency in cross-linking collagen, we performed rheology measurements (Anton Paar, Graz, Austria, Physica MCR 501) on collagen gels in cone-plate geometry, between stainless steel 40-mm-diameter plates and 0.992° truncation angle. Collagen type I solutions were isolated from rat-tail collagen by acid extraction as described previously [
29]. Collagen matrices were created by mixing HEPES 0.1 M (1 M stock, Sigma-Aldrich, H0887) and NaHCO
3 44 mM (Sigma-Aldrich, S8875) with DMEM at a collagen end concentration of 2 mg/mL as previously described [
30]. The plates were heated to 37 °C prior to loading the sample. Water was added to the solvent trap so as to maintain a moist environment. Moreover, 28 min after loading the sample, a solution of either pure DMEM or DMEM supplemented with 0.1% GTA (Sigma-Aldrich, 340855) was placed around the geometry and allowed to diffuse into the sample for 1 h. The elastic and viscous moduli of the network were probed every 5 s by applying an oscillatory deformation of 0.5% strain amplitude at a frequency of 0.5 Hz. Measurements were recorded and analyzed using software provided by the manufacturer (Anton Paar, Graz, Austria; RHEOPLUS/32 v3.41D100712).
2.5. Spheroid Formation
The collagen and buffers described in the previous paragraph were used for spheroid embedding. Collagen matrices were created by mixing with DMEM, HEPES, NaHCO
3, and growth factor-reduced basement membrane matrix, matrigel
® (Corning, Corning, NY, USA, 354230). Matrigel was added to further decrease the stiffness of the gel. Final collagen concentrations of 0.6 mg/mL and matrigel concentrations of 1.5 mg/mL were used. Fluorescent microparticles were added to the collagen mixture to a concentration of 80 particles/
L. Moreover, 30
L of the collagen mixture was polymerized in 384-well CELLSTAR
® plates (Greiner Bio-one, Kremsmünster, Austria, 781091) at 37 °C for 1 h. Non-enzymatic cross-linking was performed by incubating the gel with 0.1% GTA for 1 h. To ensure soluble GTA was completely removed, gels were subsequently washed with PBS 8 times, then twice with medium [
31].
Spheroids were injected into the 3D collagen/Matrigel matrix as described previously [
32]. In short, subconfluent monolayers of tumor cells were trypsinized and filtered (Sysmex, Norderstedt, Germany, 04-0042-2317). Cells were mixed with fluorescent microparticles (E-cadherin coated were used for 4T1, BSA coated microparticles were used for SV80) in a ratio of approximately 1000:1 and resuspended in PBS containing 2% polyvinylpyrrolidone (PVP, Sigma-Aldrich, P5288) to reach a cell concentration of approximately 50,000 cells/
L. Immediately thereafter, spheroids, 200
m in diameter and containing approximately 2500 cells, were created by automated injection of the cell-PVP mixture into the collagen/matrigel matrix at defined x-y-z positions 150
m above the bottom of the wells using an injection robot (Life Science Methods, Leiden, The Netherlands). After injection, spheroids were incubated with the appropriate medium, or medium containing 20 nM Rho kinase inhibitor (ROCK1/2 GSK 269962, Tocris, Bristol, UK, 4009) at 37 °C. As 4T1 tumor cells grew and migrated faster than SV80 fibroblast cells, 4T1 spheroids were incubated for 48 h, and SV80 spheroids for 72 h. All spheroids were fixed and stained with final concentrations of 2% formaldehyde (Sigma-Aldrich, 252549), 0.1% TritonX-100 (Sigma-Aldrich, T8787), 0.4
g/mL Hoechst (Fisher Biotech, Wembley, Australia, 33258) and 0.05
M AlexaFluor-488 Phalloidin (Invitrogen, Waltham, MA, USA, A12379) in PBS for 3 h at room temperature. The samples were washed thoroughly in PBS, followed by microscopy.
2.6. Microscopy
2.6.1. Scanning Confocal Microscopy
Images of spheroids were acquired on a Nikon C2plus Ti2 inverted scanning confocal microscope equipped with four laser lines 405/488/561/640 nm, and with a SimpleSI detector. The microscope has a Nikon-encoded and automated stage. Its camera is controlled through NIS Element Software (Nikon Instruments Inc., Melville, NY, USA; v4.11). Spheroids were imaged with 20 m distance between z-slices. ECM collagen fibers were detected by confocal reflection microscopy on a Nikon Eclipse Ti inverted scanning confocal microscope equipped with an A1R MP scanner. The collagen fibers were scanned at 561 nm excitation with a 561 nm blocking dichroic. All light in the range 400–750 nm was collected on a GaAsP-photomultiplier. Scanning confocal fluorescent microscopy of spheroids, and scanning confocal reflection microscopy of the collagen networks were performed using Plan-Apo ×20/0.75 NA, and Apo-LWD ×20/0.95 objectives (Nikon Europe B.V., Amstelveen, NL, The Netherlands), respectively.
2.6.2. Spinning Disk Confocal Microscopy
High-resolution imaging was performed on an inverted microscope (Zeiss, Oberkochen, Germany, Axiovert 200) equipped with a 20×, 0.5 NA Plan-Neofluar objective (Zeiss). The setup was expanded with a confocal spinning disk unit (Yokogawa, Musashino, Japan, CSU-X1) and an emCCD camera (Andor Technology, Belfast, Northern Ireland, iXon DU897). The hydrogel microparticles were imaged with 642 nm diode laser illumination (Spectra Physics, Utrecht, The Netherlands). A 561 nm DPSS-laser (Cobolt, Stockholm, Sweden) was used to image the AlexaFluor-561 Phalloidin. A 405 nm DPSS-laser (CrystaLaser, Reno, NV, USA) was used to illuminate the Hoechst nuclear stain. Z-stacks were used to obtain a 3D image cube of the microparticles and the surrounding cells. The mismatch between the refractive indices of the air surrounding the objective and the culture medium caused an apparent compression of the image cube, which was corrected by an experimentally determined correction factor: the apparent elongation of at least 10 stiff (>5 kPa) microparticles was determined by calculating the radius in the equatorial plane compared to the lateral radius of the particles. The ratio of both was used as a correction factor for the z-positions, rendering the effect of the refractive index mismatch negligible.
2.7. Collagen Fiber Analysis
To analyze the orientation and alignment of collagen fibers, reflection images were processed using a custom Matlab (R2021a) script. First, at the mid-plane of the spheroid, one z-plane of a reflection image stack was taken to generate a representative image of the collagen fibers. The center of mass (CoM) of the spheroid was determined, and the spheroid was separated from the background. The image was blurred with a narrow Gaussian kernel. The orientation and coherency (alignment) of the fibers were quantified using this image [
33]. These parameters were assessed at the fiber locations by means of a weighted mean over the signal intensity, and the radial alignment of the fibers was calculated relative to the CoM of the spheroid. The distance of the fibers to the edge of the spheroid was calculated using the spheroid’s foreground image. To facilitate comparison of the profile of radial fiber alignment and coherency of many spheroids, the data were binned with a bin size of 15
m based on the distance to the edge.
2.8. Migration Analysis
The home-built migration analysis in Matlab was based on a method described previously [
34]. Scanning confocal z-stacks of the actin cytoskeleton were projected using the standard deviation in the z-direction (
Figure S1A). A Gaussian filter with a narrow kernel was used to remove small fluctuations from the projected image. An adaptive threshold was used to separate the foreground from the background. The area
A and perimeter
P of the spheroid were calculated using the generated foreground image. For quantitation we defined a normalized complexity value
C as
denoting the roughness of the spheroid edges. The point in the foreground that was farthest from the background was defined as the centroid, and its distance to the background was defined as the core radius (green dot and circle in
Figure S1B). The invasive area was defined by the area of the foreground outside the core. To identify branches, skeletonization was applied to the foreground mask, with the endpoints of the resulting skeleton serving as branch points (cyan dots in
Figure S1B,C).
2.9. 3D Spheroid Reconstruction
The center of mass (CoM) and radius of a partially imaged spheroid were determined using software coded in Matlab (
Figure S2). A Gaussian filter with a wide kernel was applied to the image stacks containing the actin cytoskeleton. Subsequently, a 3D Sobel operator was used to highlight the edges of the spheroid. The foreground was separated from the background, and a least square non-linear fit was used to fit a sphere to the foreground voxels. The center and radius of this sphere defined the CoM and radius of the spheroid.
2.10. High-Resolution Microparticle Shape Reconstruction
Z-stacks of particles were taken on a spinning disk confocal fluorescence microscope. The z-slices were separated by a distance of m, which is half the depth-of-focus of the objective to comply with Nyquist’s theorem. Individual particles in the image cube were identified, and the data cubes were cropped to contain solely individual particles.
2.11. Local Stress Analysis
Fast stress analysis was performed in spherical harmonics space [
35] implemented in the Python v3.11 SHTools library [
36]. Analysis was part of a larger, home-built mixed Matlab/Python pipeline that automatically analyzed multi-color 3D image stacks from our confocal microscopes as detailed in [
28]. In short, spherical harmonics are solutions to the generalized linear elasticity continuity equation (Hooke’s law) for the mechanical equilibrium condition of a spherical boundary in an isotropic medium.
Deformations were expressed by complex coefficients,
, of the spherical harmonics:
where
are the set of complex spherical harmonics functions given by the harmonic-degree
l and order
m.
Using those solutions of the displacement field, the full stress tensor was calculated in terms of its complex stress coefficients
which are uniquely defined by the displacement coefficients
:
Any local stress on the microparticles leads to a local deformation of the particle’s surface at the location of the stress. We defined indentations as negative stress. The full stress tensor was subsequently separated into an isotropic (pressure,
P) and an anisotropic (deviatoric stress, D) component:
where
refers to Kronecker delta. Since the deviatoric stress is traceless by definition, the pressure is expressed as follows:
The spatial resolution of the stress field was limited by the maximum harmonic degree, , in the spherical harmonics expansion. Here we used since this gives a good balance between spatial resolution (≈2 m) and computational time (≈1 h per particle on an office PC).
2.12. Statistics
A one-tailed, unpaired, parametric t-test was used with Welch’s correction in order to determine statistical significance between two one-dimensional populations. For comparison of two-dimensional datasets (i.e., those containing both x- and y-coordinates), a contrast-to-noise ratio (CNR) was calculated:
where
and
are datasets depending on a spatial variable
x.
are the respective standard deviations. A one-sample
t-test on
was used to determine statistical significance between
and
. Datasets were significantly different with probabilities of
(*),
(**), and not significantly different for probabilities of
(
ns).
3. Results
3.1. Glutaraldehyde Cross-Linking Increases Collagen Network Stiffness Without Affecting Collagen Fiber Architecture
To model the extracellular matrix (ECM) surrounding tumoroids with different stiffnesses, we used non-enzymatic cross-linking of collagen gels utilizing glutaraldehyde (GTA). We first tested the effect of GTA on the elastic properties of collagen matrices and measured the elastic modulus of collagen by rheology. Collagen is a viscoelastic material for which the mechanical properties are determined by two components. The storage modulus , which represents the elastic component of a viscoelastic material, accounting for the amount of energy that is stored in the material during deformation, and the loss modulus , which represents the viscous component, accounting for the amount of energy that is dissipated during deformation.
and
were measured at a frequency of 0.5 Hz during polymerization of 2 mg/mL collagen. The collagen gels polymerized within 10 minutes, as displayed in
Figure S4A. Subsequently, GTA was added while
and
were further monitored during the process of cross-linking. On GTA cross-linking, a 4.5-fold increase in storage modulus (to
Pa, mean ± sem) was observed after 1 h incubation with 0.1% GTA, as compared to incubation with control medium (
Pa) (
Figure 1A). No change in the loss modulus was observed after adding GTA, as shown in
Figure 1B.
The architecture of the collagen gels with and without GTA was analyzed using reflection microscopy. No difference in fiber length and fiber diameter was observed, as shown in
Figure 1C. We further quantified fiber density in three independent experiments using Fiji (National Institutes of Health, Bethesda, MD, USA, version 1.53c) [
37]. A threshold was applied to a maximum projection of 5 z-slices and the area covered by the fibers was quantified (
Figure S4B). No significant increase in fiber density in GTA gels was observed as compared to control collagen gels. Likewise, the collagen architecture appeared similar in gels with and without GTA cross-linking.
These results indicated that GTA cross-linked collagen gels behave more elastic, store more energy, and return to their original shape more readily ( higher). They do not exhibit increased viscous deformation ( similar), and the collagen fiber architecture is not affected by cross-linking, supporting our aim to employ GTA-cross-linked collagen gels as an in-vitro model of the ECM surrounding tumoroids.
3.2. ECM Stiffness Increases Cell Invasion of Spheroids into the ECM with ROCK1/2 Partially Modulating This Stiffness-Induced Migration
Spheroids of SV80 fibroblasts and 4T1 breast cancer cells were cultured in GTA-cross-linked and non-cross-linked gels for three and two days, respectively. In pure 2 mg/mL collagen gels, GTA had no effect on spheroid growth and morphology. In order to expose the spheroids to even softer environments, where the impact of cross-linking was predicted to be more robust, we mixed 0.5 mg/mL collagen with 1.5 mg/mL matrigel for all further experiments. The inclusion of matrigel did not affect the collagen architecture (
Figure S3). Those gels were softer than
Pa, the resolution limit of our rheometer. We extrapolated that cross-linking with GTA would likewise lead to 4.5-fold increase in storage modulus as we had observed for 2 mg/mL pure collagen gel. Spheroids were imaged after fixation and staining.
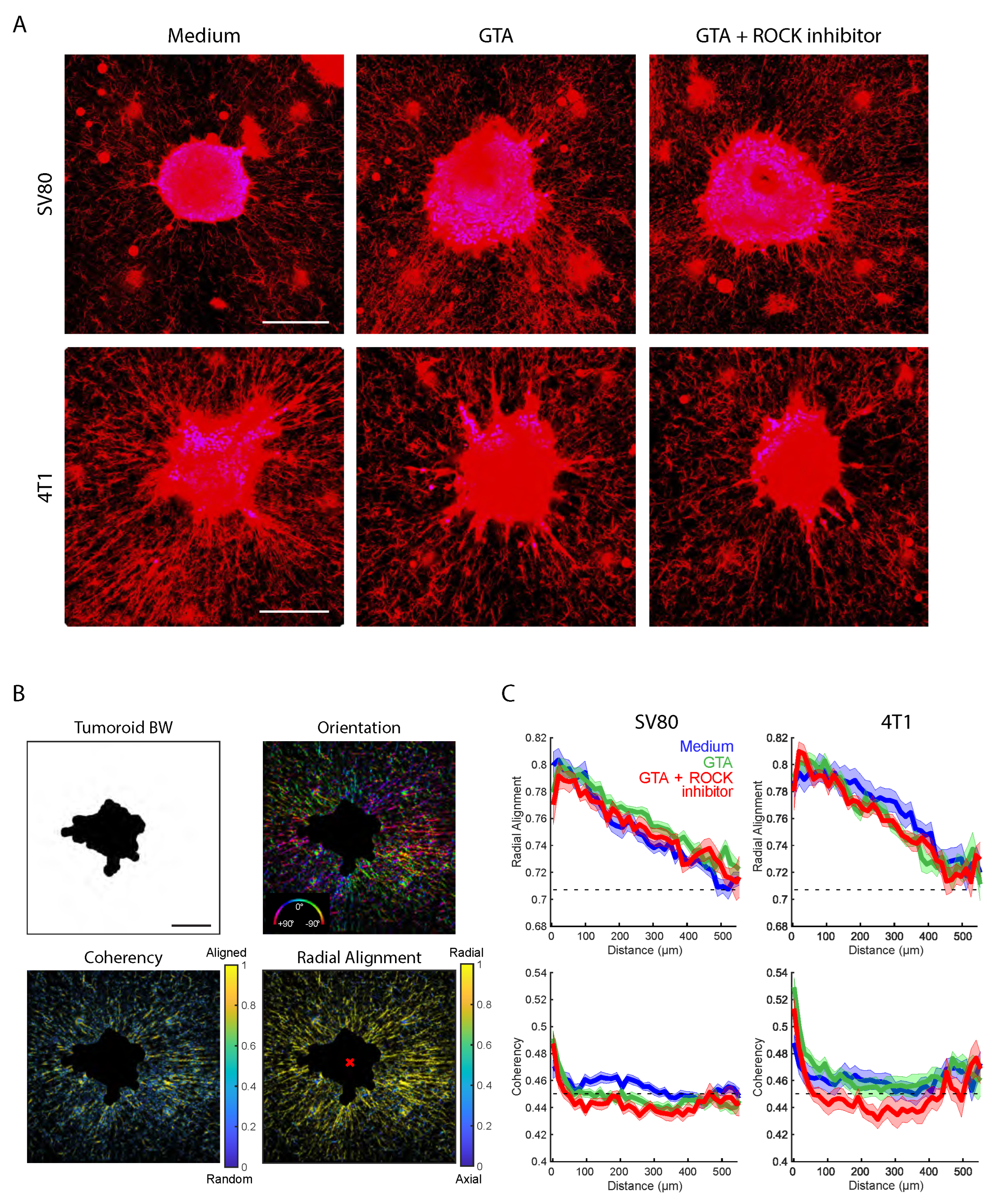
Figure 2A shows an overview of representative spheroid images.
Images were analyzed in the phalloidin channel; we labeled the cellular F-actin architecture and used a home-built spheroid invasion analysis tool. Based on a binary foreground separation of the spheroids, spheroid area, complexity, branch number, and branch area were calculated and compared between all conditions.
Figure 2B,C summarizes these results for SV80 (B) and 4T1 (C) spheroids, respectively. For both cell types, spheroids showed a significant increase in area and complexity as a measure of the spheroid’s edge ruffling, branch number, and normalized branch area in GTA cross-linked gels as compared to control gels. A minimum of 20 spheroids each was analyzed. The spheroid area was increased by a factor of 1.76 (sem medium: 0.06; sem GTA: 0.10) for 4T1 and 1.80 (sem medium: 0.05; sem GTA: 0.11) for SV80. The complexity was increased by a factor of 2.9 (sem medium: 0.13; sem GTA: 0.4) for 4T1, and 2.4 (sem medium: 0.11; sem GTA: 0.3) for SV80. Notably, while 4T1 and SV80 spheroids showed a similar area, 4T1 displayed significantly higher complexity (≈4-fold) and branch area (≈2-fold) as compared to SV80 spheroids.
As ROCK-mediated traction forces are known to increase in stiffer ECMs, we asked whether the increased migration into cross-linked ECMs may be ROCK-dependent. For this, 20 nM of the ROCK1/2 inhibitor GSK 269962 was added to spheroids in GTA gels. Indeed, for both 4T1 and SV80 spheroids exposure to ROCK1/2 inhibitor led to a decrease in complexity and branch area parameters (
Figure 2B,C). However, while the total spheroid area and the number of branches were likewise decreased for 4T1 cells in the presence of GSK 269962, SV80 spheroids showed a slight increase in spheroid area and number of branches upon ROCK1/2 inhibition. Thus, for 4T1 but not for SV80 spheroids, the inhibition of ROCK1/2 led to a shrinkage in cross-linked gels, making their behavior more similar to that observed in soft gels in the absence of the inhibitor.
Together, these data demonstrate that stiffening of the ECM increases cell invasion into the ECM for both cell types. However, the role of ROCK1/2-mediated contractility and traction differs between the two cell types, showing an involvement of the ROCK1/2 pathway in the stiffness-dependent migration of 4T1.
3.3. Cell-Type and Stiffness Affects ECM Remodeling
We next analyzed how 4T1 and SV80 spheroids remodeled the surrounding ECM fiber network, and how remodeling was affected by ECM stiffness. In soft ECM, both 4T1 and SV80 spheroids aligned the fibers of the collagen in the radial direction centered to the spheroid core. Consequently, 4T1 spheroids displayed much higher capacity to pull and create thick collagen bundles as compared to SV80 spheroids (
Figure 3A). Remarkably, while GTA cross-linking appeared to slightly increase the number of thin radially oriented fibers around SV80 spheroids, the fiber network around 4T1 spheroids was depleted. For both cell types, inhibition of ROCK1/2 minimally affected collagen remodeling, confirming our observations with respect to spheroid invasion above.
For quantitative analysis of the changes in the organization of the ECM network, we quantified the orientational order of the structure that emerged. The fiber orientation (the direction of fibers relative to the spheroid), the radial alignment relative to the centroid of the spheroid, and the coherency (a length scale of constant fiber alignment) were determined, following the methods developed by Püsköki et al. [
33] (
Figure 3B). The radial alignment decreased gradually from 0.8 at the spheroid edge to 0.71 at about 500
m from the spheroid edge. The latter value is predicted for a random network. The overall behavior was similar for all spheroids and for all conditions (
Figure 3C). In agreement with the visual results shown in
Figure 3A, the reach of ECM remodeling into the collagen gel was longer for 4T1 spheroids as compared to that for SV80 spheroids. The typical length scales found were 400 and 250
m, for 4T1 and SV80, respectively.
The coherency was increased especially close to the spheroid’s edge, which may point to active mechanical stresses applied by the cells that increase the length scale at which fibers remain aligned (
Figure 3C). Notably, the coherency measures the alignment without a given direction, which results in a non-zero offset for a random network. The coherency decreased rapidly from SV80 and 4T1 spheroid edges into the ECM, approaching the inherent fiber coherency value of 0.45 within 100
m from the spheroid edge. Following this initial drop, coherency remained slightly above the background and reached the inherent fiber coherency after 300
m for both cell lines. In a stiffer gel, coherency at the spheroid border was higher for both cell lines. Moreover, it was maintained further into the surrounding ECM, in a ROCK-dependent manner, for 4T1 but not SV80.
These findings showed that spheroids derived from both cell types strongly reorganize the collagen network on length scales of hundreds of micrometers; however, the amount of remodeling is strongly cell-type-dependent. Changes in ECM remodeling upon ECM stiffening are likewise cell type-dependent, and ECM stiffness has a limited impact on organization or length scale.
3.4. Matrix Stiffness Affects Local Mechanical Spheroid-Induced Stress
The stress originating from spheroid expansion and the traction forces applied by the cells of the spheroid onto the ECM will extend into the ECM as inferred from the emergence of fiber orientational order shown above. We quantified the local mechanical stress and pressure distribution inside and around spheroids using soft elastic hydrogel microparticles. Microparticles were mixed into the ECM solution before polymerization and mixed with the cells before injection into the ECM. We noticed that uncoated microparticles were rapidly excluded from the spheroids. Therefore, we coated the microparticles with the collagen-binding protein E-cadherin prior to co-injection into the preformed gel for 4T1 spheroids. We observed that such coated microparticles readily attached to the 4T1 cells and remained within the spheroids. As E-cadherin expression was absent in SV80 cells (
Figure S5), we used BSA-coated microparticles for SV80 spheroids, which likewise prevented exclusion of the microparticles from SV80 spheroids.
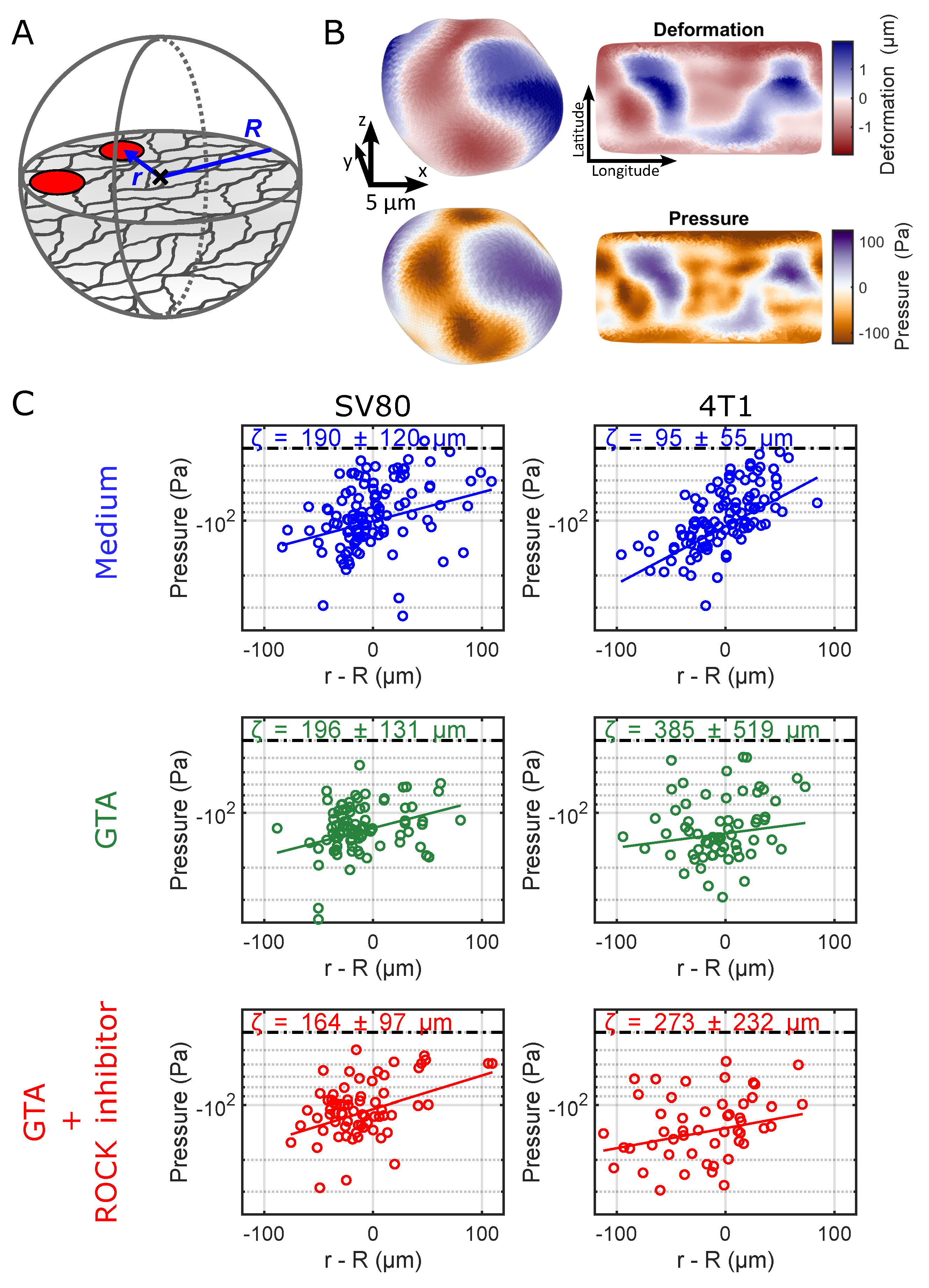
The local pressure fields were determined from the microparticle deformations as detailed in the M&M section to an accuracy of ≈40 Pa (
Figure 4A,B). As we simultaneously tracked the absolute position of each microparticle with respect to the spheroid centroid, we were able to reconstruct the local stress and pressure fields throughout the sample. One of the critical observations was the increase in absolute pressure (more negative pressure/indentation, i.e., compression) of the microparticles toward the core of the spheroid, as shown in
Figure 4C. The pressures leveled off with distance from the spheroid core. Our data revealed that pressure extended beyond the spheroid edge (the zero on the x-axis of the graphs) into the surrounding ECM. Microparticles far off from any spheroid (
m) reported on pressures of 40 Pa (dashed lines in the graphs) set by the accuracy of our measurements. The results for each individual biological replicate are shown in
Figure S6 of the
Supplementary Material.
To quantify a length scale up to which the spheroid-induced stress reaches into the ECM, we modeled an exponentially dropping absolute pressure as a function of distance
r from the spheroid core,
with core pressure
and characteristic length scale
on which the spheroid-induced mechanical stress dissipates into the gel. In the <10 Pa non-cross-linked gel, this length scale was shorter for 4T1 than for the SV80 spheroids, indicating that the SV80 fibroblasts extended pressure further into the surrounding ECM. Upon cross-linking, the effective reach of the pressure was similar in the soft (”medium”,
m) and in stiff ECM (”GTA”,
m) for SV80 fibroblast spheroids. On the other hand, the pressure reach of 4T1 spheroids increased dramatically from
m in the soft ECM to >250
m in the stiff, GTA cross-linked, ECM. The inhibition of ROCK had little effect on this behavior for SV80 and 4T1 spheroids.
These results showed that local mechanical stress in spheroids can be quantified using soft elastic hydrogel microparticles. We showed that the pressure levels are significantly increased in the core of the spheroids. Mechanical stresses and pressures level off toward the outer spheroid layers and clearly extend beyond, reaching into the ECM. In line with the extensive ECM remodeling around spheroids we showed above, the extension of mechanical stress and pressure into the surrounding ECM reaches for hundred(s) of m, length scales about or larger than the radius of a spheroid. While pressures caused by SV80 spheroids already penetrate into the ECM in soft environments, 4T1 spheroids react to ECM stiffening by an increase in their pressure reach.
4. Discussion
Our study aimed to investigate how ECM stiffness affects stresses and pressures within tumors, how it affects cell migration and ECM remodeling, and how those mechanical and biological parameters are correlated. We show that pressure gradients within and around spheroids are dependent on cell type and, for tumor spheroids, also on ECM stiffness and ROCK activity. Both tumor and fibroblast spheroids respond similarly to ECM stiffness in terms of invasion yet develop different migration patterns. Tumor spheroids exhibit a pronounced ability for collagen network remodeling, which decreases for stiffer ECM. In contrast, remodeling of the collagen network increases with ECM stiffness for fibroblast spheroids. Remodeling of the fibrous ECM is paralleled by a buildup of stress and pressure gradients extending increasingly further into the ECM in stiffer environments. Molecularly, we show that ROCK inhibition reduces tumor spheroid invasion without affecting fibroblast migration or collagen remodeling. For this study, we chose to use a spheroid model embedded in collagen I, a natural component of the ECM in many tissues, including tumor microenvironments. This decision was based on the biological relevance of collagen I in tumor biology, as it plays a significant role in cell adhesion, migration, and tumor progression [
38].
In the three-dimensional context of tissue, it is not obvious how cell migration and tumor invasion depend on the mechanical properties of the surrounding ECM. Whereas an increased stiffness is known to trigger cellular programs that lead to higher cellular forces and mobility, more stiff and dense environments will simultaneously lead to a decrease in cell mobility. Indeed we here confirmed that the relation between stiffness, motility, and invasion is more subtle. In our experiments we achieved stiffening of the low-density fibrous collagen matrix by chemical cross-linking. It should be mentioned that the mild cross-linking used solely changed the elastic behavior of the gel. We observed no change in collagen fiber architecture nor in fiber density (
Figure S4) in comparison to earlier reports suggesting that a cross-linked collagen matrix has a lower porosity than non-cross-linked controls [
39]. Thus, any change in cell behavior could be attributed to the mechanical properties of the environment. Cross-linking of the low-density collagen network led to a five-fold increase in storage modulus, consistent with earlier reports [
40]. The increase in ECM stiffness elicited an increased invasion of tumor cells and fibroblasts into the ECM. Both cell types demonstrate enhanced outward migration in response to increased ECM stiffness, indicating that they are sensitive to the mechanical properties of their microenvironment. This similarity suggests that matrix stiffness may universally promote a more migratory phenotype, possibly by enhancing cell–matrix adhesion, traction force generation, or actin cytoskeleton remodeling. Those findings are in line with earlier related observations, where it was reported that invadopodia formation and tumor cell invasion were stronger in a stiffer matrix [
15]. Likewise, interpolation of experimental results in the 2D to 3D situation in the current study indicates the stiffer ECM could provide a more rigid substrate for cancer cells to adhere to. Indeed such dependence was observed, in which cancer spheroids showed enhanced integrin adhesions in stiff ECM [
16]. Cells likely transmit forces more effectively and develop stronger adhesion to the ECM when the ECM is stiff. Enhanced cellular integrin activity in stiffer ECM would enable the cells to resist detachment from the ECM and thereby promote their ability to invade. Interestingly, we observed a higher invasion potential for 4T1 spheroids as compared to SV80 spheroids. This observation is in line with the fact that 4T1 cells highly express E-cadherin, enabling them to develop stable cell-cell contacts. Those are the prerequisites to collective migration modes that we observed as finger-like structures in our confocal images. Collective cells have been reported to migrate faster than single cells [
41]. In contrast to cancer cells, non-cancerous fibroblasts typically show no invasion and have controlled cell growth [
42]. While we do observe an expansion of fibroblast spheroids in stiffer ECM gels, we see that this expansion is without long protrusions or branch-like structures. As we see an increase in ECM remodeling for SV80 in the stiffer ECM, it could be that fibroblasts at the periphery of the spheroid may pull on each other and on the matrix, causing passive expansion of the whole structure and not active cell migration. ECM stiffness, therefore, influences cell dynamics, even in typically non-invasive cell types.
To further compare the results obtained on SV80 and 4T1, we show that the degree and pattern of ECM remodeling diverge sharply between the two cell types. In soft ECM, 4T1 spheroids remodel the surrounding matrix more extensively than SV80, reflecting the aggressive, invasive nature of cancer cells that often degrade or rearrange ECM components to facilitate invasion. This is likely due to high levels of matrix metalloproteinase (MMP) activity [
43] and dynamic cytoskeletal organization in breast cancer cells. Interestingly, when ECM stiffness is increased, SV80 fibroblasts show an increase in ECM remodeling, possibly as a result of mechanical activation into a myofibroblast-like state induced by matrix stiffening, which is characterized by enhanced contractility and matrix interaction [
44,
45].
The differential behavior between fibroblasts and 4T1 cells in terms of migration was reflected by the buildup of local stresses in and close to the spheroid and the alignment of the collagen network around the spheroids. Local stress and pressure increased toward the spheroid core to about 100–200 Pa in the about 100
m-radius spheroids investigated. There was no significant difference in core pressure for the different preparations. Even though the stiff matrix could potentially compress the spheroid and make the cells experience more stress, no increase in pressure was measured inside the spheroid. It is important to note that in addition to these mechanical stresses, increased interstitial fluid pressure (IFP), a key characteristic of the tumor microenvironment in-vivo, can also significantly influence cell migration, ECM remodeling, and the overall biomechanical landscape. While not directly measured in this in-vitro setup, elevated IFP is known to contribute to matrix stiffness and can even induce epithelial–mesenchymal transition (EMT) [
46].
It is obvious from the stress measurements, as well as from the ECM remodeling, that the internal stresses significantly extend beyond the spheroid edge into the ECM in a smooth transition. The main difference between the different experimental conditions is how far the stress reaches out into the network. In the soft environment, the reach of the mechanical stress of fibroblasts (≈200
m) is significantly larger than that of the 4T1 cells (≈100
m). Those stresses can lead to an alignment of the fibrous network of the ECM as observed in our experiments. In particular, 4T1 cancer spheroids show high, radial collagen alignment as well as rapid stress and pressure increase inside spheroids in soft matrices. High collagen remodeling was earlier attributed to local invasion [
47]; therefore, it is surprising to see that the 4T1 spheroids invade less in matrices of high remodeling compared to a matrix in which the collagen is less aligned. This suggests that a potential increase in ability to bind to the ECM rather than an increase in traction force generation needs to be considered in order to explain the reduced invasion capacity in low-stiffness gels. The stiffening of the environment by chemical cross-linking results in an increase in the mechanical reach of the stress beyond our observation volume. This suggests that the reach of traction forces is the result of increased stiffness and cross-linking of the matrix rather than the actin–myosin interactions of the cells themselves. In particular, for the 4T1 cancer cells, these results are not too surprising, as the efficiency of force transmission might be more relevant to invasion than the magnitude of these forces [
48]. The fact that despite lower collagen alignment around the tumor spheroid, more migration is seen in stiffer ECM might be due to a regulatory mechanism to manage internal pressure within the spheroid.
The results above suggested that the force-generation machinery of individual cells would have only a minor impact on the stress distribution and remodeling capacity in the context of spheroids embedded in ECM. Inhibition of ROCK only slightly changed the mechanical reach and the ability for collagen fiber alignment. The reduction in collagen alignment and invasion observed for 4T1 spheroids in the presence of a ROCK inhibitor shows that actomyosin contractility and ROCK-driven cytoskeletal tension play a role in how 4T1 cells respond to a stiffer ECM. Indeed, it has been documented that ROCK promotes collagen remodeling and facilitates tumor cell invasion [
49]. For SV80, however, we do not see a change in collagen alignment and invasion when adding a ROCK inhibitor, implying that SV80 migration is either ROCK-independent or relies on alternative mechanotransduction pathways. This points to cell-type-specific utilization of contractile machinery in response to mechanical cues. Other kinases like MLCK can also be involved in regulating actin–myosin interactions and could, therefore, be used by cells instead of ROCK, which would explain results that are opposite to those shown by Beningo et al. [
50].
The increased invasion of 4T1 tumor spheroids in the stiffer matrix, which does not show more prominent fibers, suggests that the amount of aligned collagen fibers is not related to more effective migration along such fibers. Notably, our observations are made with spheroids embedded in a relatively soft 3D environment (<100 Pa) gels. In a similar regime, a shift from 100 to 150 Pa promoted a breast cancer invasion similar to our finding for 4T1 [
5]. In much stiffer hydrogels (≥2000 Pa) spheroid expansion is attenuated, and this is overcome by ROCK inhibition, [
51]. In fact, a quantitative model showed that an intermediate ECM stiffness provides optimal conditions for cancer cells to polarize, contract, and invade [
52]. For cells attaching to a 2D substrate, the stiffness regime is very different with stiffnesses of >100 kPa promoting adhesion formation and migration [
53]. This indicates that ECM stiffness and tumor invasion exhibit non-linear behavior, potentially resembling a biphasic behavior with maximum invasion seen at medium stiffness. The behavior is influenced by the 2D versus 3D geometry and will likely be different for different cell types, which can explain the different responses of 4T1 and SV80 spheroids to stiffening in our experiments.