On the Execution and Runtime Verification of UML Activity Diagrams
Abstract
1. Introduction
- An algorithm is proposed that translates an activity diagram into an executable process in the calculus of context-aware ambients (CCA) (Section 2.3.2). This algorithm is thought of as a semantic function for UML activity diagrams. It is demonstrated that the time complexity of the algorithm is and that the size of the CCA process produced in output is in the order of , where n is the size of the UML activity diagram (Section 2.3.3).
- An implementation of the algorithm in Python is provided (as a proof of concept) to automatically generate a CCA process that describes the behaviours of a given UML activity diagram (Appendix A). The experimental results confirm the theoretical complexity in time and in the output size of the algorithm with respect to the size of the input (Section 3.1). The generated process can be executed in various scenarios using the CCA simulation tool ccaPL to better understand the behaviours of the corresponding UML activity diagram.
- We extend the syntax and the semantics of the linear temporal logic (LTL) with the CCA notion of context expression and other new predicates to support the runtime verification of CCA processes (Section 3.3.1).
- A runtime verification tool, ccaRV, is implemented in Java and can be used to verify UML activity diagrams (Section 3.3). This tool checks at runtime whether a UML activity diagram satisfies a desired property specified as an LTL formula.
- The pragmatics of the proposed approach is demonstrated using a case study in e-commerce (Section 3.4).
2. Materials and Methods
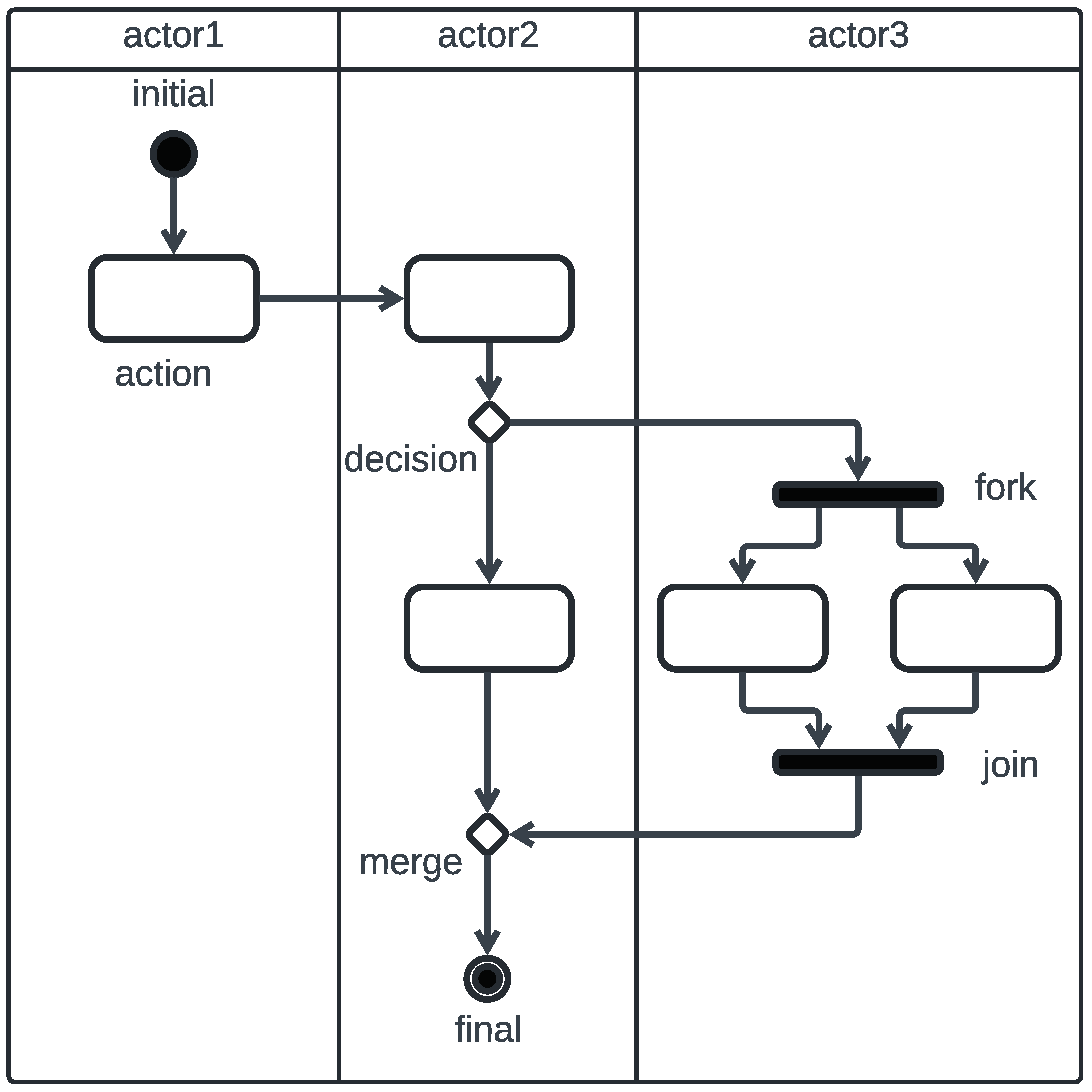
2.1. Overview of UML Activity Diagrams
2.2. Overview of CCA
2.2.1. Processes
2.2.2. Capabilities
2.2.3. Context Model
2.2.4. Context Expressions
2.2.5. An Example
| Listing 1. The ambient representing the RFID tag. |
| RFID_tag[ !@send(166).out.0 | in RFID_reader.0 ] |
| Listing 2. The ambient representing the RFID reader. |
| RFID_reader[ !recv().#recv(id).server::send(RFID_reader, ac_service, id). server::recv(status).send().0 | send().0 ] |
| Listing 3. The ambient representing the server. |
| server[ proc ac_service(client, door, id) { if < (id>100) and (id<200) > client::send(valid). door::send(open).send().0 else client::send(invalid).door::send(close).send().0 fi } | !recv().::recv(client, service, id).service(client, garage_door, id).0 | send().0 ] |
| Listing 4. The ambient representing the garage door. |
| garage_door[ !recv().server::recv(x). if < x = close and state(opened) > del opened.send().closed[0] < x = open and state(closed) > del closed.send().opened[0] else send().0 fi | send().0 | closed[0] // initially the door is closed. ] |
| Listing 5. The CCA process representing the access control system of Section 2.2.5. |
| BEGIN_DECLS def state(n) = { somewhere (this | n[0] | true) } //display code //display congruence mode random //length = 100 END_DECLS RFID_tag[ !@send(166).out.0 | in RFID_reader.0 ] | RFID_reader[ !recv().#recv(id).server::send(RFID_reader, ac_service, id). server::recv(status).send().0 | send().0 ] | server[ proc ac_service(client, door, id) { if < (id>100) and (id<200) > client::send(valid). door::send(open).send().0 else client::send(invalid).door::send(close).send().0 fi } | !recv().::recv(client, service, id).service(client, garage_door, id).0 | send().0 ] | garage_door[ !recv().server::recv(x). if < x = close and state(opened) > del opened.send().closed[0] < x = open and state(closed) > del closed.send().opened[0] else send().0 fi | send().0 | closed[0] // initially the door is closed. ] |
2.3. Mapping an Activity Diagram onto a CCA Process
2.3.1. A Mathematical Representation of an Activity Diagram
- N is a non-empty finite set of activity nodes. It is assumed that no two activity nodes have the same name.
- is a set of transitions.
- A is a finite set of actors (i.e., swimlanes).
- C is a finite set of the conditions (i.e., Boolean expressions) carried by decision nodes.
- is a type assignment to activity nodes.
- is a mapping of fork nodes to the corresponding join nodes.
- is a mapping of activity nodes to the actors that perform them.
- is a mapping of conditions to the decision node branches.
- .
- .
- .
- .
- .
- .
- .
- .
2.3.2. An Algorithm for Mapping an Activity Diagram onto a CCA Process
| Listing 6. General form of a declaration block generated by Algorithm 1. |
| BEGIN_DECLS def state(n) = { somewhere (this | n[0] | true) } def notEnd() = { somewhere (final[0] | true) } def decision1(n) = { n = c1 } … def decisionN(n) = { n = cN } //display code //display congruence mode random //length = 100 END_DECLS |
| Algorithm 1: Mapping a UML activity diagram onto a CCA process. |
 |
| Algorithm 2: mappingNode(a, x, SPACE, SPACE1). |
 |
| Listing 7. General form of an ambient corresponding to a swimlane/actor that contains no initial node and no final node. The process abstractions node1(), …, nodeN() correspond to the activity nodes that belong to that swimlane. |
| a[ proc nod1(){ … } | … | proc nodN(){ … } | !::recv(t).t().0 | !recv(t).0 ] |
| Listing 8. General form of an ambient corresponding to a swimlane/actor that contains an initial node and no final node. The process abstractions node1(), …, nodeN() correspond to the activity nodes that belong to that swimlane. |
| a[ proc initial(){ … } | initial().0 | proc nod1(){ … } | … | proc nodN(){ … } | !::recv(t).t().0 | !recv(t).0 ] |
| Listing 9. General form of an ambient corresponding to a swimlane/actor that contains no initial node but a final node. The process abstractions node1(), …, nodeN() correspond to the activity nodes that belong to that swimlane. |
| a[ proc final(){ … } | proc nod1(){ … } | … | proc nodN(){ … } | final[0] | !::recv(t).t().0 | !recv(t).0 ] |
| Listing 10. General form of an ambient corresponding to a swimlane/actor that contains an initial node and a final node. The process abstractions node1(), …, nodeN() correspond to the activity nodes that belong to that swimlane. |
| a[ proc initial(){ … } | initial().0 | proc final(){ … } | proc nod1(){ … } | … | proc nodN(){ … } | final[0] | !::recv(t).t().0 | !recv(t).0 ] |
- When the successor node is in the same swimlane, the process abstraction checks if the final node is not reached yet (using the context expression notEnd()), in which case it executes the current activity node (by sending out the name of the node, e.g., send(initial)) and then transfers the control to the successor node (by calling the process abstraction corresponding to the successor node, i.e., node().0). Otherwise it terminates. Recall that each ambient corresponding to a swimlane contains the process !recv(t).0. This process is used to handle all the statements corresponding to the execution of a local node x. For example, the process abstraction generated for the initial node of the activity diagram in Figure 2 is provided in Example 4.
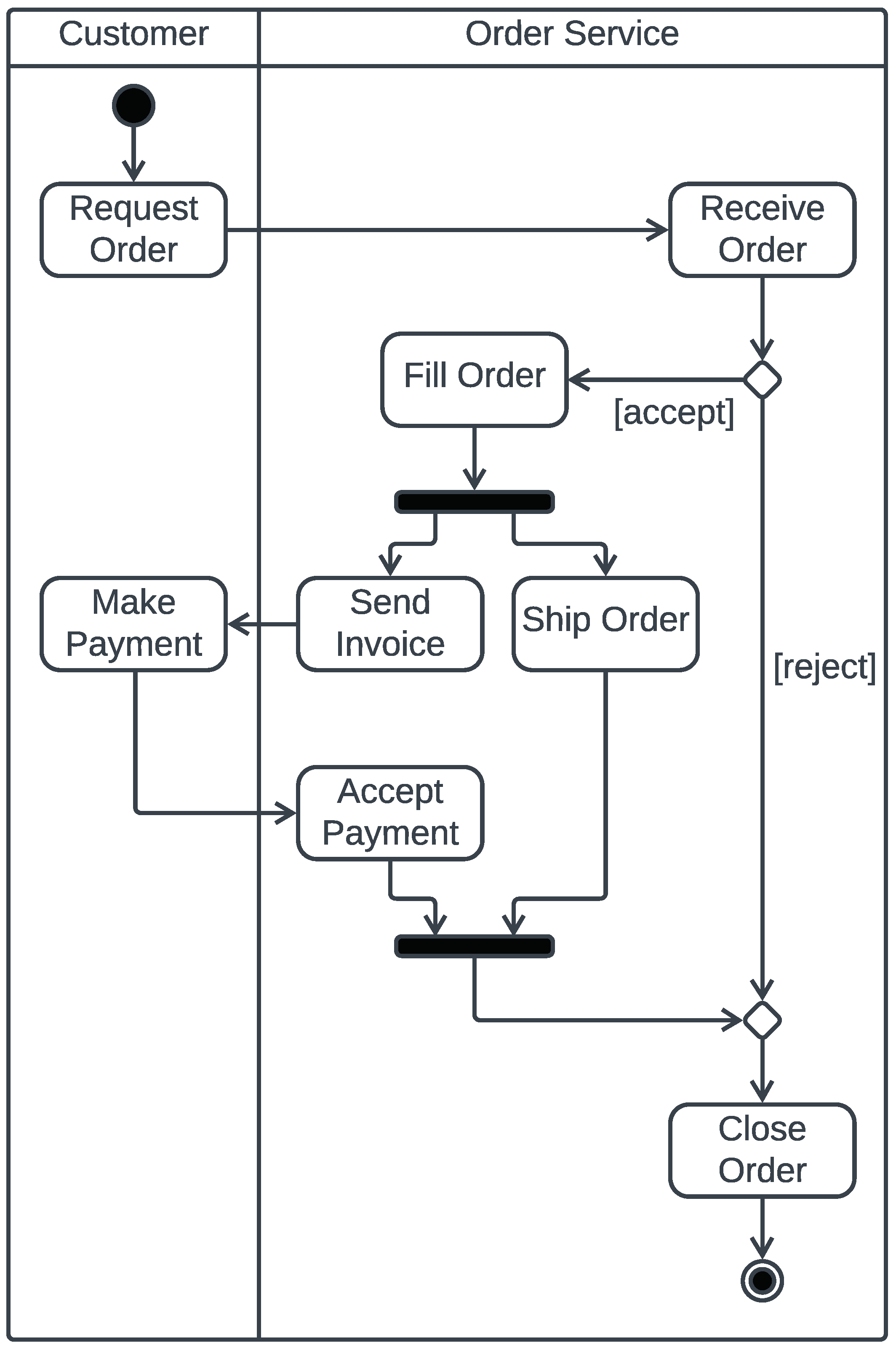
- When the successor node is in a different swimlane B, the process abstraction checks if the final node is not reached yet (using the context expression notEnd()), in which case it executes the current activity node (by sending out the name of the node, e.g., send(initial)) and then transfers the control to the successor node in the swimlane B (by sending the successor node name to B, i.e., B::send(node).0). Otherwise it terminates. Upon the receipt of the successor node name by B, the ambient B (representing the swimlane B) calls the process abstraction corresponding to that successor node using the process !::recv(t).t().0. Recall that when there are more than one swimlanes, each ambient corresponding to a swimlane contains the process !::recv(t).t().0, exactly for this purpose. For example, the process abstraction generated for the action node “Request Order” of the activity diagram in Figure 2 is provided in Example 4.
2.3.3. Complexity of the Mapping Algorithm
3. Results
3.1. Experimental Evaluation
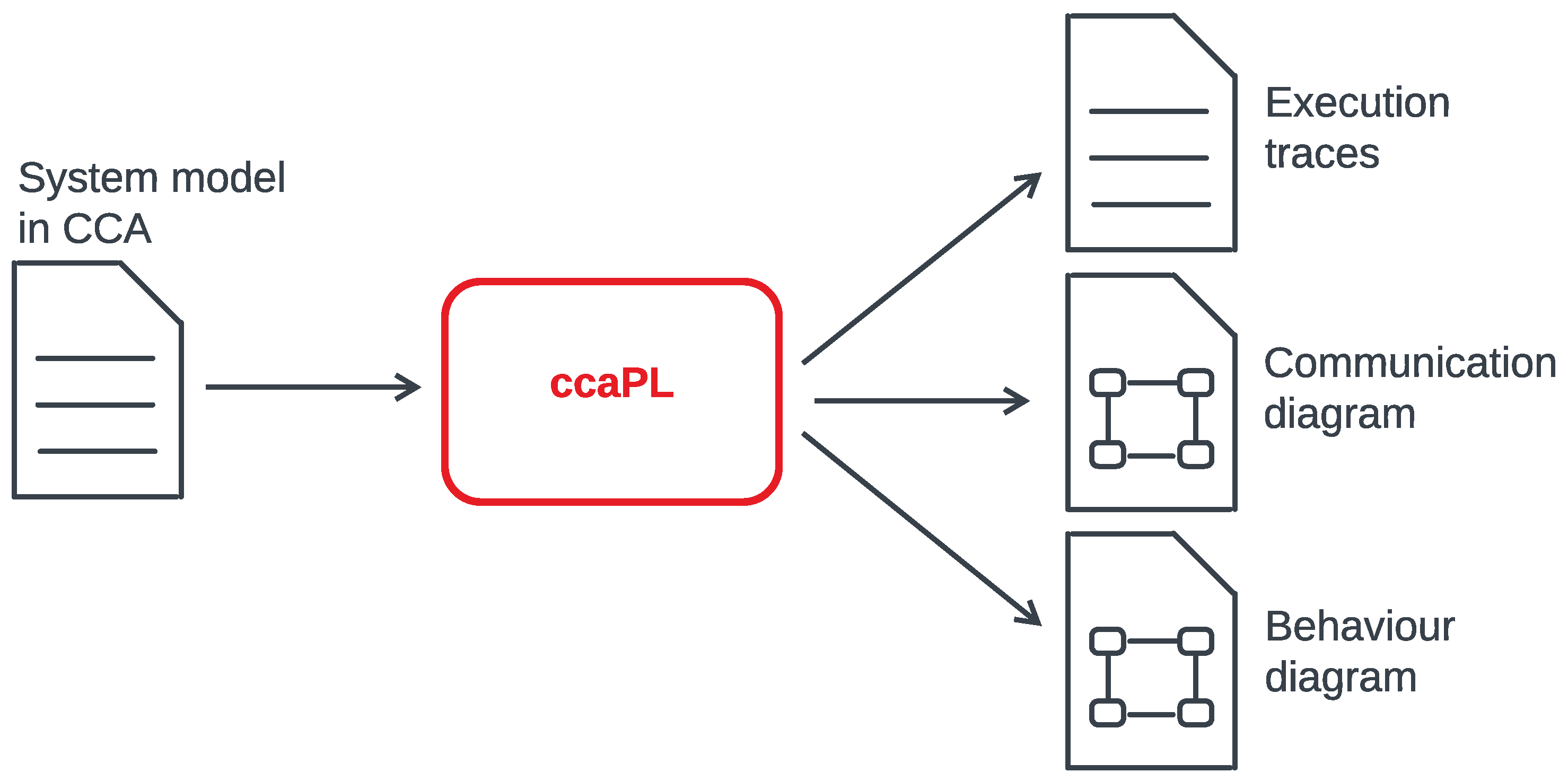
3.2. Overview of the CCA Simulator ccaPL
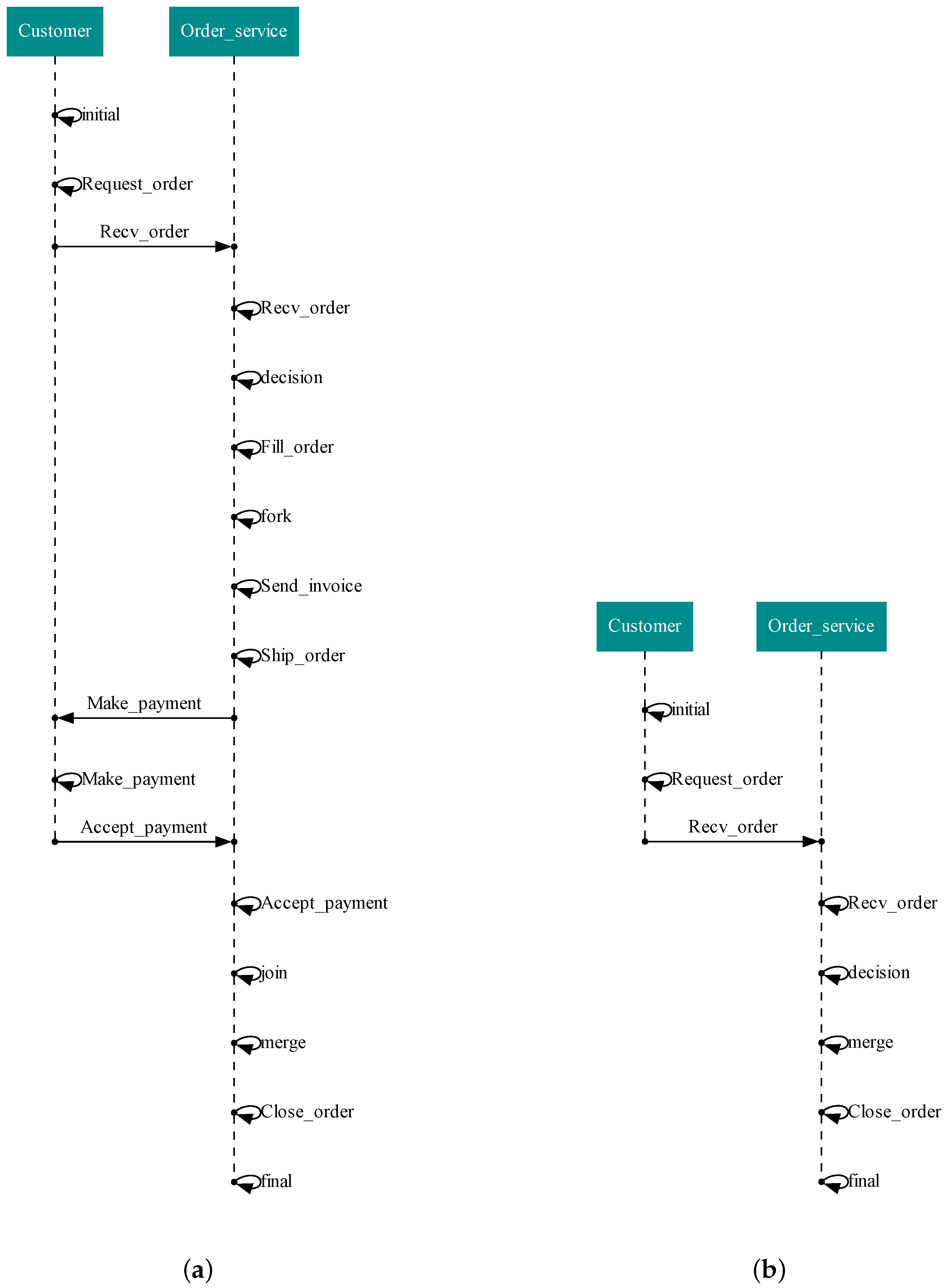
3.2.1. Textual Execution Trace
3.2.2. Communication Diagram
3.2.3. Behaviour Diagram
3.3. Overview of the CCA Runtime Verification Tool ccaRV
3.3.1. Property Specification Language
- if and r is a substring of the string .
- if and (⊧ is defined in Table 3).
- if σ
f.
- if or .
- if .
- if there exists such that and for all , .
- .
- .
- .
- .
- .
- .
- .
- , i.e., eventually f holds for ever. This formula can be used to specify safety properties, i.e., nothing bad can occur.
- , i.e., f always eventually holds. This formula can be used to specify liveness properties, i.e., always something good will eventually occur.
- , i.e., a message X has been sent/received.
- , i.e., the ambient B has received a message X.
- , i.e., the ambient A has sent a message X.
- , i.e., the ambient B has received a message X from the ambient A.
- , i.e., an activity diagram execution ends when the final node is executed.
- , i.e., ambient m is initially at ambient n, but later vanishes from n.
- , i.e., if a device d is initially in the state n, then eventually the device will change into the state m.
3.3.2. System Verification
3.4. Case Study: A Shopping Order Processing in an E-Commerce Application
3.4.1. Mapping the Activity Diagram onto a CCA Process
3.4.2. Execution of the Activity Diagram Using ccaPL
3.4.3. Runtime Verification of the Activity Diagram Using ccaRV
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. An Implementation of Algorithm 1 in Python
Appendix B. The CCA Process Generated by Algorithm 1 for the Activity Diagram of Example 1
References
- Object Management Group. OMG Unified Modeling Language (OMG UML), Superstructure. Version 2.4.1; Object Management Group: Milford, PA, USA, 2011. [Google Scholar]
- ISO/IEC 19501:2005; Information Technology—Open Distributed Processing—Unified Modeling Language (UML) Version 1.4.3. International Organization for Standardization: Geneva, Switzerland, 2005.
- Li, X.; Liu, Z.; Jifeng, H. A formal semantics of UML sequence diagram. In Proceedings of the 2004 Australian Software Engineering Conference. Proceedings., Melbourne, Australia, 13–16 April 2004; pp. 168–177. [Google Scholar] [CrossRef]
- Fernandes, F.; Song, M.A. UML-Checker: An Approach for Verifying UML Behavioral Diagrams. J. Softw. 2014, 9, 1229–1236. [Google Scholar] [CrossRef]
- Lima, V.; Talhi, C.; Mouheb, D.; Debbabi, M.; Wang, L.; Pourzandi, M. Formal Verification and Validation of UML 2.0 Sequence Diagrams using Source and Destination of Messages. Electron. Notes Theor. Comput. Sci. 2009, 254, 143–160. [Google Scholar] [CrossRef]
- Mokhati, F.; Gagnon, P.; Badri, M. Verifying UML Diagrams with Model Checking: A Rewriting Logic Based Approach. In Proceedings of the Seventh International Conference on Quality Software (QSIC 2007), Portland, OR, USA, 11–12 October 2007; pp. 356–362. [Google Scholar]
- Le, L.C. A Method for Modeling and Verifying of UML 2.0 Sequence Diagrams using SPIN. J. Sci. Technol. Inf. Secur. 2020, 1, 20–28. [Google Scholar] [CrossRef]
- Shah, K.; Grant, E. Towards Simplifying and Formalizing UML Class Diagram Generalization/Specialization Relationship with Mathematical Set Theory. In Proceedings of the 6th International Conference on Information System and Data Mining, ICISDM ’22, Silicon Valley, CA, USA, 27–29 May 2022; pp. 89–94. [Google Scholar]
- Shaikh, A.; Hafeez, A.; Wagan, A.A.; Alrizq, M.; Alghamdi, A.; Reshan, M.S.A. More Than Two Decades of Research on Verification of UML Class Models: A Systematic Literature Review. IEEE Access 2021, 9, 142461–142474. [Google Scholar] [CrossRef]
- Siewe, F.; Zedan, H.; Cau, A. The Calculus of Context-aware Ambients. J. Comput. Syst. Sci. 2011, 77, 597–620. [Google Scholar] [CrossRef]
- Siewe, F. ccaPL: A CCA Programming Environment. Available online: https://fsiewe.afrilocode.net/CCA/index.html (accessed on 23 November 2023).
- AT&T Labs-Research. Graphviz Distribution. Available online: http://www.research.att.com/sw/tools/graphviz/download.html (accessed on 23 November 2023).
- Havelund, K.; Peled, D. Runtime Verification: From Propositional to First-Order Temporal Logic. In Runtime Verification; Colombo, C., Leucker, M., Eds.; Springer: Cham, Switzerland, 2018; pp. 90–112. [Google Scholar]
- Bartocci, E.; Falcone, Y.; Francalanza, A.; Reger, G. Introduction to Runtime Verification. In Lectures on Runtime Verification: Introductory and Advanced Topics; Bartocci, E., Falcone, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–33. [Google Scholar]
- Havelund, K.; Roşu, G. Runtime Verification—17 Years Later. In Runtime Verification; Colombo, C., Leucker, M., Eds.; Springer: Cham, Switzerland, 2018; pp. 3–17. [Google Scholar]
- Broy, M.; Cengarle, M.V. UML formal semantics: Lessons learned. Softw. Syst. Model. 2011, 10, 441–446. [Google Scholar] [CrossRef]
- Daw, Z.; Cleaveland, R. An extensible formal semantics for UML activity diagrams. arXiv 2016, arXiv:1604.02386. [Google Scholar]
- Störrle, H.; Hausmann, J.H. Towards a formal semantics of UML 2.0 activities. In Proceedings of the Software Engineering 2005, Essen, Germany, 8–11 March 2005; Liggesmeyer, P., Pohl, K., Goedicke, M., Eds.; Gesellschaft für Informatik e.V.: Bonn, Germany, 2005; pp. 117–128. [Google Scholar]
- Siewe, F. Towards the Formal Analysis of UML Activity Diagrams in a Calculus of Context-aware Ambients. In Proceedings of the 2023 IEEE 47th Annual Computers, Software, and Applications Conference (COMPSAC), Torino, Italy, 27–29 June 2023; pp. 1691–1696. [Google Scholar]
- Matsumoto, A.; Yokogawa, T.; Amasaki, S.; Aman, H.; Arimoto, K. Synthesis and Consistency Verification of UML Sequence Diagrams with Hierarchical Structure. Inf. Eng. Express 2020, 6, 1–19. [Google Scholar]
- Zhou, Z.; Wang, L.; Cui, Z.; Chen, X.; Zhao, J. Jasmine: A Tool for Model-Driven Runtime Verification with UML Behavioral Models. In Proceedings of the 2008 11th IEEE High Assurance Systems Engineering Symposium, Nanjing, China, 3–5 December 2008; pp. 487–490. [Google Scholar]
- Wu, H. QMaxUSE: A new tool for verifying UML class diagrams and OCL invariants. Sci. Comput. Program. 2023, 228, 102955. [Google Scholar] [CrossRef]
- Abbas, M.; Rioboo, R.; Ben-Yelles, C.B.; Snook, C.F. Formal modeling and verification of UML Activity Diagrams (UAD) with FoCaLiZe. J. Syst. Archit. 2021, 114, 101911. [Google Scholar] [CrossRef]
- Karmakar, R.; Bera, P.; Dutta, S. FMSG: A framework for modeling and verification of a smart grid. Sadhana—Acad. Proc. Eng. Sci. 2024, 49, 131. [Google Scholar] [CrossRef]
- Halder, A.; Karmakar, R. Mapping UML Activity Diagram into Z Notation. Lect. Notes Data Eng. Commun. Technol. 2022, 96, 301–318. [Google Scholar]
- Xu, Z.; Sun, F.; Zhang, W. Research on Activity Diagram Testing method based on UML Testing Profile. In Proceedings of the 2024 6th International Conference on Electronic Engineering and Informatics (EEI), Chongqing, China, 28–30 June 2024; pp. 434–439. [Google Scholar]
- Muqsith, M.F.; Priyadi, Y.; Astuti, W. UML Artifact Extraction for Activity Diagram Based on Step Performed Using Text Mining: Case Study of SRS Sipranta Application. In Proceedings of the 2023 3rd International Conference on Electronic and Electrical Engineering and Intelligent System (ICE3IS), Yogyakarta, Indonesia, 9–10 August 2023; pp. 246–251. [Google Scholar]





| Processes | Context Expressions | ||||||
| inactivity | empty context | ||||||
| parallel composition | true | ||||||
| block | false | ||||||
| name restriction | name match | ||||||
| replication | hole | ||||||
| ambient | location context | ||||||
| context-guarded prefix | parallel composition | ||||||
| if-then | conjunction | ||||||
| … | disjunction | ||||||
| negation | |||||||
| if-then-else | spatial next modality | ||||||
| somewhere modality | |||||||
| arithmetic | |||||||
| search | |||||||
| process abstraction | |||||||
| M | Capabilities | Locations | |||||
| one transition | @ | any parent | |||||
| move into ambient n | specific parent n | ||||||
| move out of parent | # | any child | |||||
| delete ambient n | specific child n | ||||||
| receive data from | any sibling | ||||||
| send data to | specific sibling n | ||||||
| process abstraction call | locally |
| C |
| ⊧ | ||||
| C | ⊧ | if | ||
| C | ⊧ | if | ||
| C | ⊧ | if | ||
| C | ⊧ | if | C κ κ | |
| C | ⊧ | if | ||
| C | ⊧ | if | ||
| C | ⊧ | if | ||
| C | ⊧ | if | ||
| C | ⊧ | if | or |
| = | n is located at self. | ||
| = | self is located at n. | ||
| = | m is located at n. | ||
| = | self is with n. | ||
| = | n is with m. | ||
| = | current state of self is n. | ||
| = | current state of a device d is n. | ||
| = | there exists an ambient of the | ||
| form [0]. |
| (R1) | if |
| (R2) | |
| , for some i, . | |
| (R3) | |
| (R4) | |
if  . . | |
| (R5) | |
| if | |
| (R6) | |
| (R7) | |
| (R8) | |
| (R9) | |
| (R10) | , for |
| (R11) | |
| , for | |
| (R12) | |
| , for | |
| (R13) | |
| , for | |
| (R14) | |
| , for |
| UML Concepts | CCA Concepts |
|---|---|
| activity node | process abstraction |
| transition | process abstraction call |
| actor (or swimlane) | ambient |
| Activity Diagram Node | Corresponding CCA Process |
|---|---|
 |
|
 |
|
 |
|
 |
|
 |
|
| Activity Diagram Node | Corresponding CCA Process |
|---|---|
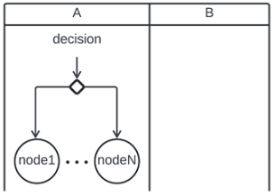 |
|
 |
|
 |
|
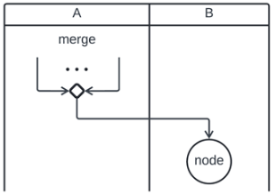 |
|
| Activity Diagram Node | Corresponding CCA Process |
|---|---|
 |
|
 |
|
 |
|
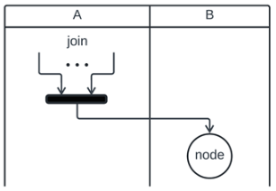 |
|
| Input Size | Execution Time (ms) | Output Size | ||
|---|---|---|---|---|
| Activity Nodes | Swimlanes | Process Abstractions | Ambients | |
| 38 | 1 | 0.40 | 38 | 1 |
| 38 | 2 | 0.40 | 38 | 2 |
| 38 | 3 | 0.40 | 38 | 3 |
| 38 | 4 | 0.41 | 38 | 4 |
| 38 | 5 | 0.44 | 38 | 5 |
| 38 | 6 | 0.46 | 38 | 6 |
| 38 | 7 | 0.48 | 38 | 7 |
| 38 | 8 | 0.51 | 38 | 8 |
| 38 | 9 | 0.54 | 38 | 9 |
| 38 | 10 | 0.56 | 38 | 10 |
| Input Size | Execution Time (ms) | Output Size | ||
|---|---|---|---|---|
| Activity Nodes | Swimlanes | Process Abstractions | Ambients | |
| 5 | 3 | 0.03 | 5 | 3 |
| 10 | 3 | 0.06 | 10 | 3 |
| 14 | 3 | 0.09 | 14 | 3 |
| 17 | 3 | 0.12 | 17 | 3 |
| 20 | 3 | 0.15 | 20 | 3 |
| 26 | 3 | 0.23 | 26 | 3 |
| 28 | 3 | 0.27 | 28 | 3 |
| 32 | 3 | 0.37 | 32 | 3 |
| 38 | 3 | 0.40 | 38 | 3 |
| 42 | 3 | 0.46 | 42 | 3 |
|
| Formula | Graphical Semantics |
|---|---|
 | |
 | |
 | |
 | |
 | |
 |
| Execution Trace | Description |
|---|---|
| “skip” | capability “skip” is executed. |
| “child to parent: A ===(X)===> B” | child ambient A sends the message X to parent ambient B. |
| “parent to child: A ===(X)===> B” | parent ambient A sends the message X to child ambient B. |
| “sibling to sibling: A ===(X)===> B” | A sends the message X to sibling ambient B |
| “local: A ===(X)===> A” | message X is sent within ambient A. |
| “ambient A moves into ambient B” | A performs the capability “in B”. |
| “ambient A moves out of ambient B” | A performs the capability “out”. |
| “delete ambient ambient A” | ambient A is deleted. |
| “binding: n -> X” | the value X is bound to the variable n by the execution of a process of the form “find n:k for P”. |
| “local call to the abstraction T in the ambient A” | A calls the local abstraction T. |
| “call to the abstraction A::T in the ambient B” | B calls abstraction T of a sibling ambient A. |
| “call to the abstraction A#T in the ambient B” | B calls abstraction T of a child ambient A. |
| “call to the abstraction A@T in the ambient B” | B calls abstraction T of a parent ambient A. |
| RFID Number | Expected Result | Actual Result |
|---|---|---|
| 0 | fail | fail |
| 70 | fail | fail |
| 100 | fail | fail |
| 101 | pass | pass |
| 166 | pass | pass |
| 199 | pass | pass |
| 200 | fail | fail |
| 201 | fail | fail |
| 300 | fail | fail |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siewe, F.; Ngounou, G.M. On the Execution and Runtime Verification of UML Activity Diagrams. Software 2025, 4, 4. https://doi.org/10.3390/software4010004
Siewe F, Ngounou GM. On the Execution and Runtime Verification of UML Activity Diagrams. Software. 2025; 4(1):4. https://doi.org/10.3390/software4010004
Chicago/Turabian StyleSiewe, François, and Guy Merlin Ngounou. 2025. "On the Execution and Runtime Verification of UML Activity Diagrams" Software 4, no. 1: 4. https://doi.org/10.3390/software4010004
APA StyleSiewe, F., & Ngounou, G. M. (2025). On the Execution and Runtime Verification of UML Activity Diagrams. Software, 4(1), 4. https://doi.org/10.3390/software4010004







