Abstract
AsymmeTree is a flexible and easy-to-use Python package for the simulation of gene family histories. It simulates species trees and considers the joint action of gene duplication, loss, conversion, and horizontal transfer to evolve gene families along the species tree. To generate realistic scenarios, evolution rate heterogeneity from various sources is modeled. Finally, nucleotide or amino acid sequences (optionally with indels, among-site rate heterogeneity, and invariant sites) can be simulated along the gene phylogenies. For all steps, users can choose from a spectrum of alternative methods and parameters. These choices include most options that are commonly used in comparable tools but also some that are usually not found, such as the innovation model for species evolution. While output files for each individual step can be generated, AsymmeTree is primarily intended to be integrated in complex Python pipelines designed to assess the performance of data analysis methods. It allows the user to interact with, analyze, and possibly manipulate the simulated scenarios. AsymmeTree is freely available on GitHub.
1. Introduction
Most proteins are part of larger families that expanded by means of gene duplications [1]. Since duplicate genes are subject to processes such as subfunctionalization and neofunctionalization [2,3,4], they are an important source of functional innovation and thus a key contribution in evolutionary adaptation. The reconstruction of gene family histories (GFHs), i.e., the identification of gene duplication, gene loss, and horizontal gene transfer (HGT) events and their placement in the species tree therefore is a prerequisite for answering many questions in evolutionary biology. In practice, however, the accurate inference of GFHs is a difficult problem in bioinformatics that, so far, has been solved partially at best.
The identification of “clusters of orthologous genes” (COGs) [5], hierarchical refinements thereof [6], as well as the pairwise orthology relation [7,8,9] are important coarse-grained representations of GFHs with a wide range of applications in evolutionary biology and phylogenetics [10]. A large portfolio of methods for orthology inference has become available, see e.g., [11,12,13] for reviews. The practical difficulties of inferring large, accurate GFHs are a severe obstacle for benchmarking computational tools and methods due to the lack of a trustworthy, fully resolved ground truth beyond simple situations and possibly a very small set of extremely well-studied gene families. Even in cases like the Hox gene clusters, not all details of the GFH have been resolved unambiguously, see, e.g., [14] for a summary.
Simulated data serve as a natural remedy and have the additional advantage that test sets can be constructed as large and as complex as desired. A second advantage of simulated data is that they can be focused to evaluate specific components of a pipeline. For instance, it is possible to separate concerns of data pre-processing, sequence comparison, or the detection of best matches from issues such as the accuracy of recognizing which reciprocal best matches do not correspond to ortholog pairs [15,16]. For some applications such as the latter, only gene tree, species tree, their reconciliation and the event types are of interest, while the generation and processing of sequence data is only a distracting overhead. AsymmeTree is therefore designed to separate the generation of the combinatorial skeleton of the GFH with weight and rate data, which we call evolutionary scenarios, from the generation of simulated sequence data.
The Python programming language has become one of the most widely used platforms in bioinformatics and in the sciences in general, and a broad spectrum of packages for phylogenetic analyses such as Bio.Phylo [17] and the ETE toolkit [18] is being actively developed. The language allows writing code that is concise, easy to read, easy to maintain, and that runs on all commonly used operating systems. A drawback of Python is its relatively low speed of execution compared to compiled languages such as C/C++. For the release version of a new method, the latter alternatives are often preferred, in particular, whenever large input data are expected. However, the (re-)implementation in such a language is usually very time-consuming. Python is therefore an ideal framework for proof-of-concept implementations that can be extensively benchmarked and validated beforehand. For these reasons, we chose Python for our library.
In order to facilitate the benchmarking of individual components of new methods and algorithms, furthermore, AsymmeTree is organized as a Python library that can be interfaced directly with target algorithms and, to our knowledge, the first tool for simulating complex GFHs that follows this paradigm instead of producing a fixed collection of output files that then need to be parsed and processed. Nevertheless, output files for individual purposes are of course available. AsymmeTree relies on our library tralda [19], which implements tree data structures and a variety of algorithms for the combinatorics of trees that frequently appear in phylogenetics, such as the construction of supertrees (e.g., [20,21]) or Bender et al.’s data structure for constant-time query of last common ancestors. The two libraries offer well-documented functions and classes that serve as the basis for easy downstream analyses. In summary, therefore, AsymmeTree allows a seamless integration into benchmarking pipelines of new methods that are implemented in Python themselves.
Our tool simulates species trees, gene trees along the species tree, and finally also sequences along trees. To that end, it implements many of the standard models used for this task but also some that are not found in (most) other simulators. For instance, we implement the innovation model [22] and the episodic birth-death process [23] for species evolution. We furthermore include the possibility to allow multifurcations in the trees on the level of both species and gene evolution. Another important novelty of our tool is the explicit modeling of neofunctionalization and subfunctionalization, i.e., the asymmetric divergence of paralogs (the name AsymmeTree alludes to this feature) after duplication. To this end, we use default parameters that we fitted to real-life data from [24]. The paralog-specific rate heterogeneity is therefore more complex than in comparable tools such as SimPhy [25] and SaGePhy [26]. Moreover, we account for essential genes by optionally prohibiting the complete extinction of the gene family within each species lineage. We account for the occurrence of additive and replacing HGT and model a transfer distance bias that prefers closer related species or genes to be chosen as recipient in an HGT event. The generated gene trees store the information about their reconciliation with the species tree. Regarding the simulation of sequences, AsymmeTree implements a variety of the standard models for nucleotide and amino acid sequence evolution, indel formation, among-site rate heterogeneity, and invariant sites. In particular, all ancestral sequences can be accessed or written to file as well as the true alignment (which is especially relevant when indels are enabled).
2. Related Work
Many different computational tools have become available in the past few decades that focus on different aspects of modeling species and/or gene family evolution and cover different ranges of tasks. Trees, of course, play a central role in any simulation of evolutionary processes. Species phylogenies are usually generated using a birth-death process [27] with constant or changing rates for speciations and extinctions. Tools that allow sampling trees conditioned on the elapsed time since the first speciation event and/or the number of extant species include the R packages TreeSim [23], its successor TreeSimGM [28], TESS [29], and castor [30]. As described in detail in Section 3.2, AsymmeTree also provides the latter functionality and, similar to castor, allows the creation of multifurcations by contraction of edges. In addition, we implement the innovation model for generating the topology of a bifurcating tree [22], a feature that is not found in any other tool.
The standard approach to evolving nucleotide or amino acid sequences along a tree are time-continuous Markov chains [31,32]. Seq-Gen [33] is a widely used tool for this task. It is written in C and supports rate heterogeneity among the individual sites of the sequence under evolution. Moreover, it allows the simulation of recombinant sequences using different trees. Seq-Gen is not able to generate insertions and deletions (indels). Well-known tools that do include models for indel formation are, e.g., Dawg [34] (for nucleotide sequences only) and INDELible [35], both of which are command line tools written in C++. Recently, the C++ tool AliSim [36] was introduced that allows the fast simulation of millions of sequences with a substantial reduction in memory usage as compared to Seq-Gen, Dawg, and INDELible. As motivated in the introduction, we focus on an easy-to-use workflow from the simulation of gene families to sequences within a single integrated package rather than optimizing our software for execution speed. Pyvolve [37] is a popular Python package with a flexible and user-friendly interface and thus, most comparable to the sequence simulation subpackage in AsymmeTree. It is able to simulate codon sequences (in addition to nucleotide and amino acid sequences). In contrast to AsymmeTree, Pyvolve does not support indels. Moreover, we shall see in Section 5 that Pyvolve is outperformed by our tool in terms of speed.
The evolution of gene families is not only shaped by speciations, but also by other phenomena such as gene duplications, losses, gene conversion, and horizontal gene transfer. Modeling these types of events and including them in the simulation is therefore crucial for a realistic assessment of phylogenetic inference and, in particular, tools that reconstruct detailed gene family histories (see, e.g., [13,38,39] for reviews). GenPhyloData [40] is written in Java and was among the first available tools considering the joint action of duplication, loss, and HGT events. In addition to the evolution of gene trees inside “host” species phylogenies, the software also generates evolution rate heterogeneity for the branches of the trees using different uncorrelated and autocorrelated models for a relaxed evolutionary clock for substitutions, and finally outputs trees with relaxed edge lengths. SaGePhy is built upon GenPhyloData [26] and implemented in Java and Python. It supports additional features such as subgene or domain level evolution inside one or multiple gene trees and the simultaneous simulation of both additive and replacing HGT, which are specified by a user-defined probability. While GenPhyloData samples species lineage recipients for HGT events uniformly at random, SaGePhy offers options for distance-biased transfers. SimPhy [25] is written in C and considers the joint action of incomplete lineage sorting (ILS), gene conversion, duplications, losses, and HGT. This is achieved by a hierarchical model that subsequently simulates (1) a species tree, (2) a locus tree (within the species tree), and (3) a gene tree (within the locus tree). SimPhy also supports a distance bias for transfer events, but no replacing HGT. Zombi [41] is written in Python and the first tool that accounts for HGT from extinct lineages of the species tree.
None of the tools GenPhyloData, SaGePhy, SimPhy, and Zombi natively implements the evolution of sequences. However, SaGePhy and SimPhy provide scripts for this task that internally call Seq-Gen and INDELible, respectively, and Zombi resorts to Pyvolve.
ALF [42] is based on the language Darwin [43] and designed for the simulation of complex genomes starting with the simulation of a species tree up to nucleotide or amino acid sequences. Features of the tool include indels, GC-content amelioration, gene duplication/loss/transfer, gene fusion and fission, as well as genome rearrangement. ALF is available both as an online version and as a stand-alone version for running simulations on a local machine. simuG [44] is designed to simulate the full suite of genomic variants from single nucleotide polymorphisms to copy number variants, inversions, and translocations. Like similar tools, its main aim is the simulation of populations, i.e., variants of a genome that are, e.g., used for benchmarking genome assembly tools, rather than macro-evolutionary distances [45,46]. Simulations of gene content and order of entire chromosomes or genomes is described, e.g., in [47].
Although our tool supports the simulation of multiple gene families along the same species tree and can produce output that collects all sequences for a given species in a single file, the focus of the tool are individual gene family histories rather than generating entire “artificial genomes”. At present, we therefore do not consider genome level events such as inversions, transpositions, tandem duplications, et cetera.
An implementation of AsymmeTree as an R package would have been an alternative to the python library, while R is the obvious choice for statistical analyses, we believe that Python is more commonly used for implementing complex methods and algorithms in bioinformatics. Furthermore, it is fairly straightforward in R to interface to Python modules, classes, and functions using the reticulate package.
3. Simulation of Species Trees and Gene Trees
3.1. Overview
Like many other tools for phylogenetic simulation [25,26,40,48], AsymmeTree generates complex gene family histories in a multilevel process that consists of the following five steps, see Figure 1: (1) A dated species tree S is simulated whose leaves correspond to extant species (thus having time stamp 0) and possibly (depending on simulation models and parameters) extinction events. (2) Along this species tree, one or multiple gene trees T are simulated using a variant of a constant-rate birth-death process [27] that considers speciations, gene duplications, and (additive) HGTs as “birth events” and gene losses as “death events”. In addition, replacing HGT and gene conversion lead to a bifurcation in one gene lineage while, at the same time, another lineage gets lost. (3) In a next step, evolution rate heterogeneity between the branches is introduced in a manner that accounts for both species effects as well as asymmetric evolution of paralogs after gene duplication. (4) The pruned gene tree is then obtained by removing all branches that lead to loss events only and suppressing all vertices that only have a single child left. The simulated species and gene trees can be visualized using AsymmeTree. An example simulation and visualization after each of steps (1)–(4) is shown in Figure 2.
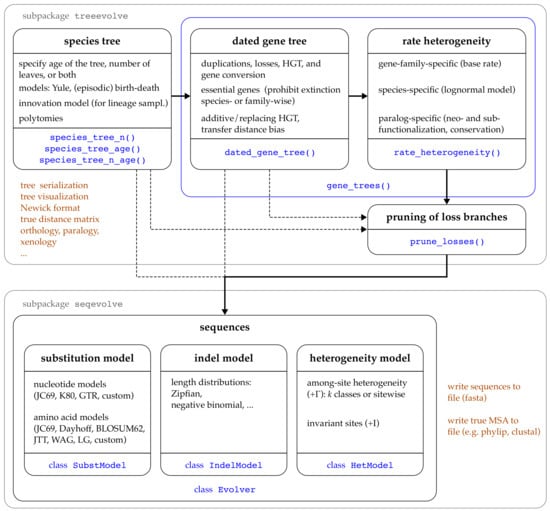
Figure 1.
Overview of the main functions and classes in AsymmeTree. The main workflow up to the simulation of is indicated by the thick arrows. Note that single steps such as introducing rate heterogeneity can be skipped. The function gene_trees() (blue box) bundles the simulation of gene trees and rate heterogeneity into one step.
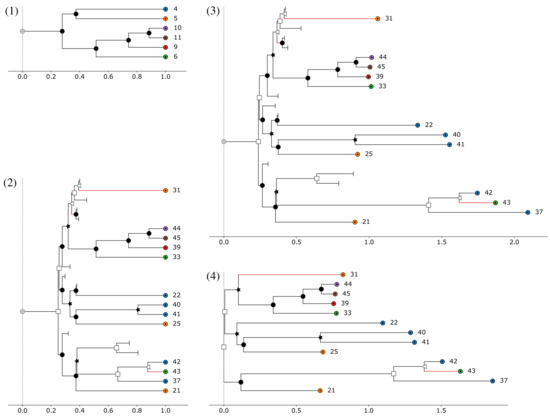
Figure 2.
Example simulation and visualization with AsymmeTree: (1) species tree, (2) dated gene tree, (3) gene tree after introduction of rate heterogeneity, and (4) pruned gene tree. The horizontal axis measures the distances of the vertices from the root of the tree. Equal colors of the leaves indicate belonging to the same species. The transferred descendant of an HGT event is marked by a red line. Symbols: ⊚—planted root, ●—speciation, □—duplication, ⊥—loss, ★—gene conversion, ◁—HGT, ⊙—leaf.
In a final step (5), nucleotide or amino acid sequences can be evolved along the gene tree using a continuous-time Markov chain, which is the standard model for this purpose [31,32]. AsymmeTree supports a variety of models for substitution, indels, and among-site heterogeneity. An overview of the basic steps is given in Figure 1.
In the following sections, the features implemented for the specific steps are described in somewhat more detail.
3.2. Species Trees
The first step in the simulation of a gene family history or even whole genomes is usually the generation of a dated rooted species tree. The species trees simulated by AsymmeTree include a so-called planted edge, i.e., the root of the tree has a single descendant, which corresponds to the first “true” speciation event of the simulated phylogeny. This accounts for the ancestral lineage in which events such as gene duplications may already occur. Available models for species evolution are the pure-birth Yule model [49], the constant-rate birth-death process (BDP) [27], and the episodic birth-death process (EBDP) [23]. The latter allows specifying “episodes” of the simulation time at the beginning of which mass extinction events or shifts of the birth and death rate occur. All rates necessary for the specific models as well as the episodes in EBDP are user-defined parameters of the function.
We provide functions for species tree sampling conditioned on
- (a)
- the number N of (extant) species,
- (b)
- the age t of the tree, i.e., the time span between the root and the (non-loss) leaves, or
- (c)
- both N and t.
We follow the methods used in TreeSim [23] to ensure accurate sampling under the specified model. In particular, we implement the backward algorithm presented in [23] to allow conditioning on N, which starts with a user-defined number N of extant species and progresses “backward in time” by drawing waiting times for speciations and extinction reducing and increasing the number of lineages, respectively, from an exponential distribution.
Under the classical birth(-death) models, the lineage for the next speciation is chosen uniformly at random among the currently extant lineages. As an alternative, we provide the option to sample the lineages using the innovation model, which captures the properties of observed phylogenies well [22]. The model associates each species lineage with a set of “features” and branching events occur as a consequence of gain or loss of a feature.
Not all combinations of options are available because some of them are specific to the different algorithms. For example, the innovation model cannot be used in combination with the backward algorithm used for conditioning on N under the (E)BDP model. Similarly, when conditioning on N and t, the resulting trees do not include the loss branches even if a death rate was specified. Table 1 gives an overview of the available combinations of options.

Table 1.
Configuration options for simulating species tree with AsymmeTree. 1,2 Times of the specified episodes are measured w.r.t. the leaves or root, respectively. 3 This is a consequence of the backward algorithm applied for (E)BDP. 4 The applied method for conditioning on N and t does not explicitly simulate the loss events [23].
It is usually assumed that cladogenesis proceeds by a series of bifurcations and that polytomies in estimated gene or species trees are “soft”, i.e., an artifact of insufficient data [50,51,52]. As a consequence, considerable efforts have been put into resolving persisting multifurcations in the tree of life, see, e.g., [53,54]. However, there is also evidence of “hard” polytomies, i.e., the generation of more than two descendant lineages from a parental species at a time [55,56,57]. We implement two models for introducing polytomies into species trees, both of which start from a bifurcating tree that was generated using one of the methods described above. The first possibility takes a probability p as input. Each inner edge (thus excluding the edges incident with leaves and the planted root) is then considered independently and contracted with probability p. The second possibility takes a fixed proportion of inner edges to be contracted as input, and, additionally, allows for specifying a bias such that edges whose endpoint have a smaller divergence time t have a higher chance to be contracted. More precisely, for the available options “inverse” and “exponential”, resp., the values and are used as weights in the sampling process, where is a user-defined intensity.
3.3. Gene Trees
Gene trees are simulated along a species tree using a constant-rate birth-death process [27] where rates for the four types of events duplication, loss, HGT, and gene conversion are user-defined. To this end, the user must specify rates for the four event types which serve as parameters for exponential distributions from which waiting times until the next events are drawn. By setting the respective rate to zero, an event type is disabled completely. The simulation starts with a single gene in the root of the species tree and proceeds stepwise in time towards the leaves by drawing waiting times until the next event and lineages in which these events take place. At each point in the simulation, the total rate is given by the sum of the four event types over the currently existing lineages in the gene tree under construction. Hence, the simulation of all gene lineages progresses synchronously. This avoids difficulties arising by the fact that some processes, such as replacing HGT as introduced below, introduce dependencies between the gene lineages. In particular, with this method, it is not necessary that simulated branches have to be invalidated as a consequence of an event in a lineage that is processed later in the simulation as it, e.g., occurs in [26].
In addition to the randomly-occurring events, speciations and species extinctions (which are determined by the species tree and therefore fixed) are included as branching and loss events, respectively, and affect all currently existing lineages in the respective species lineage. In case of a speciation, each offspring species receives one copy of each original gene lineage. On the other hand, the extinction of a species leads to loss of all of its gene lineages. If a waiting time for a duplication, loss, or HGT event is drawn such that the next event in the species tree occurs earlier, then this waiting time is discarded, the time is updated to the next species tree event, and the latter is executed.
In the following, we discuss the implementation of gene duplications, losses, HGT, and gene conversion in some more detail as well as the options for customizing the simulation that are related to these types of events.
Gene duplications. If a duplication event is drawn for some gene lineage, then the original lineage is replaced by offspring lineages (that are placed in the same species lineage). Allowing for refers to introducing polytomies on the level of gene evolution, that is, other than the multifurcations that are inherited from a (non-binary) species tree. In [16], we discussed a delayed escape from an originally concerted evolution of tandemly repeated genes [58,59] as a possible biological mechanism giving rise to (hard) polytomies at duplication vertices. Moreover, inference from biological sequences is often not able to resolve the exact chronological order of events that occurred very shortly after one another (soft polytomies). To assess a possible sensitivity of new methods to multifurcating duplication events, we model the latter by a (user-defined) parameter of a Poisson distribution from which the number k of additional copies is drawn. The default setting is , in which case no polytomies are introduced on gene tree level.
Gene losses. A loss event introduces a new leaf vertex into the gene tree which is marked as a loss event and removes the lineage from the set of currently active lineages (i.e., for which events are drawn). The final gene tree, therefore, contains as leaves the extant genes (that reached the extant species of the species tree), as well as loss events that were generated as a consequence of (a) loss event drawn for specific gene lineages, (b) extinction of species, and (c) replacing HGT (see below). As for the species tree, the complete extinction of a gene family through losses will in general not be a desirable outcome of the simulation. We therefore provide the option to prohibit the complete extinction of all paralogs in each species or, less restrictively, the extinction of all members of the gene family. We implement this feature in the simulation by temporarily setting the loss rate in a gene lineage to zero whenever this gene is currently the only surviving member of the family in its species lineage or the only overall surviving member, respectively. The former option can in particular be viewed as a way of modeling essential genes [60,61], whose complete loss is lethal but paralogs can compensate the loss of single family members in a species.
Horizontal gene transfer. Horizontal gene transfer (HGT) refers to the phenomenon that genetic material is transferred from one species into another, coexisting species. Depending on the exact mechanism, a transferred sequence may replace a homologous sequence in the recipient species (“replacing HGT”) or be integrated into the genome in an additive way (“additive HGT”) [62]. There is evidence that both modes of transfer indeed occur commonly [63,64], and first inference methods that can distinguish between them have been developed [65]. To account for replacing and additive HGT, AsymmeTree allows specifying the probability that an HGT event is replacing (rather than additive). Whenever this is the case, a gene lineage is chosen among the contemporary lineages and a simultaneous loss event is executed for this lineage. In case of an additive HGT, a species lineage (rather than a gene lineage) is chosen among the lineages that exist at the time of the event (excluding the species lineage that harbors the original gene).
Similar as SaGePhy [26] and Zombi [41], our software implements three options for a transfer distance bias, which means that closer related gene lineages (resp. species lineages in the case of additive HGT) have a higher probability to be replaced (resp. act as recipient species). The default option is no such bias, in which case the recipient gene or species lineage is chosen uniformly at random. The two other available options are “inverse” and “exponential”, in which case and are used as weights for the sampling where is the elapsed time since the last common ancestor of the transferred and the candidate replaced gene or, in case of an additive HGT, the last common ancestor of the origin and the candidate recipient species , and is a user-defined intensity. We note that, in empirical studies, a log-linear relationship of HGT frequency and phylogenetic distance was observed in archaea [66,67], indicating that the “exponential” mode models biological reality best.
Similar to Zombi [41], AsymmeTree accounts for gene transfer from species that go extinct later in the evolution since the supplied species tree may contain loss branches (as e.g., generated by the BDP model) and the genes in these branches take part in the simulation as all others until their species gets extinct.
Gene conversion refers to the replacement of a gene by a homologous gene in the same species. Therefore, it is modeled similarly to replacing HGT, except that the gene to be replaced is sampled from the contemporary homologs in the same species. In particular, analogous options for preferring closer-related genes are available. Note that a gene conversion event can only occur if at least one other contemporary homolog exists in the respective species lineage. Therefore, the effective rate for this type of event will in general be lower than the one specified by the user.
3.4. Evolution Rate Heterogeneity
Directly after simulating the gene trees, the distances in these trees, i.e., the lengths of the edges , are equal to the divergence times between u and v. The trees therefore follow a strict molecular clock [68]. However, this property is quite restrictive and usually not satisfied for biological data in general, see e.g., [69]. Different approaches to modeling rate heterogeneity have been implemented in existing tools. For example, SimPhy [25] samples different types of rate multipliers from Gamma distributions. Species-specific rate multipliers account for differences between species that arise, e.g., as a consequence of different body sizes, metabolic rates, and generation times [70,71], whereas gene-family- and paralog-specific rate multipliers capture for example differences in the selective pressure acting on individual genes. Changes of the selective pressure occur e.g., as a consequence of gene duplication. The best-known models for the divergence behavior of paralogs after duplication are neofunctionalization [1] and subfunctionalization [2], see also [72] for a review. The neofunctionalization model predicts that, after duplication, one copy acquires new functions through gain-of-function mutations and thus a higher evolution rate. Subfunctionalization, on the other hand, predicts that both paralogs evolve faster after the duplication event. ALF [42] accounts for the two phenomena by temporarily altering the mutation rate in one or both paralogs by a user-defined amount.
In AsymmeTree, we sample rate multipliers for the three different sources, similar as SimPhy [25]. In case of the paralog-specific heterogeneity, however, we explicitly account for neofunctionalization and subfunctionalization (described below). We assign to each edge of the gene tree (a) a gene-family-specific baseline rate, (b) a species-specific rate depending on the edge of the species tree into which is embedded, and (c) a series of paralog-specific rates and the time periods at which each of these rates is active. In the end, the final evolutionary distance of v from its ancestor u is obtained as the product of the divergence time between u and v and the three rate multipliers. If there are multiple periods in (c), we calculate the sum of the piecewise products according to these periods. In the following, we describe in more detail how the rate multipliers are obtained.
(a) Gene-family-specific rate heterogeneity. Gene-family-specific effects are modeled as a baseline rate that is assigned to the gene families and the same for all lineages of the gene family. The function gene_trees() simulates a user-defined number of gene trees (including rate heterogeneity) and allows to specify a distribution for the baseline rate. Available distributions are, e.g., uniform (over a user-defined interval), Gamma, and exponential.
(b) Species-specific rate heterogeneity. Deviations from a molecular clock makes estimation of divergence times and the dating of species challenging. Several “relaxed molecular clock models” to tackle this task have been proposed in the literature and their relative fitness has been assessed, e.g., in [73]. Therein, the authors come to the conclusion that autocorrelated models, which capture the idea that closely related evolutionary lineages evolve at similar rates, should be preferred in the estimation of divergence times. The lognormal model [74] is one of the most popular models of this type and implemented in AsymmeTree for the assignment of rate multipliers for the lineages of a species tree.
The lognormal model as presented in [74] assumes that, given an edge in the species tree (where u is closer to the root) and the logarithm of the rate at u, the logarithm of the rate at v has a normal distribution with variance , where is a parameter and t is the divergence time between u and v. We therefore assign rate multipliers to the nodes of the species tree S as follows: The root is assigned the rate 1. Then, we process the edges of S in a top-down order and sample the logarithm of the rate at v from a normal distribution with variance and a mean normalized in such a way that the expected value of is equal to the (already assigned) rate at u. The latter avoids a bias towards higher or lower rates. For simplicity, the rate for edge is then calculated as . The user can specify the parameter , where setting disables the species-specific rate heterogeneity. Higher values of result in smaller autocorrelation, i.e., the similarity of the rates in closely related species lineages decreases.
(c) Paralog-specific rate heterogeneity. We consider the modes neofunctionalization, subfunctionalization, and additionally conservation for the behavior of evolution rates of paralogs after a duplication event. There are not many studies that attempt to determine the extent of asymmetric evolution rates. Byrne and Wolfe [24] examined pairs of paralogs in two yeast species that arose as a consequence of whole-genome duplication (WGD). The authors introduced the parameter as measure of asymmetry, where and are the distances of paralogs a and b from the WGD event. The placement of the WGD event is determined using a homologous gene in an outgroup species that diverged before the WGD event as indicated in Figure 3. By definition, the -value always satisfies . Fitting a Gamma distribution to the values of X observed for paralog pairs in yeast yields and for the shape and scale parameters, respectively, see Figure 7 below.
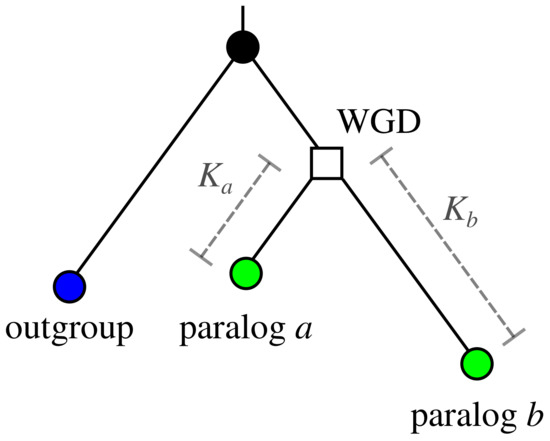
Figure 3.
Definition of the branch lengths and of a pair of paralogs used in the definition of the asymmetry parameter [24]. The ancestor, in this case the yeast WGD event, is indicated by the the square symbol.
The procedure implemented in AsymmeTree aims at modeling -values. It is already described in a rather technical fashion in [15]. In brief, we traverse the gene tree forward in time and randomly assign to each encountered duplication vertex one of the three modes (with user-defined sampling weights). In case of neofunctionalization, exactly one descendant paralog is marked with the status conserved and the others are marked with the status divergent, whereas in case of subfunctionalization and conservation, all descendant paralogs are marked with divergent and conserved, respectively. To the divergent lineages, a rate multiplier is assigned where x is drawn from a user-defined distribution. As default, we use the Gamma distribution fitted to the yeast data set. In case of a speciation event, the descendant lineages inherit the status and rate from their parent. Moreover, if a divergent lineage becomes the only surviving lineage in its species (because of loss of another lineage), its status is changed back to conserved and the rate multiplier is reset to 1. Note that, therefore, a single edge in the gene tree may be associated with multiple time periods with different rates.
3.5. Pruning of Loss Branches
The gene tree as simulated at this point may still contain branches that only lead to loss events. For downstream analyses and the simulation of sequences, however, these branches may not be of interest. AsymmeTree therefore implements the function prune_losses() which removes all of these loss branches (as well as the planted root), and suppresses all vertices that become superfluous by this procedure, i.e., vertices with a single child.
4. Simulation of Sequences
4.1. Overview
AsymmeTree supports the simulation of nucleotide and amino acid sequences using time-continuous Markov models, as usually applied for this purpose, see, e.g., [31,32,75] for textbooks. In the previous sections, we have described the simulation of (pruned) gene trees whose edges are endowed with a phylogenetic distance. Starting from the root, sequences are evolved towards the leaves of the tree where the branches are processed independently. The distance attribute of an edge always marks the expected number of substitutions per site that occur along this edge. We remark that PAM distances as, e.g., used optionally in ALF [42] are not supported in AsymmeTree. In addition, the distance of an edge (rather than the divergence time) is also used as the duration of the Markov process in which insertions and deletions are drawn.
The simulation of sequences (managed by the class Evolver in the subpackage seqevolve) takes as input a simulated gene tree, a substitution model, and optionally models for indel formation and among-site substitution rate heterogeneity. We will discuss the three types of models in the following sections. Moreover, it is possible to either specify a start sequence that is assigned to the root of the tree or alternatively the length of the sequence of the root. In the latter case, a start sequence of the specified length is generated at random based on the equilibrium frequencies of the substitution model. Note that, if indels are enabled, the lengths of the sequences will in general change during the simulation and vary between the branches of the tree.
4.2. Substitution Model
A substitution model usually comprises an exchangeability matrix S and a vector containing the equilibrium frequencies of the alphabet of nucleobases or amino acids. From this, the rate matrix Q can be computed as where [32]. The substitution probability matrix, in turn, is given by where t is the distance associated with an edge, possibly multiplied with a rate multiplier accounting for among-site rate heterogeneity (see Section 4.4). In the simulation, therefore, P has to be computed for each combination of distances (and thus edges) and rate multipliers. A single substitution probability matrix is computed efficiently by AsymmeTree using matrix diagonalization based on SciPy [76]. However, if there is a large number of classes of sites such that each class has a different rate multiplier or if the option for sitewise heterogeneity is enabled, the number of matrices that have to be computed can become very large, thus slowing down the simulation.
For this case, we evolve sequences using the Gillespie algorithm [77], which does not proceed edge-wise from one vertex to one of its children, but instead proceeds in a more fine-grained fashion. More precisely, it processes each site of the sequence individually and mutates it in a Markov process whose duration is the length of the edge. We remark that, e.g., INDELible [35] also offers both variants.
The following models for nucleotide substitution are currently available: Jukes & Cantor [78], Kimura [79], and the general time-reversible model (GTR) [80]. For the evolution of amino acid sequences, AsymmeTree includes options for the following models: Jukes & Cantor [78], Dayhoff [81], BLOSUM62 [82], JTT [83], WAG [84], and LG [85]. In [86], advances in the field of substitution models are surveyed and more sophisticated, data-specific models are advocated, see also [87]. Asymmetree is already able to utilize such recent developments since it allows the specification of custom substitution models for both nucleotide and amino acids in PAML [88] format.
4.3. Indel Model
Similar as substitutions, the formation of insertions and deletions is modeled as a time-continuous Markov process. For each edge of the gene tree, the duration of this process is given by the phylogenetic distance associated with the edge. In addition, the user specifies the per-site rates for the occurrence of insertions and deletions. The length of an indel is drawn from a user-defined distribution. Zipfian or negative binomial distributions are typically used for this purpose [34,42]. However, we also allow for the specification of, e.g., a constant value or a uniform distribution over an interval and provide the option to determine a minimal and maximal length at which the distributions are truncated. As default, we follow [42] and use a Zipfian distribution with as value of its single parameter, which was fitted to gaps in MSAs of real-life sequence in [89].
In case of an insertion, the new sites are drawn randomly from the alphabet of the specified substitution model weighted by the equilibrium frequencies. Given the current length l of the sequence, the starting position of an insertion can be drawn uniformly from the interval . In contrast, Cartwright [34] pointed out that placing a deletion is more complicated since placing it entirely within the sequence results in a higher deletion rate in the middle of the sequence than at the ends. We therefore follow the approach implemented in Dawg [34], which assumes that the sequence is embedded into a larger sequence. This ensures that deletions occur uniformly along the sequence. We note, however, that this introduces a bias towards shorter deletions and thus a lower expected value than that of the specified length distribution.
4.4. Heterogeneity Model
Selective pressure usually varies among the sites of a sequence under evolution. To model this, rate factors r for single sites or groups of sites are commonly drawn from a Gamma distribution (-model) with mean 1 and parameter [34,35,42,90] (where smaller values for correspond to higher heterogeneity). The rate matrix is then used instead of Q.
AsymmeTree supports two modes of the -model. The user can specify a number of classes to which the sites are assigned uniformly at random such that sites of the same class share a common factor r. Alternatively, sitewise heterogeneity can be enabled, i.e., every site obtains an individual rate multiplier. In both cases, the rate or class membership is inherited from the parent sites (i.e., the corresponding site in the parental lineage) during the evolution along a tree. Note that, by default, the Gillespie algorithm is used if among-site rate heterogeneity is enabled.
Another aspect of among-site heterogeneity is modeling invariant sites (-model), i.e., sites that never mutate at all as a result of very strong selective pressure [91]. To this end, the (expected) proportion p of invariant sites can be specified by the user, and each site obtains the status invariant with probability p. Note that affects the overall substitution rate. In particular, the rates of the non-invariant sites are not adjusted to compensate the decreased number of expected substitution over all sites.
4.5. True Alignment
Once the sequences have been simulated along the tree, they can be written without gaps to a file in the fasta format. In addition, AsymmeTree can construct the “true” multiple sequence alignment, i.e., introduce gaps such that the sites in one column are descendants of one another or a common site in an ancestral sequence. Constructing the true alignment is a trivial task if indels were not enabled. In the general case, AsymmeTree achieves this by assigning unique identifiers to new sites, which are then inherited by descendant sequences. The function true_alignment() of an Evolver instance can be used to construct the true MSA and optionally write it into a file. Supported formats for the MSA are, e.g., phylip and clustal.
5. Benchmarking and Validation
A series of simulation experiments was conducted to validate that AsymmeTree indeed generates evolutionary scenarios in accordance with theoretical predictions. To validate the implementation of species tree simulation conditioned on the number N of extant species, we simulated trees with AsymmeTree and TreeSim using the same combination of parameters, and compared the distributions of the tree age. There are no significant difference between the two tools (Figure 4).
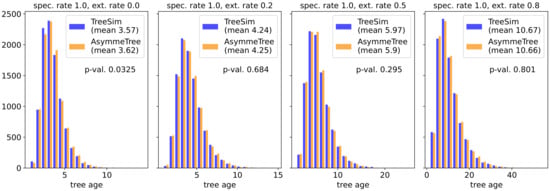
Figure 4.
Simulations of species trees conditioned on the number N of extant species. The histogram compares the distribution of the tree age with the age of trees that were simulated with TreeSim [23] with the same parameters. The speciation rate was fixed to 1 and for each extinction rate (columns), 10,000 trees with 20 extant species were generated with each of the two tools. The distributions were compared using the standard non-parametric Mann–Whitney U test. The resulting p-values are indicated.
Different options for a distance bias for selecting the replaced gene or the recipient species in HGT events affect the elapsed time between an HGT event and the last common ancestor of the two involved gene or species lineages, respectively. Scenarios simulated with the “inverse” and the “exponential” bias, as expected, result in a much lower average elapsed time compared to scenarios without distance biases. The effect is stronger in case of the “inverse” bias (Figure 5).
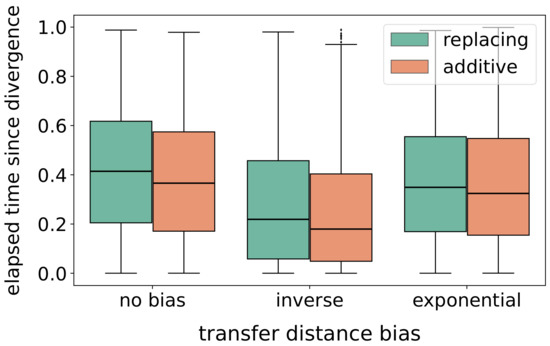
Figure 5.
Validation of the transfer distance bias. In total, 800 gene family histories were simulated each consisting of a dated species tree (no. of leaves drawn randomly from the interval ) and a dated gene tree (different combinations of duplication, loss, and HGT rates were used). The probability that an HGT event is replacing was set to . For replacing and additive HGT, the box plots represent the divergence times of the transferred and the replaced gene lineages and the divergence time of the origin and recipient species, resp., at the time of the respective HGT event.
We validated the implementation of the lognormal model for (species-specific) evolution rate heterogeneity. To this end, we simulated 10,000 species trees and assigned rates to the lineages in these tree using different values for the variance multiplier . Figure 6 shows that the assignment process along the tree is not biased towards increasing or decreasing rates and that the logarithm of the rates assigned to the leaves is indeed normally distributed. The effect of paralog-specific rate heterogeneity was investigated by measuring the -values of paralog pairs in the same species. The other two sources of rate heterogeneity were disabled for this purpose. Figure 7 (right panel) shows the distribution of the -values obtained from 5000 simulated scenarios. The Gamma distribution re-fitted to these values is very similar to the distribution used for sampling the paralog-specific rate factors, i.e., the distribution fitted to the yeast data from [24] (left panel).
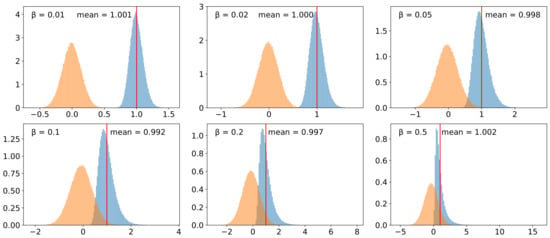
Figure 6.
Validation of the lognormal model for introducing species specific evolution rate heterogeneity. For each of the considered values of , 10,000 species trees were generated using the Yule model (duration , birth rate ). The plots show (normalized) histograms of the absolute values (blue) and the logarithm (orange) of the rate multipliers that were assigned to the leaves of the trees.
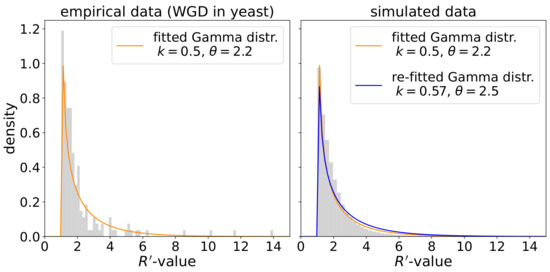
Figure 7.
Left: Histogram of -values measured for paralog pairs in yeast taken from [24]. In addition, the probability density function of the fitted Gamma distribution is shown. Right: Histogram of -values that were extracted from 5000 simulated scenarios where all paralog pairs in the same species were taken into account. The following parameters were used for all scenarios (default if not specified): species tree: 30 leaves, time span of 1, innovation model; gene tree: duplication and loss rate ; rate heterogeneity: Gamma distribution and , only neofunctionalization. The Gamma distribution that was re-fitted to the extracted -values is shown in blue.
Finally, we validated the simulation of sequence evolution represented by two models of nucleotide substitution (JC69 and K80) and two empirical model for amino acid substitution (WAG and JTT). To this end, we first simulated 100 gene trees, each having 50 leaves and covering a time span of one unit. After introducing rate heterogeneity which sets the length of the tree edges and thus the expected number of substitutions per site, we simulated sequences of length 500 nucleotides or amino acids (without indels) along these trees. For the two nucleotide models, we used the well-known formulas to calculate the pairwise maximum-likelihood distances of the sequences (see, e.g., [32]). In case of the amino acid sequences, we used TREE-PUZZLE [92] to re-estimate the distances under the same model that was used for their simulation. In Figure 8, the re-estimated pairwise distances are plotted against the true distances, i.e., the sum of the edge lengths on the path between the two respective genes. In addition, we simulated sequences along trees consisting of a single edge and assessed the effect of the length of this edge and the length of the sequence on the distance re-estimation. Figure 9 and Figure 10 show the results of this analysis for the two alternative algorithms for sequence evolution, that is, computation of the substitution probability matrix and the Gillespie algorithm, respectively. The two figures show no qualitative difference, however, we note that the Gillespie version was slightly slower on our machine. The formulas for computing the distance is not applicable if too many nucleotide substitutions occurred. Such instances are not included in the box plots, which explains the bias of the nucleotide models towards smaller estimated distances. The proportion of instances that had to be excluded as a consequence of this issue is also indicated in the plots. In contrast, the re-estimation of distances of the amino acid sequences does not yet show such a saturation effect even for the highest considered value of 5 expected substitution per site. As expected, the variance of the re-estimated distances decreases when the sequences become longer.
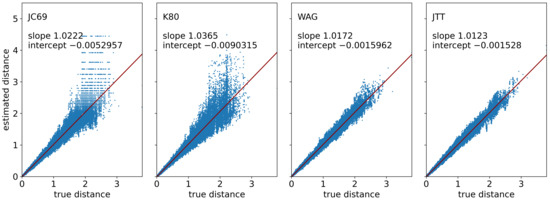
Figure 8.
Re-estimation of phylogenetic distances from simulated sequences. We generated 100 species trees each containing 50 leaves and covering a time span of one unit with the innovation model, and generated one gene tree along each of them (without duplications, losses, and HGT). After introducing species-specific rate heterogeneity with a variance parameter , we simulated sequences of length 500 along these trees for the two nucleotide substitution models JC69 and K80 and the two amino acid substitution models WAG and JTT. The distances were then re-estimated using a closed formula (JC69 and K80) [32] or, in case of the empirical models WAG and JTT, using TREE-PUZZLE [92].
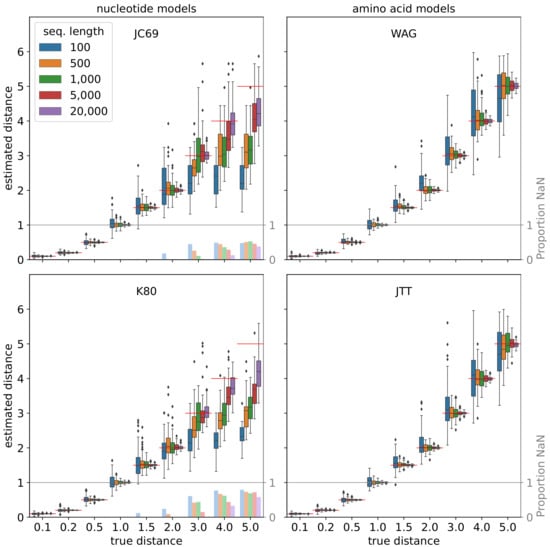
Figure 9.
Re-estimation of phylogenetic distances from sequences that were simulated using the substitution probability matrix. For each combination of a substitution model (subpanels), distance d (x-axis), and sequence length (colors), we randomly generated 100 sequences based on th equilibrium frequencies and evolve them along a tree consisting of a single edge of length d. The distances were then re-estimated using a closed formula (JC69 and K80) [32] or, in case of the empirical models WAG and JTT, using TREE-PUZZLE [92]. In the former case, the distances may be undefined (“NaN”). The red lines and the bars in faded colors indicate the true distance and the proportion of instances for which this is the case, respectively.
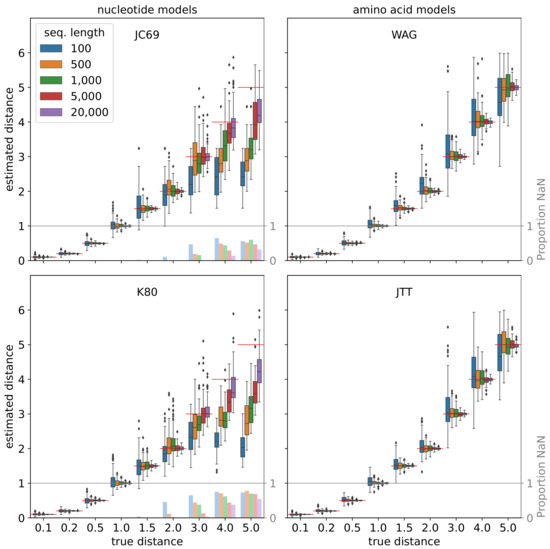
Figure 10.
Re-estimation of phylogenetic distances from sequences that were simulated using the Gillespie algorithm. See caption of Figure 9 for details.
AsymmeTree simulates species trees with 10,000 extant species and a gene family along this tree (with moderate duplication and HGT rates) typically in a few seconds. As a potential time-critical step, we benchmarked the simulation of sequences in some more detail and compared AsymmeTree to other tools for this task. Not surprisingly, Figure 11 shows that our Python package cannot compete in terms of running times with software that is written in C or C++ such as Seq-Gen [33] or INDELible [35]. However, it clearly outperforms the Python package Pyvolve [37].
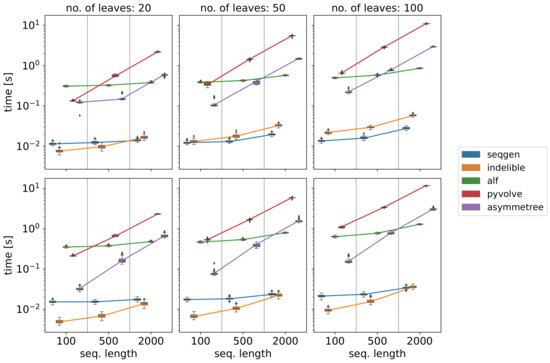
Figure 11.
Running time comparison of various tools for sequence evolution. For each combination of number of leaves (columns) and sequence length (x-axis), 100 (species) trees were simulated that cover a time span of 1 and amino acid sequences were evolved along these trees using the substitution model WAG [84] and each of the tools Seq-Gen [33], INDELible [35], ALF [42], Pyvolve [37], and AsymmeTree. In the top row, rate heterogeneity was disabled. In the bottom row, the model was used with and five classes. In the latter case, the Gillespie algorithm was used if available (i.e., in INDELible and AsymmeTree). The measures running time includes reading the tree from file (and reading a configuration file for some tools), simulation of the sequences, and writing them into a file in fasta format. All benchmarks were run on an off-the-shelf laptop (Intel® Core™ i7-4702MQ processor, 16 GB RAM, Ubuntu 20.04).
6. Availability
AsymmeTree is entirely written in Python. It requires Python version 3.7 or higher and relies on the packages NumPy, SciPy, NetworkX, Matplotlib, and tralda. It is hosted on GitHub (https://github.com/david-schaller/AsymmeTree (accessed on 6 April 2022)) and distributed under the license GNU GPL v3. The GitHub repository also provides a detailed manual and a documentation generated from the source code. For an easy installation, it is also available on PyPI (https://pypi.org/project/asymmetree/ (accessed on 6 April 2022)).
7. Concluding Remarks
AsymmeTree is a (pure-)Python package for generating complex gene family histories, including species and gene tree, as well as, sequence evolution. The simulated data are primarily intended to be used as “ground truth” in the assessment of new tools developed by the phylogenetics research community. To our knowledge, it is the first package of its kind that is implemented as a library rather than a stand-alone tool. It is therefore ideally suited for large-scale benchmarking of new algorithms and workflows, where performance assessment over a broad spectrum of parameter combinations is required. Earlier versions of AsymmeTree have been employed in a series of studies to evaluate the potential of best match graphs for the reconstruction of orthology [15,16] and to explore the information contained later-divergence-time graphs—a formal model for indirect methods of HGT inference [93]. The experiences with these applications have helped shape the current version of AsymmeTree and demonstrated the advantage of the organization as a library for automatized benchmarking purposes.
AsymmeTree focuses on gene family histories and is not intended for applications that require the detailed simulation of complete genomes. It appears possible, however, to extend AsymmeTree both towards smaller and larger scales: Local genomic organization could be introduced by adding a data layer that keeps track of local gene clusters and their internal order. Such an extension could be useful, e.g., to assess the added value of synteny data in orthology detection [94,95]. Using the fact that the gene trees simulated by AsymmeTree are dated, it would be possible to simulate a “domain tree” within the gene trees in much the same way as gene trees are constructed along a species tree. Such an extension could be used, e.g., to assess tools that evaluate (protein) domain evolution [96].
Author Contributions
D.S. implemented the library as well as the validation experiments. All authors contributed equally to concept design of the software and the writing of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded in part by the Deutsche Forschungsgemeinschaft (DFG), proj.no. STA 850/51-2 and the German Federal Ministry for Education and Research (de.NBI/RBC, grant no. 031A538B).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The Python package as well as scripts to re-run the validation experiments are available on GitHub (https://github.com/david-schaller/AsymmeTree (accessed on 6 April 2022)).
Acknowledgments
We thank Alitzel López Sánchez, Manuela Geiß, and Nicolas Wieseke for fruitful discussions in early stages of the software’s development.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| (E)BDP | (episodic) birth-death process |
| GFH | gene family history |
| HGT | horizontal gene transfer |
| MSA | multiple sequence alignment |
References
- Ohno, S. Evolution by Gene Duplication; Springer: Berlin/Heidelberg, Germany, 1970. [Google Scholar] [CrossRef]
- Force, A.; Lynch, M.; Pickett, F.B.; Amores, A.; Yan, Y.L.; Postlethwait, J. Preservation of duplicate genes by complementary, degenerative mutations. Genetics 1999, 151, 1531–1545. [Google Scholar] [CrossRef] [PubMed]
- Lynch, M.; Conery, J.S. The evolutionary fate and consequences of duplicate genes. Science 2000, 290, 1151–1155. [Google Scholar] [CrossRef] [PubMed]
- Birchler, J.A.; Yang, H. The multiple fates of gene duplications: Deletion, hypofunctionalization, subfunctionalization, neofunctionalization, dosage balance constraints, and neutral variation. Plant Cell 2022, 34, 2466–2474. [Google Scholar] [CrossRef]
- Tatusov, R.L.; Koonin, E.V.; Lipman, D.J. A genomic perspective on protein families. Science 1997, 278, 631–637. [Google Scholar] [CrossRef]
- Zahn-Zabal, M.; Dessimoz, C.; Glover, N.M. Identifying orthologs with OMA: A primer. F1000Research 2020, 9, 27. [Google Scholar] [CrossRef] [PubMed]
- Fitch, W.M. Distinguishing homologous from analogous proteins. Syst. Zool. 1970, 19, 99–113. [Google Scholar] [CrossRef]
- Roth, A.C.J.; Gonnet, G.H.; Dessimoz, C. Algorithm of OMA for large-scale orthology inference. BMC Bioinform. 2008, 9, 518. [Google Scholar] [CrossRef]
- Hellmuth, M.; Hernandez-Rosales, M.; Huber, K.T.; Moulton, V.; Stadler, P.F.; Wieseke, N. Orthology Relations, Symbolic Ultrametrics, and Cographs. J. Math. Biol. 2013, 66, 399–420. [Google Scholar] [CrossRef]
- Gabaldón, T.; Koonin, E.V. Functional and evolutionary implications of gene orthology. Nat. Rev. Genet. 2013, 14, 360–366. [Google Scholar] [CrossRef]
- Altenhoff, A.M.; Boeckmann, B.; Capella-Gutierrez, S.; Dalquen, D.A.; DeLuca, T.; Forslund, K.; Huerta-Cepas, J.; Linard, B.; Pereira, C.; Pryszcz, L.P.; et al. Standardized benchmarking in the quest for orthologs. Nat. Methods 2016, 13, 425–430. [Google Scholar] [CrossRef]
- Nichio, B.T.L.; Marchaukoski, J.N.; Raittz, R.T. New Tools in Orthology Analysis: A Brief Review of Promising Perspectives. Front. Genet. 2017, 8, 165. [Google Scholar] [CrossRef] [PubMed]
- Setubal, J.C.; Stadler, P.F. Gene Phyologenies and Orthologous Groups. In Comparative Genomics; Setubal, J.C., Stadler, P.F., Stoye, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 1704, pp. 1–28. [Google Scholar] [CrossRef]
- Pascual-Anaya, J.; D’Aniello, S.; Kuratani, S.; Garcia-Fernàndez, J. Evolution of Hox gene clusters in deuterostomes. BMC Dev. Biol. 2013, 13, 26. [Google Scholar] [CrossRef] [PubMed]
- Stadler, P.F.; Geiß, M.; Schaller, D.; López Sánchez, A.; Gonzalez Laffitte, M.; Valdivia, D.; Hellmuth, M.; Hernandez Rosales, M. From pairs of most similar sequences to phylogenetic best matches. Alg. Mol. Biol. 2020, 15, 5. [Google Scholar] [CrossRef]
- Schaller, D.; Geiß, M.; Stadler, P.F.; Hellmuth, M. Complete Characterization of Incorrect Orthology Assignments in Best Match Graphs. J. Math. Biol. 2021, 82, 20. [Google Scholar] [CrossRef] [PubMed]
- Talevich, E.; Invergo, B.M.; Cock, P.J.; Chapman, B.A. Bio.Phylo: A unified toolkit for processing, analyzing and visualizing phylogenetic trees in Biopython. BMC Bioinform. 2012, 13, 209. [Google Scholar] [CrossRef] [PubMed]
- Huerta-Cepas, J.; Serra, F.; Bork, P. ETE 3: Reconstruction, Analysis, and Visualization of Phylogenomic Data. Mol. Biol. Evol. 2016, 33, 1635–1638. [Google Scholar] [CrossRef]
- Schaller, D.; Hellmuth, M.; Stadler, P.F. A simpler linear-time algorithm for the common refinement of rooted phylogenetic trees on a common leaf set. Alg. Mol. Biol. 2021, 16, 23. [Google Scholar] [CrossRef]
- Aho, A.V.; Sagiv, Y.; Szymanski, T.G.; Ullman, J.D. Inferring a tree from lowest common ancestors with an application to the optimization of relational expressions. SIAM J. Comput. 1981, 10, 405–421. [Google Scholar] [CrossRef]
- Deng, Y.; Fernández-Baca, D. Fast Compatibility Testing for Rooted Phylogenetic Trees. Algorithmica 2018, 80, 2453–2477. [Google Scholar] [CrossRef]
- Keller-Schmidt, S.; Klemm, K. A model of macroevolution as a branching process based on innovations. Adv. Complex Syst. 2012, 15, 1250043. [Google Scholar] [CrossRef]
- Stadler, T. Simulating trees with a fixed number of extant species. Syst. Biol. 2011, 60, 676–684. [Google Scholar] [CrossRef] [PubMed]
- Byrne, K.P.; Wolfe, K.H. Consistent Patterns of Rate Asymmetry and Gene Loss Indicate Widespread Neofunctionalization of Yeast Genes After Whole-Genome Duplication. Genetics 2007, 175, 1341–1350. [Google Scholar] [CrossRef] [PubMed]
- Mallo, D.; De Oliveira Martins, L.; Posada, D. SimPhy: Phylogenomic Simulation of Gene, Locus, and Species Trees. Syst. Biol. 2016, 65, 334–344. [Google Scholar] [CrossRef] [PubMed]
- Kundu, S.; Bansal, M.S. SaGePhy: An improved phylogenetic simulation framework for gene and subgene evolution. Bioinformatics 2019, 35, 3496–3498. [Google Scholar] [CrossRef] [PubMed]
- Kendall, D.G. On the Generalized “Birth-and-Death” Process. Ann. Math. Statist. 1948, 19, 1–15. [Google Scholar] [CrossRef]
- Hagen, O.; Stadler, T. TreeSimGM: Simulating phylogenetic trees under general Bellman–Harris models with lineage-specific shifts of speciation and extinction in R. Methods Ecol. Evol. 2018, 9, 754–760. [Google Scholar] [CrossRef]
- Höhna, S.; May, M.R.; Moore, B.R. TESS: An R package for efficiently simulating phylogenetic trees and performing Bayesian inference of lineage diversification rates. Bioinformatics 2016, 32, 789–791. [Google Scholar] [CrossRef]
- Louca, S. Simulating trees with millions of species. Bioinformatics 2020, 36, 2907–2908. [Google Scholar] [CrossRef]
- Felsenstein, J. Inferring Phylogenies; Sinauer Associates: Sunderland, MA, USA, 2004. [Google Scholar]
- Yang, Z. Computational Molecular Evolution; Oxford Series in Ecology and Evolution; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Rambaut, A.; Grassly, N.C. Seq-Gen: An application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comput. Appl. Biosci. 1997, 13, 235–238. [Google Scholar] [CrossRef]
- Cartwright, R.A. DNA assembly with gaps (Dawg): Simulating sequence evolution. Bioinformatics 2005, 21, iii31–iii38. [Google Scholar] [CrossRef][Green Version]
- Fletcher, W.; Yang, Z. INDELible: A Flexible Simulator of Biological Sequence Evolution. Mol. Biol. Evol. 2009, 26, 1879–1888. [Google Scholar] [CrossRef] [PubMed]
- Ly-Trong, N.; Naser-Khdour, S.; Lanfear, R.; Minh, B.Q. AliSim: A Fast and Versatile Phylogenetic Sequence Simulator for the Genomic Era. Mol. Biol. Evol. 2022, 39, msac092. [Google Scholar] [CrossRef] [PubMed]
- Spielman, S.J.; Wilke, C.O. Pyvolve: A Flexible Python Module for Simulating Sequences along Phylogenies. PLoS ONE 2015, 10, e0139047. [Google Scholar] [CrossRef]
- Rusin, L.Y.; Lyubetskaya, E.; Gorbunov, K.Y.; Lyubetsky, V. Reconciliation of gene and species trees. BioMed Res. Int. 2014, 2014, 642089. [Google Scholar] [CrossRef] [PubMed]
- Altenhoff, A.M.; Glover, N.M.; Dessimoz, C. Inferring Orthology and Paralogy. In Evolutionary Genomics; Anisimova, M., Ed.; Springer: New York, NY, USA, 2019; Volume 1910, pp. 149–175. [Google Scholar] [CrossRef]
- Sjöstrand, J.; Arvestad, L.; Lagergren, J.; Sennblad, B. GenPhyloData: Realistic simulation of gene family evolution. BMC Bioinform. 2013, 14, 209. [Google Scholar] [CrossRef]
- Davín, A.A.; Tricou, T.; Tannier, E.; de Vienne, D.M.; Szöllosi, G.J. Zombi: A phylogenetic simulator of trees, genomes and sequences that accounts for dead linages. Bioinformatics 2020, 36, 1286–1288. [Google Scholar] [CrossRef]
- Dalquen, D.A.; Anisimova, M.; Gonnet, G.H.; Dessimoz, C. ALF—A Simulation Framework for Genome Evolution. Mol. Biol. Evol. 2012, 29, 1115–1123. [Google Scholar] [CrossRef]
- Gonnet, G.H.; Hallett, M.T.; Korostensky, C.; Bernardin, L. Darwin v. 2.0: An interpreted computer language for the biosciences. Bioinformatics 2000, 16, 101–103. [Google Scholar] [CrossRef]
- Yue, J.X.; Liti, G. simuG: A general-purpose genome simulator. Bioinformatics 2019, 35, 4442–4444. [Google Scholar] [CrossRef]
- Price, A.; Gibas, C. Simulome: A genome sequence and variant simulator. Bioinformatics 2017, 33, 1876–1878. [Google Scholar] [CrossRef]
- Pattnaik, S.; Gupta, S.; Rao, A.A.; Panda, B. SInC: An accurate and fast error-model based simulator for SNPs, Indels and CNVs coupled with a read generator for short-read sequence data. BMC Bioinform. 2014, 15, 40. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Jin, L.; Leebens-Mack, J.H.; Sankoff, D. Validation of Automated Chromosome Recovery in the Reconstruction of Ancestral Gene Order. Algorithms 2021, 14, 160. [Google Scholar] [CrossRef]
- Rasmussen, M.D.; Kellis, M. Unified modeling of gene duplication, loss, and coalescence using a locus tree. Genome Res. 2012, 22, 755–765. [Google Scholar] [CrossRef] [PubMed]
- Yule, G.U. A mathematical theory of evolution, based on the conclusions of Dr. J. C. Willis, F. R. S. Phil. Trans. R. Soc. Lond. B 1924, 213, 21–87. [Google Scholar] [CrossRef]
- Maddison, W. Reconstructing character evolution on polytomous cladograms. Cladistics 1989, 5, 365–377. [Google Scholar] [CrossRef] [PubMed]
- DeSalle, R.; Absher, R.; Amato, G. Speciation and phylogenetic resolution. Trends Ecol. Evol. 1994, 9, 297–298. [Google Scholar] [CrossRef]
- Walsh, H.E.; Kidd, M.G.; Moum, T.; Friesen, V.L. Polytomies and the power of phylogenetic inference. Evolution 1999, 53, 932–937. [Google Scholar] [CrossRef] [PubMed]
- Lafond, M.; Chauve, C.; Dondi, R.; El-Mabrouk, N. Polytomy refinement for the correction of dubious duplications in gene trees. Bioinformatics 2014, 30, i519–i526. [Google Scholar] [CrossRef]
- Larridon, I.; Villaverde, T.; Zuntini, A.R.; Pokorny, L.; Brewer, G.E.; Epitawalage, N.; Fairlie, I.; Hahn, M.; Kim, J.; Maguilla, E.; et al. Tackling Rapid Radiations with Targeted Sequencing. Front. Plant Sci. 2020, 10, 1655. [Google Scholar] [CrossRef]
- Kliman, R.M.; Andolfatto, P.; Coyne, J.A.; Depaulis, F.; Kreitman, M.; Berry, A.J.; McCarter, J.; Wakeley, J.; Hey, J. The population genetics of the origin and divergence of the Drosophila simulans complex species. Genetics 2000, 156, 1913–1931. [Google Scholar] [CrossRef]
- Takahashi, K.; Terai, Y.; Nishida, M.; Okada, N. Phylogenetic relationships and ancient incomplete lineage sorting among cichlid fishes in Lake Tanganyika as revealed by analysis of the insertion of retroposons. Mol. Biol. Evol. 2001, 18, 2057–2066. [Google Scholar] [CrossRef] [PubMed]
- Sayyari, E.; Mirarab, S. Testing for Polytomies in Phylogenetic Species Trees Using Quartet Frequencies. Genes 2018, 9, 132. [Google Scholar] [CrossRef] [PubMed]
- Liao, D. Concerted Evolution: Molecular Mechanisms and Biological Implications. Am. J. Hum. Genet. 1999, 64, 24–30. [Google Scholar] [CrossRef] [PubMed]
- Hanada, K.; Tezuka, A.; Nozawa, M.; Suzuki, Y.; Sugano, S.; Nagano, A.J.; Ito, M.; Morinaga, S.I. Functional divergence of duplicate genes several million years after gene duplication in Arabidopsis. DNA Res. 2018, 25, 327–339. [Google Scholar] [CrossRef]
- Koonin, E.V. How Many Genes Can Make a Cell: The Minimal-Gene-Set Concept. Annu. Rev. Genom. Hum. Genet. 2000, 1, 99–116. [Google Scholar] [CrossRef] [PubMed]
- Rancati, G.; Moffat, J.; Typas, A.; Pavelka, N. Emerging and evolving concepts in gene essentiality. Nat. Rev. Genet. 2018, 19, 34–49. [Google Scholar] [CrossRef]
- Thomas, C.M.; Nielsen, K.M. Mechanisms of, and barriers to, horizontal gene transfer between bacteria. Nat. Rev. Microbiol. 2005, 3, 711–721. [Google Scholar] [CrossRef]
- Choi, S.C.; Rasmussen, M.D.; Hubisz, M.J.; Gronau, I.; Stanhope, M.J.; Siepel, A. Replacing and Additive Horizontal Gene Transfer in Streptococcus. Mol. Biol. Evol. 2012, 29, 3309–3320. [Google Scholar] [CrossRef]
- Khayi, S.; Blin, P.; Pédron, J.; Chong, T.M.; Chan, K.G.; Moumni, M.; Hélias, V.; Van Gijsegem, F.; Faure, D. Population genomics reveals additive and replacing horizontal gene transfers in the emerging pathogen Dickeya solani. BMC Genom. 2015, 16, 788. [Google Scholar] [CrossRef]
- Kordi, M.; Kundu, S.; Bansal, M.S. On Inferring Additive and Replacing Horizontal Gene Transfers Through Phylogenetic Reconciliation. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, Niagara Falls, NY, USA, 7–10 September 2019; pp. 514–523. [Google Scholar] [CrossRef]
- Eppley, J.M.; Tyson, G.W.; Getz, W.M.; Banfield, J.F. Genetic exchange across a species boundary in the archaeal genus ferroplasma. Genetics 2007, 177, 407–416. [Google Scholar] [CrossRef]
- Williams, D.; Gogarten, J.P.; Papke, R.T. Quantifying homologous replacement of loci between haloarchaeal species. Genome Biol. Evol. 2012, 4, 1223–1244. [Google Scholar] [CrossRef] [PubMed]
- Zuckerkandl, E.; Pauling, L.B. Molecular disease, evolution, and genic heterogeneity. In Horizons in Biochemistry; Kasha, M., Pullman, B., Eds.; Academic Press: New York, NY, USA, 1962; pp. 189–225. [Google Scholar]
- Kawahara, Y.; Imanishi, T. A genome-wide survey of changes in protein evolutionary rates across four closely related species of Saccharomyces sensu stricto group. BMC Evol. Biol. 2007, 7, 9. [Google Scholar] [CrossRef] [PubMed]
- Martin, A.P.; Palumbi, S.R. Body size, metabolic rate, generation time, and the molecular clock. Proc. Natl. Acad. Sci. USA 1993, 90, 4087–4091. [Google Scholar] [CrossRef]
- Gillooly, J.F.; Allen, A.P.; West, G.B.; Brown, J.H. The Rate of DNA Evolution: Effects of Body Size and Temperature on the Molecular Clock. Proc. Natl. Acad. Sci. USA 2005, 102, 140–145. [Google Scholar] [CrossRef]
- Innan, H.; Kondrashov, F. The evolution of gene duplications: Classifying and distinguishing between models. Nat. Rev. Genet. 2010, 11, 97–108. [Google Scholar] [CrossRef]
- Lepage, T.; Bryant, D.; Philippe, H.; Lartillot, N. A General Comparison of Relaxed Molecular Clock Models. Mol. Biol. Evol. 2007, 24, 2669–2680. [Google Scholar] [CrossRef]
- Kishino, H.; Thorne, J.L.; Bruno, W.J. Performance of a Divergence Time Estimation Method under a Probabilistic Model of Rate Evolution. Mol. Biol. Evol. 2001, 18, 352–361. [Google Scholar] [CrossRef]
- Yang, Z. Molecular Evolution: A Statistical Approach, 1st ed.; Oxford University Press: Oxford, UK; New York, NY, USA, 2014. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Jukes, T.H.; Cantor, C.R. Evolution of Protein Molecules. In Mammalian Protein Metabolism; Elsevier: Amsterdam, The Netherlands, 1969; pp. 21–132. [Google Scholar] [CrossRef]
- Kimura, M. A Simple Method for Estimating Evolutionary Rates of Base Substitutions through Comparative Studies of Nucleotide Sequences. J. Mol. Evol. 1980, 16, 111–120. [Google Scholar] [CrossRef]
- Tavaré, S. Some Probabilistic and Statistical Problems in the Analysis of DNA Sequences. Lect. Math. Life Sci. 1986, 17, 57–86. [Google Scholar]
- Dayhoff, M.; Schwartz, R. A Model for Evolutionary Change in Proteins. In Atlas of Protein Sequence and Structure; National Biomedical Research Foundation: Washington, DC, USA, 1978; pp. 345–352. [Google Scholar]
- Henikoff, S.; Henikoff, J.G. Amino Acid Substitution Matrices from Protein Blocks. Proc. Natl. Acad. Sci. USA 1992, 89, 10915–10919. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.T.; Taylor, W.R.; Thornton, J.M. The Rapid Generation of Mutation Data Matrices from Protein Sequences. Bioinformatics 1992, 8, 275–282. [Google Scholar] [CrossRef] [PubMed]
- Whelan, S.; Goldman, N. A General Empirical Model of Protein Evolution Derived from Multiple Protein Families Using a Maximum-Likelihood Approach. Mol. Biol. Evol. 2001, 18, 691–699. [Google Scholar] [CrossRef]
- Le, S.Q.; Gascuel, O. An Improved General Amino Acid Replacement Matrix. Mol. Biol. Evol. 2008, 25, 1307–1320. [Google Scholar] [CrossRef]
- Arenas, M. Trends in substitution models of molecular evolution. Front. Genet. 2015, 6, 319. [Google Scholar] [CrossRef]
- Del Amparo, R.; Arenas, M.A. Consequences of Substitution Model Selection on Protein Ancestral Sequence Reconstruction. Mol. Biol. Evol. 2022, 39, msac144. [Google Scholar] [CrossRef]
- Yang, Z. PAML: A Program Package for Phylogenetic Analysis by Maximum Likelihood. Bioinformatics 1997, 13, 555–556. [Google Scholar] [CrossRef]
- Chang, M.S.; Benner, S.A. Empirical Analysis of Protein Insertions and Deletions Determining Parameters for the Correct Placement of Gaps in Protein Sequence Alignments. J. Mol. Biol. 2004, 341, 617–631. [Google Scholar] [CrossRef]
- Yang, Z. Maximum-likelihood estimation of phylogeny from DNA sequences when substitution rates differ over sites. Mol. Biol. Evol. 1993, 10, 1396–1401. [Google Scholar] [CrossRef]
- Gu, X.; Fu, Y.X.; Li, W.H. Maximum likelihood estimation of the heterogeneity of substitution rate among nucleotide sites. Mol. Biol. Evol. 1995, 12, 546–557. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, H.A.; Strimmer, K.; Vingron, M.; von Haeseler, A. TREE-PUZZLE: Maximum likelihood phylogenetic analysis using quartets and parallel computing. Bioinformatics 2002, 18, 502–504. [Google Scholar] [CrossRef] [PubMed]
- Schaller, D.; Lafond, M.; Stadler, P.F.; Wieseke, N.; Hellmuth, M. Indirect Identification of Horizontal Gene Transfer. J. Math. Biol. 2021, 83, 10. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.H.; Lu, F.; Wang, Z.Y.; Zhong, F.; Hoover, J.; Mural, R. Using shared genomic synteny and shared protein functions to enhance the identification of orthologous gene pairs. Bioinformatics 2005, 21, 703–710. [Google Scholar] [CrossRef] [PubMed]
- Lechner, M.; Hernandez-Rosales, M.; Doerr, D.; Wieseke, N.; Thévenin, A.; Stoye, J.; Hartmann, R.K.; Prohaska, S.J.; Stadler, P.F. Orthology Detection Combining Clustering and Synteny for Very Large Datasets. PLoS ONE 2014, 9, e105015. [Google Scholar] [CrossRef]
- Dohmen, E.; Klasberg, S.; Bornberg-Bauer, E.; Perry, S.; Kemena, C. The modular nature of protein evolution: Domain rearrangement rates across eukaryotic life. BMC Evol. Biol. 2020, 20, 30. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).