Lattice Dynamics and Thermal Properties of TixZr1-xNiSn Half-Heusler Alloys
Abstract
1. Introduction
2. Methods
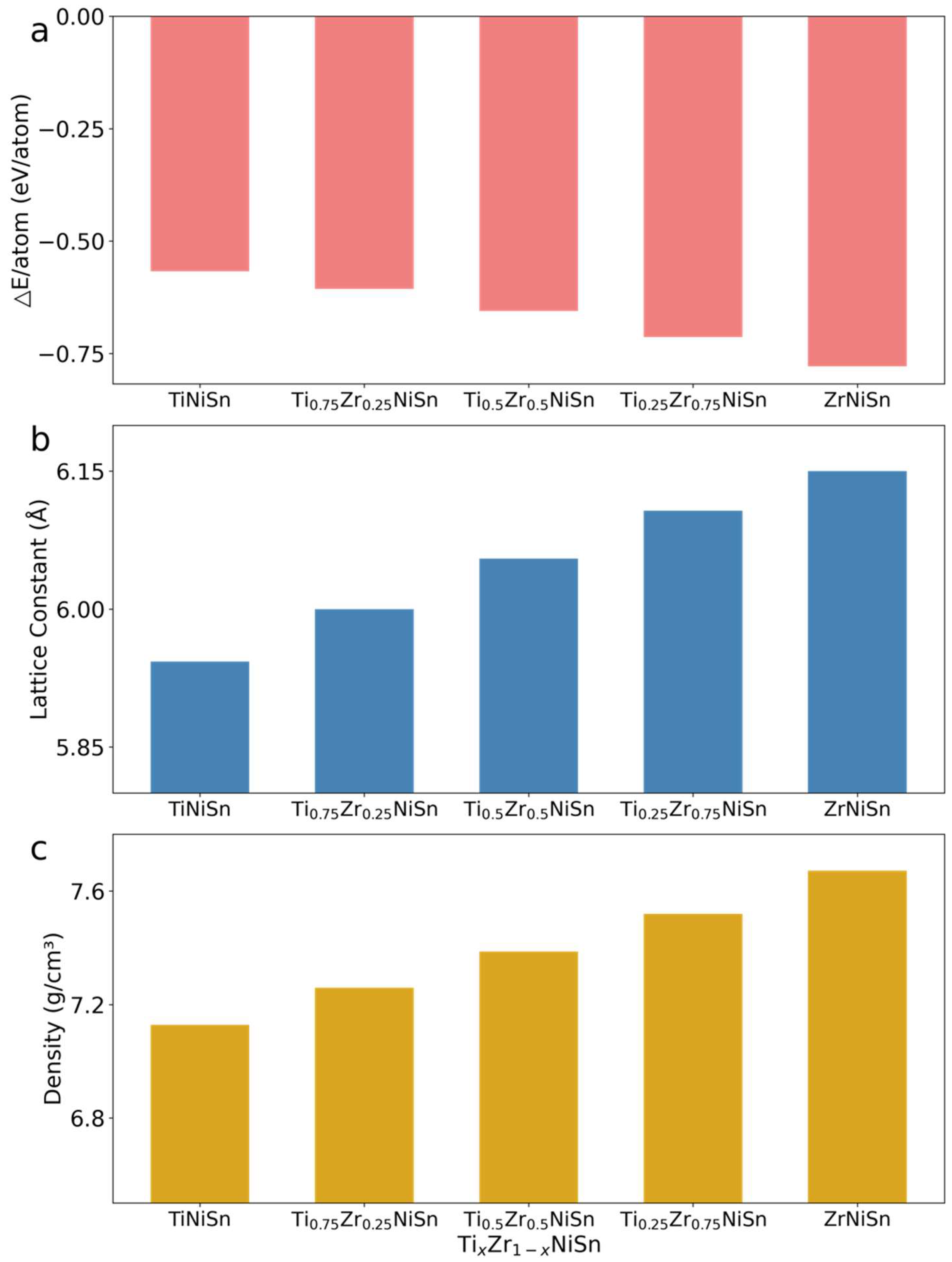
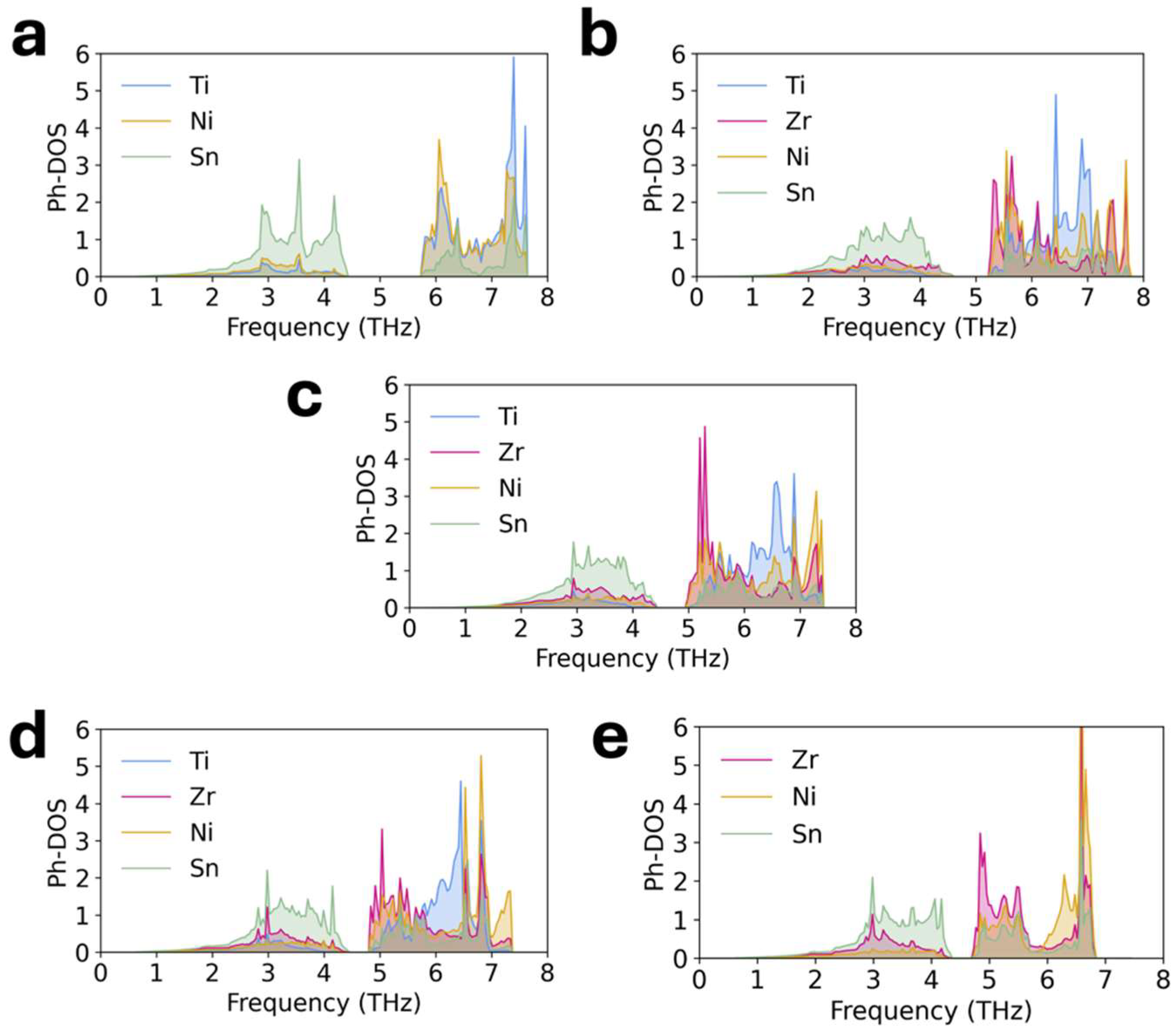
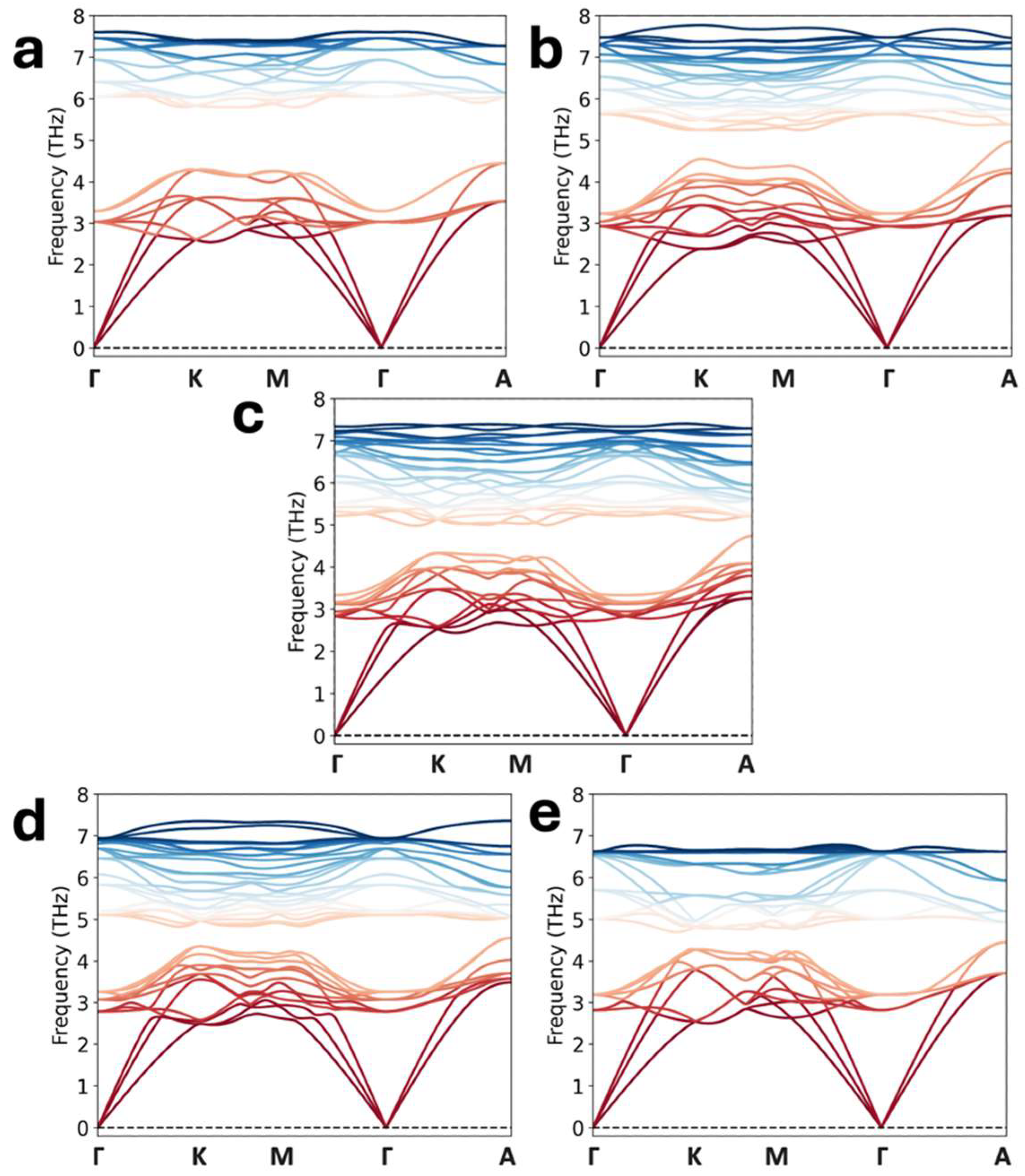
3. Results and Discussion
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bende, D.; Grin, Y.; Wagner, F.R. Chemical Bonding in MgAgAs-Type Compounds. In Heusler Alloys: Properties, Growth, Applications; Springer: Cham, Switzerland, 2016; pp. 133–156. [Google Scholar]
- Galanakis, I. Theory of Heusler and Full-Heusler Compounds. In Heusler Alloys: Properties, Growth, Applications; Springer: Cham, Switzerland, 2016; pp. 3–36. [Google Scholar]
- Sharma, P.; Singh, P.; Balasubramanian, G. Engineering Phonon Transport Through Cation Disorder in Dimensionally Constricted High Entropy MXene. Carbon 2024, 223, 119015. [Google Scholar] [CrossRef]
- Sharma, P.; Balasubramanian, G. Electronic and Lattice Distortions Induce Elastic Softening in Refractory Multicomponent Borides. Chem. Mater. 2023, 35, 7511–7520. [Google Scholar] [CrossRef] [PubMed]
- Sharma, P.; Balasubramanian, G. High Configurational Entropy Driven Increased Heat Capacity of Refractory Multicomponent Di-Silicides. Materialia 2023, 30, 101861. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Singh, P.; Smirnov, A.V.; Johnson, D.D. Effect of Substitutional Doping and Disorder on the Phase Stability, Magnetism, and Half-Metallicity of Heusler Alloys. Acta Mater. 2022, 225, 117477. [Google Scholar] [CrossRef]
- Patel, P.D.; Pillai, S.B.; Shinde, S.M.; Gupta, S.D.; Jha, P.K. Electronic, Magnetic, Thermoelectric and Lattice Dynamical Properties of Full Heusler Alloy Mn2RhSi: DFT Study. Phys. B Condens. Matter 2018, 550, 376–382. [Google Scholar] [CrossRef]
- Sharma, P.; Johnson, D.D.; Balasubramanian, G.; Singh, P. Unraveling the Connection of Electronic and Phononic Structure with Mechanical Properties of Commercial AZ80 Alloy. Mater. Lett. 2024, 366, 136501. [Google Scholar] [CrossRef]
- Sharma, P.; Gandhi, P.M.; Chintersingh, K.-L.; Schoenitz, M.; Dreizin, E.L.; Liou, S.-C.; Balasubramanian, G. Accelerated Intermetallic Phase Amorphization in a Mg-Based High-Entropy Alloy Powder. J. Magnes. Alloys 2024, 12, 1792–1798. [Google Scholar] [CrossRef]
- Sharma, P.; Naushin, N.; Rohila, S.; Tiwari, A. Magnesium Containing High Entropy Alloys. In Magnesium Alloys Structure and Properties; IntechOpen: London, UK, 2022. [Google Scholar]
- Eliassen, S.N.H.; Katre, A.; Madsen, G.K.H.; Persson, C.; Løvvik, O.M.; Berland, K. Lattice Thermal Conductivity of TixZryHf1−x−yNiSn Half-Heusler Alloys Calculated from First Principles: Key Role of Nature of Phonon Modes. Phys. Rev. B 2017, 95, 045202. [Google Scholar] [CrossRef]
- Hohl, H.; Ramirez, A.P.; Goldmann, C.; Ernst, G.; Wölfing, B.; Bucher, E. Efficient Dopants for ZrNiSn-Based Thermoelectric Materials. J. Phys. Condens. Matter 1999, 11, 1697–1709. [Google Scholar] [CrossRef]
- Shutoh, N.; Sakurada, S. Thermoelectric Properties of the TiX(Zr0.5Hf0.5)1−XNiSn Half-Heusler Compounds. J. Alloys Compd. 2005, 389, 204–208. [Google Scholar] [CrossRef]
- Sakurada, S.; Shutoh, N. Effect of Ti Substitution on the Thermoelectric Properties of (Zr,Hf)NiSn Half-Heusler Compounds. Appl. Phys. Lett. 2005, 86, 082105. [Google Scholar] [CrossRef]
- Singh, P.; Acemi, C.; Kuchibhotla, A.; Vela, B.; Sharma, P.; Zhang, W.; Mason, P.; Balasubramanian, G.; Karaman, I.; Arroyave, R.; et al. Alloying Effects on the Transport Properties of Refractory High-Entropy Alloys. Acta Mater. 2024, 276, 120032. [Google Scholar] [CrossRef]
- Chai, Y.W.; Oniki, T.; Kenjo, T.; Kimura, Y. The Effect of an Isoelectronic Ti–Zr Substitution on Heusler Nanoprecipitation and the Thermoelectric Properties of a (Ti0.2,Zr0.8)Ni1.1Sn Half-Heusler Alloy. J. Alloys Compd. 2016, 662, 566–577. [Google Scholar] [CrossRef]
- Choudhary, M.K.; Ravindran, P. First Principle Design of New Thermoelectrics from TiNiSn Based Pentanary Alloys Based on 18 Valence Electron Rule. Comput. Mater. Sci. 2022, 209, 111396. [Google Scholar] [CrossRef]
- Echevarria-Bonet, C.; Garrido-Alvarez, J.L.; Martinez-Blanco, D.; Gorria, P.; Sørby, M.H.; Riktor, M.D.; Blanco, J.A.; Hauback, B.C. Anharmonicity Effects and Thermal Expansion of Thermoelectric (M,M’,M”)NiSn (M,M’,M”=Ti, Zr, Hf) Half-Heusler Alloys. J. Alloys Compd. 2023, 959, 170583. [Google Scholar] [CrossRef]
- Graf, T.; Felser, C.; Parkin, S.S.P. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
- Jung, D.; Kurosaki, K.; Kim, C.; Muta, H.; Yamanaka, S. Thermal Expansion and Melting Temperature of the Half-Heusler Compounds: MNiSn (M = Ti, Zr, Hf). J. Alloys Compd. 2010, 489, 328–331. [Google Scholar] [CrossRef]
- Hafner, J. Ab-Initio Simulations of Materials Using VASP: Density-Functional Theory and Beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Chaput, L. Direct Solution to the Linearized Phonon Boltzmann Equation. Phys. Rev. Lett. 2013, 110, 265506. [Google Scholar] [CrossRef] [PubMed]
- Togo, A.; Chaput, L.; Tadano, T.; Tanaka, I. Implementation Strategies in Phonopy and Phono3py. J. Phys. Condens. Matter 2023, 35, 353001. [Google Scholar] [CrossRef] [PubMed]
- Togo, A.; Tanaka, I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Parlinski, K.; Li, Z.Q.; Kawazoe, Y. First-Principles Determination of the Soft Mode in Cubic ZrO2. Phys. Rev. Lett. 1997, 78, 4063–4066. [Google Scholar] [CrossRef]
- Giannozzi, P.; de Gironcoli, S.; Pavone, P.; Baroni, S. Ab Initio Calculation of Phonon Dispersions in Semiconductors. Phys. Rev. B 1991, 43, 7231–7242. [Google Scholar] [CrossRef]
- Gehringer, D.; Friák, M.; Holec, D. Models of Configurationally-Complex Alloys Made Simple. Comput. Phys. Commun. 2023, 286, 108664. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A Three-Dimensional Visualization System for Electronic and Structural Analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Böer, K.W.; Pohl, U.W. Phonon-Induced Thermal Properties. In Semiconductor Physics; Springer: Cham, Switzerland, 2018; pp. 151–179. [Google Scholar]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics, 1st ed.; Academic Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Gürth, M.; Rogl, G.; Romaka, V.V.; Grytsiv, A.; Bauer, E.; Rogl, P. Thermoelectric High ZT Half-Heusler Alloys Ti1−x−yZrxHfyNiSn (0 ≤ x ≤ 1; 0 ≤ y ≤ 1). Acta Mater. 2016, 104, 210–222. [Google Scholar] [CrossRef]
- Murray, J.L. The Ti−Zr (Titanium-Zirconium) System. Bull. Alloy Phase Diagr. 1981, 2, 197–201. [Google Scholar] [CrossRef]
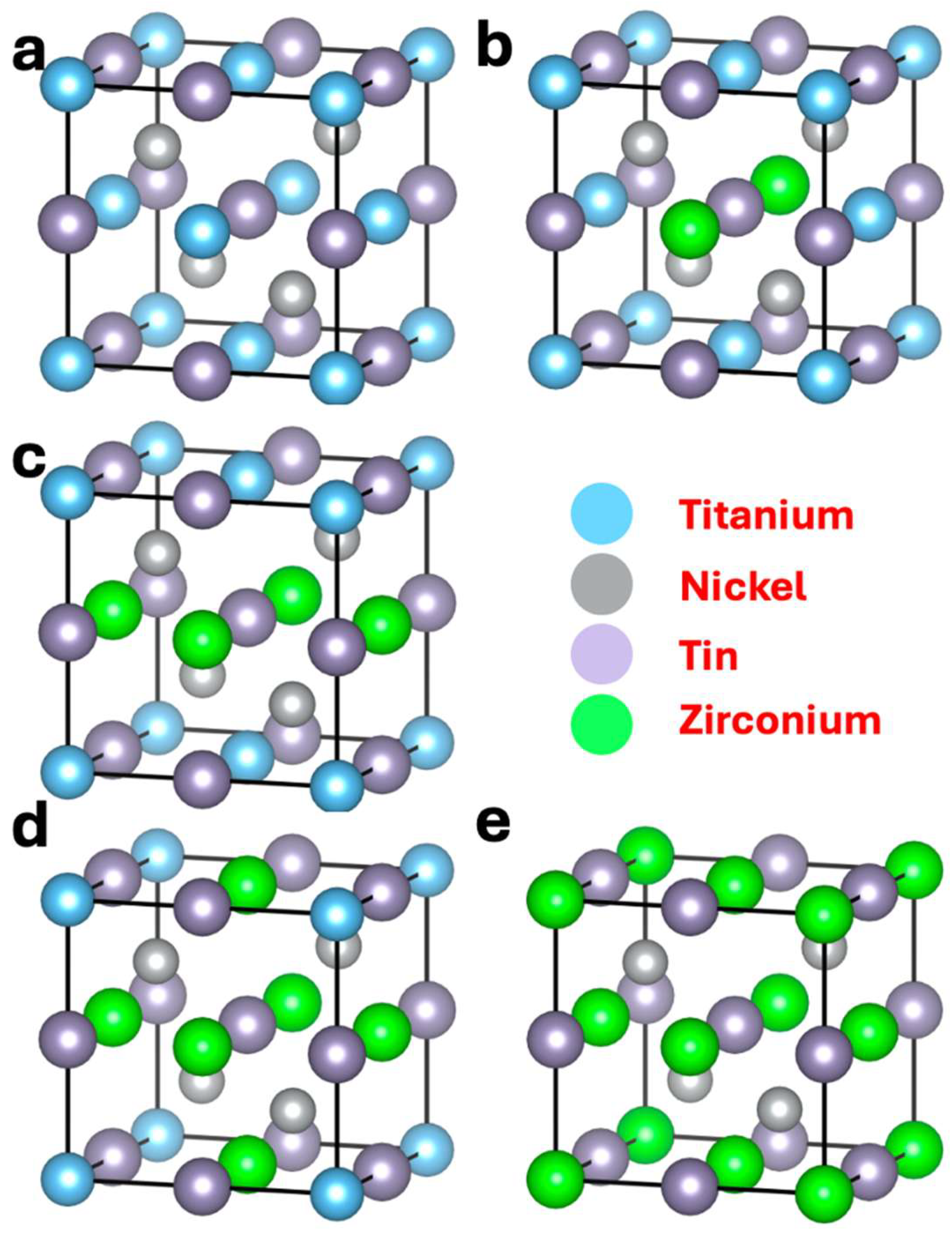

| Wyckoff | Element | Coordinates |
|---|---|---|
| 4a | Ti/Zr | (½, ½, 0) |
| 4b | Sn | (0, ½, 0) |
| 4c | Ni | (¼, ¼, ¼) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, P. Lattice Dynamics and Thermal Properties of TixZr1-xNiSn Half-Heusler Alloys. Alloys 2025, 4, 3. https://doi.org/10.3390/alloys4010003
Sharma P. Lattice Dynamics and Thermal Properties of TixZr1-xNiSn Half-Heusler Alloys. Alloys. 2025; 4(1):3. https://doi.org/10.3390/alloys4010003
Chicago/Turabian StyleSharma, Prince. 2025. "Lattice Dynamics and Thermal Properties of TixZr1-xNiSn Half-Heusler Alloys" Alloys 4, no. 1: 3. https://doi.org/10.3390/alloys4010003
APA StyleSharma, P. (2025). Lattice Dynamics and Thermal Properties of TixZr1-xNiSn Half-Heusler Alloys. Alloys, 4(1), 3. https://doi.org/10.3390/alloys4010003






