Abstract
In this work, the structural, magnetic, thermal, and transport properties of the arc-melted polycrystalline Heusler alloy Co2Ti1.5Sn0.5 are investigated. The alloy crystallizes in an L21 structure with a space group of Fm-3m. The magnetic properties of the alloy depict its antiferromagnetic nature and the alloy exhibits magnetic ordering around Neel Temperature TN = 8.5 K. The effective magnetic moment value obtained from the Curie –Weiss law suggests that the cobalt atom in the alloy is in the low-spin state. From the heat capacity studies, the Sommerfeld coefficient and Debye temperature were determined. In addition, electrical resistivity shows a linear response with increasing temperature, indicating the metallic nature of the alloy.
1. Introduction
Heusler alloys have received a great deal of attention in recent decades due to their diverse applications, which include high-temperature ferri- and ferromagnets, shape memory alloys, multi-ferroics, and topological insulators with significant potential for spintronic, energy, and magnetocaloric applications. These alloys consist of intermetallic materials containing ternary X2YZ or XYZ compositions comprising transition metals (X and Y) and a p-block element (Z) that crystallizes in a structure belonging to space group Cb1 or L21. In particular, cobalt-based Heusler alloys were considered to be good candidates for research on itinerant electron ferromagnetism and spintronic applications [1,2]. In spintronics devices such as magnetic tunnel junctions (MTJs) [3,4] and giant magnetoresistance (GMR) devices [5], Heusler alloys based on Co2 can be employed as electrode devices. Co2FeAl [6] is a potential MTJ, while Co2FeAl0.5Si0.5/Ag/Co2FeAl0.5Si0.5 [7] is found to have a GMR ratio of 34% at 290 K (80% at 14 K) [8]. Magnetic tunnel junctions, spin valves, and magnetic random access memory are just a few examples of spintronic devices where 100% spin polarization is present due to the material’s metallicity in one spin channel and semiconductor property in the other spin channel, which is very useful in half-metallic ferromagnetic applications [9,10]. Studies on Co2TiX (X = Si, Ge, and Sn) alloys demonstrate their half-metallic nature and thermoelectric properties [11]. Further research on these materials reveals that their transition temperature and physical properties are significantly dependent on the transition and p-block stoichiometry. For instance, in Co2TiAl1-xSix alloy, the substitution of silicon for aluminum increases the Curie temperature [12]. Whereas, in Co2Ti1-xMnxGa, transition temperature increases with an increase in “x” until x = 0.7 and becomes independent of doping concentration for x > 0.7 [13]. In the case of CoTi1−xVxSb, an increase in electrical resistivity is observed when vanadium is slightly substituted for titanium [14]. Additionally, pseudo-binary alloys such as CoTi1-xAlx [15] and CoTi1-xGax [16], and quaternary Heusler alloys such as Co2Ti1−xFexAs [17] and Co2Ti1-xFexSn[18] show notable changes with doping.
Co2TiSn is one of the technologically advantageous materials in this Heusler family as it demonstrates a half-metallic property [19,20]. It undergoes a semiconductor–metal transition around room temperature (Tc = 350 K), which is associated with a paramagnetic to ferromagnetic transition. The near room temperature ferromagnetic property of Co2TiSn makes this material a strong candidate for magnetic applications. Our prior work on Co2Ti0.5Sn1.5 and Co2Ti0.75Sn1.25 [21] also produced promising results. These alloys had high-temperature ferromagnetic characteristics, and the transition temperature of these alloys shifted upward with increasing Sn concentration. The attractive behavior of this alloy with the change in stoichiometry makes this series interesting for further studies. In this work, to obtain further insight into this series, we synthesized a Co2Ti1.5Sn0.5 alloy, and its magnetic, thermal, and transport properties were thoroughly examined.
2. Materials and Methods
Co2Ti1.5Sn0.5 alloy was prepared by arc-melting of pure Co (99.95%), Ti (99.98%), and Sn (99.999%) under an inert argon atmosphere. The ingot was remelted several times to improve homogeneity. To enhance crystallinity, the resultant alloy was sealed in an evacuated quartz tube and annealed at 1273 K for 8 days. A Panalytical XPert PRO diffractometer with Cu-Kα radiation was used to confirm phase purity from the X-ray powder diffraction data. Using the FULLPROF program [22], diffraction data were refined to understand the crystal structure. The sample composition was examined using backscattered electron analysis (BSE) and Energy Dispersive X-ray Electron Spectroscopy (EDAX). We added error values to the EDAX measurements to make it more quantitative. Study of the magnetization, heat capacity, and electrical resistivity of the prepared samples was carried out using a Vibrating Sample Magnetometer (VSM) and Physical Property Measurement System (PPMS) in a DYNACOOL device from Quantum Design in the temperature range of 2–400 K and in an applied magnetic field of 0–9 T. Both zero-field cooling (ZFC) and field cooling (FC) magnetization investigations were carried out for the samples.
3. Results and Discussion
The room-temperature XRD pattern of the Co2Ti1.5Sn0.5 alloy was analyzed using the FULLPROF program [14], which is displayed in Figure 1a. It confirms that the sample crystallizes in a Cu2MnAl-type ordered L21 structure with a space group of Fm-3m. The lattice parameter a, determined from Rietveld refinement, is 5.95 Å, which is less than the lattice parameter of Co2TiSn alloy (6.07 Å) and could be due to the addition of titanium, which has a smaller atomic radius than tin [20].
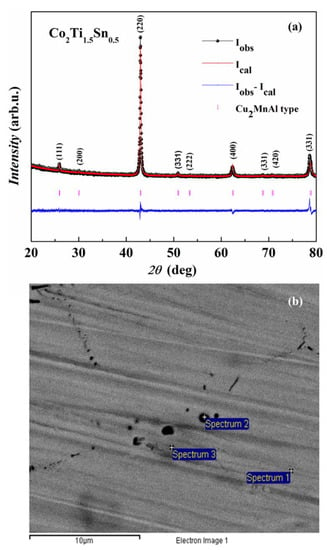
Figure 1.
(a). Rietveld refined room temperature XRD pattern of Co2Ti1.5Sn0.5. (b) BSE image of Co2Ti1.5Sn0.5 alloy.
The refinement’s quality of fit parameter is . Further, the stoichiometric formation of the phase is verified through BSE and EDAX analysis of the sample. The analysis of sample surfaces with BSE imaging, along with EDAX, confirms the single-phase nature; the stoichiometry of the composition is found to be 2:1.5:0.5 as per the result listed in Table 1.

Table 1.
EDAX result for Co2Ti1.5Sn0.5 alloy.
The temperature dependence of magnetic susceptibilities (M/B(T)) in ZFC and FC at various magnetic fields measured in the temperature range of 2–300 K is shown in Figure 2. In an applied magnetic field of B = 0.01 T, magnetic susceptibility displays an antiferromagnetic transition at TN = 8.5 K (see Figure 2a). This antiferromagnetic transition is further confirmed by a shift toward the low-temperature range in the first-order derivative of ZFC magnetization, as shown in Figure 2b. A drastic change in magnetic behavior and transition temperature for Co2Ti1.5Sn0.5 is observed when comparing it to the Co2TiSn parent alloy. This change from high-temperature (350 K) ferromagnetism to low-temperature (8.5 K) antiferromagnetism could be attributed to a reduction in the lattice parameter and the corresponding change in magnetic interactions. Additionally, in M/B(T) in applied magnetic fields of 0.01 T and 0.1 T, thermomagnetic irreversibility is visible (see Figure 2a,c) and disappears as B approaches 1 T (Figure 2d). Hence, the bifurcation in the ZFC and FC curves may be due to the domain wall pinning effect [23].
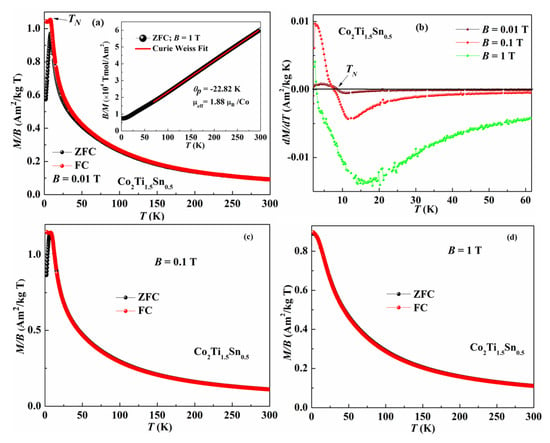
Figure 2.
(a) Variation in magnetic susceptibility (M/B(T)) with temperature in an applied magnetic field of B = 0.01 T. The linear fit of Equation (1) is shown in the inset. (b) First-order derivative of ZFC magnetization with temperature for the applied magnetic fields of B = 0.01 T, 0.1 T, and 1 T. ZFC and FC M/B(T) in an applied magnetic field of B = 0.1 T (c) and 1 T (d).
The inset of Figure 2a depicts the Curie–Weiss behavior of the alloy in a temperature range of 80–300 K at B = 1 T, obeying the Equation (1)
where C is the Curie constant and denotes Curie–Weiss temperature. The obtained Curie–Weiss temperature and Curie constants are and 0.8335, respectively. The negative Curie–Weiss temperature signifies an antiferromagnetic type of interaction in the paramagnetic region. The effective magnetic moment of the cobalt atom, calculated from the Curie constant, is measured as 1.8 (8) μB/Co, which is in close agreement with the magnetic moment of a cobalt atom in the low-spin state.
Variation in isothermal magnetization M(B) up to a magnetic field of B = 9 T in the vicinity of the transition temperature of Co2Ti1.5Sn0.5 alloy is demonstrated in Figure 3a. Isothermal magnetization curves follow the antiferromagnetic behavior detected in the magnetic susceptibility measurements. We did not observe a tendency toward the saturation of magnetization at high magnetic fields.
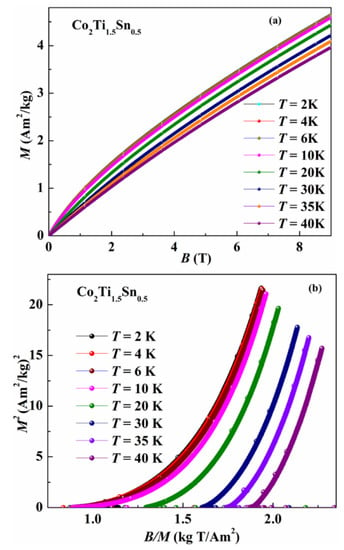
Figure 3.
(a) Field-dependent isothermal magnetization M(B) of Co2Ti1.5Sn0.5 alloy at various temperatures. (b) Arrott plot of Co2Ti1.5Sn0.5 alloy.
In order to understand the order of magnetic transition, an Arrott plot was constructed around the transition temperature and is depicted in Figure 3b. According to the Banerjee criterion [16], an Arrott plot with a positive slope indicates a phase transition that is second-order in nature, whereas a negative slope or inflection point in an Arrott plot indicates that the transition is of a first-order nature [17]. As shown in Figure 3b, the positive slope of Arrott plot curves around transition temperature denotes that the antiferromagnetic transition is second-order in nature at TN. Additionally, magnetic hysteresis studies of Co2Ti1.5Sn0.5 alloy support the suggestion that the magnetic transition is second-order in nature as it is hysteresis free (see Figure 4); second-order transition materials will usually display negligible or low magnetic hysteresis [24,25,26]. For practical applications, the absence of magnetic hysteresis is more advantageous.
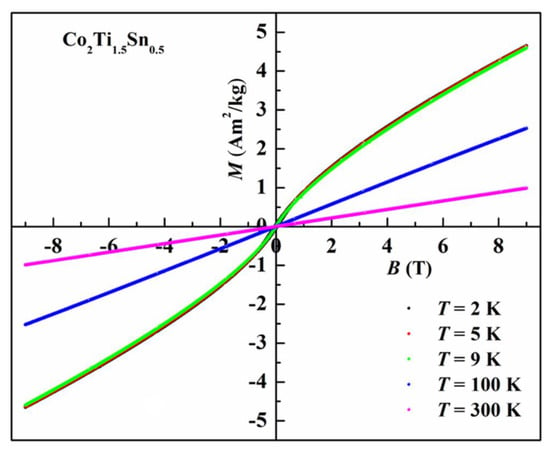
Figure 4.
Magnetic hysteresis at selected temperatures (T = 2 K, 5 K, 9 K, 100 K, and 300 K).
To gather a deeper insight into the system, heat capacity as a function of the temperature C(T) of Co2Ti1.5Sn0.5 is presented without an applied magnetic field (B = 0 T) in Figure 5. No clear anomaly around the antiferromagnetic transition temperature TN is discernible for heat capacity.
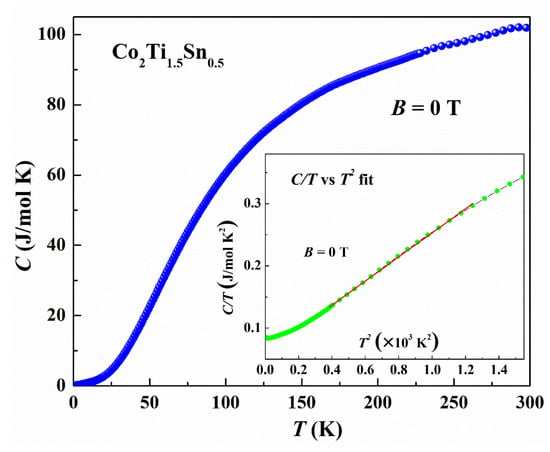
Figure 5.
Variation in heat capacity C(T) in the absence of an applied magnetic field. Inset shows the least square linear fit of C/T vs. T2.
The variation in heat capacity C/T(T) follows the relation
where γ and β are the Sommerfeld coefficient and Debye coefficient, respectively. From the C/T vs. T2 fit (seen in the inset of Figure 4), γ and β values were obtained as 59.57 mJ/mol K2 and 0.1937 mJ/mol K4, respectively. Further, Debye temperature was found to be 232 K using the following equation:
Electrical resistivity (ρ(T)) in the temperature range of 2–300 K for applied magnetic fields of 0 T and 9 T is displayed in Figure 6. The temperature dependence has typical metallic behavior. We determined the residual resistivity ratio, RRR = ρ (300 K)/ρ (2 K), to be 1.43.
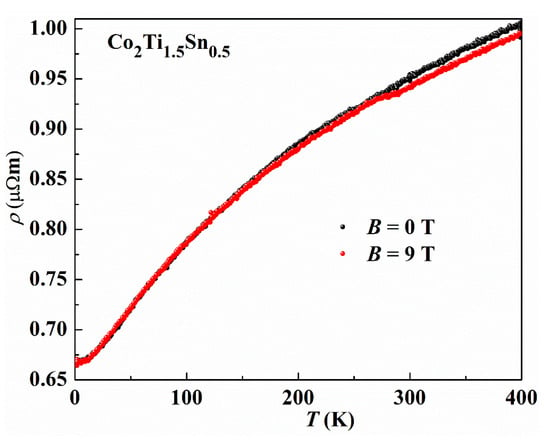
Figure 6.
Temperature dependence of resistivity for Co2Ti1.5Sn0.5 in B = 0 T and B = 9 T.
4. Conclusions
The structural, magnetic, thermodynamic, and transport properties of polycrystalline Co2Ti1.5Sn0.5 have been systematically investigated. Crystallographic studies confirm that the alloy crystallizes in an L21 structure with a space group of Fm-3m, and the lattice parameter was found to be 5.950 Å. Compositional analysis asserts that the Heusler alloy exhibits a homogenous single-phase with 2:1.5:0.5 stoichiometry. Variation in magnetic susceptibility with temperature indicates the antiferromagnetic transition has a transition temperature of TN = 8.5 K. Thermomagnetic irreversibility in temperature-dependent magnetic susceptibility at the lower applied fields indicates a significant domain wall pinning effect in the alloy. The effective magnetic moment of cobalt obtained experimentally from the Curie –Weiss fit is comparable to the low-spin state magnetic moment of the cobalt atom. Further, from temperature-dependent heat capacity studies, the value of Sommerfeld coefficient, Debye coefficient, and Debye temperature were determined as 59.57 mJ/mol K2, 0.1937 mJ/mol K4, and 232 K, respectively. The observed behavior of electrical resistivity demonstrates the typical metallic behavior of the alloy.
Author Contributions
S.R.A.: conceptualization, investigation, formal analysis, and writing—original draft; K.A.: investigation and writing—review and editing; S.S.: investigation and writing—review and editing; U.D.R.: investigation and writing—review and editing; A.D.: data curation; M.R.: data curation, writing—review and editing, and funding acquisition; R.N.: validation, writing—review and editing, funding acquisition, and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
S.R. Athul thanks CSIR, Govt. India for awarding JRF through a CSIR fellowship (No. 09/895(0013)/2019-EMR-I). The authors are grateful to Mr. Nilesh Kulkarni and Mrs. Bhagyashree Chalke from the Department of Condensed Matter Physics, Tata Institute of Fundamental Research, Mumbai, India for their help with structural measurements. This research study is a part of the implementation of the University Science Park TECHNICOM for Innovation Applications Supported by Knowledge Technology project, ITMS: 313011D232, supported by the Research & Development Operational Programme funded by the ERDF, and also by VEGA 1/0705/20, 1/0404/21 and VVGS-2022-2117.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interests.
References
- Varaprasad, B.; Srinivasan, A.; Takahashi, Y.; Hayashi, M.; Rajanikanth, A.; Hono, K. Spin polarization and Gilbert damping of Co2Fe(GaxGe1−x) Heusler alloys. Acta Mater. 2012, 60, 6257–6265. [Google Scholar] [CrossRef]
- Bainsla, L.; Mallick, A.I.; Raja, M.M.; Nigam, A.K.; Varaprasad, B.S.D.C.S.; Takahashi, Y.K.; Alam, A.; Suresh, K.G.; Hono, K. Spin gapless semiconducting behavior in equiatomic quaternary CoFeMnSi Heusler alloy. Phys. Rev. B-Condens. Matter Mater. Phys. 2015, 91, 104408. [Google Scholar] [CrossRef]
- Kubota, H.; Nakata, J.; Oogane, M.; Ando, Y.; Sakuma, A.; Miyazaki, T. Large Magnetoresistance in Magnetic Tunnel Junctions Using Co-Mn-Al Full Heusler Alloy. Jpn. J. Appl. Phys. 2004, 43, L984–L986. [Google Scholar] [CrossRef]
- Feng, Y.; Ding, H.; Li, X.; Wu, B.; Chen, H. Spin Transport Properties of Highly Lattice- Matched All-Heusler-Alloy Magnetic Tunnel Junction Spin Transport Properties of Highly Lattice-Matched All-Heusler-Alloy Magnetic Tunnel Junction. J. Applied Phys. 2022, 131, 133901. [Google Scholar] [CrossRef]
- Sakuraba, Y.; Iwase, T.; Saito, K.; Mitani, S.; Takanashi, K. Enhancement of spin-asymmetry by L21-ordering in Co2MnSi/Cr/Co2MnSi current-perpendicular-to-plane magnetoresistance devices. Appl. Phys. Lett. 2009, 94, 012511. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z.; Xu, J.; Zuo, S.; Zhang, Y.; Liu, D.; Zheng, X.; Wang, L.; Zhao, T.; Hu, F.; et al. Multiple Transitions and Wide Refrigeration Temperature Range in R3NiSi2 (R = Tb, Dy) Compounds. J. Magn. Magn. Mater. 2020, 502, 166551. [Google Scholar] [CrossRef]
- Wang, W.; Liu, E.; Kodzuka, M.; Sukegawa, H.; Wojcik, M.; Jedryka, E.; Wu, G.H.; Inomata, K.; Mitani, S.; Hono, K. Coherent Tunneling and Giant Tunneling Magnetoresistance in Co2FeAl/MgO/CoFe Magnetic Tunneling Junctions. Phys. Rev. B 2010, 81, 1–4. [Google Scholar] [CrossRef]
- Nakatani, T.M.; Furubayashi, T.; Kasai, S.; Sukegawa, H.; Takahashi, Y.K.; Mitani, S.; Hono, K. Bulk and interfacial scatterings in current-perpendicular-to-plane giant magnetoresistance with Co2Fe(Al0.5Si0.5) Heusler alloy layers and Ag spacer. Appl. Phys. Lett. 2010, 96, 212501. [Google Scholar] [CrossRef]
- Cui, Z.; Ding, H.; Xu, K.; Feng, Y. Electronic Structures of Various (001) and (111) Surfaces, Interfaces and Spin Transport Properties of Half-Metallic Fully Compensated Ferrimagnet Cr2Se. J. Alloys Compd. 2021, 884, 5–13. [Google Scholar] [CrossRef]
- Cui, Z.; Ding, H.; Feng, Y. Investigation of the half-metallicity, magnetism and spin transport properties of double half-Heusler alloys Mn2CoCrZ2 (Z = P, As). Phys. Chem. Chem. Phys. 2021, 23, 17984–17991. [Google Scholar] [CrossRef] [PubMed]
- Barth, J.; Fecher, G.H.; Balke, B.; Ouardi, S.; Graf, T.; Felser, C.; Shkabko, A.; Weidenkaff, A.; Klaer, P.; Elmers, H.J.; et al. Itinerant Half-Metallic Ferromagnets Co2TiZ (Z=Si, Ge, Sn ): Ab Initio Calculations and Measurement of the Electronic Structure and Transport Properties. Phys. Rev. B Condens. Matter Mater. Phys. 2010, 81, 1–20. [Google Scholar] [CrossRef]
- Graf, T.; Barth, J.; Balke, B.; Populoh, S.; Weidenkaff, A.; Felser, C. Tuning the Carrier Concentration for Thermoelectrical Application in the Quaternary Heusler Compound Co2TiAl1-xSiX. Scr. Mater. 2010, 63, 925–928. [Google Scholar] [CrossRef]
- Okubo, A.; Umetsu, R.Y.; Kainuma, R.; Ishida, K. Magnetic Properties and Phase Stability of Co2(Ti1-xMnx)Ga Heusler Alloys. J. Phys. Conf. Ser. 2010, 200, 14–18. [Google Scholar] [CrossRef]
- Nakatsu, R.; Hiroi, M.; Tareuchi, N.; Kawakami, M. Transport and Magnetic Properties of the Half-Heusler Compounds CoTi1-xVxSb. AIP Conf. Proc. 2006, 850, 1247–1248. [Google Scholar] [CrossRef]
- Waterman, E.H.; Franse, J.J.M. Magnetic and Electronic Properties of CoTi1-xAlx Compounds. J. Phys. F Met. Phys. 1980, 10, 947–958. [Google Scholar] [CrossRef]
- Ooiwa, K. The Magnetic Moment of Co in a Heusler Alloy Co2TiGa and a Pseudobinary Alloy System CoTi1-yGaY. J. Phys. Soc. Japan 1985, 54, 1581–1591. [Google Scholar] [CrossRef]
- Mostefa, Z.; Cherifi, F.; Boukra, A.; Meghoufel, Z.F.; Boukortt, A. Martensitic Phase Transformations in Quaternary Heusler Alloys Co2Ti1-xFexAs. Acta Phys. Pol. A 2021, 140, 175–180. [Google Scholar] [CrossRef]
- Rani, D.; Suresh, K.G.; Alam, A. Effect of Fe Substitution for Ti on the Structural and Magnetic Properties of Half-Metallic Ferromagnet Co2TiSn. AIP Conf. Proc. 2018, 1953, 1–5. [Google Scholar] [CrossRef]
- Majumdar, S.; Chattopadhyay, M.K.; Sharma, V.K.; Sokhey, K.J.S.; Roy, S.B.; Chaddah, P. Transport Properties of the Ferromagnetic Heusler Alloy Co2TiSn. Phys. Rev. B-Condens. Matter Mater. Phys. 2005, 72, 1–4. [Google Scholar] [CrossRef]
- van Engen, P.G.; Buschow, K.H.J.; Erman, M. Magnetic Properties and Magneto-Optical Spectroscopy of Heusler Alloys Based on Transition Metals and Sn. J. Magn. Magn. Mater. 1983, 30, 374–382. [Google Scholar] [CrossRef]
- Remya, U.D.; Athul, S.R.; Arun, K.; Swathi, S.; Dzubinska, A.; Reiffers, M.; Ramamoorthi, N. Investigations on Magnetic, Magnetocaloric and Transport Properties of Co2Ti1-xSn1+x(x = 0.25, 0.5) Heusler Alloys. AIP Conf. Proc. 2021, 2369, 1–6. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent Advances in Magnetic Structure Determination by Neutron Powder Diffraction. Phys. B Condens. Matter 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Aryal, A.; Bakkar, S.; Samassekou, H.; Pandey, S.; Dubenko, I.; Stadler, S.; Ali, N.; Mazumdar, D. Mn2FeSi: An antiferromagnetic inverse-Heusler alloy. J. Alloy. Compd. 2020, 823, 153770. [Google Scholar] [CrossRef]
- Banerjee, B.K. On a Generalised Approach to First and Second Order Magnetic Transitions. Phys. Lett. 1964, 12, 16–17. [Google Scholar] [CrossRef]
- Duc, N.H.; Kim Anh, D.T.; Brommer, P.E. Metamagnetism, Giant Magnetoresistance and Magnetocaloric Effects in RCo2-Based Compounds in the Vicinity of the Curie Temperature. Phys. B Condens. Matter 2002, 319, 1–8. [Google Scholar] [CrossRef]
- Nehla, P.; Kareri, Y.; Gupt, G.D.; Hester, J.; Babu, P.D.; Ulrich, C.; Dhaka, R.S. Neutron Diffraction and Magnetic Properties of Co2Cr1-xTixAl Heusler Alloys. Phys. Rev. B 2019, 100, 1–11. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).