New Die-Compaction Equations for Powders as a Result of Known Equations Correction—Part 3: Modernization of Plasticity Equations for a Porous Body

Abstract

Equations of plasticity of a porous body proposed by different authors and obtained under the condition that the yield surface of a porous body has the shape of an ellipsoid of revolution are considered in this paper. Such equations have two independent parameters which are the functions of relative density. Various theoretical dependences of these parameters on the relative density and, as a result, various equations for describing the die-compaction of powders are presented. It is shown that the correction of two density-dependent parameters, taking into account the initial density, makes it possible to significantly increase the accuracy of approximation of experimental data on the powder compaction process (PCP) of various powders. Among the considered “continuum” equations of powder die-compaction, the PCP to a density of 0.95 is the most accurately described by the equation in which the corrected Skorokhod’s theoretical density functions are used and which contains one constant as a result. Another equation which contains four constants allows one to accurately (R² > 0.9990–0.9999) describe the PCP to a density of >0.95. This equation is obtained by replacing one of two independent parameters in the traditional continuum equation with the lateral pressure coefficient followed by substituting, instead of those parameters, their dependencies on the density in the form of power function. The adequacy of the PCP description by this equation was verified by approximating experimental data on the die-compaction of iron powders to a relative density greater than 0.95, as well as highly plastic powders with a final density of ~1.0.

1. Introduction

In Part 1 of this work [1], frequently used equations for describing the process of powders compaction (PCP) in a rigid die have been considered, and in some cases, refined. For an adequate description of PCP, these equations were proposed mainly in the form of mathematical functions as well as in the form of semi-empirical equations which contain some physical parameters of the powder material, such as the yield strength and hardening law, the forces of internal and external friction of powders, and in which such physical phenomena as the rearrangement of particles and their plastic deformation are taken into account. In Part 2 [2], two new equations were proposed to describe PCP through correction and generalization of the well-known Balshin’s equations. The new equations contain three constants, in one case, and four constant parameters, in another case, and they allow description of PCP with high accuracy when the relative density changes from the initial value to the maximum possible one.

The formulation of these equations was stipulated by the fallacy of the assertion of many researchers that it is impossible to describe the entire powder compaction process in a rigid die with one equation. By this reason, a need arose to explain the situation and obtain an answer to the question of how a multi-stage powder compaction process with different mechanisms can be described by a single equation. There is no answer to this question yet. In addition, new equations can resolve the dispute about when the particles rearrangement process ends, and what is the true deformation of particles when the powder is compacted to a practically non-porous state. No less interesting is the ability of new equations to determine the true strength of particles of different sizes and different origins, as well as the law of their strengthening. Knowledge of the true characteristics of ordinary and unusual powders opens up the prospect of obtaining more accurate data on the distribution of stress state and density in samples of complex shape when using the finite element method.

Note that new equations for compaction of powders in a rigid die were found as a result of an analysis of the equations obtained by M. Balshin within the framework of the discrete theory of compaction. But there is another approach for describing PCP in a die, which considers a powder sample as a solid body with pores. Here, the equation for PCP is a special case of the general process of a porous body deformation, which provides various schemes of the stress–strain state, such as upsetting, extrusion, radial compression of a cylinder with fixed ends, etc. From the theory of metal forming under pressure, it is known that plastic deformation under stress or axial pressure, e.g., during upsetting, occurs when the stress reaches the yield strength of the sample material. In a volume-stressed state, that is, when stress occurs in different directions, a certain combination of stresses different in direction is required for deformation to start. Since the stress state of a body under load is characterized by a stress tensor in which the stresses depend on the chosen coordinate system, stress invariants are used that do not depend on the axis direction. Of three stress invariants (linear I_1σ, quadratic I_2σ, and cubic I_3σ), the first and second ones have gained widespread use. The condition, under which plastic deformation of a solid body occurs, written in terms of the stress invariants, has the following form [3]:

$$I_{1\sigma }^2-3I_{2\sigma }={\sigma }_s^2,$$

(1)

where σ_s is the yield strength of deformable material.

When the usual stress tensor is represented as the sum of two tensors responsible for changes in the body volume (spherical tensor) and shape (stress deviator), the plasticity condition for a solid body can be written as

$$3I_{2\sigma }^{\prime }+{\sigma }_s^2=0,$$

(2)

where $I_{2\sigma }^{\prime }=I_{2\sigma }+{\displaystyle \frac{1}{3}}{I}_{1\sigma }^2$ is the second invariant of the stress deviator.

If expressing the second invariant of the stress deviator in terms of principal stresses, the plasticity condition for a solid body will have the form [3]:

$${\displaystyle \frac{1}{\sqrt{2}}}\sqrt{{({\sigma }_1-{\sigma }_2)}^2+{({\sigma }_2-{\sigma }_3)}^2+{({\sigma }_3-{\sigma }_1)}^2}={\sigma }_{s },$$

(3)

where σ₁, σ₂, σ₃ are the principal stresses in a rectangular coordinate system.

The above plasticity condition has a geometric meaning that consists in the fact that this condition in the coordinate system with the axes of principal stresses σ₁, σ₂, and σ₃ is displayed as a cylinder equally inclined to the three axes with a radius equal to $r={\sigma }_S\sqrt{2/3}$ and infinite length. In accordance with this condition, any point on the cylinder surface or any stress vector emerging from the origin of coordinates and touching the cylinder surface causes a plastic flow of a solid body.

2. Plasticity Equation for a Porous Body

2.1. General Aspects

Unlike a solid continuous body, a porous material is capable of changing its volume under the action of both tensile and compressive stress. Therefore, the plasticity condition for a porous body must take into account volumetric changes, which are absent in a solid body. Taking these volumetric changes into account leads to another form of the plasticity condition and another geometric form of the plasticity surface. Moreover, if a porous body is isotropic and the yield strength does not change with increasing strain, then one of the most effective conditions for the yield of such a body is, as noted in [4] with reference to the work of H. Kuhn and C. L. Downey [5], the following equation:

$$3I_{2\sigma }^{\prime }-\left(1-2\nu \right)I_{2\sigma }-Y^2=0,$$

(4)

where $I_{2\sigma }^{\prime }$ is the second invariant of the deviator of stress acting on the porous body, ν is the transverse strain coefficient of the porous body, and Y is the yield stress of the porous material under uniaxial compression.

If we take into account that $I_{2\sigma }={ I}_{2\sigma }^{\prime }-{\displaystyle \frac{1}{3}}{I}_{1\sigma }^2$ and Y = f(θ) × σ_s, where f(θ) is a function showing the change in the yield strength of the body in the presence of porosity θ, and make appropriate substitutions in Equation (4), we obtain the equation:

$$3I_{2\sigma }^{\prime }-{\displaystyle \frac{\left(1-2\nu \right)}{2(1+\nu )}}{I}_{1\sigma }^2-{\displaystyle \frac{3f^2\left(\theta \right)}{2(1+\nu )}}{\sigma }_s^2=0$$

(5)

On replacing the factors before the first invariant and before the yield strength with simple symbols, we obtain a simpler equation which, by its geometric meaning, reflects an ellipsoid of revolution:

$$3I_{2\sigma }^{\prime }+\alpha I_{1\sigma }^2-\beta {\sigma }_s^2=0,$$

(6)

where $\alpha =(1-2\nu )/2(1+\nu )$, $\beta =3f^2\left(\theta \right)/2(1+\nu )$.

Since the coefficient of transverse deformation of a porous body ν depends on the porosity as well, the coefficients α and β can be expressed in terms of porosity by various formulas with varying degrees of complexity, e.g., A.M. Laptev has suggested [6] the following simple approximation expressions for these coefficients:

$$\alpha =a·{\theta }^m \mathrm{and} \beta ={\left(1-\theta \right)}^{2n},$$

(7)

in which the parameters a, m, and n are determined by experiment. However, there are theoretical dependences of the coefficients α and β on porosity, e.g., the dependences proposed by R. Green [7]:

$$\alpha ={\displaystyle \frac{1}{4}}{\left[{\displaystyle \frac{3(1-{\theta }^{1/3})}{(3-2{\theta }^{1/4})ln\theta }}\right]}^2 \mathrm{and} \beta ={\left[{\displaystyle \frac{3(1-{\theta }^{1/3})}{(3-2{\theta }^{1/4})}}\right]}^2,$$

(8)

where θ is the sample porosity.

It should be noted that there are other dependences of the coefficients α and β on porosity. There are also other expressions for the plasticity equation for porous bodies with their own coefficients, but they all refer to an isotropic porous material with an ellipsoidal yield surface which, as follows from many works, most successfully describes the process of compaction of porous and powder samples. Another record of the porous body plasticity equation is given, e.g., in the article by A. Smyslov [8]:

$$S_{ij}{S}_{ij}+{\alpha }^{\prime }{\sigma }_{kk}^2-{\beta }^{\prime }{k}^2=0,$$

(9)

where S_ij are the components of the stress deviator, σ_kk are the diagonal members of the stress tensor, k is the plasticity parameter which is related to the yield strength of the particle material by the relationship $k={\sigma }_s\sqrt{2/3}$.

At the same time, A. Smyslov also offered his own theoretical dependences of coefficients α′ and β′ on porosity [8], in which we will replace porosity with relative density ρ = 1 − θ:

$$\alpha \prime ={\displaystyle \frac{\left(1-\rho \right)}{2\left(5-2\rho \right)}} \mathrm{and} \beta \prime ={\displaystyle \frac{3{\rho }^2}{\left(5-2\rho \right)}}$$

(10)

Another version of the plasticity equation for a porous body was given in V. Segal’s work [9], but the plasticity equation proposed by V. Skorokhod, I. Martynova, and M. Shtern [10,11] has become more widespread:

$${\displaystyle \frac{p^2}{\psi }}+{\displaystyle \frac{{\tau }^2}{\phi }}-\rho ·k^2=0,$$

(11)

where $\mathrm{p}={\displaystyle \frac{1}{3}}\times {\mathrm{I}}_{1\mathsf{\sigma }}=({\mathsf{\sigma }}_1+{\mathsf{\sigma }}_2+{\mathsf{\sigma }}_3)/3$ is the hydrostatic pressure, $\tau =\sqrt{2\times I_{2\sigma }^{\prime }}={\displaystyle \frac{1}{\sqrt{3}}}\sqrt{{({\sigma }_1-{\sigma }_2)}^2+{({\sigma }_2-{\sigma }_3)}^2+{({\sigma }_3-{\sigma }_1)}^2}$ is the shear stress intensity, k is the same plasticity parameter as in Equation (9), and ψ and φ are functions of porosity or relative density that characterize the change in the body porosity with change in its volume and shape, respectively.

It is important to note that in the theory of metal forming, the intensity of shear stress is interpreted as the square root of the second invariant of the stress deviator: $T=\sqrt{I_{2\sigma }^{\prime }}$ [3] and, therefore, $\tau =T\sqrt{2}$.

Theoretical porosity functions ψ and φ were proposed by V. Skorokhod [12], and in the case of replacing porosity with relative density these functions acquire the form:

$$\psi ={\displaystyle \frac{2}{3}}·{\displaystyle \frac{{\rho }^3}{\left(1-\rho \right)}} \mathrm{and} \phi ={\rho }^2$$

(12)

Since Equations (6), (9), and (11) describe the same yield surface, there is a certain relationship between the coefficients α, α′, β, β′, and ψ, φ, which is easy to obtain after writing these equations using the components of the stress tensor in the coordinate system of principal stress. After the disclosure of Equations (6), (9), and (11) using the principal stress, they are converted respectively to the following forms:

$${\displaystyle \frac{1}{2}}\left[{({\sigma }_1-{\sigma }_2)}^2+{({\sigma }_2-{\sigma }_3)}^2+{({\sigma }_3-{\sigma }_1)}^2\right]+\alpha {({\sigma }_1+{\sigma }_2+{\sigma }_3)}^2-\beta {\sigma }_s^2=0$$

(13)

$${\displaystyle \frac{1}{3}}\left[{({\sigma }_1-{\sigma }_2)}^2+{({\sigma }_2-{\sigma }_3)}^2+{({\sigma }_3-{\sigma }_1)}^2\right]+{\alpha }^{\prime }{({\sigma }_1+{\sigma }_2+{\sigma }_3)}^2-{\beta }^{\prime }{\displaystyle \frac{2}{3}}{\sigma }_s^2=0$$

(14)

$${\displaystyle \frac{1}{3\phi }}\left[{({\sigma }_1-{\sigma }_2)}^2+{({\sigma }_2-{\sigma }_3)}^2+{({\sigma }_3-{\sigma }_1)}^2\right]+{\displaystyle \frac{1}{\psi }}{\displaystyle \frac{{({\sigma }_1+{\sigma }_2+{\sigma }_3)}^2}{9}}-\rho {\displaystyle \frac{2}{3}}{\sigma }_s^2=0$$

(15)

From these equations, the following relations between the coefficients and density functions are obtained:

$$\alpha ={\displaystyle \frac{3}{2}}\alpha \prime ={\displaystyle \frac{1}{6}}{\displaystyle \frac{\phi }{\psi }} \mathrm{and} \beta =\beta \prime =\phi \rho$$

(16)

For the case of compacting powder in a rigid cylindrical die, when introducing a cylindrical coordinate system with axis z (height), r (radius), and φ (angle in the plane perpendicular to the z axis), Figure 1, and also taking into account that the radial and tangential stresses are equal and make a certain part of axial stress (expressed through the coefficient of lateral pressure, ξ) σ_r = σ_φ = ξσ_z, the above Equations (13)–(15) are transformed to the corresponding forms:

$${\sigma }_z={\sigma }_s{\displaystyle \frac{2}{3}}\sqrt{\left({\displaystyle \frac{1}{4\alpha }}+1\right)\beta }$$

(17)

$${\sigma }_z={\sigma }_s{\displaystyle \frac{2}{3}}\sqrt{\left({\displaystyle \frac{1}{6\alpha }}+1\right){\beta }^{\prime }}$$

(18)

$${\sigma }_z={\sigma }_s\sqrt{{\displaystyle \frac{2}{3}}}\sqrt{\left(\psi +{\displaystyle \frac{2}{3}}\phi \right)\rho }=k\sqrt{\left(\psi +{\displaystyle \frac{2}{3}}\phi \right)\rho }$$

(19)

Equations (17)–(19) describe the same PCP although they are written differently in forms acceptable to different researchers. In order to describe the PCP with these equations, it is necessary to know the yield strength of the powder material and the dependences of coefficients α, β, α′ and β′, or ψ and φ on relative density. For a more accurate description of PCP, it is also necessary to know the hardening law of the powder material during deformation, since plastic deformation of the powder occurs during compaction. As for the use of density-dependent coefficients, there are two possibilities. In one case, theoretical dependences α(ρ) and β(ρ) or ψ(ρ) and φ(ρ) can be used, and, in the other case, experimental ones. Experimental dependences of density functions are rarely used because they are relatively difficult to be obtained due to the need in special dies, and the theoretical dependences are quite diverse with an under-determined degree of accuracy or adequacy of them to the actual PCP. As theoretical density functions, the expressions (8), (10), and (12) are used, as well as expressions proposed by other authors, e.g., by M. Koval’chenko [13]:

$$\psi ={\displaystyle \frac{1}{6}}{\rho }^{{\displaystyle \frac{\left(2.5-\rho \right)}{\rho }}}{\displaystyle \frac{\left(2+{\rho }^{2/\rho }\right)}{\left(1-{\rho }^{2/\rho }\right)}} \mathrm{and} \phi ={\rho }^{{\displaystyle \frac{\left(2.5-\rho \right)}{\rho }}}$$

(20)

On substituting the coefficients or density functions into Equations (17)–(19), one can obtain equations that establish the relationship between the axial stress or densification pressure σ_z and the relative density ρ of the powder compacted in a rigid die. Taking into account various density functions, these equations acquire the following forms:

By R. Green [7],

$${\sigma }_z=-{\sigma }_s{\displaystyle \frac{2}{3}}\mathrm{l}\mathrm{n}(1-\rho )\sqrt{1+{\left\{{\displaystyle \frac{3[1-{(1-\rho )}^{1/3}]}{[3-2{(1-\rho )}^{1/4}]\mathrm{l}\mathrm{n}(1-\rho )}}\right\}}^2}$$

(21)

By A. Smyslov [8],

$${\sigma }_z={\sigma }_s{\displaystyle \frac{2}{3}}\sqrt{{\displaystyle \frac{(8-5\rho ){\rho }^2}{(1-\rho )(5-2\rho )}}}$$

(22)

By V. Skorokhod and M. Shtern [10,11],

$${\sigma }_z={\sigma }_s{\displaystyle \frac{2}{3}}\sqrt{{\displaystyle \frac{{\rho }^3}{(1-\rho )}}}=k\sqrt{{\displaystyle \frac{2}{3}}{\displaystyle \frac{{\rho }^3}{(1-\rho )}}}$$

(23)

By M. Koval’chenko [13],

$${\sigma }_z={\sigma }_s{\displaystyle \frac{1}{\sqrt{3}}}\sqrt{{\rho }^{2.5/\rho }{\displaystyle \frac{(2-{\rho }^{2/\rho })}{\left(1-{\rho }^{2/\rho }\right)}}}=k\sqrt{{\rho }^{2.5/\rho }{\displaystyle \frac{(2-{\rho }^{2/\rho })}{2\left(1-{\rho }^{2/\rho }\right)}}}$$

(24)

An important parameter in the above equations is the yield strength σ_s or the plasticity constant k of the powder material. In one case, researchers prefer to use the usual yield strength under uniaxial compression or the tension σ_s. In the other case, preference is given to the plasticity constant k which reflects the material resistance to shear. Considering that during tension or compression the material is actually deformed by shearing along the glide planes of dislocations rather than by stretching or compressing interatomic distances, it would be more correct to use the yield strength of the material under shear, which is reflected in the parameter k or the shear yield strength τ_s. Unfortunately, k is determined indirectly through the usual yield strength and by different formulas. In particular, in powder metallurgy, some authors determine it by the formula $k={\sigma }_s\sqrt{2/3}$ [8,13], whereas in metal forming, this parameter is obtained as $k={\sigma }_s\sqrt{1/3}$ [3]. Therefore, in powder compaction equations, it is better to use the usual and unambiguous yield strength σ_s.

The equations presented above, which relate the axial pressure to the sample density, make it possible to quantitatively describe the PCP in a rigid die. As can be seen, the same compaction process, that is, of the same powder, cannot be theoretically described unambiguously. Different authors give their own descriptions of PCP which may reflect the actual PCP with different degrees of accuracy. To assess the degree of accuracy, it is necessary to compare the theoretical compaction curve for a particular powder with the experimental compaction curve of this powder. It should be noted that in the literature, there is a large number of experimental data on the compaction of various powders, which makes it possible to check the adequacy or accuracy of the description of the real PCP by a theoretical equation. However, a certain problem in assessing the accuracy of a theoretical equation lies in the difficulty of constructing a theoretical curve because of the lack of information about the value of the yield strength and the hardening law for small (several micrometers) and even large (tens of micrometers) powder particles.

Sometimes, to construct a theoretical curve, step-by-step actions are performed such as (1) determination of the true deformation of particles at a small degree of compaction, (2) substitution of the deformation value into the known law of hardening of the bulk material from which the powder is made to determine a new yield strength, (3) substitution of a new yield strength into the theoretical equation, and (4) determination of compaction pressure for new values of density and yield strength. By repeating these actions with a stepwise increase in density, one can finally construct a theoretical compaction curve that takes into account the strengthening of particles during deformation. However, to implement such a technique, it is necessary to know the true value of particle deformation at a given density level. Here are the equations that allow determining the value of the true deformation of particles for PCP in a rigid die, depending on the compaction density and specific coefficients or density functions present in Equations (17) and (19):

For Equation (17) with coefficients α and β:

$${ϵ}_p={\displaystyle \frac{2}{3}}\underset{{\rho }_0}{\overset{\rho }{\int }}\sqrt{\left({\displaystyle \frac{1}{4\alpha }}+1\right)\beta }{\displaystyle \frac{d\rho }{{\rho }^2}}$$

(25)

For Equation (19) with coefficients ψ and φ:

$${ϵ}_p=\sqrt{{\displaystyle \frac{2}{3}}}\underset{{\rho }_0}{\overset{\rho }{\int }}\sqrt{\left(\psi +{\displaystyle \frac{2}{3}}\phi \right)\rho }{\displaystyle \frac{d\rho }{{\rho }^2}}$$

(26)

When considering the above equations for determining the true deformation of particles, two points deserve special attention. The first point is that the theoretical deformation of particles is an ambiguous quantity and depends on the form of coefficients or density functions. Consequently, different authors propose their own density functions, according to which the amount of the true deformation happens to be different and to a different extent correspond to the real deformation of particles. The second point is related to the physical concept of powder deformation, since deformation, like the yield strength, is determined in two ways. In one case, the deformation reflects the change in the sample length under tension or compression; in the other, it reflects the degree of shear under the same tension or compression. Since the real deformation is practically due to shear, it is more correct to operate with shear strain, which is not directly measured but can be calculated from the true tensile or compression strain. In particular, in [11,12,14], the shear strain is determined by the formula:

$$\mathsf{\gamma }=\sqrt{{\displaystyle \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}·{ϵ}_p,$$

(27)

while in the theory of metal forming, a different formula is used:

$$\mathsf{\Lambda }=\sqrt{3}·{ϵ}_p,$$

(28)

where ${ϵ}_p$ is the true deformation equivalent to compression or tension.

If we dwell on the former relation, then in order to obtain the average shear deformation of powders under their compaction, Formulas (25) and (26) must be rewritten in such a way:

$${\mathsf{\gamma }}_p=\sqrt{{\displaystyle \frac{2}{3}}}{\int }_{{\rho }_0}^{\rho }\sqrt{\left({\displaystyle \frac{1}{4\alpha }}+1\right)\beta }{\displaystyle \frac{d\rho }{{\rho }^2}}$$

(29)

$${\mathsf{\gamma }}_p={\int }_{{\rho }_0}^{\rho }\sqrt{\left(\psi +{\displaystyle \frac{2}{3}}\phi \right)\rho }{\displaystyle \frac{d\rho }{{\rho }^2}}$$

(30)

Thus, knowing the density functions, it is possible to determine the degree of the true deformation of powder, which is similar to the deformation of tension or compression, using Formulas (25) and (26), respectively, as well as the value of the true shear deformation using Formulas (29) and (30). Since the hardening law for plastic deformation of a material is determined under tension or compression, then in order to estimate the yield strength of powders as a result of their deformation under compaction, it is necessary to determine the degree of this deformation using Formulas (25) and (26). If we substitute the theoretical density functions proposed by V. Skorokhod [12] or M. Koval’chenko [13] into Formula (26), we obtain, respectively, the final equation showing the dependence of the true linear deformation of particles on the relative density of the powder sample:

$${ϵ}_p={\displaystyle \frac{2}{3}}{\int }_{{\rho }_0}^{\rho }\sqrt{{\displaystyle \frac{1}{\left(1-\rho \right)\rho }}} d\rho$$

(31)

or

$${ϵ}_p=\sqrt{{\displaystyle \frac{2}{3}}}{\int }_{{\rho }_0}^{\rho }{\rho }^{\left(2.5-4\rho \right)/2\rho }\sqrt{{\displaystyle \frac{\left(2-{\rho }^{2/\rho }\right)}{2\left(1-{\rho }^{2/\rho }\right)}}}d\rho .$$

(32)

Numerical integration of expressions (31) and (32), although the integral in (31) is taken in elementary functions, makes it possible to determine the degree of powder deformation when the relative density changes within the given limits, e.g., when changing the relative density from 0.3 to 0.99, the degree of plastic deformation of the particles is 1.188 by Formula (31) and 0.649 by Formula (32). Thus, different density functions applied to the same Formula (26) lead to significantly different values of the true powder deformation under compaction in the same density range. Therefore, even if the hardening law of the powder material is known, due to different theoretical density functions and, consequently, different degrees of particle deformation, it is difficult to unambiguously determine the real yield strength of the powder as it is densified and strengthened.

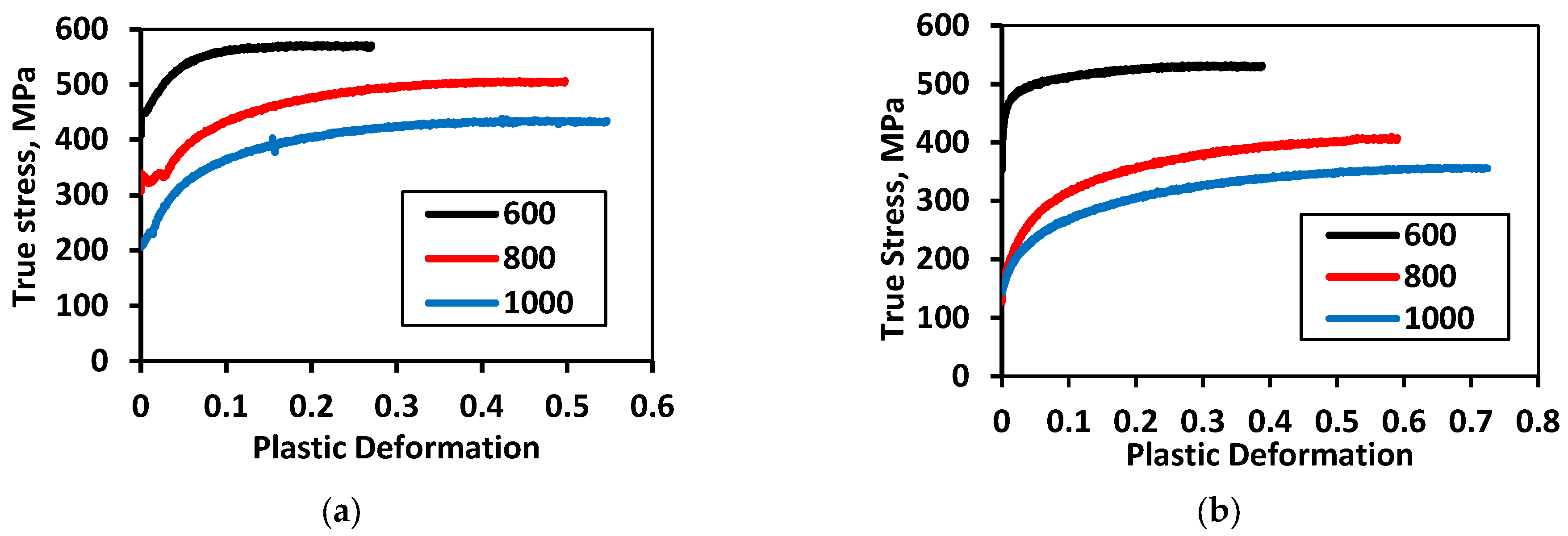
Along with the ambiguous situation in determining the true deformation of powder particles, there is also a similar situation with the hardening law for micron-sized metal particles. The hardening law for fine powder particles can differ significantly from that for massive compact materials due to the differences in their structure. To confirm this thesis, we present the results of our own research on compression at room temperature of samples obtained from the same powder, but having different microstructures due to compaction of the powder at different temperatures. The compression test results for specimens made from two different iron powders, which were obtained by impact compaction at different temperatures, are shown in Figure 2. More detailed information about the structure and properties of samples made from coarse-grained and fine-grained iron powders by impact sintering at different temperatures is given in article [15].

It is important to note that Figure 2 shows only irreversible deformation, that is, deformation without an elastic component, which can be easily subtracted from the total deformation during computer processing of the compression diagram obtained on the testing machine. In the presented graphs, there is either obvious yield strength, Figure 2a, or the conditional yield strength which corresponds to a relative plastic deformation equal to 0.002, Figure 2b. Relative plastic strain was defined as the natural logarithm of the ratio of the initial height of the sample to its current height during compression.

Figure 2 demonstrates that the hardening laws for the same material but obtained from powder at different temperatures differ significantly. Consequently, the laws of hardening of a microscopic metal particle and a monolithic sample of the same metal can be fundamentally different as well. The particle hardening law is generally unknown, and it is rather difficult to establish it. Therefore, it is almost impossible to construct a theoretical powder compaction curve using equations, e.g., (23) and (24), without knowing the true yield stress and the particle hardening law.

2.2. Correction of “Continual” Equations

When compacting the powder in a rigid die, some experts, in particular, A. M. Laptev [6], admit that the yield strength can be constant during the whole PCP and depend on the material and type of powder. In this case, it becomes possible to use the above equations for compaction of a porous sample in a rigid die to approximate the experimental data on compaction of various powders and, as a result, determine the average yield strength of the powder particles. However, before using Equations (21)–(24), it is necessary to bear in mind the fact that they provide changes in relative density from zero to one, whereas in reality the axial pressure begins to increase from a relative density equal to the initial powder density ρ₀. Therefore, it is advisable to correct the compaction equations with respect of the powder initial density. Since the final form of the equations depends on the form of the density functions, it is necessary first of all to correct these density functions according to Formulas (10) and (12). The coefficients in Formula (8) are quite complex, and the density functions according to Formula (20) implicitly take into account a certain level of initial density.

The correction of coefficients and density functions according to Formulas (10) and (12), taking into account the initial density, resulted in the corresponding forms:

$$\alpha \prime ={\displaystyle \frac{\left(1-\rho \right)}{2\left(5-3{\rho }_0-2\rho \right)}} \mathrm{and} \beta \prime ={\displaystyle \frac{3{\left(\rho -{\rho }_0\right)}^2}{\left(1-{\rho }_0\right)\left(5-3{\rho }_0-2\rho \right)}}$$

(33)

$$\psi ={\displaystyle \frac{2}{3}}·{\displaystyle \frac{{\left(\rho -{\rho }_0\right)}^3}{{\left(1-{\rho }_0\right)}^2·\left(1-\rho \right)}} \mathrm{and} \phi ={\displaystyle \frac{{\left(\rho -{\rho }_0\right)}^2}{{\left(1-{\rho }_0\right)}^2}}$$

(34)

On substituting Formulas (33) and (34) into Equations (18) and (19), respectively, we obtain new dependences of axial pressure on the relative density, in which the axial pressure is zero at the initial density ρ₀:

$${\sigma }_z={\sigma }_s{\displaystyle \frac{2}{3}}\sqrt{{\displaystyle \frac{(8-3{\rho }_0-5\rho )·{\left(\rho -{\rho }_0\right)}^2}{\left(1-{\rho }_0\right)(1-\rho )(5-3{\rho }_0-2\rho )}}}$$

(35)

$${\sigma }_z={\sigma }_s{\displaystyle \frac{2}{3}}\sqrt{{\displaystyle \frac{{\left(\rho -{\rho }_0\right)}^3}{{\left(1-{\rho }_0\right)}^2·(1-\rho )}}}=k\sqrt{{\displaystyle \frac{2}{3}}{\displaystyle \frac{{\left(\rho -{\rho }_0\right)}^3}{{\left(1-{\rho }_0\right)}^2(1-\rho )}}}.$$

(36)

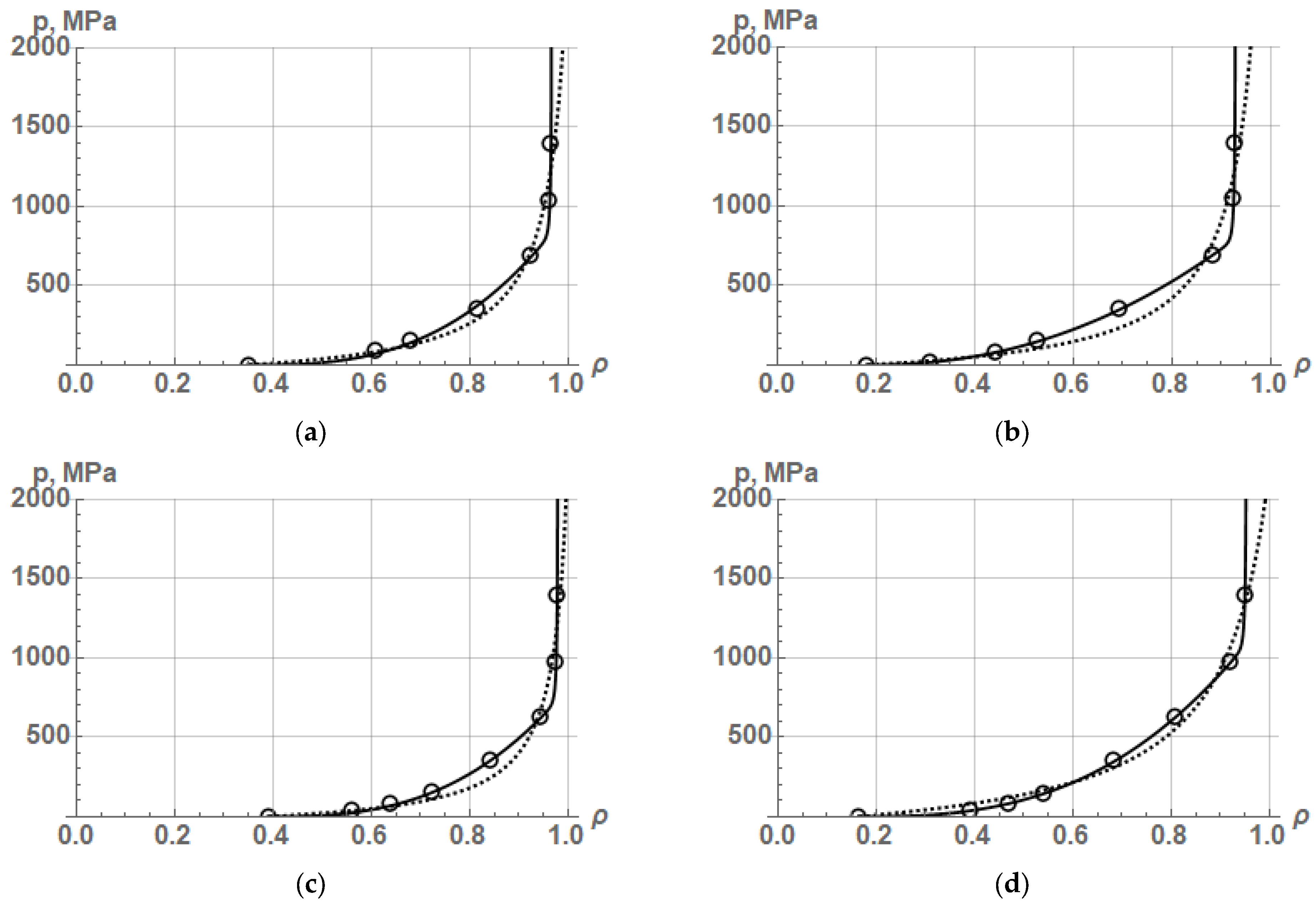
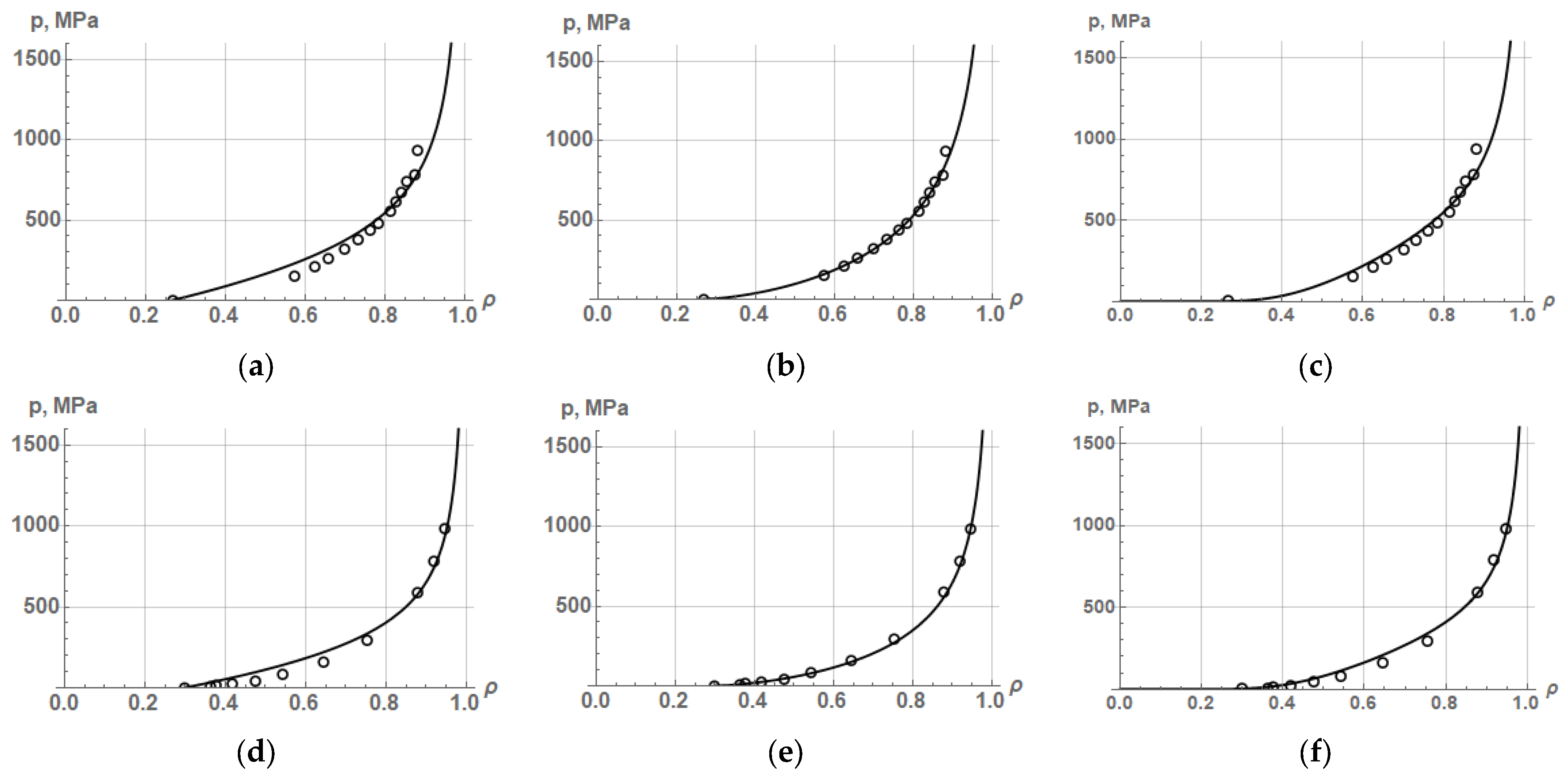
Let us approximate the experimental data on the compaction of iron, copper, nickel, and titanium powders presented in [16,17,18,19], respectively, using the corrected Equations (35) and (36), and the initial Equation (24). The results of approximation of experimental data on the compaction of iron and copper powders by Equations (24), (35), and (36) are shown in Figure 3, and the values of the average yield strength and the coefficient of determination R² are listed in

Table 1. Yield strength σ_s and coefficient of determination R² obtained through approximation of experimental data on PCP of iron [16] and copper [17] using the corrected equations of Smyslov (35) and Skorokhod–Martynova–Shtern (36), as well as the original Koval’chenko Equation (24).

Parameter	Powder
	Iron			Cooper
	Equation			Equation
	(35)	(36)	(24)	(35)	(36)	(24)
ρ0	0.268			0.3
σs, MPa	528.38	668.26	737.22	405.85	461.56	551.27
R2	0.94752	0.99802	0.96597	0.98477	0.99735	0.99304

.

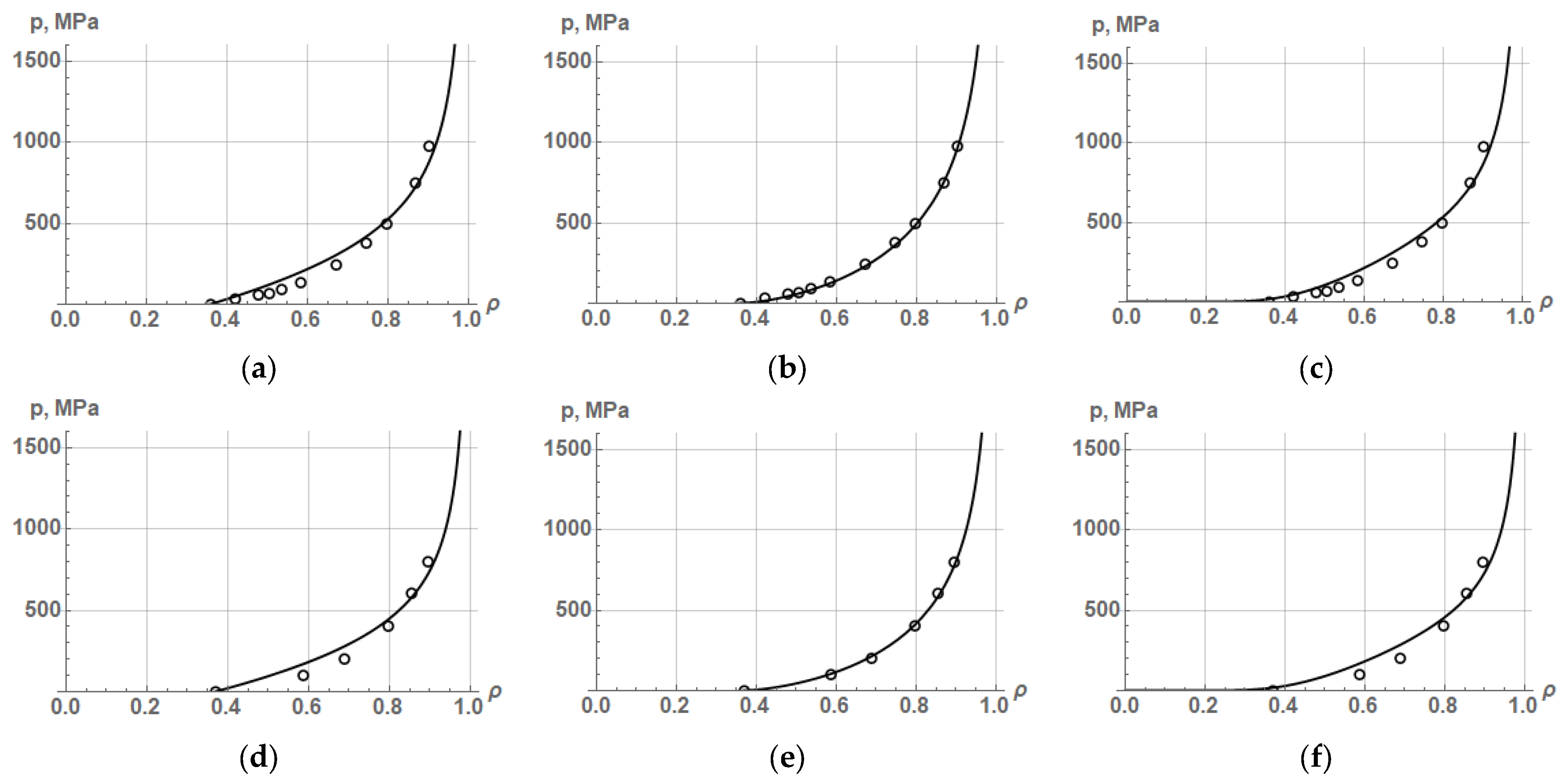
The results of approximation of experimental data on the compaction of nickel and titanium powders by Equations (24), (35), and (36) are shown in Figure 4, and the values of the average yield strength and the coefficient of determination R² are listed in

Table 2. Yield stress and coefficient of determination R² obtained through approximation of experimental data on the compaction of nickel [18] and titanium [19] powders using the corrected equations of Smyslov (35) and Skorokhod–Martynova–Stern (36), as well as the original Kovalchenko Equation (24).

Parameter	Powder
	Nickel			Titanium
	Equation			Equation
	(35)	(36)	(24)	(35)	(36)	(24)
ρ0	0.36			0.37
σs, MPa	569.61	724.36	717.13	494.50	622.86	612.79
R2	0.97104	0.99941	0.97127	0.96307	0.99918	0.95646

.

The results of approximation by Equations (24), (35), and (36) of experimental data on the compaction of various powders show that the highest accuracy of the PCP description (R² = 0.997–0.999) is provided by the corrected Skorokhod–Martynova–Shtern Equation (36). This means that the theoretical density functions proposed by V. Skorokhod, after their correction, are very close to real or experimental density functions. However, this is true for the compaction of plastic powders in the range of relative density from the initial density to a density of 0.9–0.95.

Quite remarkable is the fact that Equation (36) is similar in form to the new equation, which is based on the analysis of the discrete Balshin’s equation and presented in Part 2 of this work ([2] Equation (9)). Let us compare these equations:

Equation (36) on a continuum basis: ${\sigma }_z={\sigma }_s{\displaystyle \frac{2}{3}}·{\displaystyle \frac{1}{{\left(1-{\rho }_0\right)}^{(1.5-0.5)}}}·{\displaystyle \frac{{\left(\rho -{\rho }_0\right)}^{1.5}}{{(1-\rho )}^{0.5}}}$;

Equation (9) from [2] on a discrete basis: $p=w·{\displaystyle \frac{1}{{(1-{\rho }_0)}^{(n-m)}}}·{\displaystyle \frac{{(\rho -{\rho }_0)}^n}{{(1-\rho )}^m}}$.

A visual comparison of the equations makes it evident that Equation (36) with corrected theoretical density functions is a special case of the new equation on a discrete basis with arbitrary exponents in the numerator and denominator of the equation. Therefore, Equation (36) can describe quite accurately some experimental PCPs.

In particular, when approximating the compaction process of titanium powder, Equation (36) (that is, an equation with one constant) provides a description of the experimental curve with an accuracy of R² = 0.99918. However, the new equation on a discrete basis (9) from [2] gives higher approximation accuracy, R² = 0.99989, and more accurate values of exponents n = 1.59301 (instead of n = 1.5) and m = 0.51491 (instead of m = 0.5).

When approximating the compaction process of other powders, the discrepancy between the experimental values of n and m and their theoretical values, n = 1.5 and m = 0.5, increases, e.g., for copper powder from [17], it turned out that n = 1.8683 and m = 0.3453 along with a higher accuracy R² = 0.99985 versus R² = 0.99735, and for nickel powder from [18], n = 1.3527 and m = 0.5394 along with a higher accuracy of R² as well: R² = 0.99977 versus R² = 0.99941. These examples show that the corrected equation on a continuum basis with the theoretical density functions of V. Skorokhod is able to accurately describe the process of compaction of various powders. However, the new Equation (9) from [2] on a discrete basis is more flexible and more accurate when describing PCP in a rigid die.

A more accurate description of the PCP by Equation (36) makes it possible to determine more accurately the degree of plastic deformation of particles under compaction in a given range of density changes. The formula for determining linear plastic deformation in this case will be the following:

$${ϵ}_p={\displaystyle \frac{2}{3}}·{\displaystyle \frac{1}{(1-{\rho }_0)}}{\int }_{{\rho }_0}^{\rho }\sqrt{{\displaystyle \frac{{(\rho -{\rho }_0)}^3}{\left(1-\rho \right)}}}·{\displaystyle \frac{d\rho }{{\rho }^2}}.$$

(37)

Moreover, the degree of deformation can be calculated even more accurately using the new Equation (9) from [2], assuming that the constant w = σ_S(2/3). In this case, the formula for determining the degree of linear deformation will look as

$${ϵ}_p={\displaystyle \frac{2}{3}}·{\displaystyle \frac{1}{{(1-{\rho }_0)}^{(n-m)}}}{\int }_{{\rho }_0}^{\rho }{\displaystyle \frac{{(\rho -{\rho }_0)}^n}{{\left(1-\rho \right)}^m}}·{\displaystyle \frac{d\rho }{{\rho }^2}}.$$

(38)

It is of interest to compare the results of approximation of experimental data on PCP for iron, copper, nickel, and titanium powders using Equation (36) and the new Equation (9) from Part 2 [2] in order to compare the values of the yield strength of particles, their plastic deformation, work of plastic deformation, and accuracy of the approximation by the coefficient of determination R². All these data are given in

Table 3. Yield strength, plastic deformation, and work of deformation of iron, copper, nickel, and titanium particles, obtained through approximating the experimental PCP by Equation (36) and Equation (9) from [2].

Parameter	Powder
	Fe		Cu		Ni		Ti
	Equation		Equation		Equation		Equation
	(36)	(9) [2]	(36)	(9) [2]	(36)	(9) [2]	(36)	(9) [2]
Δρ = ρ − ρ0	0.616		0.649		0.543		0.528
σS, MPa	668.26	464.06	461.56	687.72	724.36	654.56	622.86	622.98
εP	0.4506	0.6703	0.5284	0.3599	0.3527	0.4027	0.3323	0.3182
WP, J/cm3	301.09	311.08	243.88	247.49	255.47	263.57	206.97	198.21
R2	0.99154	0.99333	0.99735	0.99985	0.99941	0.99977	0.99918	0.99989

.

Table 3 indicates that the corrected Skorokhod–Martynova–Shtern Equation (36) and new Equation (9) presented in Part 2 [2] describe the process of compaction of metal powders to a density of 0.9–0.95 quite accurately, and give almost the same values for the work of powder deformation but different values for the yield strength and the plastic deformation of particles. Herein, the values of the strength and plasticity characteristics of the particles obtained by Equation (9) can be closer to real values.

2.3. Second Correction of “Continual” Equations

When considering the powders compaction process (PCP) in a rigid die, it is necessary to pay attention to the fact that the new Equation (9) on a discrete basis from Part 2 [2], as well as Equation (36) obtained here on a continuous basis, cannot describe the PCP with high accuracy in cases where compaction reaches an extremely high density, which is less than 1 and does not increase with a significant increase in the compaction pressure. For such a case, another equation on a continuum basis has been derived.

As known, the density functions ψ and φ characterize the influence of relative density or porosity on the change in bulk modulus of elasticity K and shear modulus G of a porous material under elastic deformation. These modules reflect the change in the volume and shape of material under effect of a certain stress state. There are two more constants used in the theory of elasticity, through which the bulk modulus of elasticity K and the shear modulus G can be expressed. They are Young’s modulus E and Poisson’s ratio ν. Experimentally, it is much easier to determine Young’s modulus and Poisson’s ratio of a porous material, and therefore in the literature there are experimental dependences of these characteristics on the porosity, from which it is easy to determine the constants of the bulk modulus and the shear modulus:

$$K={\displaystyle \frac{E}{3\left(1-2\nu \right)}} \mathrm{and} G={\displaystyle \frac{E}{2\left(1+\nu \right)}}$$

(39)

In order not to replace one constant with another, one sometimes uses Poisson’s ratio ν (with its well-known dependence on density) as one of the density functions. In particular, for PCP in a rigid die, A. M. Laptev has proposed the following equation containing Poisson’s ratio [20]:

$${\sigma }_z=\sqrt{{\displaystyle \frac{2}{3}}}\sqrt{{\displaystyle \frac{\left(1-\nu \right)}{\left(1-2\nu \right)}}}·{\phi }_0{\sigma }_s,$$

(40)

where ν and φ₀ are density-dependent parameters.

In this case, the author [20] proposes to use the following dependences of Poisson’s ratio $\nu$ and parameter φ₀ on the relative density:

$$\nu =0.5{\rho }^{1.92} \mathrm{and} {\phi }_0={\rho }^{2.5}$$

(41)

On substituting these dependences into Equation (40), a simple equation is obtained to describe the PCP in a rigid die:

$${\sigma }_z={\sigma }_s\sqrt{{\displaystyle \frac{2}{3}}}\sqrt{{\displaystyle \frac{\left(2-{\rho }^{1.92}\right)}{2\left(1-{\rho }^{1.92}\right)}}}{\rho }^{2.5}$$

(42)

An attempt to replace one of the density functions with Poisson’s ratio was also made by M. Koval’chenko [13], where one of the formulas for describing PCP in a rigid die does not contain the density function ψ but includes the density-dependent Poisson’s ratio ν:

$${\sigma }_z={\tau }_s\sqrt{{\displaystyle \frac{\left(1-\nu \right)\rho \phi }{\left(1-2\nu \right)}}}={\sigma }_s\sqrt{{\displaystyle \frac{2}{3}}}\sqrt{{\displaystyle \frac{\left(1-\nu \right)\rho \phi }{\left(1-2\nu \right)}}}.$$

(43)

On substituting the Poisson’s ratio proposed by M. Koval’chenko for a porous body in the form $\nu =0.5{\rho }^{2/\rho }$ and the density function φ in the form $\phi ={\rho }^{\left(2.5-\rho \right)/\rho }$ into this equation, it becomes just the same as Equation (24).

Thus, the equation derived from the theory of plasticity of a porous body, which describes PCP in a rigid die, contains two parameters that depend on relative density. At the same time, taking into account the fact that during powder compaction the volume and the shape of the compact change, it is quite reasonable to use parameters or density functions in the powder compaction equation, which characterize the change in volume, i.e., parameter ψ, and the change in shape, i.e., parameter φ. Moreover, the use of them is suitable for different powder compaction schemes, such as upsetting, radial compression of the cylinder, pressing in a rigid die, or uniform compression. At the moment, particularly the scheme of pressing in a rigid die is of interest to us, where, as shown above, sometimes an equation is used in which, instead of the parameter responsible for the change in volume, a parameter characterizing the relative transverse change in the size of the powder blank during compaction is used, i.e., parameter ν. However, when compacting a powder blank in a rigid die, there is no transverse deformation of the blank, and therefore the use of parameter ν in the equation is illogical.

It seems quite reasonable to use another parameter for PCP in a rigid die, namely, the lateral pressure coefficient ξ instead of the transverse deformation coefficient ν. This is easy to do, since there is a relationship between the lateral pressure coefficient and the Poisson’s ratio [16,21]:

$$\xi ={\displaystyle \frac{\nu }{1-\nu }} \mathrm{or} \nu ={\displaystyle \frac{\xi }{1+\xi }}.$$

(44)

On substituting relation (44) into Equation (43), the simplest equation is obtained to describe PCP in a rigid die:

$${\sigma }_z={\sigma }_s\sqrt{{\displaystyle \frac{2}{3}}}\sqrt{{\displaystyle \frac{\rho \phi }{\left(1-\xi \right)}}}=k\sqrt{{\displaystyle \frac{\rho \phi }{\left(1-\xi \right)}}}.$$

(45)

Equation (19) can be transformed to the same form as well if we replace the parameter ψ with the relation between ψ and ξ, which, taking into account the relation from [11,21]:

$$\nu =\left(\psi -{\displaystyle \frac{1}{3}}\phi \right)/\left(2\psi +{\displaystyle \frac{1}{3}}\phi \right)$$

(46)

and the relation (44), looks as:

$$\psi ={\displaystyle \frac{1}{3}}\phi {\displaystyle \frac{1+2\xi }{1-\xi }}$$

(47)

Equation (45) can also be obtained from Equation (17) if we replace the coefficient α with its expression in terms of the lateral pressure coefficient ξ from [6]:

$$\alpha ={\displaystyle \frac{(1-\xi )}{2(1+2\xi )}}$$

(48)

Substituting this relation into Equation (17) leads to the following equation:

$${\sigma }_z={\sigma }_s\sqrt{{\displaystyle \frac{2\beta }{3(1-\xi )}}}=k\sqrt{{\displaystyle \frac{\beta }{1-\xi }}}$$

(49)

Equations (49) and (45) are identical, since β = φρ (see relation (16)).

It is important to emphasize that Equation (45) (or Equation (49)) is not original: it repeats the well-known plasticity equation but with other parameters or density functions. It turned out to be very effective for approximating experimental data on the compaction of various powder using the simplest dependences on density for parameters β and ξ:

$$\beta ={\rho }^n \mathrm{and} \xi =a{\rho }^m$$

(50)

On substituting these dependences into Equation (49), the simplest plasticity equation is obtained which makes it possible to approximate the PCP in a rigid die and obtain approximate dependences with parameters or constants for each specific powder:

$${\sigma }_z={\sigma }_s\sqrt{{\displaystyle \frac{2}{3}}}\sqrt{{\displaystyle \frac{{\rho }^n}{(1-a{\rho }^m)}}}=k{\displaystyle \frac{{\rho }^{0.5n}}{\sqrt{1-a{\rho }^m}}}=k{\displaystyle \frac{{\rho }^{n^{\prime }}}{\sqrt{1-a{\rho }^m}}},$$

(51)

where σ_s, n, a, and m are generally unknown parameters determined from the experiment by approximating specific experimental data on PCP using this equation.

At the same time, attention should be paid to the fact that approximation by Equation (51) of experimental data on PCP implies the fulfillment of the condition under which the yield strength of powder particles remains constant during the whole PCP. The question of the legitimacy of accepting such a condition for an adequate description of the plastic powder compaction process is still open, but the fulfillment of this condition allows Equations (36) and (51) to describe the PCP with a very high accuracy. With this, Equation (51) allows describing PCP up to the limiting density with high accuracy, despite the absence of initial density.

In addition, Equation (51) can be modified, taking into account the initial density. For this, we substitute the expression (ρ − ρ₀)/(1 − ρ₀) instead of ρ in Equation (51). As a result, it takes the following form:

$${\sigma }_z={\overline{\sigma }}_s\sqrt{{\displaystyle \frac{2}{3}}}·\sqrt{{\displaystyle \frac{{\left(1-{\rho }_0\right)}^{\left(\overline{m}-\overline{n}\right)}{\left(\rho -{\rho }_0\right)}^{\overline{n}}}{{\left(1-{\rho }_0\right)}^{\overline{m}}-\overline{a}{\left(\rho -{\rho }_0\right)}^{\overline{m}}}}}={\overline{\sigma }}_s\sqrt{{\displaystyle \frac{2}{3}}}·{\displaystyle \frac{{(1-{\rho }_0)}^{0.5(\overline{m}-\overline{n})}{(\rho -{\rho }_0)}^{0.5\overline{n}}}{{\left[{(1-{\rho }_0)}^{\overline{m}}-\overline{a}{(\rho -{\rho }_0)}^{\overline{m}}\right]}^{0.5}}}.$$

(52)

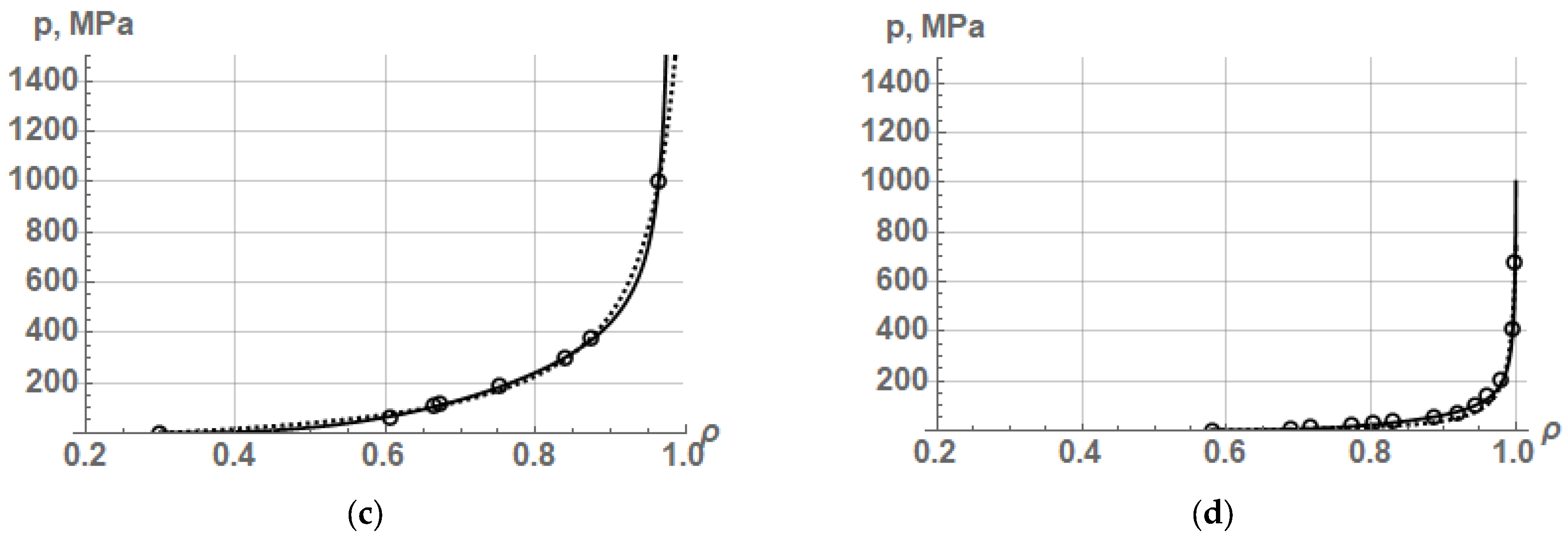
There are four constants in this equation, ${\overline{\sigma }}_s$, $\overline{n}$, $\overline{a}$, and $\overline{m}$, which can be determined through approximating experimental data on the compaction of various powders. Let us show examples of approximation by this equation of unique experimental data on the compaction of various iron powders given in the book by R. Kieffer and W. Hotop [22]. We have already partially used them in [1] (Table 5) and in [2] (Table 4). Here, we use all nine powders for the approximation and will perform approximation using not only the new Equation (52) but also the well-known Kawakita–Ludde Equation [23], which was converted in [1] into the dependence of pressure on relative density—Equation (16). The results of approximation of nine iron powders by the new Equation (52) and Equation (16) by K. Kawakita and K.H. 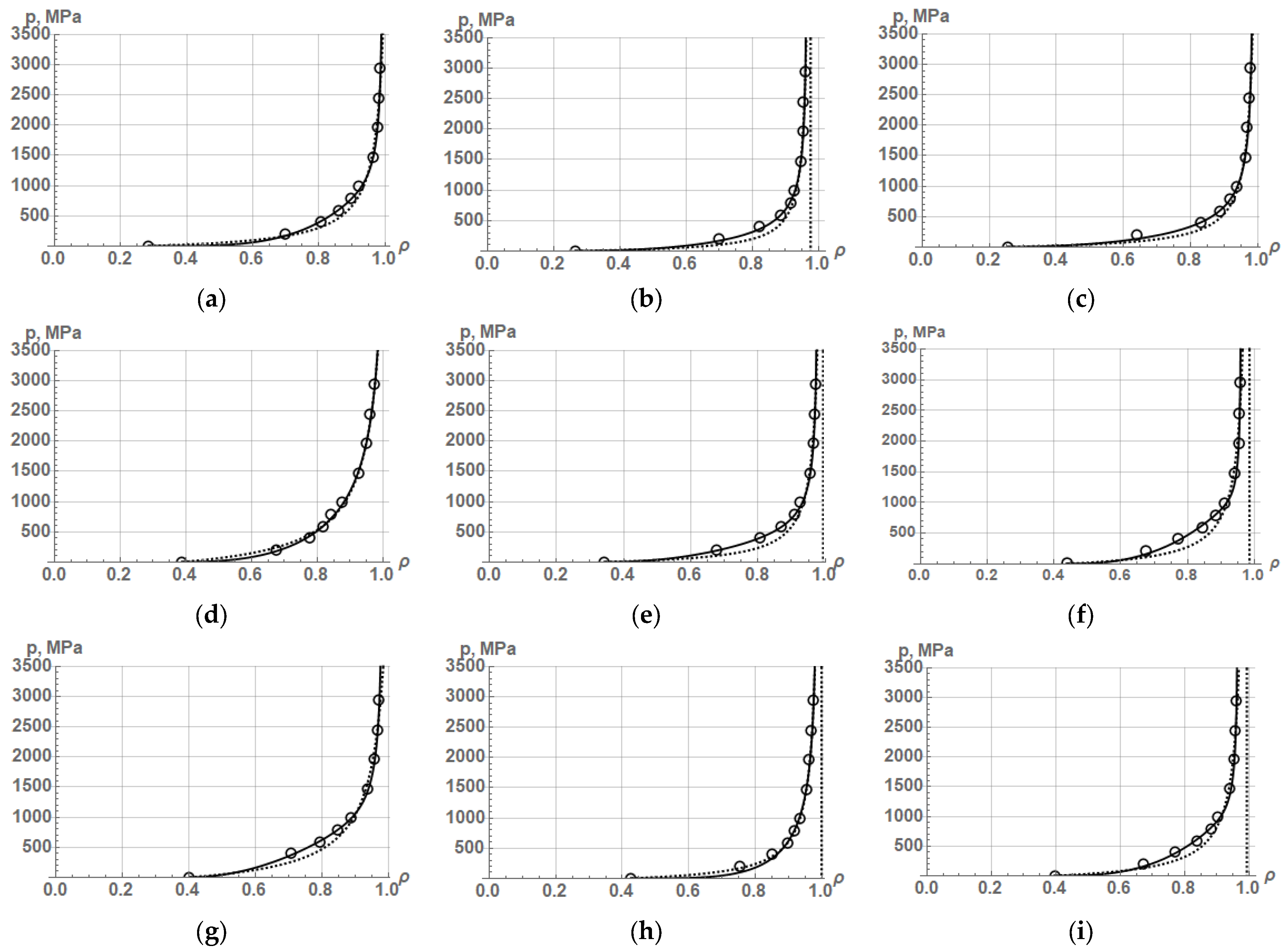Lüdde from [1] are shown in Figure 5, and the obtained values of the constants of Equation (52) and Equation (16) from [1] along with the coefficient of determination R² are presented in

Table 4. Constant parameters and coefficient of determination R² obtained through approximation by Equation (52) and Equation (16) from [1] of the experimental data on compaction of various iron powders from [22], as well as the values of the specific work of PCP, W_pd, and plastic deformation of particles under compaction, ε_p.

Parameter	Iron Powders Obtained in Various Ways
	FeKH1	FeKH2	FeKH3	FeKH4	FeKH5	FeKH6	FeKH7	FeKH8	FeKH9
ρ0	0.285	0.266	0.256	0.389	0.344	0.439	0.403	0.427	0.397
	Equation (52)
σS, MPa	1675	450	390	570	980	1770	1655	530	1845
$\overline{n}$	3.8135	2.0252	1.7970	2.1369	2.1326	2.5733	1.9253	3.5912	2.8892
$\overline{a}$	1.1919	1.0926	1.0198	0.9949	1.2824	8.9231	1.3568	1.0177	4.0591
$\overline{m}$	20.749	1.7984	1.1693	0.3968	7.1418	30.449	10.580	0.7733	23.973
ρ∞	0.9940	0.9647	0.9876	1.0079	0.9775	0.9610	0.9830	0.9871	0.9657
R2	0.99821	0.98811	0.99590	0.99694	0.99838	0.99331	0.99755	0.99464	0.99879
Wpd, J/cm3	288.62	249.83	296.62	377.51	291.46	266.78	418.36	179.79	284.14
εp	0.1723	0.5552	0.7613	0.6623	0.2959	0.1507	0.2528	0.3392	0.1540
	Equation (16) [1]
b, ×10−2	2.7753	5.6503	4.5114	0.86996	2.8926	1.5898	0.94425	1.8345	1.6416
b′ = 1/b, MPa	36.03	17.70	22.17	114.95	34.57	62.9	105.90	54.51	60.92
a	0.72048	0.72736	0.74478	0.62472	0.65408	0.55488	0.60821	0.57276	0.60027
ρ∞	1.0196	0.9756	1.0015	1.0366	0.9944	0.9862	1.0286	0.9995	0.9932
R2	0.98164	0.98056	0.99014	0.99658	0.98282	0.95471	0.98071	0.99761	0.97384
Wpd, J/cm3	306.93	198.62	249.81	429.55	224.64	220.07	370.87	222.25	260.26

.

As seen from the graphs in Figure 5 and the values of the determination coefficient R² in Table 4, the new Equation (52) provides a fairly accurate description of the compaction process for almost all iron powders. The Kawakita–Ludde equation, in which there are only two constants, in some cases, namely, FeKH3, FeKH4, and FeKH8 powders, is capable to describe the compaction process with a high accuracy as well. However, it is difficult to determine the degree of plastic deformation of particles from the Kawakita–Ludde equation, whereas from Equation (53), the linear plastic deformation can be determined by the following formula:

$${ϵ}_p=\sqrt{{\displaystyle \frac{2}{3}}}·{(1-{\rho }_0)}^{0.5(\overline{m}-\overline{n})}{\int }_{{\rho }_0}^{\rho }\sqrt{{\displaystyle \frac{{(\rho -{\rho }_0)}^{\overline{n}}}{\left[{\left(1-{\rho }_0\right)}^{\overline{m}}-\overline{a}{\left(\rho -{\rho }_0\right)}^{\overline{m}}\right]}}}·{\displaystyle \frac{d\rho }{{\rho }^2}}.$$

(53)

Numerical integration of Equation (53) within the limits of relative density change from the initial density to the density corresponding to the compaction pressure of 2940 MPa makes it possible to determine the degree of plastic deformation of particles under compaction. Apart from the value of plastic deformation, the work of plastic deformation or the work of powder densification is also important. The formula for determining the densification work has been given at the very beginning of Part 1 [1]. The results of calculating the specific compaction work of iron powders using Equation (52) and the Kawakita–Ludde Equation (16) from [1] are given in

Table 5. Specific work of plastic deformation W_pd under compaction of iron powders calculated by Equations (16) and (52) from [1] and degree of plastic deformation ε_p calculated by Equation (53), as well as the degree of the change in relative density due to plastic deformation Δρ_d by Equation (54) and due to the rearrangement of particles by the formula $\mathsf{\Delta }{\rho }_r=\mathsf{\Delta }\rho -\mathsf{\Delta }{\rho }_d$.

Parameter	Iron Powders Obtained in Various Ways
	FeKH1	FeKH2	FeKH3	FeKH4	FeKH5	FeKH6	FeKH7	FeKH8	FeKH9
ρf	0.987	0.96	0.981	0.976	0.972	0.958	0.972	0.976	0.961
Δρ = ρf–ρ0	0.702	0.694	0.725	0.587	0.628	0.519	0.569	0.549	0.564
	Equation (52)
Wpd, J/cm3	288.62	249.83	296.92	377.51	291.46	266.78	418.36	179.79	284.14
	Equation (16) [1]
Wpd, J/cm3	306.93	198.62	249.81	429.55	224.64	220.07	370.87	222.25	260.26
	Equation (53)
εp	0.1723	0.5552	0.7613	0.6623	0.2959	0.1507	0.2528	0.3392	0.1540
	Change in relative density due to deformation Δρd and rearrangement Δρr
Δρd	0.156	0.409	0.523	0.472	0.249	0.134	0.217	0.281	0.137
Δρr	0.546	0.285	0.202	0.115	0.379	0.385	0.352	0.268	0.427

. In addition, this table shows the data on the degree of plastic deformation of iron powders calculated by Equation (53), as well as the degree of change in relative density Δρ_d due to plastic deformation, which is determined by the formula:

$$∆{\rho }_d={\rho }_f·\left[1-\mathrm{e}\mathrm{x}\mathrm{p}(-{ϵ}_p)\right],$$

(54)

where ρ_f is the final relative density of powder samples corresponding to a pressure of 2940 MPa.

Knowing the change in relative density due to plastic deformation, it is possible to determine the change in relative density due to the rearrangement of particles $\mathsf{\Delta }{\rho }_r=\mathsf{\Delta }\rho -\mathsf{\Delta }{\rho }_d$, which is shown in Table 5 as well.

The data in Table 5 indicate that different powder compaction equations lead to different values of the powder compaction work. A more accurate value of the compaction work corresponds to a more accurate approximation of the experimental data, i.e., the approximation by Equation (52). This equation makes it possible to more accurately determine the degree of plastic deformation of the particles and, as a result, to calculate the degree of change in the relative density of the powder due to both plastic deformation and rearrangement.

Of interest is the possibility of Equation (52) to describe with high accuracy the processes of compaction of coarse and fine powders of iron and copper from [24], which are difficult to accurately describe by many known equations. Experimental data on the compaction of these powders have been given in [1] (Table 8). The results of approximating the compaction of these powders by Equation (52) are shown in Figure 6, and the values of the parameters and the coefficient of determination are listed in

Table 6. Constant parameters and coefficient of determination R² obtained through approximation by Equations (16) and (52) from [1] of experimental data on compaction of coarse and fine iron and copper powders from [24], as well as the values of plastic deformation ε_p and specific plastic deformation work W_pd under compaction.

Parameter	Powder
	Fe (Coarse)		Fe (Fine)		Cu (Coarse)		Cu (Fine)
	Equation		Equation		Equation		Equation
	(52)	(16) [1]	(52)	(16) [1]	(52)	(16) [1]	(52)	(16) [1]
ρ0	0.35		0.183		0.391		0.165
ρf	0.965		0.927		0.978		0.95
σS, MPa	1190	-	1190	-	995	-	1565	-
$\overline{n}$, b	2.8563	0.02174	2.1833	0.03755	2.7848	0.02642	2.7453	0.02718
$\overline{a}$, a	6407.4	0.66092	5233480	0.81999	151.57	0.61890	188084	0.84893
$\overline{m}$	166.44	-	169.63	-	145.43		211.53	-
ρ∞	0.9666	1.0322	0.9287	1.0166	0.9793	1.0260	0.9534	1.0922
R2	0.99951	0.96683	0.99999	0.96167	0.99976	0.95341	0.99997	0.98561
εp	0.1493	-	0.3267	-	0.1664	-	0.2688	-
Wpd, J/cm3	201.31	205.66	388.81	342.92	165.59	151.54	420.65	501.94

. In addition, for comparison, Figure 6 shows the results of the approximation of these powders by the Kawakita–Ludde Equation (16) from [1].

Figure 6 and Table 6 demonstrate that the transformed continuum plasticity equation for a porous body (52) makes it possible to describe the PCP of iron and copper powders to a high density with very high accuracy: R² > 0.9990. Herein, the process of compaction of fine iron powder, Figure 6b, is described almost absolutely exactly with R² = 0.9999985. However, the use of the Kawakita–Ludde equation with two constant parameters to approximate these experimental data does not allow one to describe PCP with high accuracy. Moreover, the Kawakita–Ludde equation shows the possibility of achieving a pore-free state for the samples, while the experimental data indicate that it is impossible to reduce the porosity to zero even at very high pressure.

Also noteworthy is the ability of the continuum Equation (52) to accurately describe the process of compaction of highly plastic powders which can be compacted to a practically pore-free state at a relatively low pressure. In this regard, we will perform an approximation by Equation (52) and, for comparison, by Equation (16) from [1], of the experimental data on the compaction of powders of tin, lead, and annealed copper given in [25] and lead in [17], which we have already used for approximation by other equations in Part 2 [2]. The results of this approximation are shown in Figure 7 and

Table 7. Constant parameters and coefficient of determination R² obtained through approximation by Equations (16) from [1] and Equation (52) of experimental data on compaction of powders of tin, lead, and annealed copper [25] and lead [17], as well as the degree of plastic deformation ε_p and specific work of plastic deformation W_pd under compaction.

Parameter	Powder
	Sn [25]		Pb [25]		Cu [25]		Pb [17]
	Equation		Equation		Equation		Equation
	(52)	(16) [1]	(52)	(16) [1]	(52)	(16) [1]	(52)	(16) [1]
ρ0	0.501		0.439		0.3		0.58
ρf	0.997		0.995		0.964		0.999
σS, MPa	78	-	16	-	692	-	128	-
$\overline{n}$, b	2.1752	0.32714	3.6815	0.66983	2.5956	0.032411	2.4022	0.13571
$\overline{a}$, a	1.0048	0.50298	1.0017	0.56311	1.3233	0.71006	0.9891	0.42419
$\overline{m}$	8.65484	-	0.64765	-	10.5886	-	5.3766	-
ρ∞	0.9997	1.0080	0.9985	1.0048	0.9817	1.0347	1.0009	1.0073
R2	0.99793	0.97893	0.99876	0.99538	0.99981	0.99910	0.99917	0.98332
εp	0.2106	-	0.4457	-	0.2368	-	0.1812	-
Wpd, J/cm3	16.424	10.831	7.132	7.427	163.86	185.36	23.195	18.862

.

These findings evidence that Equation (52) provides high accuracy of approximation of highly plastic powders. The Kawakita–Ludde equation provides sufficiently high approximation accuracy in two of four cases, but the accuracy is still somewhat lower than the approximation accuracy by Equation (52). Therefore, the continuum Equation (52) with four constant parameters makes it possible to describe PCP with high accuracy from the beginning to end (when an extremely high density is achieved). Such cases are practically impossible to be described with high accuracy by the known equations for PCP in a rigid die. The new Equation (52) also makes it possible to determine the yield strength of the powder material and the degree of plastic deformation of particles under compaction from initial to final density. In addition, Equation (52) allows one to establish the functional dependence of the lateral pressure coefficient on density due to the determination of the parameters $\overline{a}$ and $\overline{m}$ as a result of the approximation: ${\xi }_{ex}=\overline{a}·{\left({\displaystyle \frac{\rho -{\rho }_0}{1-{\rho }_0}}\right)}^{\overline{m}}$. By knowing $\overline{a}$, $\overline{m,}$ and $\overline{n}$, one can determine the experimental dependences of the coefficients α and β or ψ and φ on the relative density as follows:

$${\alpha }_{ex}={\displaystyle \frac{(1-\overline{a}{\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)}^{\overline{m}})}{2(1+2\overline{a}{\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)}^{\overline{m}})}} \mathrm{and} {\beta }_{ex}={\left({\displaystyle \frac{\rho -{\rho }_0}{1-{\rho }_0}}\right)}^{2\overline{n}}$$

(55)

$${\psi }_{ex}={\displaystyle \frac{1}{3}}{\left({\displaystyle \frac{\rho -{\rho }_0}{1-{\rho }_0}}\right)}^{2\overline{n}-1}{\displaystyle \frac{\left[1+2a{\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)}^{\overline{m}}\right]}{\left[1-a{\left(\frac{\rho -{\rho }_0}{1-{\rho }_0}\right)}^{\overline{m}}\right]}} \mathrm{and} {\phi }_{ex}={\left({\displaystyle \frac{\rho -{\rho }_0}{1-{\rho }_0}}\right)}^{2\overline{n}-1}$$

(56)

It is also of interest that this continuum Equation (52) is similar to the discrete Equation (15) proposed in Part 2 [2]. It is advisable to compare these equations:

Discrete Equation (15) from [2]: $p=H·{\displaystyle \frac{{\left(1-{\rho }_0\right)}^{\left(c-b\right)}·{\left(\rho -{\rho }_0\right)}^b}{\left[{\left(1-{\rho }_0\right)}^c-a{\left(\rho -{\rho }_0\right)}^c\right]}}$,

Continuum Equation (52): ${\sigma }_z={\overline{\sigma }}_s\sqrt{{\displaystyle \frac{2}{3}}}·\sqrt{{\displaystyle \frac{{(1-{\rho }_0)}^{(\overline{m}-\overline{n})}{(\rho -{\rho }_0)}^{\overline{n}}}{\left[{(1-{\rho }_0)}^{\overline{m}}-\overline{a}{(\rho -{\rho }_0)}^{\overline{m}}\right]}}}$.

Recall that Equation (15) was derived through generalizing the discrete Balshin’s equations, and Equation (52) was derived through transforming the continuum plasticity equation for a porous sample and using the power-law density dependences for the two coefficients in this equation. That is, when deriving these equations, different approaches were applied, but in the end, almost the same equations were obtained. Of particular interest is also the fact that when approximating some experimental data on powder compaction by these equations, almost complete coincidence of the values for the determination coefficient and compaction work, the equality between the parameters b and n, as well as the equality between the values of H and ${\overline{\mathsf{\sigma }}}_{\mathrm{s}}\sqrt{2/3}$ take place. Such a situation is observed, in particular, in compacting coarse and fine powders of iron and copper when we compare the approximations according to Equations (15) and (52) (see Table 2.9 [2] and Table 6) as well as in compacting annealed copper powder when we compare Table 10 [2] and Table 7. At the same time, there are powders in the approximation of which by Equations (15) and (52) there is no high degree of coincidence for some parameters but the values of the determination coefficient, compaction work, parameters b and n, as well as the values of H and ${\overline{\sigma }}_s\sqrt{2/3}$ are close. Such cases take place in compaction of iron powders FeKH1, FeKH6, FeKH7, and FeKH9. Finally, there is a third group of powders, the approximation of which is accompanied with significant differences in the approximation accuracy, compaction work, parameters b and n, as well as the values of H and ${\overline{\sigma }}_s\sqrt{2/3}$. This group includes FeKH2, FeKH3, FeKH4, FeKH5, and FeKH8 powders, as well as tin and lead powders. Thus, with all the above, it is still difficult to clarify the reasons for the differences in the approximation of PCP of different powders by Equations (15) and (52), but they can be clarified in the course of the further theoretical and experimental studies.

At the same time, there are limitations on the use of Equation (52) for approximation of experimental data on PCP. First, this equation, when approximating PCP to a density of 0.8–0.9, in many cases, gives an ambiguous result, that is, it is possible to obtain different values of the yield strength for the powder material, at which a high level of approximation accuracy is ensured. Second, it is not always possible to obtain the optimal value of the yield strength, because for a given yield strength below a certain value, the computer approximation does not work.

3. Conclusions

• Correction of two density-dependent parameters of the continuum equations with respect to taking into account the initial density allows us to significantly improve the accuracy of the description of the powder compaction process in a rigid die. In this case, a higher accuracy of approximation is achieved when using the Skorokhod–Martynova–Shtern equation with theoretical density functions. This equation contains one constant, which corresponds to the yield stress of particles and is determined from experiment. Such an equation can describe the powder compaction process up to a density of 0.9–0.95 with high accuracy.
• The equation obtained from the plasticity equation of a porous body by replacing one of the density functions with a lateral pressure coefficient and using power-law dependences on the relative density of both one of the density functions and the lateral pressure coefficient has wider possibilities in describing the PCP in a rigid die. In this case, the number of constant parameters increases to four, which provides a highly accurate description of the powder compaction process to both a non-porous state and a state in which the sample has a certain level of porosity at infinite pressure.
• The physical meaning of the four constants requires clarification. However, now we can assume that one constant having the dimension of pressure characterizes the strength of particles in the form of yield strength or hardness. The other three constants reflect the influence on the powder compaction process in the die of the shape and size of particles, as well as of internal friction forces and adhesion forces between particles. At the same time, the physical essence of each of those three dimensionless constants for the powder compaction process is still unknown.
• High-precision approximation of the experimental compaction process in a die of various powders by an equation with four constants makes it possible to establish dependence on the relative density of two parameters which are used in the plasticity equations for a porous body, as well as of the lateral pressure coefficient without additional experiments suggesting using of special devices.