Exploring the Effects of Cramped-Impact-Type Mechanical Action on Active Pharmaceutical Ingredient (Levofloxacin)—Prospects for Pharmaceutical Applications
Abstract
1. Introduction
2. Materials and Methods
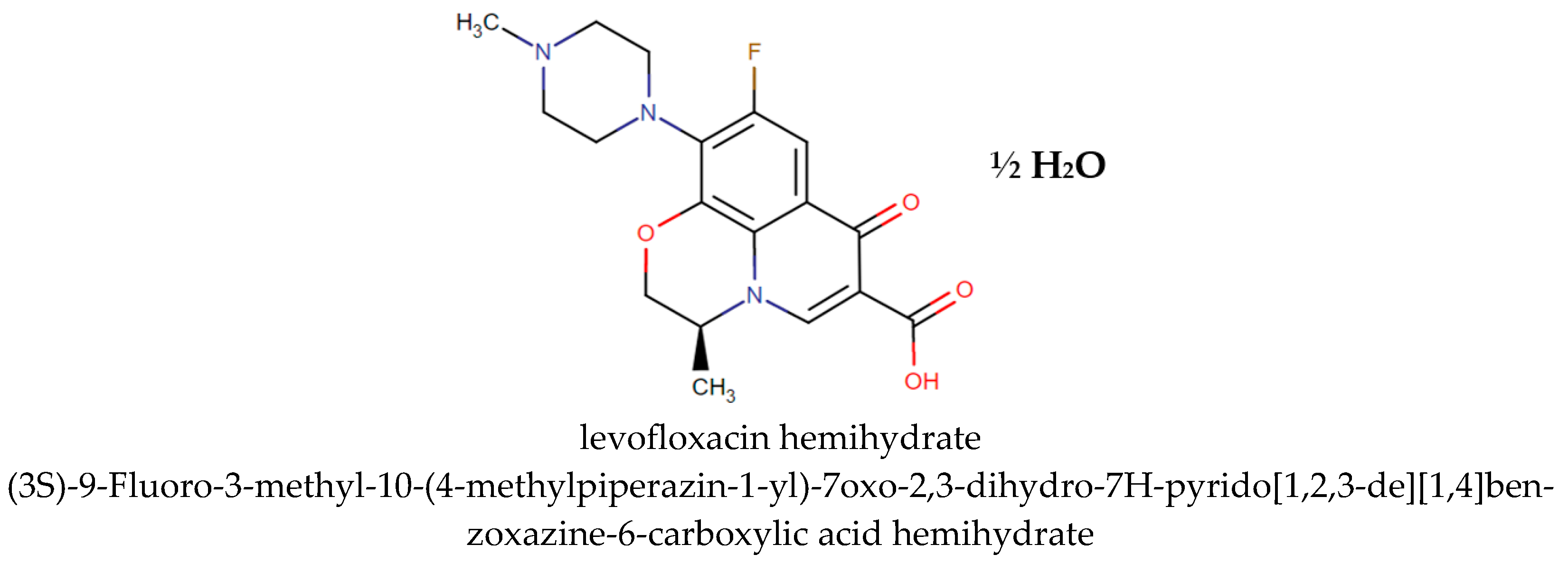
2.1. Fluoroquinolone Sample Substance
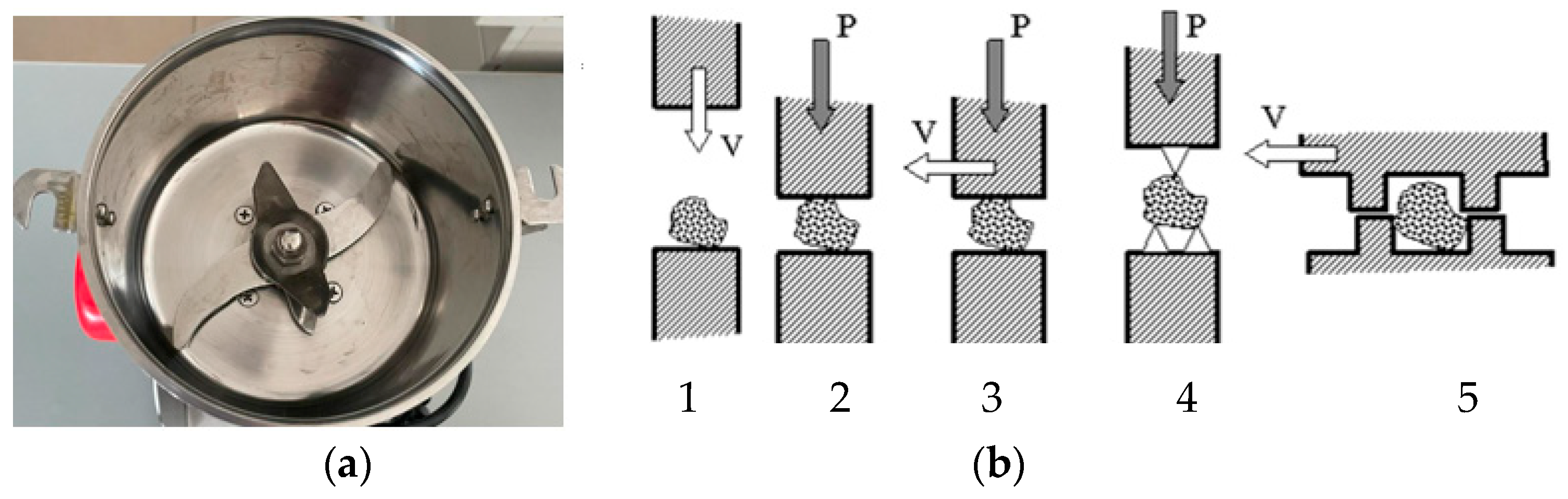
2.2. Tribochemical Equipment
Study Design
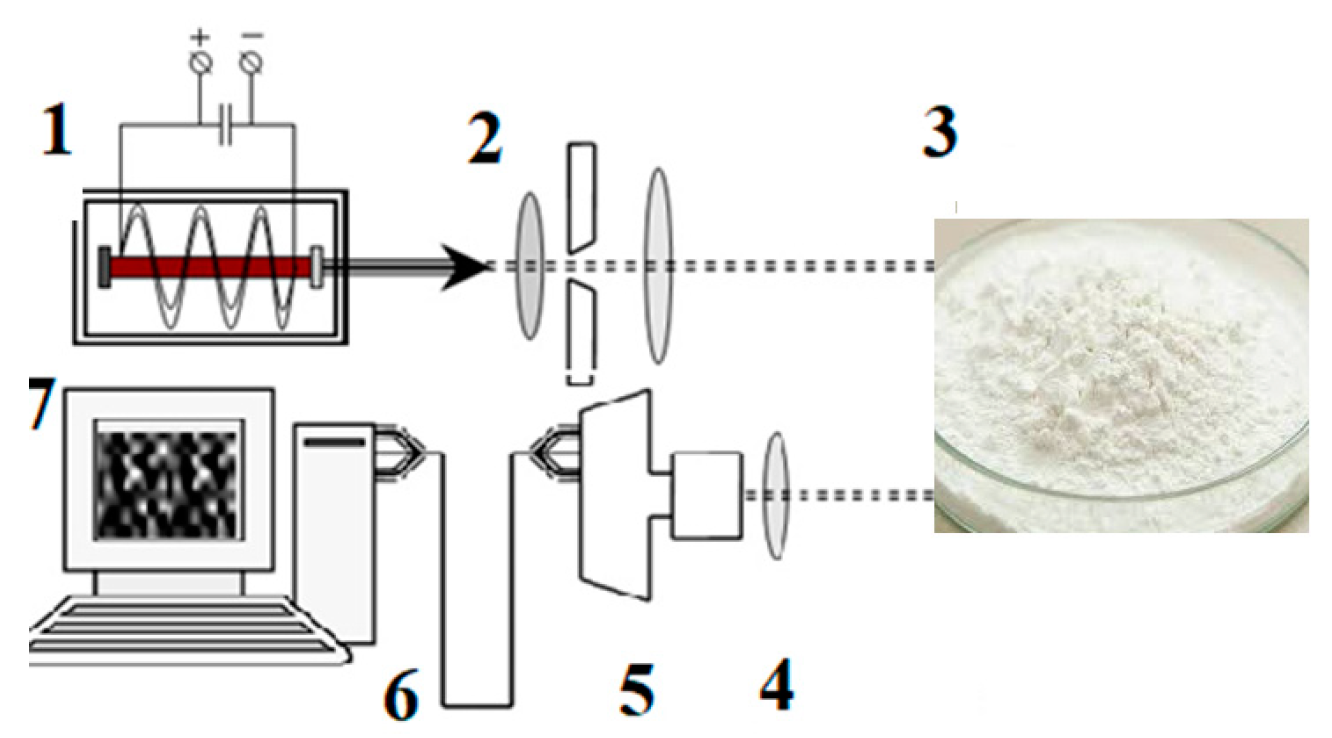
2.3. Determination of Disperse-Phase Particle Size and Particle Size Distribution
2.3.1. Static Light Scattering (SLS)
2.3.2. Dynamic Light Scattering (DLS)
2.3.3. Optical and Digital Microscopy (OM and DM)
2.4. LALLS Study of Dissolution Rate Kinetics Design
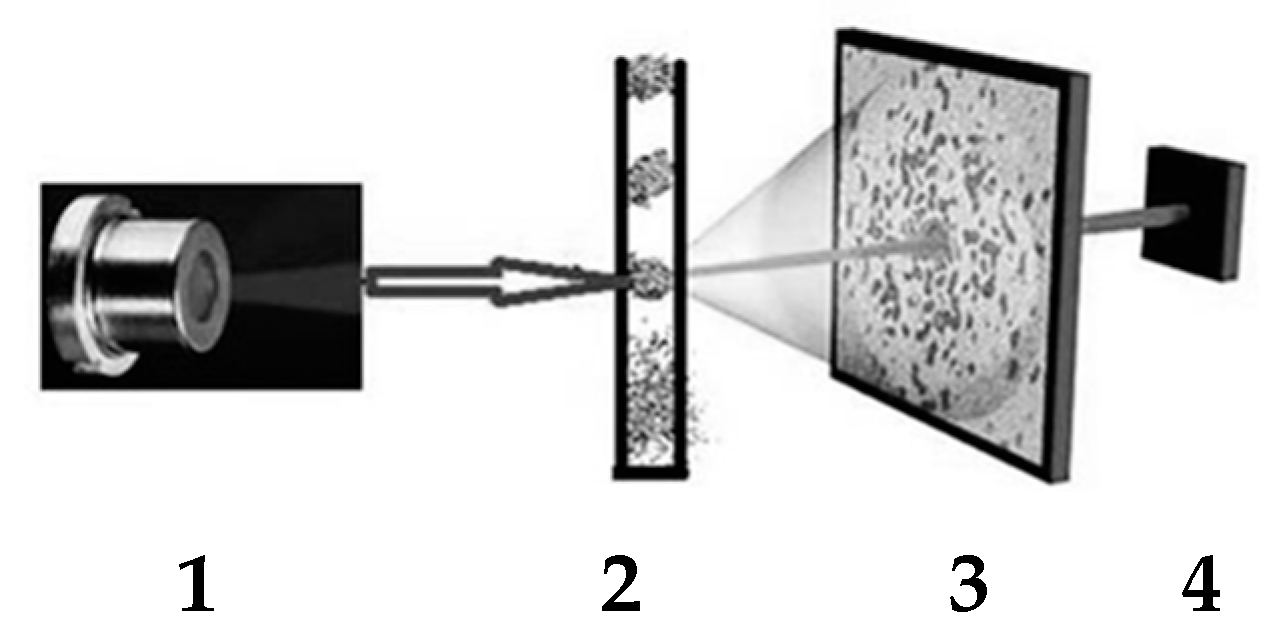
2.5. 2D Light Scattering (2D-LS) Method
2.6. Fourier-Transform IR Spectroscopy
2.7. Molecular Docking Studies
2.8. Spirotox Method
Spirotox Study Design
2.9. Statistical Data Processing
3. Results
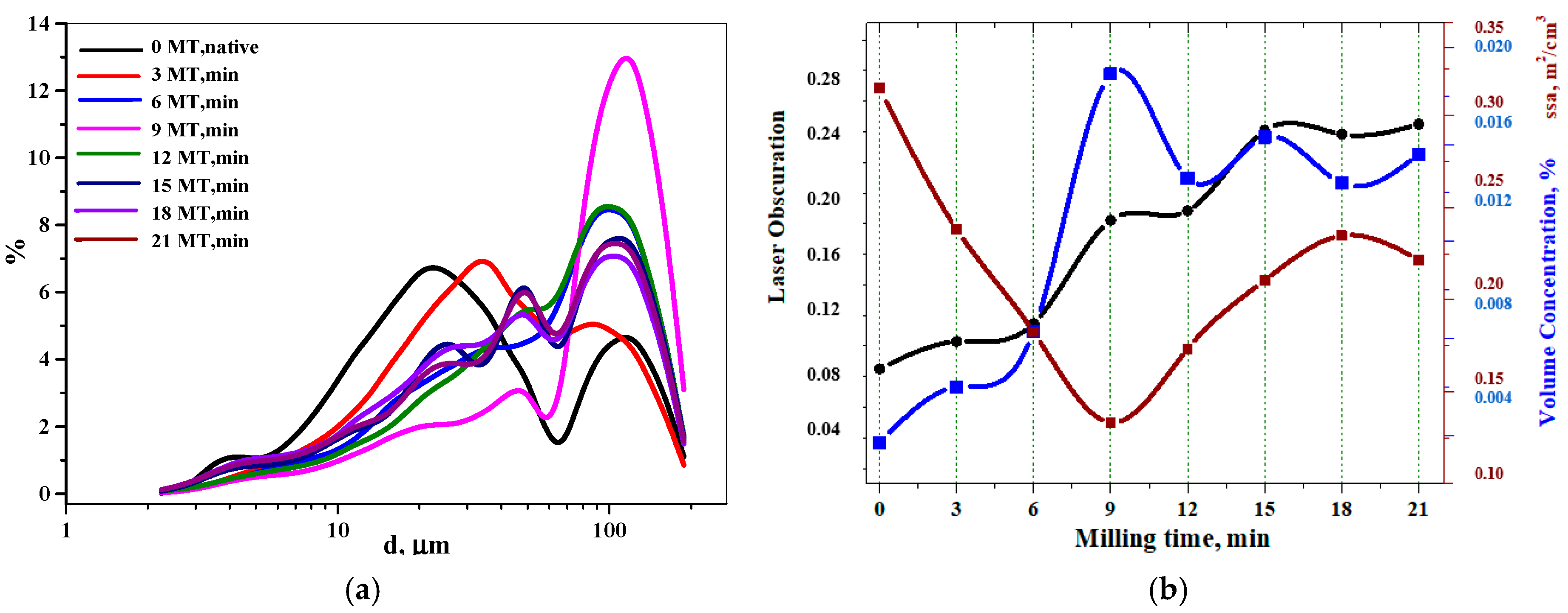
3.1. Disperse-Phase Particle Size and Particle Size Distribution
3.1.1. Static Laser Scattering Data
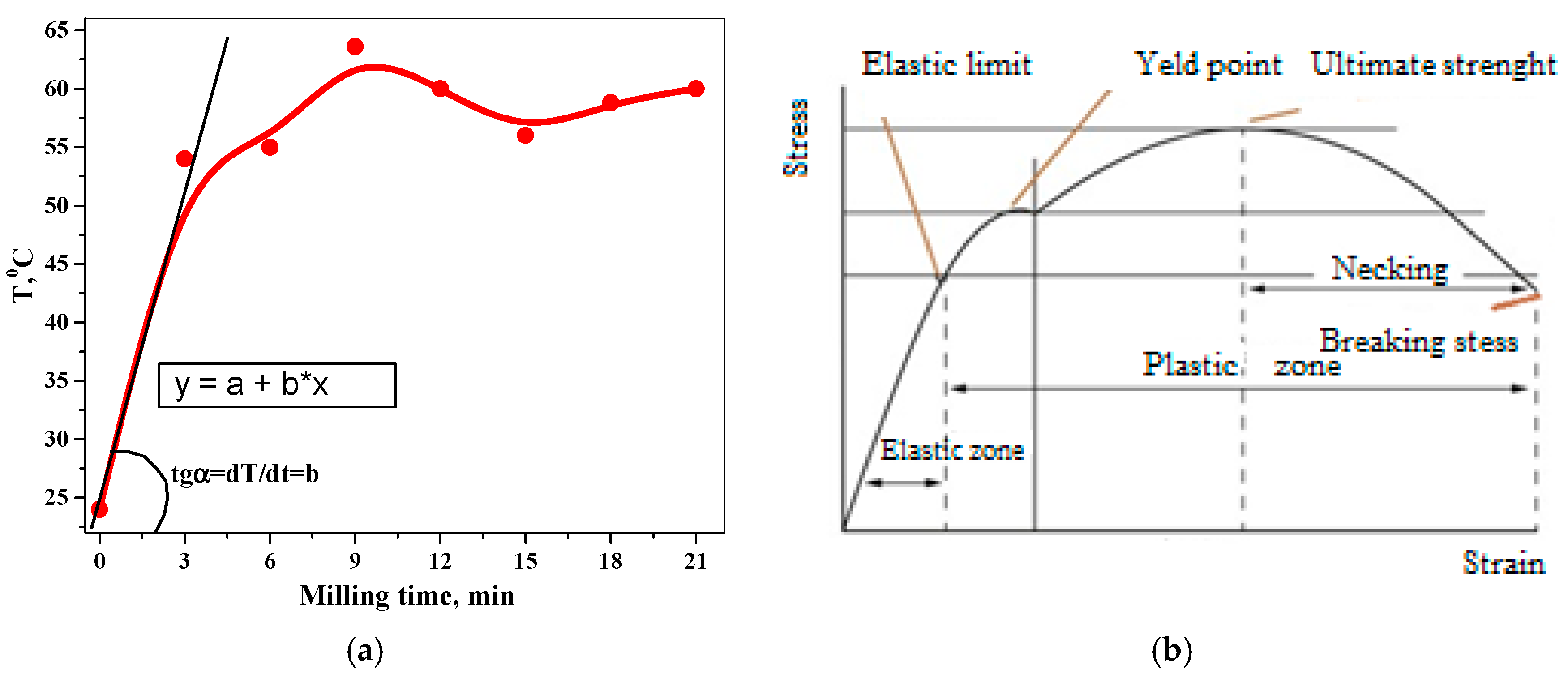
3.1.2. Stress–Strain Relationships
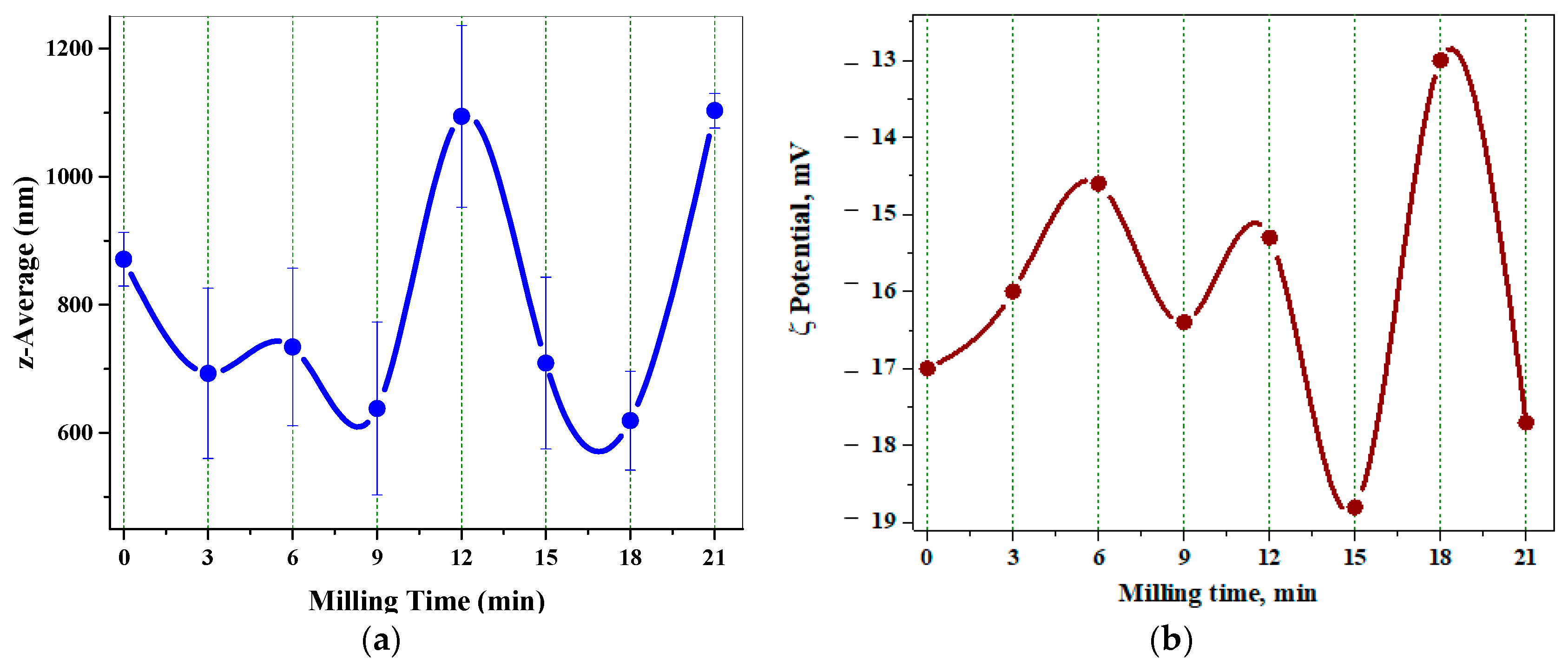
3.1.3. Dynamic Laser Scattering Data
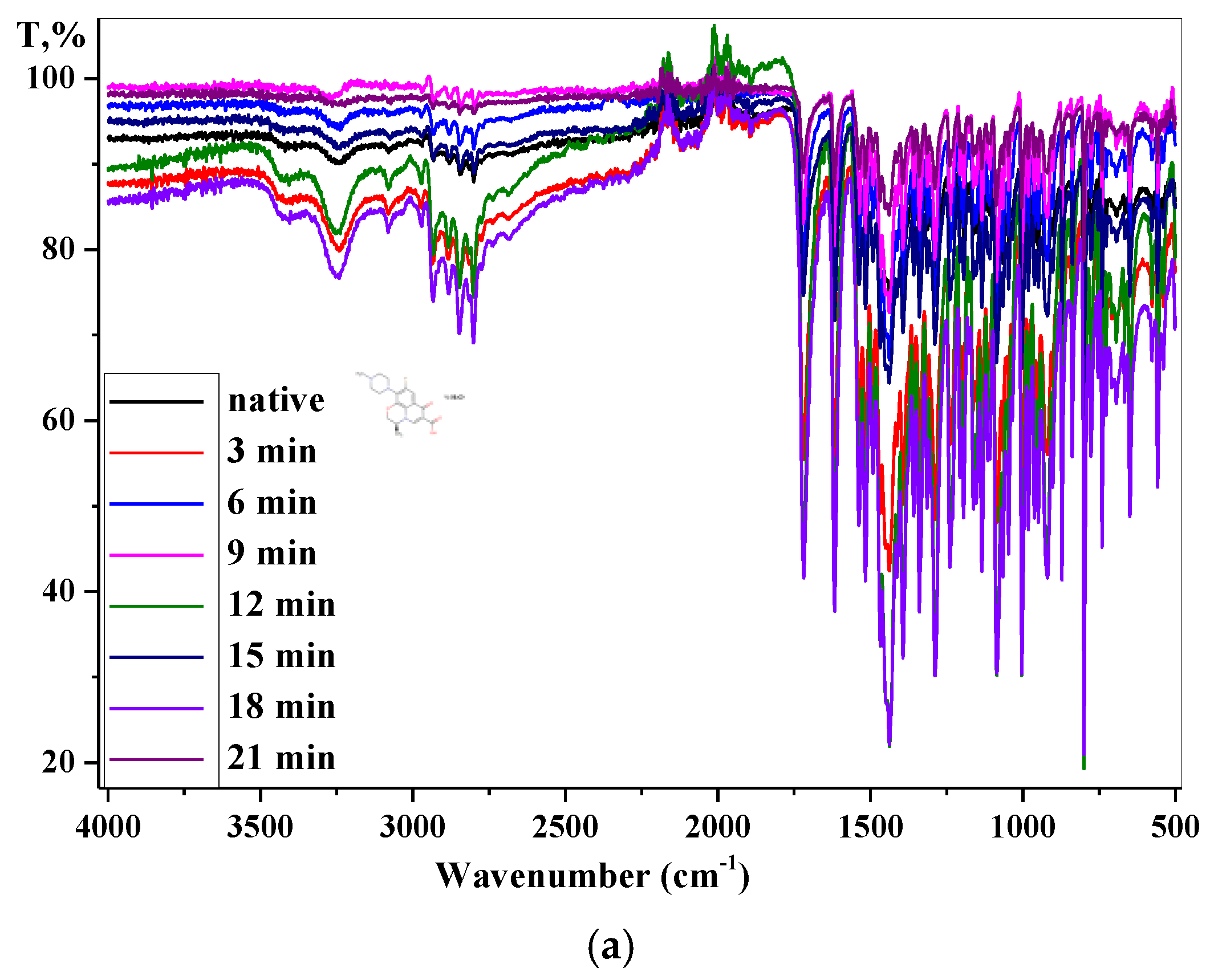
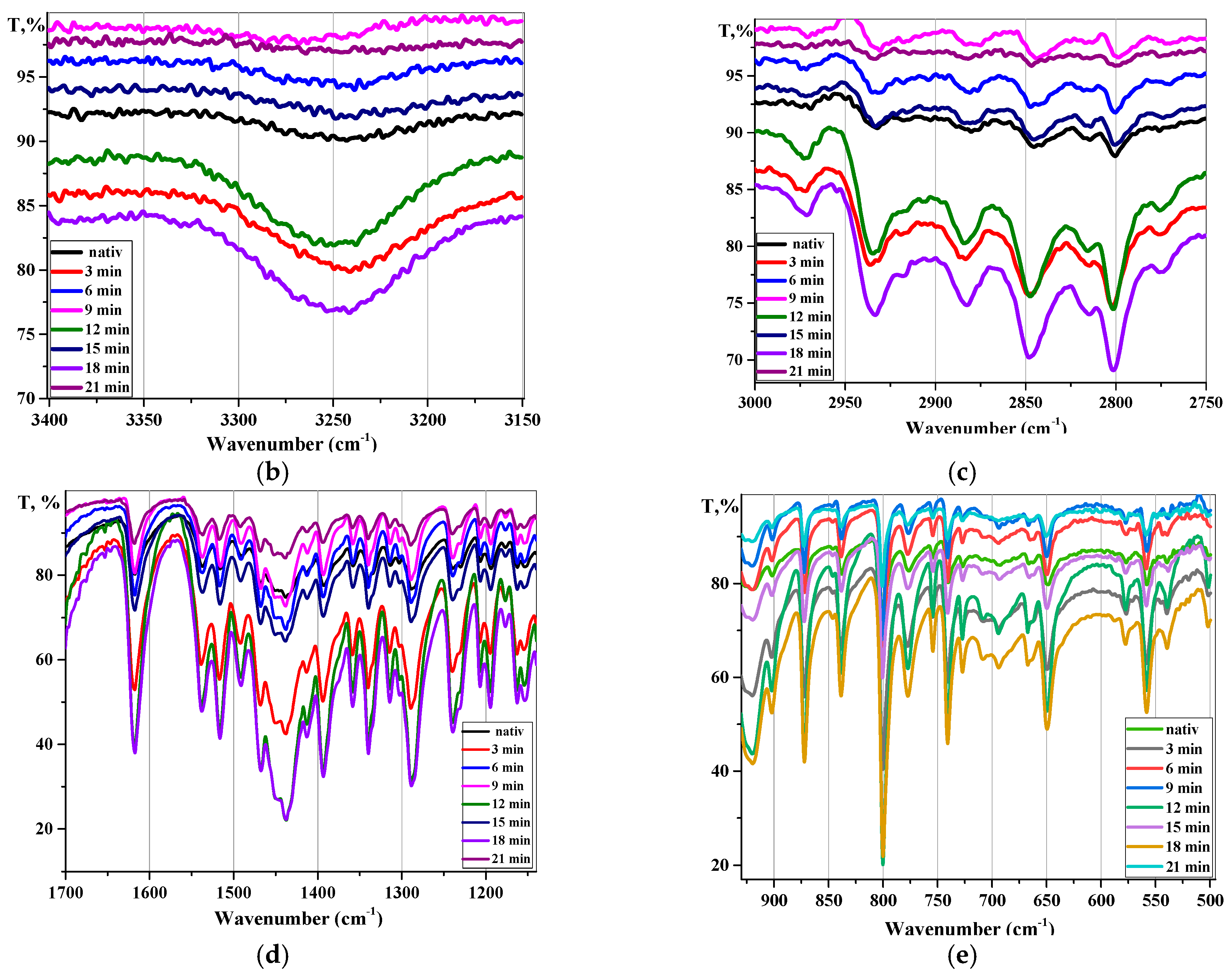
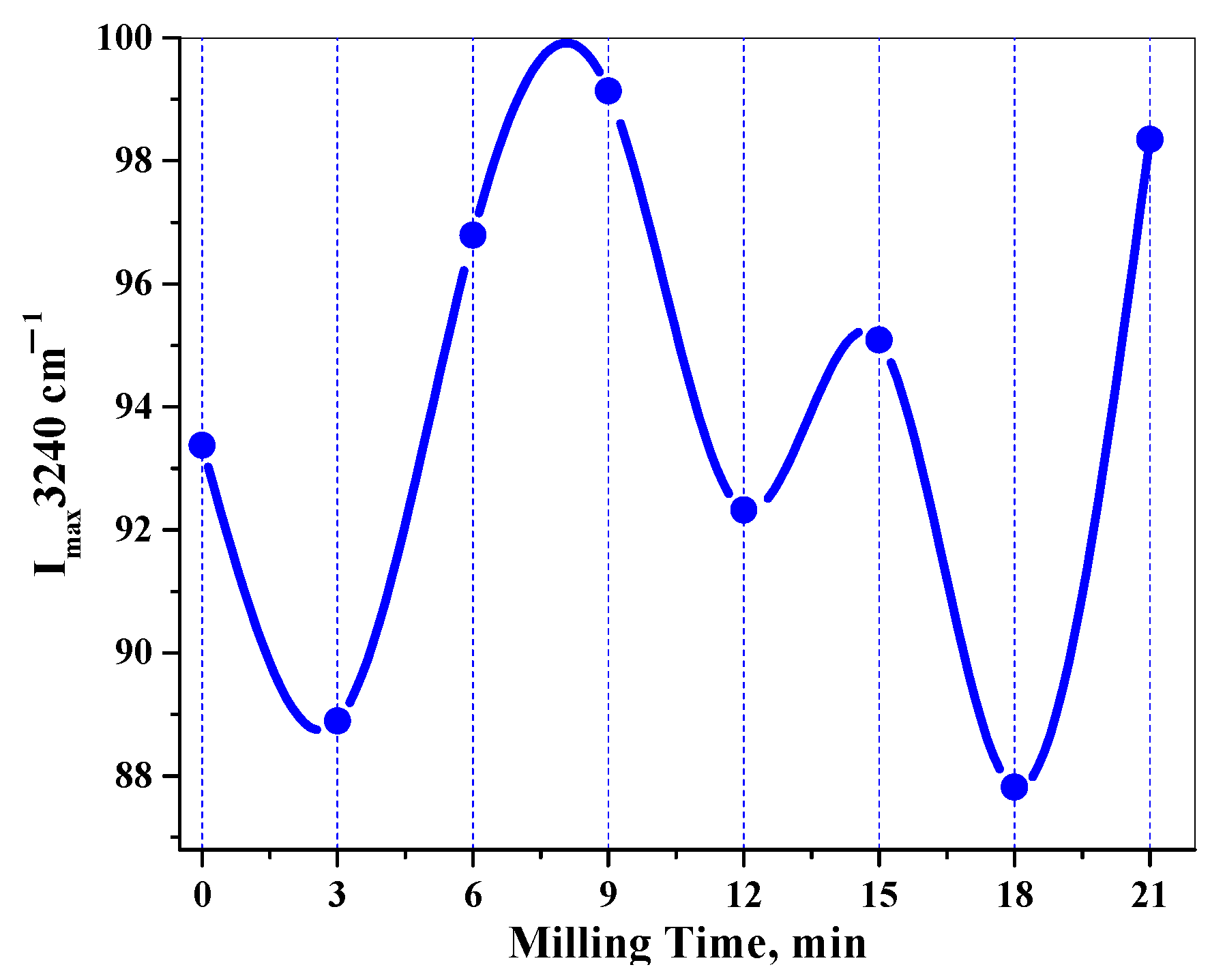
3.2. Fourier-Transform Infrared Spectroscopy Analysis
3.3. 2D Light Scattering Method
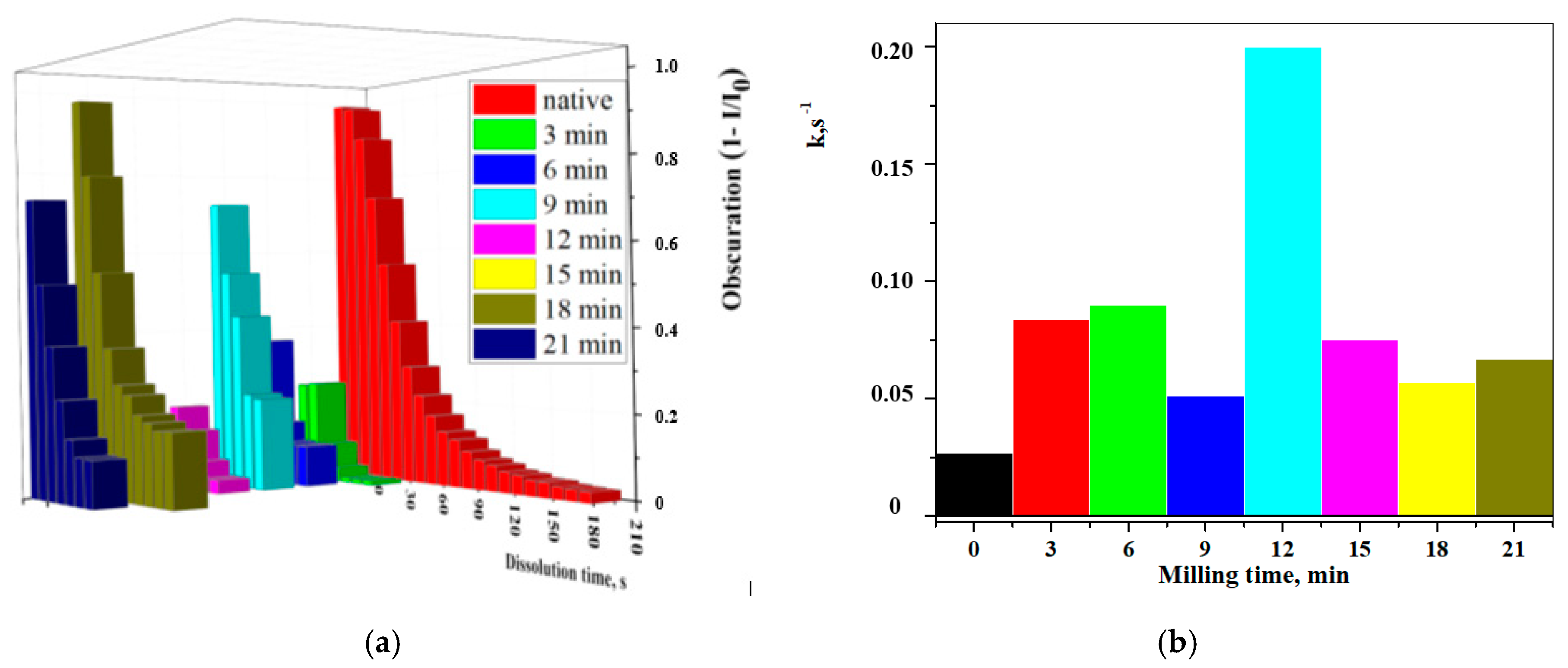
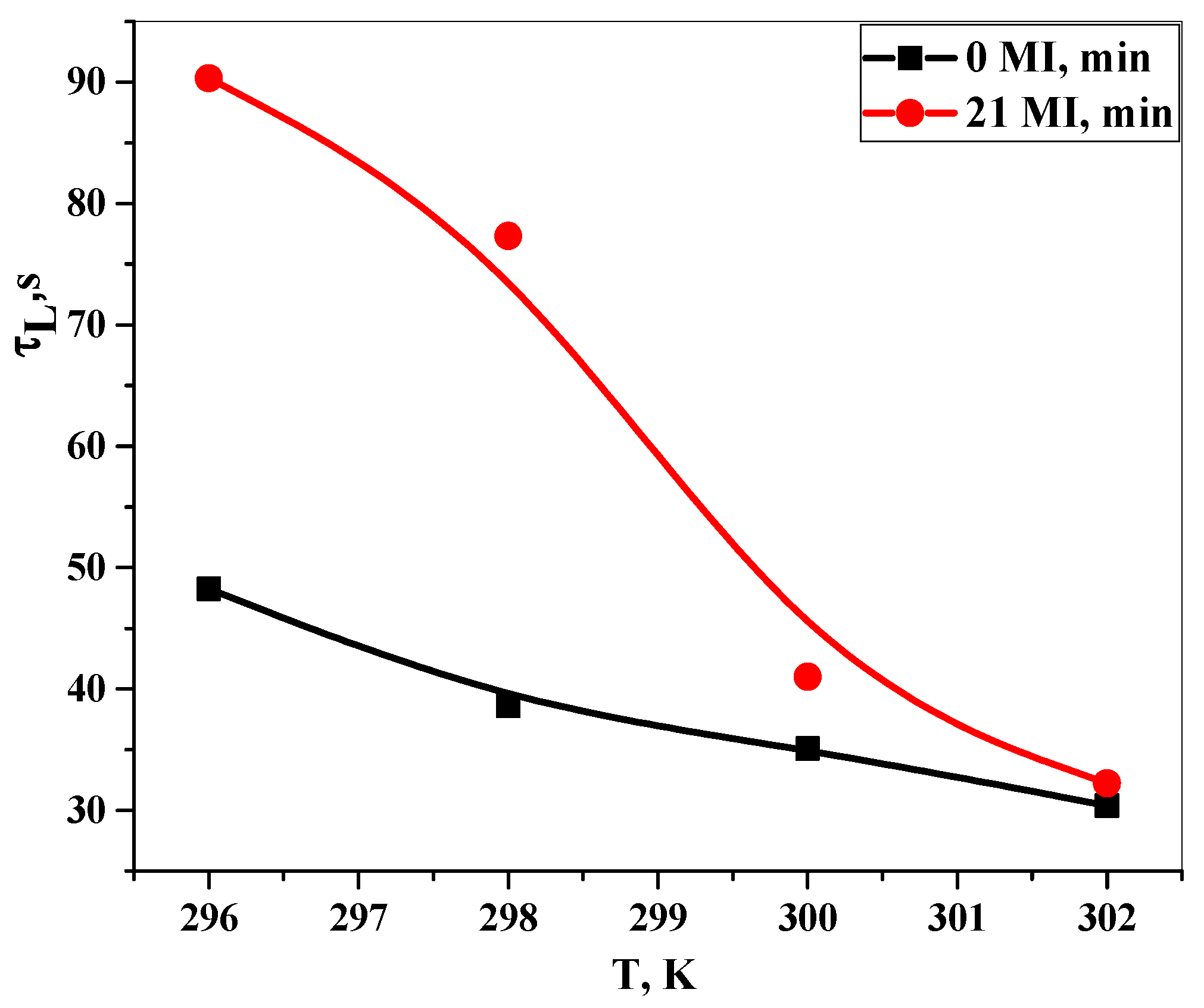
3.4. Study of Dissolution Kinetics in Water by the LALLS Method
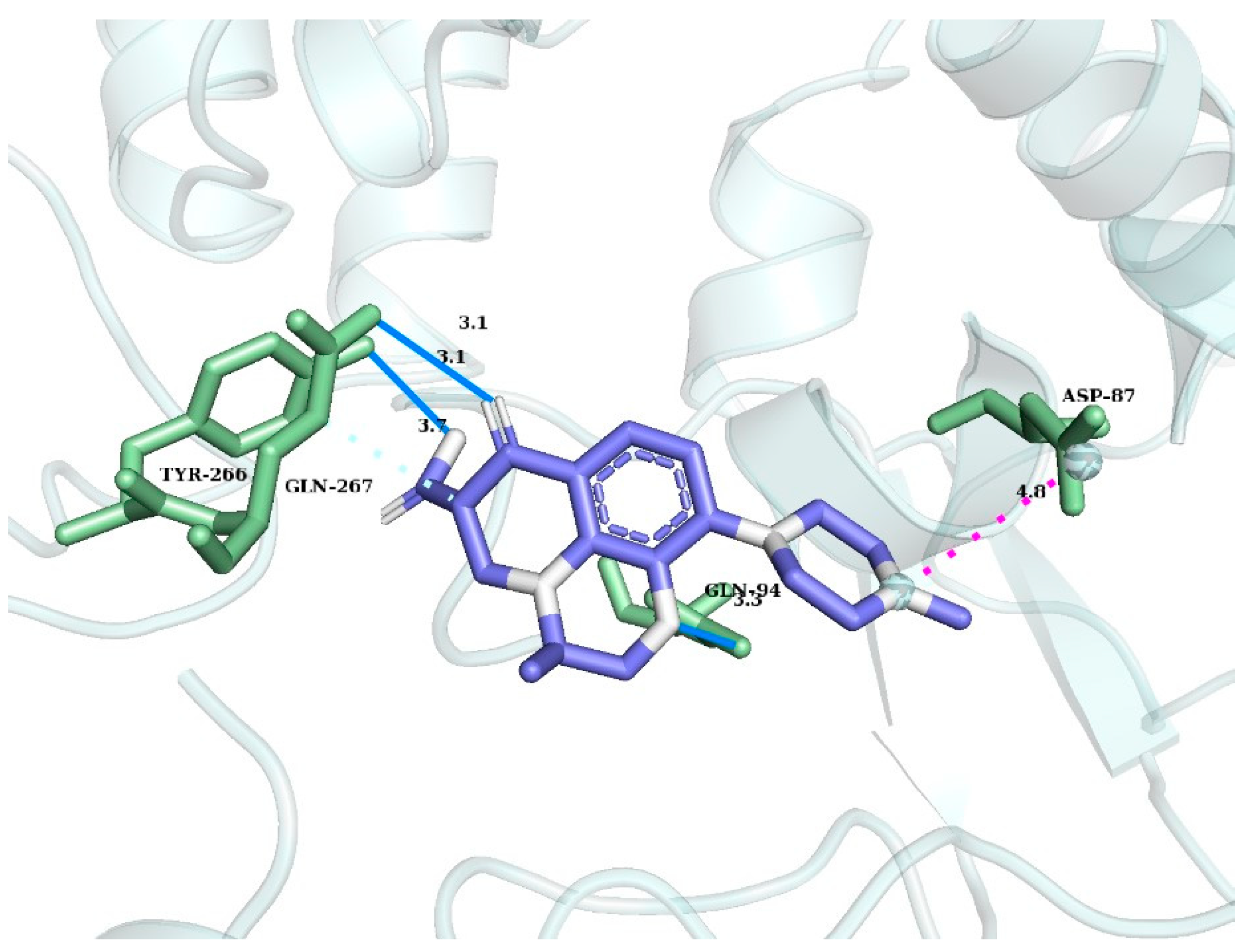
3.5. Biological Activity Studies Using the Spirotox as Well as Molecular Computer Docking Methods
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| MCh | mechanochemistry |
| MAct | mechanoactivation |
| IUPAC | international union of pure and applied chemistry |
| SMComplex | supramolecular complex |
| DLS | dynamic light scattering |
| SB | solid body |
| obsEa | observed activation energy |
| TrbCh | tribochemical |
| Lvf·Hh | levofloxacin hemihydrate |
| FQs | fluoroquinolones |
| SLS | static light scattering |
| VC | volumetric concentration |
| HS | hydrodynamic size |
| ZP | zeta potential |
| PdI | polydispersity index |
| NPs | nanoparticles |
| QSAR | quantitative structure activity relationship |
| FTIR | Fourier-transform IR spectroscopy |
| MI | mechanic impact |
| DPh | dispersion phenomenon |
| LALLS | low-angle laser light scattering |
| OM | optical microscopy |
| IR | infra-red |
| DSA | dynamic strain aging |
| 2D-LS | two-dimensional dynamic backscattering |
| ChRS | chemometric reference sample |
| DIS | dynamic impurity subsystem selectivity index |
| SLS | static light scattering |
| Spirotox test | Spirostomum ambiguum acute toxicity test |
References
- Lyakhov, N.; Grigoreva, T.; Talako, T.; Udalova, T.; Vosmerikov, S.; Devyatkina, E. A Carbon-Free Way for Obtaining Nanoscale Silicon. Powders 2022, 1, 18–32. [Google Scholar] [CrossRef]
- Bose, A.; Mal, P. Mechanochemistry of supramolecules. Beilstein J. Org. Chem. 2019, 15, 881–900. [Google Scholar] [CrossRef]
- Hernández, J.G. Mechanochemistry. Beilstein J. Org. Chem. 2017, 13, 2372–2373. [Google Scholar] [CrossRef]
- Gomollón-Bel, F. Ten Chemical Innovations that will change our world: IUPAC identifies emerging technologies in chemistry with potential to make our planet more sustainable. Chem. Int. 2019, 41, 12–17. [Google Scholar] [CrossRef]
- Feng, X.; Dong, C.; Wang, X.; Wang, J. Mechanochemical treatment for degradation of ciprofloxacin (CIP) in solutions. Water Sci. Technol. 2022, 86, 1958–1968. [Google Scholar] [CrossRef] [PubMed]
- Friščić, T.; Mottillo, C.; Titi, H.M. Mechanochemistry for Synthesis. Angew. Chem. Int. Ed. 2020, 59, 1018–1029. [Google Scholar] [CrossRef]
- Lavalle, P.; Boulmedais, F.; Schaaf, P.; Jierry, L. Soft-mechanochemistry: Mechanochemistry inspired by nature. Langmuir 2016, 32, 7265–7276. [Google Scholar] [CrossRef]
- Castro, J. Elastic potentials as yield surfaces for isotropic materials. PLoS ONE 2022, 17, e0275968. [Google Scholar] [CrossRef]
- Kiener, D.; Fritz, R.; Alfreider, M.; Leitner, A.; Pippan, R.; Maier-Kiener, V. Rate limiting deformation mechanisms of BCC metals in confined volumes. Acta Mater. 2019, 166, 687–701. [Google Scholar] [CrossRef]
- Michalchuk, A.A.; Boldyreva, E.V.; Belenguer, A.M.; Emmerling, F.; Boldyrev, V.V. Tribochemistry, mechanical alloying, mechanochemistry: What is in a name? Front. Chem. 2021, 9, 685789. [Google Scholar] [CrossRef] [PubMed]
- Alex, T.C.; Kailath, A.J.; Kumar, R. Al-monohydrate (boehmite) to al-trihydrate (bayerite/gibbsite) transformation during high-energy milling. Metall. Mater. Trans. B 2020, 51, 443–451. [Google Scholar] [CrossRef]
- Thammajaruk, P.; Blatz, M.B.; Buranadham, S.; Guazzato, M.; Wang, Y. Shear bond strength of composite cement to alumina-coated versus tribochemical silica-treated zirconia. J. Mech. Behav. Biomed. Mater. 2020, 105, 103710. [Google Scholar] [CrossRef] [PubMed]
- Thiessen, K.P. Tribochemistry versus Nano-Tribology I. Theoretical Considerations on Making a Tandem Nanoscope. Eur. Chem. Bull 2016, 5, 420–422. [Google Scholar]
- Knyazeva, A.G.; Evstigneev, N.K. Interrelations between heat and mechanical processes during solid phase chemical conversion under loading. Procedia Comput. Sci. 2010, 1, 2619–2628. [Google Scholar] [CrossRef]
- Kloskowski, T.; Szeliski, K.; Fekner, Z.; Rasmus, M.; Dąbrowski, P.; Wolska, A.; Siedlecka, N.; Adamowicz, J.; Drewa, T.; Pokrywczyńska, M. Ciprofloxacin and levofloxacin as potential drugs in genitourinary cancer treatment—The effect of dose–response on 2D and 3D cell cultures. Int. J. Mol. Sci. 2021, 22, 11970. [Google Scholar] [CrossRef] [PubMed]
- Lungu, I.-A.; Moldovan, O.-L.; Biriș, V.; Rusu, A. Fluoroquinolones hybrid molecules as promising antibacterial agents in the fight against antibacterial resistance. Pharmaceutics 2022, 14, 1749. [Google Scholar] [CrossRef]
- Mühlenweg, H.; Hirleman, E.D. Laser diffraction spectroscopy: Influence of particle shape and a shape adaptation technique. Part. Part. Syst. Charact. 1998, 15, 163–169. [Google Scholar] [CrossRef]
- De Boer, A.H.; Gjaltema, D.; Hagedoorn, P.; Schaller, M.; Witt, W.; Frijlink, H.W. Design and application of a new modular adapter for laser diffraction characterization of inhalation aerosols. Int. J. Pharm. 2002, 5, 233–245. [Google Scholar] [CrossRef]
- Sourav Bhattacharjee, S. DLS and Zeta potential—What they are and what they are not? J. Control. Release 2016, 235, 337–351. [Google Scholar] [CrossRef]
- Mondal, S.; Mondal, H.; Saha, K.; Roul, B. Development of a low-cost smartphone-connected Digital Microscope. J. Microsc. Ultrastruct. 2020, 8, 51. [Google Scholar] [CrossRef]
- Uspenskaya, E.V.; Pleteneva, T.V.; Syroeshkin, A.V.; Kazimova, I.V.; Elizarova, T.E.; Odnovorov, A.I. Role of stable hydrogen isotope variations in water for drug dissolution managing. Curr. Issues Pharm. Med. Sci. 2020, 33, 94–101. [Google Scholar] [CrossRef]
- Vladimirovich, S.A.; Valerievna, L.O.; Vadimovna, P.T.; Valerievna, U.E.; Antonovna, T.-L.M.; Vladimirovna, T.I. The new two-dimensional light scattering method for recognition of pharmaceutical enantiomers. J. Appl. Pharm. Sci. 2020, 10, 029–034. [Google Scholar] [CrossRef]
- Ludwig, B.; Burke, T.T. Infrared Spectroscopy Studies of Aluminum Oxide and Metallic Aluminum Powders, Part I: Thermal Dehydration and Decomposition. Powders 2022, 1, 47–61. [Google Scholar] [CrossRef]
- Mourin, M.; Bhattacharjee, A.; Wai, A.; Hausner, G.; O’Neil, J.; Dibrov, P. Pharmacophore based screening & modification of amiloride analogs for targeting the NHAP-type cation-proton antiporter in vibrio cholerae. Can. J. Microbiol. 2021, 67, 835–849. [Google Scholar]
- Janson, G.; Zhang, C.; Prado, M.G.; Paiardini, A. PyMod 2.0: Improvements in protein sequence-structure analysis and homology modeling within pymol. Bioinformatics 2016, 33, 444–446. [Google Scholar] [CrossRef]
- Cravotto, G.; Gaudino, E.C.; Cintas, P. On the mechanochemical activation by ultrasound. Chem. Soc. Rev. 2013, 42, 7521. [Google Scholar] [CrossRef]
- Malygin, G.A. Mechanism of plastic collapse of nanosized crystals with BCC lattice under uniaxial compression. Phys. Solid State 2018, 60, 1244–1249. [Google Scholar] [CrossRef]
- Semenova, O.; Sosunov, A.; Prokhorov, N.; Ponomarev, R. Temperature dependence of LINBO3 dislocation density in the near-surface layer. Chin. Opt. Lett. 2022, 20, 061601. [Google Scholar] [CrossRef]
- Odnobokova, M.; Belyakov, A.; Kaibyshev, R. Development of Nanocrystalline 304L Stainless Steel by Large Strain Cold Working. Metals 2015, 5, 656–668. [Google Scholar] [CrossRef]
- Jitendra, P.; Swadesh, V. 3-Raw materials for terry fabrics. Woven Terry Fabr. Manuf. Qual. Manag. 2017, 19–28. [Google Scholar]
- Petukhov, B.V. The mechanism of the anomalous behavior of the plastic flow of materials with high crystal relief caused by the dynamic impurity subsystem. Fizika Tverdogo Tela 2021, 64, 2126–2133. [Google Scholar]
- Mayerhöfer, T.G.; Popp, J. Quantitative Evaluation of Infrared Absorbance Spectra-Lorentz Profile versus Lorentz Oscillator. Chemphyschem 2019, 20, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Butyagin, P.Y. Problems in mechanochemistry and prospects for its development. Russ. Chem. Rev. 1994, 63, 965–976. [Google Scholar] [CrossRef]
- Suganandha, J.B.; Mani, M.R. Correlation Study of 3D Surface Roughness of Milled Surfaces with Laser Speckle Pattern. Sensors 2022, 22, 2842. [Google Scholar]
- Guntram, J.; Werner, R. Dissolution rates and activation energy for dissolution of brucite (001): A new method based on the microtopography of crystal surfaces. Geochim. Et Cosmochim. Acta 1996, 60, 5055–5062. [Google Scholar]
- Andini, S.; Bolognese, A.; Formisano, D.; Manfra, M.; Montagnaro, F.; Santoro, L. Mechanochemistry of ibuprofen pharmaceutica. Chemosphere 2012, 88, 548–553. [Google Scholar] [CrossRef]
- Stanzione, F.; Giangreco, I.; Cole, J.C. Use of molecular docking computational tools in drug discovery. Prog. Med. Chem. 2021, 60, 273–343. [Google Scholar]
- Xu, L.X.; Bhamla, M.S. Biophysical mechanism of ultrafast helical twisting contraction in the giant unicellular ciliate Spirostomum ambiguum. bioRxiv 2019, 854836. [Google Scholar] [CrossRef]
- Petukhov, B.V. Kinetics of plastic deformation of impurity covalent crystals. Phys. Solid State 2015, 57, 2264–2270. [Google Scholar] [CrossRef]
- Carlton, H.; Huitink, D.; Liang, H. Tribochemistry as an Alternative Synthesis Pathway. Lubricants 2020, 8, 87. [Google Scholar] [CrossRef]





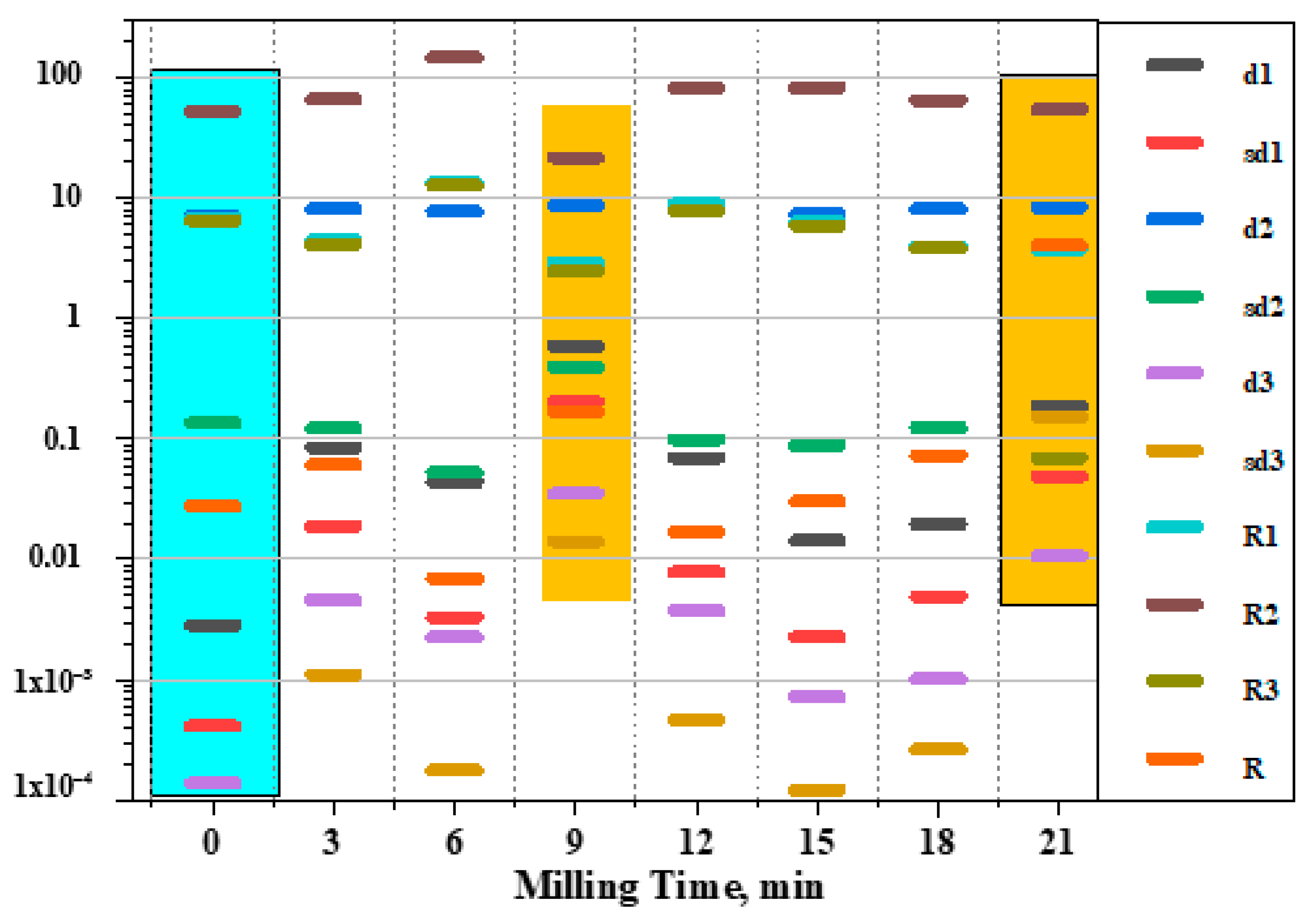

| Descriptor | Mathematical Representation | Description |
|---|---|---|
| d1 | it is the total number of elements. ∆Si is the value of differences in the signal level of the elements of two interference patterns. Sb is the threshold level of the signal. | The number of different elements, regardless of the degree of difference. |
| d2 | ∑∆Si>Sb ∆Si is the average value of the signal level of all the elements of the original interference pattern. | The degree of difference for each discrete element based on the original interference pattern and the total intensity of the level of its signal. |
| d3 | ∆Smax is the sum of max possible differences in terms of the signal level of all the relevant elements of the interference patterns of absolute black and absolute white. | The max value of possible differences between the interference patterns of absolute black and absolute white. |
| Frequency Range, cm−1 | Group | Compound Class | Appearance/Comments |
| 3400–3450 | O-H stretching | H2O | medium |
| ~3250 | O-H stretching | carboxylic acid | strong, intramolecular H-bonded |
| 3000–2800 | N-R stretching | amine | medium |
| 3000–2840 | C-H stretching | alkane | medium |
| 1720–1706 | C=O stretching | carboxylic acid | strong |
| 1685–1666 | C=O stretching | conjugated ketone | strong |
| 1650–1580 | N-H bending | amine | medium |
| ~1650 | O-H bending | H2O | strong |
| 1606–1550 | C=C stretching | quinolone | strong |
| 1465–1450 | C-H bending | methyl | medium |
| 1342–1266 | C-N stretching | aromatic amine | strong |
| 1045–1000 | C-F stretching | fluoro compound | strong |
| 1275–1200 | C-O stretching | alkyl aryl ether | strong |
| ~1000 | C-N stretching | piperazine | strong |
| 880 ± 20 | C-H bending | alkane substituted | strong |
| Milling Time, min | T, K (Reaction Mill Bowl) | Dissolution Time, s | K·102, s−1 | Ea, kJ·mol−1 |
|---|---|---|---|---|
| 0 | 297 | 200 | 2.7 | - |
| 3 | 327 | 50 | 8.4 | 30 |
| 6 | 328 | 30 | 9.0 | 32 |
| 9 | 336 | 40 | 5.1 | 14 |
| 12 | 333 | 40 | 20.0 | 46 |
| 15 | 329 | 30 | 7.5 | 26 |
| 18 | 332 | 90 | 5.7 | 17 |
| 21 | 333 | 60 | 6.7 | 10 |
| Milling Time, min | obsEa ± SD, kJ·mol−1 |
|---|---|
| 0 | 56 ± 5 |
| 21 | 138 ± 23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uspenskaya, E.; Simutina, A.; Kuzmina, E.; Sukhanova, V.; Garaev, T.; Pleteneva, T.; Koldina, A.; Kolyabina, E.; Petrov, G.; Syroeshkin, A. Exploring the Effects of Cramped-Impact-Type Mechanical Action on Active Pharmaceutical Ingredient (Levofloxacin)—Prospects for Pharmaceutical Applications. Powders 2023, 2, 464-483. https://doi.org/10.3390/powders2020028
Uspenskaya E, Simutina A, Kuzmina E, Sukhanova V, Garaev T, Pleteneva T, Koldina A, Kolyabina E, Petrov G, Syroeshkin A. Exploring the Effects of Cramped-Impact-Type Mechanical Action on Active Pharmaceutical Ingredient (Levofloxacin)—Prospects for Pharmaceutical Applications. Powders. 2023; 2(2):464-483. https://doi.org/10.3390/powders2020028
Chicago/Turabian StyleUspenskaya, Elena, Anastasia Simutina, Ekaterina Kuzmina, Vasilisa Sukhanova, Timur Garaev, Tatiana Pleteneva, Alena Koldina, Ekaterina Kolyabina, Gleb Petrov, and Anton Syroeshkin. 2023. "Exploring the Effects of Cramped-Impact-Type Mechanical Action on Active Pharmaceutical Ingredient (Levofloxacin)—Prospects for Pharmaceutical Applications" Powders 2, no. 2: 464-483. https://doi.org/10.3390/powders2020028
APA StyleUspenskaya, E., Simutina, A., Kuzmina, E., Sukhanova, V., Garaev, T., Pleteneva, T., Koldina, A., Kolyabina, E., Petrov, G., & Syroeshkin, A. (2023). Exploring the Effects of Cramped-Impact-Type Mechanical Action on Active Pharmaceutical Ingredient (Levofloxacin)—Prospects for Pharmaceutical Applications. Powders, 2(2), 464-483. https://doi.org/10.3390/powders2020028










