Why Above-Average Rainfall Occurred in Northern Northeast Brazil during the 2019 El Niño?
Abstract
1. Introduction
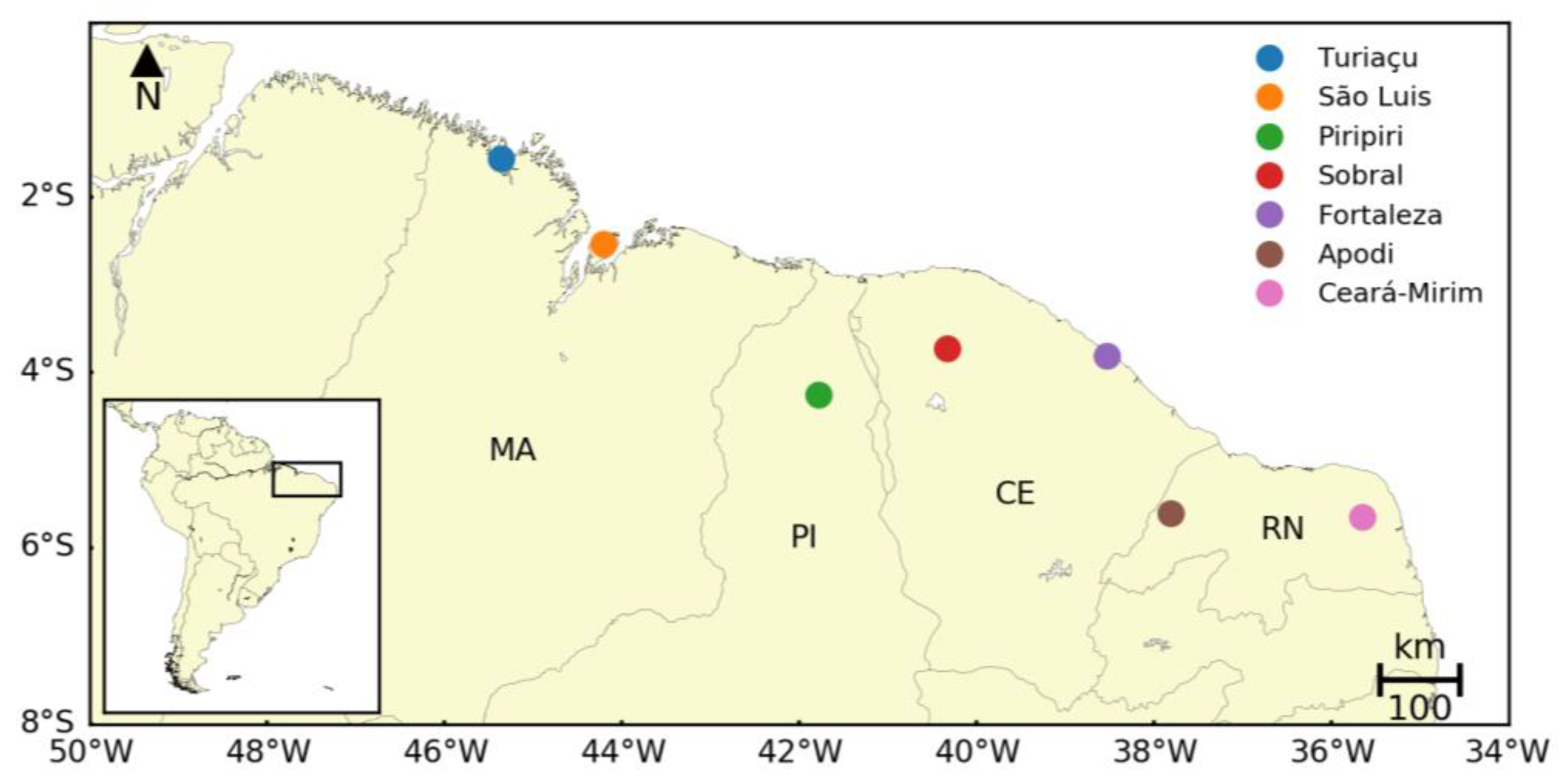
2. Data and Methods
2.1. Datasets
2.2. ENSO-Related Variability
2.3. Model Simulations
2.4. MJO Activity
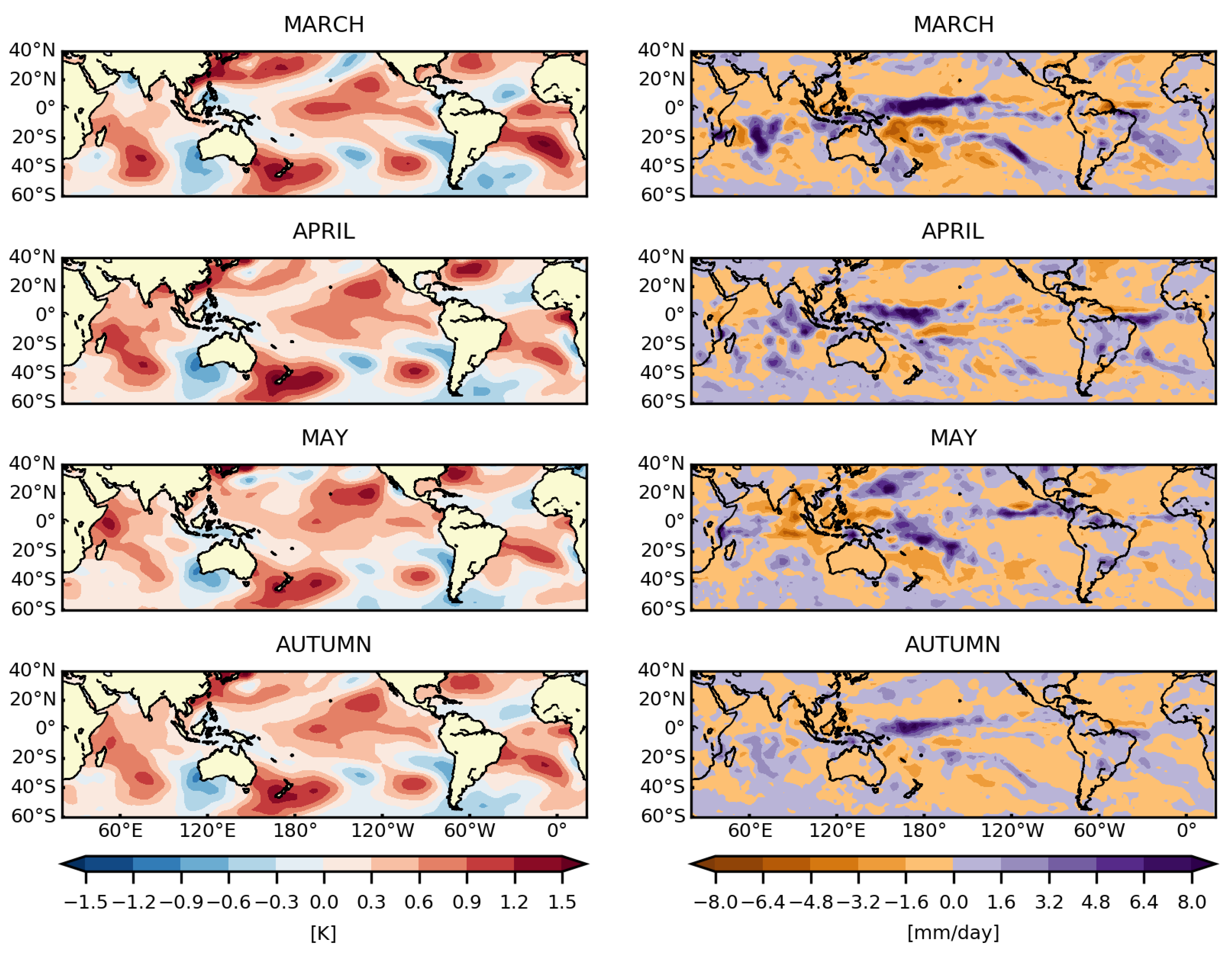
3. Overview of El Niño-Related Conditions in the Austral Autumn
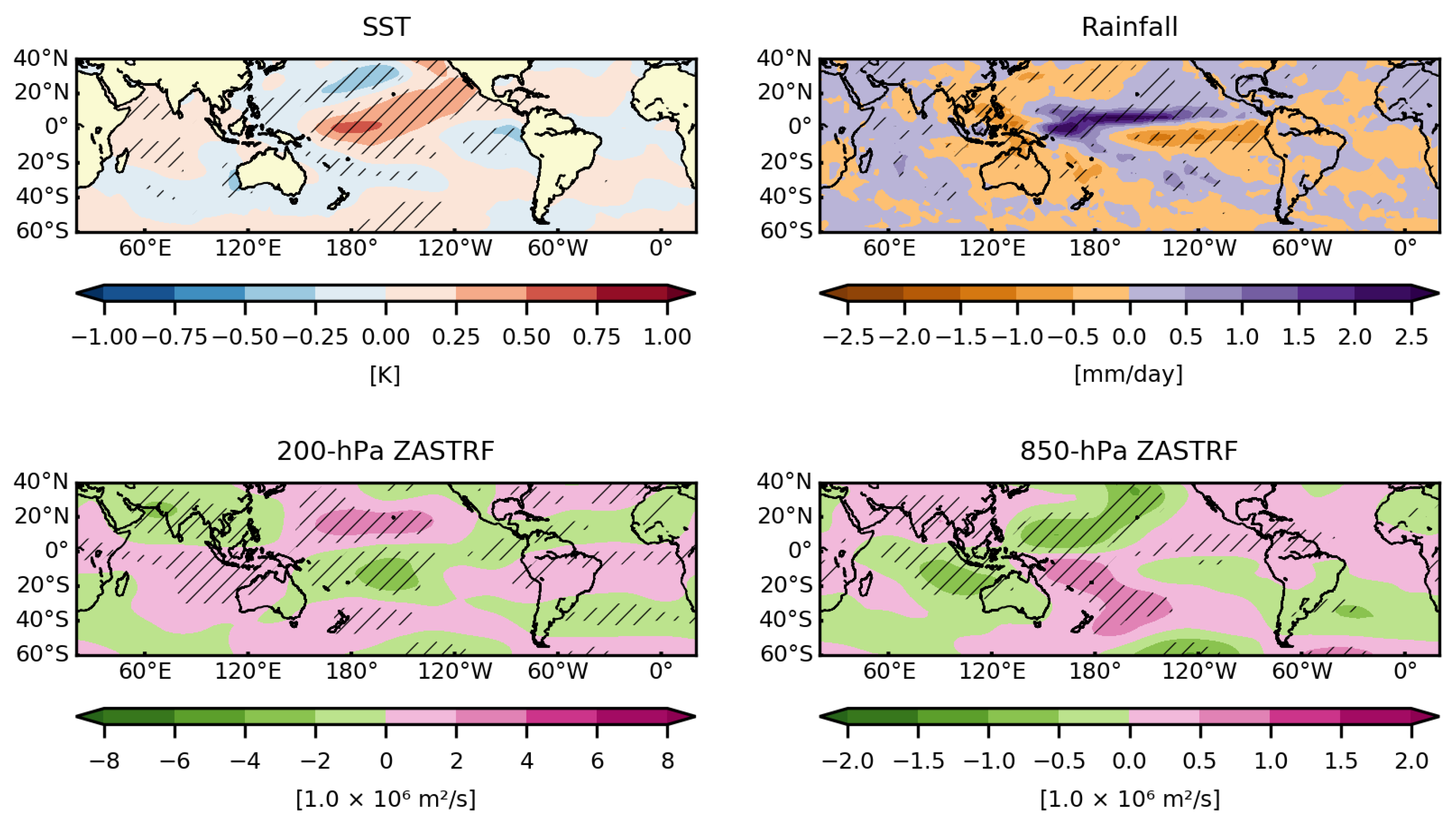
4. Oceanic and Atmospheric Conditions in the 2019 Austral Autumn
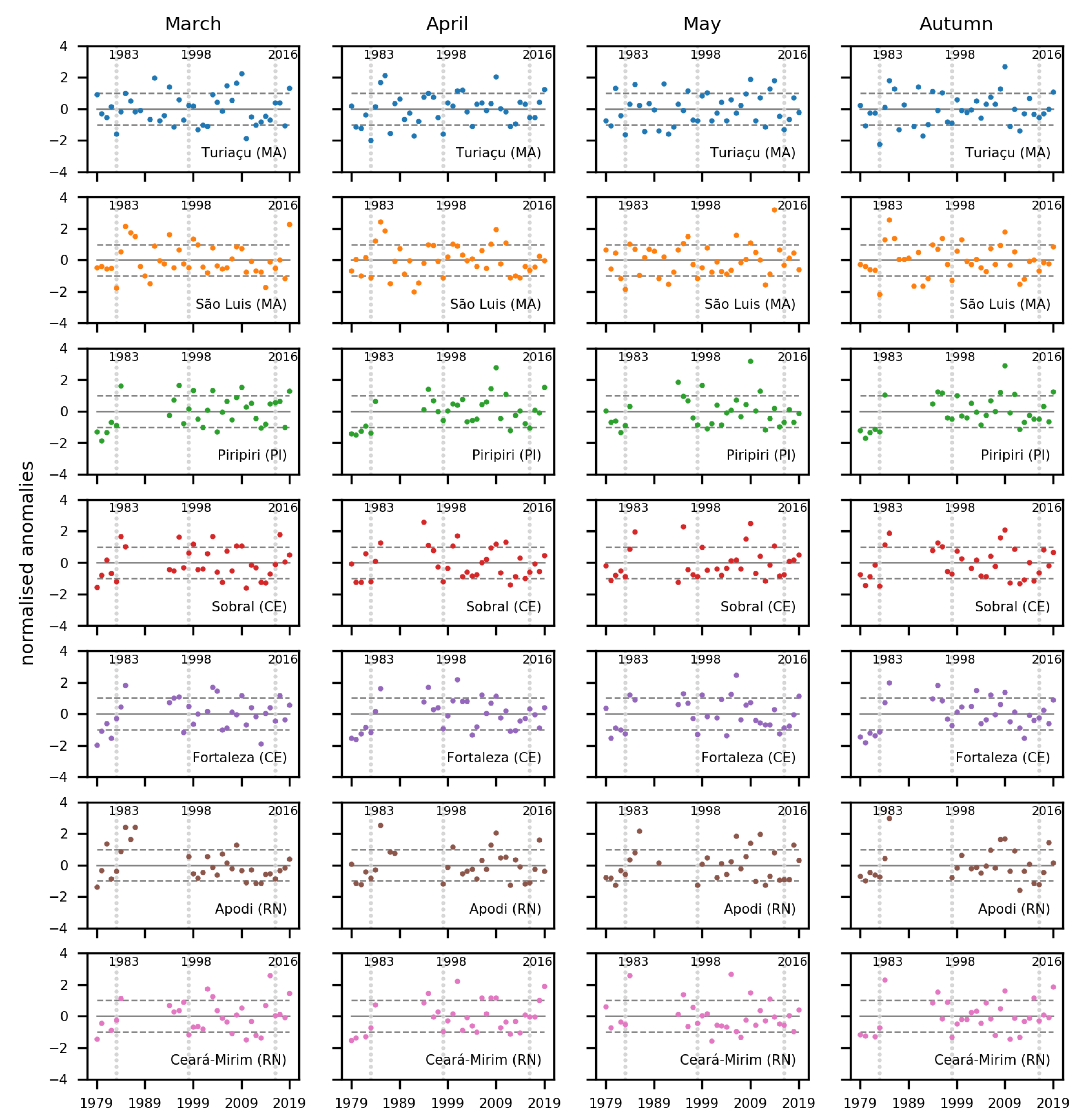
4.1. SST and Rainfall Anomalies
4.2. Atmospheric Circulation Anomalies
5. Model Results
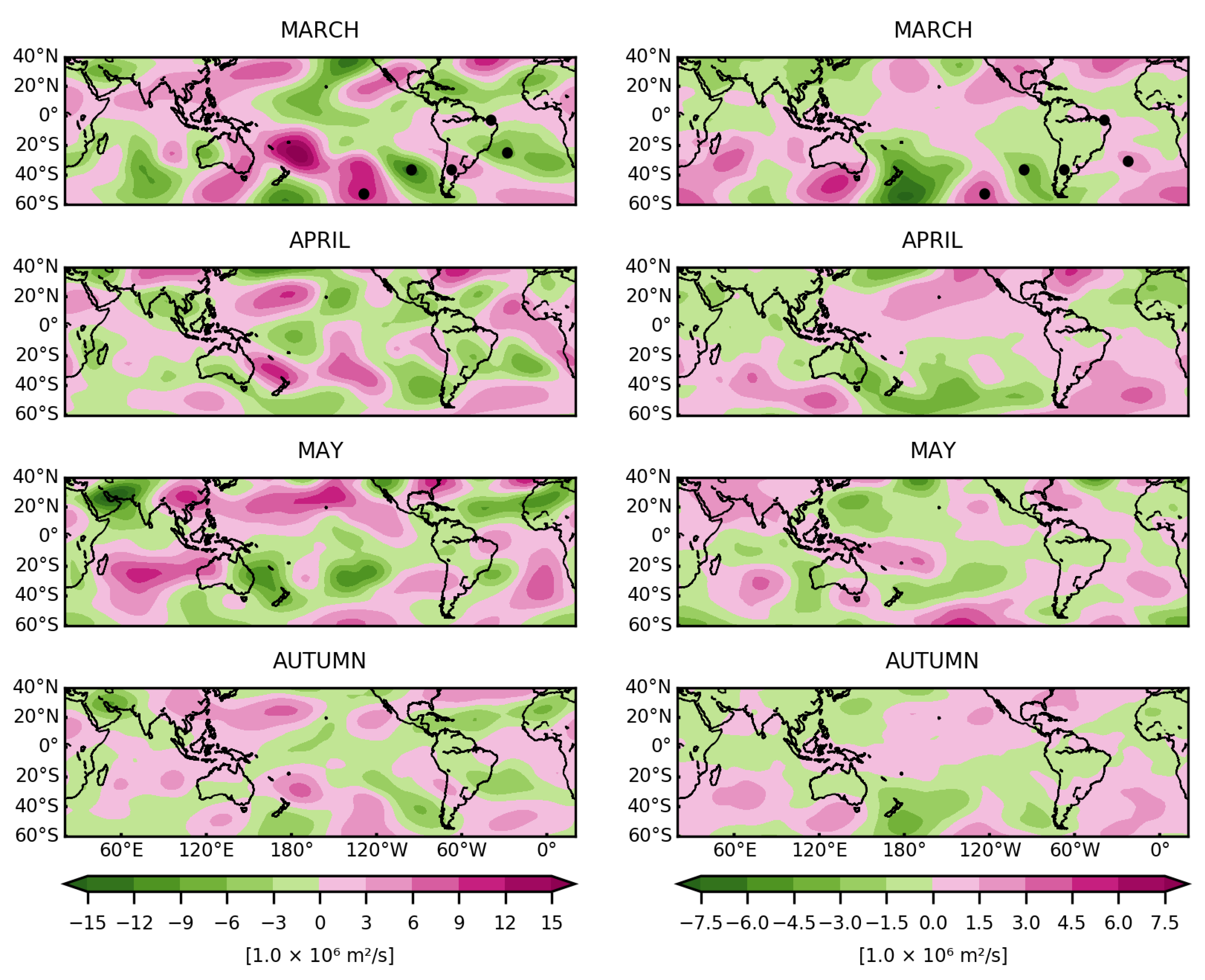
5.1. Influence Functions
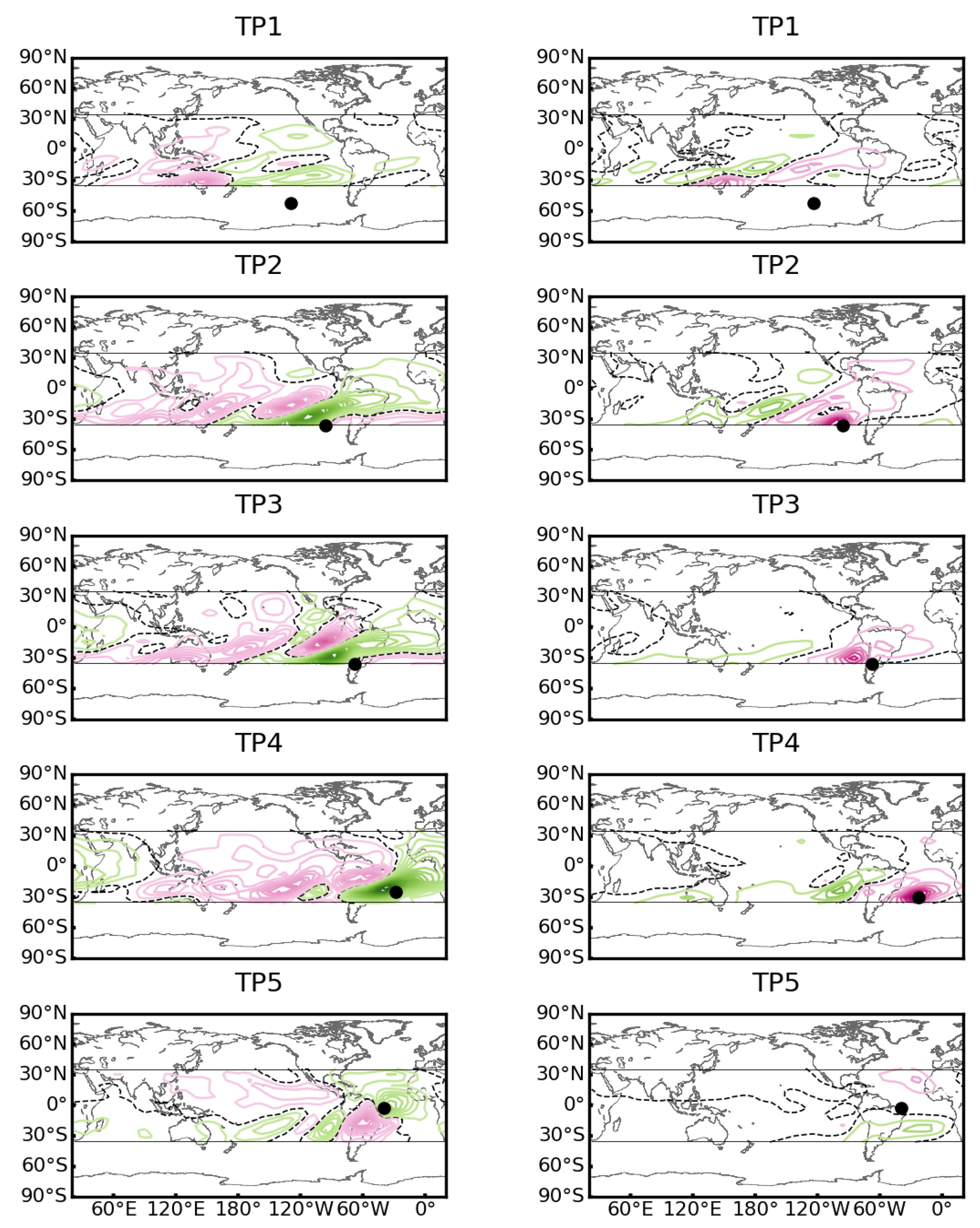
5.2. Vertical and Horizontal Distributions of Thermal Forcings
5.3. Modelled ZASTRF Anomalies
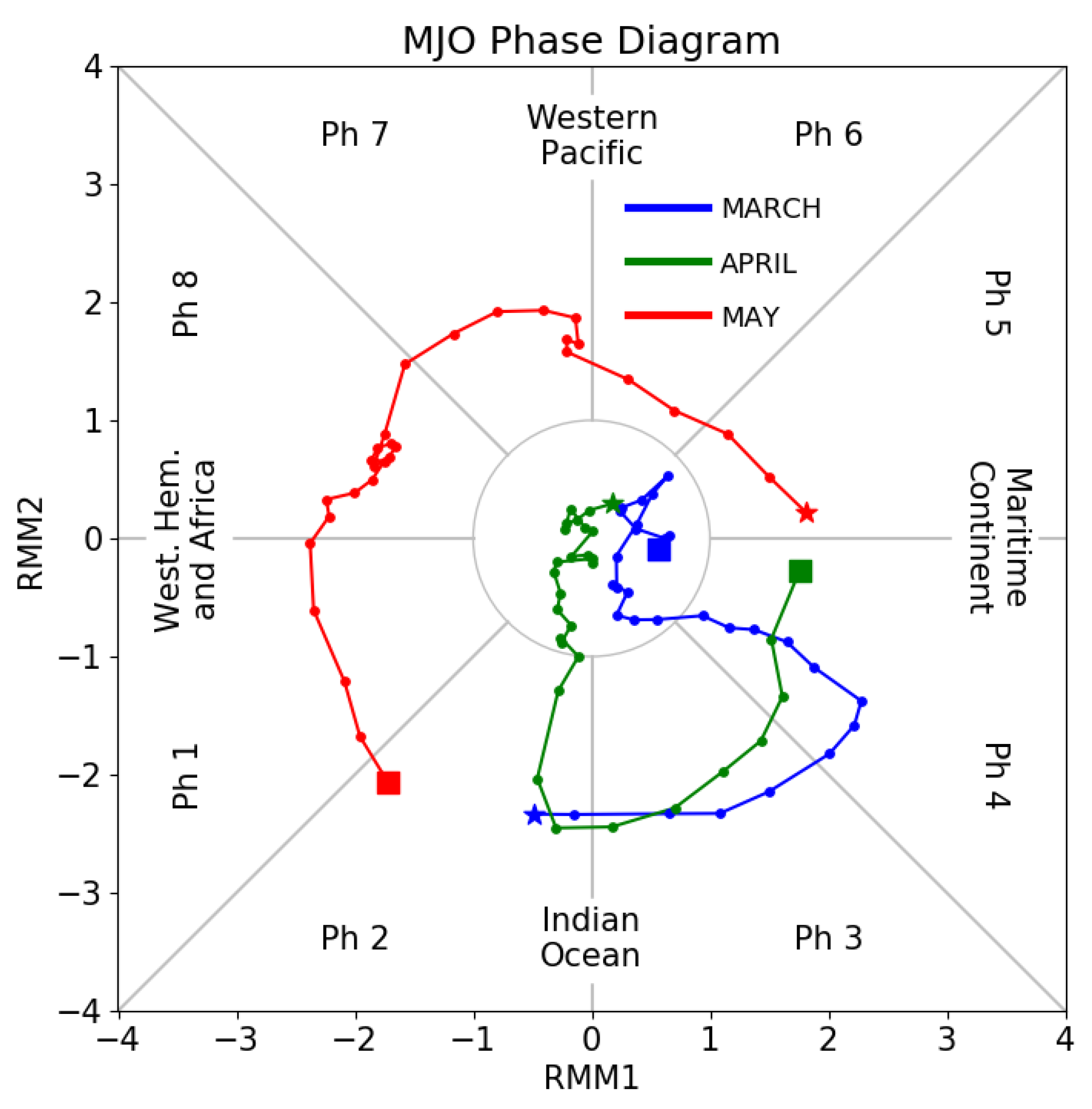
6. MJO Contributions to the MAM 2019 Rainfall in NNEB
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wallace, J.M.; Hobbs, P.V.; McMurdie, L.; Houze, R.A. Weather Systems. In Atmospheric Science—An Introductory Survey, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 313–373. [Google Scholar] [CrossRef]
- Houze, R.A. Cumulonimbus and Severe Storms. Cloud Dyn. 2014, 104, 187–236. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R. The Pacific Decadal Oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Walker, G.T.; Bliss, E.W. World Weather V. Mem. R. Meteorol. Soc. 1932, 4, 53–84. [Google Scholar] [CrossRef]
- Walker, G.T.; Bliss, E.W. World Weather V. Mem. R. Meteorol. Soc. 1937, 4, 119–139. [Google Scholar] [CrossRef]
- Bjerknes, J. “El Niño” study based on analysis of ocean surface temperatures 1935–1957. Inter. Am. Trop. Tuna Comm. Bull. 1961, 5, 217–303. [Google Scholar]
- Bjerknes, J. A possible response of the atmospheric Hadley circulation to equatorial anomalies of ocean temperature. Tellus 1966, 18, 820–829. [Google Scholar] [CrossRef]
- Wyrtki, K. El Niño—The dynamic response of the equatorial Pacific Ocean to atmospheric forcing. J. Phys. Oceanogr. 1975, 5, 572–584. [Google Scholar] [CrossRef]
- Neelin, J.D.; Battisti, D.S.; Hirst, A.C.; Jin, F.-F.; Wakata, Y.; Yamagata, T.; Zebiak, S.E. ENSO theory. J. Geophys. Res. Oceans 1998, 103, 14261–14290. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Hurrell, J.W. Decadal atmosphere-ocean variations in the Pacific. Clim. Dyn. 1994, 9, 303–319. [Google Scholar] [CrossRef]
- Cane, M.A. The evolution of El Niño, past and future. Earth Planet. Sci. Lett. 2005, 230, 227–240. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Zebiak, S.E.; Glantz, M.H. ENSO as an Integrating Concept in Earth Science. Science 2006, 314, 1740–1745. [Google Scholar] [CrossRef]
- Chase, T.N.; Pielke Sr, R.A.; Avissa, R. Teleconnections in the Earth System. In Encyclopedia of Hydrological Sciences; Anderson, M.G., Ed.; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Lin, J.; Qian, T. A New Picture of the Global Impacts of El Nino-Southern Oscillation. Sci. Rep. 2019, 9, 17543. [Google Scholar] [CrossRef]
- Nicholls, N. Towards the prediction of major Australian droughts. Aust. Met. Mag. 1985, 33, 161–166. [Google Scholar]
- Nicholls, N. The El Niño/Southern Oscillation and Australian vegetation. Plant Ecol. 1991, 91, 23–36. [Google Scholar] [CrossRef]
- Cai, W.; Cowan, T. Dynamics of late autumn rainfall reduction over southeastern Australia. Geophys. Res. Lett. 2008, 35, L09708. [Google Scholar] [CrossRef]
- Taschetto, A.S.; England, M.H. El Niño Modoki Impacts on Australian Rainfall. J. Clim. 2009, 22, 3167–3174. [Google Scholar] [CrossRef]
- Cai, W.; van Rensch, P.; Cowan, T.; Hendon, H.H. Teleconnection Pathways of ENSO and the IOD and the Mechanisms for Impacts on Australian Rainfall. J. Clim. 2011, 24, 3910–3923. [Google Scholar] [CrossRef]
- Davey, M.; Brookshaw, A.; Ineson, S. The probability of the impact of ENSO on precipitation and near-surface temperature. Clim. Risk Manag. 2014, 1, 5–24. [Google Scholar] [CrossRef]
- Cai, W.; McPhaden, M.J.; Grimm, A.M.; Rodrigues, R.R.; Taschetto, A.S.; Garreaud, R.D.; Dewitte, B.; Poveda, G.; Ham, Y.-G.; Santoso, A.; et al. Climate impacts of the El Niño–Southern Oscillation on South America. Nat. Rev. Earth Environ. 2020, 1, 215–231. [Google Scholar] [CrossRef]
- Grimm, A.M.; Ambrizzi, T. Teleconnections into South America from the tropics and extratropics on interannual and intraseasonal timescales. In Past Climate Variability in South America and Surrounding Regions; Vimeux, F., Sylvestre, F., Khodri, M., Eds.; Developments in Paleoenvironmental Research; Springer: Dordrecht, The Netherland, 2009; pp. 159–191. [Google Scholar] [CrossRef]
- Stan, C.; Straus, D.M.; Frederiksen, J.S.; Lin, H.; Maloney, E.D.; Schumacher, C. Review of Tropical-Extratropical Teleconnections on Intraseasonal Time Scales. Rev. Geophys. 2017, 55, 902–937. [Google Scholar] [CrossRef]
- Shimizu, M.H.; de Albuquerque Cavalcanti, I.F. Variability patterns of Rossby wave source. Clim. Dyn. 2011, 37, 441–454. [Google Scholar] [CrossRef]
- L’heureux, M.L.; Thompson, D.W.J. Observed Relationships between the El Niño–Southern Oscillation and the Extratropical Zonal-Mean Circulation. J. Clim. 2006, 19, 276–287. [Google Scholar] [CrossRef]
- Grimm, A.M. Interannual climate variability in South America: Impacts on seasonal precipitation, extreme events, and possible effects of climate change. Stoch. Environ. Res. Risk Assess. 2011, 25, 537–554. [Google Scholar] [CrossRef]
- Tedeschi, R.G.; Grimm, A.M.; Cavalcanti, I.F.A. Influence of Central and East ENSO on extreme events of precipitation in South America during austral spring and summer. Int. J. Clim. 2015, 35, 2045–2064. [Google Scholar] [CrossRef]
- Tedeschi, R.G.; Grimm, A.M.; Cavalcanti, I.F.A. Influence of Central and East ENSO on precipitation and its extreme events in South America during austral autumn and winter. Int. J. Clim. 2016, 36, 4797–4814. [Google Scholar] [CrossRef]
- Saravanan, R.; Chang, P. Interaction between tropical Atlantic variability and El Niño–Southern Oscillation. J. Clim. 2000, 13, 2177–2194. [Google Scholar] [CrossRef]
- Hastenrath, S. Circulation and teleconnection mechanisms of Northeast Brazil droughts. Prog. Oceanogr. 2006, 70, 407–415. [Google Scholar] [CrossRef]
- Rodrigues, R.R.; Haarsma, R.J.; Campos, E.J.D.; Ambrizzi, T. The Impacts of Inter–El Niño Variability on the Tropical Atlantic and Northeast Brazil Climate. J. Clim. 2011, 24, 3402–3422. [Google Scholar] [CrossRef]
- Lucena, D.B.; Servain, J.; Filho, M.F.G. Rainfall Response in Northeast Brazil from Ocean Climate Variability during the Second Half of the Twentieth Century. J. Clim. 2011, 24, 6174–6184. [Google Scholar] [CrossRef]
- Hastenrath, S.; Greischar, L. Circulation mechanisms related to northeast Brazil rainfall anomalies. J. Geophys. Res. Atmos. 1993, 98, 5093–5102. [Google Scholar] [CrossRef]
- Chiang, J.C.H.; Vimont, D.J. Analogous Pacific and Atlantic Meridional Modes of Tropical Atmosphere–Ocean Variability in the tropical Pacific and tropical Atlantic. J. Clim. 2004, 17, 4143–4158. [Google Scholar] [CrossRef]
- Wagner, R.G. Mechanisms Controlling Variability of the Interhemispheric Sea Surface Temperature Gradient in the Tropical Atlantic. J. Clim. 1996, 9, 2010–2019. [Google Scholar] [CrossRef]
- Chang, P.; Ji, L.; Li, H. A decadal climate variation in the tropical Atlantic Ocean from thermodynamic air-sea interactions. Nature 1997, 385, 516–518. [Google Scholar] [CrossRef]
- Goddard, L.; Aitchellouche, Y.; Baethgen, W.; Dettinger, M.; Graham, R.; Hayman, P.; Kadi, M.; Martínez, R.; Meinke, H. Providing Seasonal-to-Interannual Climate Information for Risk Management and Decision-making. Procedia Environ. Sci. 2010, 1, 81–101. [Google Scholar] [CrossRef]
- Creedy, T.J.; Asare, R.A.; Morel, A.C.; Hirons, M.; Mason, J.; Malhi, Y.; McDermott, C.L.; Opoku, E.; Norris, K. Climate change alters impacts of extreme climate events on a tropical perennial tree crop. Sci. Rep. 2022, 12, 19653. [Google Scholar] [CrossRef]
- Nobre, G.G.; Muis, S.; Veldkamp, T.I.; Ward, P.J. Achieving the reduction of disaster risk by better predicting impacts of El Niño and La Niña. Prog. Disaster Sci. 2019, 2, 100022. [Google Scholar] [CrossRef]
- Giovannettone, J.; Paredes, F.; Barbosa, H.; Dos Santos, C.A.C.; Kumar, T.V.L. Characterization of links between hydro-climate indices and long-term precipitation in Brazil using correlation analysis. Int. J. Clim. 2020, 40, 5527–5541. [Google Scholar] [CrossRef]
- Valadão, C.E.A.; Carvalho, L.M.V.; Lucio, P.S.; Chaves, R.R. Impacts of the Madden-Julian oscillation on intraseasonal precipitation over Northeast Brazil. Int. J. Clim. 2016, 37, 1859–1884. [Google Scholar] [CrossRef]
- Junior, F.D.C.V.; Jones, C.; Gandu, A.W.; Martins, E.S.P.R. Impacts of the Madden-Julian Oscillation on the intensity and spatial extent of heavy precipitation events in northern Northeast Brazil. Int. J. Clim. 2021, 41, 3628–3639. [Google Scholar] [CrossRef]
- Mo, K.C.; Nogues-Paegle, J. Pan-America. In Intraseasonal Variability in the Atmosphere-Ocean Climate System; Springer Praxis Books (Environmental Sciences); Springer: Berlin/Heidelberg, Germany, 2005; pp. 95–124. [Google Scholar] [CrossRef]
- Shimizu, M.H.; Ambrizzi, T. MJO influence on ENSO effects in precipitation and temperature over South America. Theor. Appl. Clim. 2015, 124, 291–301. [Google Scholar] [CrossRef]
- Shimizu, M.H.; Ambrizzi, T.; Liebmann, B. Extreme precipitation events and their relationship with ENSO and MJO phases over northern South America. Int. J. Climatol. 2017, 37, 2977–2989. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Nichols, G.P.; Fontenot, J.D.; Gibbons, J.P.; Sanders, M. Evaluation of volumetric modulated Arc therapy for postmastectomy treatment. Radiat. Oncol. 2017, 30, 8179–8205. [Google Scholar] [CrossRef] [PubMed]
- Adler, R.F.; Sapiano, M.R.P.; Huffman, G.J.; Wang, J.-J.; Gu, G.; Bolvin, D.; Chiu, L.; Schneider, U.; Becker, A.; Nelkin, E.; et al. The Global Precipitation Climatology Project (GPCP) Monthly Analysis (New Version 2.3) and a Review of 2017 Global Precipitation. Atmosphere 2018, 9, 138. [Google Scholar] [CrossRef] [PubMed]
- Liebmann, B.; Smith, C.A. Description of a complete (interpolated) outgoing longwave radiation dataset. Bull. Am. Meteorol. Soc. 1996, 77, 1275–1277. [Google Scholar]
- Junker, N.W.; Grumm, R.H.; Hart, R.; Bosart, L.F.; Bell, K.M.; Pereira, F.J. Use of Normalized Anomaly Fields to Anticipate Extreme Rainfall in the Mountains of Northern California. Weather. Forecast. 2008, 23, 336–356. [Google Scholar] [CrossRef]
- Allen, M.P. The t test for the simple regression coefficient. In Understanding Regression Analysis; Springer: Boston, MA, USA, 1997; pp. 66–70. [Google Scholar] [CrossRef]
- Trenberth, K.E. The definition of el nino. Bull. Am. Meteorol. Soc. 1997, 78, 2771–2778. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Stepaniak, D.P. Indices of El Niño evolution. J. Clim. 2001, 14, 1697–1701. [Google Scholar] [CrossRef]
- Ashok, K.; Behera, S.K.; Rao, S.A.; Weng, H.; Yamagata, T. El Niño Modoki and its possible teleconnection. J. Geophys. Res. Ocean. 2007, 112, C11007. [Google Scholar] [CrossRef]
- Lo, F.; Hendon, H.H. Empirical Extended-Range Prediction of the Madden–Julian Oscillation. Mon. Weather. Rev. 2000, 128, 2528–2543. [Google Scholar] [CrossRef]
- Livezey, R.E.; Chen, W.Y. Statistical field significance and its determination by Monte Carlo techniques. Mon. Wea. Rev. 1983, 111, 46–59. [Google Scholar] [CrossRef]
- Branstator, G. Analysis of General Circulation Model Sea-Surface Temperature Anomaly Simulations Using a Linear Model. Part I: Forced Solutions. J. Atmos. Sci. 1985, 42, 2225–2241. [Google Scholar] [CrossRef]
- Grimm, A.M.; Silva Dias, P.L. Analysis of tropical–extratropical interactions with influence functions of a barotropic model. J. Atmos. Sci. 1995, 52, 3538–3555. [Google Scholar] [CrossRef]
- Watanabe, M.; Kimoto, M. Atmosphere-ocean thermal coupling in the North Atlantic: A positive feedback. Q. J. R. Meteorol. Soc. 2000, 126, 3343–3369. [Google Scholar] [CrossRef]
- Tseng, K.-C.; Maloney, E.; Barnes, E. The Consistency of MJO Teleconnection Patterns: An Explanation Using Linear Rossby Wave Theory. J. Clim. 2018, 32, 531–548. [Google Scholar] [CrossRef]
- Kasahara, A.; Silva Dias, P.L. Response of planetary waves to stationary tropical heating in a global atmosphere with me-ridional and vertical shear. J. Atmos. Sci. 1986, 43, 1893–1912. [Google Scholar] [CrossRef]
- Majda, A.J.; Biello, J.A. The Nonlinear Interaction of Barotropic and Equatorial Baroclinic Rossby Waves. J. Atmos. Sci. 2003, 60, 1809–1821. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Solomon, A. Implications of Global Atmospheric Spatial Spectra for Processing and Displaying Data. J. Clim. 1993, 6, 531–545. [Google Scholar] [CrossRef]
- Tseng, K.-C.; Maloney, E.; Barnes, E.A. The Consistency of MJO Teleconnection Patterns on Interannual Time Scales. J. Clim. 2020, 33, 3471–3486. [Google Scholar] [CrossRef]
- Jin, F.; Hoskins, B.J. The Direct Response to Tropical Heating in a Baroclinic Atmosphere. J. Atmos. Sci. 1995, 52, 307–319. [Google Scholar] [CrossRef]
- Ambrizzi, T.; Hoskins, B.J. Stationary rossby-wave propagation in a baroclinic atmosphere. Q. J. R. Meteorol. Soc. 1997, 123, 919–928. [Google Scholar] [CrossRef]
- Seo, K.-H.; Son, S.-W. The Global Atmospheric Circulation Response to Tropical Diabatic Heating Associated with the Madden–Julian Oscillation during Northern Winter. J. Atmos. Sci. 2012, 69, 79–96. [Google Scholar] [CrossRef]
- Zhang, C.; Hagos, S.M. Bi-modal Structure and Variability of Large-Scale Diabatic Heating in the Tropics. J. Atmos. Sci. 2009, 66, 3621–3640. [Google Scholar] [CrossRef]
- Schumacher, C.; Houze, R.A., Jr.; Kraucunas, I. The tropical dynamical response to latent heating estimates derived from the TRMM precipitation radar. J. Atmos. Sci. 2004, 61, 1341–1358. [Google Scholar] [CrossRef]
- Schumacher, C.; Zhang, M.H.; Ciesielski, P.E. Heating Structures of the TRMM Field Campaigns. J. Atmos. Sci. 2007, 64, 2593–2610. [Google Scholar] [CrossRef]
- Liu, A.Z.; Ting, M.; Wang, H. Maintenance of Circulation Anomalies during the 1988 Drought and 1993 Floods over the United States. J. Atmos. Sci. 1998, 55, 2810–2832. [Google Scholar] [CrossRef]
- Zhou, G. Atmospheric Response to Sea Surface Temperature Anomalies in the Mid-latitude Oceans: A Brief Review. Atmos. Ocean. 2019, 57, 319–328. [Google Scholar] [CrossRef]
- Teng, H.; Branstator, G. Amplification of Waveguide Teleconnections in the Boreal Summer. Curr. Clim. Chang. Rep. 2019, 5, 421–432. [Google Scholar] [CrossRef]
- Yanai, M.; Esbensen, S.; Chu, J.H. Determination of bulk properties of tropical cloud clusters from large-scale heat and moisture budgets. J. Atmos. Sci. 1973, 30, 611–627. [Google Scholar] [CrossRef]
- Wheeler, M.C.; Hendon, H.H. An all-season real-time multivariate MJO index: Development of an index for monitoring and prediction. Mon. Wea. Rev. 2004, 132, 1917–1932. [Google Scholar] [CrossRef]
- Duchon, C.E. Lanczos filtering in one and two dimensions. J. Appl. Meteorol. Climatol. 1979, 18, 1016–1022. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Caron, J.M. The Southern Oscillation Revisited: Sea Level Pressures, Surface Temperatures, and Precipitation. J. Clim. 2000, 13, 4358–4365. [Google Scholar] [CrossRef]
- NOAA Monthly Climate Time Series: Atlantic Meridional Mode (AMM) SST Index. Available online: https://psl.noaa.gov/data/timeseries/monthly/AMM/ammsst.data (accessed on 18 June 2023).
- Hu, Z.; McPhaden, M.J.; Kumar, A.; Yu, J.; Johnson, N.C. Uncoupled El Niño Warming. Geophys. Res. Lett. 2020, 47, e2020GL087621. [Google Scholar] [CrossRef]
- Andreoli, R.V.; de Oliveira, S.S.; Kayano, M.T.; Viegas, J.; de Souza, R.A.F.; Candido, L.A. The influence of different El Niño types on the South American rainfall. Int. J. Clim. 2017, 37, 1374–1390. [Google Scholar] [CrossRef]
- van Rensch, P.; Arblaster, J.; Gallant, A.J.E.; Cai, W.; Nicholls, N.; Durack, P.J. Mechanisms causing east Australian spring rainfall differences between three strong El Niño events. Clim. Dyn. 2019, 53, 3641–3659. [Google Scholar] [CrossRef]
- Kayano, M.T.; Capistrano, V.B. How the Atlantic multidecadal oscillation (AMO) modifies the ENSO influence on the South American rainfall. Int. J. Clim. 2014, 34, 162–178. [Google Scholar] [CrossRef]
- Levine, A.F.Z.; McPhaden, M.J.; Frierson, D.M.W. The impact of the AMO on multidecadal ENSO variability. Geophys. Res. Lett. 2017, 44, 3877–3886. [Google Scholar] [CrossRef]
- L’heureux, M.L.; Takahashi, K.; Watkins, A.B.; Barnston, A.G.; Becker, E.J.; Di Liberto, T.E.; Gamble, F.; Gottschalck, J.; Halpert, M.S.; Huang, B.; et al. Observing and Predicting the 2015/16 El Niño. Bull. Am. Meteorol. Soc. 2017, 98, 1363–1382. [Google Scholar] [CrossRef]
- Johnson, N.C.; L’Heureux, M.L.; Chang, C.; Hu, Z. On the Delayed Coupling Between Ocean and Atmosphere in Recent Weak El Niño Episodes. Geophys. Res. Lett. 2019, 46, 11416–11425. [Google Scholar] [CrossRef]
- Mo, K.C.; Paegle, J.N. The Pacific-South American modes and their downstream effects. Int. J. Climatol. A J. R. Meteorol. Soc. 2001, 10, 1211–1229. [Google Scholar] [CrossRef]
- Alvarez, M.S.; Vera, C.; Kiladis, G.N.; Liebmann, B. Influence of the Madden Julian Oscillation on precipitation and surface air temperature in South America. Clim. Dyn. 2016, 46, 245–262. [Google Scholar] [CrossRef]
- Seo, K.-H.; Lee, H.-J. Mechanisms for a PNA-Like Teleconnection Pattern in Response to the MJO. J. Atmos. Sci. 2017, 74, 1767–1781. [Google Scholar] [CrossRef]
- Adames, F.; Wallace, J.M.; Monteiro, J.M. Seasonality of the Structure and Propagation Characteristics of the MJO. J. Atmos. Sci. 2016, 73, 3511–3526. [Google Scholar] [CrossRef]
- Sutton, R.; Jewson, S.P.; Rowell, D.P. The Elements of Climate Variability in the Tropical Atlantic Region. J. Clim. 2000, 13, 3261–3284. [Google Scholar] [CrossRef]
- Xie, S.-P.; Carton, J.A. Tropical Atlantic variability: Patterns, mechanisms, and impacts. Earth Climate: The Ocean-Atmosphere Interaction. Geophys. Monogr. Amer. Geophys. Union 2004, 147, 121–142. [Google Scholar] [CrossRef]
- Utida, G.; Cruz, F.W.; Etourneau, J.; Bouloubassi, I.; Schefuß, E.; Vuille, M.; Novello, V.F.; Prado, L.F.; Sifeddine, A.; Klein, V.; et al. Tropical South Atlantic influence on Northeastern Brazil precipitation and ITCZ displacement during the past 2300 years. Sci. Rep. 2019, 9, 1698. [Google Scholar] [CrossRef]
- McPhaden, M.J. Playing hide and seek with El Niño. Nat. Clim. Chang. 2015, 5, 791–795. [Google Scholar] [CrossRef]

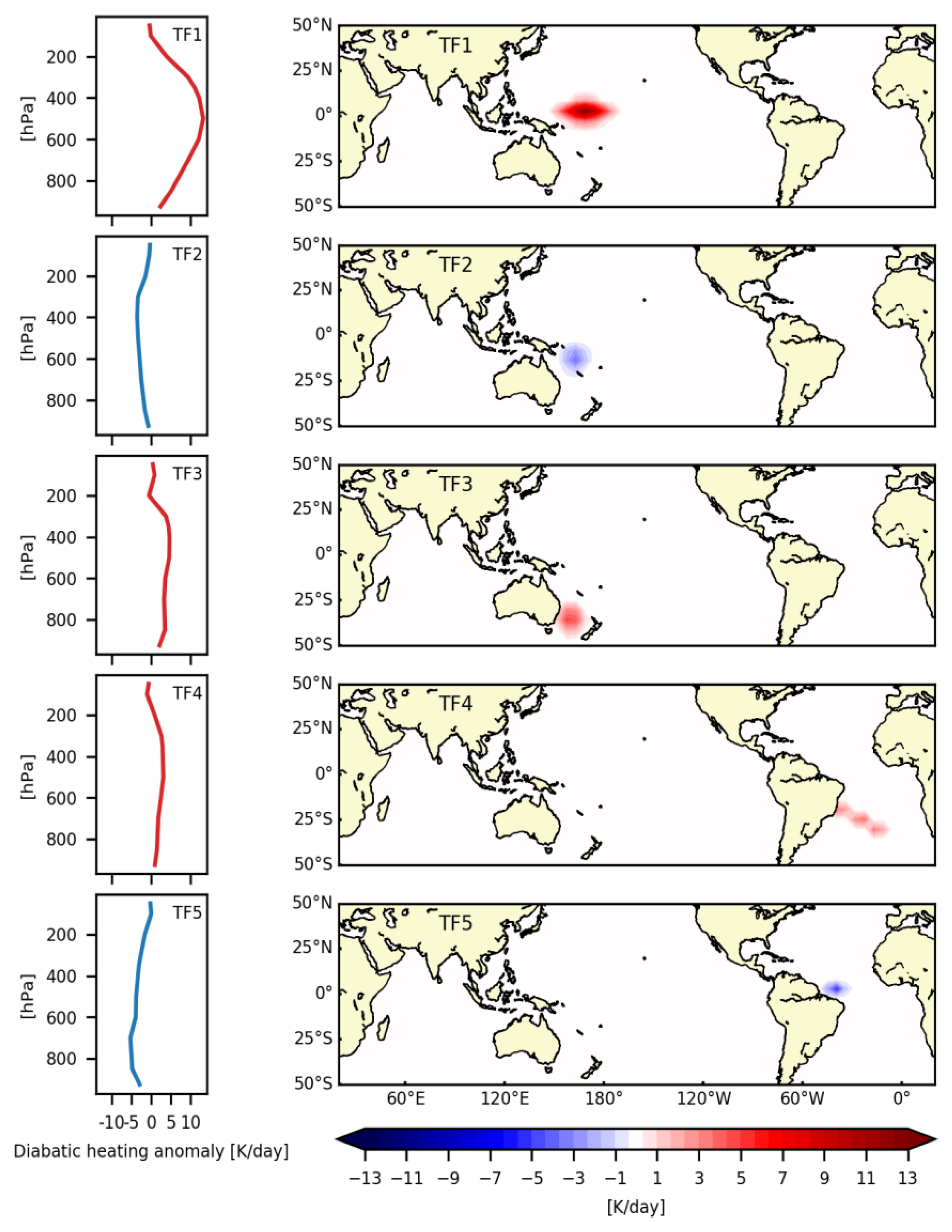


| Experiment | Amplitude (K Day−1) | Peaking Level (hPa) | Vertical Profile | Location |
|---|---|---|---|---|
| IFs | 5 | 400 | Deep | Grid point: 35° S–35° N/0–360° |
| TF1 | 13.1 | 500 | Deep | Area: ~5° S–7.5° N/150° E–170° W |
| TF2 | −3.6 | 400 | Deep | Area: ~20°–5° S/155°–170° E |
| TF3 | 4.6 | 400 | Deep | Area: ~40°–25° S/152°–168° E |
| TF4 | 3.1 | 500 | Deep | Area: ~35°–15° S/43°–10° W |
| TF5 | −5.3 | 700 | Shallow | Area: ~2.5°S–7.5° N/48°–32° W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Andrade, F.M.; Godoi, V.A.; Aravéquia, J.A. Why Above-Average Rainfall Occurred in Northern Northeast Brazil during the 2019 El Niño? Meteorology 2023, 2, 307-328. https://doi.org/10.3390/meteorology2030019
de Andrade FM, Godoi VA, Aravéquia JA. Why Above-Average Rainfall Occurred in Northern Northeast Brazil during the 2019 El Niño? Meteorology. 2023; 2(3):307-328. https://doi.org/10.3390/meteorology2030019
Chicago/Turabian Stylede Andrade, Felipe M., Victor A. Godoi, and José A. Aravéquia. 2023. "Why Above-Average Rainfall Occurred in Northern Northeast Brazil during the 2019 El Niño?" Meteorology 2, no. 3: 307-328. https://doi.org/10.3390/meteorology2030019
APA Stylede Andrade, F. M., Godoi, V. A., & Aravéquia, J. A. (2023). Why Above-Average Rainfall Occurred in Northern Northeast Brazil during the 2019 El Niño? Meteorology, 2(3), 307-328. https://doi.org/10.3390/meteorology2030019







