The Status of the Astrophysical Parameters of Upper Main Sequence Stars
Abstract
1. Introduction
2. Target Selection and Catalogues
3. Methods
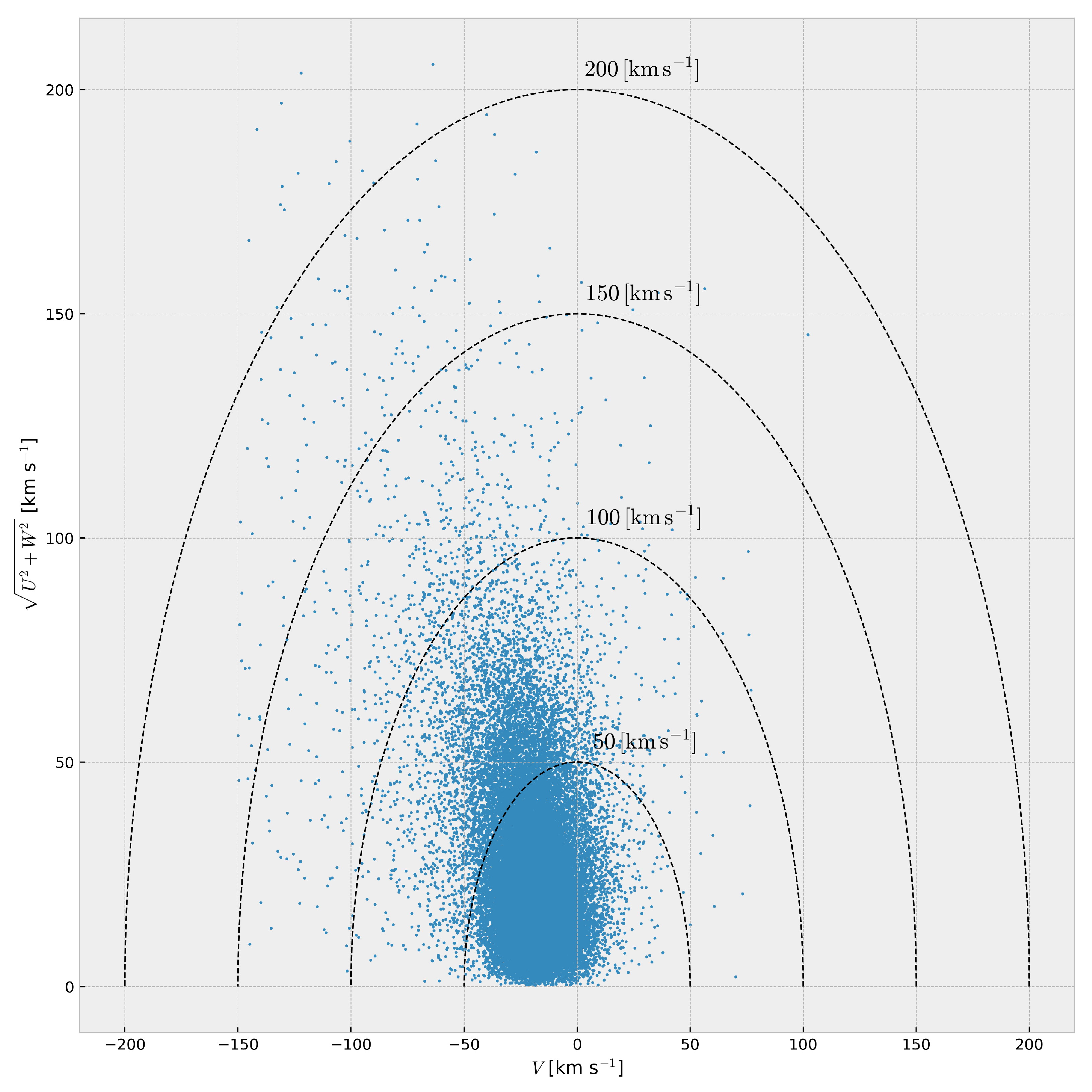
3.1. Kinematic Selection
3.2. Extinction Measurements
- Mean ();
- Standard deviation ();
- Skewness ();
- Kurtosis ().
4. Results
4.1. Effective Temperature
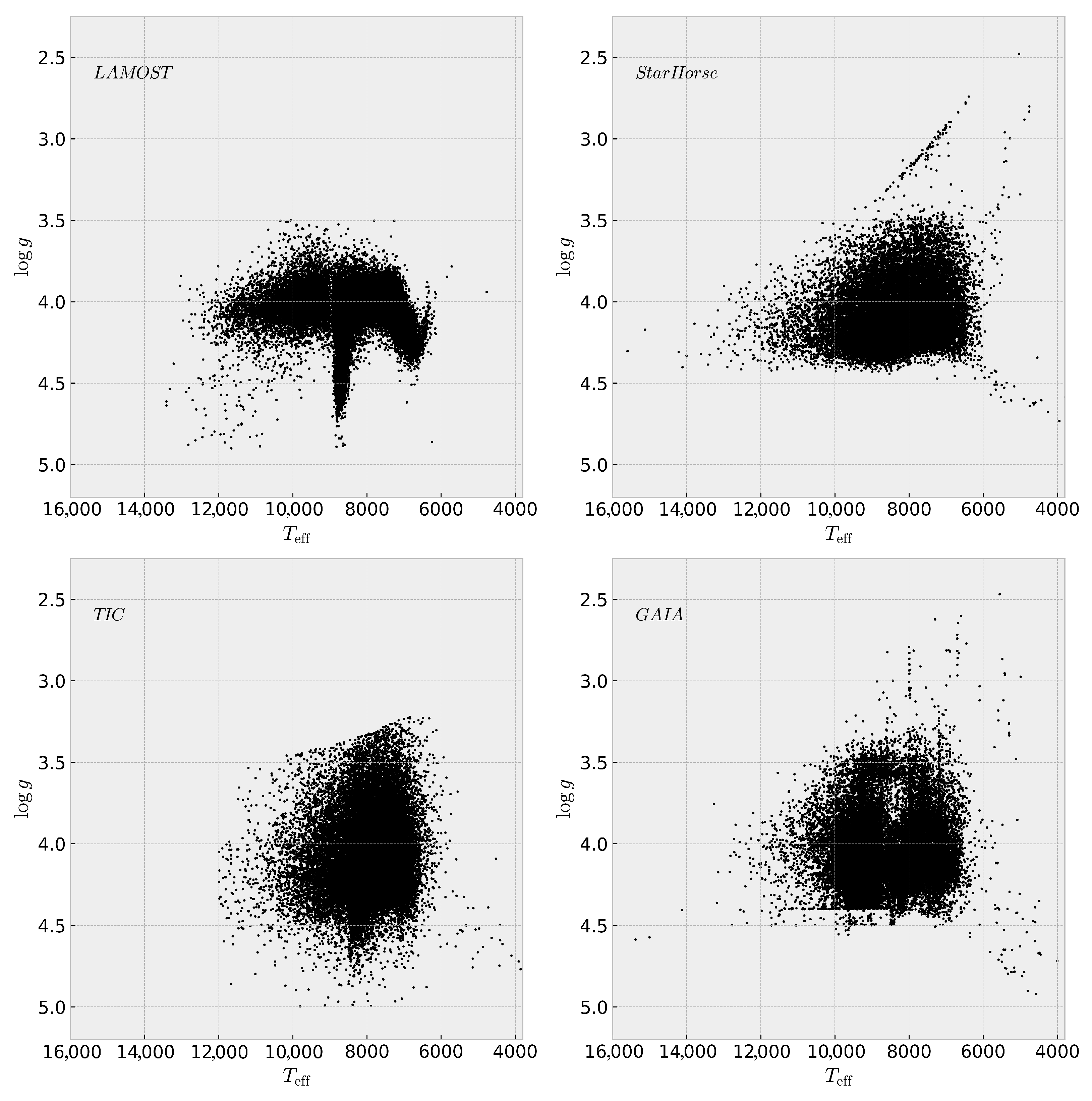
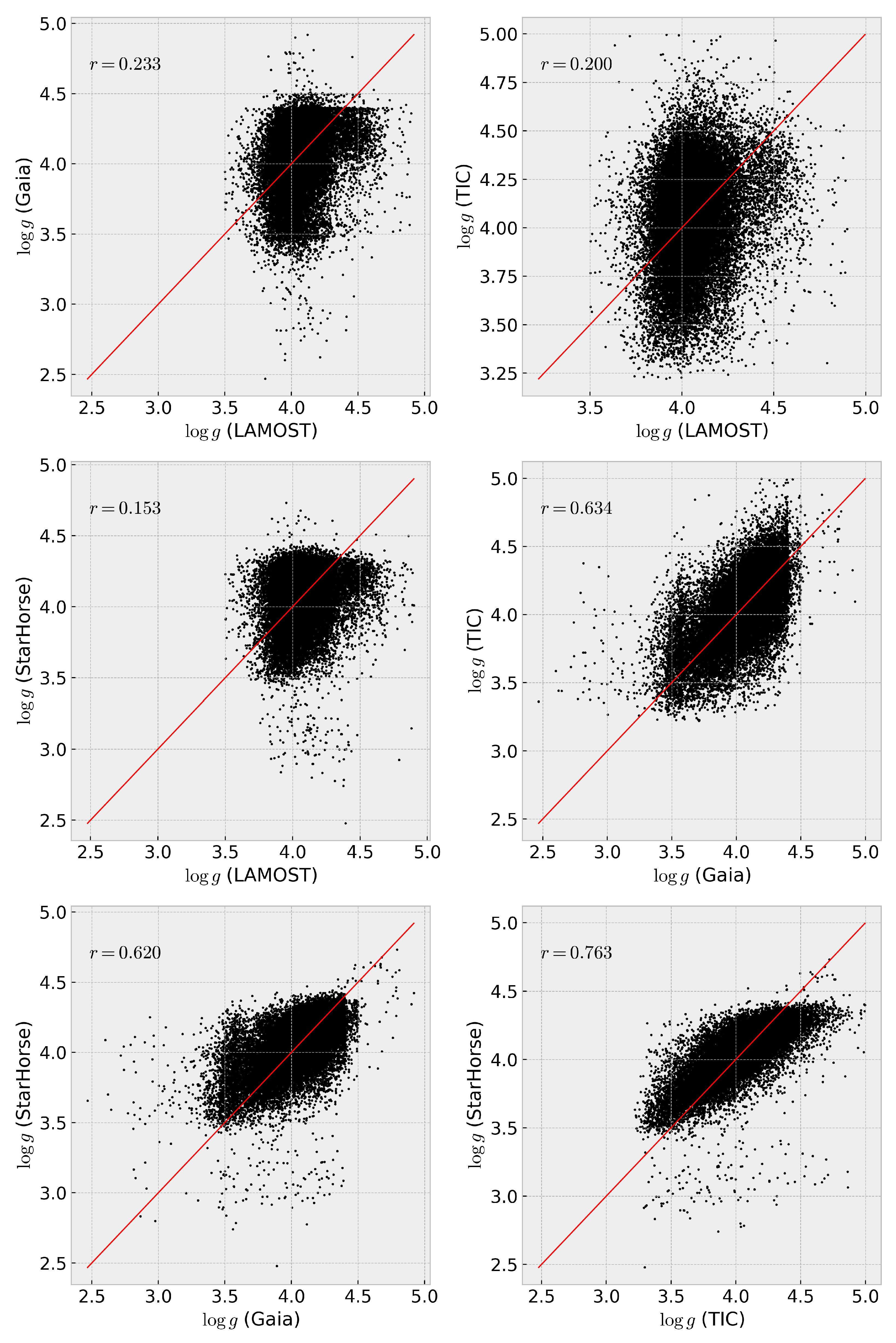
4.2. Surface Gravity
4.3. Correlation with
4.4. Bolometric Correction
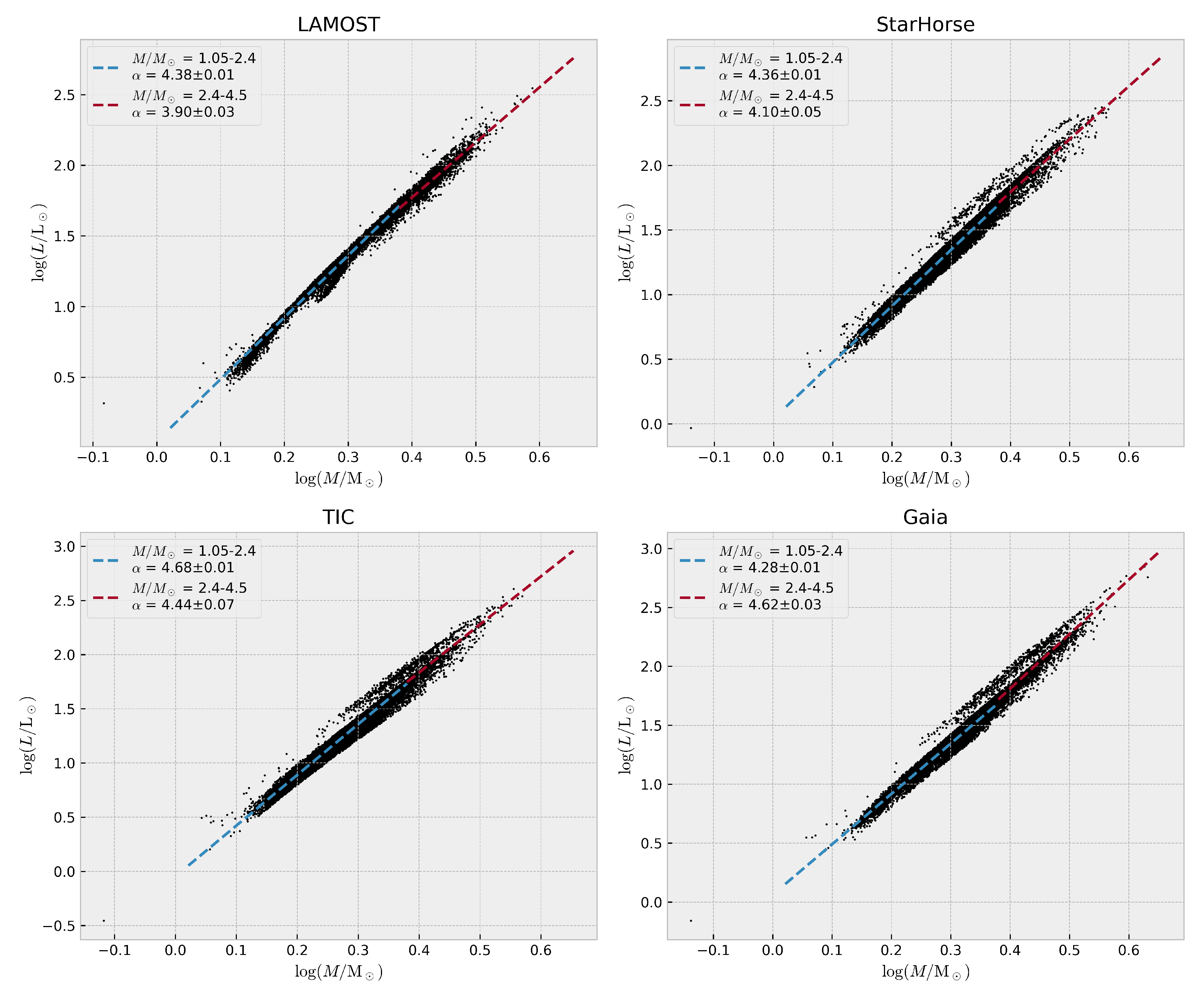
4.5. Mass-Luminosity Relation
4.6. Mass-Radius Relation
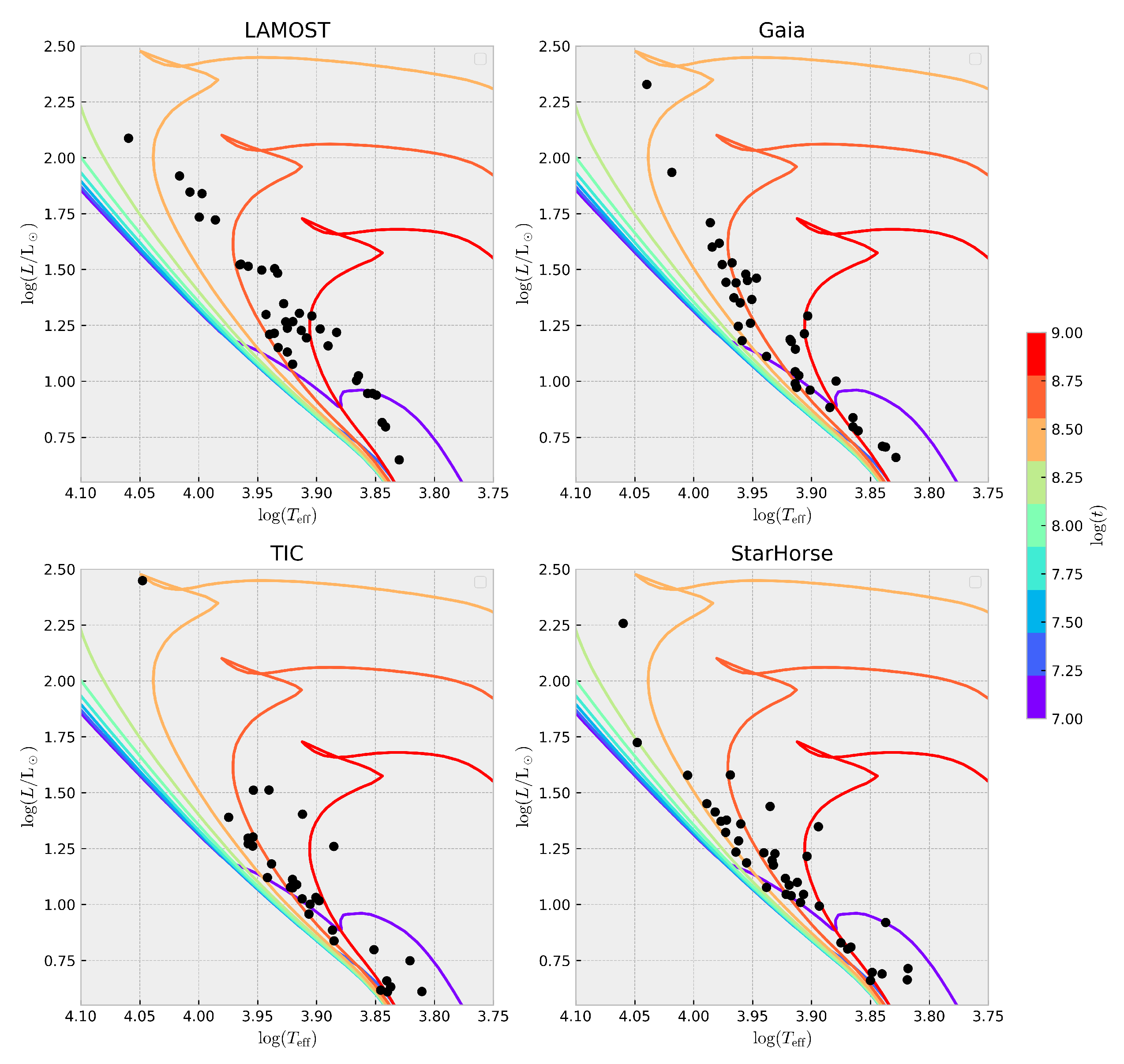
4.7. Ages of Star Clusters
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
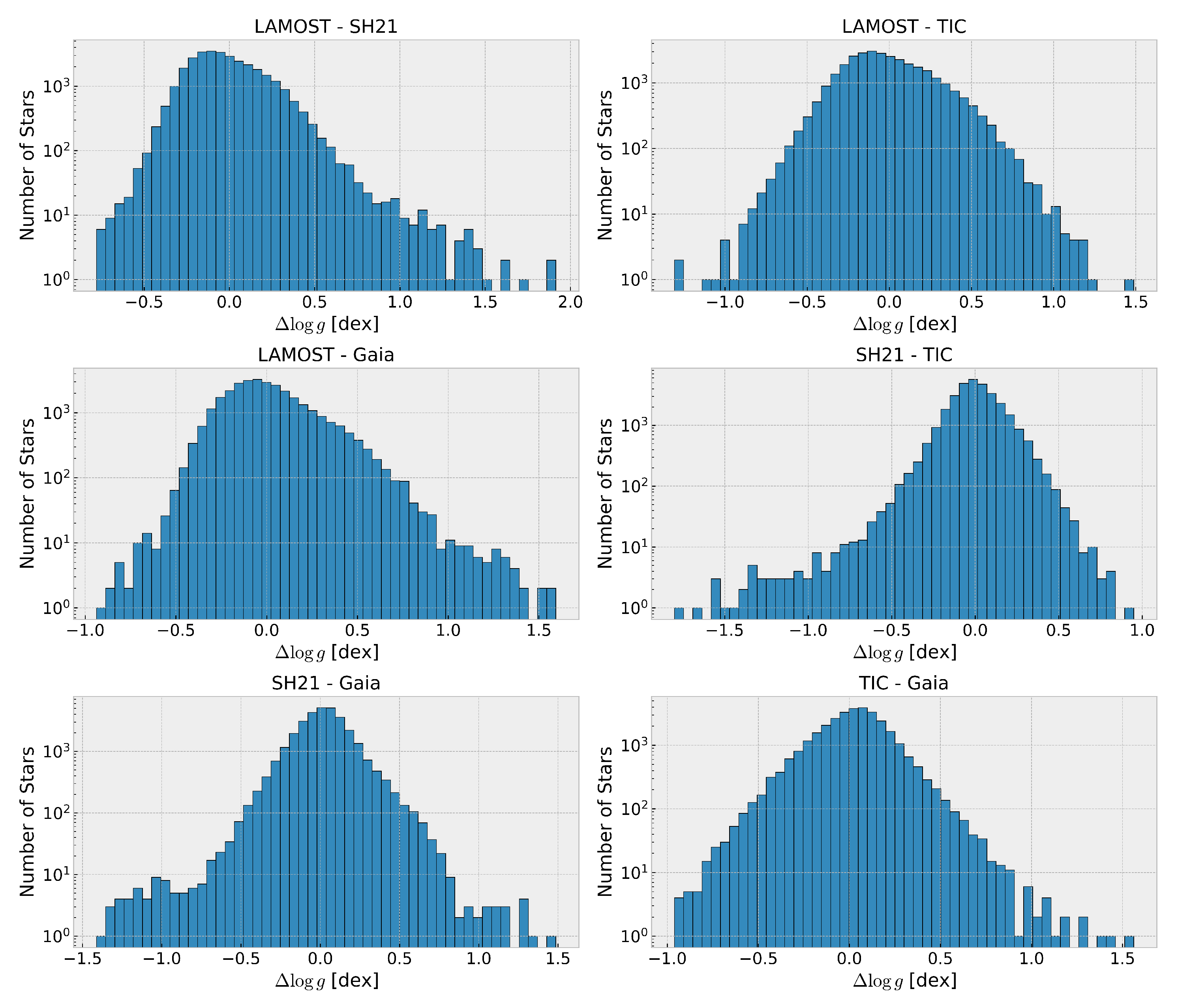
Appendix A. Histograms of the Differences in Teff and log g

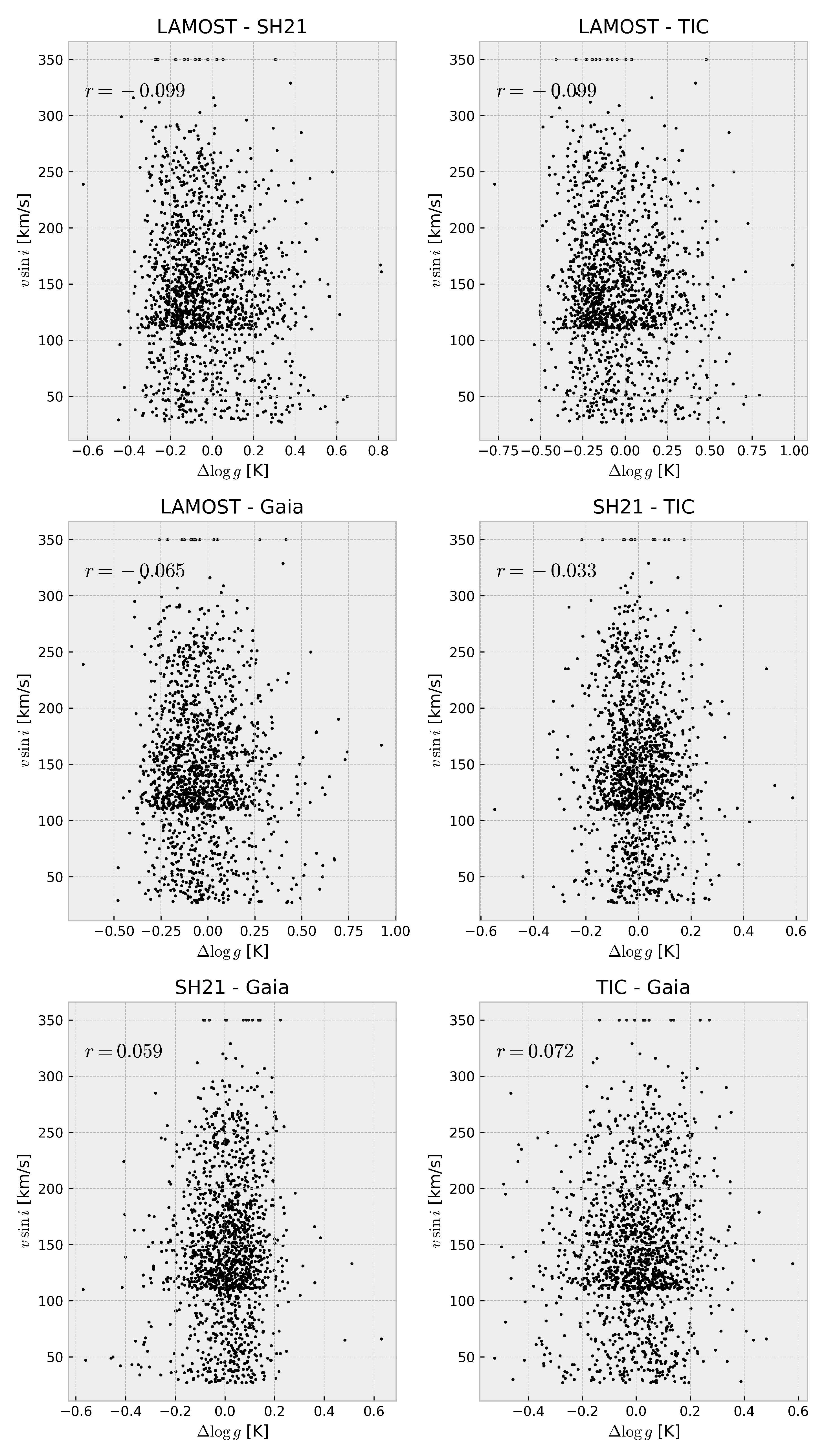
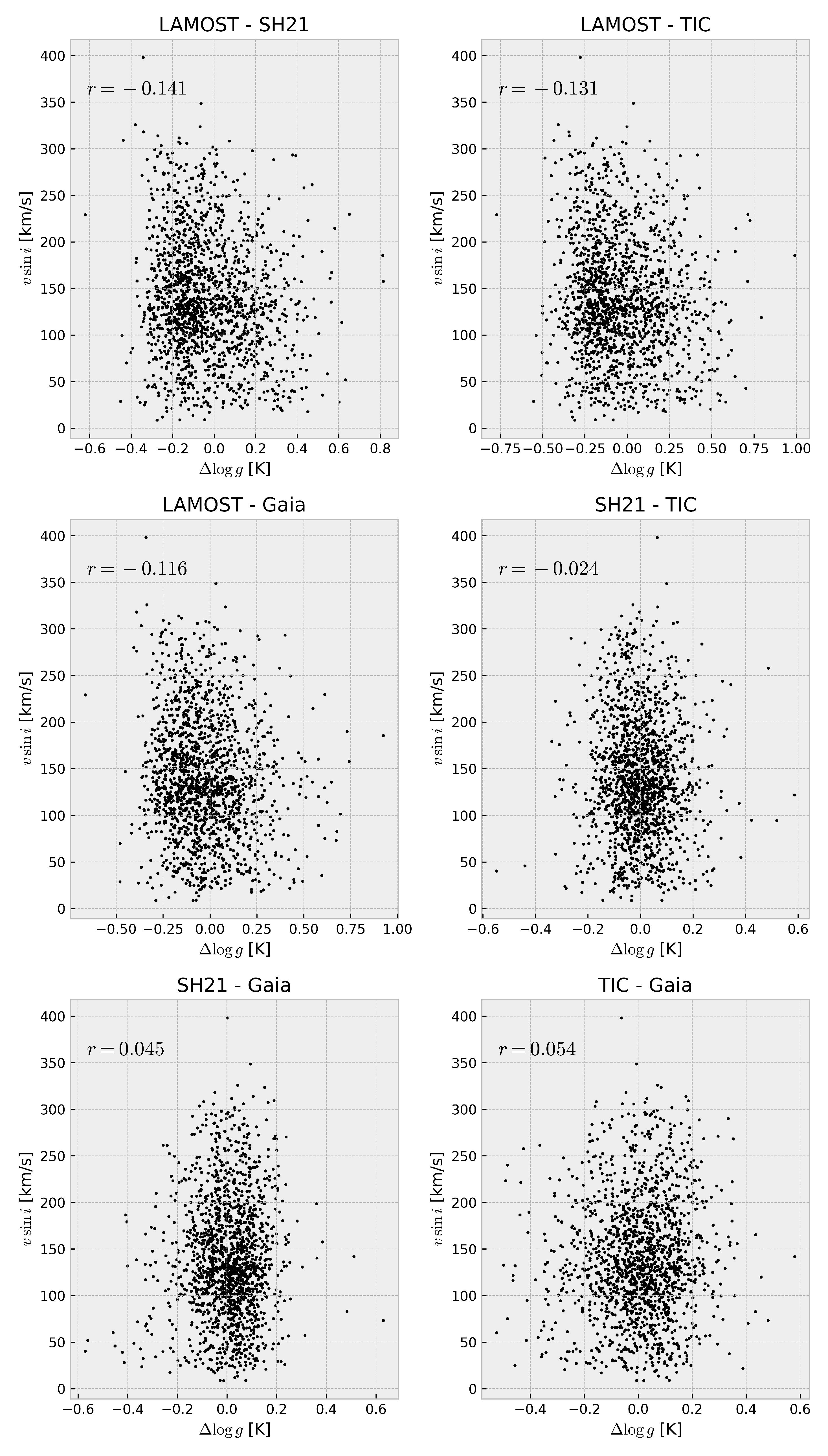
Appendix B. Plots of the Correlation with υ sin i

References
- Jermyn, A.S.; Anders, E.H.; Lecoanet, D.; Cantiello, M. An Atlas of Convection in Main-sequence Stars. Astrophys. J. Suppl. Ser. 2022, 262, 19. [Google Scholar] [CrossRef]
- Pamyatnykh, A.A. Pulsational Instability Domains in the Upper Main Sequence. ActaA 1999, 49, 119–148. [Google Scholar]
- D’Antona, F.; Montalbán, J.; Kupka, F.; Heiter, U. The Böhm-Vitense Gap: The Role of Turbulent Convection. Astrophys. J. Suppl. Ser. 2002, 564, L93–L96. [Google Scholar] [CrossRef]
- Charbonneau, P.; Michaud, G. Meridional Circulation and Diffusion in A and Early F Stars. Astrophys. J. 1991, 370, 693. [Google Scholar] [CrossRef]
- Moss, D. Magnetic Fields in the Ap and Bp Stars: A Theoretical Overview. In Proceedings of the Magnetic Fields Across the Hertzsprung-Russell Diagram; Astronomical Society of the Pacific Conference Series; Mathys, G., Solanki, S.K., Wickramasinghe, D.T., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2001; Volume 248, p. 305. [Google Scholar]
- Antoci, V.; Cunha, M.S.; Bowman, D.M.; Murphy, S.J.; Kurtz, D.W.; Bedding, T.R.; Borre, C.C.; Christophe, S.; Daszyńska-Daszkiewicz, J.; Fox-Machado, L.; et al. The first view of δ Scuti and γ Doradus stars with the TESS mission. Mon. Not. R. Astron. Soc. 2019, 490, 4040–4059. [Google Scholar] [CrossRef]
- Walczak, P.; Fontes, C.J.; Colgan, J.; Kilcrease, D.P.; Guzik, J.A. Wider pulsation instability regions for β Cephei and SPB stars calculated using new Los Alamos opacities. Astron. Astrophys. 2015, 580, L9. [Google Scholar] [CrossRef]
- Maury, A.C.; Pickering, E.C. Spectra of bright stars photographed with the 11-inch Draper Telescope as part of the Henry Draper Memorial. Ann. Harv. Coll. Obs. 1897, 28, 1–128. [Google Scholar]
- Alecian, G. Diffusion velocity of metals in Ap star atmospheres: The effect of ambipolar diffusion of H. Mon. Not. R. Astron. Soc. 2023, 519, 5913–5921. [Google Scholar] [CrossRef]
- ud-Doula, A.; Krtička, J.; Kubátová, B. Horizontal flows in the atmospheres of chemically peculiar stars. Astron. Astrophys. 2025, 694, A270. [Google Scholar] [CrossRef]
- Pinsonneault, M.H.; Kawaler, S.D.; Demarque, P. Rotation of Low-Mass Stars: A New Probe of Stellar Evolution. Astrophys. J. Suppl. Ser. 1990, 74, 501. [Google Scholar] [CrossRef]
- Abt, H.A.; Levato, H.; Grosso, M. Rotational Velocities of B Stars. Astrophys. J. 2002, 573, 359–365. [Google Scholar] [CrossRef]
- Holmberg, J.; Nordström, B.; Andersen, J. The Geneva-Copenhagen survey of the Solar neighbourhood II. New uvby calibrations and rediscussion of stellar ages, the G dwarf problem, age-metallicity diagram, and heating mechanisms of the disk. Astron. Astrophys. 2007, 475, 519–537. [Google Scholar] [CrossRef]
- Teixeira, G.D.C.; Sousa, S.G.; Tsantaki, M.; Monteiro, M.J.P.F.G.; Santos, N.C.; Israelian, G. New Teff and [Fe/H] spectroscopic calibration for FGK dwarfs and GK giants. Astron. Astrophys. 2016, 595, A15. [Google Scholar] [CrossRef]
- Paunzen, E.; Schnell, A.; Maitzen, H.M. An empirical temperature calibration for the Δ a photometric system . I. The B-type stars. Astron. Astrophys. 2005, 444, 941–946. [Google Scholar] [CrossRef]
- Paunzen, E.; Schnell, A.; Maitzen, H.M. An empirical temperature calibration for the Δ a photometric system. II. The A-type and mid F-type stars. Astron. Astrophys. 2006, 458, 293–296. [Google Scholar] [CrossRef]
- Cardelli, J.A.; Clayton, G.C.; Mathis, J.S. The Relationship between Infrared, Optical, and Ultraviolet Extinction. Astrophys. J. 1989, 345, 245. [Google Scholar] [CrossRef]
- McDonald, I.; Zijlstra, A.A.; Cox, N.L.J.; Alexander, E.L.; Csukai, A.; Ramkumar, R.; Hollings, A. PYSSED: An automated method of collating and fitting stellar spectral energy distributions. RAS Tech. Instruments 2024, 3, 89–107. [Google Scholar] [CrossRef]
- Marigo, P.; Girardi, L.; Chiosi, C.; Wood, P.R. Zero-metallicity stars. I. Evolution at constant mass. Astron. Astrophys. 2001, 371, 152–173. [Google Scholar] [CrossRef]
- Allende Prieto, C.; Barklem, P.S.; Lambert, D.L.; Cunha, K. S4N: A spectroscopic survey of stars in the solar neighborhood. The Nearest 15 pc. Astron. Astrophys. 2004, 420, 183–205. [Google Scholar] [CrossRef]
- Gebran, M.; Vick, M.; Monier, R.; Fossati, L. Chemical composition of A and F dwarfs members of the Hyades open cluster. Astron. Astrophys. 2010, 523, A71. [Google Scholar] [CrossRef]
- Shejeelammal, J.; Meléndez, J.; Rathsam, A.; Martos, G. The [Y/Mg] chemical clock in the Galactic disk: The influence of metallicity and the Galactic population in the solar neighbourhood. Astron. Astrophys. 2024, 690, A107. [Google Scholar] [CrossRef]
- Netopil, M.; Oralhan, İ.A.; Çakmak, H.; Michel, R.; Karataş, Y. The Galactic metallicity gradient shown by open clusters in the light of radial migration. Mon. Not. R. Astron. Soc. 2022, 509, 421–439. [Google Scholar] [CrossRef]
- Zhao, G.; Zhao, Y.H.; Chu, Y.Q.; Jing, Y.P.; Deng, L.C. LAMOST spectral survey—An overview. Res. Astron. Astrophys. 2012, 12, 723–734. [Google Scholar] [CrossRef]
- Gaia Collaboration; Creevey, O.L.; Sarro, L.M.; Lobel, A.; Pancino, E.; Andrae, R.; Smart, R.L.; Clementini, G.; Heiter, U.; Korn, A.J.; et al. Gaia Data Release 3. A golden sample of astrophysical parameters. Astron. Astrophys. 2023, 674, A39. [Google Scholar] [CrossRef]
- Gray, R.O.; Corbally, C.J. An Expert Computer Program for Classifying Stars on the MK Spectral Classification System. Astron. J. 2014, 147, 80. [Google Scholar] [CrossRef]
- Hümmerich, S.; Paunzen, E.; Bernhard, K. A plethora of new, magnetic chemically peculiar stars from LAMOST DR4. Astron. Astrophys. 2020, 640, A40. [Google Scholar] [CrossRef]
- Anders, F.; Khalatyan, A.; Chiappini, C.; Queiroz, A.B.; Santiago, B.X.; Jordi, C.; Girardi, L.; Brown, A.G.A.; Matijevič, G.; Monari, G.; et al. Photo-astrometric distances, extinctions, and astrophysical parameters for Gaia DR2 stars brighter than G = 18. Astron. Astrophys. 2019, 628, A94. [Google Scholar] [CrossRef]
- Anders, F.; Khalatyan, A.; Queiroz, A.B.A.; Chiappini, C.; Ardèvol, J.; Casamiquela, L.; Figueras, F.; Jiménez-Arranz, Ó.; Jordi, C.; Monguió, M.; et al. Photo-astrometric distances, extinctions, and astrophysical parameters for Gaia EDR3 stars brighter than G = 18.5. Astron. Astrophys. 2022, 658, A91. [Google Scholar] [CrossRef]
- Magnier, E.A.; Schlafly, E.; Finkbeiner, D.; Juric, M.; Tonry, J.L.; Burgett, W.S.; Chambers, K.C.; Flewelling, H.A.; Kaiser, N.; Kudritzki, R.P.; et al. The Pan-STARRS 1 Photometric Reference Ladder, Release 12.01. Astrophys. J. Suppl. Ser. 2013, 205, 20. [Google Scholar] [CrossRef]
- Skrutskie, M.F.; Cutri, R.M.; Stiening, R.; Weinberg, M.D.; Schneider, S.; Carpenter, J.M.; Beichman, C.; Capps, R.; Chester, T.; Elias, J.; et al. The Two Micron All Sky Survey (2MASS). Astron. J. 2006, 131, 1163–1183. [Google Scholar] [CrossRef]
- Cutri, R.M.; Wright, E.L.; Conrow, T.; Fowler, J.W.; Eisenhardt, P.R.M.; Grillmair, C.; Kirkpatrick, J.D.; Masci, F.; McCallon, H.L.; Wheelock, S.L.; et al. VizieR Online Data Catalog: AllWISE Data Release (Cutri+ 2013); VizieR Online Data Catalog: Strasbourg, France, 2013; p. II/328. [Google Scholar]
- Onken, C.A.; Wolf, C.; Bessell, M.S.; Chang, S.W.; Da Costa, G.S.; Luvaul, L.C.; Mackey, D.; Schmidt, B.P.; Shao, L. SkyMapper Southern Survey: Second data release (DR2). Publ. Astron. Soc. Aust. 2019, 36, e033. [Google Scholar] [CrossRef]
- Queiroz, A.B.A.; Anders, F.; Santiago, B.X.; Chiappini, C.; Steinmetz, M.; Dal Ponte, M.; Stassun, K.G.; da Costa, L.N.; Maia, M.A.G.; Crestani, J.; et al. StarHorse: A Bayesian tool for determining stellar masses, ages, distances, and extinctions for field stars. Mon. Not. R. Astron. Soc. 2018, 476, 2556–2583. [Google Scholar] [CrossRef]
- Fouesneau, M.; Frémat, Y.; Andrae, R.; Korn, A.J.; Soubiran, C.; Kordopatis, G.; Vallenari, A.; Heiter, U.; Creevey, O.L.; Sarro, L.M.; et al. Gaia Data Release 3. Apsis. II. Stellar parameters. Astron. Astrophys. 2023, 674, A28. [Google Scholar] [CrossRef]
- Li, X.; Zeng, S.; Wang, Z.; Du, B.; Kong, X.; Liao, C. Estimating atmospheric parameters from LAMOST low-resolution spectra with low SNR. Mon. Not. R. Astron. Soc. 2022, 514, 4588–4600. [Google Scholar] [CrossRef]
- Stassun, K.G.; Oelkers, R.J.; Paegert, M.; Torres, G.; Pepper, J.; De Lee, N.; Collins, K.; Latham, D.W.; Muirhead, P.S.; Chittidi, J.; et al. The Revised TESS Input Catalog and Candidate Target List. Astron. J. 2019, 158, 138. [Google Scholar] [CrossRef]
- Husser, T.O.; Wende-von Berg, S.; Dreizler, S.; Homeier, D.; Reiners, A.; Barman, T.; Hauschildt, P.H. A new extensive library of PHOENIX stellar atmospheres and synthetic spectra. Astron. Astrophys. 2013, 553, A6. [Google Scholar] [CrossRef]
- Stassun, K.G.; Oelkers, R.J.; Pepper, J.; Paegert, M.; De Lee, N.; Torres, G.; Latham, D.W.; Charpinet, S.; Dressing, C.D.; Huber, D.; et al. The TESS Input Catalog and Candidate Target List. Astron. J. 2018, 156, 102. [Google Scholar] [CrossRef]
- Sun, W.; Chiappini, C. Exploring the stellar rotation of early-type stars in the LAMOST medium-resolution survey: III. Evolution. Astron. Astrophys. 2024, 689, A141. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, C.; Deng, L.C. Deriving the Stellar Labels of LAMOST Spectra with the Stellar LAbel Machine (SLAM). Astrophys. J. Suppl. Ser. 2020, 246, 9. [Google Scholar] [CrossRef]
- Castelli, F. ATLAS12: How to use it. Mem. Della Soc. Astron. Ital. Suppl. 2005, 8, 25. [Google Scholar]
- Zuo, F.; Luo, A.L.; Du, B.; Li, Y.; Jones, H.R.A.; Song, Y.h.; Kong, X.; Guo, Y.x. Projected Rotational Velocities for LAMOST Stars with Effective Temperatures Lower than 9000 K. Astrophys. J. Suppl. Ser. 2024, 271, 4. [Google Scholar] [CrossRef]
- Majewski, S. The APO Galactic Evolution Experiment (APOGEE). In Proceedings of the The Milky Way and its Stars: Stellar Astrophysics, Galactic Archaeology, and Stellar Populations, Santa Barbara, CA, USA, 2–6 February 2015; p. 47. [Google Scholar]
- Bensby, T.; Feltzing, S.; Oey, M.S. Exploring the Milky Way stellar disk. A detailed elemental abundance study of 714 F and G dwarf stars in the solar neighbourhood. Astron. Astrophys. 2014, 562, A71. [Google Scholar] [CrossRef]
- Straizys, V.; Jodinskiene, E.; Kurliene, G. The calibration of the Vilnius photometric system in temperatures and gravities. Vilnius Astron. Obs. Biul. 1982, 60, 16. [Google Scholar]
- Karataş, Y.; Schuster, W.J. Metallicity and absolute magnitude calibrations for UBV photometry. Mon. Not. R. Astron. Soc. 2006, 371, 1793–1812. [Google Scholar] [CrossRef]
- Paunzen, E.; Netopil, M. On the current status of open-cluster parameters. Mon. Not. R. Astron. Soc. 2006, 371, 1641–1647. [Google Scholar] [CrossRef]
- Holmberg, J.; Nordström, B.; Andersen, J. The Geneva-Copenhagen survey of the solar neighbourhood. III. Improved distances, ages, and kinematics. Astron. Astrophys. 2009, 501, 941–947. [Google Scholar] [CrossRef]
- Flower, P.J. Transformations from Theoretical Hertzsprung-Russell Diagrams to Color-Magnitude Diagrams: Effective Temperatures, B-V Colors, and Bolometric Corrections. Astrophys. J. 1996, 469, 355. [Google Scholar] [CrossRef]
- Torres, G. On the Use of Empirical Bolometric Corrections for Stars. Astron. J. 2010, 140, 1158–1162. [Google Scholar] [CrossRef]
- Wang, J.; Zhong, Z. Revisiting the mass-luminosity relation with an effective temperature modifier. Astron. Astrophys. 2018, 619, L1. [Google Scholar] [CrossRef]
- Griffiths, S.C.; Hicks, R.B.; Milone, E.F. A re-examination of mass-luminosity relations from binary-star data. J. R. Astron. Soc. Can. 1988, 82, 1–12. [Google Scholar]
- Demircan, O.; Kahraman, G. Stellar Mass / Luminosity and Mass / Radius Relations. Astrophys. Space Sci. 1991, 181, 313–322. [Google Scholar] [CrossRef]
- Eker, Z.; Soydugan, F.; Soydugan, E.; Bilir, S.; Yaz Gökçe, E.; Steer, I.; Tüysüz, M.; Şenyüz, T.; Demircan, O. Main-Sequence Effective Temperatures from a Revised Mass-Luminosity Relation Based on Accurate Properties. Astron. J. 2015, 149, 131. [Google Scholar] [CrossRef]
- Moya, A.; Zuccarino, F.; Chaplin, W.J.; Davies, G.R. Empirical Relations for the Accurate Estimation of Stellar Masses and Radii. Astrophys. J. Suppl. Ser. 2018, 237, 21. [Google Scholar] [CrossRef]
- Malkov, O.Y.; Sichevskij, S.G.; Kovaleva, D.A. Parametrization of single and binary stars. Mon. Not. R. Astron. Soc. 2010, 401, 695–704. [Google Scholar] [CrossRef]
- Bressan, A.; Marigo, P.; Girardi, L.; Salasnich, B.; Dal Cero, C.; Rubele, S.; Nanni, A. PARSEC: Stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. Mon. Not. R. Astron. Soc. 2012, 427, 127–145. [Google Scholar] [CrossRef]
- Eker, Z.; Bakış, V.; Bilir, S.; Soydugan, F.; Steer, I.; Soydugan, E.; Bakış, H.; Aliçavuş, F.; Aslan, G.; Alpsoy, M. Interrelated main-sequence mass-luminosity, mass-radius, and mass-effective temperature relations. Mon. Not. R. Astron. Soc. 2018, 479, 5491–5511. [Google Scholar] [CrossRef]
- Hunt, E.L.; Reffert, S. Improving the open cluster census. II. An all-sky cluster catalogue with Gaia DR3. Astron. Astrophys. 2023, 673, A114. [Google Scholar] [CrossRef]
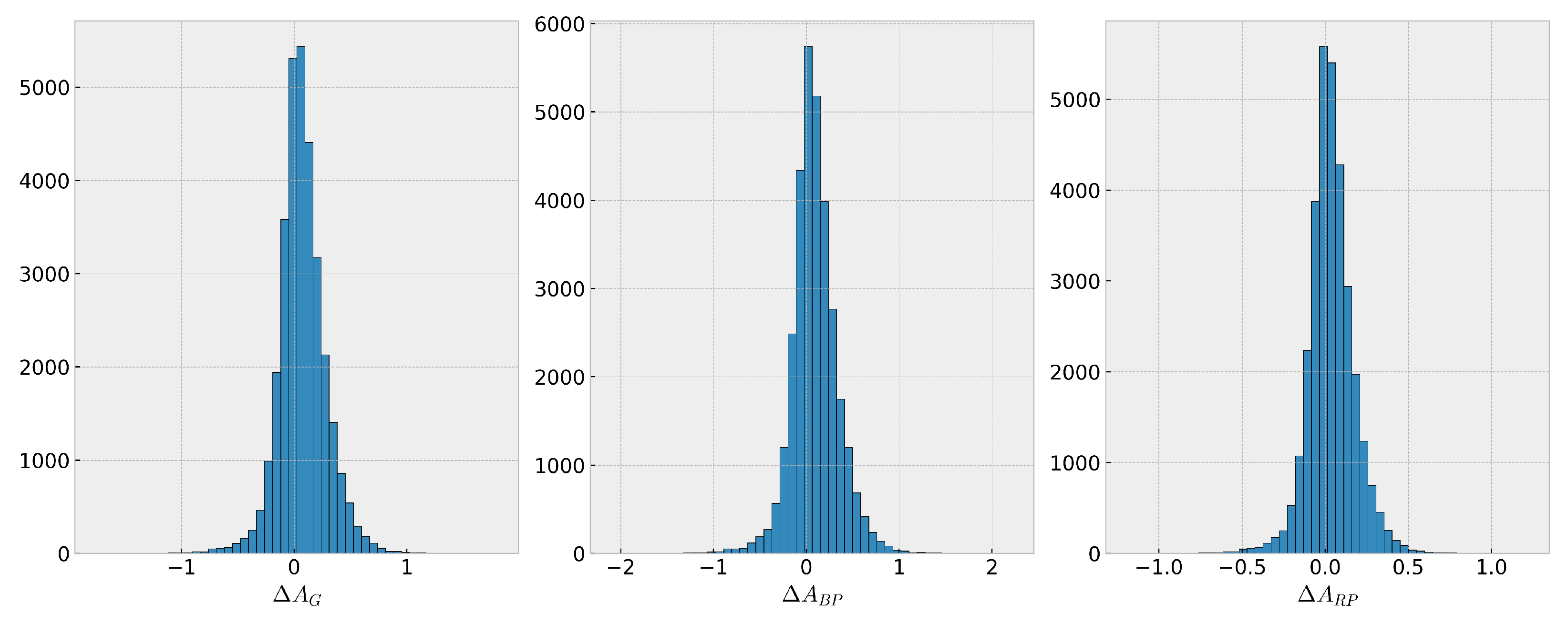
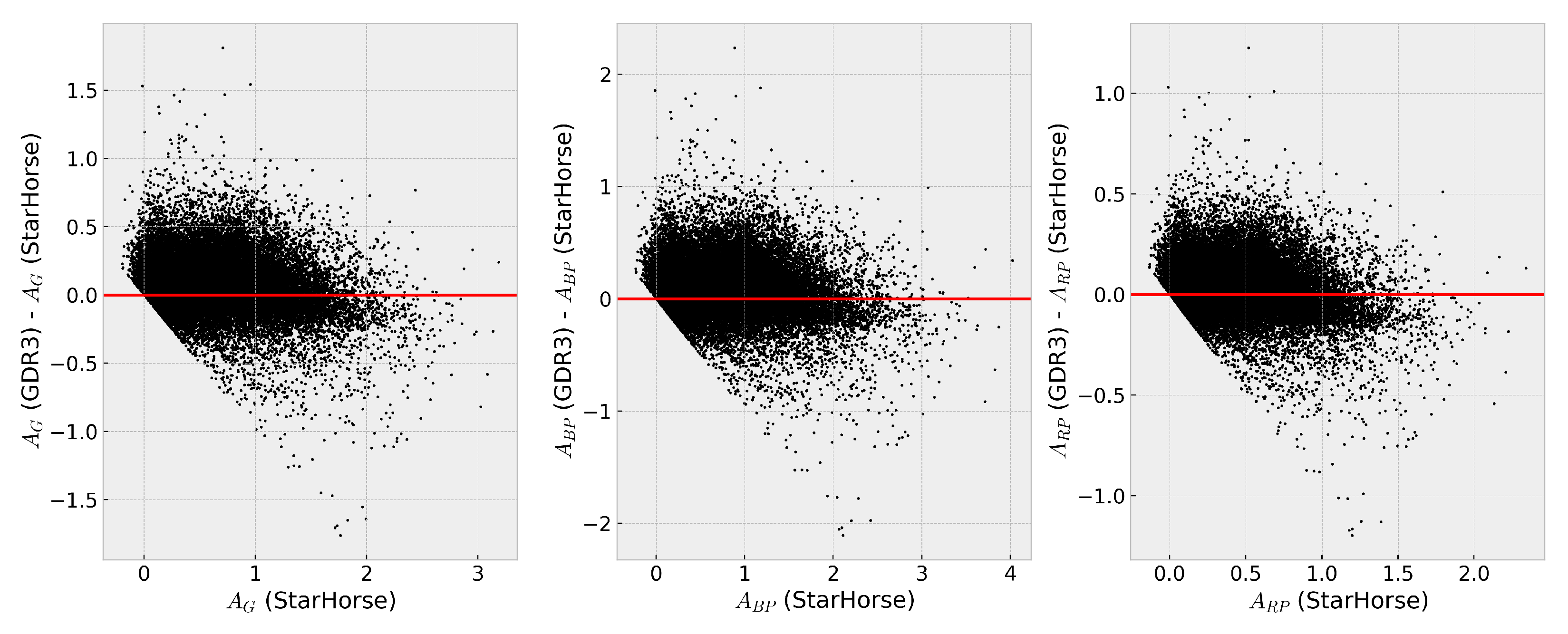

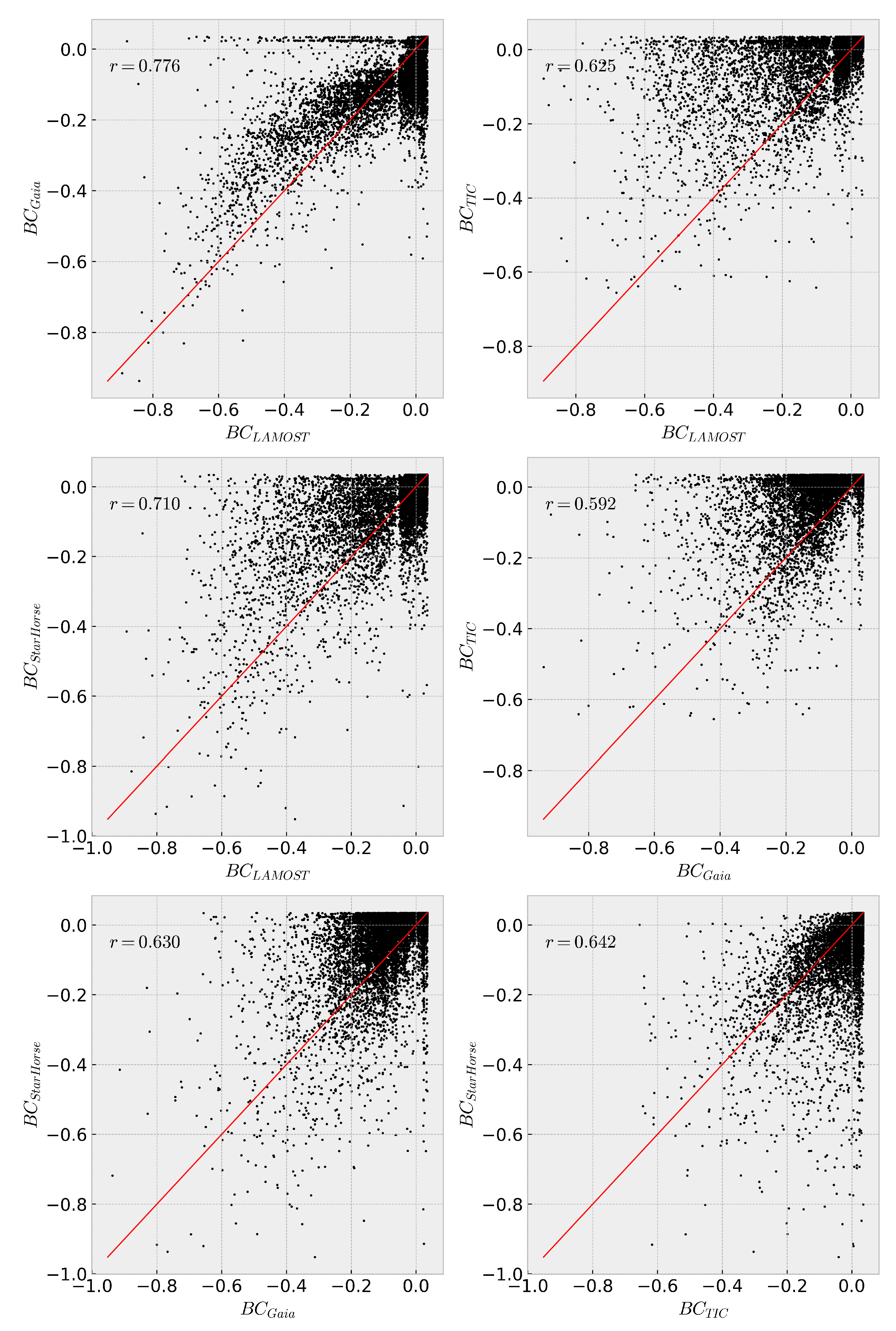


| Difference | [Mag] | [Mag] | ||
|---|---|---|---|---|
| +0.072 | +0.211 | −0.013 | +4.111 | |
| +0.091 | +0.251 | +0.034 | +4.248 | |
| +0.037 | +0.140 | −0.026 | +4.297 |
| Difference | [K] | [K] | ||
|---|---|---|---|---|
| LAMOST—SH21 | +55.404 | 703.794 | +0.505 | +4.959 |
| LAMOST—TIC | +249.421 | 721.973 | +1.204 | +4.724 |
| LAMOST—Gaia | −205.857 | 708.814 | +0.014 | +8.502 |
| SH21—TIC | +194.017 | 574.952 | +1.432 | +7.976 |
| SH21—Gaia | −261.262 | 700.037 | −0.101 | +5.162 |
| TIC—Gaia | −455.278 | 662.693 | −0.695 | +3.810 |
| Difference | [dex] | [dex] | ||
|---|---|---|---|---|
| LAMOST—SH21 | −0.009 | +0.211 | +0.829 | +1.724 |
| LAMOST—TIC | −0.012 | +0.251 | +0.616 | +0.435 |
| LAMOST—Gaia | +0.022 | +0.217 | +0.885 | +1.652 |
| SH21—TIC | −0.002 | +0.125 | +0.233 | +2.923 |
| SH21—Gaia | +0.032 | +0.138 | +0.013 | +4.137 |
| TIC—Gaia | +0.034 | +0.165 | −0.146 | +2.056 |
| Mass Range [] | Reference | |
|---|---|---|
| 2.440 | [53] | |
| 4.160 | ||
| 3.510 | ||
| 2.62 | [54] | |
| 3.92 | ||
| 4.841 | [55] | |
| 4.328 | ||
| 3.962 | ||
| 2.726 |
| Survey | for | for |
|---|---|---|
| LAMOST | ||
| StarHorse | ||
| TIC | ||
| Gaia |
| Survey | Mass–Radius Relation (MRR) |
|---|---|
| LAMOST | Lower mass |
| Higher mass | |
| StarHorse | Lower mass |
| Higher mass | |
| TIC | Lower mass |
| Higher mass | |
| Gaia | Lower mass |
| Higher mass | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kueß, L.; Paunzen, E. The Status of the Astrophysical Parameters of Upper Main Sequence Stars. Astronomy 2025, 4, 15. https://doi.org/10.3390/astronomy4030015
Kueß L, Paunzen E. The Status of the Astrophysical Parameters of Upper Main Sequence Stars. Astronomy. 2025; 4(3):15. https://doi.org/10.3390/astronomy4030015
Chicago/Turabian StyleKueß, Lukas, and Ernst Paunzen. 2025. "The Status of the Astrophysical Parameters of Upper Main Sequence Stars" Astronomy 4, no. 3: 15. https://doi.org/10.3390/astronomy4030015
APA StyleKueß, L., & Paunzen, E. (2025). The Status of the Astrophysical Parameters of Upper Main Sequence Stars. Astronomy, 4(3), 15. https://doi.org/10.3390/astronomy4030015






