Core–Corona Decomposition of Very Compact (Neutron) Stars: Accounting for Current Data of XTE J1814-338
Abstract
1. Introduction
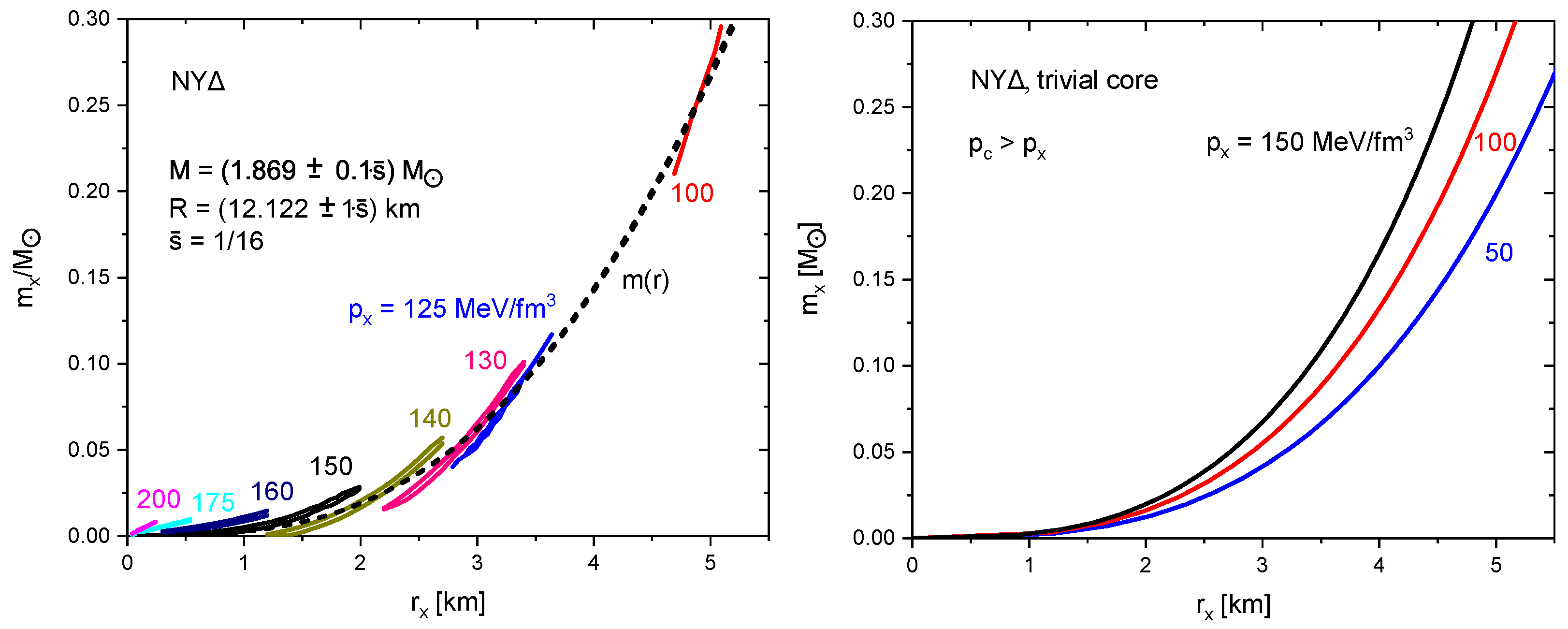
2. Outline of Core–Corona Decomposition
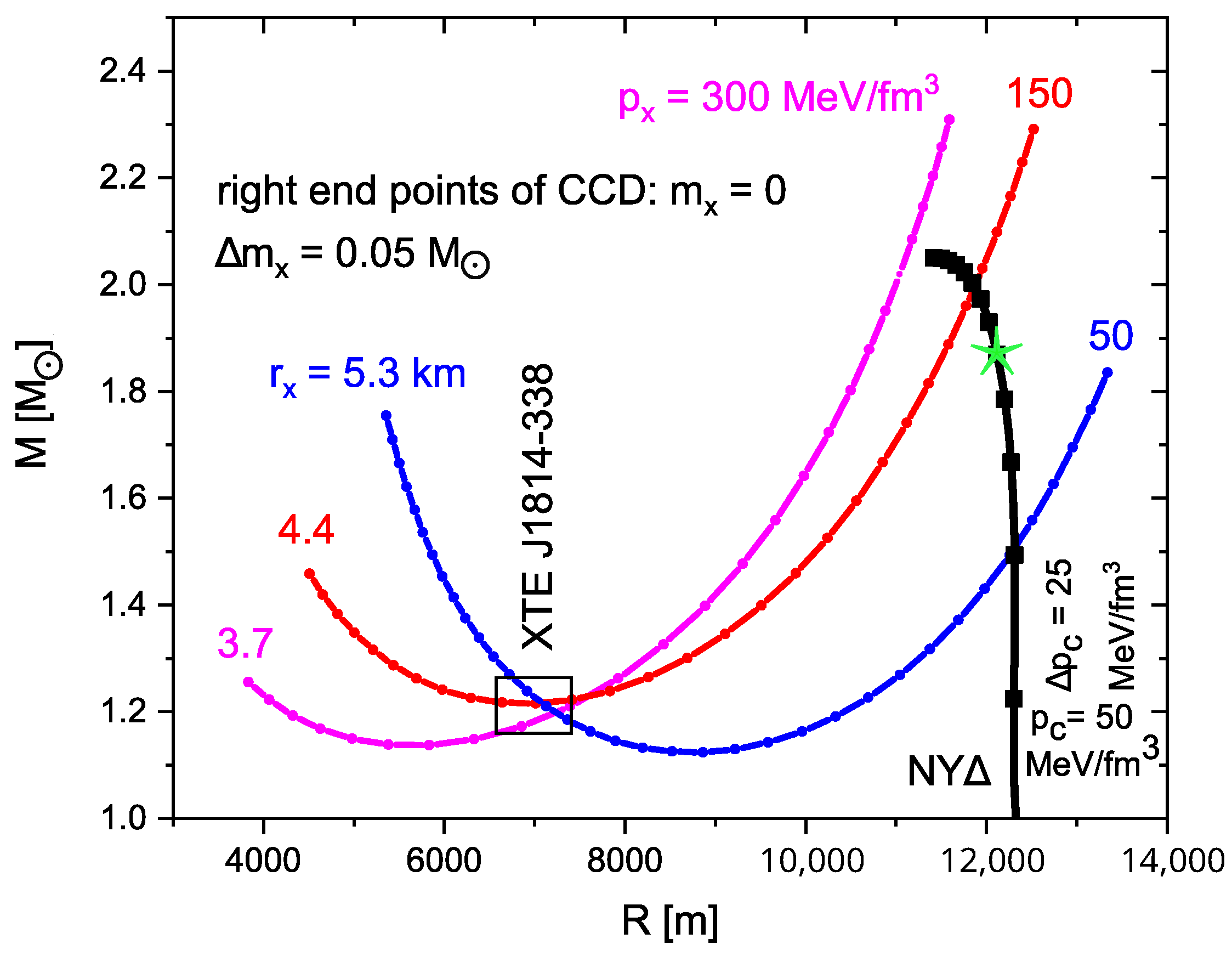
3. Catching Current Data of XTE J1814-338 by CCD
3.1. Selecting a Reference EoS
3.2. Masses and Radii
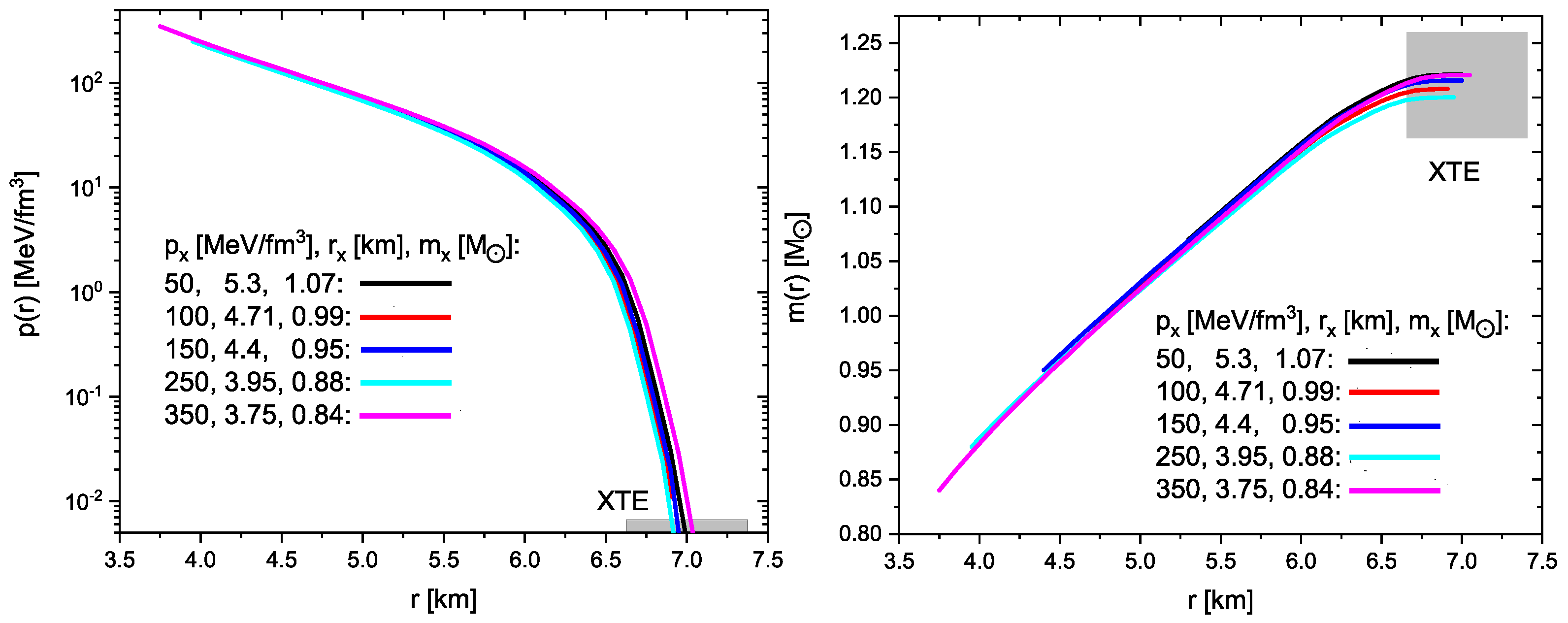
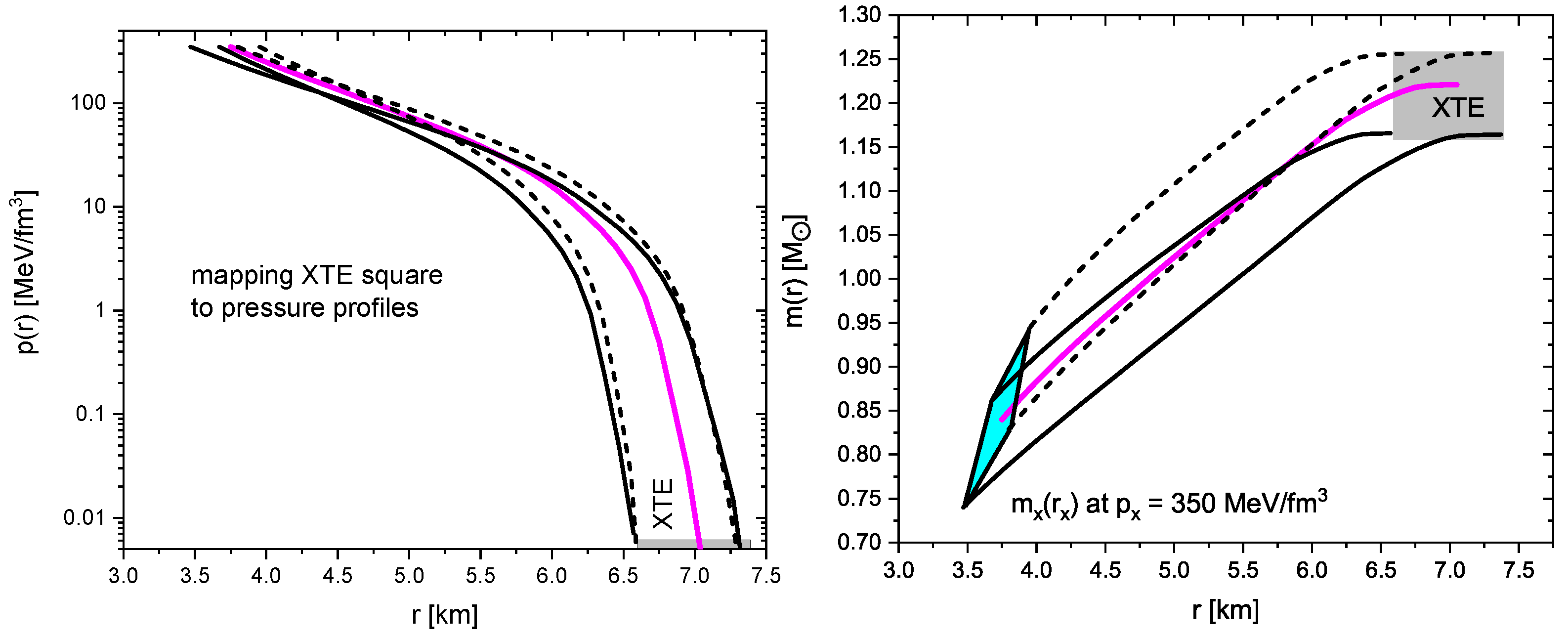
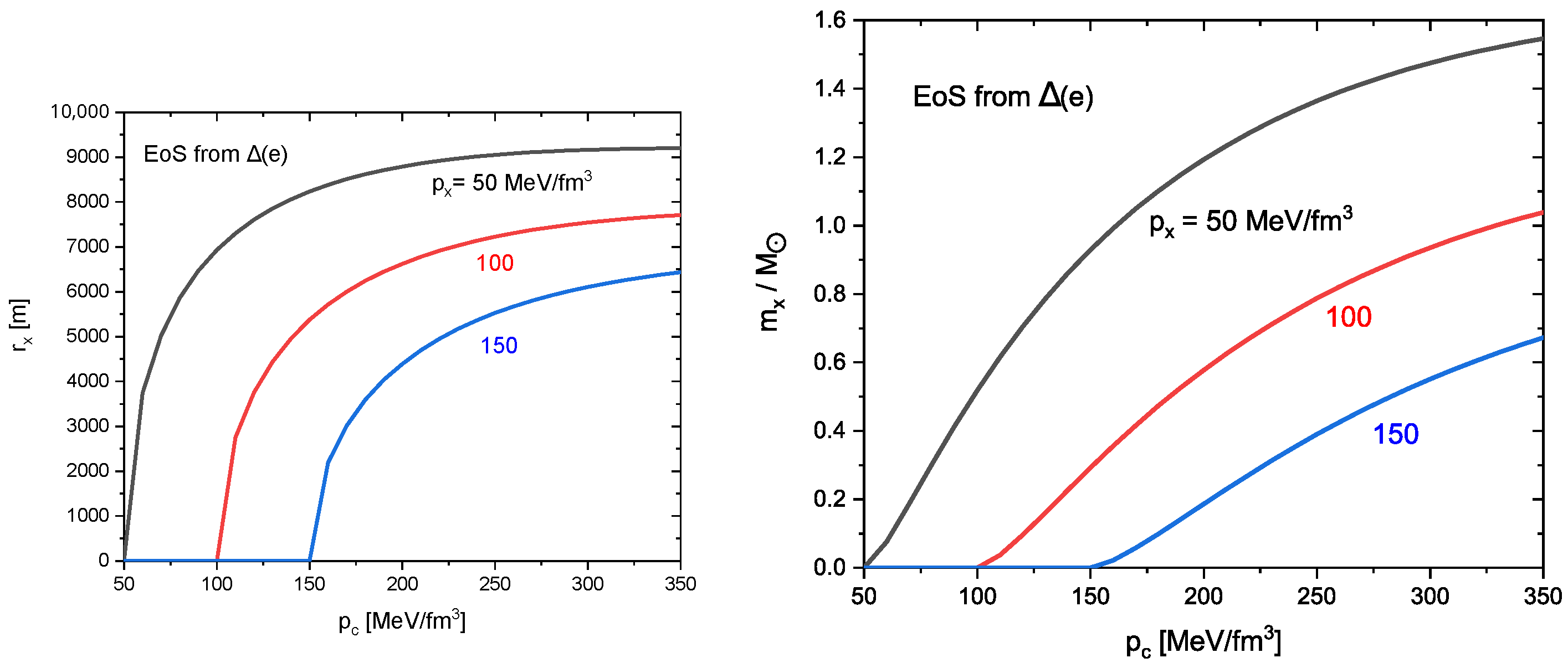
3.3. Pressure and Mass Profiles in the Corona
4. Considering One-Fluid Core Examples
4.1. Using Core Model with EoS Related to QCD Trace Anomaly
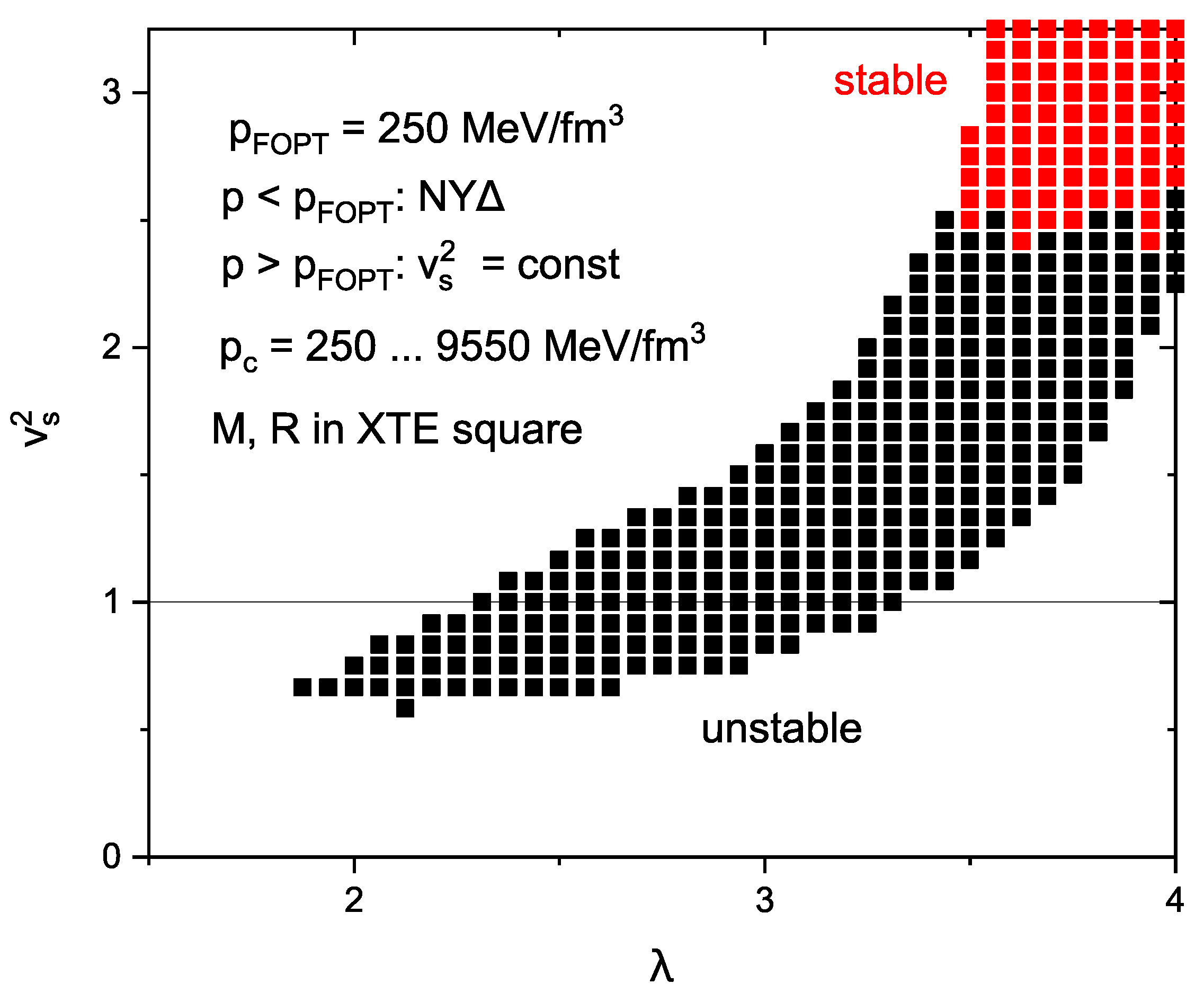
4.2. First-Order Phase Transition
5. Summary
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCD | core–corona decomposition |
| DM | Dark Matter |
| EoS | equation of state |
| FOPT | first-order phase transition |
| HESS | high-energy stereoscopic system |
| NICER | Neutron Star Interior Composition Explorer |
| SM | Standard Model |
| TOV | Tolman–Oppenheimer–Volkoff |
Appendix A. What If No Core Is Required?


| 1 | The very small mass value is scrutinized in [5]. |
| 2 | Our notion “corona” is a synonym for “mantel”, “crust”, “envelope”, “shell” or “halo”. It refers to the complete part of the compact star outside the core, where . |
| 3 | There are various possibilities to constrain the (, , ) parameter space, e.g., fixing px as the pressure at the nuclear saturation density—thus defining the “core” as a part with supra-nuclear density, if the above one-fluid TOV equations are supposed to hold, or selecting the radius as the locus where the pressure of a DM admixture vanishes, meaning that the core is to be dealt with in two-fluid TOV equations. Other side conditions are conceivable, e.g., employing the same value of for several compact (neutron) stars, such as HESS J1731-347 and XTE J1814-338 considered in [11]. Here, we do not impose constraints and assume the applicability of the EoS NY in the corona up to the maximum pressure and energy density tabulated in [17] and study the range of core parameters delivering the XTE J1814-338 mass and radius. |
| 4 | Actually, we combine the EoS N (purely nucleonic matter based on DD-ME2 functional described in [17]) for with NY (hyperson––excitation admixed matter) for . At , we use a linear interpolation to with . Analog linear interpolations apply for the tabulated values in Table I in [17], where further details can be found. |
| 5 | A specific model of a core of asymmetric DM surrounded by an SM envelope is presented in Figure 9—right in [23]. (We thank J. Schaffner-Bielich for bringing this reference to our attention.) The explicitly given EoSs of core and corona allow for stability analyses and tidal deformability evaluations. |
References
- Kini, Y.; Salmi, T.; Vinciguerra, S.; Watts, A.L.; Bilous, A.; Galloway, D.K.; van der Wateren, E.; Khalsa, G.P.; Bogdanov, S.; Buchner, J.; et al. Constraining the properties of the thermonuclear burst oscillation source XTE J1814-338 through pulse profile modelling. Mon. Not. Roy. Astron. Soc. 2024, 535, 1507–1525. [Google Scholar] [CrossRef]
- Zöllner, R.; Ding, M.; Kämpfer, B. Masses of compact (neutron) stars with distinguished cores. Particles 2023, 6, 217–238. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.; Dittmann, A.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.; Guillot, S.; Ho, W.; Lattimer, J.; Loewenstein, M.; et al. The radius of PSR J0740+ 6620 from NICER and XMM-Newton data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Doroshenko, V.; Suleimanov, V.; Pühlhofer, G.; Santangelo, A. A strangely light neutron star within a supernova remnant. Nat. Astron. 2022, 6, 1444–1451. [Google Scholar] [CrossRef]
- Salmi, T.; Deneva, J.S.; Ray, P.S.; Watts, A.L.; Choudhury, D.; Kini, Y.; Vinciguerra, S.; Cromartie, H.T.; Wolff, M.T.; Arzoumanian, Z.; et al. A NICER View of PSR J1231- 1411: A Complex Case. Astrophys. J. 2024, 976, 58. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952- 0607: The fastest and heaviest known galactic neutron star. Astrophys. J. Lett. 2022, 934, L17. [Google Scholar] [CrossRef]
- Ecker, C.; Rezzolla, L. Impact of large-mass constraints on the properties of neutron stars. Mon. Not. Roy. Astron. Soc. 2023, 519, 2615–2622. [Google Scholar] [CrossRef]
- Pitz, S.L.; Schaffner-Bielich, J. Generating ultracompact neutron stars with bosonic dark matter. Phys. Rev. D 2025, 111, 043050. [Google Scholar] [CrossRef]
- Yang, S.H.; Pi, C.M.; Weber, F. Strange stars admixed with mirror dark matter: Confronting observations of XTE J1814-338. Phys. Rev. D 2025, 111, 043037. [Google Scholar] [CrossRef]
- Laskos-Patkos, P.; Moustakidis, C.C. XTE J1814-338: A potential hybrid star candidate. arXiv 2024, arXiv:2410.18498. [Google Scholar] [CrossRef]
- Zöllner, R.; Kämpfer, B. Core-corona decomposition of compact (neutron) stars compared to NICER data including XTE J1814-338. arXiv 2024, arXiv:2411.08068. [Google Scholar]
- Lopes, L.L. Macroscopic properties of the XTE J1814-338 as a dark matter admixed strange star. arXiv 2025, arXiv:2501.06379. [Google Scholar]
- Lopes, L.L.; Issifu, A. XTE J1814-338 as a dark matter admixed neutron star. arXiv 2024, arXiv:2411.17105. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Alford, M. Ultracompact hybrid stars consistent with multimessenger astrophysics. Phys. Rev. D 2023, 107, 023018. [Google Scholar] [CrossRef]
- Zöllner, R.; Kämpfer, B. Exotic Cores with and without Dark-Matter Admixtures in Compact Stars. Astronomy 2022, 1, 36–48. [Google Scholar] [CrossRef]
- Schaffner-Bielich, J. Compact Star Physics; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Li, J.J.; Sedrakian, A.; Alford, M. Relativistic hybrid stars with sequential first-order phase transitions and heavy-baryon envelopes. Phys. Rev. D 2020, 101, 063022. [Google Scholar] [CrossRef]
- Choudhury, D.; Salmi, T.; Vinciguerra, S.; Riley, T.E.; Kini, Y.; Watts, A.L.; Dorsman, B.; Bogdanov, S.; Guillot, S.; Ray, P.S.; et al. A nicer view of the nearest and brightest millisecond pulsar: Psr j0437–4715. Astrophys. J. Lett. 2024, 971, L20. [Google Scholar] [CrossRef]
- Salmi, T.; Choudhury, D.; Kini, Y.; Riley, T.E.; Vinciguerra, S.; Watts, A.L.; Wolff, M.T.; Arzoumanian, Z.; Bogdanov, S.; Chakrabarty, D.; et al. The Radius of the High-mass Pulsar PSR J0740+ 6620 with 3.6 yr of NICER Data. Astrophys. J. 2024, 974, 294. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Alford, M. Confronting new NICER mass-radius measurements with phase transition in dense matter and twin compact stars. JCAP 2025, 2025, 002. [Google Scholar] [CrossRef]
- Marczenko, M.; Redlich, K.; Sasaki, C. Curvature of the energy per particle in neutron stars. Phys. Rev. D 2024, 109, L041302. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Fukushima, K.; McLerran, L.D.; Praszałowicz, M. Trace anomaly as signature of conformality in neutron stars. Phys. Rev. Lett. 2022, 129, 252702. [Google Scholar] [CrossRef] [PubMed]
- Gresham, M.I.; Zurek, K.M. Asymmetric dark stars and neutron star stability. Phys. Rev. D 2019, 99, 083008. [Google Scholar] [CrossRef]
- Di Clemente, F.; Drago, A.; Pagliara, G. Merger of a Neutron Star with a Black Hole: One-family versus Two-families Scenario. Astrophys. J. 2022, 929, 44. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zöllner, R.; Kämpfer, B. Core–Corona Decomposition of Very Compact (Neutron) Stars: Accounting for Current Data of XTE J1814-338. Astronomy 2025, 4, 10. https://doi.org/10.3390/astronomy4020010
Zöllner R, Kämpfer B. Core–Corona Decomposition of Very Compact (Neutron) Stars: Accounting for Current Data of XTE J1814-338. Astronomy. 2025; 4(2):10. https://doi.org/10.3390/astronomy4020010
Chicago/Turabian StyleZöllner, Rico, and Burkhard Kämpfer. 2025. "Core–Corona Decomposition of Very Compact (Neutron) Stars: Accounting for Current Data of XTE J1814-338" Astronomy 4, no. 2: 10. https://doi.org/10.3390/astronomy4020010
APA StyleZöllner, R., & Kämpfer, B. (2025). Core–Corona Decomposition of Very Compact (Neutron) Stars: Accounting for Current Data of XTE J1814-338. Astronomy, 4(2), 10. https://doi.org/10.3390/astronomy4020010




