Abstract
We revisit 77 relaxed (extra)solar multibody (sub)systems containing 2–9 bodies orbiting about gravitationally dominant central bodies. The listings are complete down to (sub)systems with 5 orbiting bodies and additionally contain 33 smaller systems with 2–4 orbiting bodies. Most of the multiplanet systems (68) have been observed outside of our solar system, and very few of them (5) exhibit classical Laplace resonances (LRs). The remaining 9 subsystems have been found in our solar system; they include 7 well-known satellite groups in addition to the four gaseous giant planets and the four terrestrial planets, and they exhibit only one classical Laplace resonant chain, the famous Galilean LR. The orbiting bodies (planets, dwarfs, or satellites) appear to be locked in/near global mean-motion resonances (MMRs), as these are determined in reference to the orbital period of the most massive (most inert) body in each (sub)system. We present a library of these 77 multibody subsystems for future use and reference. The library listings of dynamical properties also include regular spacings of the orbital semimajor axes. Regularities in the spatial configurations of the bodies were determined from patterns that had existed in the mean tidal field that drove multibody migrations toward MMRs, well before the tidal field was erased by the process of `gravitational Landau damping’ which concluded its work when all major bodies had finally settled in/near the global MMRs presently observed. Finally, detailed comparisons of results help us discern the longest commonly-occurring MMR chains, distinguish the most important groups of triple MMRs, and identify a new criterion for the absence of librations in triple MMRs.
Keywords:
exoplanet dynamics; extrasolar systems; gravitational Landau damping; orbital resonances; solar-system subsystems; tidal interactions PACS:
96.15.Wx; 96.30.–t; 97.82.–j
1. Introduction
We have analyzed the orbital configurations of 77 planetary and satellite subsystems and we have collected the results in a library for future use and reference. The study involves the global mean-motion resonances (MMRs) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] observed in solar and extrasolar settings, as well as the few classical Laplace resonances (LRs) so far discovered in exoplanetary systems and the Galilean satellites (Refs. [15,16,17,18,19,20,21,22,23,24] and [23,24,25,26,27,28], respectively). The regular spatial layouts of the orbits resulting from gravitational Landau damping of the long-gone mean tidal field [14,15,16,29,30,31,32,33,34,35] are also analyzed and included in the library (for a guide to previous analyses see the references in the first note1).
The library extensively covers 40 exosystems with 5–9 orbiting bodies. Another 28 exosystems with 2–4 orbiting bodies are included to provide a basis for comparisons with the more populous exosystems; in this group, only 3 four-body systems exhibit LRs (GJ 876, HR 8799, and K-176).
The extrasolar orbiting objects are categorized as planets or dwarf planets according to their surface gravities g; the critical solar threshold applied also to exoplanets is m [35]. Furthermore, the solar-system satellites are also divided by size into small-sized (mean diameter Mm)2, large-sized ( Mm), and the few largest of the large satellites (seven moons with Mm), although surface gravity is used again as a qualifier with corresponding threshold values of m and m [35].
For each (sub)system, the input parameters (central host masses and radii, orbiting object masses and radii, orbital semimajor axes, and orbital periods) and the output modeled parameters (individual tidal-field wavelengths and systemic mean Landau wavelengths, nearest global MMRs and their deviations relative to the observed periods of the orbiting objects) are listed in separate tables that are included in the archive (folder Analysis_Files) that constitutes supplementary material to this paper (DOI link: https://doi.org/10.5281/zenodo.14577621, accessible any time past 30 December2024). Here, we illustrate the main results from comparisons concerning the orbital periods, the global resonances, the surface gravities, and the regularly-spaced semimajor-axis configurations in each (sub)system. In particular:
In Section 2, we summarize our modeling assumptions and the adopted physical constraints.
In Section 3, we show some representative plots of the main results that illustrate the global MMR layouts and the spatial configurations of the orbiting bodies in these (sub)systems. In this section, we also classify the various subsystems into three general MMR groups:
- (a)
- Six Laplace resonances, including the famous Galilean LR (Section 3.1, Figures 1–5).
- (b)
- Seven global solar-system MMRs and our local terrestrial MMR (Section 3.2, Figures 6–10).
- (c)
- Sixty-three extrasolar non-LR MMRs with 2–9 orbiting planets (Section 3.3,Figures 11–18).
In Section 4, we compare extensively the results from modeling of the 77 multibody systems. This section is divided in 12 parts as follows:
- 1.
- Classical Laplace resonances.
- 2.
- Solar-system: Gaseous giant planets.
- 3.
- Solar-system: Terrestrial planets.
- 4.
- Solar-system: Satellite systems.
- 5.
- Exosystems with 2–9 planets and no classical LRs.
- 6.
- Commonly-occurring triple MMR chains.
- 7.
- Tidal-field wavelengths and theoretical Landau wavelengths [16].
- 8.
- Extrasolar dwarf planets with surface gravities m [35].
- 9.
- Bodies on or near the so-called “critical orbital period” of each system [16].
- 10.
- Summary of the longest global MMR chains and the geometric sequences [24].
- 11.
- Beyond the classical LRs: Summary of important groups of triple MMR chains.
- 12.
- A criterion for the absence of librations in triple MMR chains.
2. Modeling Assumptions and Adopted Constraints
In modeling the nearest MMRs to orbiting bodies, we take the following steps:
- 1.
- The most massive (and most inert) body is assigned to the 1:1 MMR at the “center” of the MMR chain.
- 2.
- In the few cases where the most massive body is too distant from the group of the other bodies, the most massive body of the group is assigned to the 1:1 MMR for a better look at the resonant chain (e.g., K-90, K-176, K-254).
- 3.
- If the masses of the bodies are not known, then the largest body is assigned to the 1:1 MMR. When mass information will be obtained, the adopted global MMR chain can be easily rescaled if necessary.
- 4.
- Distant outer bodies (say, beyond the 5:1 MMR) are assigned only to principal exterior MMRs of the form k:1, where is an integer.
- 5.
- Inner bodies orbiting near the host (say, inward of the 1:5 MMR) are also assigned only to principal interior MMRs of the form 1:k, where is an integer.
- 6.
- Rational secondary MMRs of the form k:ℓ with integer are limited, as much as possible, to single-digit values of k and ℓ, i.e., . Important exceptions in this case are some geometric MMR sequences (e.g., K-444) and some distant MMRs disconnected from the inner compact chains (e.g., 14:5 for K2-268 f and HD 191939 g that are obviously displaced inward from 3:1 for some unknown reason).
- 7.
- When peculiar fractions appear to be necessary in long MMR chains, the MMRs are fitted by a single denominator, if possible (see, e.g., the MMR chain (1:3:13:40: in GJ 163).
In modeling the regular spacings of the orbits, we take the following steps:
- 1.
- In each system, the empirically determined (by trial and error) wavelength of the long-gone mean tidal field [15] cannot be longer than the theoretical Landau wavelength calculated from the Hill radius H of the most massive body [16].
- 2.
- The empirically determined wavelength is maximized, subject to the constraintin order to specify the longest possible wavelength that is not Jeans unstable [31,34].
- 3.
- The nearest neighbors of the most massive body should be separated from it by a distance of at least . Low-mass bodies may, however, be separated by a distance of only .
- 4.
- The local Landau wavelength of each body i (, where is the body’s Hill radius) should not overlap with the wavelengths of its nearest neighbors.
- 5.
- Some very low-mass bodies (e.g., the innermost Neptunian moons Naiad, Thalassa, Despina [36] and the three innermost planets b-c-i of K90 [37,38,39]) are caught orbiting inside the same tidal potential trough, yet their orbits do obey comfortably the no-overlap condition 4.
- 6.
- The mean tidal field is expected to show a minimum at the location of the central host. In some systems, this precise condition is not achieved (e.g., the Galilean moons and TRAPPIST-1 (TR-1) shown below); then, the actual wavelength is expected to be somewhat different than our best-fit value, and the orbiting bodies are by all means displaced off of the actual minima of their tidal potential troughs.
3. Library Setup and Details
The library archive is located at the DOI address https://doi.org/10.5281/zenodo.14577621 (accessible any time past 30 December 2024). The files are organized in groups in the main folder The_77_Systems, and their contents are described in the top-level file README.txt. The text files (*.txt and *.m) contain listings of the following dynamical parameters, most of which are collected in the Output.txt file of each system:
- 1.
- Central host mass , radius , and surface gravity .
- 2.
- Orbiting-body periods , semimajor axes , masses , radii , and surface gravities .
- 3.
- Orbiting-body period ratios , nearest global MMRs, and their relative deviations.
- 4.
- Subsystem critical orbital period [16] and whether a body is orbiting to within <8%.
- 5.
- Theoretical Landau wavelength and empirical wavelength of the mean tidal field [16].
- 6.
- Orbiting-body Hill radii and local Landau wavelengths .
- 7.
- For each pair of adjacent orbiting bodies i and , a comparison between and . It is generally expected that the adjacent local Landau wavelengths should not overlap (certainly not substantially), viz.
- 8.
- Pairs of bodies in which condition (2) is violated (marginally or decidedly) are noted by *** in the Output.txt files. The systems that show clear violations should be revisited in future studies. The systems that show “marginal” overlaps are not considered as cause for concern.
- 9.
- Certain issues and peculiarities encountered during modeling are noted under the heading “Needs more work” in the following 21 Output.txt files of the library: 55 Cnc, GJ 163, HD 20781, HD 108236, HD 158259, HR 8799, K-11, K-33, K-36, K-55, K-80, K-102, K-150, K-238, K-254, K-292, K-363, K-1542, K2-384, TOI-270, Teegarden’s Star (TS).
- 10.
- In particular, peculiar, or at least unusual, MMR chains are found in the following 18 systems (see the corresponding files System_Name.m and System_Name.eps): 12 also found in the preceding list, GJ 163, HD 108236, K-11, K-33, K-36, K-80, K-238, K-292, K-363, K-1542, TOI-270, TS; and additionally, HD 191939, K-32, K-154, K2-38, K2-268, TOI-700.
Specific open-source reference works (papers) concerning observations and dynamical modeling of the various (sub)systems are also included in the library in PDF format (files Author1_Year.pdf).
The EPS file figures included in the library (and the representative subset of figures shown below) delineate the following pieces of information:
- 1.
- The title displays the names of the orbiting bodies.
- a.
- A number in parentheses denotes the radial location (n) of the most massive body.
- b.
- The names of solar-system bodies are abbreviated by their initials.
- c.
- Names of bodies not shown in the plots are enclosed in parentheses.
- 2.
- The top frame shows the spatial distribution of semimajor axes.
- a.
- The empirically determined value of “Minimum Separation” is displayed.
- b.
- The value of is determined from the most massive body and its neighbors [16].
- c.
- Vertical dotted lines are drawn in intervals of .
- d.
- Vertical dashed lines are midlines of the corresponding intervals.
- e.
- Blue circles denote the semimajor axes of the orbits.
- 3.
- The bottom frame shows the distribution of orbital-period ratios.
- a.
- The nearest global MMRs are displayed in k:ℓ form.
- b.
- Nearest MMRs to bodies not shown in the plots are enclosed in parentheses.
- c.
- Presence of a Laplace resonance in the MMR chain is indicated by the symbol (LR).
- d.
- Vertical dotted lines denote the precise locations of the nearest MMRs.
- e.
- Red circles denote the normalized orbital periods .
- f.
- The normalizing period is , where n is specified in item 1a above.
Some representative examples are shown in the following three subsections (Figures 1–18, all of them selected from the EPS files of the library).
3.1. Laplace Resonances: The Galilean LR and the 5 Extrasolar LRs
Notes:
- 1.
- These 6 LRs have also been discussed extensively in Ref. [23].
- 2.
- The LR in HD 219134 (HR 8832) is unconfirmed [40,41].
- 3.
- In K-176, the most massive planet b is not part of the c-d-e LR [24,42].
- 4.
- In K-176, the most massive planet of the LR (planet d) is assigned to the 1:1 MMR.
- 5.
- SI units of Mm ( m) and Gm ( m) are used for the Galilean-moon subsystem.
- 6.
- Units of au and mau ( au) are used for the extrasolar systems.
- 7.
Figures:
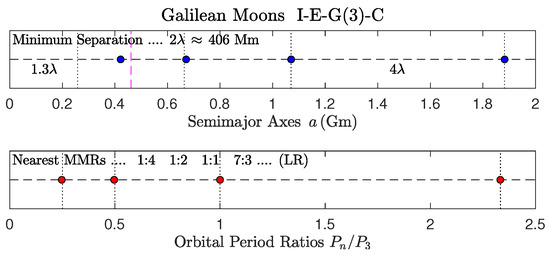
Figure 1.
Galilean moons.
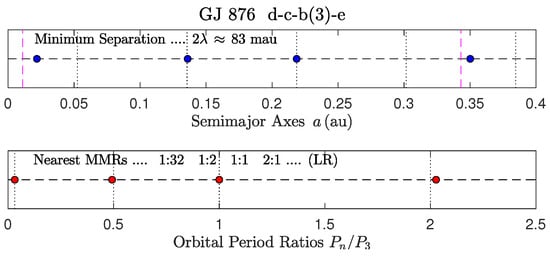
Figure 2.
GJ 876.
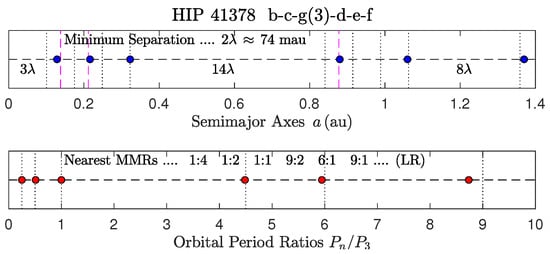
Figure 3.
HIP 41378.
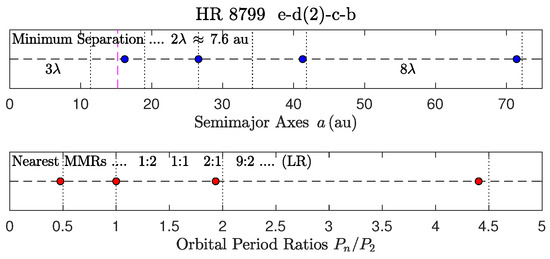
Figure 4.
HR 8799.
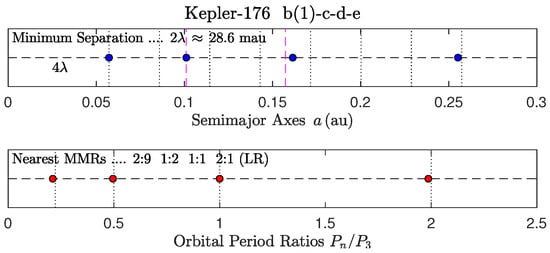
Figure 5.
K-176.
3.2. Solar Subsystems: The Terrestrial Local MMR and the 7 Global Non-LR MMRs
Notes:
- 1.
- Units of au are used for the planetary subsystems.
- 2.
- SI units of Mm are used for the satellite subsystems.
- 3.
- Venus and Ceres are shown with the gaseous giants, but they are not included in the fit.
- 4.
- Asteroid Toro [43] is shown with the terrestrial planets, but it is not included in the fit.
- 5.
- The five inner moons of Neptune with semimajor axes Mm [36] are also plotted separately for clarity (file Solar_8/Neptune_moons_9s/Neptune_Inner.m in the library).
- 6.
Figures:
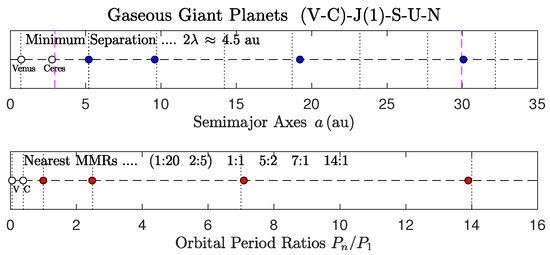
Figure 6.
Gaseous giant planets.
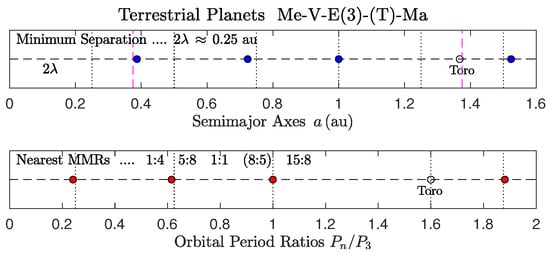
Figure 7.
Terrestrial planets.
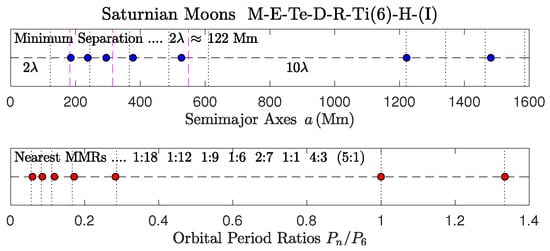
Figure 8.
Saturnian moons.
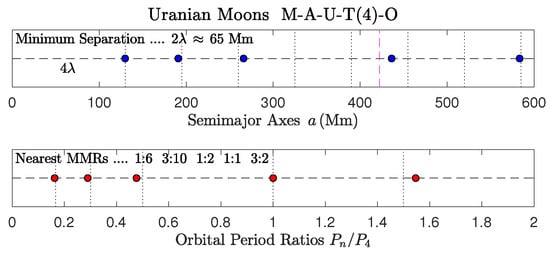
Figure 9.
Uranian moons.
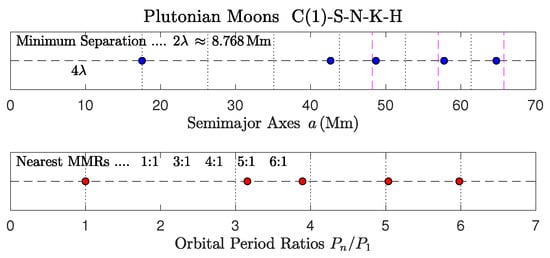
Figure 10.
Plutonian moons.
3.3. Extrasolar Planetary Systems: The 63 Global Non-LR MMRs
Notes:
- 1.
- Units of au and mau ( au) are used for the extrasolar systems.
- 2.
- In HD 10180, planets i and j [48,49,50] are not confirmed, but they fit very well in the chain.
- 3.
- In K-444 [51,52,53], planets d-e-f display a geometric MMR sequence with common ratio , viz. ::1 [24].
- 4.
- The triple MMR chain of K-60 [54,55,56] shows a phase angle that librates about and that was analyzed in depth in Refs. [18,24].
- 5.
- Pulsar B1257+12 [57,58,59,60] is also included in the subset of exosystems with three orbiting planets (folder 3p_15/B1257_12 in the library).
- 6.
Figures:
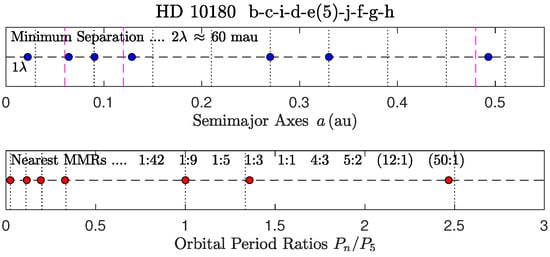
Figure 11.
HD 10180.
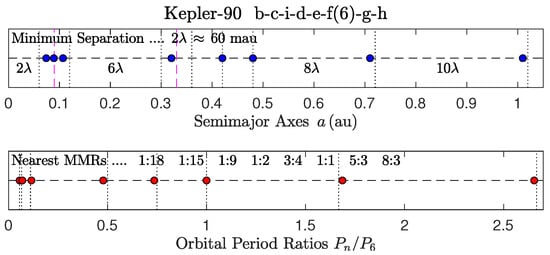
Figure 12.
K-90.
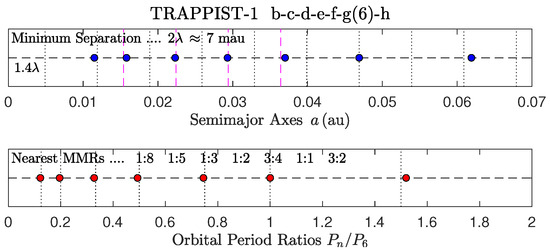
Figure 13.
TRAPPIST-1 (TR-1).
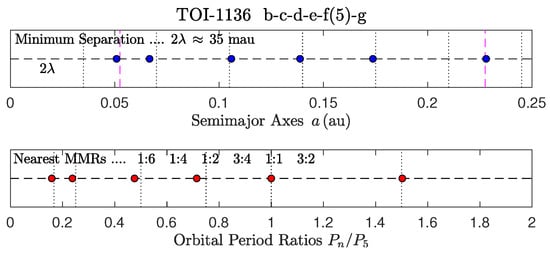
Figure 14.
TOI-1136.
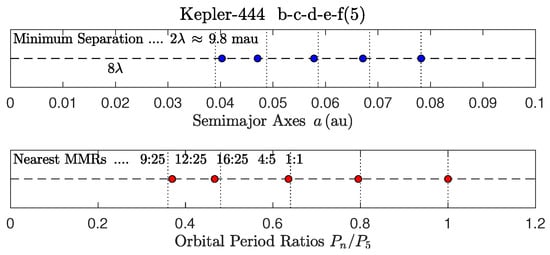
Figure 15.
K-444.
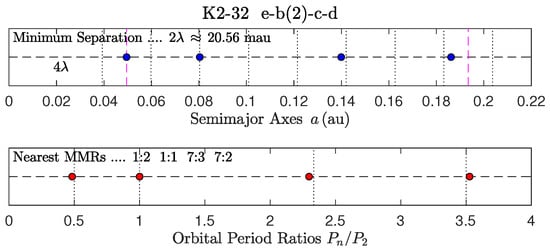
Figure 16.
K2-32 [61,62,63].
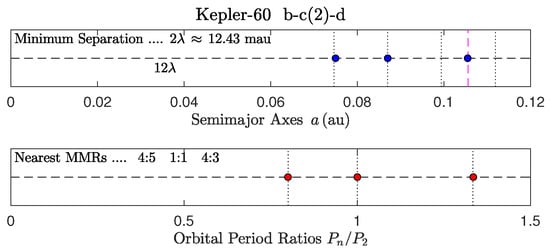
Figure 17.
K-60 [18,54,55,56].
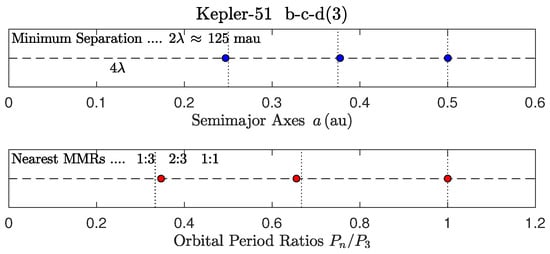
Figure 18.
K-51 [64,65,66].
4. Comparisons of Results
4.1. Classical Laplace Resonances
Table 1 summarizes the systems that exhibit classical LRs (see also Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 and Refs. [23,24]):

Table 1.
Six systems with global MMR chains exhibiting classical LRs.
- (a)
- The Galilean-moon subsystem has been analyzed in Ref. [16].
- (b)
- The LR of HIP 41378 is the only one that has the same layout as the famous Galilean LR.
- (c)
- No LR has been found with the most massive body at radial position (viz. 1:2:4).
- (d)
- The 9:2/2:9 MMRs are not too uncommon in LR-systems (or in non-LR systems; e.g., K-48, K-332, HD 23472).
- (e)
- Callisto’s 7:3 MMR is unique in LR-systems, and the 3:7 interior MMR does not occur—although these resonances are quite common in non-LR systems.3
4.2. Solar System: Gaseous Giant Planets
Figure 6 shows the spatial and MMR arrangements of the gaseous giants of our solar system:
- (a)
- This subsystem has been analyzed in Ref. [16].
- (b)
- Beyond Jupiter, the semimajor axes of the gaseous planets form approximately an arithmetic progression with common difference au, in which dwarf Pluto also participates. This type of layout also occurs in the Mercury–Venus–Earth subsystem ( au), and these two arithmetic progressions are sufficient to invalidate the empirical Titius–Bode rule [67] on both ends of the solar planetary sequence.
- (c)
- Pluto is orbiting near the 21:1 MMR, and together with Uranus (7:1) and Neptune (14:1), the bodies form a triple MMR of the reduced ratio 1:2:3. This reduced ratio is quite common in exosystems, but the actual integer 1:2:3 MMR does not occur in multibody systems, thus supporting the vacancy of the 2:1 MMR.4
- (d)
- The 2:1 global MMR of Jupiter is vacant (see also Refs. [15,68]). Saturn could not occupy this MMR because then the local Landau wavelengths would overlap substantially. Nonetheless, Saturn (presently at 5:2) seems to violate marginally the no-overlap condition (2): au, whereas au, an overlap width of 0.6 au (13.7% of the separation ).
- (e)
- Saturn’s orbital period ( yr) is close to the critical orbital period ( yr) of the subsystem ( is actually longer by 34 days) [16].
4.3. Solar System: Terrestrial Planets
Figure 7 shows the arrangements of orbits and orbital periods for the terrestrial planets of our solar system:
- (a)
- The MMR chain is local with the Earth taken at the 1:1 MMR.
- (b)
- It is obvious that Mars did not settle anywhere near the 2:1 local MMR of the subsystem.
- (c)
- The empirical tidal wavelength is mau, but the local Landau wavelength set by the Earth is only mau. For consistency, the empirical value has to be halved, so that the actual wavelength will be set to 62.5 mau in close agreement with . This subdivision of -values has to be implemented in a number of other systems as well (see below).
- (d)
- The planets fit within a single potential trough of the global mean tidal field ( au), yet pairs of adjacent orbits do not violate the no-overlap condition (2) since the largest -sum, viz. au, does not exceed the smallest (V-E) separation of 0.27 au.
- (e)
- Asteroid Toro [43] fits well in both layouts shown in Figure 7 (the local MMR chain and the arrangement of semimajor axes), although it was not part of the fit.
4.4. Solar System: Satellite Systems
Figure 8, Figure 9 and Figure 10 show the configurations of the major satellites of Saturn, Uranus, and Pluto:
- (a)
- The disturbed inner satellite system of Neptune [36] is also included in the library (section Solar_8/Neptune_moons_9s).
- (b)
- The surprising proximity of pumice-moon Hyperion to Saturn’s giant moon Titan has been discussed in detail in Refs. [24,44].
- (c)
- In Uranus, the adjacent small moons Ariel and Umbriel are presumed to be in a 5:3 local MMR [69], which produces a reduced integer MMR chain of 3:5:10 with Titania (Figure 9). The same layout occurs in TOI-270 (i.e., :1:2), where the occupied 2:1 MMR proved to be a major concern in a recent study [23].
- (d)
- However, a more accurate solution for the MMR of Ariel is 2:7 leading to the unusual reduced chain of 6:10:21:33 (or the global MMR ::1:) with Titania. This model makes it clear that Umbriel is displaced off of the 1:2 MMR by about % and Oberon lies off of the 3:2 MMR by +3% (library file Uranus_alt.m in folder Solar_8/Uranus_moons_5s).
- (e)
- The group of the five Plutonian satellites is the prototypical example of a regular multibody system with an obviously vacant 2:1 MMR (Figure 10).
- (f)
- The satellites are organized in three subsets by surface gravity g [35]:
- (i)
- The largest of the large satellites with m : Earth’s moon, Jupiter’s Galilean moons, and Saturn’s Titan.
- (ii)
- The 10 large satellites with m : Tethys, Dione, Rhea, Iapetus (Saturn); Ariel, Umbriel, Titania, Oberon (Uranus); Neptune’s Triton; and Pluto’s Charon.
- (iii)
- The small satellites with m .
The thresholds are effectively mean values delimited by the Callisto ( m )–Triton ( m ) gap and by the Tethys ( m )–Enceladus ( m ) gap, respectively.
4.5. Exosystems with 2–9 Planets and No Classical LRs
Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 show some representative examples of multibody extrasolar systems. Furthermore:
- (a)
- TOI-270 [70,71,72,73] has been investigated in Ref. [23] and the key systems HD 110067 [14], K-176 [42,74], and K-223 [4,75] have been discussed in depth in Ref. [24].
- (b)
- Ref. [24] also contains a detailed study of three-body and four-body MMRs occurring in many exosystems.
- (c)
- Few body systems are usually not compact (or `closely-packed’), and the empirically determined wavelength is too long to satisfy the Landau condition (1), in which case has to be subdivided to match (see below). But, as far as we can tell, these systems appear to satisfy the no-overlap condition (2) quite comfortably.
- (d)
- The commonly-occurring triple MMRs are summarized in Table 2, Table 3, Table 4 and Table 5 and some unusual scarce MMRs are listed in Table 6.
 Table 2. Commonly-occurring triple chains: Interior MMRs not including 1:1.
Table 2. Commonly-occurring triple chains: Interior MMRs not including 1:1. Table 3. Commonly-occurring triple chains: Interior MMRs up to 1:1.
Table 3. Commonly-occurring triple chains: Interior MMRs up to 1:1. Table 4. Commonly-occurring triple chains: MMRs centered around 1:1.
Table 4. Commonly-occurring triple chains: MMRs centered around 1:1. Table 5. Commonly-occurring triple chains: Exterior MMRs starting from 1:1.
Table 5. Commonly-occurring triple chains: Exterior MMRs starting from 1:1. Table 6. Notable unusual MMR chains.
Table 6. Notable unusual MMR chains. - (e)
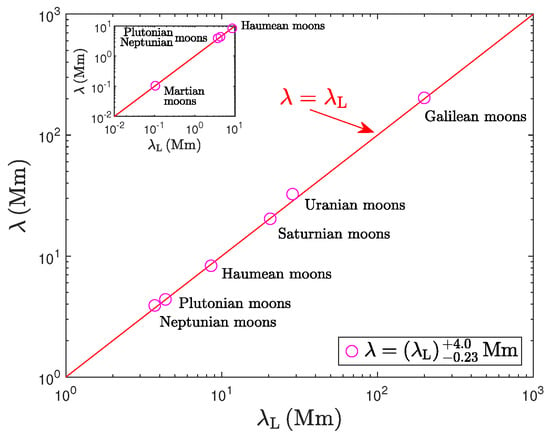
- The distributions of the fundamental wavelengths and are summarized in Figure 19, Figure 20 and Figure 21 for systems at mau-, au-, and Mm-scales, respectively.
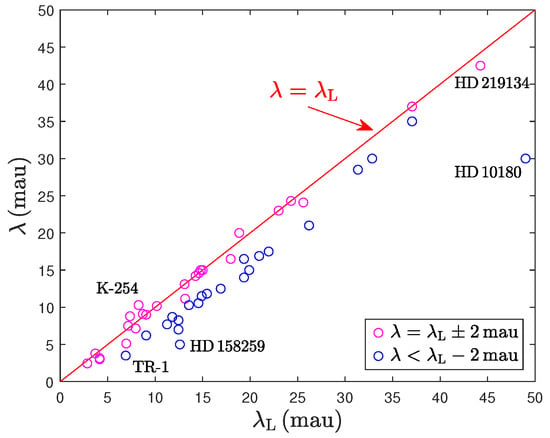 Figure 19. Empirically determined tidal-field wavelengths versus the corresponding Landau wavelengths of exosystems with more than 2 planets (Table 7). We use 47 points with mau in this plot. More systems listed in Table 8 generally show (like HD 10180 and HD 158259 depicted here). Magenta points are clustered around the red line (to within mau). Blue points lie at mau. Systems for which could not be determined (Table 7, bottom) are assumed to lie on the red line.
Figure 19. Empirically determined tidal-field wavelengths versus the corresponding Landau wavelengths of exosystems with more than 2 planets (Table 7). We use 47 points with mau in this plot. More systems listed in Table 8 generally show (like HD 10180 and HD 158259 depicted here). Magenta points are clustered around the red line (to within mau). Blue points lie at mau. Systems for which could not be determined (Table 7, bottom) are assumed to lie on the red line.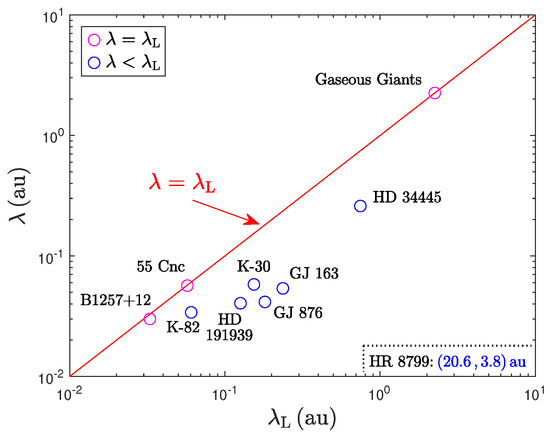 Figure 20. As in Figure 19, but for planetary systems of au scales. The gaseous giants of our solar system and the exoplanets of 55 Cnc and the pulsar B1257+12 effectively have (magenta points), whereas the remaining exosystems have au (blue points).
Figure 20. As in Figure 19, but for planetary systems of au scales. The gaseous giants of our solar system and the exoplanets of 55 Cnc and the pulsar B1257+12 effectively have (magenta points), whereas the remaining exosystems have au (blue points). - (f)
- Some of the 63 exoplanetary systems show peculiarities and/or unique properties that are noted in the Output.txt files of the library (see also items 9, 10 at the top of Section 3).
4.6. Commonly-Occurring Triple MMR Chains
4.7. Tidal-Field Wavelengths
For scaling reasons, we have to analyze solar satellite subsystems and multiplanetary systems separately:
- (a)
- Table 7 and Table 8 and Figure 19 summarize exosystems at mau scales. The top group in Table 7 shows sparse systems in which the empirically determined had to be scaled down (mostly by a factor of 2) to satisfy the Landau condition (1).
 Table 7. Exosystems with more than 2 planets: empirically determined tidal-field wavelengths compared to the corresponding Landau wavelengths .
Table 7. Exosystems with more than 2 planets: empirically determined tidal-field wavelengths compared to the corresponding Landau wavelengths . Table 8. Exosystems with more than 2 planets: empirically determined tidal-field wavelengths .
Table 8. Exosystems with more than 2 planets: empirically determined tidal-field wavelengths . - (b)
- Planetary systems at au scales are shown separately and named individually in Figure 20. The gaseous giants of our solar system appear in this plot on the line. HR 8799 is off-scale (), as noted at the bottom right of the figure.
- (c)
- Table 9 and Figure 21 summarize the solar satellite systems. The values of the inner moons of Saturn and Neptune had to be scaled down to satisfy the Landau condition (1). This is shown in rows 3 and 6 of Table 9, where the empirical -values were trisected.
 Table 9. Solar satellite systems: empirically determined tidal-field wavelengths and the corresponding Landau wavelengths of the inner moons. The inner moon that provides the value of for each subsystem is shown in the third column.
Table 9. Solar satellite systems: empirically determined tidal-field wavelengths and the corresponding Landau wavelengths of the inner moons. The inner moon that provides the value of for each subsystem is shown in the third column. - (d)
- The Martian satellite system is shown in the inset of Figure 21, and it also fits the condition well. With only two moons present in the system, the empirical -value had to be divided by 45 (row 7 of Table 9) to match the Landau wavelength of km derived theoretically for the inner and more massive moon Phobos.
4.8. Extrasolar Dwarf Planets by Their Surface Gravities
Table 10 and Figure 22 and Figure 23 show the exosystems for which we could determine the surface gravities g of the orbiting bodies with m . We use the threshold value of m from Ref. [35] to determine whether the bodies are likely to be planets (P) or dwarf planets (DP). The lowest-occurring g-value (if any) that is larger than is listed for each system along with all values that are smaller than . We determine that:

Table 10.
Lowest-occurring surface gravities m s−2 of exoplanets (P) and identification of likely dwarf planets (DP) with m s−2 [35].
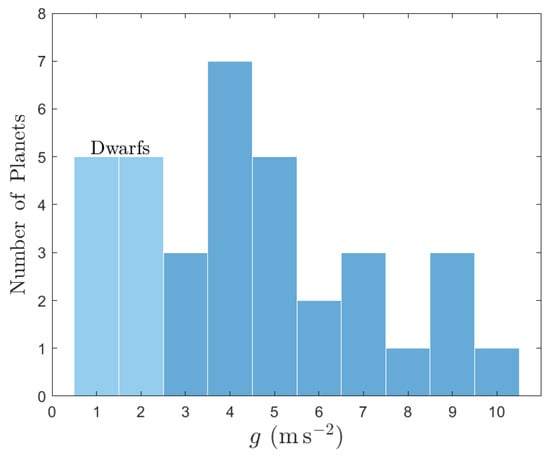
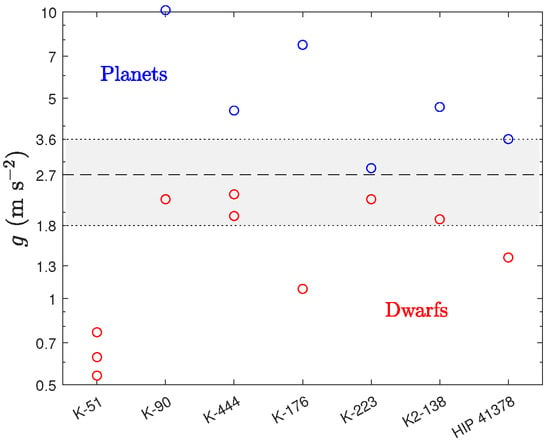
Figure 23.
From the top section of Table 10: Ten planets with m s−2 (red circles) are classified as dwarfs. Two of the planets (blue circles) fall within the gray strip of width m s−2 centered about [35]. All three planets of K-51 [64,65,66] are classified as dwarfs, which makes the K-51 system unique.
- (a)
- Dwarf planets appear in 7 of 27 exosystems (i.e., 26% of the tabulated systems).
- (b)
- All 3 planets of K-51 with m are certainly dwarfs.
- (c)
- Two of 5 planets of K-444 (d and e) are likely dwarfs.
- (d)
- K-444 d ( m ), K-223 e, and K-90 g ( m ) are marginally identified as dwarfs (Figure 23).
- (e)
- The three bodies named d in HD 191939, K-30, and K-223, all with m , are marginally identified as planets.
4.9. Bodies on or near the Critical Orbital Period of Each System
Table 11 lists orbiting bodies occupying the critical orbit [16] (top group) and pairs of adjacent bodies orbiting on either side of in a symmetric configuration (bottom group). Multibody model simulations of angular momentum transfer (Appendix A in Ref. [16]) have indicated that such configurations could be commonly-occurring in real systems. The relative deviations from precise symmetry of the identified library systems are all smaller than 7.5% (last column in the table):

Table 11.
Bodies on or on either side of the critical orbital period of their systems (top and bottom group, respectively). For the bottom group of 2 adjacent bodies (i and ) in each system, .
- (a)
- The top group of 15 bodies includes the satellites of the 3 gaseous giants except Uranus. All other entries represent well-known exoplanets.
- (b)
- Neptune’s satellite system was severely disturbed by the capture of Triton, so it is remarkable that Larissa (L) managed to settle so close to the critical orbit; its period ( min) is shorter by only 18 min, whereas it is longer than the nearest assigned 1:11 MMR by 30.5 min. The critical orbit of the system and the moons of Neptune interior to the orbit of Triton are shown in Figure 24.
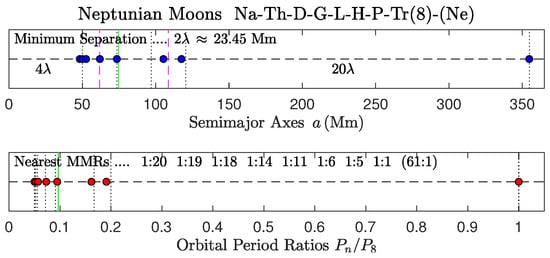 Figure 24. The Neptunian moons [36]. Nereid (Ne) is not shown in this plot. The small innermost moons Naiad (Na), Thalassa (Th), and Despina (D) are orbiting inside the same tidal potential well without violating the no-overlap condition (2). The fifth moon, Larissa (L), has settled closer to the critical orbit of the system (, Mm; vertical green lines) than the nearest assigned 1:11 MMR.
Figure 24. The Neptunian moons [36]. Nereid (Ne) is not shown in this plot. The small innermost moons Naiad (Na), Thalassa (Th), and Despina (D) are orbiting inside the same tidal potential well without violating the no-overlap condition (2). The fifth moon, Larissa (L), has settled closer to the critical orbit of the system (, Mm; vertical green lines) than the nearest assigned 1:11 MMR. - (c)
- The bottom group of 11 pairs includes Ariel–Umbriel whose orbital periods nearly form an arithmetic progression with as well. All other entries represent well-known exoplanet pairs with periods symmetrically located about the values of their systems.
- (d)
- Planets b and c of pulsar B1257+12 are also included in the bottom group. This is also a remarkable symmetry because the innermost planet b is less massive than its neighbors (), and it appears to be unimportant for the overall layout of this unique pulsar planetary system. Of course, this particular orbital symmetry indicates the opposite (see also Ref. [16], Appendix A).
Table 12 lists two additional bodies orbiting very near the critical orbit of their systems, with the relevant periods being of order of 30 years or longer. The relative deviations from precise symmetry are smaller than 4%:

Table 12.
Bodies nearly on the critical orbital period of the order of 30 years or longer.
- (1)
- (2)
- HR 8799 d is also notable. It is orbiting close to the critical orbit of the system of 4 exoplanets, and its long orbital period ( yr) is shorter by only 4.5 yr (). The planetary system of HR 8799 is depicted in Figure 4 above.
4.10. Summary of the Longest Global MMR Chains and the Geometric Sequences
Table 13 summarizes the longest global MMR chains derived from combinations of triple chains listed in Table 2, Table 3, Table 4 and Table 5 above:
- (a)
- Triple geometric sequences are denoted by the acronym GS and their common ratio . All triple GSs found in exosystems have been summarized in Ref. [24].
- (b)
- There exist three types of triple GSs with , viz. ::, :1:, and ::1.
- (c)
- (d)
- (e)
- The entire quintuple MMR chain in K2-138 and HD 158259 is approximately geometric with a common ratio of . This raises the issue of whether this chain could actually be precisely geometric:
- (i)
- The unusual resonances 2/7 and 3/7 were chosen for the inner planets because these values are very close (to within <1%) to the measured orbital period ratios of 0.285 and 0.430, respectively; but the corresponding geometric resonances () are also nearby (to within <4%).
- (ii)
- If we assume that the MMR chains of K2-138 and HD 158259 (including the additional planets not listed in Table 13) may be precise GSs, then their MMRs are all powers of the ratio 2/3 as follows:
- ✩
- K2-138 MMR sequence (6 confirmed planets): , where for planets b–c–d–e(4)–f–g, respectively.
- ✩
- HD 158259 MMR sequence (5 confirmed planets plus a strong candidate, planet g): , where for planets b–c–d–e–f(5)–g, respectively.
- (iii)
- Similar issues of difficult choices between nearby MMRs are raised in another two cases listed in Table 13:
- ①
- Instead of the best-fitting 5:9 MMR, K-186 and K-296 may have a 4:7 MMR.
- ②
- Instead of the adopted 3:4 MMR, TOI-1136 and K2-384 may have a 5:7 MMR. However, no such issue exists in the case of the 3:4 MMRs identified in K-90, K-226, and TR-1 (relative deviations of <2% from 3/4).
- (iv)
- A summary of 4 markedly similar global MMR chains is listed at the bottom of Table 13. The prototypical sequence occurs in TR-1 and in TOI-1136:
- ➣
- The 1:5 and 1:4 inner MMRs (blue color) occur sufficiently far away from the 1:1 MMR (where the density of consecutive principal MMRs is too high), so failure to match the nearby 1:6 and 1:3 MMRs, respectively, is not a cause for concern.
- ➣
- The unusual 4:9 and 2:3 MMRs in HD 110067 cannot be overlooked in the same way because these resonances are not far away from 1:1, but their appearance is understood: these MMRs are exact elements of the GS with .
- ➣
- It is interesting that the 3:2 MMR in K2-384 is the only 3:2 MMR that is vacant in the markedly similar systems listed at the bottom of Table 13. We searched for another planet at d, but we did not find a signal in the archival Kepler data.
- ➣
- On the other hand, the 2:1 MMR in HD 110067 is not vacant. This resonance has drawn much attention recently [14,15,16,23,24]. It turns out that the pristine 6 triple MMR 1::2 observed in HD 110067 [14] represents a stable `Laplace-like resonance’ [23] whose double Laplace phase angle () most likely librates near (based on the results of Ref. [13]).7
- ➣
- This leaves only one surprising 2:1 MMR, that occupied by planet TOI-270 d [70,71,72,73] (see Figure 1 in Ref. [23] that shows the entire :1:2 MMR chain). The MMR chain of TOI-270 may be a Laplace-like resonance as well, although its apparent stability is presently unexplained.
- (v)
- The issues highlighted in items (i)–(iv) above will have to be addressed by future studies.
- (f)
- Summary of recently studied global MMRs and the librations of their phase angles:
- (i)
- The global MMR chains of TR-1 and TOI-1136 at the bottom of Table 13 are nearly identical. In TR-1, all planet pairs and all triple MMRs appear to be locked in librations [6,79,80,81,82,83,84].
- (ii)
- Three-body and four-body resonances of the 6 planets in HD 110067 have been extensively studied in Ref. [24].
- (iii)
- The geometric sequences, the four-body MMRs of K-223 and HD 110067, and the unusual LR encountered in K-176 (that does not include the most massive planet) have been extensively studied in Ref. [24].
- (iv)
- The 6 known LRs (folder LRs_6 in the library) and the Laplace-like MMR of HD 110067 (folder 6p_10/HD_110067 in the library) have been studied in Refs. [15,23].
- (v)
- The surprising triple MMR chain of TOI-270 listed in Table 4 (viz. :1:2, probably a new type of Laplace-like resonance, though unproven) was the main subject of the study in Ref. [23].

Table 13.
The longest global MMR chains and 5 commonly-occurring triple chains ★.
Table 13.
The longest global MMR chains and 5 commonly-occurring triple chains ★.
| A Chain of 5 MMRs | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2/7 | 3/7 | 2/3 | 1 | 3/2 | HD 158259, K2-138 (GS: 2/3:1:3/2, ) | ||||
| Chains of 4 MMRs | |||||||||
| 1/3 | 1/2 | 3/4 | 1 | TR-1, K2-384 (GS: 1/3:1/2:3/4, ) | |||||
| 1/2 | 3/4 | 1 | 3/2 | TR-1, TOI-1136 | |||||
| 4/9 | 2/3 | 1 | 3/2 | HD 110067 (Quadruple GS: ) | |||||
| 2/7 | 5/9 | 1 | 5/3 | K-186, K-296 | |||||
| Commonly-occurring Chains of 3 MMRs | |||||||||
| 3/4 | 1 | 3/2 | TR-1, TOI-1136, K-226 | ||||||
| 2/3 | 1 | 3/2 | HD 110067, HD 158259, K-11, K2-138 (GS: ) | ||||||
| 4/9 | 2/3 | 1 | HD 110067, HD 23472 (GS: ) | ||||||
| 1/2 | 3/4 | 1 | TR-1, TOI-1136, K-90, K2-384 | ||||||
| 1/3 | 1/2 | 3/4 | TR-1, K2-384 (GS: ) | ||||||
| Summary: Markedly Similar Long MMR Chains | |||||||||
| 1/6 | 1/3 | 1/2 | 3/4 | 1 | K2-384 | ||||
| 1/8 | 1/5 | 1/3 | 1/2 | 3/4 | 1 | 3/2 | TR-1 | ||
| 1/6 | 1/4 | 1/2 | 3/4 | 1 | 3/2 | TOI-1136 | |||
| 4/9 | 2/3 | 1 | 3/2 | 2 | 8/3 | HD 110067 | |||
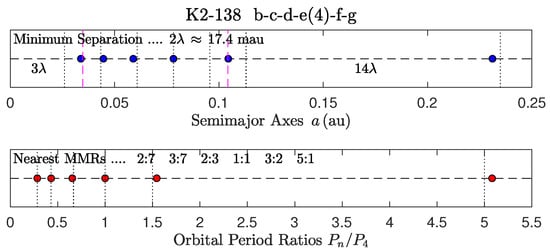
Figure 25.
K2-138 [8,11,88,89].
4.11. Beyond the Classical LRs: Summary of Important Groups of Triple MMR Chains
Table 14 and Table 15 summarize triple MMR chains reduced to integer ratios . With the exception of the famous Plutonian satellite sequence (1:3:4:5:6), these integer MMR sequences do not occur in real exosystems; but they are naturally classified in groups of which the top 6 groups in Table 14 and Table 15 are quite common in rational forms. In contrast, the bottom groups (7)–(10) in Table 14 are not common at all; they are highlighted here for the benefit of future investigations.

Table 14.
Beyond the famous Laplace resonance: groups of triple MMRs reduced to ratios of integers ≤9. The top 6 groups are by far the most common; they are analyzed further in Table 15. The top 3 groups are understood to a large extent [18,19,20,21,22,23,24,25,26,27,28,102,103,104,105]. The next 3 groups (4)–(6) are isolated here for the first time, and they should be investigated in future studies.

Table 15.
Groups (1)–(6) of integer ratios: analysis of local MMR pairs and their corresponding phase angles and their likely libration centers (LCs) [13,24] ★.
For the 6 main groups listed at the top of Table 14 and in Table 15, we summarize the following general characteristics:
- (a)
- All triple MMRs are combinations of local pairs chosen from the set {2:1, 3:2, 4:3}. Of the 9 possible combinations, three pairs do not appear in the tables:
- (i)
- The pair 4:3 and 4:3—This GS occurs in HD 110067 (:2: [14]), but it is not otherwise common (which may be surprising).
- (ii)
- The pair 2:1 and 4:3—This :1: MMR does not occur in real systems, probably because it is too close to the dominant Laplace-like resonance :1: (the MMRs mostly overlap).
- (iii)
- The pair 4:3 and 2:1—This MMR of type :1:2 does not occur in real systems either, although it is not close to the dominant LR :1:2. If it can be formed in exosystems, it is expected to not show librations because of the unique composition of its phase (, where () are the mean longitudes of the orbits [24]), the only one among the 9 combinations from set in which . More details are given in Section 4.12 below.
- (iv)
- We note that the pair 3:2 and 2:1, which is closer to the LR than the 4:3 and 2:1 pair, does occur in real systems, but its phase angle ( is defined in the notes to Table 15) does not librate either (see also group (6) in item (3) below).
- (b)
- Group (1): These are the 2 types of classical LRs with phase angle . The third type (the integer MMR chain 1:2:4) does not occur in any real system [23]; the reason is unknown. The libration centers of the GJ 876 LR and the Galilean LR are and , respectively [17,25].
- (c)
- Group (2): These are the most common GSs, and they have a common ratio of [24].
- (d)
- Group (3): These are the 3 types of Laplace-like resonances (::1, :1:, and 1::2) with phase angle and libration centers in the vicinity of (see Table 15).
For the local MMR layouts of the triple resonances and the phase angles and LCs of the 10 groups listed in Table 14, we also summarize the following specific properties:
- (1)
- Groups (1)–(3): These triple MMRs are expected to show librations irrespective of whether the individual local MMRs librate or not [17,18,19,20,21].
- (2)
- Groups (4) and (5): The trailing local MMR is 3:2, the same in both groups. Other than that, these groups are very different, although the global MMRs may both show LCs located at ∼180°. These MMRs have not been explored in the past. They are also listed in Table 2 of Ref. [24].
- (3)
- Group (6): These MMRs are not locked in librations. The reason appears to be the trailing 2:1 local MMR, which is not viable outside of the classical LR and the Laplace-like resonances (see Endnote 7). As mentioned above, a single puzzling exception occurs in TOI-270, which shows a trailing 2:1 MMR and an unusual phase angle [23]:
- •
- In TOI-270, the MMR chain :1:2 has the same phase () as the uncommon first-order MMR pair 4:3 and 4:3, the GS described in item (a)–(i) above. In this case, (); therefore, phase librations are feasible in principle.
- •
- This phase is expected to librate about a center in the vicinity of , but N-body simulations have not been carried out for long enough to check the results [72].
- •
- The MMR chain :1:2 is closer to the dominant LR :1:2 than the MMR pairs listed in items (a)-(iii, iv) above. The two chains mostly overlap. Yet, the TOI-270 MMR survives intact, unlike the 2:1 and 4:3 pair of MMRs discussed in items (a)–(ii) above.
- •
- Thus, the pair 2:1 and 4:3 is suppressed by the Laplace-like pair 3:2 and 4:3, whereas the pair 5:3 and 2:1 is unaffected by the LR pair 2:1 and 2:1. This disparity could characterize a fundamental difference between LRs and Laplace-like MMRs, with the latter being dominant over the range of their resonances and the former being incapable of suppressing nearly overlapping MMRs.
- •
- For the above reasons, the stability of the :1:2 MMR of TOI-270 remains a mystery, and the problem needs to be studied in more detail in the future.8
- (4)
- Groups (7)–(10): These are 14 global MMRs that appear rarely in individual exosystems:
- (i)
- They are unusual (they show large “integer gaps” between their MMRs), and it remains to be seen whether the same types of reduced MMR chains will be discovered in exosystems in the future.
- (ii)
- The set is dominated by the pristine principal MMR chain of Plutonian moons (1:3:4:5:6), whose triple MMRs appear in the list in all possible consecutive combinations (despite the striking vacancy of the 2:1 global MMR).
- (iii)
- The unusual chain :1: (huge gap beyond 1:1) appears in both K-48 and HIP 41378.
- (iv)
- The unusual chain :1: (gap at 4:3 – 3:2) appears in both HD 23472 and K-102.
- (v)
- Two very different MMRs of the 2:4:9 form appear in two very different exosystems (K-332 and HR 8799).
- (vi)
- Notable MMRs of future interest are ::1 (HD 20781), :1: (HD 10180, gap at 2:3), :1: (K-80, gaps at 2:3 and at 4:3), and :: (K2-268, gap at 1:3).
4.12. A Criterion for the Absence of Librations in Triple MMR Chains
The preceding analysis (item (a)–(iii) in Section 4.11) revealed a criterion, viz.
for the absence of librations in triple MMR chains (or, equivalently, in local adjacent resonant pairs). We reduce inequality (3) to first principles as follows:
We consider a pair of MMRs in the form of irreducible fractions, viz. , where subscripts and correspond to the leading and the trailing MMR, respectively, and is the order parameter of the MMR. From Ref. [24], we obtain expressions for A and B in the general case with , viz.
In the case of a trailing 2:1 MMR, and Equation (6) gives . Since , leading MMRs with (e.g., 4:3 or 5:4) are predicted to show no librations, if they are found in real systems in the future.
Absence of such MMRs was discovered empirically in past work (note rows 12, 13 in Table 2 of Ref. [24]). In row 11 of the same table, it was pointed out that the pair 4:3 and 5:4 has not been observed either (see Endnote 8). The fractions , do not satisfy the inequality (6), in which case, the triple MMR chain of the integer form 3:4:5 (observed in Pluto’s moons) is not precluded from locking into librations (see also the unusual top entry in group (9) of Table 14 for K-1542).
The :1: MMR of K-90 (, ) at the bottom of Table 4 is another example. This triple MMR (Figure 12) is expected to not be librating because , , and the no-libration criterion (6) is amply satisfied.
On the other hand, the 20 integer MMR ratios listed in Table 14 do not satisfy the no-libration criterion (6), which is consistent with their appearance in real systems. These MMRs are tested in the program Analysis_Files/Phases/Criterion_1.m of the library. In contrast, the related program Criterion_2.m produces a set of hypothetical, single-digit integer, MMR ratios that do satisfy the criterion (6) for the absence of librations.
5. Summary of Contents and Cross-References
The following table provides a detailed guide of the many cross-references that occur between the text, the tables, and the figures.
| Description of Contents and Cross-References | ||||
| Section 2 | ||||
| Items 1–7 | Assumptions on modeling the nearest MMRs | |||
| Items 1–6 | Conditions on modeling the spacings of the orbits | |||
| Section 3 | ||||
| Items 1–10 | Notes on the dynamical parameters listed in the library | |||
| Items 1–3 | Notes on the EPS file figures included in the library | |||
| Section 3.1 | ||||
| Items 1–7 | Notes on Laplace resonances | |||
| Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 | Figures of 5 LR systems | |||
| Section 3.2 | ||||
| Items 1–6 | Notes on solar subsystems | |||
| Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 | Figures of 5 solar subsystems | |||
| Section 3.3 | ||||
| Items 1–6 | Notes on extrasolar planetary systems | |||
| Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 | Figures of 8 extrasolar planetary systems | |||
| Section 4 | ||||
| Section 4.1 | Items (a)–(e) | Classical Laplace resonances (Table 1) | ||
| Section 4.2 | Items (a)–(e) | Gaseous giant planets (Figure 6) | ||
| Section 4.3 | Items (a)–(e) | Terrestrial planets (Figure 7) | ||
| Section 4.4 | Items (a)–(f) | Satellite systems (Figure 8, Figure 9 and Figure 10 and Figure 24) | ||
| Section 4.5 | Items (a)–(f) | Exosystems (Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 and Figure 25) | ||
| Section 4.6 | Items (a)–(c) | Triple MMR chains (Table 2, Table 3, Table 4, Table 5 and Table 6) | ||
| Section 4.7 | Items (a)–(d) | Tidal-field wavelengths (Table 7, Table 8 and Table 9, Figure 19 and Figure 21) | ||
| Section 4.8 | Items (a)–(e) | Extrasolar dwarf planets (Table 10, Figure 22 and Figure 23) | ||
| Section 4.9 | Items (a)–(d) | Critical orbital periods (Table 11) | ||
| Items (1)–(2) | Bodies with yr (Table 12) | |||
| Section 4.10 | Items (a)–(f) | Longest MMRs and geometric sequences (Table 13) | ||
| Section 4.11 | Items (a)–(d) | Characteristics of the 6 main groups of triple MMRs | ||
| Items (1)–(4) | Properties of 10 groups of triple MMRs (Table 14 and Table 15) | |||
| Section 4.12 | Equations (3)–(6) | Criterion for the absence of librations (Equation (6)) | ||
| Tables | ||||
| Table 1 | Section 4.1 | The 6 classical Laplace resonances | ||
| Table 2, Table 3, Table 4, Table 5 and Table 6 | Section 4.6 | Common and uncommon triple MMRs | ||
| Table 7, Table 8 and Table 9 | Section 4.7 | Tidal-field wavelengths and Landau wavelengths | ||
| Table 10 | Section 4.8 | Dwarf planets by surface gravity g | ||
| Table 11 and Table 12 | Section 4.9 | Bodies on/near the critical orbital periods | ||
| Table 13 | Section 4.10 | The longest global MMR chains | ||
| Table 14 and Table 15 | Section 4.11 | Groups of triple integer MMR chains | ||
| Figures | ||||
| Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 | LR systems | Galilean moons, GJ 876, HIP 41378, HR 8799, K-176 | ||
| Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 | Solar subsystems | Planets: Gas giants, Terrestrial; Moons: Saturn, Uranus, Pluto | ||
| Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 | Extrasolar planets | HD 10180, K-90, TR-1, TOI-1136, K-444, K2-32, K-60, K-51 | ||
| Figure 19 | Table 7 exosystems | Landau tidal-field wavelengths | ||
| Figure 20 | -au-scale systems | Landau tidal-field wavelengths | ||
| Figure 21 | Inner-moon systems | Landau tidal-field wavelengths | ||
| Figure 22 | Table 10 exoplanets | Distribution of surface gravities m | ||
| Figure 23 | Table 10 exodwarfs | Surface gravities m | ||
| Figure 24 | Neptunian moons | MMRs and semimajor axes | ||
| Figure 25 | K2-138 | MMRs and semimajor axes | ||
| Endnotes | ||||
| Note 1 | Section 1 | Citation guide to previous analyses | ||
| Note 2 | Section 1 and Section 3.1(5–6) | SI unit multiples and milli-au (mau) unit | ||
| Note 3 | Section 4.1(e) | The 7:3 exterior MMR | ||
| Note 4 | Section 4.1(e) | The 3:7 interior MMR | ||
| Note 5 | Section 4.2(c) | The reduced 1:2:3 MMR ratio | ||
| Note 6 | Table 8 | Long Landau wavelengths | ||
| Note 7 | Section 4.10(e)–(iv) | The 1::2 MMR in HD 110067 | ||
| Note 8 | Section 4.10(e)–(iv) | Four-planet resonant angles in HD 110067 | ||
| Note 9 | Table 15 | No librations for the 3:2 and 2:1 MMR pair | ||
| Note 10 | Table 15 | The unobserved 4:3 and 5:4 MMR pair | ||
| Note 11 | Section 4.11(3) | Beyond the LRs: The global 2:1 MMR in K-9 | ||
| Note 12 | Section 4.11(3) | Summary of occupied 2:1 non-LR MMRs | ||
Author Contributions
Conceptualization, formal analysis, and investigation, D.M.C., S.G.T.L., and D.K.; methodology, D.M.C. and D.K.; validation and resources, S.G.T.L.; software, data curation, visualization, and writing—original draft preparation, D.M.C.; writing—review and editing, S.G.T.L. and D.K.; supervision and project administration, D.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The library of data and models generated in the course of this study can be downloaded from the DOI link https://doi.org/10.5281/zenodo.14577621 (accessible any time past 30 December 2025). MATLAB programs (version 24.2.0.2740171 (R2024b) Update 1) that produce the results are included in the library files.
Acknowledgments
We thank the reviewers of this work for comments and suggestions that helped us improve the presentation of data and results. NASA, NSF, and LoCSST support over the years is gratefully acknowledged by the authors. S.G.T.L. and D.M.C. acknowledge support from NSF-AAG grant No. AST-2109004.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DOI | Digital Object Identifier |
| DP | Dwarf Planet (Table 10) |
| EPS | Encapsulated PostScript |
| GS | Geometric Sequence |
| K- | Kepler- |
| K2- | Kepler2- |
| LC | Libration Center |
| LR | Laplace Resonance |
| MMR | Mean-Motion Resonance |
| P | Planet (Table 10) |
| Portable Document Format | |
| SI | Système International d’unités |
| TR-1 | TRAPPIST-1 |
| TS | Teegarden’s Star [76,77,78] |
Notes
| 1 | Global MMRs are studied in Ref. [15]; few-body Landau damping is presented in Ref. [16]; LRs are studied in Ref. [23]; Laplace-like MMRs and their phase angles are collected in Ref. [24]; and surface gravities of (exo)planets and satellites are analyzed in Ref. [35]. |
| 2 | In the SI system of units, m and m. Furthermore, we use au, where au is the astronomical unit. |
| 3 | The 7:3 exterior MMR occurs in K-30, K-80, K2-32, TOI-700, Teegarden’s system, and the Galilean moons. The 3:7 interior MMR occurs in K2-138, TOI-178, and HD 158259. |
| 4 | The reduced 1:2:3 MMR ratio does not occur in this precise form (so the 2:1 MMR remains vacant), but its rational scalings occur in Uranus (Umbriel–Titania–Oberon), K-32, K-51, K-62, K-82, K-84, K2-384, TOI-1136, and HD 23472. |
| 5 | An extreme ratio of (such as those at the bottom of Table 8) implies that the most massive planet is orbiting at the outer end of the MMR chain while the less massive inner planets are in a compact configuration characterized by . Additional solar-system examples are the Uranian and Neptunian moon systems, respectively. |
| 6 | In the 1::2 MMR section of HD 110067, the planets are orbiting to within <0.05% of their respective MMRs. Outside this section, the planets continue to exhibit tiny relative deviations of ≤0.093% from the corresponding MMRs. The relative deviations from the empirically determined MMRs in the HD 110067 system (viz. [ 0.0 4.4 4.7 9.3]) are the smallest ones among all systems in the library. |
| 7 | Furthermore, two four-planet resonant phase angles were calculated for HD 110067 in Ref. [24]. |
| 8 | We note that planet K-9 c was also found to be near the 2:1 MMR of the three-planet system K-9 d–b–c [106,107,108], but we do not consider it a mystery. Planet d is too distant to participate in a triple MMR, and the two massive planets b and c form a single pair that is kept off of the exact 2:1 MMR, which was shown to be unstable [109]. It was also shown in Ref. [109] that the long-term stability of the pair is maintained by the libration of the difference of apsidal angles about ∼180° with amplitude . A summary of chains with an occupied non-LR 2:1 MMR follows: 1::2 in HD 110067 d–e–f, a Laplace-like resonance [24]; :1:2 in TOI-270 b–c–d, unexplained [23]; :1:2 in K-9 d-b-c, apsidal difference librates about ∼180° maintaining long-term stability [109]. |
References
- Goldreich, P. An explanation of the frequent occurrence of commensurable mean motions in the solar system. Mon. Not. R. Astron. Soc. 1965, 130, 159. [Google Scholar] [CrossRef]
- Lissauer, J.J.; Ragozzine, D.; Fabrycky, D.C.; Steffen, J.H.; Ford, E.B.; Jenkins, J.M.; Shporer, A.; Holman, M.J.; Rowe, J.F.; Quintana, E.V.; et al. Architecture and dynamics of Kepler’s candidate multiple transiting planet systems. Astrophys. J. Suppl. 2011, 197, 8. [Google Scholar] [CrossRef]
- Papaloizou, J.C.B. Three body resonances in close orbiting planetary systems: Tidal dissipation and orbital evolution. Int. J. Astrobiol. 2015, 14, 291. [Google Scholar] [CrossRef]
- Mills, S.M.; Fabrycky, D.C.; Migaszewski, C.; Ford, E.B.; Petigura, E.; Isaacson, H. A resonant chain of four transiting, sub-Neptune planets. Nature 2016, 533, 509. [Google Scholar] [CrossRef]
- MacDonald, M.G.; Ragozzine, D.; Fabrycky, D.C.; Ford, E.B.; Holman, M.J.; Isaacson, H.T.; Lissauer, J.J.; Lopez, E.D.; Mazeh, T.; Rogers, L.; et al. A dyamical analysis of the Kepler-80 system of five transiting planets. Astron. J. 2016, 152, 105. [Google Scholar] [CrossRef]
- Luger, R.; Sestovic, M.; Kruse, E.; Grimm, S.L.; Demory, B.-O.; Agol, E.; Bolmont, E.; Fabrycky, D.; Fernandes, C.S.; Van Grootel, V.; et al. A seven-planet resonant chain in TRAPPIST-1. Nat. Astron. 2017, 1, 0129. [Google Scholar] [CrossRef]
- Delisle, J.B. Analytical model of multi-planetary resonant chains and constraints on migration scenarios. Astron. Astrophys. 2017, 605, A96. [Google Scholar] [CrossRef]
- Christiansen, J.L.; Crossfield, I.J.M.; Barentsen, G.; Lintott, C.J.; Barclay, T.; Simmons, B.D.; Petigura, E.; Schlieder, J.E.; Dressing, C.D.; Vanderburg, A.; et al. The K2-138 System: A near-resonant chain of five sub-Neptune planets discovered by Citizen Scientists. Astron. J. 2018, 155, 57. [Google Scholar] [CrossRef]
- Millholland, S.; Laughlin, G.; Teske, J.; Butler, R.P.; Burt, J.; Holden, B.; Vogt, S.; Crane, J.; Shectman, S.; Thompson, I. New constraints on Gliese 876—Exemplar of mean-motion resonance. Astron. J. 2018, 155, 106. [Google Scholar] [CrossRef]
- MacDonald, M.G.; Dawson, R.I. Three pathways for observed resonant chains. Astron. J. 2018, 156, 228. [Google Scholar] [CrossRef]
- Lopez, T.A.; Barros, S.C.C.; Santerne, A.; Deleuil, M.; Adibekyan, V.; Almenara, J.-M.; Armstrong, D.J.; Brugger, B.; Barrado, D.; Bayliss, D.; et al. Exoplanet characterisation in the longest known resonant chain: The K2-138 system seen by HARPS. Astron. Astrophys. 2019, 631, A90. [Google Scholar] [CrossRef]
- Morrison, S.J.; Dawson, R.I.; MacDonald, M. Chains of planets in mean motion resonances arising from oligarchic growth. Astrophys. J. 2020, 904, 157. [Google Scholar] [CrossRef]
- Siegel, J.C.; Fabrycky, D. Resonant chains of exoplanets: Libration centers for three-body angles. Astron. J. 2021, 161, 290. [Google Scholar] [CrossRef]
- Luque, R.; Osborn, H.P.; Leleu, A.; Pallé, E.; Bonfanti, A.; Barragán, O.; Wilson, T.G.; Broeg, C.; Collier Cameron, A.; Lendl, M.; et al. A resonant sextuplet of sub-Neptunes transiting the bright star HD 110067. Nature 2023, 623, 932. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Laycock, S.G.T.; Kazanas, D. The global 2:1 mean-motion resonance in HD 110067 is not vacant! Res. Not. AAS 2023, 7, 275. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Kazanas, D. Landau tidal damping and major-body clustering in solar and extrasolar subsystems. Astronomy 2024, 3, 139. [Google Scholar] [CrossRef]
- Rivera, E.J.; Laughlin, G.; Butler, R.P.; Vogt, S.S.; Haghighipour, N.; Meschiari, S. The Lick-Carnegie exoplanet survey: A Uranus-mass fourth planet for GJ 876 in an extrasolar Laplace configuration. Astrophys. J. 2010, 719, 890. [Google Scholar] [CrossRef]
- Goździewski, K.; Migaszewski, C.; Panichi, F.; Szuszkiewicz, E. The Laplace resonance in the Kepler-60 planetary system. Mon. Not. R. Astron. Soc. 2016, 455, L104. [Google Scholar] [CrossRef]
- Charalambous, C.; Martí, J.G.; Beaugé, C.; Ramos, X.S. Resonance capture and dynamics of three-planet systems. Mon. Not. R. Astron. Soc. 2018, 477, 1414. [Google Scholar] [CrossRef]
- Goździewski, K.; Migaszewski, C. An exact, generalized Laplace resonance in the HR 8799 planetary system. Astrophys. J. Lett. 2020, 902, L40. [Google Scholar] [CrossRef]
- Celletti, A.; Karampotsiou, E.; Lhotka, C.; Pucacco, G.; Volpi, M. Laplace-like resonances with tidal effects. Astron. Astrophys. 2021, 655, A94. [Google Scholar] [CrossRef]
- Zurlo, A.; Goździewski, K.; Lazzoni, C.; Mesa, D.; Nogueira, D.; Desidera, S.; Gratton, R.; Marzari, F.; Langlois, M.; Pinna, E.; et al. Orbital and dynamical analysis of the system around HR8799. New astrometric epochs from VLT/SPHERE and LBT/LUCI. Astron. Astrophys. 2022, 666, A133. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Sorabella, N.M.; Bhattacharya, S.; Laycock, S.G.T.; Kazanas, D. Global mean-motion resonances: Part I—An exceptional multiplanetary resonant chain in TOI-270 and an exact Laplace-like resonance in HD 110067. Galaxies 2025, 13, 42. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Sorabella, N.M.; Bhattacharya, S.; Laycock, S.G.T.; Kazanas, D. Global mean-motion resonances: Part II—Laplace-like phase angles to facilitate libration searches in multiplanetary N-body simulations. Galaxies 2025, 13, 41. [Google Scholar] [CrossRef]
- Murray, C.D.; Dermott, S.F. Solar System Dynamics; Cambridge University Press: Cambridge, UK, 1999; pp. 364–371, 396–399. [Google Scholar]
- Lieske, J.H. Galilean satellite ephemerides E5. Astron. Astrophys. Suppl. Ser. 1998, 129, 205. [Google Scholar] [CrossRef]
- Musotto, S.; Varadi, F.; Moore, W.; Schubert, G. Numerical simulations of the orbits of the Galilean satellites. Icarus 2002, 159, 500. [Google Scholar] [CrossRef]
- Lainey, V.; Duriez, L.; Vienne, A. Synthetic representation of the Galilean satellites’ orbital motions from L1 ephemerides. Astron. Astrophys. 2006, 456, 783. [Google Scholar] [CrossRef]
- Landau, L. Oscillations of an electron plasma. J. Phys. 1946, 10, 25, (English Translation). [Google Scholar]
- Lynden-Bell, D. The stability and vibrations of a gas of stars. Mon. Not. R. Astron. Soc. 1962, 124, 279. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics; Princeton University Press: Princeton, NJ, USA, 1987; pp. 347, 412, 437–439, 677. [Google Scholar]
- Kandrup, H.E. Violent relaxation, phase mixing, and gravitational Landau damping. Astrophys. J. 1998, 500, 120. [Google Scholar] [CrossRef]
- Vandervoort, P.O. On stationary oscillations of galaxies. Mon. Not. R. Astron. Soc. 2003, 339, 537. [Google Scholar] [CrossRef]
- Trigger, S.A.; Ershkovich, A.I.; van Heijst, G.J.F.; Schram, P.P.J.M. Kinetic theory of Jeans instability. Phys. Rev. E 2004, 69, 066403. [Google Scholar] [CrossRef] [PubMed]
- Christodoulou, D.M.; Laycock, S.G.T.; Kazanas, D. An objective classification scheme for solar-system bodies based on surface gravity. Galaxies 2024, 12, 74. [Google Scholar] [CrossRef]
- Showalter, M.R.; de Pater, I.; Lissauer, J.J.; French, R.S. The seventh inner moon of Neptune. Nature 2019, 566, 350. [Google Scholar] [CrossRef]
- Cabrera, J.; Csizmadia, S.Z.; Lehmann, H.; Dvorak, R.; Gandolfi, D.; Rauer, H.; Erikson, A.; Dreyer, C.; Eigmüller, P.H.; Hatzes, A.; et al. The planetary system to KIC 11442793: A compact analogue to the solar system. Astrophys. J. 2015, 781, 18. [Google Scholar] [CrossRef]
- Shallue, C.J.; Vanderburg, A. Identifying exoplanets with deep learning: A five-planet resonant chain around Kepler-80 and an eighth planet around Kepler-90. Astron. J. 2018, 155, 94. [Google Scholar] [CrossRef]
- Fulton, B.J.; Petigura, E.A. The California-Kepler Survey. VII. Precise planet radii leveraging Gaia DR2 reveal the stellar mass dependence of the planet radius gap. Astron. J. 2018, 156, 264. [Google Scholar] [CrossRef]
- Vogt, S.S.; Burt, J.; Meschiari, S.; Butler, R.P.; Henry, G.W.; Wang, S.; Holden, B.; Gapp, C.; Hanson, R.; Arriagada, P. Six planets orbiting HD 219134. Astrophys. J. 2015, 814, 12. [Google Scholar] [CrossRef]
- Rosenthal, L.J.; Fulton, B.J.; Hirsch, L.A.; Isaacson, H.T.; Howard, A.W.; Dedrick, C.M.; Sherstyuk, I.A.; Blunt, S.C.; Petigura, E.A.; Knutson, H.A.; et al. The California Legacy Survey. I. A catalog of 178 planets from precision radial velocity monitoring of 719 nearby stars over three decades. Astrophys. J. Suppl. 2021, 255, 8. [Google Scholar] [CrossRef]
- Judkovsky, Y.; Ofir, A.; Aharonson, O. Kepler multitransiting system physical properties and impact parameter variations. Astron. J. 2024, 167, 103. [Google Scholar] [CrossRef]
- Danielsson, L. The orbital resonances between the asteroid Toro and the Earth and Venus. Moon Planets 1978, 18, 265. [Google Scholar] [CrossRef]
- Jacobson, R.A. The orbits of the main Saturnian satellites, the Saturnian system gravity field, and the orientation of Saturn’s pole. Astron. J. 2022, 164, 199. [Google Scholar] [CrossRef]
- Jacobson, R.A. The orbits of the Uranian satellites and rings, the gravity field of the Uranian system, and the orientation of the pole of Uranus. Astron. J. 2014, 148, 76. [Google Scholar] [CrossRef]
- Showalter, M.R.; Hamilton, D.P. Resonant interactions and chaotic rotation of Pluto’s small moons. Nature 2015, 522, 45. [Google Scholar] [CrossRef]
- Stern, S.A.; Grundy, W.M.; McKinnon, W.B.; Weaver, H.A.; Young, L.A. The Pluto system after New Horizons. Ann. Rev. Astron. Astrophys. 2018, 56, 357. [Google Scholar] [CrossRef]
- Lovis, C.; Ségransan, D.; Mayor, M.; Udry, S.; Benz, W.; Bertaux, J.-L.; Bouchy, F.; Correia, A.C.M.; Laskar, J.; Lo Cuorto, G.; et al. The HARPS search for southern extra-solar planets XXVIII. Up to seven planets orbiting HD 10180: Probing the architecture of low-mass planetary systems. Astron. Astrophys. 2011, 528, A112. [Google Scholar] [CrossRef]
- Tuomi, M. Evidence for nine planets in the HD10180 system. Astron. Astrophys. 2012, 543, A52. [Google Scholar] [CrossRef]
- Kiefer, F.; Hébrard, G.; Etangs, A.L.d.; Martioli, E.; Dalal, S.; Vidal-Madjar, A. Determining the true mass of radial-velocity exoplanets with Gaia. Astron. Astrophys. 2021, 645, A7. [Google Scholar] [CrossRef]
- Mills, S.M.; Fabrycky, D.C. Mass, density, and formation constraints in the compact, sub-Earth Kepler-444 system including two Mars-mass planets. Astrophys. J. Lett. 2017, 838, L11. [Google Scholar] [CrossRef]
- Buldgen, G.; Farnir, M.; Pezzotti, C.; Eggenberger, P.; Salmon, S.J.A.J.; Montalban, J.; Ferguson, J.W.; Khan, S.; Bourrier, V.; Rendle, B.M.; et al. Revisiting Kepler-444, Astron. Astrophys. 2019, 630, A126. [Google Scholar]
- Weiss, L.M.; Isaacson, H.; Howard, A.W.; Fulton, B.J.; Petigura, E.A.; Fabrycky, D.; Jontof-Hutter, D.; Steffen, J.H.; Schlichting, H.E.; Wright, J.T.; et al. The Kepler Giant Planet Search. I. A decade of Kepler planet-host radial velocities from W. M. Keck Observatory. Astrophys. J. Suppl. 2024, 270, 8. [Google Scholar] [CrossRef]
- Rowe, J.F.; Coughlin, J.L.; Antoci, V.; Barclay, T.; Batalha, N.M.; Borucki, W.J.; Burke, C.J.; Bryson, S.T.; Caldwell, D.A.; Campbell, J.R.; et al. Planetary candidates observed by Kepler. V. Planet sample from Q1-Q12 (36 months). Astrophys. J. Suppl. 2015, 217, 16. [Google Scholar] [CrossRef]
- Jontof-Hutter, D.; Ford, E.B.; Rowe, J.F.; Lissauer, J.J.; Fabrycky, D.C.; Van Laerhoven, C.; Agol, E.; Deck, K.M.; Holczer, T.; Mazeh, T. Erratum: “Secure mass measurements from transit timing: 10 Kepler exoplanets between 3 and 8 M⊕ with diverse densities and incident fluxes”. Astrophys. J. 2021, 911, 154. [Google Scholar] [CrossRef]
- Leleu, A.; Deslisle, J.-B.; Udry, S.; Mardling, R.; Turbet, M.; Egger, J.A.; Alibert, Y.; Chatel, G.; Eggenberger, P.; Stalport, M. Removing biases on the density of sub-Neptunes characterised via transit timing variations. Astron. Astrophys. 2023, 669, A117. [Google Scholar] [CrossRef]
- Wolszczan, A.; Frail, D.A. A planetary system around the millisecond pulsar PSR1257+12. Nature 1992, 355, 145. [Google Scholar] [CrossRef]
- Konacki, M.; Wolszczan, A. Masses and orbital inclinations of planets in the PSR B1257+12 system. Astrophys. J. Lett. 2003, 591, L147. [Google Scholar] [CrossRef]
- Goździewski, K.; Konacki, M.; Wolszczan, A. Long-term stability and dynamical environment of the PSR 1257+12 planetary system. Astrophys. J. 2005, 619, 1084. [Google Scholar] [CrossRef]
- Wolszczan, A. Discovery of pulsar planets. New Astron. Rev. 2012, 56, 2. [Google Scholar] [CrossRef]
- Heller, R.; Rodenbeck, K.; Hippke, M. Transit least-squares survey. I. Discovery and validation of an Earth-sized planet in the four-planet system K2-32 near the 1:2:5:7 resonance. Astron. Astrophys. 2019, 625, A31. [Google Scholar] [CrossRef]
- Lillo-Box, J.; Lopez, T.A.; Santerne, A.; Nielsen, L.D.; Barros, S.C.C.; Deleuil, M.; Acuña, L.; Mousis, O.; Sousa, S.G.; Adibekyan, V.; et al. Masses for the seven planets in K2-32 and K2-233. Astron. Astrophys. 2020, 640, A48. [Google Scholar] [CrossRef]
- Rowe, J.F.; Bryson, S.T.; Marcy, G.W.; Lissauer, J.J.; Jontof-Hutter, D.; Mullally, F.; Gilliland, R.L.; Issacson, H.; Ford, E.; Howell, S.B.; et al. Validation of Kepler’s multiple planet candidates. III. Light curve analysis and announcement of hundreds of new multi-planet systems. Astrophys. J. 2014, 784, 45. [Google Scholar] [CrossRef]
- Steffen, J.H.; Fabrycky, D.C.; Agol, E.; Ford, E.B.; Morehead, R.C.; Cochran, W.D.; Lissauer, J.J.; Adams, E.R.; Borucki, W.J.; Bryson, S.; et al. Transit timing observations from Kepler—VII. Confirmation of 27 planets in 13 multiplanet systems via transit timing variations and orbital stability. Mon. Not. R. Astron. Soc. 2013, 428, 1077. [Google Scholar] [CrossRef]
- Masuda, K. Very low density planets around Kepler-51 revealed with transit timing variations and an anomaly similar to a planet-planet eclipse event, Astrophys. J. 2014, 783, 53. [Google Scholar] [CrossRef]
- Libby-Roberts, J.E.; Berta-Thompson, Z.K.; Désert, J.-M.; Masuda, K.; Morley, C.V.; Lopez, E.D.; Deck, K.M.; Fabrycky, D.; Fortney, J.J.; Line, M.R.; et al. The featureless transmission spectra of two super-puff planets. Astron. J. 2020, 159, 57. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Kazanas, D. A physical interpretation of the Titius-Bode rule and its connection to the closed orbits of Bertrand’s theorem. Res. Astron. Astrophys. 2017, 17, 129. [Google Scholar] [CrossRef]
- Steffen, J.H. Kepler’ s missing planets. Mon. Not. R. Astron. Soc. 2013, 433, 3246. [Google Scholar] [CrossRef]
- Ćuk, M.; El Moutamid, M.; Tiscareno, M.S. Dynamical history of the Uranian system. Planet. Sci. J. 2020, 1, 22. [Google Scholar] [CrossRef]
- Günther, M.N.; Pozuelos, F.J.; Dittman, J.A.; Dragomir, D.; Kane, S.R.; Daylan, T.; Feinstein, A.D.; Huang, C.X.; Morton, T.D.; Bonfanti, A.; et al. A super-Earth and two sub-Neptunes transiting the nearby and quiet M dwarf TOI-270. Nat. Astron. 2019, 3, 1099. [Google Scholar] [CrossRef]
- Van Eylen, V.; Astudillo-Defru, N.; Bonfils, X.; Livingston, J.; Hirano, T.; Luque, R.; Lam, K.W.F.; Justesen, A.B.; Winn, J.N.; Gandolfi, D.; et al. Masses and compositions of three small planets orbiting the nearby M dwarf L231-32 (TOI-270) and the M dwarf radius valley. Mon. Not. R. Astron. Soc. 2021, 507, 2154. [Google Scholar] [CrossRef]
- Kaye, L.; Vissapragada, S.; Günther, M.N.; Aigrain, S.; Mikal-Evans, T.; Jensen, E.L.N.; Parviainen, H.; Pozuelos, F.J.; Abe, L.; Acton, J.S.; et al. Transit timings variations in the three-planet system: TOI-270. Mon. Not. R. Astron. Soc. 2022, 510, 5464. [Google Scholar] [CrossRef]
- Mikal-Evans, T.; Madhusudhan, N.; Dittman, J.; Günther, M.N.; Welbanks, L.; Van Eylen, V.; Crossfield, I.J.M.; Daylan, T.; Kreidberg, L. Hubble Space Telescope transmission spectroscopy for the temperate sub-Neptune TOI-270 d: A possible hydrogen-rich atmosphere containing water vapor. Astron. J. 2023, 165, 84. [Google Scholar] [CrossRef]
- MacDonald, M.G.; Polania Vivas, M.S.; D’Angiolillo, S.; Fernandez, A.N.; Quinn, T. exoMMR: A new python package to confirm and characterize mean motion resonances. Astron. J. 2023, 166, 94. [Google Scholar] [CrossRef]
- Borucki, W.J.; Koch, D.G.; Basri, G.; Batalha, N.; Brown, T.M.; Bryson, S.T.; Caldwell, D.; Christensen-Dalsgaard, J.; Cochran, W.D.; DeVore, E.; et al. Characteristics of planetary candidates observed by Kepler II. Analysis of the first four months of data. Astrophys. J. 2011, 736, 19. [Google Scholar] [CrossRef]
- Teegarden, B.J.; Pravdo, S.H.; Hicks, M.; Lawrence, K.; Shaklan, S.B.; Covey, K.; Fraser, O.; Hawley, S.L.; McGlynn, T.; Reid, I.N. Discovery of a new nearby star. Astrophys. J. Lett. 2003, 589, L51. [Google Scholar] [CrossRef][Green Version]
- Zechmeister, M.; Dreizler, S.; Ribas, I.; Reiners, A.; Caballero, J.A.; Bauer, F.F.; Béhar, V.J.S.; González-Cuesta, L.; Herrero, E.; Lalitha, S.; et al. The CARMENES search for exoplanets around M dwarfs. Astron. Astrophys. 2019, 627, A49. [Google Scholar] [CrossRef]
- Dreizler, S.; Luque, R.; Ribas, I.; Koseleva, V.; Ruh, H.L.; Nagel, E.; Pozuelos, F.J.; Zechmeister, M.; Reiners, A.; Caballero, J.A.; et al. Teegarden’s star revisited. Astron. Astrophys. 2024, 684, A117. [Google Scholar] [CrossRef]
- Gillon, M.; Triaud, A.H.M.J.; Demory, B.-O.; Jehin, E.; Agol, E.; Deck, K.M.; Lederer, S.M.; de Wit, J.; Burdanov, A.; Ingalls, J.G.; et al. Seven temperate terrestrial planets around the nearby ultracool dwarf star TRAPPIST-1. Nature 2017, 542, 456. [Google Scholar] [CrossRef]
- Agol, E.; Dorn, C.; Grimm, S.L.; Turbet, M.; Ducrot, E.; Delrez, L.; Gillon, M.; Demory, B.-O.; Burdanov, A.; Barkaoui, K.; et al. Refining the transit-timing and photometric analysis of TRAPPIST-1: Masses, radii, densities, dynamics, and ephemerides. Planet. Sci. J. 2021, 2, 1. [Google Scholar] [CrossRef]
- Mah, J. Formation and Dynamics of the Resonant Chain in the TRAPPIST-1 Exoplanet System. Master’s Thesis, The University of Hong Kong, Hong Kong, 2018. [Google Scholar]
- Ducrot, E.; Gillon, M.; Delrez, L.; Agol, E.; Rimmer, P.; Turbet, M.; Günther, M.N.; Demory, B.-O.; Triaud, A.H.M.J.; Bolmont, E.; et al. TRAPPIST-1: Global results of the Spitzer exploration science program Red Worlds. Astron. Astrophys. 2020, 640, A112. [Google Scholar] [CrossRef]
- Hirano, T.; Gaidos, E.; Winn, J.N.; Dai, F.; Fukui, A.; Kuzuhara, M.; Kotani, T.; Tamura, M.; Hjorth, M.; Albrecht, S.; et al. Evidence for spin-orbit alignment in the TRAPPIST-1 system. Astrophys. J. Lett. 2020, 890, L27. [Google Scholar] [CrossRef]
- Pichierri, G.; Morbidelli, A.; Batygin, K.; Brasser, R. The formation of the TRAPPIST-1 system in two steps during the recession of the disk inner edge. Nat. Astron. 2024, 8, 1408. [Google Scholar] [CrossRef]
- Dai, F.; Masuda, K.; Beard, C.; Robertson, P.; Goldberg, M.; Batygin, K.; Bouma, L.; Lissauer, J.J.; Knudstrup, E.; Albrecht, S.; et al. TOI-1136 is a young, coplanar, aligned planetary system in a pristine resonant chain. Astron. J. 2023, 165, 33. [Google Scholar] [CrossRef]
- Beard, C.; Robertson, P.; Dai, F.; Holcomb, R.; Lubin, J.; Akana Murphy, J.M.; Batalha, N.M.; Blunt, S.; Crossfield, I.; Dressing, C.; et al. The TESS-Keck Survey. XVII. Precise mass measurements in a young, high-multiplicity transiting planet system using radial velocities and transit timing variations. Astron. J. 2024, 167, 70. [Google Scholar] [CrossRef]
- Polanski, A.S.; Lubin, J.; Beard, C.; Akana Murphy, J.M.; Rubenzahl, R.; Hill, M.L.; Crossfield, I.J.M.; Chontos, A.; Robertson, P.; Isaacson, H.; et al. The TESS-Keck Survey. XX. 15 new TESS planets and a uniform RV analysis of all survey targets. Astrophys. J. Suppl. 2024, 272, 32. [Google Scholar] [CrossRef]
- Hardegree-Ullman, K.K.; Christiansen, J.L.; Ciardi, D.R.; Crossfield, I.J.M.; Dressing, C.D.; Livingston, J.H.; Volk, K.; Agol, E.; Barclay, T.; Barentsen, G.; et al. K2-138 g: Spitzer spots a sixth planet for the Citizen Science System. Astron. J. 2021, 161, 219. [Google Scholar] [CrossRef]
- MacDonald, M.G.; Feil, L.; Quinn, T.; Rice, D. Confirming the 3:2 resonance chain of K2-138. Astron. J. 2022, 163, 162. [Google Scholar] [CrossRef]
- Hara, N.C.; Bouchy, F.; Stalport, M.; Boisse, I.; Rodrigues, J.; Delisle, J.-B.; Santerne, A.; Henry, G.W.; Arnold, L.; Astudillo-Defru, N.; et al. The SOPHIE search for northern extrasolar planets. XVI. HD 158259: A compact planetary system in a near-3:2 mean motion resonance chain. Astron. Astrophys. 2020, 636, L6. [Google Scholar] [CrossRef]
- Vallenari, A.; Brown, A.G.A.; Prusti, T.; de Bruijne, J.H.J.; Arenou, F.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Ducourant, C.; Evans, D.W.; et al. (Gaia Collaboration) Gaia Data Release 3. Summary of the content and survey properties. Astron. Astrophys. 2023, 674, A1. [Google Scholar]
- Barros, S.C.C.; Demangeon, O.D.S.; Alibert, Y.; Leleu, A.; Adibekyan, V.; Lovis, C.; Bossini, D.; Sousa, S.G.; Hara, N.; Bouchy, F.; et al. HD 23472: A multi-planetary system with three super-Earths and two potential super-Mercuries. Astron. Astrophys. 2022, 665, A154. [Google Scholar] [CrossRef]
- Christiansen, J.L.; Bhure, S.; Zink, J.K.; Hardegree-Ullman, K.K.; Adkins, B.D.; Hedges, C.; Morton, T.D.; Bieryla, A.; Ciardi, D.R.; Cochran, W.D.; et al. Scaling K2. V. Statistical validation of 60 new exoplanets from K2 campaigns 2–18. Astron. J. 2022, 163, 244. [Google Scholar] [CrossRef]
- Lissauer, J.J.; Jontof-Hutter, D.; Rowe, J.F.; Fabrycky, D.C.; Lopez, E.D.; Agol, E.; Marcy, G.W.; Deck, K.M.; Fischer, D.A.; Fortney, J.J.; et al. All six planets known to orbit Kepler-11 have low densities. Astrophys. J. 2013, 770, 131. [Google Scholar] [CrossRef]
- Bedell, M.; Bean, J.L.; Meléndez, J.; Mills, S.M.; Fabrycky, D.C.; Freitas, F.C.; Ramírez, I.; Asplund, M.; Liu, F.; Yong, D. Kepler-11 is a solar twin: Revising the masses and radii of benchmark planets via precise stellar characterization. Astrophys. J. 2017, 839, 94. [Google Scholar] [CrossRef]
- Quintana, E.V.; Barclay, T.; Raymond, S.N.; Rowe, J.F.; Bolmont, E.; Caldwell, D.A.; Howell, S.B.; Kane, S.R.; Huber, D.; Crepp, J.R.; et al. An Earth-sized planet in the habitable zone of a cool star. Science 2014, 344, 277. [Google Scholar] [CrossRef] [PubMed]
- Berger, T.A.; Huber, D.; Gaidos, E.; van Saders, J.L. Revised radii of Kepler stars and planets using Gaia Data Release 2. Astrophys. J. 2018, 866, 99. [Google Scholar] [CrossRef]
- Thompson, S.E.; Coughlin, J.L.; Hoffman, K.; Mullally, F.; Christiansen, J.L.; Burke, C.J.; Bryson, S.; Batalha, N.; Haas, M.R.; Catanzarite, J.; et al. Planetary candidates observed by Kepler. VIII. A fully automated catalog with measured completeness and reliability based on Data Release 25. Astrophys. J. Suppl. 2018, 235, 38. [Google Scholar] [CrossRef]
- Quinn, T.; MacDonald, M.G. Confirming resonance in three transiting systems. Astron. J. 2023, 166, 58. [Google Scholar] [CrossRef]
- Barclay, T.; Quintana, E.V.; Adams, F.C.; Ciardi, D.R.; Huber, D.; Foreman-Mackey, D.; Montet, B.T.; Caldwell, D. The five planets in the Kepler-296 binary system all orbit the primary: A statistical and analytical analysis. Astrophys. J. 2015, 809, 7. [Google Scholar] [CrossRef]
- Becker, J.C.; Adams, F.C. Effects of unseen additional planetary perturbers on compact extrasolar planetary systems. Mon. Not. R. Astron. Soc. 2017, 468, 549. [Google Scholar] [CrossRef]
- Lari, G.; Saillenfest, M. The nature of the Laplace resonance between the Galilean moons. Celest. Mech. Dyn. Astr. 2024, 136, 19. [Google Scholar] [CrossRef]
- Henrard, J.; Lemaitre, A. A second fundamental model for resonance. Celest. Mech. 1983, 30, 197. [Google Scholar] [CrossRef]
- Delisle, J.-B.; Laskar, J.; Correia, A.C.M.; Boué, G. Dissipation in planar resonant planetary systems. Astron. Astrophys. 2012, 546, A71. [Google Scholar] [CrossRef]
- Batygin, K.; Morbidelli, A. Analytical treatment of planetary resonances. Astron. Astrophys. 2013, 556, A28. [Google Scholar] [CrossRef]
- Torres, G.; Fressin, F.; Batalha, N.M.; Borucki, W.J.; Brown, T.M.; Bryson, S.T.; Buchhave, L.A.; Charbonneau, D.; Ciardi, D.R.; Dunham, E.W.; et al. Modeling Kepler light curves as false positives: Rejection of blend scenarios for Kepler-9, and validation of Kepler-9 d, a super-Earth-size planet in a multiple system. Astrophys. J. 2011, 727, 24. [Google Scholar] [CrossRef]
- Borsato, L.; Malavolta, L.; Piotto, G.; Buchhave, L.A.; Mortier, A.; Rice, K.; Cameron, A.C.; Coffinet, A.; Sozzetti, A.; Charbonneau, D.; et al. HARPS-N radial velocities confirm the low densities of the Kepler-9 planets. Mon. Not. R. Astron. Soc. 2019, 484, 3233. [Google Scholar] [CrossRef]
- Faridani, T.H.; Naoz, S.; Li, G.; Rice, M.; Inzunza, N. More likely than you think: Inclination-driving secular resonances are common in known exoplanet systems. Astrophys. J. 2025, 978, 18. [Google Scholar] [CrossRef]
- Antoniadou, K.I.; Libert, A.-S. Exploiting periodic orbits as dynamical clues for Kepler and K2 systems. Astron. Astrophys. 2020, 640, A55. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).