Axion Mass and the Ground State of Deconfining SU(2) Yang–Mills Thermodynamics
Abstract
1. Introduction
2. Axion Mass Squared via the Veneziano–Witten Formula at a Finite Temperature
3. The Veneziano–Witten Integral for Deconfining SU(2) Yang–Mills Thermodynamics
3.1. The Topological Susceptibility on a Harrington–Shepard (HS) (Anti)Caloron
3.2. Do Thermal Quasiparticle Fluctuations Contribute to ?
4. Cosmological Implications: Bose Condensation of Axion Particles
5. Summary and Outlook
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
 .
.Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Factorized χ(T) in the Model of the Stochastic Yang–Mills Vacuum at T>T c
Appendix A.2. Contributions to Topological Susceptibility Due to Massless and Massive Quasi-Particles
| 1 | Since the correlator of Q is computed on one field configuration only using a Harrington–Shepard caloron, it naturally factorizes into a local and a nonlocal part. Note that the contribution and weight of the anticaloron is identical and, therefore, the average over both caloron and anticaloron reduces to the caloron contribution. |
| 2 | For useful relations on the contractions of bilinears in see [36]. |
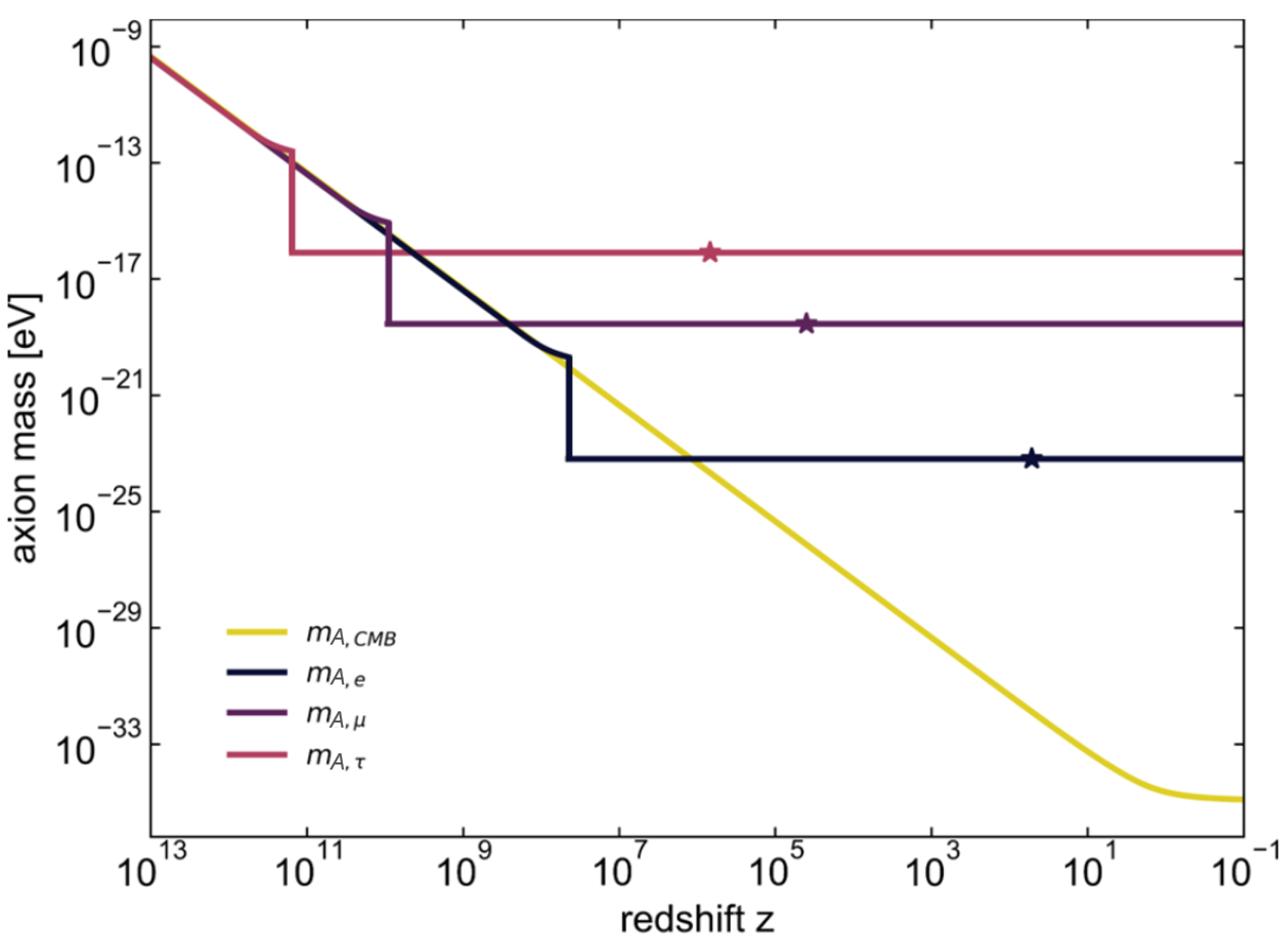
| 3 | In cosmology, axion particles can be shown to be nonrelativistic [11]: Roughly speaking, their speed is bounded from above by where denotes the entire mass of the instantaneously gravitating system at redshift z after virialization [11]. To axions that presently form a super-horizon sized, self-gravitating Bose condensate to represent dark energy we associate the gauge group SU(2)CMB [20,31,45]. In this system presently gravitates subject to a mass made from the axion condensate, dark matter, and baryons. For a spatial ball of present Hubble radius —the causally connected, selfgravitating region to which a typical axion particle virializes—we have . Using eV and [46,47,48] yields eV. Setting eV [35], one thus arrives at . In a spatially flat, matter-dominated universe, evolves as . With [49], this produces . In a radiation-dominated universe, does not evolve in z. Ignoring a small regime in redshift of dark-energy domination and taking the redshift of radiation-matter equality as , the axion-particle speed thus increases from its present value by a factor of . Therefore, axions that associate with SU(2)CMB are non-relativistic throughout the entire expansion history. Axion particles of species that are associated with fuzzy dark matter receive their redshift independent masses due to the Veneziano–Witten formula applied to confining phases of SU(2) Yang–Mills theories for redshifts [31], where topological charge is carried by round-point center-vortex loops [23]. Presently, they are similarly slow to the axions of SU(2)CMB [11,31]. With increasing z, and for , the velocities of these axion particles remains constant until the percolation of their selfgravitating lumps sets in at . For , axion velocities either decay with (matter domination) or with (radiation domination) as z increases, and so are guaranteed to be non-relativistic. In the deconfining phases of the associated SU(2) Yang–Mills theories, i.e., in the very early, radiation dominated universe, axion velocities do not evolve. |
| 4 | One can readily see that the horizon size remains smaller than the Compton wavelength in a radiation dominated universe. Namely, . This shows that no gravitational back reaction occurs while maintaining the condensed state of axion particles. Thus, the condition to determine the critical temperature for condensation is solely Equation (16). |
References
- Gross, D.J.; Pisarski, R.D.; Yaffe, L.G. QCD and instantons at finite temperature. Rev. Mod. Phys. 1981, 53, 43–80. [Google Scholar] [CrossRef]
- Schäfer, T.; Shuryak, E.V. Instantons in QCD. Rev. Mod. Phys. 1998, 70, 323–425. [Google Scholar] [CrossRef]
- Berkowitz, E.; Buchoff, M.I.; Rinaldi, E. Lattice QCD input for axion cosmology. Phys. Rev. D 2015, 92, 034507. [Google Scholar] [CrossRef]
- Borsanyi, S.; Dierigl, M.; Fodor, Z.; Katz, S.D.; Mages, S.W.; Nogradi, D.; Redondo, J.; Ringwald, A.; Szabo, K.K. Axion cosmology, lattice QCD and the dilute instanton gas. Phys. Lett. B 2016, 752, 175–181. [Google Scholar] [CrossRef]
- Gattringer, C.; Göckeler, M.; Rakow, P.; Schaefer, S.; Schäfer, A. A comprehensive picture of topological excitations in finite temperature lattice QCD. Nucl. Phys. B 2001, 618, 205–240. [Google Scholar] [CrossRef]
- Gattringer, C.; Hoffmann, R.; Schaefer, S. The topological susceptibility of SU(3) gauge theory near Tc. Phys. Lett. B 2002, 535, 358–362. [Google Scholar] [CrossRef]
- Jahn, P.T.; Moore, G.D.; Robaina, D. χtop(T ≫ Tc) in pure-glue QCD through reweighting. Phys. Rev. D 2018, 98, 054512. [Google Scholar] [CrossRef]
- Burger, F.; Ilgenfritz, E.M.; Lombardo, M.P.; Müller-Preussker, M.; Trunin, A. Topology (and axion’s properties) from lattice QCD with a dynamical charm. Nucl. Phys. A 2017, 967, 880–883. [Google Scholar] [CrossRef]
- Giusti, L.; Lüscher, M. Topological susceptibility at T > Tc from master-field simulations of the SU(3) gauge theory. Eur. Phys. J. C 2019, 79, 207. [Google Scholar] [CrossRef]
- Antonov, D. Topological Susceptibility of the Gluon Plasma in the Stochastic-Vacuum Approach. Universe 2024, 10, 377. [Google Scholar] [CrossRef]
- Sin, S.J. Late time cosmological phase transition and galactic halo as Bose liquid. Phys. Rev. D 1994, 50, 3650–3654. [Google Scholar] [CrossRef] [PubMed]
- Suárez, A.; Robles, V.H.; Matos, T. A Review on the Scalar Field/Bose-Einstein Condensate Dark Matter Model. Astrophys. Space Sci. Proc. 2014, 38, 107–142. [Google Scholar] [CrossRef]
- Magana, J.; Matos, T. A brief Review of the Scalar Field Dark Matter model. J. Phys. Conf. Ser. 2012, 378, 012012. [Google Scholar] [CrossRef]
- Schive, H.Y.; Chiueh, T.; Broadhurst, T. Cosmic Structure as the Quantum Interference of a Coherent Dark Wave. Nat. Phys. 2014, 10, 496–499. [Google Scholar] [CrossRef]
- Martinez-Medina, L.A.; Robles, V.H.; Matos, T. Dwarf galaxies in multistate scalar field dark matter halos. Phys. Rev. D 2015, 91, 023519. [Google Scholar] [CrossRef]
- Hui, L.; Ostriker, J.P.; Tremaine, S.; Witten, E. Ultralight scalars as cosmological dark matter. Phys. Rev. D 2017, 95, 043541. [Google Scholar] [CrossRef]
- Niemeyer, J.C. Small-scale structure of fuzzy and axion-like dark matter. Prog. Part. Nucl. Phys. 2020, 113, 103787. [Google Scholar] [CrossRef]
- Perez, A.; Rovelli, C. Physical effects of the Immirzi parameter in loop quantum gravity. Phys. Rev. D 2006, 73, 044013. [Google Scholar] [CrossRef]
- Candelas, P.; Raine, D.J. General-relativistic quantum field theory: An exactly soluble model. Phys. Rev. D 1975, 12, 965. [Google Scholar] [CrossRef]
- Giacosa, F.; Hofmann, R.; Neubert, M. A model for the very early Universe. JHEP 2008, 02, 077. [Google Scholar] [CrossRef]
- Meinert, J.; Hofmann, R. Electroweak Parameters from Mixed SU(2) Yang–Mills Thermodynamics. Symmetry 2024, 16, 1587. [Google Scholar] [CrossRef]
- Trombetti, T.; Burigana, C. Semi-analytical description of clumping factor and cosmic microwave background free–free distortions from reionization. Mon. Not. R. Astron. Soc. 2013, 437, 2507–2520. [Google Scholar] [CrossRef]
- Hofmann, R. The Thermodynamics of Quantum Yang-Mills Theory: Theory and Applications, 2nd ed.; World Scientific Publishing Co. Pte Ltd.: Singapore, 2016. [Google Scholar]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Peccei, R.; Quinn, H.R. Constraints Imposed by CP Conservation in the Presence of Instantons. Phys. Rev. D 1977, 16, 1791–1797. [Google Scholar] [CrossRef]
- Wantz, O.; Shellard, E.P.S. Axion cosmology revisited. Phys. Rev. D 2010, 82, 123508. [Google Scholar] [CrossRef]
- Harrington, B.J.; Shepard, H.K. Periodic Euclidean solutions and the finite-temperature Yang-Mills gas. Phys. Rev. D 1978, 17, 2122–2125. [Google Scholar] [CrossRef]
- Hofmann, R. Nonperturbative approach to Yang-Mills thermodynamics. Int. J. Mod. Phys. A 2005, 20, 4123–4216. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Ultraviolet Behavior of Nonabelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343–1346. [Google Scholar] [CrossRef]
- Politzer, H.D. Reliable Perturbative Results for Strong Interactions? Phys. Rev. Lett. 1973, 30, 1346–1349. [Google Scholar] [CrossRef]
- Meinert, J.; Hofmann, R. Axial Anomaly in Galaxies and the Dark Universe. Universe 2021, 7, 198. [Google Scholar] [CrossRef]
- Veneziano, G. U(1) without instantons. Nucl. Phys. B 1979, 159, 213–224. [Google Scholar] [CrossRef]
- Witten, E. Current algebra theorems for the U(1) “Goldstone boson”. Nucl. Phys. B 1979, 156, 269–283. [Google Scholar] [CrossRef]
- Ma, C.P.; Bertschinger, E. Cosmological Perturbation Theory in the Synchronous and Conformal Newtonian Gauges. Astrophys. J. 1995, 455, 7. [Google Scholar] [CrossRef]
- Hofmann, R. Low-frequency line temperatures of the CMB. Ann. Phys. 2009, 18, 634. [Google Scholar] [CrossRef]
- Herbst, U. The Deconfining Phase of SU(2) Yang-Mills Thermodynamics. arXiv 2005, arXiv:hep-th/0506004. [Google Scholar]
- Kraan, T.C.; van Baal, P. Exact T duality between calorons and Taub - NUT spaces. Phys. Lett. B 1998, 428, 268–276. [Google Scholar] [CrossRef]
- Kraan, T.C.; van Baal, P. Periodic instantons with nontrivial holonomy. Nucl. Phys. B 1998, 533, 627–659. [Google Scholar] [CrossRef]
- Kraan, T.C.; van Baal, P. Monopole constituents inside SU(n) calorons. Phys. Lett. B 1998, 435, 389–395. [Google Scholar] [CrossRef]
- Hofmann, R.; Kaviani, D. The quantum of action and finiteness of radiative corrections: Deconfining SU(2) Yang-Mills thermodynamics. Quant. Matt. 2012, 1, 41–52. [Google Scholar] [CrossRef]
- Rabinowitch, A.S. On a new class of progressive waves in Yang–Mills fields with SU(2) symmetry. Nucl. Phys. B 2024, 1001, 116505. [Google Scholar] [CrossRef]
- Seiler, E. Some more remarks on the Witten–Veneziano formula for the η’ mass. Phys. Lett. B 2002, 525, 355–359. [Google Scholar] [CrossRef]
- Azakov, S.; Joos, H.; Wipf, A. Witten–Veneziano relation for the Schwinger model. Phys. Lett. B 2000, 479, 245–248. [Google Scholar] [CrossRef]
- Hahn, S.; Hofmann, R. Exact determination of asymptotic CMB temperature-redshift relation. Mod. Phys. Lett. A 2018, 2016, 1850029. [Google Scholar] [CrossRef]
- Frieman, J.A.; Hill, C.T.; Stebbins, A.; Waga, I. Cosmology with ultralight pseudo Nambu-Goldstone bosons. Phys. Rev. Lett. 1995, 75, 2077–2080. [Google Scholar] [CrossRef] [PubMed]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% Determination of The Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Riess, A.G.; Anand, G.S.; Yuan, W.; Casertano, S.; Dolphin, A.; Macri, L.M.; Breuval, L.; Scolnic, D.; Perrin, M.; Anderson, I.R. JWST Observations Reject Unrecognized Crowding of Cepheid Photometry as an Explanation for the Hubble Tension at 8σ Confidence. Astrophys. J. Lett. 2024, 962, L17. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Breuval, L.; Brink, T.G.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team. arXiv 2021, arXiv:2112.04510. [Google Scholar] [CrossRef]
- Hofmann, R. SU(2) Yang-Mills Theory: Waves, Particles, and Quantum Thermodynamics. Entropy 2016, 18, 310. [Google Scholar] [CrossRef]
- Einstein, A. Quantentheorie des einatomigen idealen Gases—Zweite Abhandlung. In Sitzungsberichte der Preussischen Akademie der Wissenschaften; Wiley: Hoboken, NJ, USA, 1925; p. 3. [Google Scholar]
- Matos, T.; Guzman, F.S. Scalar fields as dark matter in spiral galaxies. Class. Quant. Grav. 2000, 17, L9–L16. [Google Scholar] [CrossRef]
- D’Elia, M.; Di Giacomo, A.; Meggiolaro, E. Gauge invariant field strength correlators in pure Yang-Mills and full QCD at finite temperature. Phys. Rev. D 2003, 67, 114504. [Google Scholar] [CrossRef]
- Vicari, E.; Panagopoulos, H. θ dependence of SU(N) gauge theories in the presence of a topological term. Phys. Rep. 2009, 470, 93–150. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofmann, R.; Meinert, J.; Antonov, D. Axion Mass and the Ground State of Deconfining SU(2) Yang–Mills Thermodynamics. Astronomy 2024, 3, 319-333. https://doi.org/10.3390/astronomy3040020
Hofmann R, Meinert J, Antonov D. Axion Mass and the Ground State of Deconfining SU(2) Yang–Mills Thermodynamics. Astronomy. 2024; 3(4):319-333. https://doi.org/10.3390/astronomy3040020
Chicago/Turabian StyleHofmann, Ralf, Janning Meinert, and Dmitry Antonov. 2024. "Axion Mass and the Ground State of Deconfining SU(2) Yang–Mills Thermodynamics" Astronomy 3, no. 4: 319-333. https://doi.org/10.3390/astronomy3040020
APA StyleHofmann, R., Meinert, J., & Antonov, D. (2024). Axion Mass and the Ground State of Deconfining SU(2) Yang–Mills Thermodynamics. Astronomy, 3(4), 319-333. https://doi.org/10.3390/astronomy3040020






