An Investigation of the Entropy Associated with a Collapsing Molecular Cloud

Abstract

The investigation of entropy variation during the star formation process within collapsing molecular clouds represents a significant field of inquiry in astrophysics. As the cloud contracts, the presence of gaseous components contributes to an increase in entropy; however, the degree of this entropy change is contingent upon the spatial constraints imposed on the gases. In this research endeavor, I perform a comprehensive analysis of entropy dynamics on a microcosmic level within the contracting cloud, adhering to the tenets of the second law of thermodynamics. The initial focus centers on a turbulent cloud consisting of N particles, each with a mass of M, which succumbs to gravitational forces. It becomes evident that for the collapse to transpire, the gravitational energy must surpass the opposing pressure forces, resulting in the swift movement of particles throughout the cloud and ultimately facilitating a shift in entropy.

1. Introduction

It has been stated by [1] that the arrow of time arises from the Universe being at some distance from equilibrium in a nation of low entropy. This implies that the Second Law of Thermodynamics tells us that the entropy of the Universe does now not minimize [2]. According to a paper by [2], a homogeneous Universe with an outstanding fluid expands adiabatically with constant entropy. It has additionally been inferred that the rate of change of entropy increases entropy for the duration of expansion and minimizes the entropy in the course of contraction [2,3,4]. As refs. [5,6] cited, black holes are the largest accumulations of entropy due to the fact they have the strongest gravity. Physically speaking, gravitational collapse leads to the greatest feasible quantity of disorder. In addition, refs. [7,8] have calculated the entropy inside the observable Universe. This has been observed by means of [7], which have introduced correct consequences and outlined the entropy of the cosmological horizon. But what about the entropy of the collapsing molecular cloud throughout the formation star? How can the entropy of small-scale constructions be calculated from the perspective of thermodynamic laws? This question is in need of a detailed analysis and of appreciation due to the fact the gravitation pressure of a star-forming core is much lower than that of black holes. Many studies have stated that the cooling time and entropy thresholds are a consequence of thermal instabilities that develop in hot gases when the ratio of crossing time to free-fall time is less than 10 [9,10,11].

The formation of massive compact (MC) structures seems to take place when the diffuse interstellar medium (ISM) undergoes significant compression due to various factors, such as supernovae explosions, magnetorotational instability, or gravitational instability, within the stellar and gaseous disks of galaxies [12].

Over the recent ten years, there have been significant advancements in our understanding of the initial stages of low-mass star formation through observations. The utilization of sensitive receivers on large radio telescopes like the JCMT and IRAM 30 m MRT has allowed us to detect young protostars during the early accretion phase, known as ‘Class 0’ objects. This breakthrough has also enabled us to explore the inner density structure of pre-collapse cores, which was previously unattainable. Class 0 objects exhibit strong dust continuum emissions at submillimeter wavelengths, minimal emissions below 10 microns, and display powerful jet-like outflows. Furthermore, we have directly observed evidence of gravitational infall in several of these objects [13].

How would gravity possibly increase entropy in the early collapse phase than the late one in the process of star formation is an other problem to be understood in support of the existing star formation theory. Do diffuse systems have a higher entropy than that of condensed systems, or vice versa? And, in fact, the entropy of the early Universe was lower than at present when I consider the whole Universe. Of course, there are some diffuse systems higher in entropy than some condensed systems [14], and vice versa. Here, ‘lower’ is a relative term. Considering the attractive nature of gravity, it has been claimed that a uniform state has much lower entropy than a much more dispersed state. The early Universe seems to have had a higher entropy than the present-day Universe, which after all is not a very hot, very uniform gas. But a moment’s thought shows that this is at best not obvious [14].

Turbulence in the interstellar medium of Milky Way-type galaxies can be attributed to accretion, assuming that the galaxies are accumulating mass at a similar pace to their star formation. This phenomenon is especially significant in the outer disks beyond the region where stars are actively forming. However, in dwarf galaxies, the accretion rate must surpass the rate of star formation by a significant margin in order to drive turbulence, indicating that other factors are likely to play a more prominent role in these smaller galaxies [15]. Turbulence serves a dual purpose, as it not only generates areas of increased density that trigger gravitational contraction or collapse but also counteracts the gravitational effects within these regions of higher density [16]. Compressible turbulence is a significant factor in shaping the structure of the interstellar medium within our Galaxy, and it is believed to have a crucial role in the formation of structures in the early Universe as well. The density probability distribution function (PDF) and the power spectrum of this compressible, supersonic turbulence are essential components in theories related to star formation [17].

The Second Law of Thermodynamics remains a perplexing puzzle in the field of physics. The progression of the Universe involves a rise in disorder, known as entropy, which cannot be derived from our current understanding of the fundamental laws of physics, nor can it be elucidated solely through statistical reasoning. Notably, the Second Law establishes a distinction between the flow of time in the past and future [18].

Entropy fluctuations are unstable in a thermal self-gravitating cloud due to its negative heat capacity. The negative heat capacity of a star is properly understood. As a star loses complete poIr by means of radiation, the contraction will increase the thermal velocities, equivalent to an growth in temperature, to maintain equilibrium with the increase in the absolute value of the potential energy. The entropy of a star decreases in conjunction with whole energy. More generally, if a phase of a cloud loses energy, then the temperature rises while the entropy decreases inside this contracting region. Conversely, the section of a cloud that gains energy expands with an ensuing reduction in temperature and an increase in entropy.

It has been discussed by [2] that the arrow of time arises from the Universe being far from equilibrium in a state of low entropy. The Second Law of Thermodynamics requires that the entropy of the Universe does not decrease. Hence, the Universe must have initially been in a state of very low entropy [2]. According to the past hypothesis by [3], entropy of the entire Universe was very low (compared to now) about 15 billion years ago.

At a large scale, the early Universe used to be very hot and very dense; as it expanded and cooled, it grew to be much less hot, and much less dense. Since entropy is a measure of phase/space volume, it has been suggested by [19] that one can associate entropy with an event horizon proportional to its area [19]. In addition, ref. [20] estimated the entropy increase in Hawking evaporation. However, my work focuses on a star-forming region named molecular cloud, which is different from the case of compact objects. It was described by [14] that the early Universe was at a local thermal equilibrium and was highly uniform, but it was not at a global thermal equilibrium because of the expansion of the Universe. The process of becoming non-uniform leads to an increase in entropy. The conversion of gravitational energy to internal energy and the emission of electromagnetic radiation result in the growth of entropy. However, the dominating entropy-increasing processes comprise the formation of black holes. However, this paper particularly deals with the entropy of a collapsing star-forming molecular cloud.

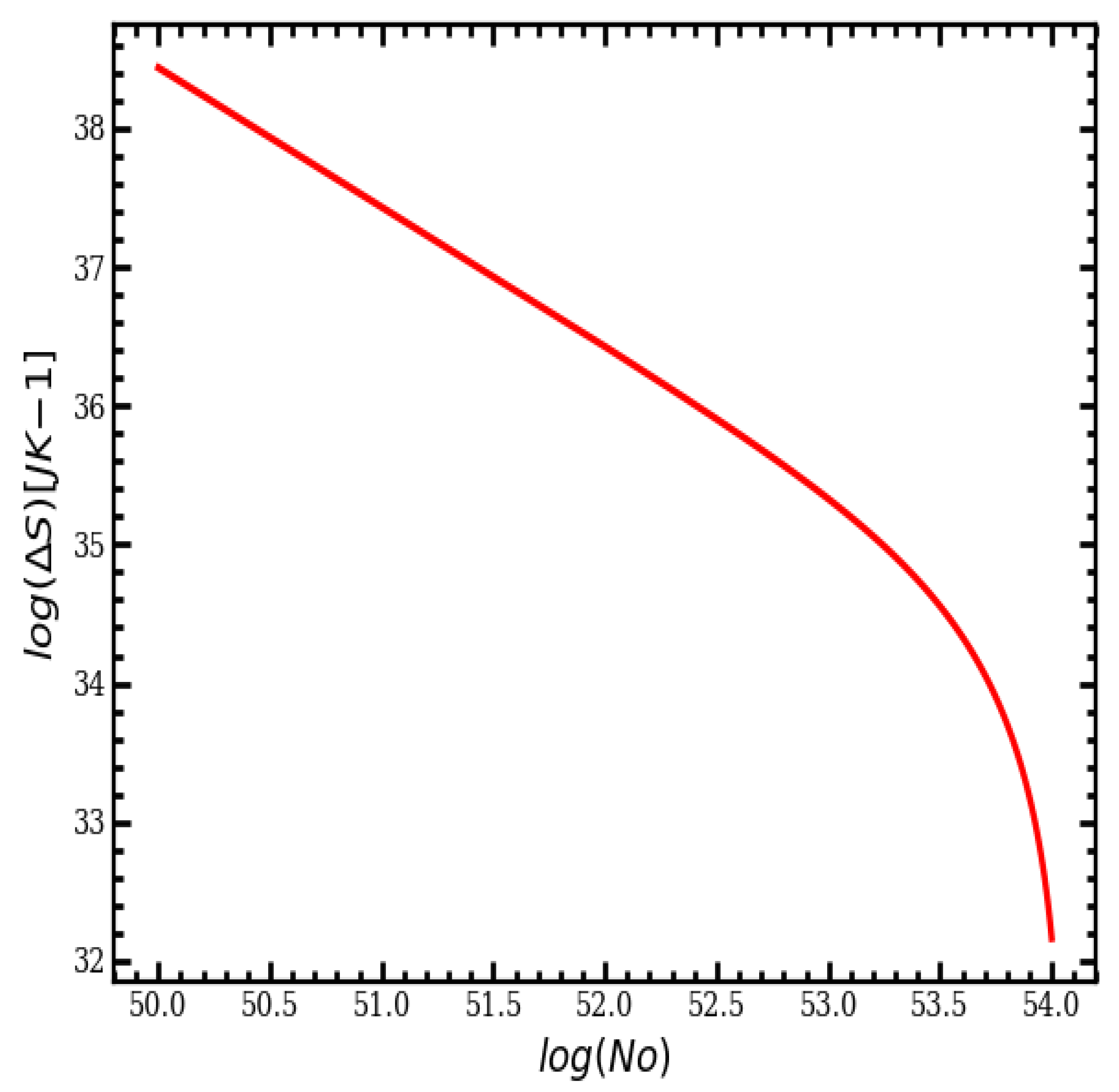
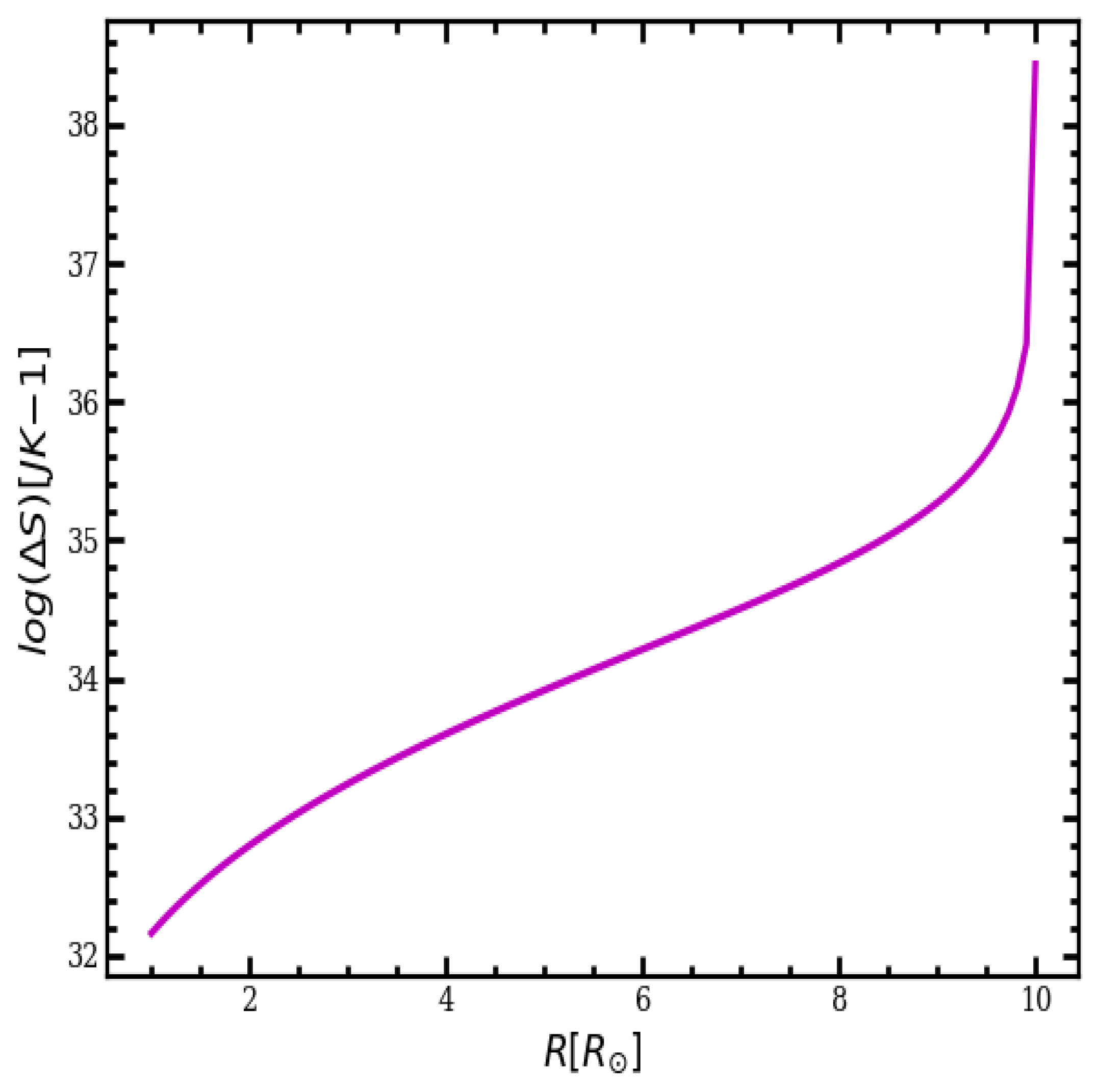
This research aims to examine the changes in entropy associated with a collapsing cloud by comparing its initial and final dimensions through mathematical modeling, which is subsequently followed by the derivation of numerical results based on theoretical principles. While the expansion of a self-gravitating gas results in an increase in both volume and entropy, the role of turbulence within a cloud is still uncertain. This study integrates isotropic turbulent velocity dispersion, the particle count, and the dimensions of a cloud to assess the variations in entropy within the system being analyzed.

2. Theoretical Background

Entropy is a thermodynamic measure that indicates the extent to which a system’s thermal energy cannot be transformed into mechanical work, as well as the level of disorder or randomness present within the system. In this context, I focus on macroscopic systems consisting of a large number of particles represented as N. To establish a foundation for this discussion, I will first reference the First Law of Thermodynamics, which is expressed as follows:

$$dE=dQ-PdV$$

(1)

The total variation in the internal energy of a system is expressed as the aggregate of the heat supplied to the system and the work performed on it. The Second Law of Thermodynamics is as follows:

$$dQ=TdS$$

(2)

It asserts that processes occur in a particular direction and that energy has both qualitative and quantitative attributes. By integrating Equations (1) and (2), I have obtained the following result:

$$dE=TdS-PdV$$

(3)

3. Mathematical Modeling

Given that both energy and entropy are subject to temporal variations, one can derive the time derivative of Equation (3) to obtain the following:

$${\displaystyle \frac{dE}{dt}}={\displaystyle \frac{TdS}{dt}}-{\displaystyle \frac{PdV}{dt}}$$

(4)

By reorganizing the equation and substituting dQ for TdS, as indicated in Equation (2), I arrive at the following expression:

$${\displaystyle \frac{dQ}{dt}}={\displaystyle \frac{dE}{dt}}+{\displaystyle \frac{PdV}{dt}}$$

(5)

$$E={\displaystyle \frac{3}{2}}{K}_{B}T={\displaystyle \frac{3M}{2}}{\sigma }^2$$

(6)

where $K_B$ is the Boltzmann constant. The methodology presented by [21] leads to the representation of energies and volume on a per-unit-mass basis. As a result, the energy contained within a turbulent cloud, which is defined by a one-dimensional velocity dispersion $\sigma$, is articulated as follows:

$$E={\displaystyle \frac{3M}{2}}{\sigma }^2$$

(7)

Pressure in a turbulent cloud with one-dimensional velocity dispersion $\sigma$ is

$$p={\displaystyle \frac{P}{M}}={\displaystyle \frac{1}{V}}{\sigma }^2=\rho {\sigma }^2/M$$

(8)

Thus,

$${\displaystyle \frac{dQ}{dt}}={\displaystyle \frac{3}{2}}{\displaystyle \frac{d{\sigma }^2}{dt}}+{\sigma }^2{\displaystyle \frac{3}{R}}{\displaystyle \frac{dR}{dt}},$$

(9)

In this context, R represents the radius of a cloud that possesses a mass M, as indicated by Equation (8). Consequently, Equation (8) provides the following information:

$${\displaystyle \frac{dQ}{dt}}=k\left({\sigma }^{-2}{\displaystyle \frac{d{\sigma }^2}{dt}}+{\displaystyle \frac{2}{R}}{\displaystyle \frac{dR}{dt}}\right)$$

(10)

This suggests the following:

$${\displaystyle \frac{dQ}{dt}}=2k{\displaystyle \frac{d}{dt}}ln\left(\sigma R\right),$$

(11)

In this context, k represents turbulent kinetic energy. The expression ln$\left(\sigma R\right)$ bears a resemblance to the entropy associated with thermodynamic systems or heat engines, as illustrated in the equation dQ/dt = TdS/dt, where kinetic energy is comparable to thermal temperature, T.

4. Results

Entropy of Turbulent-Gravitating Molecular Cloud

In this section, I aim to integrate the chemical potential ($\mu$) into Equation (3). The chemical potential ($\mu$) characterizes the influence of variations in number density. The component $\mu$ dN was omitted from the fundamental Equation (3). Consequently, I have added this term and restructured Equation (3) accordingly.

$$dE=TdS-PdV+\mu dN,$$

(12)

In this context, N represents the total number of particles contained within the volume V of a cloud. The chemical potential of a given phase increases as its internal energy, E, rises, while it concurrently decreases with a reduction in the phase’s entropy, S, at a constant temperature. This relationship indicates that the change in entropy diminishes as the chemical potential increases, as illustrated in Equation (12). Consequently, the disparity between the initial and final entropies becomes progressively smaller over time, particularly as the chemical potential continues to rise. By applying Equation (2) to Equation (12), taking the time derivative of both sides, and subsequently rearranging the terms, I arrive at the following result:

$${\displaystyle \frac{dQ}{dt}}={\displaystyle \frac{dE}{dt}}+{\displaystyle \frac{PdV}{dt}}-\mu {\displaystyle \frac{dN}{dt}}$$

(13)

Utilizing the foundational structure established previously and applying Equations (7) and (8) within Equation (13), I derive the following result:

$${\displaystyle \frac{dQ}{dt}}={\displaystyle \frac{3M}{2}}{\displaystyle \frac{d{\sigma }^2}{dt}}+{\sigma }^2{\displaystyle \frac{3}{R}}{\displaystyle \frac{dR}{dt}}-\mu {\displaystyle \frac{dN}{dt}}$$

(14)

which yields

$${\displaystyle \frac{dQ}{dt}}={\displaystyle \frac{3M}{2}}{\displaystyle \frac{d{\sigma }^2}{dt}}+{\sigma }^2{\displaystyle \frac{3}{R}}{\displaystyle \frac{dR}{dt}}-\mu {\displaystyle \frac{dN}{dt}}$$

(15)

The ideal gas equation of state, expressed as P = n$K_{B}T$, can also be represented in the form $\rho c_s^2=\rho {\displaystyle \frac{K_{B}T}{\mu m_H}}$, where n is defined as N/v. This leads to the conclusion that $\mu$ can be calculated using the formula $\mu ={\displaystyle \frac{\rho V}{N{m}_H}}$. In this context, $c_s$ denotes the speed of sound, while $m_H$ refers to the mass of a hydrogen atom.

$${\displaystyle \frac{dQ}{Mdt}}={\displaystyle \frac{3}{2}}{\displaystyle \frac{d{\sigma }^2}{dt}}+{\sigma }^2{\displaystyle \frac{3}{MR}}{\displaystyle \frac{dR}{dt}}-{\displaystyle \frac{\rho V}{N{m}_{H}M}}{\displaystyle \frac{dN}{dt}}$$

(16)

This results in

$${\displaystyle \frac{dQ}{Mdt}}={\displaystyle \frac{3}{2}}{\displaystyle \frac{d{\sigma }^2}{dt}}+{\sigma }^2{\displaystyle \frac{3}{MR}}{\displaystyle \frac{dR}{dt}}-{\displaystyle \frac{1}{N{m}_H}}{\displaystyle \frac{dN}{dt}}$$

(17)

This yields

$$dQ={\displaystyle \frac{3M}{2}}d{\sigma }^2+3{\sigma }^2{\displaystyle \frac{dR}{R}}-{\displaystyle \frac{M}{m_H}}{\displaystyle \frac{dN}{N}}$$

(18)

This leads to

$$TdS={\displaystyle \frac{3}{2}}Md{\sigma }^2+3{\sigma }^2{\displaystyle \frac{dR}{R}}-{\displaystyle \frac{M}{m_H}}{\displaystyle \frac{dN}{N}}$$

(19)

The chemical potential of a given phase increases as its internal energy, U, is elevated, whereas it concurrently diminishes when the phase’s entropy, S, declines at a constant temperature.

$${\int }_{So}^{S}TdS={\displaystyle \frac{3}{2}}{\int }_{\sigma }^{{\sigma }_f}M\sigma d\sigma +3{\sigma }^2{\int }_{R_o}^R{\displaystyle \frac{dR}{R}}-{\displaystyle \frac{M}{m_H}}{\int }_{N_o}^N{\displaystyle \frac{dN}{N}}$$

(20)

In this context, $m_H$ represents the mass of a hydrogen atom, $R_o$ denotes the initial radius of a cloud, while R indicates the final radius of a cloud. Additionally, $N_o$ refers to the initial total number of particles within the cloud, $N_f$ signifies the final total number of particles, and M is the mass of the initial cloud. The term $\sigma$ is used to describe the initial turbulent velocity dispersion, whereas ${\sigma }_f$ represents the final turbulent velocity dispersion. where $N_o$ and $N_f$ represent the initial and final total number of particles, respectively.

$$T(S-S_o)={\displaystyle \frac{3M}{2}}\left({\sigma }_f^2-{\sigma }^2\right)+3{\sigma }^{2}ln\left({\displaystyle \frac{R}{R_o}}\right)-{\displaystyle \frac{M}{m_H}}ln\left({\displaystyle \frac{N_f}{N_o}}\right)$$

(21)

$$\Delta S={\displaystyle \frac{3{\sigma }^2}{2T}}\left[M{\sigma }^{-2}\left({\sigma }_f^2-{\sigma }^2\right)+{\displaystyle \frac{2}{3}}ln\left({\displaystyle \frac{R}{R_o}}\right)-{\displaystyle \frac{{\sigma }^{-2}M}{m_H}}ln\left({\displaystyle \frac{N_f}{N_o}}\right)\right]$$

(22)

Applying the virial theorem for a cloud of mass M, contracting to a radius R, the temperature to which the matter becomes heated up to is $T=T_v={\displaystyle \frac{GM\mu m_H}{6K_{B}R}}$. Using this in Equation (22), we obtain

$$\Delta S={\displaystyle \frac{3{\sigma }^2}{2\frac{GM\mu m_H}{6K_{B}R}}}\left[M{\sigma }^{-2}\left({\sigma }_f^2-{\sigma }^2\right)+{\displaystyle \frac{2}{3}}ln\left({\displaystyle \frac{R}{R_o}}\right)-{\displaystyle \frac{{\sigma }^{-2}M}{m_H}}ln\left({\displaystyle \frac{N_f}{N_o}}\right)\right]$$

(23)

where G is the gravitational constant, $k_B$ is the Boltzmann constant, and ${\sigma }_{SB}$ is the Stefan–Boltzmann constant. One can write M = $N_o\mu m_H$; then, Equation (22) becomes

$$\Delta S={\displaystyle \frac{9K_B}{G{\left(\mu m_H\right)}^2}}{\displaystyle \frac{R}{N_o}}\left[M\left({\sigma }_f^2-{\sigma }^2\right)+{\displaystyle \frac{2{\sigma }^{-2}}{3}}ln\left({\displaystyle \frac{R}{R_o}}\right)-{\displaystyle \frac{M}{m_H}}ln\left({\displaystyle \frac{N_f}{N_o}}\right)\right]$$

(24)

5. Discussion

The information depicted in Figure 1, Figure 2 and Figure 3 underscores the crucial influence of the total particle count on both the initial and final states of a collapsing cloud being analyzed. Additionally, these figures reveal that a rise in the total number of particles is associated with a reduction in the change in entropy. Equation (24) indicates that the entropy change within a collapsing molecular cloud is directly proportional to the total number of particles present. This connection implies that the entropy linked to baryonic matter in the Universe has significantly diminished compared to earlier cosmic periods. As matter contracts and aggregates, this clumping process generates heat, which, despite raising the temperature, is released as radiation with very high entropy. Figure 4 shows that an increase in velocity dispersion results in a decrease in entropy change during the initial phase of collapse. Conversely, turbulence contributes to an increase in entropy change by promoting chaotic particle motion, as illustrated in Figure 5. Furthermore, Figure 6 highlights the relationship between the dispersion of initial and final turbulent velocities of gas, confirming that entropy is affected by the velocity of gas particles within a molecular cloud. This finding emphasizes that the motion of gas particles is predominantly chaotic rather than laminar. Lastly, Figure 7 and Figure 8 demonstrate that as size increases, so does entropy.

6. Conclusions

This study explores the relationship between entropy and the radius of a turbulent-gravitating system. The findings indicate that as a cloud with an initial radius of $R_o$ collapses to a much smaller radius $R\ll R_o$, the change in entropy increases depending on the total number of particles that a cloud and the core hold. The existence of sufficient space for particles to move allows the entropy to grow. The field of star formation presents a multitude of unresolved challenges, particularly concerning the entropy associated with star-forming molecular clouds. Previous research has often overlooked the chemical potential when addressing the entropy of these clouds. This paper investigated how dynamic factors, such as turbulence, size, chemical potential, and particle concentration, affect the entropy of collapsing molecular clouds. There remain significant gaps in our understanding of other dynamic processes that are essential for a thorough comprehension of entropy over time. The results indicate that entropy behavior is complex and significantly shaped by various dynamic processes and properties of a cloud, including the time scale of star formation. At the onset of collapse, entropy levels are elevated; however, as a central core develops, the molecules within that core exhibit a greater degree of order compared to the earlier collapse phase. This understanding contributes important insights to the theory of star formation. However, a further detailed examination is required to fully grasp the implications of entropy in both the formation and evolution of stars. Therefore, it is necessary to further examine the various dynamic factors that affect entropy. I suggest conducting a study on the role of entropy in the broader development of the Universe, particularly emphasizing its influence on the process of star formation.