Landau Tidal Damping and Major-Body Clustering in Solar and Extrasolar Subsystems
Abstract
1. Introduction
- In Appendix A, we describe few-body systems evolving by exchanging angular momentum and lowering their total mechanical energies.
- In Appendix B, we formulate a self-consistent calculation of the characteristic tidal dissipation time and the corresponding radial velocity fluctuations in such systems.
- In Appendix C, we analyze gravitational Landau damping of the tidal field in few-body systems, a unique mechanism responsible for settling of the bodies near mean-motion resonances over times comparable to —where they no longer exchange substantial amounts of angular momentum, and so they send the global tidal field to oblivion.
2. Dynamical Evolution of Interacting Keplerian Fluid Elements
3. Secular Evolution of Interacting Planets and Satellites
3.1. Quasistatic Equilibria
3.2. Papaloizou Approach
3.3. Free-Energy Variational Approach
4. Summary and Discussion
4.1. Summary
4.2. Global Mean-Motion Resonances
4.3. The Critical Orbit in Solar Subsystems
4.4. The Critical Orbit in Exoplanets
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GLD | Gravitational Landau Damping |
| LD | Landau Damping |
| LR | Laplace Resonance |
| MMR | Mean-Motion Resonance |
| MRI | Magnetorotational Instability |
Appendix A. Angular Momentum Transfer between Multiple Bodies
Appendix A.1. Three Bodies
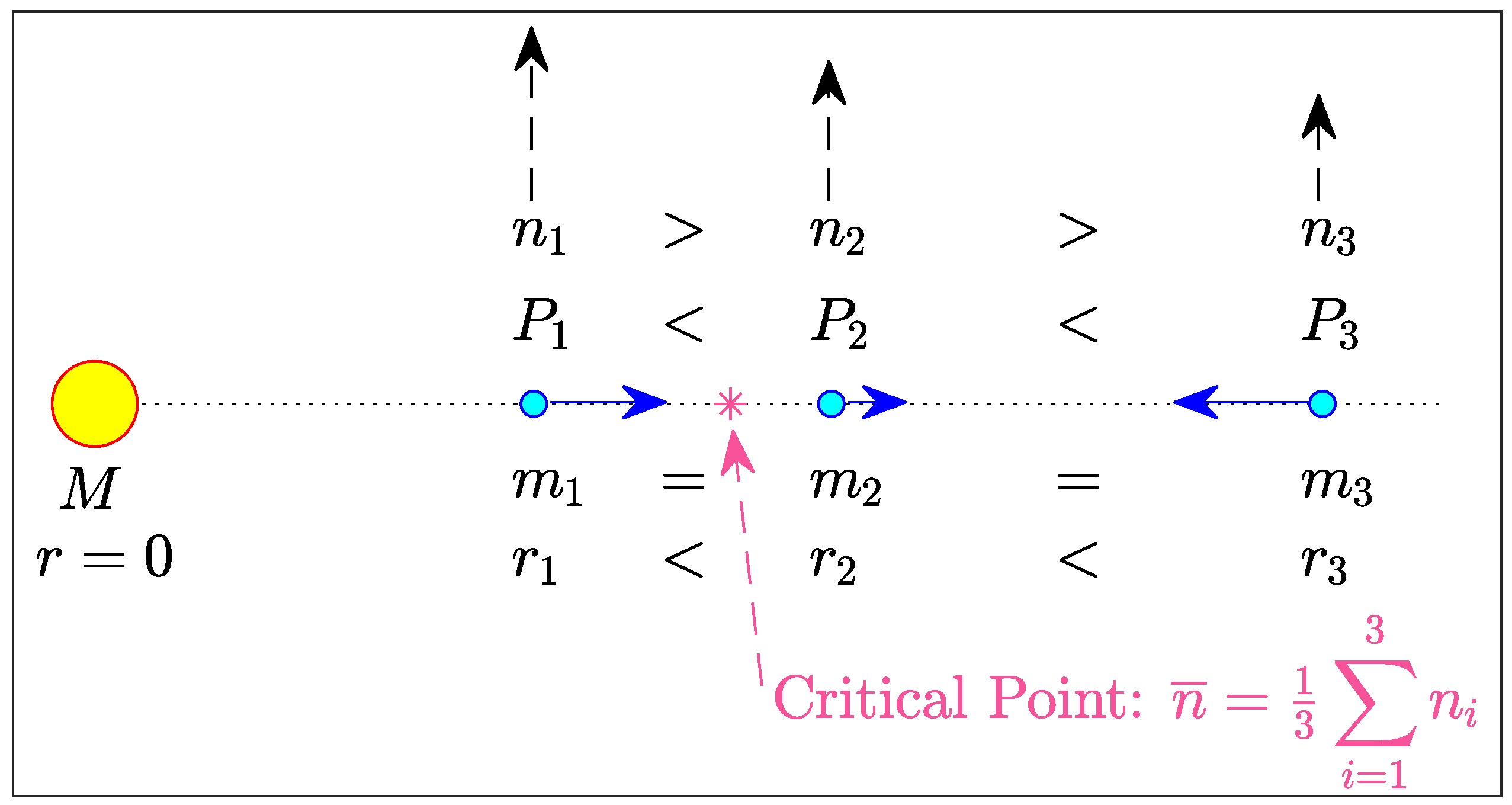
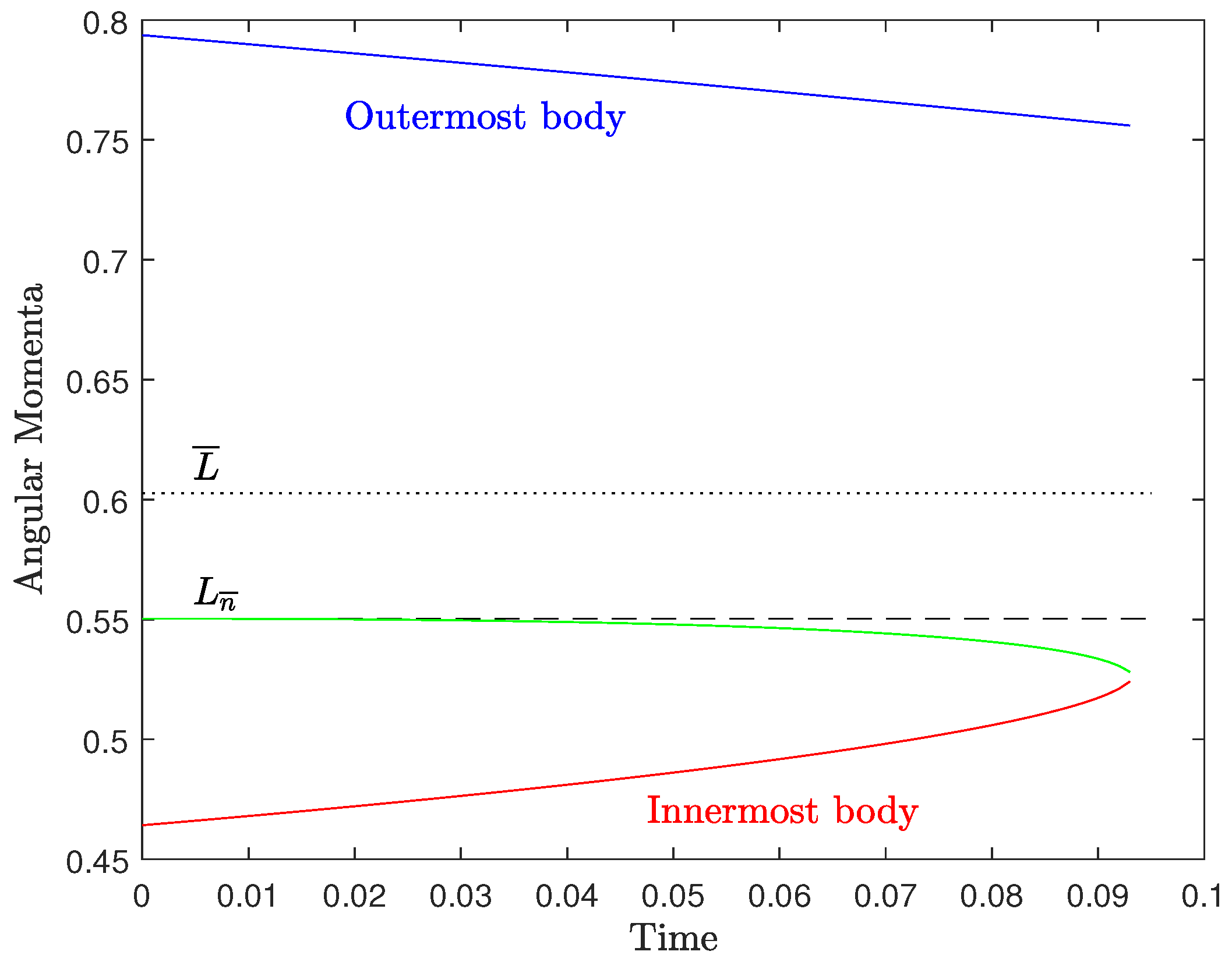
Appendix A.2. Four Bodies
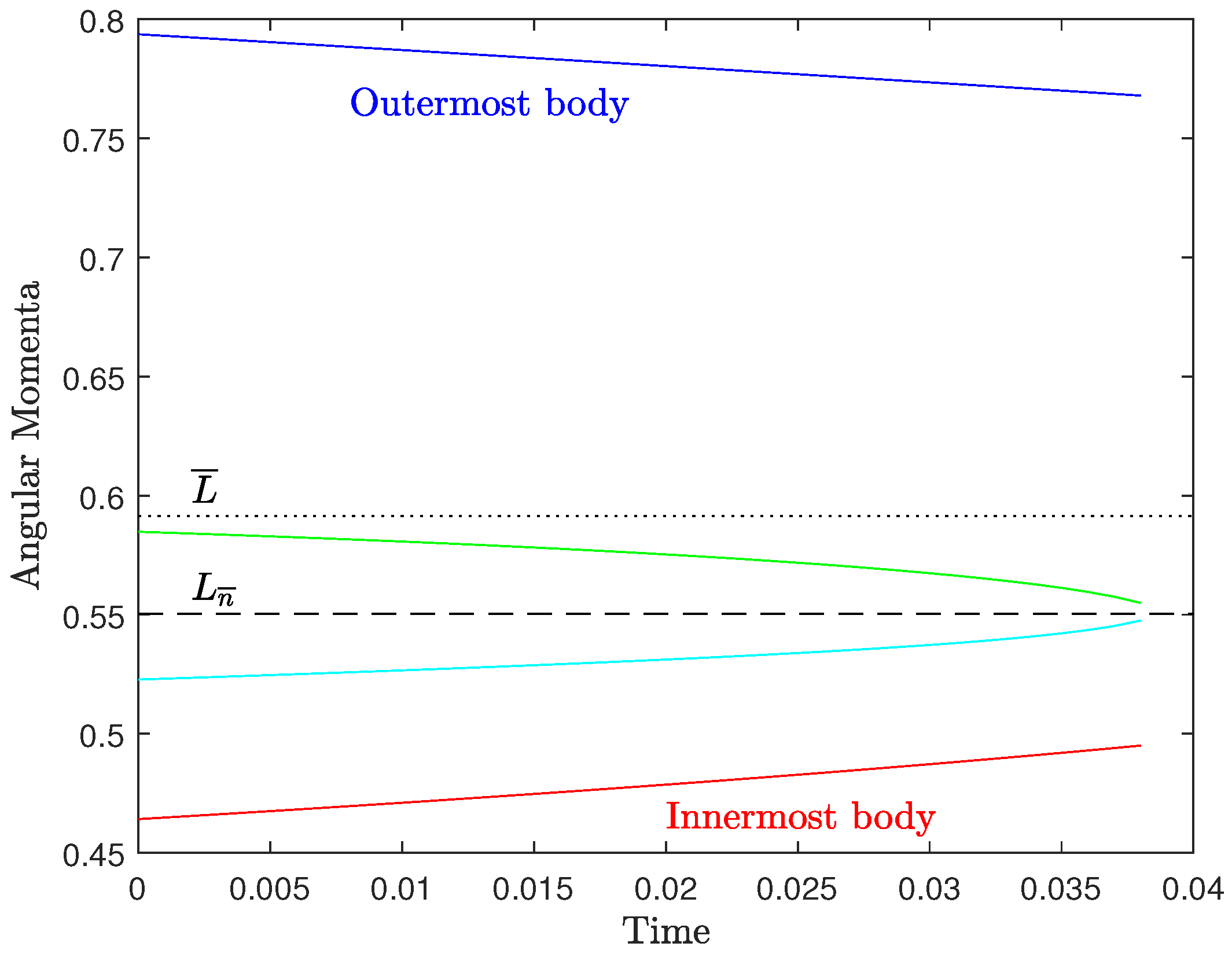
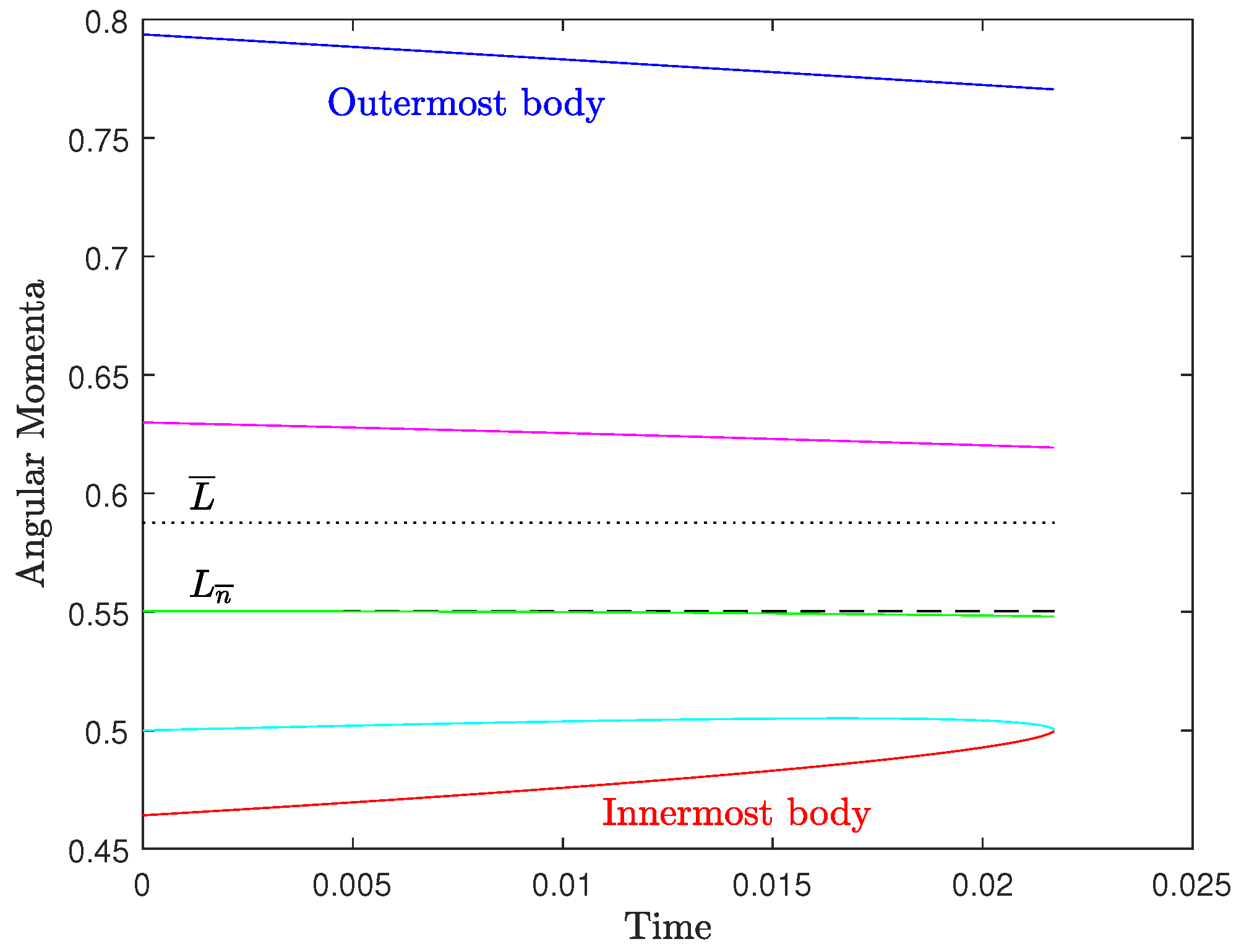
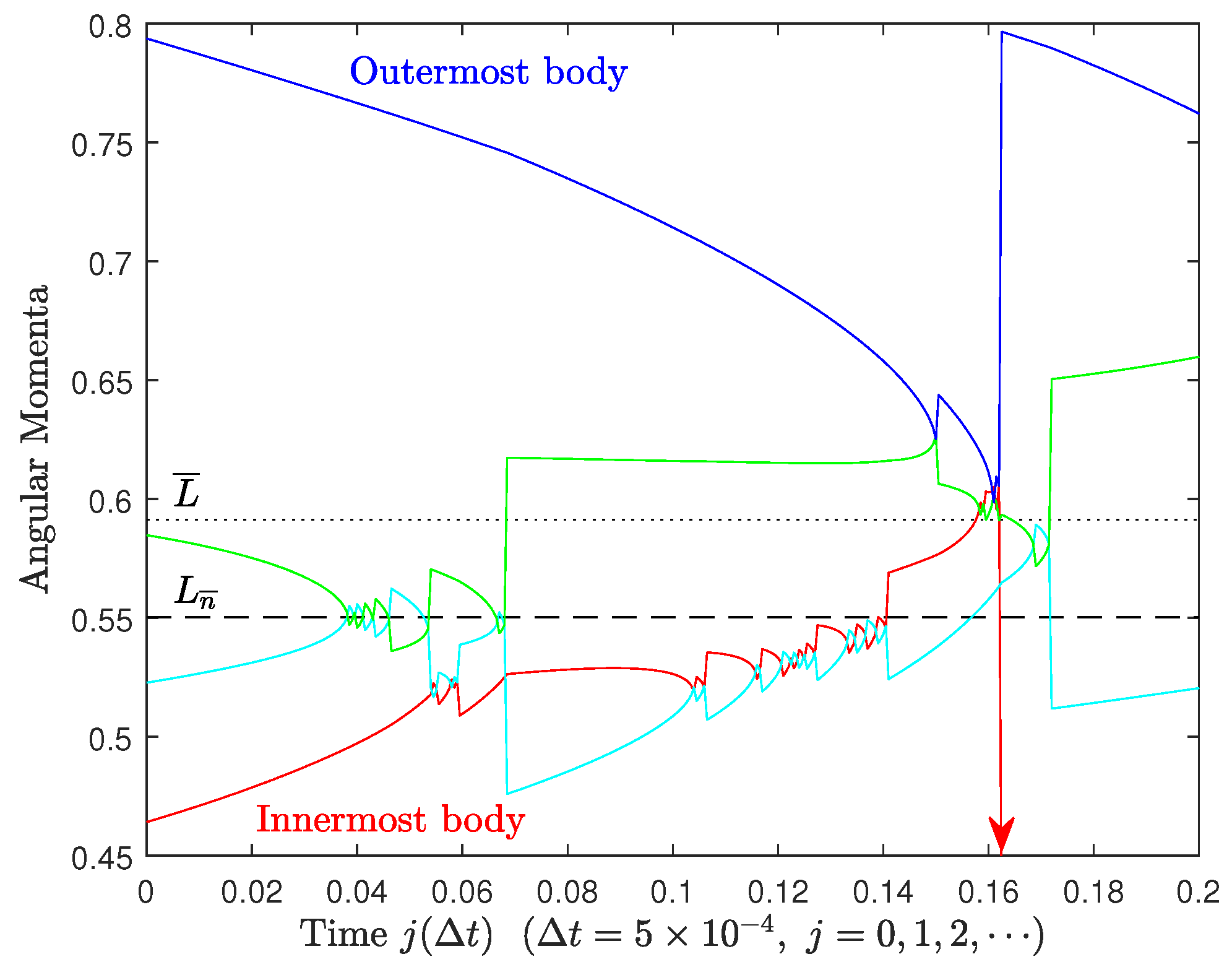
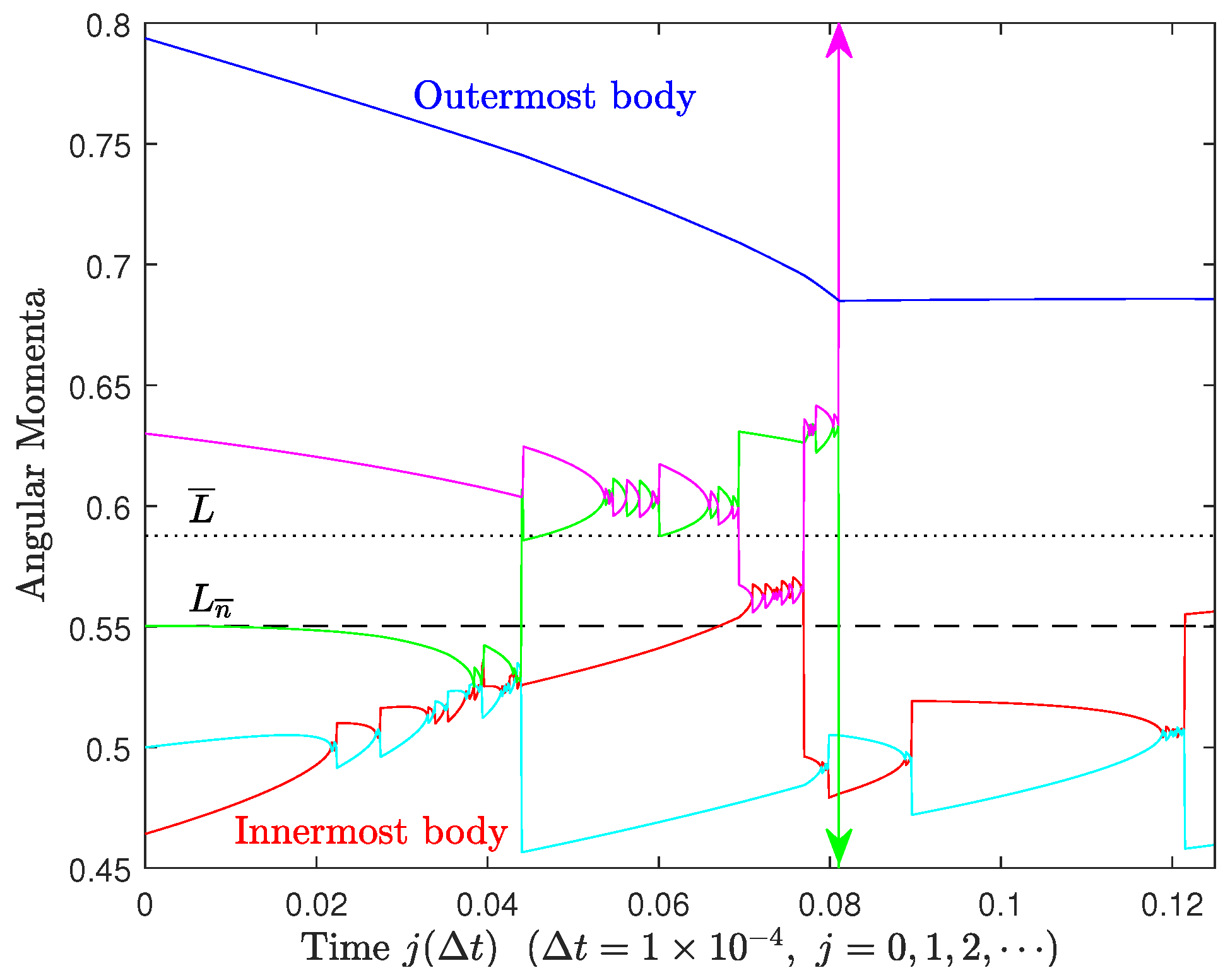
Appendix A.3. Five Bodies
Appendix A.4. Time Evolution of the Critical Orbit
Appendix B. Dissipation Timescale, Velocity Fluctuations, and Related Scales
Appendix B.1. Dissipation Timescale
Appendix B.2. Velocity Fluctuations
Appendix B.3. Integral Length
Appendix B.4. Damping Rate
Appendix B.5. Remarks on Protostellar Disks
Appendix C. Landau Damping of Tidal Waves near Mean-Motion Resonances
Appendix C.1. Damping Mechanism
Appendix C.2. Jeans Wavenumber and Hill Radius
Appendix C.3. Regimes of Jeans Instability and Gravitational Landau Damping
- (a)
- TEvS considered an ‘infinite’ self-gravitating collection of masses with uniform density , in which case the Hill frequency is a constant defined by the equation
- (b)
- This idealized system contains two species of particles with masses m and . To rewrite as a ‘global’ quantity, we imagine a spherical volume of radius r containing a mass M (smaller masses are neglected) with mean density , in which case we obtainor , which is the same as Equation (A40) for few-body systems. Now it becomes evident why we used the symbol here for the frequency (TEvS call it ), just as we did in Appendix C.2 above. The need for radius r to be taken around a mass M stems from the peculiarities of this infinite uniform self-gravitating model (any mass M can be a central mass in its vicinity, where the geometry then becomes spherically symmetric).
- (c)
- The linear stability analysis of this Jeans-like model also establishes the local ‘Debye length’ D, viz.,which TEvS call the Debye–Jeans radius, although they point out that this D is not related to screening (a minor oversight that neglects the role of the Hill radius in gravitating bodies). Here, is the thermal velocity of fast particles belonging to the m-species in three dimensions. In one dimension, the velocity dispersion will then beand then we find thatThus, the precise correspondence between parameters in the two models (Appendix C.2 and Appendix C.3) is formally established.
- (d)
- Collisions between heavy and light particles must be included in the TEvS model, otherwise the number of particles is not conserved. On the other hand, few-body systems are collisionless in the long run (some ejections of lower-mass bodies by the massive bodies are expected in early evolution); thus, for our application, we reduce the equations of TEvS to the limit of zero collision frequency ().
- (e)
- The TEvS dispersion relation in the limit of (their Equation (15)) readswhere k is the wavenumber andof a radial mode with frequency . The function is given bywhere, in our case, , with the asymptotic behavior
Appendix C.4. Bodies Interacting with Their Collective Tidal Field
- (a)
- It is certainly not the case that slightly faster-moving bodies will lose energy and slightly slower-moving bodies will gain energy from the wave, as is commonly quoted. This misconception invalidates the analogy with the famous example of a surfer riding an ocean wave. Whether a resonant body will gain or lose energy depends on the phase of the wave upon energy exchange. In other words, a radially oscillating body trapped within its Hill radius with radial velocity near the wave’s phase velocity will rob the wave of some of its energy only if its oscillation is in phase with the wave (see Appendix C.5 below).
- (b)
- (c)
- Considering only resonant bodies starting with velocities , if they gain energy, they will move away from resonance, whereas if they lose energy, they will move closer to the resonant velocity . The end result is that the latter bodies interact more efficiently with the wave and, on average, the field gains energy from bodies with . The opposite holds for bodies with for which the gainers are more efficient and the field is damped.
- (d)
- In a Maxwellian radial velocity distribution (even a sparse one with just 4–7 bodies), or in any other distribution with a roughly similar (bell-shaped) profile, there will be more bodies with ; thus, on average, the wave will have to push on most of them and it will be damped. It is for this reason that the negative gradient of the distribution function at determines the damping rate [60].
Appendix C.5. A Resonant Body Trapped in the Tidal Potential

Appendix C.6. Signatures of Tidal Fields Long Gone
References
- Lovis, C.; Ségransan, D.; Mayor, M.; Udry, S.; Benz, W.; Bertaux, J.L.; Bouchy, F.; Correia, A.C.M.; Laskar, J.; Curto, G.L.; et al. The HARPS search for southern extra-solar planets XXVIII. Astron. Astrophys. 2011, 528, A112. [Google Scholar] [CrossRef]
- Shallue, C.J.; Vanderburg, A. Identifying exoplanets with deep learning: A five-planet resonant chain around Kepler-80 and an eighth planet around Kepler-90. Astron. J. 2018, 155, 94. [Google Scholar] [CrossRef]
- Delrez, L.; Gillon, M.; Triaud, A.H.; Demory, B.O.; de Wit, J.; Ingalls, J.G.; Agol, E.; Bolmont, E.; Burdanov, A.; Burgasser, A.J.; et al. Early 2017 observations of TRAPPIST-1 with Spitzer. Mon. Not. R. Astron. Soc. 2018, 475, 3577. [Google Scholar] [CrossRef]
- Grimm, S.L.; Demory, B.O.; Gillon, M.; Dorn, C.; Agol, E.; Burdanov, A.; Delrez, L.; Sestovic, M.; Triaud, A.H.; Turbet, M. The nature of the TRAPPIST-1 exoplanets. Astron. Astrophys. 2018, 613, A68. [Google Scholar] [CrossRef]
- Bonfanti, A.; Gillon, M. MCMCI: A code to fully characterise an exoplanetary system. Astron. Astrophys. 2020, 635, A6. [Google Scholar] [CrossRef]
- Johnson, M.C.; Endl, M.; Cochran, W.D.; Meschiari, S.; Robertson, P.; MacQueen, P.J.; Brugamyer, E.J.; Caldwell, C.; Hatzes, A.P.; Ramírez, I.; et al. A 12-year activity cycle for the nearby planet host star HD 219134. Astrophys. J. 2016, 821, 74. [Google Scholar] [CrossRef]
- Vogt, S.S.; Burt, J.; Meschiari, S.; Butler, R.P.; Henry, G.W.; Wang, S.; Holden, B.; Gapp, C.; Hanson, R.; Arriagada, P.; et al. Six planets orbiting HD 219134. Astrophys. J. 2015, 814, 12. [Google Scholar] [CrossRef]
- Christiansen, J.L.; Crossfield, I.J.; Barentsen, G.; Lintott, C.J.; Barclay, T.; Simmons, B.D.; Petigura, E.; Schlieder, J.E.; Dressing, C.D.; Vanderburg, A.; et al. The K2-138 system: A near-resonant chain of five sub-Neptune planets discovered by citizen scientists. Astron. J. 2018, 155, 57. [Google Scholar] [CrossRef]
- Lopez, T.A.; Barros, S.C.C.; Santerne, A.; Deleuil, M.; Adibekyan, V.; Almenara, J.M.; Armstrong, D.J.; Brugger, B.; Barrado, D.; Bayliss, D.; et al. Exoplanet characterisation in the longest known resonant chain: The K2-138 system seen by HARPS. Astron. Astrophys. 2019, 631, A90. [Google Scholar] [CrossRef]
- Lissauer, J.J.; Ragozzine, D.; Fabrycky, D.C.; Steffen, J.H.; Ford, E.B.; Jenkins, J.M.; Shporer, A.; Holman, M.J.; Rowe, J.F.; Quintana, E.V.; et al. Architecture and dynamics of Kepler’s candidate multiple transiting planet systems. Astrophys. J. Suppl. Ser. 2011, 197, 8. [Google Scholar] [CrossRef]
- Mills, S.M.; Fabrycky, D.C.; Migaszewski, C.; Ford, E.B.; Petigura, E.; Isaacson, H. A resonant chain of four transiting, sub-Neptune planets. Nature 2016, 533, 509. [Google Scholar] [CrossRef] [PubMed]
- Millholland, S.; Laughlin, G.; Teske, J.; Butler, R.P.; Burt, J.; Holden, B.; Vogt, S.; Crane, J.; Shectman, S.; Thompson, I. New constraints on Gliese 876—Exemplar of mean-motion resonance. Astron. J. 2018, 155, 106. [Google Scholar] [CrossRef]
- Rivera, E.J.; Laughlin, G.; Butler, R.P.; Vogt, S.S.; Haghighipour, N.; Meschiari, S. The Lick-Carnegie exoplanet survey: A Uranus-mass fourth planet for GJ 876 in an extrasolar Laplace configuration. Astrophys. J. 2010, 719, 890. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. Instability, turbulence, and enhanced transport in accretion disks. Rev. Mod. Phys. 1998, 70, 1. [Google Scholar] [CrossRef]
- Goldreich, P. An explanation of the frequent occurrence of commensurable mean motions in the solar system. Mon. Not. R. Astron. Soc. 1965, 130, 159. [Google Scholar] [CrossRef]
- Lynden-Bell, D.; Pringle, J.E. The evolution of viscous discs and the origin of the nebular variables. Mon. Not. R. Astron. Soc. 1974, 168, 603. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Gunn, J.E. On the nature of pulsars. I. Theory. Astrophys. J. 1969, 157, 1395. [Google Scholar] [CrossRef]
- Page, D.N.; Thorne, K.S. Disk-accretion onto a black hole. Time-averaged structure of accretion disk. Astrophys. J. 1974, 191, 499. [Google Scholar]
- Papaloizou, J.C.B. Tidal interactions in multi-planet systems. Celest. Mech. Dyn. Astr. 2011, 111, 83. [Google Scholar] [CrossRef]
- Trigger, S.A.; Ershkovich, A.I.; van Heijst, G.J.F.; Schram, P.P.J.M. Kinetic theory of Jeans instability. Phys. Rev. E 2004, 69, 066403. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Kazanas, D.; Shlosman, I.; Tohline, J.E. Phase-transition theory of instabilities. I. Second-harmonic instability and bifurcation points. Astrophys. J. 1995, 446, 472. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. A powerful local shear instability in weakly magnetized disks. I. Linear analysis. Astrophys. J. 1991, 376, 214. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Contopoulos, J.; Kazanas, D. Interchange method in incompressible magnetized Couette flow: Structural and magnetorotational instabilities. Astrophys. J. 1996, 462, 865. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Contopoulos, J.; Kazanas, D. Interchange method in compressible magnetized Couette flow: Magnetorotational and magnetoconvective instabilities. Astrophys. J. 2003, 586, 372. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000; pp. 147, 153. [Google Scholar]
- Binney, J.; Tremaine, S. Galactic Dynamics; Princeton University Press: Princeton, NJ, USA, 1987; pp. 347, 412, 437–439, 677. [Google Scholar]
- Chandrasekhar, S. Ellipsoidal Figures of Equilibrium; Yale University Press: New Haven, CT, USA, 1969; pp. 71, 124. [Google Scholar]
- Fabrycky, D.C.; Lissauer, J.J.; Ragozzine, D.; Rowe, J.F.; Steffen, J.H.; Agol, E.; Barclay, T.; Batalha, N.; Borucki, W.; Ciardi, D.R.; et al. Architecture of Kepler’s multi-transiting systems. II. New investigations with twice as many candidates. Astrophys. J. 2014, 790, 146. [Google Scholar] [CrossRef]
- Luque, R.; Osborn, H.P.; Leleu, A.; Pallé, E.; Bonfanti, A.; Barragán, O.; Wilson, T.G.; Broeg, C.; Cameron, A.C.; Lendl, M.; et al. A resonant sextuplet of sub-Neptunes transiting the bright star HD 110067. Nature 2023, 623, 932. [Google Scholar] [CrossRef]
- Morbidelli, A. Modern Celestial Mechanics; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Murray, C.D.; Dermott, S.F. Solar System Dynamics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Roy, A.E.; Ovenden, M.W. On the occurrence of commensurable mean motions in the solar system. Mon. Not. R. Astron. Soc. 1954, 114, 232. [Google Scholar] [CrossRef][Green Version]
- Wisdom, J. The resonance overlap criterion and the onset of stochastic behavior in the restricted three-body problem. Astrophys. J. 1980, 85, 1122. [Google Scholar] [CrossRef]
- Wisdom, J. Canonical solution of the two critical argument problem. Celest. Mech. 1986, 38, 175. [Google Scholar] [CrossRef]
- Batygin, K.; Morbidelli, A. Dissipative divergence of resonant orbits. Astron. J. 2013, 145, 1. [Google Scholar] [CrossRef]
- Lithwick, Y.; Wu, Y. Resonant repulsion of Kepler planet pairs. Astrophys. J. Lett. 2012, 756, L11. [Google Scholar] [CrossRef]
- Landahl, M.T.; Mollo-Christensen, E. Turbulence and Random Processes in Fluid Mechanics; Cambridge University Press: Cambridge, UK, 1992; p. 10. [Google Scholar]
- George, W.K. Lectures in Turbulence for the 21st Century. 2013, pp. 64–66. Available online: http://www.turbulence-online.com/publication.html (accessed on 16 April 2024).
- Goldreich, P.; Soter, S. Q in the solar system. Icarus 1966, 5, 375. [Google Scholar] [CrossRef]
- MacDonald, G.J.F. Tidal friction. Rev. Geophys. 1964, 2, 467. [Google Scholar] [CrossRef]
- Munk, W.H.; MacDonald, G.J.F. The Rotation of the Earth; Cambridge University Press: Cambridge, UK, 1960. [Google Scholar]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity, 4th ed.; Dover: New York, NY, USA, 1927; p. 259. [Google Scholar]
- Wang, H.; George, W.K. The integral scale in homogeneous isotropic turbulence. J. Fluid Mech. 2002, 459, 429. [Google Scholar] [CrossRef]
- Mora, D.O.; Obligado, M. Estimating the integral length scale on turbulent flows from the zero crossings of the longitudinal velocity fluctuation. Exp. Fluids 2020, 61, 199. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Sykes, J.B.; Reid, W.H., Translators; Pergamon Press: Oxford, UK, 1987; pp. 31–33, 92–93. [Google Scholar]
- Haisch, K.E., Jr.; Lada, E.A.; Lada, C.J. Disk frequencies and lifetimes in young clusters. Astrophys. J. 2001, 553, L153. [Google Scholar] [CrossRef]
- Hillenbrand, L.A. Observational constraints on dust disk lifetimes: Implications for planet formation. In A Decade of Extrasolar Planets around Normal Stars, 19th ed.; STScI Symp Ser.; Livio, M., Sahu, K., Valenti, J., Eds.; Cambridge University Press: Cambridge, UK, 2008; p. 84. [Google Scholar]
- Wadhwa, M.; Russell, S.S. Timescales of accretion and differentiation in the early solar system: The meteoritic evidence. In Protostars and Planets IV; Mannings, V., Boss, A.P., Russell, S.S., Eds.; University of Arizona Press: Tucson, AZ, USA, 2000; p. 995. [Google Scholar]
- Landau, L. On the vibrations of the electronic plasma. J. Phys. 1946, 10, 25. (In English) [Google Scholar]
- Kandrup, H.E. Violent relaxation, phase mixing, and gravitational Landau damping. Astrophys. J. 1998, 500, 120. [Google Scholar] [CrossRef]
- Lynden-Bell, D. The stability and vibrations of a gas of stars. Mon. Not. R. Astron. Soc. 1962, 124, 279. [Google Scholar] [CrossRef]
- Vandervoort, P.O. On stationary oscillations of galaxies. Mon. Not. R. Astron. Soc. 2003, 339, 537. [Google Scholar] [CrossRef]
- Jeans, J.H. I. The stability of a spherical nebula. Phil. Trans. R. Soc. Lond. 1902, 199, 1. [Google Scholar]
- Chen, C.H.K.; Klein, K.G.; Howes, G.G. Evidence for electron Landau damping in space plasma turbulence. Nat. Commun. 2019, 10, 740. [Google Scholar] [CrossRef]
- Doveil, F.; Escande, D.F.; Macor, A. Experimental observation of nonlinear synchronization due to a single wave. Phys. Rev. Lett. 2005, 94, 085003. [Google Scholar] [CrossRef]
- Klimas, A.J.; Viñas, A.F.; Araneda, J.A. Simulation study of Landau damping near the persisting to arrested transition. J. Plasma Phys. 2017, 83, 905830405. [Google Scholar] [CrossRef]
- Herr, W. Introduction to Landau damping. In Proceedings of the CAS-CERN Accelerator School: Advanced Accelerator Physics; Herr, W., Ed.; CERN: Geneva, Switzerland, 2014; p. 377. [Google Scholar]
- Dawson, J. On Landau damping. Phys. Fluids 1961, 4, 869. [Google Scholar] [CrossRef]
- Ryutov, D.D. Landau damping: Half a century with the great discovery. Plasma Phys. Control. Fusion 1999, 41, A1. [Google Scholar] [CrossRef]
- Wesson, J. Landau damping. Phys. Plasmas 2015, 22, 022519. [Google Scholar] [CrossRef]
- Bellan, P.M. Fundamentals of Plasma Physics; Cambridge University Press: Cambridge, UK, 2006; p. 155. [Google Scholar]
- Bittencourt, J.A. Fundamentals of Plasma Physics; Springer: New York, NY, USA, 2004; p. 500. [Google Scholar]
- Fitzpatrick, R. Plasma Physics; CRC Press: Boca Raton, FL, USA, 2015; pp. 229–241. [Google Scholar]
- Stix, T.H. Waves in Plasmas; Springer: New York, NY, USA, 1992; pp. 169–193. [Google Scholar]
- Souami, D.; Cresson, J.; Biernacki, C.; Pierret, F. On the local and global properties of gravitational spheres of influence. Mon. Not. R. Astron. Soc. 2020, 496, 4287. [Google Scholar] [CrossRef]
- Makarov, V.V.; Efroimsky, M. Pathways of survival for exomoons and inner exoplanets. Astron. Astrophys. 2023, 672, A78. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Laycock, S.G.T.; Kazanas, D. The global 2:1 mean-motion resonance in HD 110067 is not vacant! Res. Notes AAS 2023, 7, 275. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Kazanas, D. A physical interpretation of the Titius-Bode rule and its connection to the closed orbits of Bertrand’s theorem. Res. Astron. Astrophys. 2017, 17, 129. [Google Scholar] [CrossRef]
- Laskar, J. On the spacing of planetary systems. Phys. Rev. Lett. 2000, 84, 3240. [Google Scholar] [CrossRef]
- Gerlach, E.; Haghighipour, N. Can GJ 876 host four planets in resonance? Celest. Mech. Dyn. Astr. 2012, 113, 35. [Google Scholar] [CrossRef]
- Martí, J.G.; Giuppone, C.A.; Beaugé, C. Dynamical analysis of the Gliese-876 Laplace resonance. Mon. Not. R. Astron. Soc. 2013, 433, 928. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christodoulou, D.M.; Kazanas, D. Landau Tidal Damping and Major-Body Clustering in Solar and Extrasolar Subsystems. Astronomy 2024, 3, 139-166. https://doi.org/10.3390/astronomy3020010
Christodoulou DM, Kazanas D. Landau Tidal Damping and Major-Body Clustering in Solar and Extrasolar Subsystems. Astronomy. 2024; 3(2):139-166. https://doi.org/10.3390/astronomy3020010
Chicago/Turabian StyleChristodoulou, Dimitris M., and Demosthenes Kazanas. 2024. "Landau Tidal Damping and Major-Body Clustering in Solar and Extrasolar Subsystems" Astronomy 3, no. 2: 139-166. https://doi.org/10.3390/astronomy3020010
APA StyleChristodoulou, D. M., & Kazanas, D. (2024). Landau Tidal Damping and Major-Body Clustering in Solar and Extrasolar Subsystems. Astronomy, 3(2), 139-166. https://doi.org/10.3390/astronomy3020010






