Frequency–Redshift Relation of the Cosmic Microwave Background
Abstract
:1. Introduction
2. Observational T-z Relation Extractions from a Prescribed v-z Relation
2.1. Absorber Clouds in the Line of Sight of a Quasar or a Bright Galaxy
2.2. The Thermal Sunyaev-Zel’dovich Effect
3. T-z Relation and v-z Relation in SU(2)CMB: Theoretical Basis
3.1. T-z Relation in SU(2)CMB
3.2. Anisotropic Photon Emission by Electrons or Isotropic and Homogeneous Thermalisation
3.3. Thermalisation-Dependent Mixing of Two SU(2) Gauge Theories
4. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
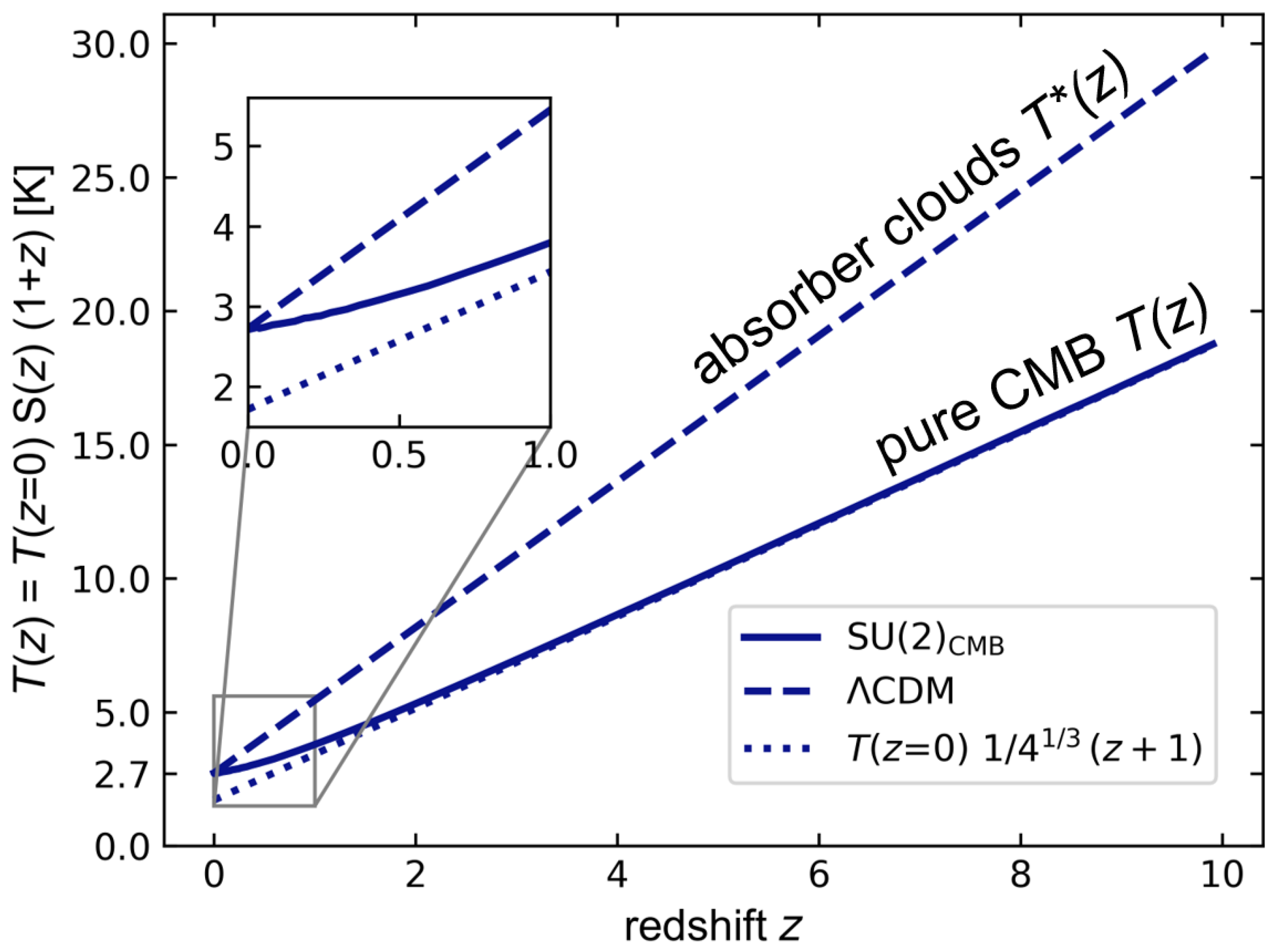
| 1 | One may think of the true CMB temperature (which would be lower in SU(2)) and participating CMB frequency being elevated by the same factor to and of a rotational excitation, respectively, by the incoherent mixing of a Cartan mode in SU(2) and a Cartan mode of SU(2) as the observer moves from empty space outside the cloud towards its interior. |
| 2 | According to a very good approximation, the spectral intensity of today’s CMB is given as [1]. If we assume a T-z relation of and a -z relation of with , then the Stefan–Boltzmann law would still have redshifted according to the T-z relation: . However, the maximum of the distribution converts to a maximum of the distribution . Thus, would no longer be a blackbody spectrum. |
| 3 | This admixture would arise due to phase tunnelling occurring when supercooling the deconfining phase into the preconfining phase in SU(2). |
| 4 | Charge carriers subject to SU(2) theories of larger Yang–Mills scales, represented by the charged leptons of the standard model and , are unstable due to weak decay and therefore do not qualify as material within the emitting surfaces of a blackbody cavity. |
References
- Mather, J.C.; Cheng, E.S.; Cottingham, D.A.; Eplee, R.E., Jr.; Fixsen, D.J.; Hewagama, T.; Isaacman, R.B.; Jensen, K.A.; Meyer, S.S.; Noerdlinger, P.D.; et al. Measurement of the Cosmic Microwave Background Spectrum by the COBE FIRAS Instrument. Astrophys. J. 1994, 420, 439. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Hofmann, R. SU(2) Yang-Mills Theory: Waves, Particles, and Quantum Thermodynamics. Entropy 2016, 18, 310. [Google Scholar] [CrossRef]
- Hahn, S.; Hofmann, R. Exact determination of asymptotic CMB temperature-redshift relation. Mod. Phys. Lett. A 2018, 2016, 1850029. [Google Scholar] [CrossRef]
- Hofmann, R.; Meinert, J.; Balaji, S.S. Cosmological Parameters from Planck Data in SU(2)CMB, Their Local LCDM Values, and the Modified Photon Boltzmann Equation. Ann. Phys. 2023, 535, 2200517. [Google Scholar] [CrossRef]
- Hahn, S.; Hofmann, R.; Kramer, D. SU(2)CMB and the cosmological model: Angular power spectra. Mon. Not. R. Astron. Soc. 2019, 482, 4290. [Google Scholar] [CrossRef]
- Szopa, M.; Hofmann, R. A Model for CMB anisotropies on large angular scales. J. Cosmol. Astropart. Phys. 2008, 3, 001. [Google Scholar] [CrossRef]
- Hofmann, R. The fate of statistical isotropy. Nat. Phys. 2013, 9, 686–689. [Google Scholar] [CrossRef]
- Hahn, S.; Hofmann, R. SU(2)CMB at high redshifts and the value of H0. Mon. Not. R. Astron. Soc. 2017, 469, 1233. [Google Scholar] [CrossRef]
- Meinert, J.; Hofmann, R. Axial Anomaly in Galaxies and the Dark Universe. Universe 2021, 7, 198. [Google Scholar] [CrossRef]
- Hofmann, R. Relic photon temperature versus redshift and the cosmic neutrino background. Ann. Phys. 2015, 527, 254–264. [Google Scholar] [CrossRef]
- Fixsen, D.J.; Kogut, A.; Levin, S.; Limon, M.; Lubin, P.; Mirel, P.; Seiffert, M.; Singal, J.; Wollack, E.; Villela, T.; et al. ARCADE 2 Measurement of the Extra-Galactic Sky Temperature at 3–90 GHz. Astrophys. J. 2011, 734, 5. [Google Scholar] [CrossRef]
- Dowell, J.; Taylor, G.B. The Radio Background below 100 MHz. Astrophys. J. Lett. 2018, 858, L9. [Google Scholar] [CrossRef]
- Hofmann, R. The Isolated Electron: De Broglie’s Hidden Thermodynamics, SU(2) Quantum Yang-Mills Theory, and a Strongly Perturbed BPS Monopole. Entropy 2017, 19, 575. [Google Scholar] [CrossRef]
- Hofmann, R.; Grandou, T. On Emergent Particles and Stable Neutral Plasma Balls in SU(2) Yang-Mills Thermodynamics. Universe 2022, 8, 117. [Google Scholar] [CrossRef]
- Hofmann, R. The Thermodynamics of Quantum Yang-Mills Theory: Theory and Applications; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2016. [Google Scholar] [CrossRef]
- Riechers, D.A.; Weiss, A.; Walter, F.; Carilli, C.L.; Cox, P.; Decarli, R.; Neri, R. Microwave background temperature at a redshift of 6.34 from H2O absorption. Nature 2022, 602, 58–62. [Google Scholar] [CrossRef]
- Songaila, A.; Cowie, L.L.; Vogt, S.; Keane, M.; Wolfei, A.M.; Hu, E.M.; Oren, A.L.; Tytleri, D.R.; Lanzetta, K.M. Measurement of the microwave background temperature at a redshift of 1.776. Nature 1994, 371, 43–45. [Google Scholar] [CrossRef]
- Ge, J.; Bechtold, J.; Black, J.H. A New Measurement of the Cosmic Microwave Background Radiation Temperature at z = 1.97. Astrophys. J. 1997, 474, 67–73. [Google Scholar] [CrossRef]
- Srianand, R.; Petitjean, P.; Ledoux, C. The cosmic microwave background radiation temperature at a redshift of 2.34. Nature 2000, 408, 931–935. [Google Scholar] [CrossRef] [PubMed]
- Molaro, P.; Levshakov, S.A.; Dessauges-Zavadsky, M.; D’Odorico, S. The cosmic microwave background radiation temperature 67 at zabs = 3.025 toward QSO 0347-3819. Astron. Astrophys. 2002, 381, L64–L67. [Google Scholar] [CrossRef]
- Noterdaeme, P.; Petitjean, P.; Srianand, R.; Ledoux, C.; López, S. The evolution of the cosmic microwave background temperature. Measurements of TCMB at high redshift from carbon monoxide excitation. Astron. Astrophys. 2011, 526, L7. [Google Scholar] [CrossRef]
- Noterdaeme, P.; Krogager, J.K.; Balashev, S.; Ge, J.; Gupta, N.; Krühler, T.; Ledoux, C.; Murphy, M.T.; Pâris, I.; Petitjean, P.; et al. Discovery of a Perseus-like cloud in the early Universe. H I-to-H2 transition, carbon monoxide and small dust grains at zabs≈ 2.53 towards the quasar J0000+0048. Astron. Astrophys. 2017, 597, A82. [Google Scholar] [CrossRef]
- Maeder, A. Scale-invariant Cosmology and CMB Temperatures as a Function of Redshifts. Astrophys. J. 2017, 847, 65. [Google Scholar] [CrossRef]
- Muller, S.; Beelen, A.; Black, J.H.; Curran, S.J.; Horellou, C.; Aalto, S.; Combes, F.; Guélin, M.; Henkel, C. A precise and accurate determination of the cosmic microwave background temperature at z = 0.89. Astron. Astrophys. 2013, 551, A109. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Sunyaev, R.A. The Interaction of Matter and Radiation in a Hot-Model Universe. Astrophys. Space Sci. 1969, 4, 301–316. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, Y.B. The Observations of Relic Radiation as a Test of the Nature of X-ray Radiation from the Clusters of Galaxies. Comm. Astrophys. Space Phys. 1972, 4, 173. [Google Scholar]
- Bahcall, J.N.; Wolf, R.A. Fine-Structure Transitions. Astrophys. J. 1968, 152, 701. [Google Scholar] [CrossRef]
- Roth, K.C.; Meyer, D.M.; Hawkins, I. Interstellar Cyanogen and the Temperature of the Cosmic Microwave Background Radiation. Astrophys. J. 1993, 413, L67. [Google Scholar] [CrossRef]
- Hurier, G.; Aghanim, N.; Douspis, M.; Pointecouteau, E. Measurement of the TCMB evolution from the Sunyaev-Zel’dovich effect. Astron. Astrophys. 2014, 561, A143. [Google Scholar] [CrossRef]
- Hofmann, R. Low-frequency line temperatures of the CMB. Ann. Phys. 2009, 18, 634. [Google Scholar] [CrossRef]
- Giacosa, F.; Hofmann, R. A Planck-scale axion and SU(2) Yang Mills dynamics: Present acceleration and the fate of the photon. Eur. Phys. J. C 2007, 50, 635–646. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Ultraviolet Behavior of Nonabelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343–1346. [Google Scholar] [CrossRef]
- Politzer, H.D. Reliable Perturbative Results for Strong Interactions? Phys. Rev. Lett. 1973, 30, 1346–1349. [Google Scholar] [CrossRef]
- Trombetti, T.; Burigana, C. Semi-analytical description of clumping factor and cosmic microwave background free–free distortions from reionization. Mon. Not. R. Astron. Soc. 2013, 437, 2507–2520. [Google Scholar] [CrossRef]
- Oh, S.P. Observational Signatures of the First Luminous Objects. Astrophys. J. 1999, 527, 16. [Google Scholar] [CrossRef]
- Fornengo, N.; Lineros, R.; Regis, M.; Taoso, M. Possibility of a Dark Matter Interpretation for the Excess in Isotropic Radio Emission Reported by ARCADE. Phys. Rev. Lett. 2011, 107, 271302. [Google Scholar] [CrossRef] [PubMed]
- Seiffert, M.; Fixsen, D.J.; Kogut, A.; Levin, S.M.; Limon, M.; Lubin, P.M.; Mirel, P.; Singal, J.; Villela, T.; Wollack, E.; et al. Interpretation of the arcade 2 absolute sky brightness measurement. Astrophys. J. 2011, 734, 6. [Google Scholar] [CrossRef]
- Baiesi, M.; Burigana, C.; Conti, L.; Falasco, G.; Maes, C.; Rondoni, L.; Trombetti, T. Possible nonequilibrium imprint in the cosmic background at low frequencies. Phys. Rev. Res. 2020, 2, 013210. [Google Scholar] [CrossRef]
- Biermann, P.L.; Nath, B.B.; Caramete, L.I.; Harms, B.C.; Stanev, T.; Tjus, J.B. Cosmic backgrounds due to the formation of the first generation of supermassive black holes. Mon. Not. R. Astron. Soc. 2014, 441, 1147–1156. [Google Scholar] [CrossRef]
- Bowman, J.; Rogers, A.; Monsalve, R.; Mozdzen, T.J.; Mahesh, N. An absorption profile centred at 78 megahertz in the sky-averaged spectrum. Nature 2018, 555, 67. [Google Scholar] [CrossRef]
- Barkana, R. Possible interaction between baryons and dark-matter particles revealed by the first stars. Nature 2018, 555, 71. [Google Scholar] [CrossRef] [PubMed]
- Fodor, G.; Rácz, I. What Does a Strongly Excited ’t Hooft–Polyakov Magnetic Monopole Do? Phys. Rev. Lett. 2004, 92, 151801. [Google Scholar] [CrossRef] [PubMed]
- Forgács, P.; Volkov, M.S. Resonant Excitations of the ’t Hooft–Polyakov Monopole. Phys. Rev. Lett. 2004, 92, 151802. [Google Scholar] [CrossRef] [PubMed]
- De Broglie, L. Recherches sur la théorie des Quanta. Ann. Phys. 1925, 10, 22–128. [Google Scholar] [CrossRef]
- De Broglie, L. The Thermodynamics of the Isolated Particle (or the Hidden Thermodynamics of Particles); Gauthier-Villars: Paris, France, 1964. [Google Scholar]
- Hofmann, R.; Meinert, J. Electroweak parameters from mixed SU(2) Yang-Mills Thermodynamics. Phys. Rev. D 2023. submitted. [Google Scholar]
- Schrödinger, E. Quantisierung als Eigenwertproblem. Ann. Phys. 1926, 384, 361–376. [Google Scholar] [CrossRef]
- Born, M. Zur Quantenmechanik der Stoßvorgänge. Z. Phys. 1926, 37, 863. [Google Scholar] [CrossRef]
- Meinert, J.; Morejón, L.; Sandrock, A.; Eichmann, B.; Kreidelmeyer, J.; Kampert, K.H. The impact of modified temperature redshift relation on UHECR propagation and cosmogenic neutrinos. arXiv 2023, arXiv:2309.08451. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofmann, R.; Meinert, J. Frequency–Redshift Relation of the Cosmic Microwave Background. Astronomy 2023, 2, 286-299. https://doi.org/10.3390/astronomy2040019
Hofmann R, Meinert J. Frequency–Redshift Relation of the Cosmic Microwave Background. Astronomy. 2023; 2(4):286-299. https://doi.org/10.3390/astronomy2040019
Chicago/Turabian StyleHofmann, Ralf, and Janning Meinert. 2023. "Frequency–Redshift Relation of the Cosmic Microwave Background" Astronomy 2, no. 4: 286-299. https://doi.org/10.3390/astronomy2040019
APA StyleHofmann, R., & Meinert, J. (2023). Frequency–Redshift Relation of the Cosmic Microwave Background. Astronomy, 2(4), 286-299. https://doi.org/10.3390/astronomy2040019






