Schwarzschild Black Holes in Extended Spacetime with Two Time Dimensions
Abstract
1. Introduction
2. 5D Schwarzschild Equations
3. Solution of 5D Equations
3.1. Existence of a Solution
3.2. Solution Classes
- (i)
- : In this case, it follows from that for all .
- (ii)
- : In this case, .
- (iii)
- : In this case, .
- (iv)
- : In this last case, and for all . With , Equation can be written as
3.3. Approximate Solution Close to
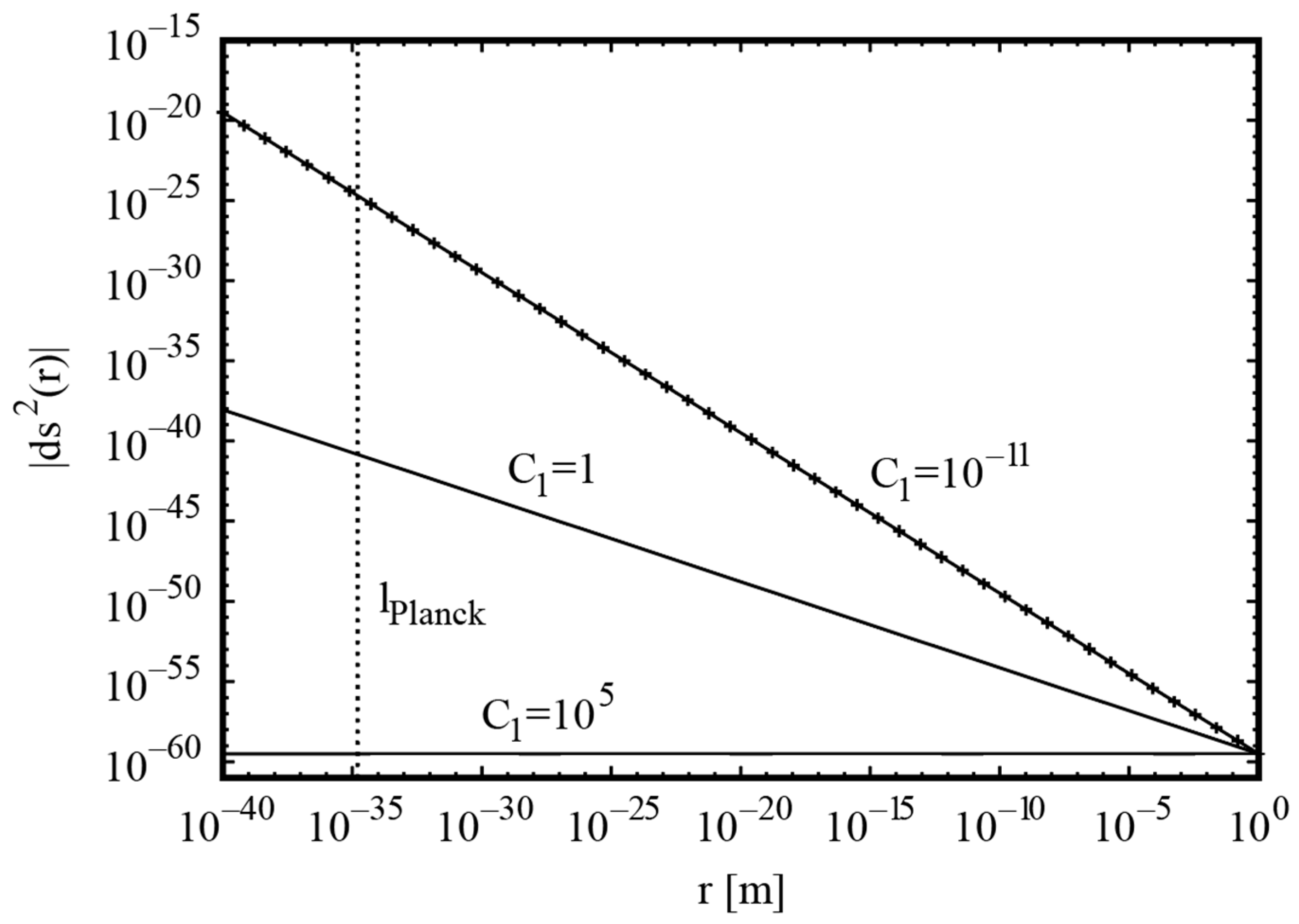
4. Physical Interpretation
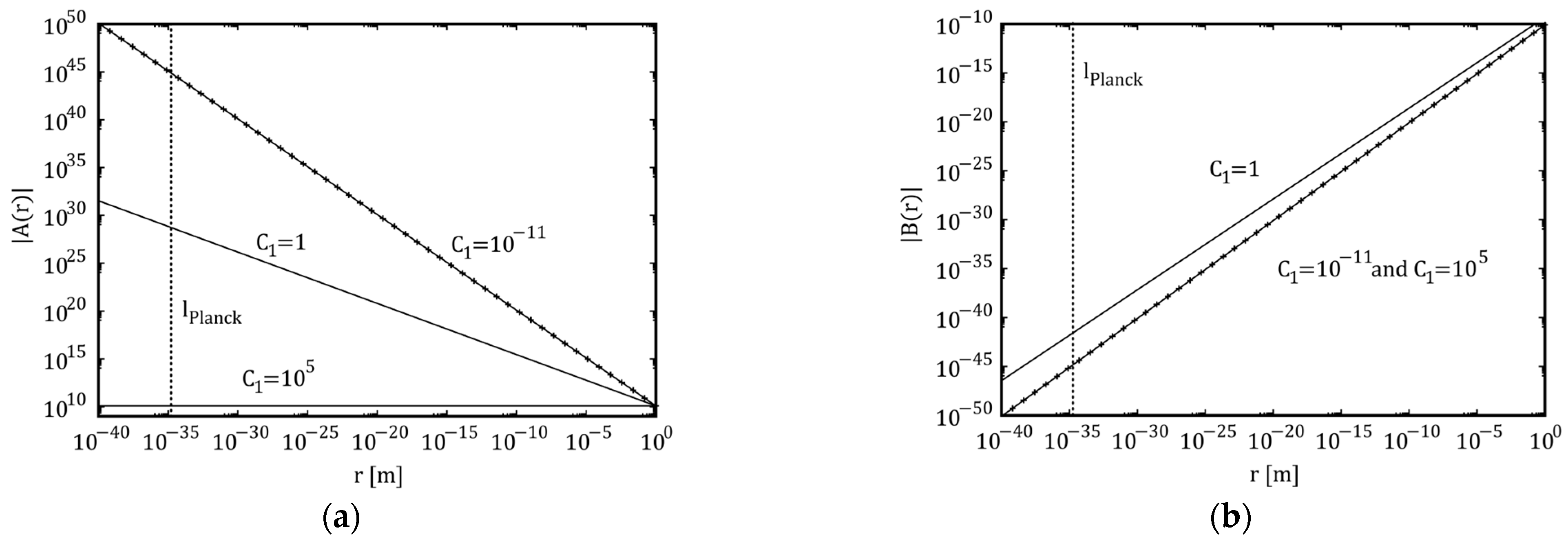
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Brügmann, B.; Ghez, A.M.; Greiner, J. Black holes. Proc. Natl. Acad. Sci. USA 2001, 98, 10525–10526. [Google Scholar] [CrossRef] [PubMed]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman and Company: San Francisco, CA, USA, 1970. [Google Scholar]
- Einstein, A. Relativity: The Special and General Theory; Henry Holt and Company: New York, NY, USA, 1920. [Google Scholar]
- Schwarzschild, K. On the Gravitational Field of a Mass Point According to Einstein’s Theory. Sitzungsber. Kgl. Preuß. Akad. Wiss. 1916, 7, 189–196. [Google Scholar]
- Kerr, R.P. Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics. Phys. Rev. Lett. 1963, 11, 237. [Google Scholar] [CrossRef]
- Newman, E.T.; Couch, E.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. Metric of a Rotating, Charged Mass. J. Math. Phys. 1965, 6, 918. [Google Scholar] [CrossRef]
- Reissner, H. Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie. Ann. Phys. 1916, 355, 106–120. [Google Scholar] [CrossRef]
- Weyl, H. Zur Gravitationstheorie. Ann. Phys. 1917, 359, 117–145. [Google Scholar] [CrossRef]
- Nordström, G. On the Energy of the Gravitation field in Einstein’s Theory. K. Ned. Akad. Wet. Proc. 1918, 20, 1238–1245. [Google Scholar]
- Jeffery, G.B. The field of an electron on Einstein’s theory of gravitation. Proc. R. Soc. A 1921, 99, 123. [Google Scholar]
- Penrose, R. Gravitational Collapse and Space-Time Singularities. Phys. Rev. Lett. 1965, 14, 57. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, 17. [Google Scholar]
- Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.-K.; Ball, D.; Baloković, M.; et al. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, 21. [Google Scholar]
- Gambini, R.; Pullin, J. Black Holes in Loop Quantum Gravity: The Complete Space-Time. Phys. Rev. Lett. 2008, 101, 1301. [Google Scholar] [CrossRef] [PubMed]
- Pullin, J.; Gambini, R. A First Course in Loop Quantum Gravity; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Zwiebach, B. A First Course in String Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Vaz, C. Black holes as gravitational atoms. J. Mod. Phys. 2014, D23, 1441002. [Google Scholar] [CrossRef]
- Corda, C. Black Hole Spectra from Vaz’s Quantum Gravitational Collapse. Fortschr. Phys. 2023, 71, 2300028. [Google Scholar] [CrossRef]
- Bars, I. Supersymmetry, p-brane duality, and hidden spacetime dimensions. Phys. Rev. D 1996, 54, 5203. [Google Scholar] [CrossRef]
- Bars, I.; Kounnas, C. Theories with Two Times. Phys. Lett. B 1997, 402, 25–32. [Google Scholar] [CrossRef]
- Bars, I.; Kounnas, C. String and particle with two times. Phys. Rev. D 1997, 56, 3664. [Google Scholar] [CrossRef]
- Tegmark, M. On the dimensionality of spacetime. Class. Quantum Gravity 1997, 14, L69. [Google Scholar] [CrossRef]
- Köhn, C. The Planck Length and the Constancy of the Speed of Light in Five Dimensional Spacetime Parametrized with Two Time Coordinates. J. High Energy Phys. Gravit. Cosmol. 2017, 3, 635–650. [Google Scholar] [CrossRef]
- Chen, X. Three Dimensional Time Theory: To Unify the Principles of Basic Quantum Physics and Relativity. arXiv 2005, arXiv:quant-ph/0510010. [Google Scholar]
- Köhn, C. A Solution to the Cosmological Constant Problem in Two Time Dimensions. J. High Energy Phys. Gravit. Cosmol. 2020, 6, 640–655. [Google Scholar] [CrossRef]
- Elsborg, J.; Köhn, C. Magnetic monopoles in two time dimensions. Int. J. Mod. Phys. A 2022, 37, 2250141. [Google Scholar] [CrossRef]
- Weinstein, S. Multiple Time Dimensions. arXiv 2008, arXiv:0812.3869. [Google Scholar]
- Craig, W.; Weinstein, S. On determinism and well-posedness in multiple time dimensions. Proc. R. Soc. A 2009, 465, 3023–3046. [Google Scholar] [CrossRef]
- Lindelöf, E. Sur l’application de la méthode des approximations successives aux équations différentielles ordinaires du premier ordre. C. R. Hebd. Séances Acad. Sci. 1894, 118, 454–457. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields, 3rd ed.; Pergamon Press: London, UK, 1971; Volume 2. [Google Scholar]
- Debono, I.; Smoot, G.F. General Relativity and Cosmology: Unsolved Questions and Future Directions. Universe 2016, 2, 23. [Google Scholar] [CrossRef]
- Lo, K.Y.; Shen, Z.-Q.; Zhao, J.-H.; Ho, P.T.P. Intrinsic Size of Sagittarius A*: 72 Schwarzschild Radii. Astrophys. J. 1998, 508, L61. [Google Scholar] [CrossRef]
| Solution Classes | |
|---|---|
| (i) | |
| (ii) | |
| (iii) | |
| (iv) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paiman, M.; Cornean, H.; Köhn, C. Schwarzschild Black Holes in Extended Spacetime with Two Time Dimensions. Astronomy 2023, 2, 269-285. https://doi.org/10.3390/astronomy2040018
Paiman M, Cornean H, Köhn C. Schwarzschild Black Holes in Extended Spacetime with Two Time Dimensions. Astronomy. 2023; 2(4):269-285. https://doi.org/10.3390/astronomy2040018
Chicago/Turabian StylePaiman, Mechid, Horia Cornean, and Christoph Köhn. 2023. "Schwarzschild Black Holes in Extended Spacetime with Two Time Dimensions" Astronomy 2, no. 4: 269-285. https://doi.org/10.3390/astronomy2040018
APA StylePaiman, M., Cornean, H., & Köhn, C. (2023). Schwarzschild Black Holes in Extended Spacetime with Two Time Dimensions. Astronomy, 2(4), 269-285. https://doi.org/10.3390/astronomy2040018