Physical Origin of the Dark Spot in the First Image of Supermassive Black Hole SgrA*
Abstract
1. Introduction
2. Basic Equations
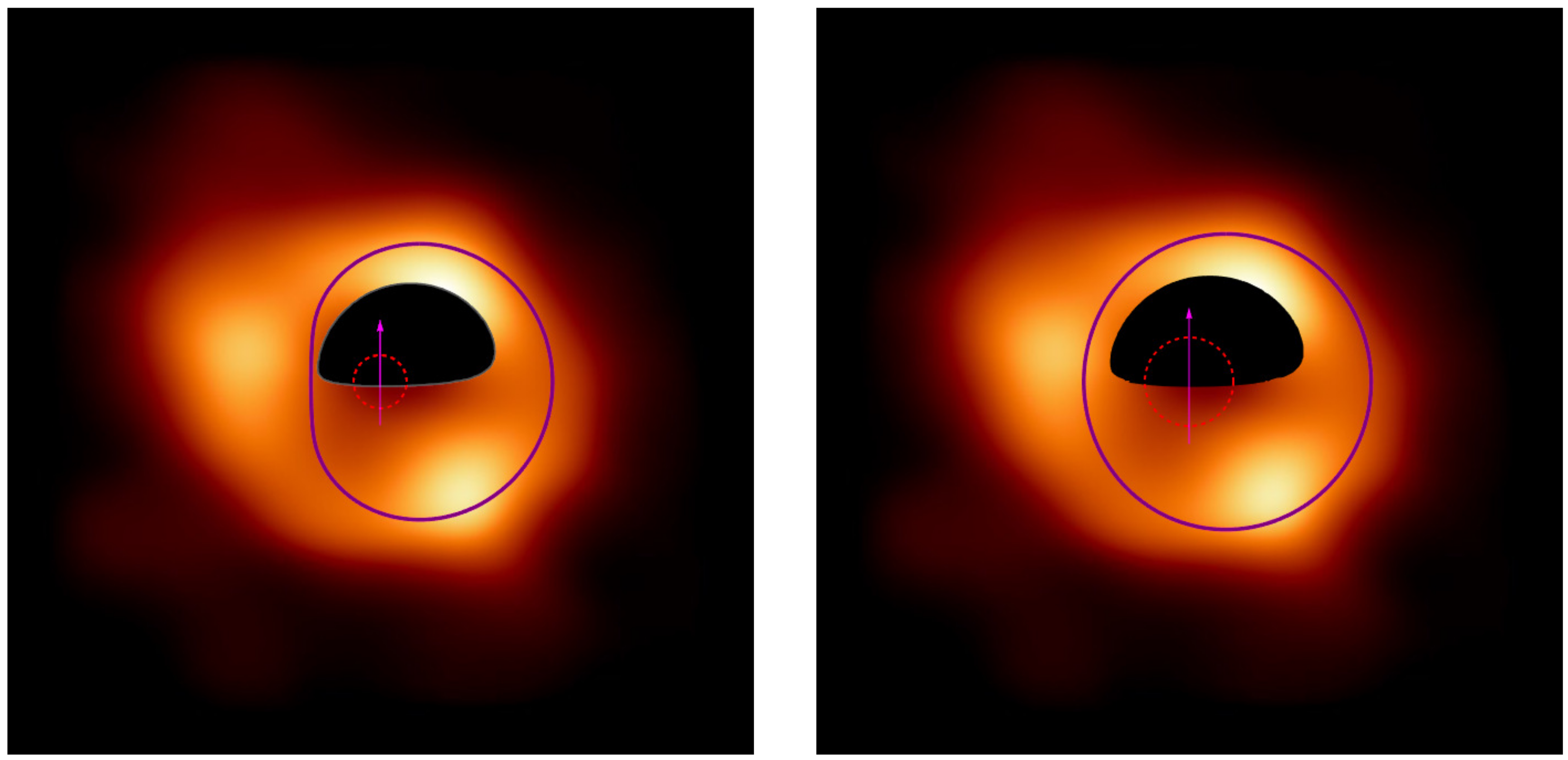
3. Physical Origin of the Dark Spot in the First Image of SgrA*
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. 2022, 930, L12. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. II. EHT and Multiwavelength Observations, Data Processing, and Calibration. Astrophys. J. 2022, 930, L13. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. III. Imaging of the Galactic Center Supermassive Black Hole. Astrophys. J. 2022, 930, L14. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. IV. Variability, Morphology, and Black Hole Mass. Astrophys. J. 2022, 930, L15. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. V. Testing Astrophysical Models of the Galactic Center Black Hole. Astrophys. J. 2022, 930, L16. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. Astrophys. J. 2022, 930, L17. [Google Scholar]
- Luminet, J.-P. Image of a spherical black hole with thin accretion disk. Astron. Astrophys. 1979, 75, 228–235. [Google Scholar]
- Bromley, B.C.; Chen, K.; Miller, W.A. Line emission from an accretion disk around a rotating black hole: Toward a measurement of frame dragging. Astrophys. J. 1997, 475, 57–64. [Google Scholar] [CrossRef]
- Falcke, H.; Melia, F.; Agol, E. Viewing the Shadow of the Black Hole at the Galactic Center. Astrophys. J. 2000, 528, L13–L16. [Google Scholar] [CrossRef]
- Luminet, J.-P. An illustrated history of black hole imaging: Personal recollections (1972–2002). arXiv 2019, arXiv:1902.11196. [Google Scholar]
- Bardeen, J.M. Black Holes; DeWitt, C., DeWitt, B.S., Eds.; Gordon and Breach Science Publishers: New York, NY, USA, 1973; pp. 215–239. [Google Scholar]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; The International Series of Monograph on Physics; Clarendon Press: Oxford, UK, 1983; Volume 69, Chapter 7. [Google Scholar]
- Dokuchaev, V.I.; Nazarova, N.O.; Smirnov, V.P. Event horizon silhouette: Implications to supermassive black holes in the galaxies M87 and Milky Way. Gen. Relativ. Gravit. 2019, 51, 81. [Google Scholar] [CrossRef]
- Dokuchaev, V.I. To see the invisible: Image of the event horizon within the black hole shadow. Int. J. Mod. Phys. D 2019, 28, 1941005. [Google Scholar] [CrossRef]
- Dokuchaev, V.I. Spin and mass of the nearest supermassive black hole. Gen. Relativ. Gravit. 2014, 46, 1832–1845. [Google Scholar] [CrossRef]
- Dokuchaev, V.I.; Nazarova, N.O. Gravitational lensing of a star by a rotating black hole. JETP Lett. 2017, 106, 637–642. [Google Scholar] [CrossRef][Green Version]
- Dokuchaev, V.I.; Nazarova, N.O. Star Motion around Rotating Black Hole. Available online: https://youtu.be/P6DneV0vk7U (accessed on 27 January 2018).
- Dokuchaev, V.I.; Nazarova, N.O. Silhouettes of invisible black holes. Phys. Usp. 2020, 63, 583–600. [Google Scholar] [CrossRef]
- Dokuchaev, V.I.; Nazarova, N.O. Event horizon image within black hole shadow. JETP 2019, 128, 578–585. [Google Scholar] [CrossRef]
- Dokuchaev, V.I.; Nazarova, N.O. Infall of the Star into Rotating Black Hole Viewed by a Distant Observer. Available online: https://youtu.be/fps-3frL0AM (accessed on 16 April 2018).
- Dokuchaev, V.I.; Nazarova, N.O. The Brightest Point in Accretion Disk and Black Hole Spin: Implication to the Image of Black Hole M87*. Universe 2019, 5, 183. [Google Scholar] [CrossRef]
- Blandford R., D.; Znajek R., L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astr. Soc. 1977, 179, 433. [Google Scholar] [CrossRef]
- McKinney, J.C.; Tchekhovskoy, A.; Blandford, R.D. General relativistic magnetohydrodynamic simulations of magnetically choked accretion flows around black holes. Mon. Not. R. Astr. Soc. 2012, 423, 3083. [Google Scholar] [CrossRef]
- Kerr, R.P. Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics. Phys. Rev. Lett. 1963, 11, 237–238. [Google Scholar] [CrossRef]
- Boyer, R.H.; Lindquist, R.W. Maximal Analytic Extension of the Kerr Metric. J. Math. Phys. 1967, 8, 265. [Google Scholar] [CrossRef]
- Carter, B. Global Structure of the Kerr Family of Gravitational Fields. Phys. Rev. 1968, 174, 1559–1571. [Google Scholar] [CrossRef]
- De Felice, F. Equatorial geodesic motion in the gravitational field of a rotating source. Nuovo Cimento B 1968, 57, 351–388. [Google Scholar] [CrossRef]
- Bardeen, J.M. Stability of Circular Orbits in Stationary, Axisymmetric Space-Times. Astrophys. J. 1970, 161, 103–109. [Google Scholar] [CrossRef]
- Bardeen, J.M. A Variational Principle for Rotating Stars in General Relativity. Astrophys. J. 1970, 162, 71–95. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347–370. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Gal’tsov, D.V. Particles and Fields in the Vicinity of Black Holes; Moscow Univ. Press: Moscow, Russia, 1986. (In Russian) [Google Scholar]
- Cunningham, C.T.; Bardeen, J.M. The Optical Appearance of a Star Orbiting an Extreme Kerr Black Hole. Astrophys. J. 1972, 173, L137–L142. [Google Scholar] [CrossRef]
- Cunningham, C.T.; Bardeen, J.M. The Optical Appearance of a Star Orbiting an Extreme Kerr Black Hole. Astrophys. J. 1973, 183, 237–264. [Google Scholar] [CrossRef]
- Kardashev, N.S.; Novikov, D.; Lukash, V.N.; Pilipenko, S.V.; Mikheeva, E.V.; Bisikalo, D.V.; Wiebe, D.S.; Doroshkevich, A.G.; Zasov, A.V.; Zinchenko, I.I. Review of scientific topics for the Millimetron space observatory. Phys. Usp. 2014, 57, 1199–1228. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dokuchaev, V.I. Physical Origin of the Dark Spot in the First Image of Supermassive Black Hole SgrA*. Astronomy 2022, 1, 93-98. https://doi.org/10.3390/astronomy1020009
Dokuchaev VI. Physical Origin of the Dark Spot in the First Image of Supermassive Black Hole SgrA*. Astronomy. 2022; 1(2):93-98. https://doi.org/10.3390/astronomy1020009
Chicago/Turabian StyleDokuchaev, Vyacheslav I. 2022. "Physical Origin of the Dark Spot in the First Image of Supermassive Black Hole SgrA*" Astronomy 1, no. 2: 93-98. https://doi.org/10.3390/astronomy1020009
APA StyleDokuchaev, V. I. (2022). Physical Origin of the Dark Spot in the First Image of Supermassive Black Hole SgrA*. Astronomy, 1(2), 93-98. https://doi.org/10.3390/astronomy1020009





