MW-Level Performance Comparison of Contra Rotating Generators for Wind Power Applications
Abstract
1. Introduction
2. Methodology
2.1. Mathematical Sizing
2.1.1. PMVM Mathematical Sizing
2.1.2. WFFSM Mathematical Sizing
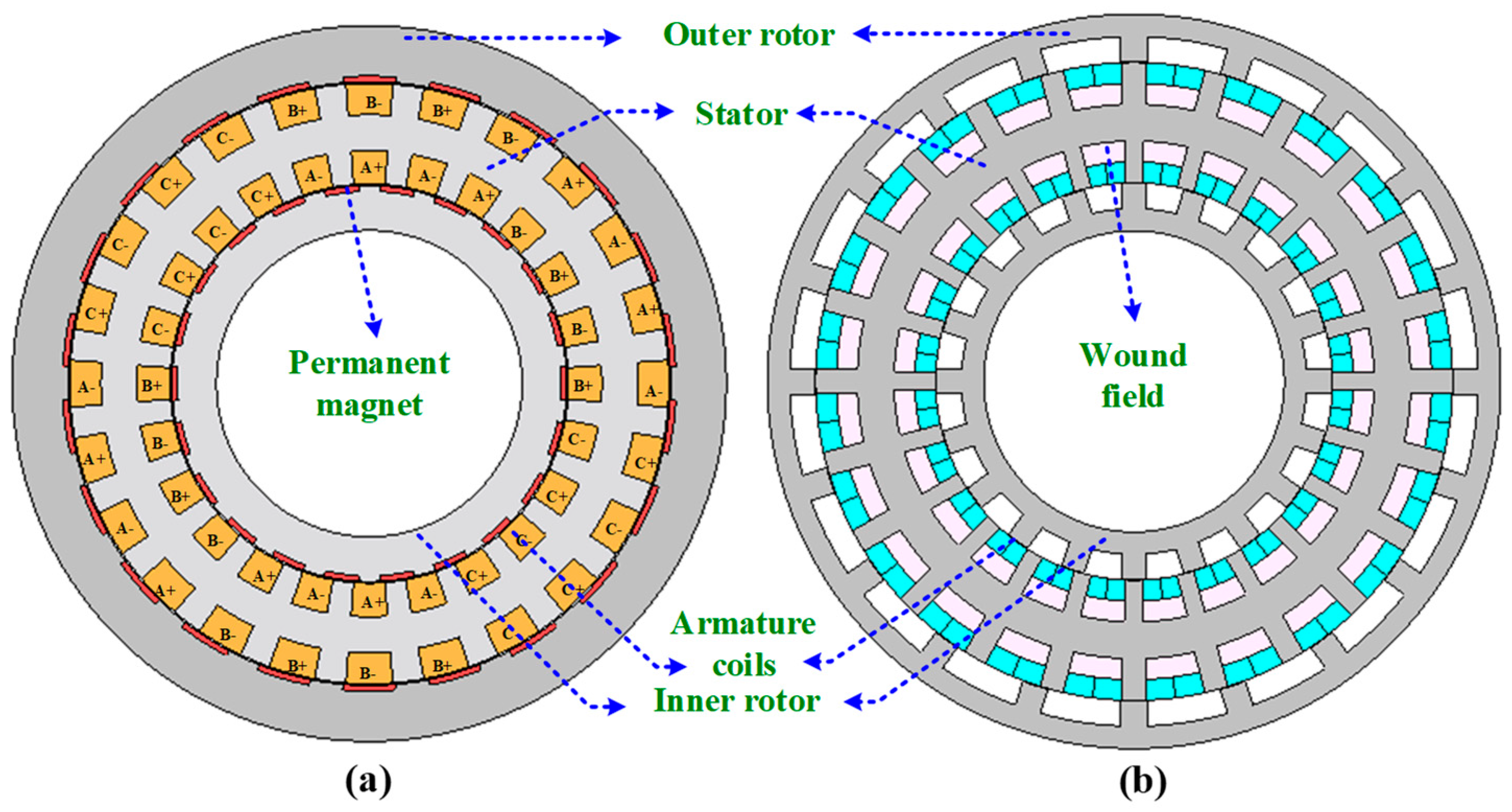
2.2. Machine Topologies and Slot/Poles Combinations
3. Results and Discussions
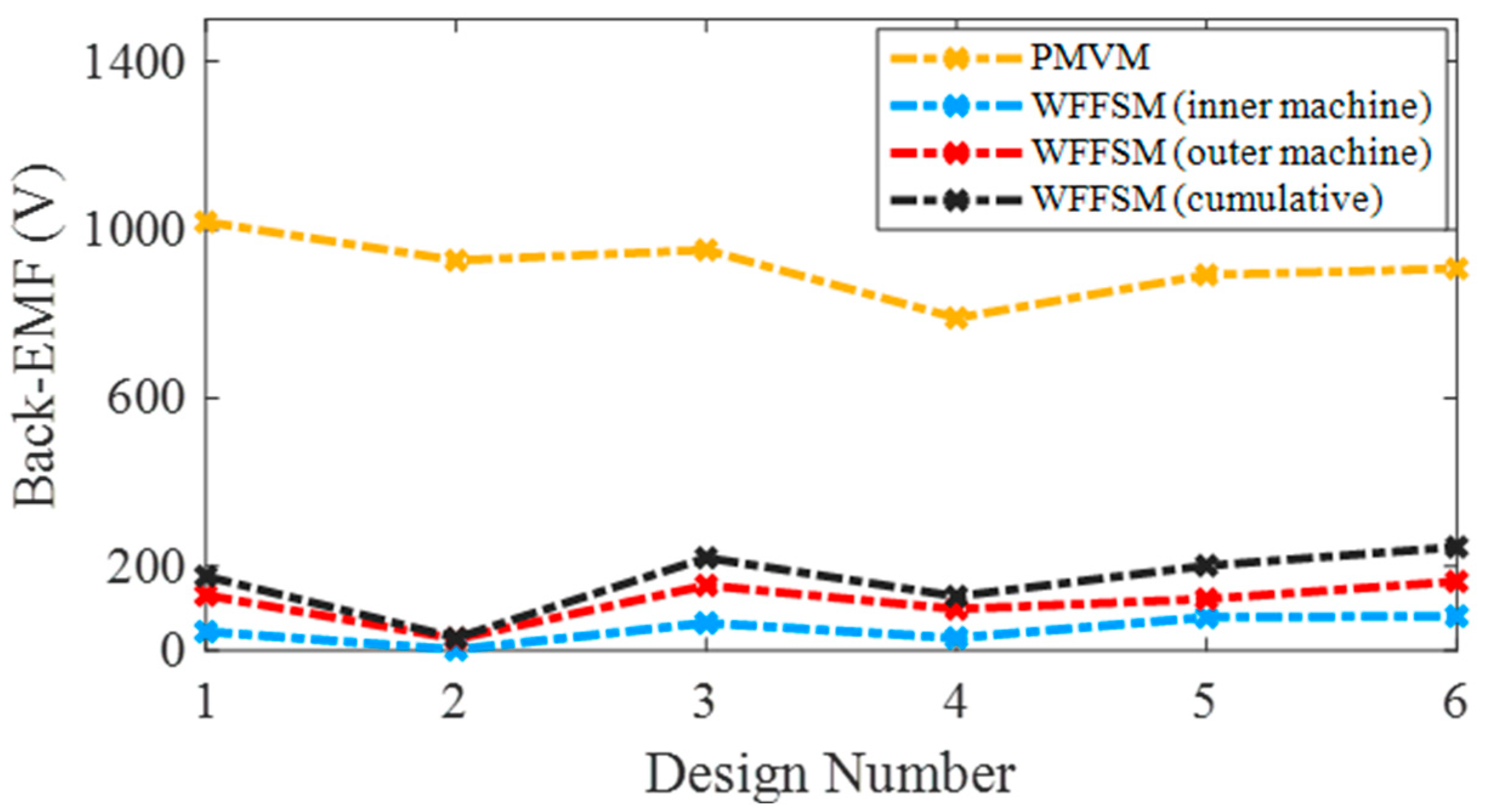
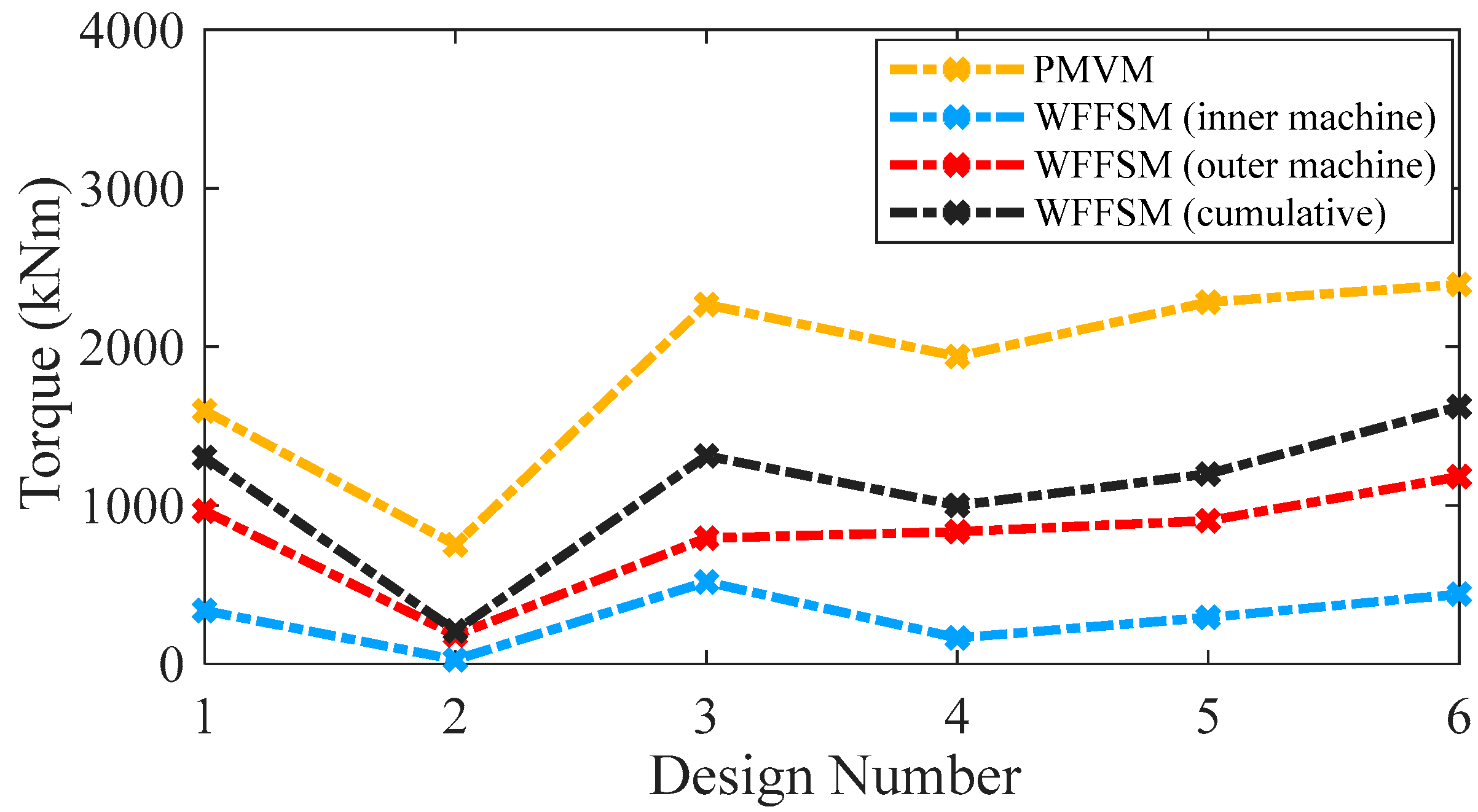
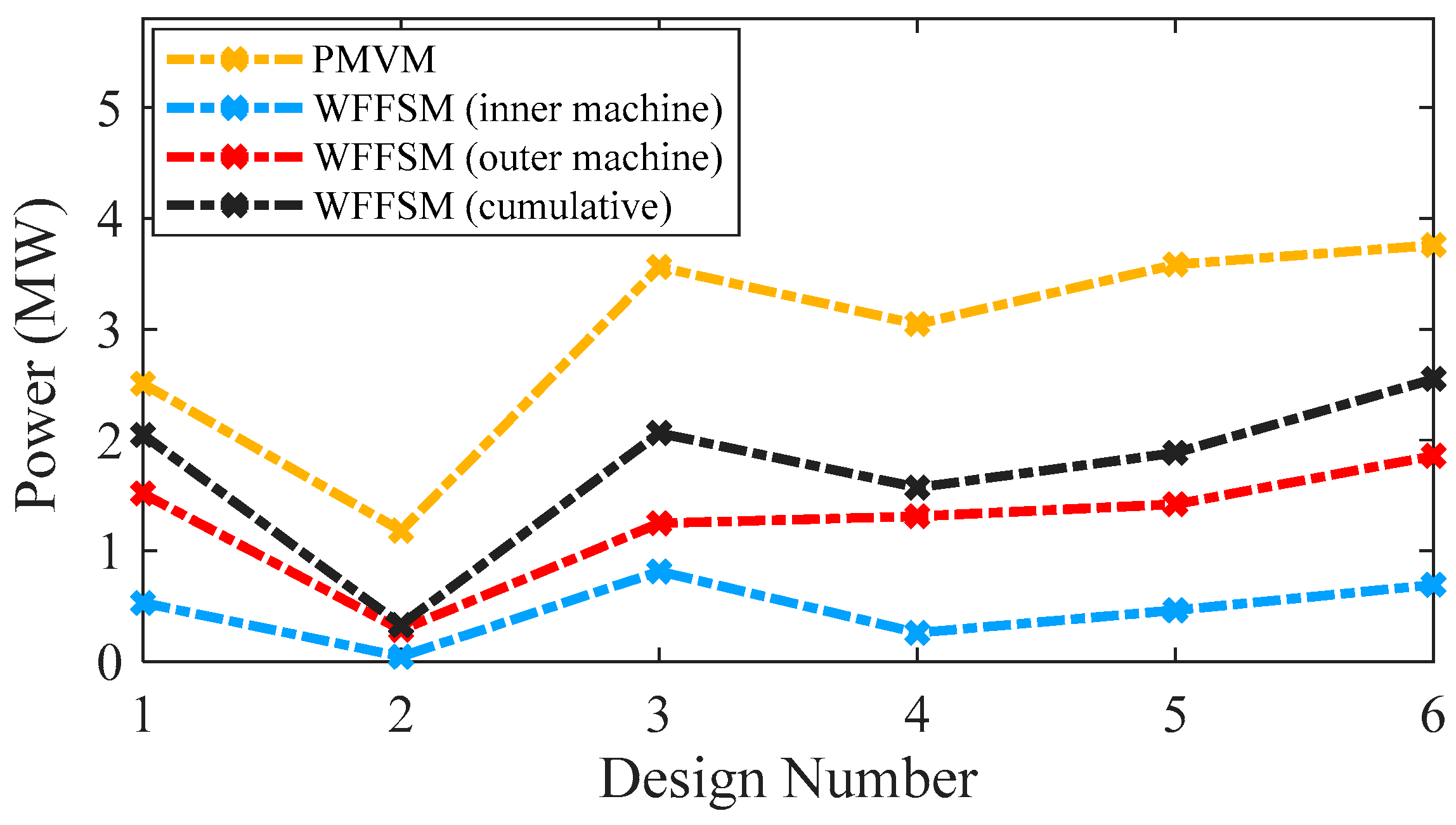
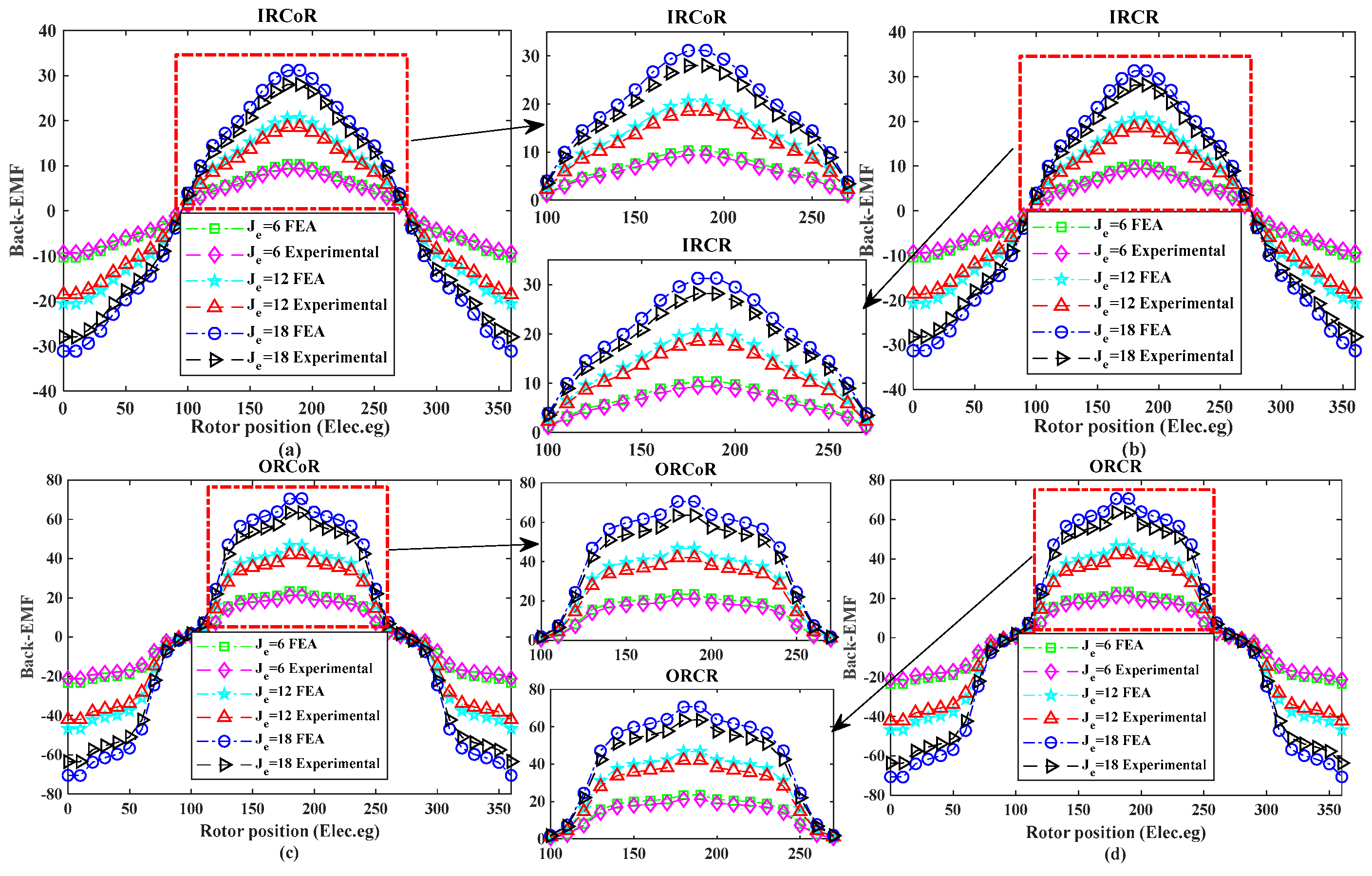
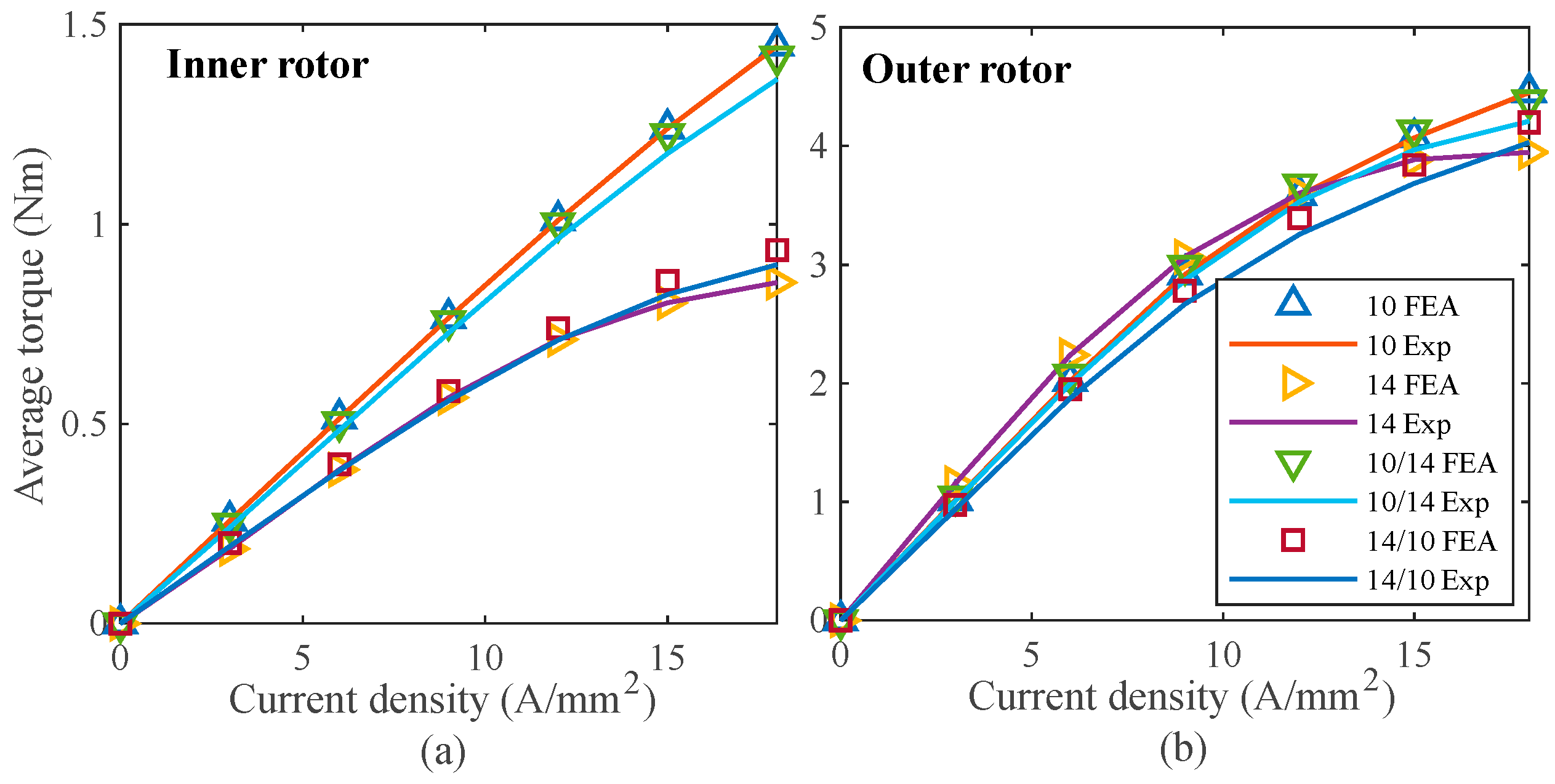
3.1. No-Load Back-EMF, Cogging Torque, and On-Load Torque
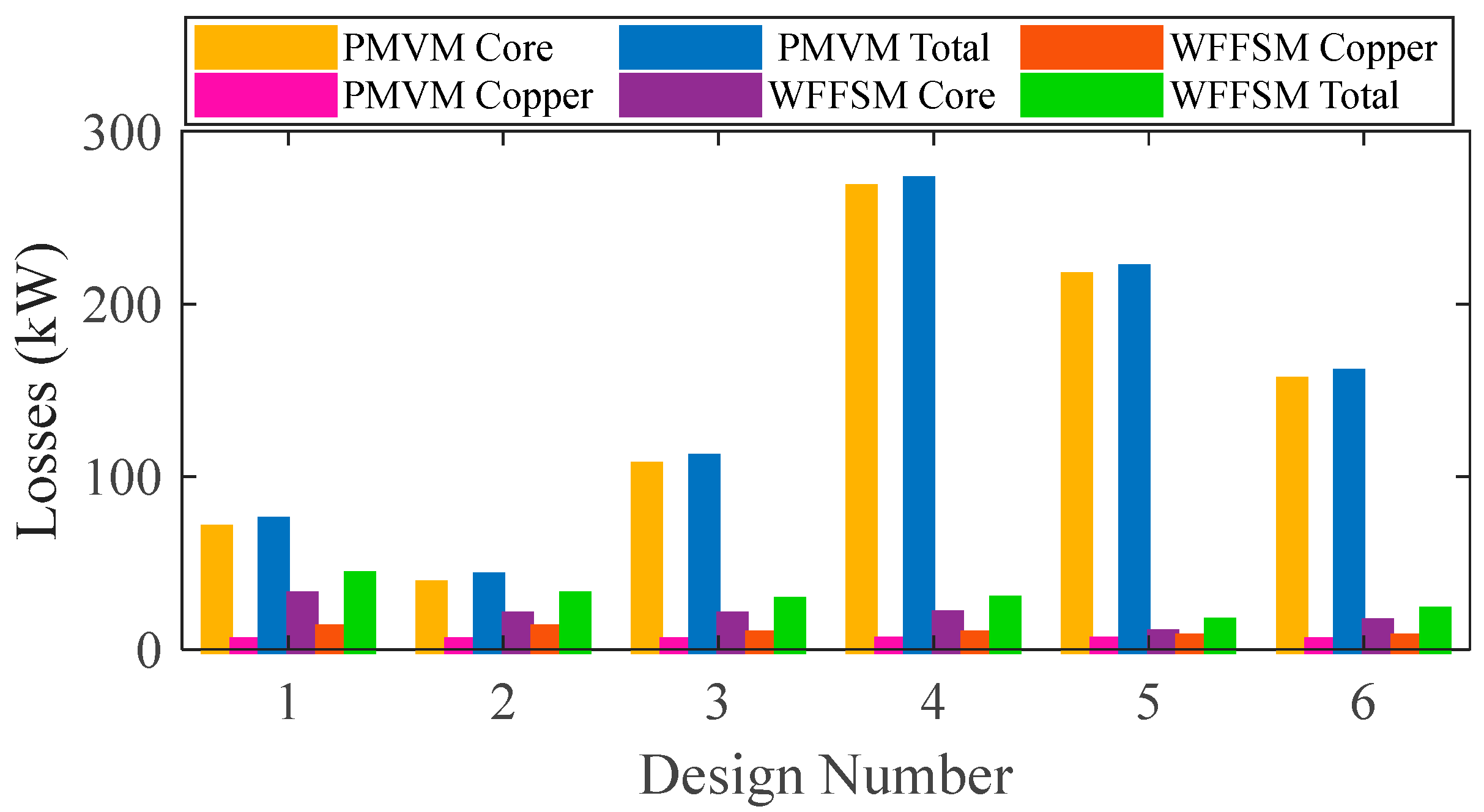
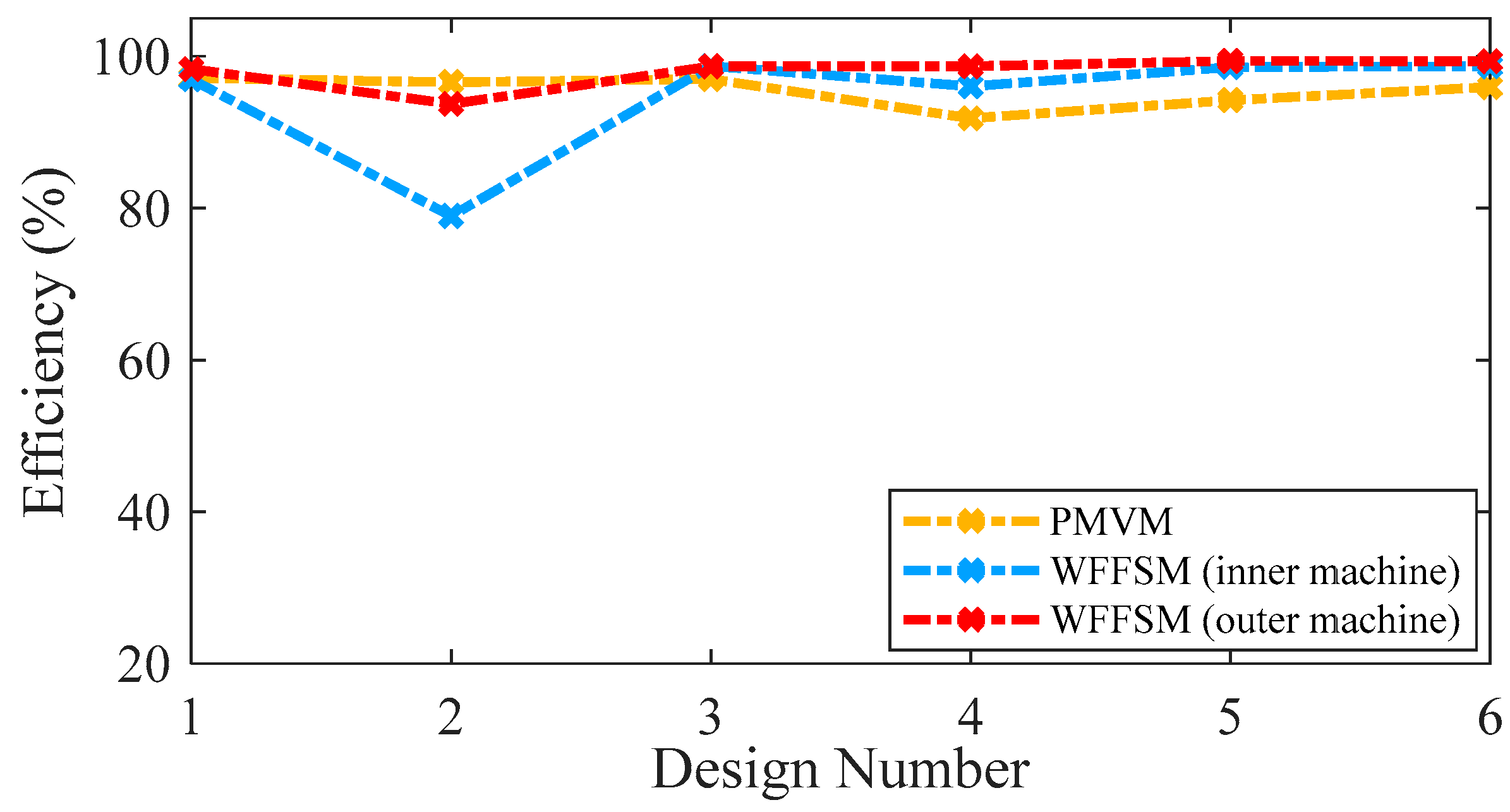
3.2. Losses and Efficiency
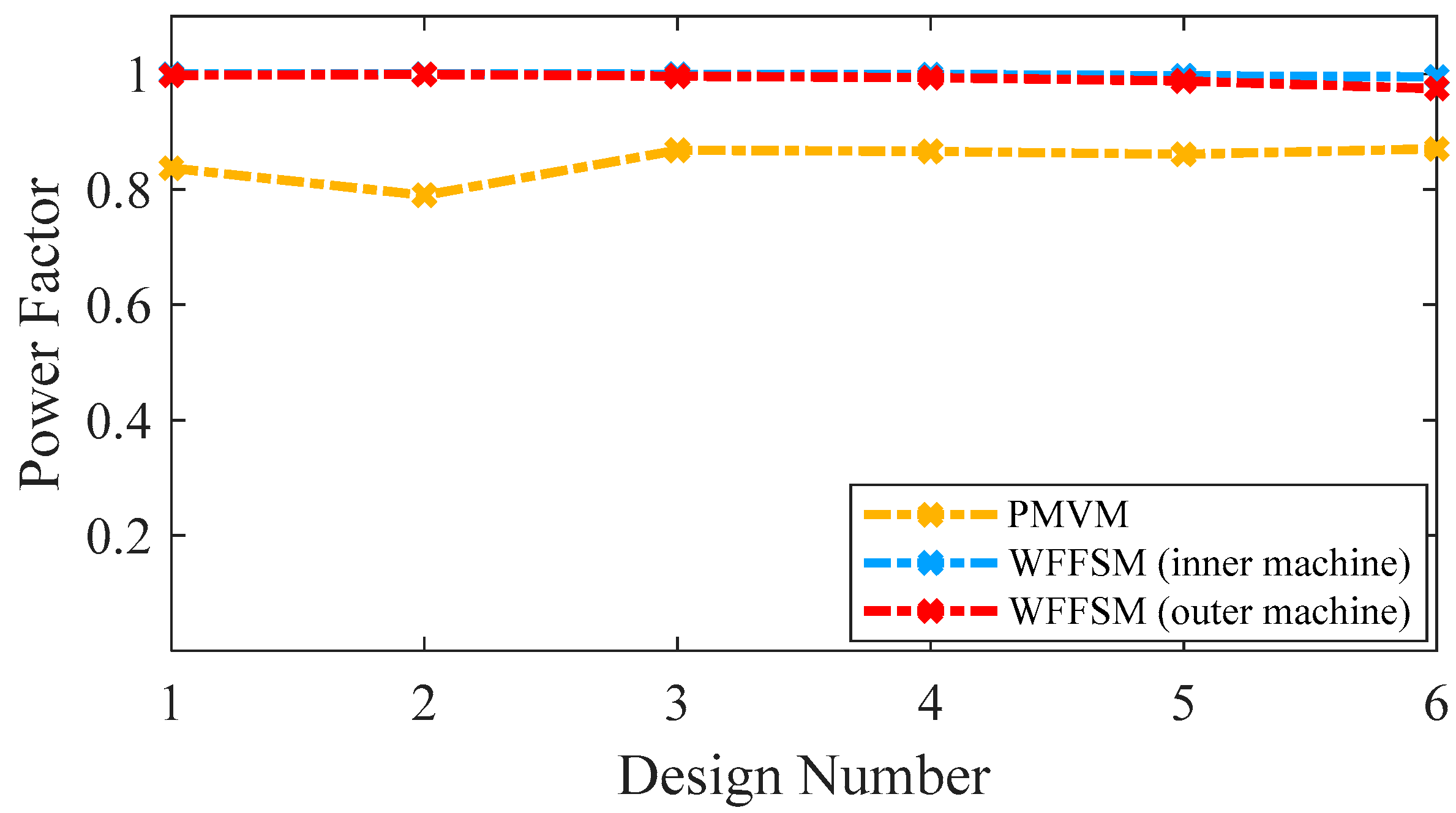
3.3. Power Factor
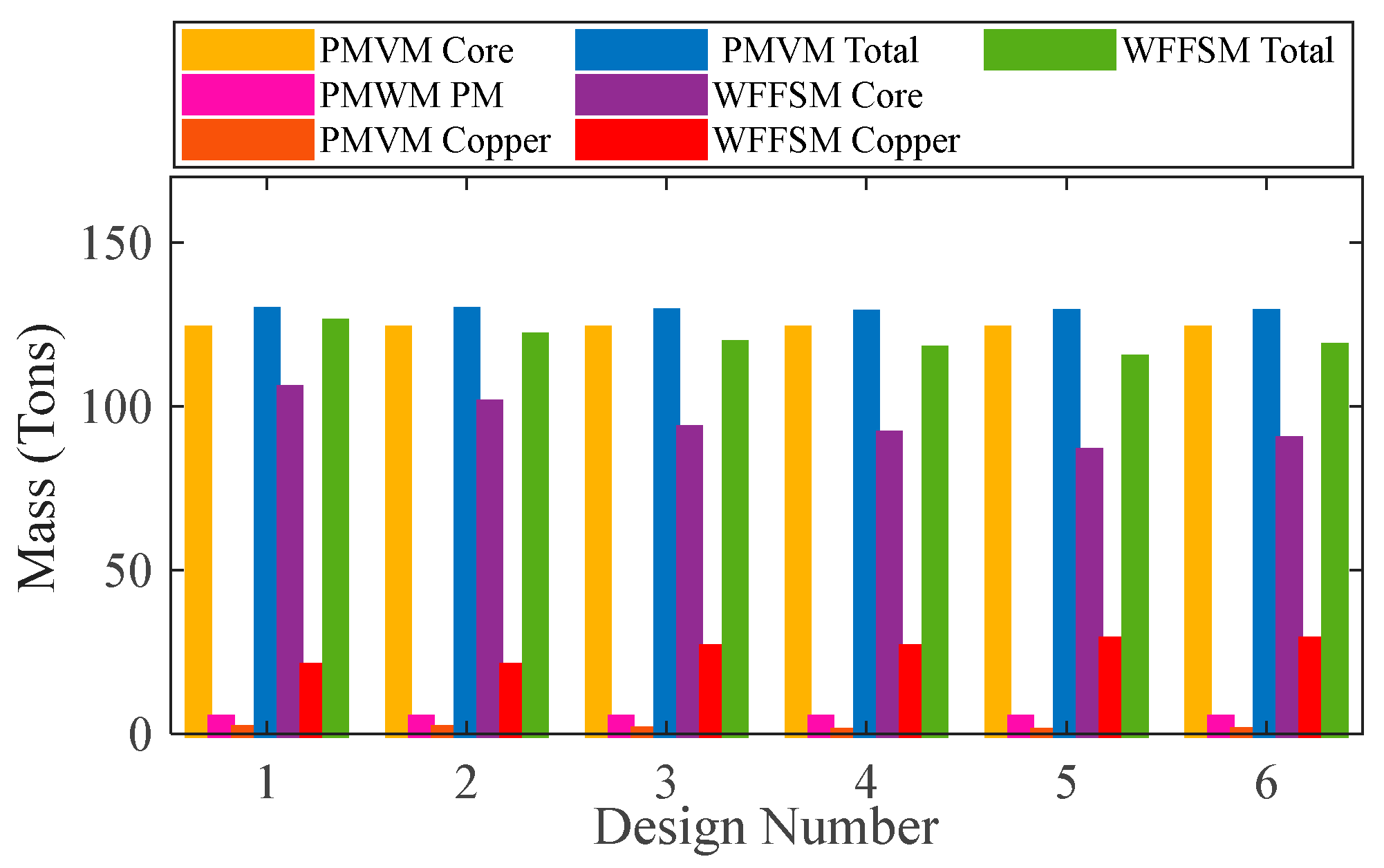
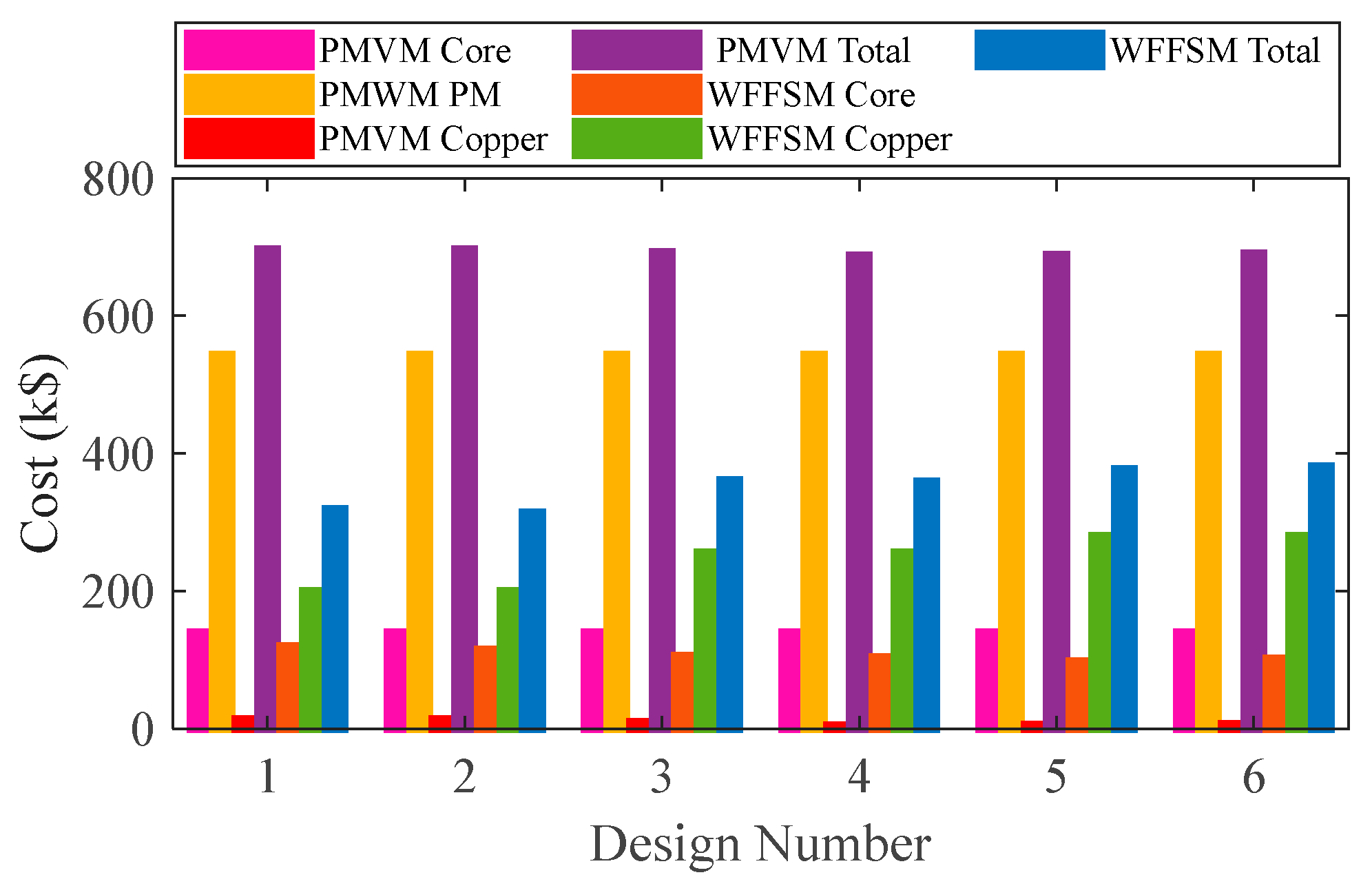
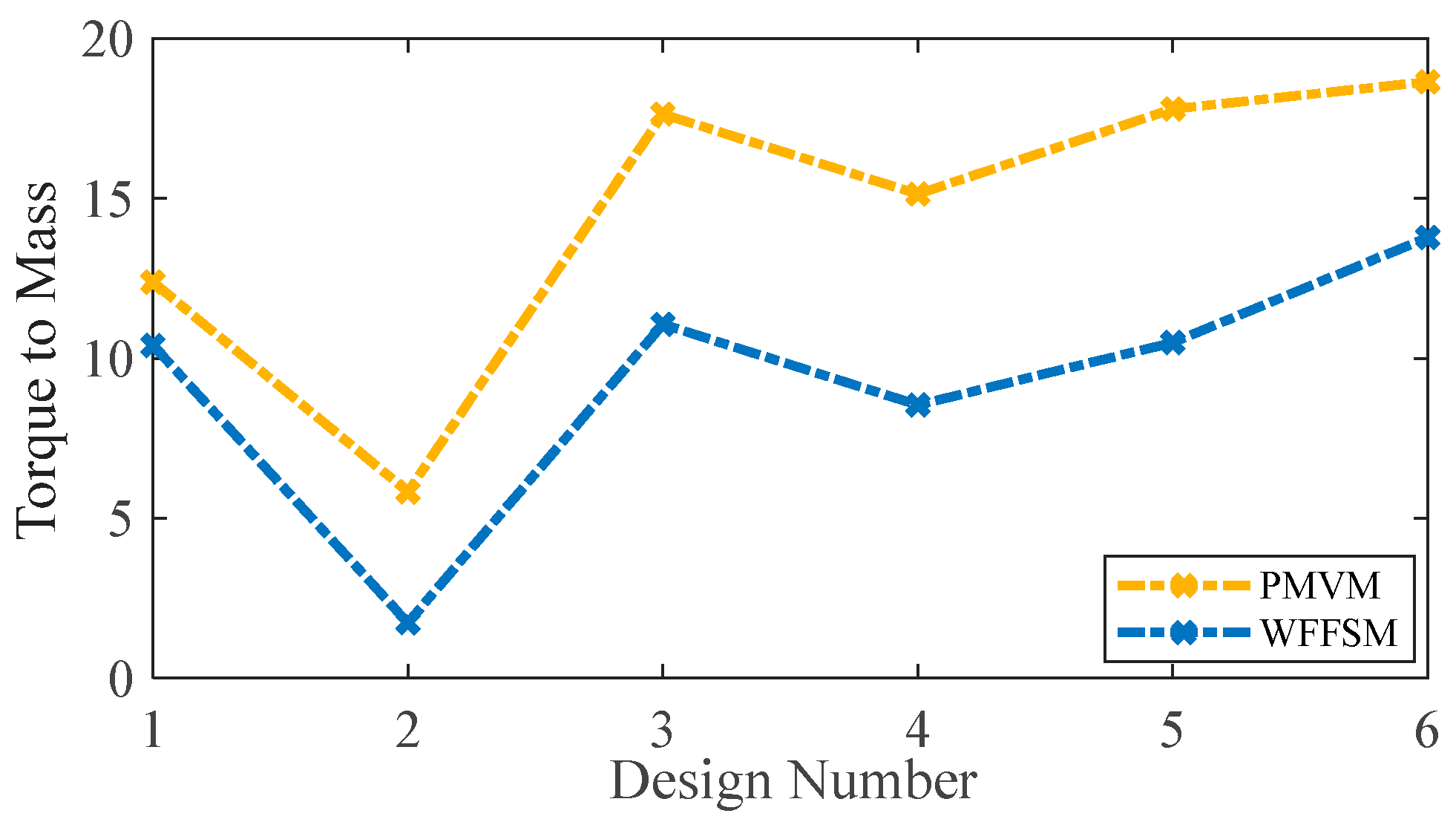
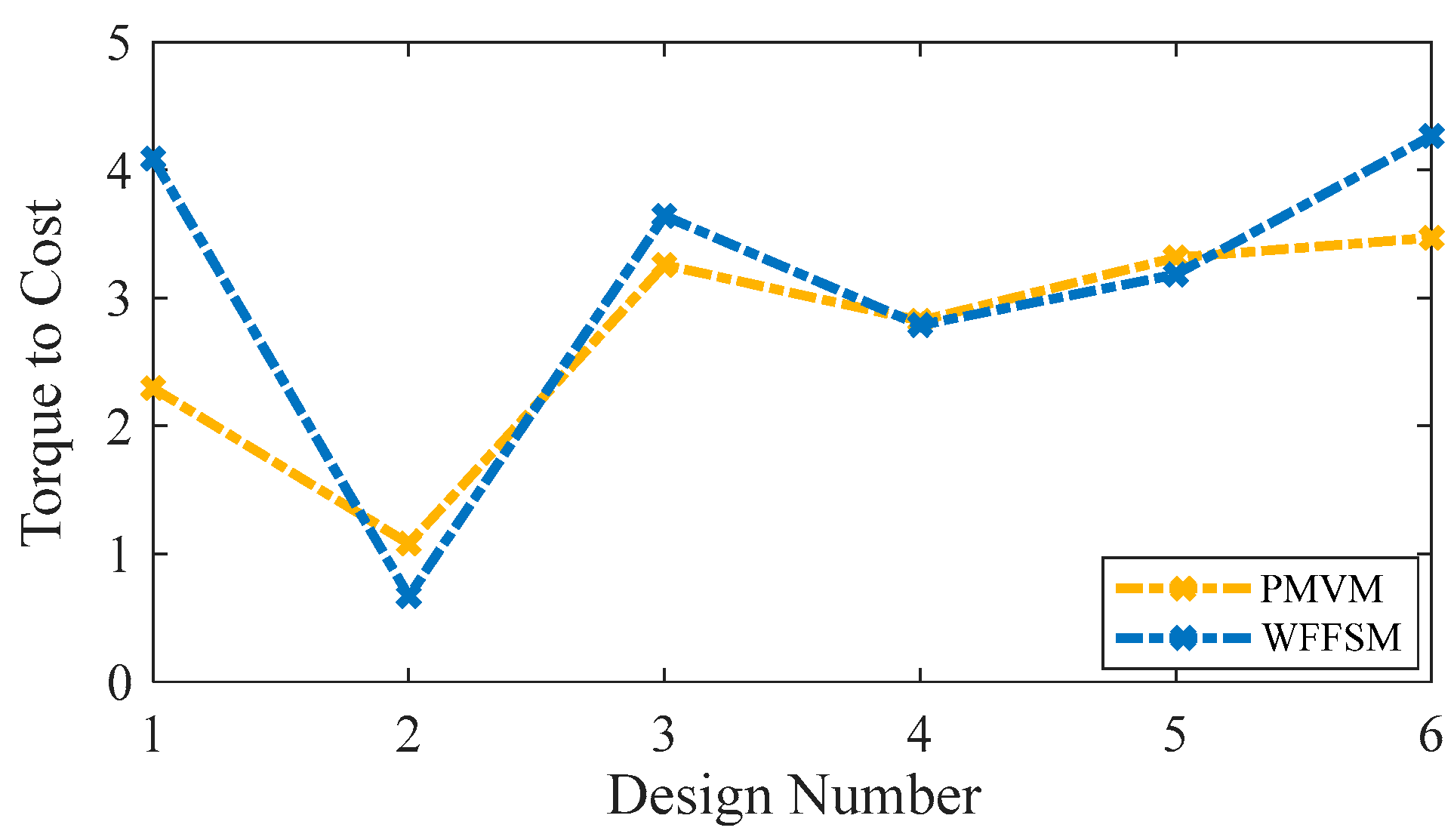
3.4. Torque/Mass and Torque/Cost
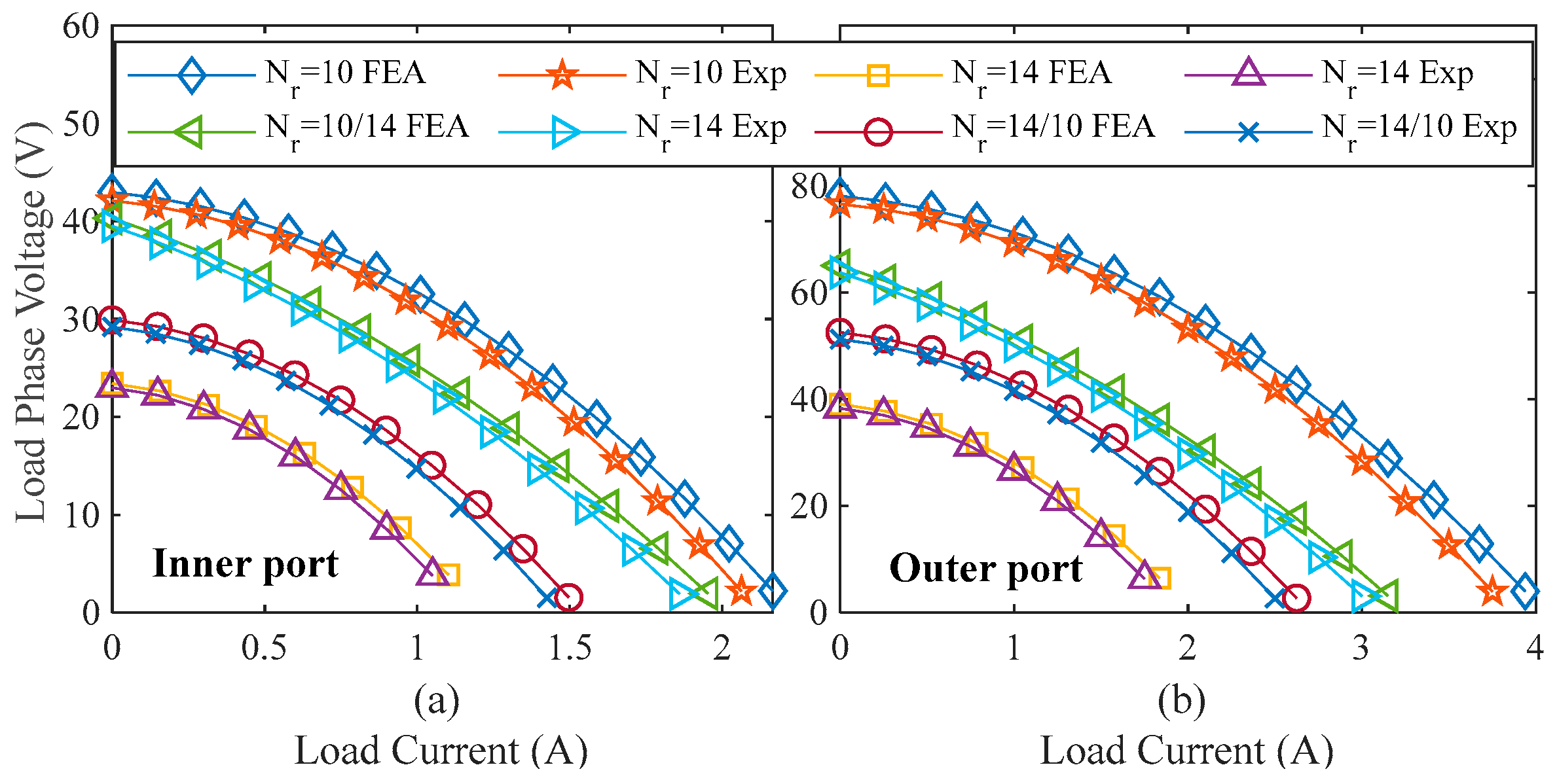
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| List of Symbols | |
|---|---|
| Symbols | Definition |
| Pole pair number | |
| Current per phase | |
| Magnetic flux linkage | |
| Phase number | |
| Angle between magnetic field and current | |
| Number of turns per phase | |
| Winding factor | |
| Flux per stator phase | |
| Rotor pole arc | |
| Leakage factor | |
| Stator pole pair number | |
| Outer diameter of the rotor | |
| Stack length | |
| Peak value of the inner air gap flux density | |
| Machine electrical loading | |
| Rotor pole number | |
| Stator slot number | |
| Gear ratio | |
| Flux | |
| d-axis inductance | |
| q-axis inductance | |
| d-axis current | |
| q-axis current | |
| Air-gap region | |
| Air-gap magnetic flux density | |
| Maximum air-gap flux density | |
References
- #WWEAwebinar: Wind Power Around the World (Recordings Available). 2021. Available online: https://wwindea.org/wweawebinar-wind-power-around-the-world (accessed on 9 November 2024).
- Simon, E.; Maureen, H.; Joachim, S.; Bentham, P. Analysis: Record-Low Price for U.K. Offshore Wind Cheaper Than Existing Gas Plants by 2023. 2019. Available online: https://www.carbonbrief.org/analysis-record-low-uk-offshore-wind-cheaper-than-existing-gas-plants-by-2023/ (accessed on 10 November 2024).
- Chen, H.; Zuo, Y.; Chau, K.T.; Zhao, W.; Lee, C.H.T. Modern electric machines and drives for wind power generation: A review of opportunities and challenges. IET Renew. Power Gener. 2021, 15, 1864–1887. [Google Scholar] [CrossRef]
- Padinharu, D.K.K.; Li, G.-J.; Zhu, Z.-Q.; Clark, R.; Thomas, A.; Azar, Z.; Duke, A. Permanent Magnet Vernier Machines for Direct-Drive Offshore Wind Power: Benefits and Challenges. IEEE Access 2022, 10, 20652–20668. [Google Scholar] [CrossRef]
- Fernando, N.; Nutkani, I.U.; Saha, S.; Niakinezhad, M. Flux switching machines: A review on design and applications. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017; pp. 1–6. [Google Scholar]
- Kumar, P.S.; Abraham, A.; Bensingh, R.J.; Ilangovan, S. Computational and experimental analysis of a counter-rotating wind turbine system. J. Sci. Ind. Res. 2013, 72, 300–306. [Google Scholar]
- Li, Z.; Wang, Y.; Xiao, H. Experimental study on structures of counter-rotating wind turbines. In Proceedings of the 2013 International Conference on Materials for Renewable Energy and Environment, Chengdu, China, 19–21 August 2013; pp. 368–372. [Google Scholar]
- Li, Z.; Wang, Y.; Zhang, Y. Experimental study on interaction of the counter-rotating rotors in a wind turbine. In Proceedings of the 2011 International Conference on Materials for Renewable Energy & Environment, Shanghai, China, 20–22 May 2011; pp. 570–574. [Google Scholar]
- Bayron, P.; Kelso, R.; Chin, R. Experimental analysis of co-rotating and counter-rotating tandem horizontal-axis wind turbine performance and wake dynamics. J. Wind. Eng. Ind. Aerodyn. 2024, 253, 105840. [Google Scholar] [CrossRef]
- Ullah, W.; Khan, F.; Hussain, S.; Yousuf, M.; Akbar, S. A Novel Dual Port Dual Rotor Wound Field Flux Switching Generator with Uniform and Non-Uniform Rotor Poles for Counter-Rotating Wind Power Generation. IEEE Trans. Energy Convers. 2023, 38, 2420–2433. [Google Scholar] [CrossRef]
- Ullah, W.; Khan, F.; Akuru, U.B.; Hussain, S.; Yousuf, M.; Akbar, S. A Novel Dual Electrical and Dual Mechanical Wound Field Flux Switching Generator for Co-Rotating and Counter-Rotating Wind Turbine Applications. IEEE Trans. Ind. Appl. 2024, 60, 184–195. [Google Scholar] [CrossRef]
- Allahyari, A.; Torkaman, H. A Novel High-Performance Consequent Pole Dual Rotor Permanent Magnet Vernier Machine. IEEE Trans. Energy Convers. 2020, 35, 1238–1246. [Google Scholar] [CrossRef]
- Alavijeh, M.M.; Mirsalim, M. Design and optimization of a new dual-rotor Vernier machine for wind-turbine application. In Proceedings of the 2020 28th Iranian Conference on Electrical Engineering (ICEE), Tabriz, Iran, 4–6 August 2020; pp. 1–6. [Google Scholar]
- Fatima, M.; Khan, F.; Ullah, W.; Akuru, U.B. Mathematical sizing and design analysis of permanent magnet vernier machine for contra-rotating wind power applications. IET Electr. Power Appl. 2025, 19, e12531. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Z.Q. Influence of gear ratio on electromagnetic performance and geometries of vernier permanent magnet synchronous machines. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 2453–2460. [Google Scholar]
- Allahyari, A.; Bostanci, E.; Mahmoudi, A. High-Performance Vernier Machines with Halbach Array Permanent Magnets for Direct Drive Applications. Machines 2023, 11, 525. [Google Scholar] [CrossRef]
- Padinharu, D.K.K.; Li, G.J.; Zhu, Z.Q.; Foster, M.P.; Stone, D.A.; Griffo, A.; Clark, R.; Thomas, A. Scaling Effect on Electromagnetic Performance of Surface-Mounted Permanent-Magnet Vernier Machine. IEEE Trans. Magn. 2020, 56, 8100715. [Google Scholar] [CrossRef]



| Design Number | PMVM | WFFSM | ||
|---|---|---|---|---|
| Ss | Pr | Ss | Pr | |
| 1 | 96 | 80 | 48 | 40 |
| 2 | 48 | 40 | 48 | 28 |
| 3 | 144 | 120 | 24 | 20 |
| 4 | 288 | 240 | 24 | 28 |
| 5 | 240 | 200 | 12 | 10 |
| 6 | 192 | 160 | 12 | 14 |
| Key Parameters | Values |
|---|---|
| Rated Speed (rpm) | 15 |
| Rated Power (MW) | 3 |
| Outer Diameter (mm) | 5000 |
| Stack Length (mm) | 1200 |
| Air Gap Length (mm) | 5 |
| Magnet Volume (m3) | 0.536 |
| Field Current Density, Je (A/mm2) | 10 |
| Armature Current (A) | 7000 |
| Cost of PM ($/kg) | 135 |
| Cost of steel core ($/kg) | 1.25 |
| Cost of Copper ($/kg) | 10.85 |
| Performance Indicators (Units) | Machine Type | |||
|---|---|---|---|---|
| PMVM | ) | ) | WFFSM | |
| Cogging torque (%) | = 8.96/7.19 | 41.61 | 42.6 | - |
| Back-EMF (V) | 907.52 | 81.79 | 164.11 | 245.91 |
| Torque (kNm) | 2393.52 | 441.51 | 1182.87 | 1624.38 |
| Power (MW) | 3.75 | 0.69 | 1.85 | 2.54 |
| Power factor | 0.87 | 0.99 | 0.97 | - |
| Core losses (kW) | 155.19 | 6.5 | 8.8 | 15.3 |
| Copper losses (kW) | 4.55 | 2.8 | 3.9 | 6.7 |
| Efficiency (%) | 95.92 | 98.66 | 99.31 | - |
| Design Number | PMVM | WFFSM | ||
|---|---|---|---|---|
| 1 | 11.63 | 8.81 | 136.91 | 50.75 |
| 2 | 60.5 | 36.81 | 1194.32 | 195.1 |
| 3 | 5.85 | 15.28 | 45.05 | 26.12 |
| 4 | 17.59 | 16.09 | 145.54 | 39.98 |
| 5 | 19.9 | 13.12 | 45.46 | 39.7 |
| 6 | 8.96 | 7.19 | 41.61 | 42.63 |
| Performance Indicator | Machine Type | ||
|---|---|---|---|
| PMVM | WFFSM | ||
| Core | Mass (Tons) | 123.26 | 84.46 |
| Cost (k$) | 139.78 | 101.4 | |
| Copper | Mass (Tons) | 0.658 | 28.38 |
| Cost (k$) | 6.48 | 279.4 | |
| PM | Mass (Tons) | 4.43 | - |
| Cost (k$) | 543.41 | - | |
| Cumulative | Mass (Tons) | 128.36 | 117.84 |
| Cost (k$) | 689.68 | 380.84 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fatima, M.; Ullah, W.; Khan, F.; Akuru, U.B. MW-Level Performance Comparison of Contra Rotating Generators for Wind Power Applications. Wind 2025, 5, 30. https://doi.org/10.3390/wind5040030
Fatima M, Ullah W, Khan F, Akuru UB. MW-Level Performance Comparison of Contra Rotating Generators for Wind Power Applications. Wind. 2025; 5(4):30. https://doi.org/10.3390/wind5040030
Chicago/Turabian StyleFatima, Mehroz, Wasiq Ullah, Faisal Khan, and U. B. Akuru. 2025. "MW-Level Performance Comparison of Contra Rotating Generators for Wind Power Applications" Wind 5, no. 4: 30. https://doi.org/10.3390/wind5040030
APA StyleFatima, M., Ullah, W., Khan, F., & Akuru, U. B. (2025). MW-Level Performance Comparison of Contra Rotating Generators for Wind Power Applications. Wind, 5(4), 30. https://doi.org/10.3390/wind5040030







