A Systematic Review of Wind Energy Forecasting Models Based on Deep Neural Networks

Abstract

The present study focuses on wind power forecasting (WPF) models based on deep neural networks (DNNs), aiming to evaluate current approaches, identify gaps, and provide insights into their importance for the integration of Renewable Energy Sources (RESs). The systematic review was conducted following the methodology of Kitchenham and Charters, including peer-reviewed articles from 2020 to 2024 that focused on WPF using deep learning (DL) techniques. Searches were conducted in the ACM Digital Library, IEEE Xplore, ScienceDirect, Springer Link, and Wiley Online Library, with the last search updated in April 2024. After the first phase of screening and then filtering using inclusion and exclusion criteria, risk of bias was assessed using a Likert-scale evaluation of methodological quality, validity, and reporting. Data extraction was performed for 120 studies. The synthesis established that the state of the art is dominated by hybrid architectures (e.g., CNN-LSTM) integrated with signal decomposition techniques like VMD and optimization algorithms such as GWO and PSO, demonstrating high predictive accuracy for short-term horizons. Despite these advancements, limitations include the variability in datasets, the heterogeneity of model architectures, and a lack of standardization in performance metrics, which complicate direct comparisons across studies. Overall, WPF models based on DNNs demonstrate substantial promise for renewable energy integration, though future work should prioritize standardization and reproducibility. This review received no external funding and was not prospectively registered.

1. Introduction

The efficient operation of the electricity sector has a direct impact on social and economic development. Consequently, it is crucial to ensure continuous maintenance to guarantee this sector. However, the production of electrical energy stands out as the primary cause of pollution [1]. As a result, Renewable Energy Sources (RESs) have emerged as a significant alternative solution to mitigate the harmful effects of pollution. Specifically, wind energy has proven to be more economical than other RESs, thanks to the rapid advancements in wind turbine technology [2].

Wind and solar energy generation has a major drawback due to the intermittency and unpredictability of the variables [3]. Power generation from intermittent sourced disrupts typical methods for planning and operating energy systems; therefore, it represents a strong challenge to wind power’s future prospects [4]. Ref. [5] notes that the principal obstacles to achieving a high share of wind energy are effective scheduling, system management, and optimization. In addition, ref. [1] claims wind energy forecasting is an issue of vital importance for wind energy development.

As wind power deployment continues to grow, accurately predicting the energy output of operating wind turbines has become even more critical, thus contributing to its overall dependability and security [6]. The complexity of predicting wind power arises from the presence of significant nonlinearities in wind speed [7].

Developing more accurate wind power forecasting tools offers significant benefits to traders, schedulers, and dispatchers. For instance, over the past 10 years, a few energy-specialized forecasting companies have been acquired by large organizations, which offer full or partial power forecasting services. Generally, renewable-energy forecasts serve two primary audiences: energy-market participants and power-system operators [8]. Nonetheless, although forecasting tools have become increasingly accurate, integrating large-scale wind farms into the grid still presents significant challenges. In future power systems with renewable-energy penetration approaching 100%, new use-cases for uncertainty forecasting will arise, necessitating the creation of next-generation forecasting methods [8].

Wind power forecasting (WPF) techniques are classified according to their modeling theory or time horizon. According to [1], the short-term forecasting horizon is the most widely adopted because it fulfils several critical objectives: safeguarding system reliability, optimizing resource utilization, meeting demand in real time, and securing supply. Its versatility makes it the preferred choice for tasks such as next-day energy dispatch and day-ahead market operations. Moreover, short-term forecasts typically achieve lower error margins than medium- and long-term predictions, further reinforcing their practical value.

Regarding forecasting horizons, prior work commonly distinguishes very short-term (seconds to 30 min), short-term (30 min to 6 h), medium-term (6 h to 1 day), and long-term (1 day to 1 week) horizons [1,5], though boundaries may vary by application. In practice, short-term forecasts support secure grid operation and intraday market trading, medium-term forecasting aligns with day-ahead markets and physical power exchange, and long-term forecasting informs capacity assessments and identification of wind-power generation potential [4,9].

WPF has progressed from physical approaches and statistical time-series models to machine learning (ML) methods, with deep neural networks (DNNs) gaining traction in recent years [4,5,10]. DNNs are multilayer neural models with many hidden layers that learn data representations in supervised or unsupervised settings [11]. Despite this progress, operational adoption remains limited, as traditional techniques are still prevalent due to lower computational demand and stronger adaptation or extrapolation capabilities [12]. Even so, DNN-based approaches are widely viewed as promising for WPF [1,12]. Representative DNN families include convolutional neural networks (CNNs) and recurrent architectures (RNN, LSTM, GRU, BiLSTM, BiGRU), as well as deep belief networks (DBNs) and autoencoders; these models can learn deep nonlinear features of wind series and have shown strong predictive performance [5,13].

The forecast accuracy depends on choices such as input selection and training setup. In practice, many works combine signal decomposition, neural models, and metaheuristic optimization to reduce errors, and some apply post-processing to refine results. Using several models together can lower variance, while denoising helps capture wind-speed variability [1].

Despite extensive research aimed at mitigating power-output fluctuations and the intrinsic randomness of wind-power forecasts, important challenges remain. Reliable large-scale integration demands short-term forecasting models that couple high accuracy with robustness and computational efficiency, motivating advanced hybrid algorithms that fuse complementary techniques [12].

According to the above, there is a clear need to conduct a systematic review of the literature on wind power and/or wind speed prediction models based on deep neural networks. This review covers the full spectrum of DNN families applied to wind forecasting with a primary emphasis on short-term horizons, while also considering closely related ranges (ultra/very-short-term ranges) given that horizon definitions vary across studies. In addition to outlining the state of the art in feature extraction, pre-processing pipelines, optimization algorithms, and evaluation methodologies; the trends in short-term forecasting; dataset characteristics; dataset use in training and validation; and current processing times, this work clarifies horizon mapping, consolidates recent evidence from the last few years, and situates its contribution with respect to earlier surveys by discussing dataset practices and simple benchmarking guidance, together with brief notes on efficiency and interpretability relevant to deployment. The remainder of the paper is organized as follows: Section 2 describes the systematic review methodology; Section 3 presents the findings mapped to Research Questions RQ1–RQ5, and discusses implications and limitations; Section 4 concludes with key results and research gaps.

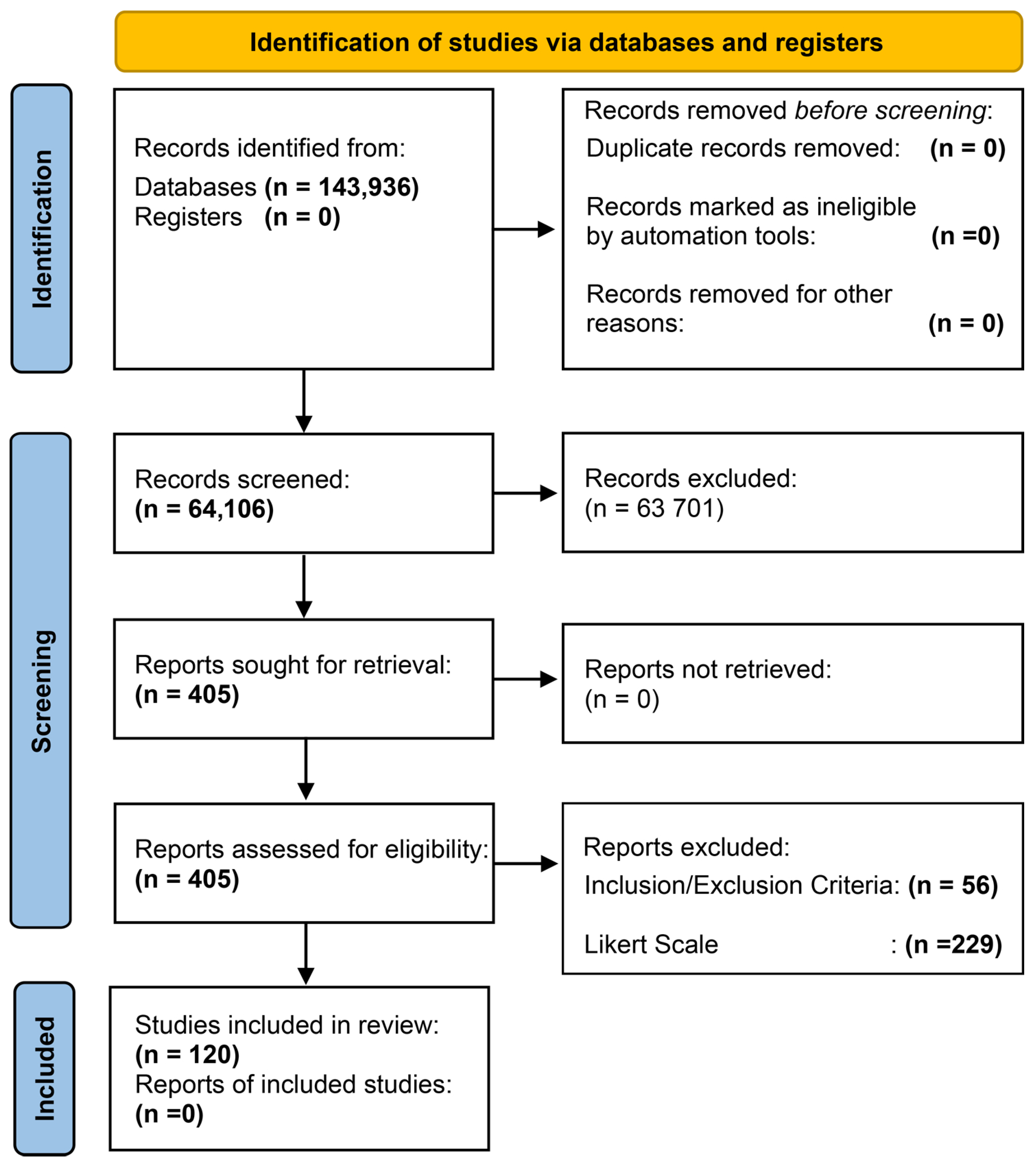
2. Systematic Literature Review Methodology

This systematic review followed the Kitchenham and Charters (2007) methodology for systematic reviews in software engineering [14]. The review protocol was not prospectively registered in a public database (e.g., PROSPERO, OSF, INPLASY), and no amendments were made during the process.

We considered established alternatives such as PRISMA 2020 and guidelines for systematic mapping studies. PRISMA is optimized for clinical evidence syntheses, with a strong emphasis on protocol registration and trial-style reporting. We adopt its transparency elements and include a PRISMA flow diagram, but our object of study (model architectures, datasets, and metrics in engineering papers) aligns better with the Kitchenham and Charters methodology, which is widely used in software and machine-learning reviews and provides concrete guidance on formulating research questions and inclusion and exclusion criteria and performing quality assessment and data extraction. Given the heterogeneity of modeling studies, rather than clinical outcomes, the framework by Kitchenham and Charters was the most appropriate. Although the review was not prospectively registered, which is common in this area, we provide the full search strings, screening stages, and quality criteria in Section 2 to support reproducibility.

The Kitchenham and Charters methodology consists of three phases. In the planning phase, a protocol was established to avoid bias, defining research questions, selection criteria, and quality assessment procedures. The conducting phase involved identifying and selecting relevant studies, followed by extracting and synthesizing the data. In the reporting phase, the findings were interpreted, limitations were discussed, and the applicability of the conclusions was evaluated. This structured methodology provides a comprehensive and unbiased overview of deep learning-based WPF models, while also highlighting current research trends and outlining potential future directions [15].

2.1. Planning Phase

This phase assesses whether existing reviews on the topic are available and establishes a protocol to address the research phenomenon. First of all, a review of prior literature reviews is conducted to determine whether the issue has already been examined. If so, relevant details and findings are collected to evaluate the progress made in the field.

2.1.1. Review Summary

For this study, the search strategy combined keywords such as systematic review, state of the art, review, survey, WPF, wind speed prediction (WSP), deep neural network, and deep learning. The literature reviewed includes articles published in journals and conference proceedings, retrieved from reputable databases such as IEEE Xplore, ACM Digital Library, Wiley Online Library, ScienceDirect, and Springer Link. To reduce potential bias and ensure broader coverage, supplementary searches were also conducted via Google Scholar to rapidly identify prior surveys. The most relevant studies identified through this process are described in the following paragraph.

Ref. [9] presents an extensive review of research on wind power generation based on a systematic literature network analysis covering 145 articles. Their study applies several approaches, including citation network analysis, to examine the main methods used in the field. One of the key findings is that most of the attention has been directed toward Measure–Correlate–Predict (MCP) models. The review also addresses central questions regarding the methods and models applied, how these have evolved over time, the types of analyses conducted, and the variables and evaluation metrics considered.

In [5], an extensive review of forecasting methods using DNNs is presented. The paper surveys a range of approaches to WS and WP forecasting, highlighting the strengths and limitations of different DNN models. It also discusses hybrid DNN architectures, preprocessing strategies, feature extraction techniques, and the optimizers commonly applied in these studies. In addition, the review identifies current challenges and outlines future research directions, offering a detailed examination of the performance metrics employed. The authors stress the importance of optimizing model configurations and examine how different forecasting methods have developed and evolved over time.

Ref. [16] presents a comprehensive review of current methodologies for forecasting electricity generation in wind farms. The paper discusses state-of-the-art techniques in WPF, with particular emphasis on intelligent methods for predicting energy output. The authors also highlight challenges related to data preparation and utilization, including difficulties in data analysis, cleaning, and filtering.

Ref. [12] provides a comprehensive examination of contemporary techniques for forecasting wind power generation. The review concentrates on ultra-short-term and short-term forecasting methods, emphasizing the main contributions of different models along with their respective strengths and limitations. It surveys a wide range of approaches, including neural network-based methods, ML techniques, deep learning (DL) models, hybrid predictive frameworks, and statistical approaches. The authors also identify several key challenges, such as complex model structures and hardware requirements, excessive parameter tuning, growing input vector dimensions, high demands for data quality, difficulties in achieving model generalization, and persistent issues in evaluating forecasting accuracy.

Ref. [1] presents a thorough review and classification of wind speed forecasting (WSF) models. The study examines several key aspects, including model input types, forecasting horizons, preprocessing and post-processing techniques, and evaluation metrics. It reviews a variety of artificial neural network (ANN) models and assesses their performance using regression-based metrics. The paper also discusses optimization strategies and extraction methods. Overall, the authors provide valuable insights into the current state of AI applications in wind speed forecasting and highlight future challenges in this area.

The scientific literature reveals a lack of recent systematic reviews focused on DL-based WPF. In this context, the objective of this review is to collect and analyze relevant primary studies, identify emerging trends, uncover research gaps, and evaluate existing approaches. Like prior surveys, we apply a structured review framework with defined research questions, explicit inclusion and exclusion criteria, and a quality assessment. Compared with prior surveys [1,5,9,12,16], this study places a clear emphasis on short-term wind power forecasting with consistent horizon mapping; covers the full spectrum of DNN families, including hybrid pipelines; synthesizes recent evidence from 2020 to 2024; examines dataset practices (public vs. private sources, size, resolution, temporal splits); offers simple benchmarking guidance; and brings deployment-oriented aspects to the fore by discussing processing-time reporting, computational efficiency/complexity, and interpretability as directions for future work.

2.1.2. Research Questions

According to the methodology proposed by [15], defining research questions is a crucial step in a systematic literature review, focusing on extracting information from primary studies.

• General research question:

• What is the current state of the art in wind power forecasting models based on deep neural networks?

• Specific research questions:

• What are the current architectures for wind power forecasting models that utilize deep neural networks, pre-processing and feature extraction techniques, and optimization algorithms?
• What are the current performance metrics for validating models?
• What is the typical forecasting time frame for short-term forecasting models?
• What are the currently accepted datasets for training wind power forecasting models using deep neural networks, and how are these datasets distributed for use?
• What are the typical processing times for current wind power forecasting models that utilize deep neural networks?

2.2. Conducting Phase

This phase involves identifying primary studies related to the research questions and extracting key information from them. To ensure impartial selection, the process follows a strict protocol, including inclusion and exclusion criteria and quality validation.

2.2.1. Strategy for Searching for Primary Studies

This systematic literature review aims to gather and evaluate relevant information from primary studies on WPF, also referred as WSP models based on DNNs. This subsection details the scientific databases used to retrieve the initial studies and the keywords employed to construct the search strings. The review was conducted using the following online databases: ACM Digital Library, IEEE Xplore, ScienceDirect, Springer Link, and Wiley Online Library on 30 April 2024.

The keywords for constructing the search strings include wind power forecasting (WPF), wind speed forecasting (WSF), wind power prediction (WPP), wind speed prediction (WSP), deep neural network (DNN), and deep learning (DL). These terms were chosen to address a wide range of research questions and to reduce the risk of missing relevant studies by including synonyms identified through related articles. The search strings for this review combine these topics, synonyms, and logical operators (AND, OR) to ensure a thorough search, as detailed in

Table 1. Initial search string.

Databases	Search String
ACM Digital Library	wind AND (power OR speed) AND (forecasting OR prediction) AND (deep neural network OR DNN OR deep learning)
IEEE Xplore	((wind AND (power OR speed) AND (forecasting OR prediction) AND (deep neural network OR DNN OR deep learning))
ScienceDirect	wind AND (power OR speed) AND (forecasting OR prediction) AND (deep neural network OR DNN OR deep learning)
Springer Link	wind AND power AND speed AND forecasting AND prediction AND (deep OR neural OR network OR learning OR DNN)
Wiley Online Library	wind AND (power OR speed) AND (forecasting OR prediction) AND (deep neural network OR DNN OR deep learning)

.

2.2.2. Procedure for Relevant Study Selection

The search for primary studies was conducted exclusively within the databases mentioned previously. From this search, only articles published in journals or presented at conferences will be considered. The selection process will proceed as follows:

• Database Search: Execute each search string in the selected databases, as indicated in Table 1.
• Filter by Date and Source Type: Limit the search results to publications from 2020 to 2024, including only journal articles and conference papers. The initial search results are summarized in

  Table 2. Initial results after using search strings and applying constraints (articles from 2020 to 2024).

  Databases	Initial Results	Constrain (2020–2024)
  ACM Digital Library	61,157	23,442
  IEEE Xplore	1003	821
  ScienceDirect	25,850	16,419
  Springer Link	22,297	10,376
  Wiley Online Library	33,629	13,048
  TOTAL	143,936	64,106

  .
• Title-Based Selection: Select all studies whose titles include the following keywords: “Wind Speed OR Wind Power” AND “Forecasting OR Prediction”.
• Abstract and Keyword Screening: If a title does not explicitly mention the terms from step 3, the abstract, keywords, and conclusions should be reviewed to check for the presence of any of the following terms: deep learning, deep neural network, or DNN.

  Table 3. Configuration of the first evaluation.

  Databases	Search String
  ACM Digital Library	[All: wind] AND [[All: power] OR [All: speed]] AND [[All: forecasting] OR [All: prediction]] AND [[All: deep neural network] OR [All: dnn] OR [All: deep learning]] AND [[Title: “wind speed”] OR [Title: “wind power”]] AND [[Title: forecasting] OR [Title: forecast] OR [Title: prediction]] AND [E-Publication Date: (1 January 2020 TO 31 December 2024)]
  IEEE Xplore	(((wind AND (power OR speed) AND (forecasting OR prediction) AND (deep neural network OR DNN OR deep learning)) AND ((“Document Title”:“Wind Speed” OR “Document Title”:“Wind Power”) AND (“Document Title”:“Forecasting” OR “Document Title”:“prediction”))) AND (“Abstract”:“deep learning” OR “Abstract”:“deep neural network” OR “Abstract”:“DNN”))
  ScienceDirect	wind AND (power OR speed) AND (forecasting OR prediction) AND (deep neural network OR DNN OR deep learning) AND [Title, abstract or keywords: (“deep learning” OR “deep neural network” OR DNN)] AND [Title: (“Wind Speed” OR “Wind Power”) AND (Forecasting OR forecast OR prediction)]
  Springer Link	“wind AND power AND speed AND forecasting AND prediction AND (deep OR neural OR network OR learning OR DNN)” within 2020–2024 Remove this filter
  Wiley Online Library	“wind AND (power OR speed) AND (forecasting OR prediction) AND (deep neural network OR DNN OR deep learning)” anywhere and “(“Wind Speed” OR “Wind Power”) AND (Forecasting OR forecast OR prediction)” in Title and “deep learning” OR “deep neural network” OR “DNN” in Keywords

  presents the specific database configurations applied during this first evaluation.
• Second Evaluation, Inclusion/Exclusion Criteria: Apply the inclusion and exclusion criteria (detailed in a later section) to filter the studies selected in the previous step.
• Third Evaluation, Scientific Validity Assessment: Use a Likert scale to evaluate the scientific quality and validity of the remaining articles.
• Data Extraction: Extract relevant information from the articles identified in step 6 to address the research questions of the study.

2.2.3. Inclusion and Exclusion Criteria

The inclusion criteria for this review require that studies focus specifically on wind power forecasting models based on deep neural networks and be published in peer-reviewed journals. Eligible articles must be directly related to wind power forecasting, employ deep learning or deep neural network techniques, and appear in recognized academic journals.

Conversely, the exclusion criteria eliminate studies that are not related to wind power or wind speed forecasting, do not utilize deep learning or deep neural networks, do not rely solely on Numerical Weather Prediction (NWP) methods, or do not merely present applications without proposing or developing a forecasting model.

The selection process was performed by the authors—Edgar A. Manzano and Ruben Nogales—who screened the titles, abstracts, and full texts according to the inclusion and exclusion criteria. In cases of disagreement, the author Alberto Rios acted as an arbitrator to reach consensus. No automation tools were used during this process.

2.2.4. Quality Assessment

After selecting the articles based on the inclusion and exclusion criteria, each article was evaluated using a Likert scale. This scale is used to assess the quality of the studies in terms of methodology, results, and presentation. Each reported criterion is assigned a weight based on the response level, as shown in

Table 4. Likert scale categories and assigned weights.

Category	Description	Weight
a. Strongly Disagree	Clearly lacking	−1.00
b. Disagree	Weakly addressed	−0.50
c. Neither Agree nor Disagree	Moderately addressed or unclear	0.25
d. Agree	Adequately addressed	0.50
e. Strongly Agree	Thoroughly addressed	1.00

.

To ensure balance, the sum of the weights from categories “a”, “b”, “d”, and “e” is calculated. For example, if (1) is met, the article is placed at the midpoint of the quality scale.

$$\sum (a+b+d+e)=0$$

(1)

The values from category “c” are used to define the threshold $\tau$ in (2).

$$\tau =\sum \left(c\right)=n_c\times 0.25$$

(2)

where $n_c$ is the number of responses in category “c”.

Inclusion Rule: An article is included in the review if it meets (3).

$$\sum (a+b+d+e)\ge \tau$$

(3)

Only studies that meet or exceed this threshold, based on the quality assessment criteria, are included in the final systematic literature review. The following items detail the different criteria considered in this work:

• The results are reliable.
• The results hold significant value.
• The study contributes new insights.
• The evaluation effectively addresses its original objectives and proposal.
• The theoretical contributions, perspectives, and values of the research are well-defined.
• The research explores a diverse range of perspectives and contexts.
• The research design is justifiable.
• The problem’s approach, formulation, and analysis are thoroughly executed.
• The design of the sample and selection of target classes are well-documented.
• The data collection process was conducted effectively.
• The criteria for evaluating the results are clearly established.
• The connections between data, interpretation, and conclusions are evident.
• The research scope allows for further investigation.
• The research process is well-documented.
• The reporting is clear and logically structured.

Data extraction was carried out independently by the two aforementioned authors, using a predefined form to record study characteristics (e.g., forecasting horizons, datasets, architectures, performance metrics). Any disagreements were resolved by consultation with the third author. No automation tools were employed in this stage.

Initially, 405 papers were identified from indexed databases, marking the completion of the first phase. The second phase involved evaluating the papers against inclusion and exclusion criteria, while the third phase consisted of assessing the papers using the Likert scale.

Table 5. Results after completing the procedure.

Databases	First Phase	Second Phase	Third Phase
ACM	9	5	1
IEEE Xplore	130	116	4
ScienceDirect	231	207	114
Springer Link	26	13	0
Wiley	9	8	1
TOTAL	405	349	120

details the results.

We summarize the conducting phase of the Kitchenham and Charters methodology in a PRISMA 2020 flow diagram (Figure 1).

2.3. Reporting Phase

To gather information about the primary studies, we developed a generic model designed to evaluate the proposed architectures across various works in the scientific literature (Figure 2). This model consists of the following components:

• Preprocessing and Feature Extraction Techniques: Before applying forecasting models, it is crucial to preprocess the raw data and extract meaningful features. Signal decomposition methods are used in this phase to break down the complex time-series data into simpler components.
• DNN Models: Algorithms use the learned patterns and relationships from the data to make accurate predictions about future wind power generation, continuously adapting to new data and improving forecasts over time by learning from historical data patterns.
• Optimization Algorithms: These methods ensure that the DNN model achieves the best possible performance by optimizing its parameters and hyperparameters, speed up the training process, and achieve better convergence.

2.3.1. Preprocessing and Feature Extraction Techniques

Basic pre-processing techniques remain essential for reducing noise and standardizing wind-speed data. Standard normalization, including z-score scaling, is applied in [17]. Missing values are imputed with the k-Nearest Neighbours (kNN) algorithm in [18,19,20,21], and unsupervised grouping with k-means clustering appears in [22,23]. These lightweight operations prepare the data for more sophisticated decomposition.

Among the multi-scale transforms, the wavelet transform (WT) is the most frequently cited because it captures non-stationary patterns in distinct frequency bands that can be separately modeled. Recent studies employ WT for denoising [24,25,26] or convert WS series into matrix form to represent strong temporal fluctuations [27]. A stationary variant (stationary wavelet transform, SWT) appears in [28]. The discrete wavelet transform (DWT) separates low- and high-frequency components, which makes each sub-series more stationary and therefore easier to model, leading to improved forecasting accuracy [29,30]. The empirical wavelet transform (EWT), an adaptive spectral method, was used to extract fluctuating features in [31,32] and has been paired with spectral clustering [33] and combined with other methods [24].

At an intermediate level of complexity, Singular Spectrum Analysis (SSA) excels at isolating trend and periodic components while suppressing noise [34,35]. Its performance improves when paired with Extreme Gradient Boosting (XGBoost), Convolutional Long Short-Term Memory (ConvLSTM), or Categorical Boosting (CatBoost), as shown in [21,22,36]. The family of empirical decomposition methods begins with the classical iterative filter–sifting approach, which appears in wind speed research such as [37,38]. Its modern successor is Empirical Mode Decomposition (EMD), which was applied in [20]. A time-adaptive version named Time Variant Filter EMD (TVF-EMD) is combined with the Empirical Wavelet Transform in [24]. By retuning the filter at every iteration, TVF-EMD limits mode mixing and edge artefacts, as shown in [39].

Building on EMD, Ensemble EMD (EEMD) averages many noise-perturbed runs and produces more repeatable intrinsic mode functions, an idea used in [20,24,37,40,41]. Complementary EEMD (CEEMD) refines this strategy by adding pairs of positive and negative noise so that the injected noise cancels in expectation, as reported in [42,43,44]. Complete Ensemble EMD with Adaptive Noise (CEEMDAN) further injects adaptive noise at each iteration and then removes it which yields perfectly reconstructable and cleaner components [20,45,46,47,48,49]. The most recent variant Improved CEEMDAN (ICEEMDAN) recursively refines the residual, suppresses mode mixing more effectively, and needs far fewer ensemble runs [50,51,52,53,54].

Finally, Variational Mode Decomposition (VMD) optimizes the extraction of band-limited modes with less edge effects than classical EMD. Baseline implementations appear in [55,56,57,58,59,60,61,62,63]. Optimized variants tune parameters through Particle Swarm Optimization (PSO), Genetic Algorithms (GAs), or other metaheuristic strategies [64,65,66,67,68,69]. VMD has also been integrated with Hue–Saturation–Value (HSV) color-space imaging [70], denoising autoencoders [71], and Graph Neural Network (GNN)-based temporal modules [72]. In addition, multi-method frameworks that combine VMD with CEEMDAN and SSA have demonstrated greater robustness when dealing with noisy and highly non-stationary data [73].

These approaches span fundamental transforms to variational and meta-optimized decomposition, offering researchers a versatile toolbox that can be adapted to signal complexity and the required level of forecasting accuracy.

2.3.2. DNN-Based Models

Standard recurrent neural networks (RNNs) introduce feedback connections but struggle with long-range dependencies. Long Short-Term Memory (LSTM) solves that limitation thanks to its input, forget and output gates, which let the cell track intermittent, long-term patterns in wind speed series [19,27,37,43,48,56,74,75,76,77]. The Gated Recurrent Unit (GRU) retains much of that memory power with fewer parameters, which is useful when data are scarce [28,53,67,78,79]. Bidirectional LSTM (BiLSTM) processes the sequence forward and backward, injecting future context into every time step, a popular choice in wind-prediction studies [20,22,24,55,69,80,81,82,83].

Many variants combine recurrent cells only. Examples include Deep EDLSTM [84], encoder–decoder LSTM [85], and a family of LSTM/BiLSTM hybrids [46,66,68,86,87,88]. GRU-centred designs appear as well: GRU-SNN for spiking processing [31] and multi-stage or ensemble GRU systems [33,62,89,90,91]. Bidirectional GRU (BiGRU) plays the same role in dual models [39,92].

A second line of research intertwines classical statistical models and shallow neural networks with deep-learning blocks. Linear components are typically handled by AutoRegressive Integrated Moving Average (ARIMA) and Seasonal ARIMA (SARIMA), which provide fast, interpretable baselines. Among shallow nets, the Extreme Learning Machine (ELM) is prized for single-pass training: hidden weights are frozen at random and output weights are obtained analytically, so ELM is exceptionally fast on large datasets. The Adaptive Neuro-Fuzzy Inference System (ANFIS) exploits fuzzy rules plus neural-network learning to capture nonlinear relationships with a small number of interpretable parameters. Deep Belief Networks (DBNs) stack Restricted Boltzmann Machines to deliver unsupervised pre-training, while the Multilayer Perceptron (MLP) and its error-back-propagation variant (BPNN) continue to serve as standard benchmarks.

These elements are combined in many hybrid architectures, for example, DBN–LSTM–ARIMA–BPNN–ELM [50], BPNN–LSTM [45], SARIMA–LSTM [29], MLP–LSTM [93], BPNN–ELM–ANFIS–LSTM [54], ensembles that run RNN, GRU and LSTM in parallel [36,94], BiLSTM - ELM [44], GRU–BiLSTM [32], and BiLSTM–BiGRU pairings [30].

Temporal Convolutional Networks (TCNs) use causal dilated convolutions to reach long contexts while remaining highly parallelizable [95]. They have inspired hybrids such as TCN-LSTM [38] or the LSTM-TCN-NTF scheme, where Non-stationary Transformers (NTFs) tackle regime shifts [96].

The Attention mechanism (ATT) dynamically re-weights inputs and hidden states. It has been grafted onto MLP [97], GRU [7,40], BiGRU [63], LSTM [98], and BiLSTM (pure or with a TCN) [13,47,64].

Transformers discard recurrence entirely: self-attention captures global dependencies and scales smoothly to long sequences. Pure Transformer wind predictors exist [25], as do Transformer modules nested inside larger hybrids [99].

Graph Neural Networks (GNNs) model stations as nodes and wind flows as edges, learning the implicit spatio-temporal topology [100]. They also appear inside broader systems that blend GNNs with GRU, LSTM, MLP and Transformer [72] or with BiGRU plus attention [49]. Other variants include graph-attention models [101] and spatio-temporal graph networks (STGNs) [102].

Convolutional LSTM (ConvLSTM) inserts convolutions into LSTM gates so it can handle 2D grids over time—ideal for wind maps. It is used on its own [23], paired with Kernel ELM [103], extended in novel variants [104], or combined with ConvGRU inside multi-branch schemes [105].

Convolutional Neural Networks (CNNs) extract local spatial patterns (e.g., 3 × 3 filters in a regional wind-farm map [106]) and are applied directly [11,61,65,70,107] or enhanced with attention [41]. For 2D gridded inputs, U-Net (a CNN architecture) is also used in [108].

Finally, there are many CNN hybrids: the CNN–LSTM fusion marries CNN spatial encoding with LSTM temporal memory, spawning a vast family; CNN-GRU [42]; LSTM-CNN variants [18,109,110]; the dual-branch CNN-SP-LSTM [111]; industry-inspired designs [17,112]; multi-model ensembles (ANFIS–LSTM–CNN–ELM) [52]; CNN-BiLSTM systems [21,59,113,114,115]; and attention-augmented versions such as CNN-BiLSTM-ATT [57,116]. Broader pipelines such as those in [117] and the CNN-BiGRU-TCN triad presented in [73] illustrate the current trend toward increasingly rich composite architectures.

2.3.3. Optimization Algorithms

The Grey Wolf Optimizer (GWO) is a nature-inspired metaheuristic algorithm that simulates the leadership hierarchy and hunting strategy of grey wolves. Introduced for continuous optimization problems, the standard GWO has been used in [31,64]. More recent studies have proposed enhancements to GWO, for instance, an Improved Grey Wolf Optimizer (IGWO) was introduced in [11] to improve the convergence speed and avoid local optima through adaptive control parameters. Multi-objective GWO (MOGWO) is applied in [52], extending GWO to handle multiple forecasting objectives simultaneously, such as accuracy and robustness. Further refinements include the Two-phase Mutation GWO (TMGWO) in [87], which integrates a mutation strategy to enhance diversity in the search process, and the social rank updating GWO (SGWO) in [88], where social behavior is modified to prioritize more promising search directions. Lastly, GWO is also used as part of integrated optimization schemes in hybrid models such as [77], showing its versatility in various WSF contexts.

Several newer carnivore-inspired swarms share GWO’s hierarchical hunting logic such as Improved Chimp Optimization (ICHOA) in [39] or Multi-objective Enhanced Golden Jackal Optimization (MOEGJO) in [82].

Hybrid and swarm intelligence algorithms combining hawk or tunicate behavior have gained attention for solving complex forecasting tasks. In [103], a hybrid swarm optimizer (Mutation Harris Hawks Optimization and Grey Wolf Optimizer, MHHOGWO) is proposed by combining Harris Hawks Optimization (HHO) with GWO. This method leverages the exploitation power of GWO and the exploratory dynamics of HHO, further enhanced with mutation operations, to escape local optima and improve forecasting accuracy. In the domain of bio-inspired improvements, [51] introduces the Modified Multi-objective Tunicate Swarm Algorithm (MMOTA), a modified Tunicate Swarm Algorithm (TSA) enhanced with elite opposition learning and multi-objective strategies. This allows for better exploration while preserving convergence efficiency. Another tunicate-based improvement, ITSA (Improved Tunicate Swarm Algorithm), can be found in [34], aiming to refine search strategies in dynamic forecasting environments.

Genetic Algorithms (GAs) are classical evolutionary optimization methods inspired by natural selection. They have been applied in [43]. More advanced evolutionary designs include the Multi-objective Binary Backtracking Search Algorithm (MOBBSA) in [85], tailored to handle binary decision spaces in feature selection or model structure optimization. Furthermore, [69] presents the Differential Evolution Sparrow Search Algorithm (DESSA), which provides adaptive exploration capabilities in dynamic environments. Another examples is the Heap-Based Optimizer (HBO), which introduces a memory heap that adjusts weights dynamically in [75].

The Dragonfly Algorithm (DA) mimics static and dynamic swarming behaviors found in nature. The authors of [50] proposed a Modified Multi-objective Dragonfly Algorithm (MMODA) to handle nonlinear WS data, offering improved convergence to a Pareto front. Similarly, ref. [55] presents Multi-objective Opposition-based Firefly Algorithm with Dragonfly Algorithm (MOOFADA), aimed at avoiding premature convergence and ensuring global exploration.

Kindred terrestrial swarms enrich the aforementioned behavioral template: Improved Reptile Search (IRSA) incorporates adaptive control factors to maintain diversity during the exploit phase [44]. Coati Optimization (COA) leverages cooperative foraging of coatis, alternating scout and exploitation moves to navigate rugged landscapes [109]. The Multi-objective Slime Mould Algorithm (MOSMA) models slime–mould oscillatory motion, maintaining exploration pressure near the global optimum [89].

Particle Swarm Optimization (PSO) is a widely used optimization technique based on the social behavior of bird flocking; it is employed in [56,65,96] to tune model parameters or select relevant input features. Ref. [33] enhances this with Improved PSO (IPSO), addressing the challenge of stagnation by incorporating inertia weight adaptation. Hybrid models like that in [65] utilize PSO for feature extraction and combine it with Wild Horse Optimization (WHO) for hyperparameter tuning, showing that PSO variants can be highly flexible. In [118], Chaotic PSO (CPSO) is applied, leveraging chaos theory to diversify the particle trajectories and prevent premature convergence.

The Ant Colony Optimization (ACO) algorithm models pheromone-guided search behavior in ants. Ref. [119] employs a variational version of ACO for optimizing forecasting parameters, achieving robust performance in nonlinear conditions. Similarly, ref. [22] uses the Cuckoo Search (CS) algorithm with early stopping to prevent overtraining. The Crisscross Optimization Algorithm (CSO) in [40] is a lesser-known but efficient search method designed to explore multidimensional spaces through cross-dimensional operations; this was improved in [21] by introducing Multi-objective CSO (MOCSA).

Bayesian Optimization (BO) is a probabilistic approach to optimize black-box functions by building a surrogate model and selecting the most promising configurations using acquisition functions. It is applied in [36,48,81] for hyperparameter tuning. In a more heuristic manner, ref. [59] proposes Adaptive Greedy Optimization (AGO) to adaptively search the hyperparameter space. Another example is the Multi-objective Multi-Verse Optimizer (MOMVO), used to adaptively expand or contract candidate regions, producing diverse Pareto solutions at modest costs [54].

Marine-based and newer swarm algorithms are increasingly used in multi-objective settings. Ref. [120] introduces the Multi-objective Opposition Elite Marine Predator Optimization Algorithm (MOEMPA), a strategy that enhances convergence through opposition-based mechanisms. Similarly, ref. [98] applies the Whale Optimization Algorithm (WOA), known for its bubble-net strategy that models encircling behavior.

After completing the reporting phase—which examined preprocessing techniques, signal-decomposition methods, deep learning models and optimization algorithms—we developed a detailed workflow diagram for DNN-based wind power forecasting (Figure 3). This diagram summarizes the entire prediction methodology. In addition, the evaluation metrics extracted from the literature are incorporated and discussed in a later section.

2.3.4. Corpus vs. Narrative Scope

We retained 120 primary studies. In this section, we cite only the subset that directly addresses our three axes: preprocessing and feature extraction, DNN models, and optimization algorithms. Several studies are not cited individually here because they pursue aims outside of the scope of this section (e.g., few-shot/meta-learning and generative augmentation, online/continual learning, distribution-shift handling, or parametric probabilistic formulations). Nevertheless, all 120 references were considered in the quantitative evidence used to answer our research questions: every retained study contributed to the aggregate statistics (e.g., performance criteria, forecasting horizon, data sources, and distributions) that support our answers. For completeness and proper acknowledgment, we explicitly cite the studies used in the statistics but not discussed in the narrative [121,122,123,124,125,126,127,128,129,130,131,132].

3. Discussion

Given the methodological heterogeneity among the included studies—in terms of datasets (private/public, country-specific), forecasting horizons, model architectures, and performance metrics (RMSE, MAE, R², MAPE)—a statistical meta-analysis was not appropriate. Instead, we applied a narrative synthesis by grouping studies according to the defined research questions (RQ1–RQ5). No formal statistical heterogeneity tests or sensitivity analyses were conducted.

3.1. RQ1: What Are the Current Architectures for Wind Power Forecasting Models That Utilize Deep Neural Networks, Feature Extraction Techniques, and Optimization Algorithms?

To address this first research question, a comprehensive analysis of all reviewed papers has been conducted, dividing the analysis into the wind power prediction models used in the studies, preprocessing and feature extraction techniques employed, and the optimization algorithms considered by the same research. Thus,

Table 6. Pure DNN models used in WPF studies.

Model (Single Family)	Studies
LSTM	10
BiLSTM	10
Other Variants of LSTM	2
GRU	5
BiGRU	2
Other Variants of GRU	7
Transformer	1
GNN (2D)	1
CNN (2D)	6

,

Table 7. Hybrid DNN architectures used in WPF studies.

Architecture (Two or More Families/Blocks)	Studies
BiLSTM-BiGRU	1
TCN-LSTM	4
ATT-GRU	2
ATT-BiGRU	1
ATT-LSTM	1
ATT-BiLSTM	3
GNN-LSTM	1
GNN-GRU	1
GNN-BiGRU	1
GNN-Transformer	1
CNN-GRU	1
CNN-LSTM	3
CNN-BiLSTM	5
CNN-BiLSTM-ATT	2
CNN-BiGRU-TCN	2
Hybrid LSTM/BiLSTM	6
Hybrid ConvLSTM	4
Other Hybrid LSTM	6
Other Hybrid GRU	2
Other Hybrid BiLSTM	2
Other Hybrid Transformer	1
Other Hybrid GNN (2D)	3
Other Hybrid CNN (2D)	6

and

Table 8. Totals by hybrid family.

Hybrid Family	Total Occurrences
Total Hybrid LSTM	26
Total Hybrid GRU	6
Total Hybrid BiLSTM	19
Total Hybrid BiGRU	6
Total Hybrid Transformer	2
Total Hybrid GNN	5
Total Hybrid CNN	18

Notes. Counts reflect occurrences of model families, not unique papers. A study can contribute to multiple families if its architecture includes several blocks (e.g., CNN–BiLSTM contributes to both CNN and BiLSTM).

display the counts of core models used across the corpus. The values are occurrences rather than unique papers: a single study can contribute to multiple rows if it employs more than one model. Pure models are listed only in Table 6; hybrid combinations are listed only in Table 7 and Table 8. Family totals in bold highlight occurrences within each family and may therefore exceed the total number of studies (N = 120).

3.1.1. WPF Models Based on DNNs

Based on the analysis of the information found, the dominance of LSTM, GRU, and BiLSTM models in WPF can be attributed to several factors, particularly their strengths in handling time-series data, efficiency, and interpretability in capturing complex temporal dependencies. Below we analyze the trends found.

First, LSTM models are the most widely used due to their ability to handle long-term dependencies and mitigate the vanishing gradient problem, which is crucial in time-series forecasting like wind power forecasting. Wind power generation data often has irregular and complex temporal patterns, and LSTMs excel in learning from these historical dependencies over longer periods. LSTM models are preferred due to its long-term memory retention, high adaptability, maturity and effectiveness. Second, BiLSTM networks are increasingly used and are likely to see even more applications in future research due to their ability to capture both past and future information in a sequence. This makes BiLSTM well-suited for scenarios where understanding the full context (before and after a particular point) is critical.

Third, GRU models are a simplified version of LSTMs, designed to achieve a comparable performance with fewer parameters and a less complex architecture. GRU models are popular because of their faster training times, similar performances to LSTM models, and less need for long-term memory for certain applications where short-term memory may be prioritized.

Finally, hybrid models are more widely used in WPF research because they combine the strengths of multiple methods to improve performance and accuracy. In such a complex and dynamic field as WPF, no single model is sufficient to handle all the challenges involved, which is why hybrid approaches have become increasingly prevalent. Hybrid models combine different techniques to capture different aspects of the data, leading to better overall predictions. For example, LSTM models are excellent for capturing temporal patterns, while CNN models can capture spatial dependencies; this allows hybrid models to account for both the spatial and temporal characteristics of wind power data, improving the model’s ability to generalize and generate accurate forecasts.

Therefore, hybrid LSTM models are the most commonly used in WPF because they effectively combine the strengths of LSTM with other methods, such as CNNs, statistical models, or attention mechanisms. LSTMs excel at capturing long-term temporal dependencies in wind power data, but integrating them with complementary techniques improves overall forecasting accuracy. Their flexibility and proven reliability make them a preferred choice for hybrid models, allowing researchers to enhance performance by addressing both temporal and spatial complexities in wind data.

In addition, hybrid BiLSTM models are gaining popularity because they offer bidirectional learning, capturing both past and future dependencies in the data, which is particularly useful for WPF. These models improve prediction accuracy by providing a more comprehensive view of temporal relationships. As computational power increases and more complex models become feasible, the use of BiLSTM-based hybrids is expected to grow, as they deliver richer insights for forecasting in highly dynamic systems like wind power systems.

3.1.2. Signal Decomposition Methods

Wind power data is inherently complex, with non-stationary and nonlinear characteristics due to the irregular nature of wind patterns. The trend in feature extraction techniques for WPF in

Table 9. Signal decomposition methods used in studies as part of preprocessing and feature extraction processes.

Signal Decomposition Methods	Studies
Hybrid VMD	10
VMD	9
CEEMDAN	6
ICEEMDAN	5
SSA	5
EEMD	5
EWT	4
WT	3
EMD	3
CEEMD	3
DWT	2
ED	2
SWT	1

reveals a preference for methods that effectively handle these aspects. VMD excels in decomposing these signals into discrete modes that represent different frequency components, allowing for a more precise understanding of underlying patterns. VMD operates within a more well-defined mathematical framework, minimizing mode mixing (a common issue with Empirical Mode Decomposition methods like ICEEMDAN), leading to more accurate decomposition and feature extraction.

Hybrid VMD models combine VMD with other techniques to further enhance signal decomposition and feature extraction. These hybrid approaches take advantage of VMD’s precise mode extraction and integrate it with advanced methods that can better handle noise, outliers, or short-term fluctuations in wind data.

ICEEMDAN and its variants (like CEEMDAN and EEMD) are designed to handle noise and improve upon the original EMD (Empirical Mode Decomposition) technique, but they come with some inherent limitations like noise sensitivity, mode decomposition control and slower convergence.

3.1.3. Optimization Algorithms

WPF involves dealing with highly nonlinear and volatile data, making the optimization landscape multimodal (with many local optima). According to

Table 10. Optimization algorithms considered in proposals.

Optimization Algorithms	Studies
GWO and enhancements	8
PSO and enhancements	6
GA variants	4
BO	3
Other types of terrestrial swarm algorithms	3
Hybrid and swarm algorithms	3
DA variants	2
Other carnivore-inspired swarm algorithms	2
ACO, CD, CSO, MOCSA, AGO, MOMVO, MOEMPA, WOA	1

, GWO and its hybrid form are the most used algorithms, probably because they are particularly well-suited for these types of problems because they adapt to complex search spaces without relying on derivative information, allowing them to efficiently navigate and optimize the nonlinear parameters involved in model training.

PSO and GA, though capable of handling nonlinearity, tend to exhibit premature convergence or struggle with complex multimodal landscapes in cases where the optimization problem is highly nonlinear. GWO, with its hierarchical hunting mechanism, can better navigate through these challenging landscapes by encouraging wolves to explore diverse solutions before narrowing down on the best ones.

The shift towards hybrid GWO and PSO highlights the trend of combining traditional algorithms with advanced techniques to improve forecasting accuracy and efficiency in WPF models.

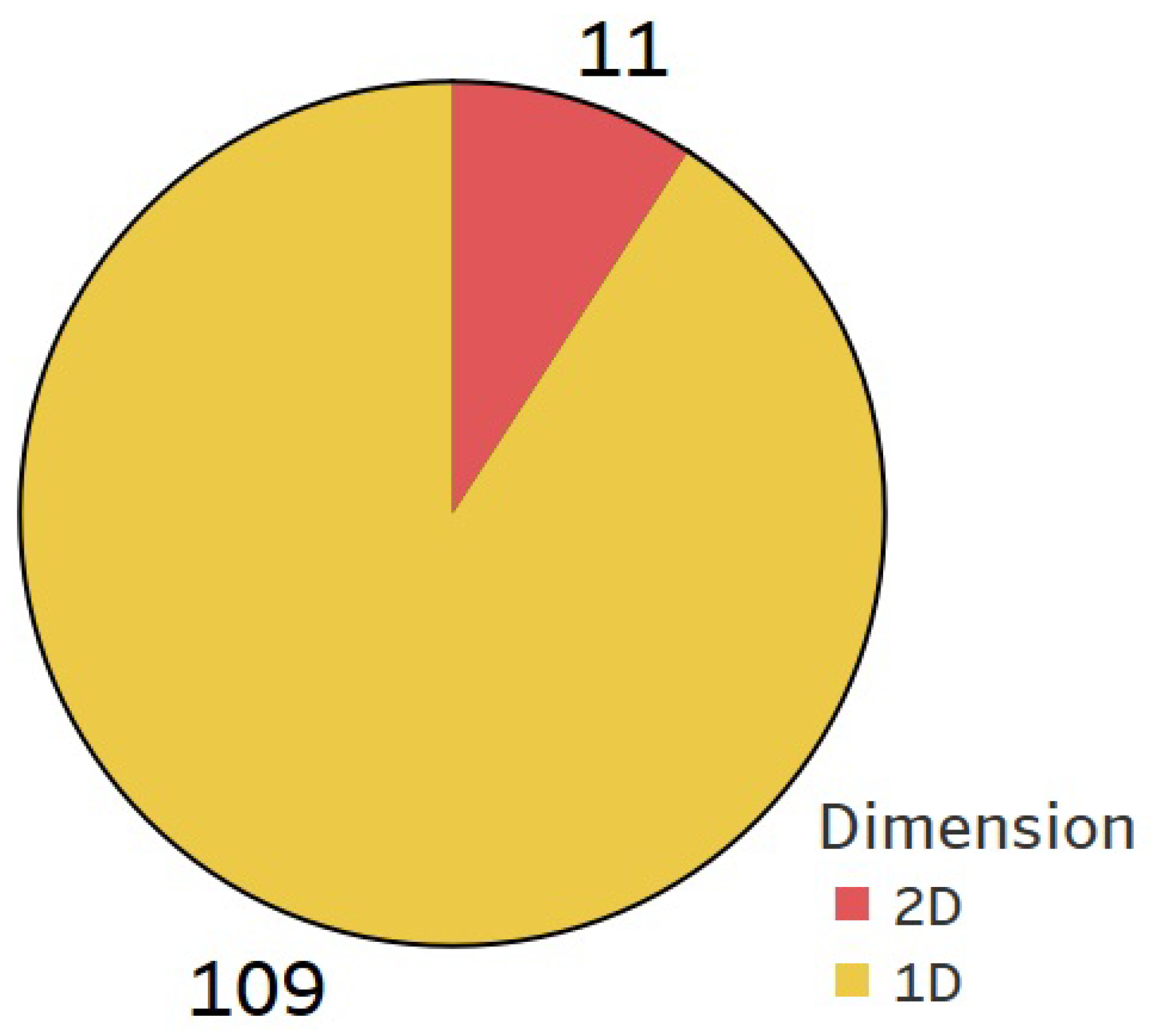
3.1.4. Dimensions

Analyzing the type of dimension focused on by researchers, we found a dominance of 1D techniques in WPF over 2D techniques, as observed in Figure 4. This can be attributed to their strengths and practical advantages. 1D models, such as LSTM and GRU, are highly effective at capturing temporal patterns in time-series data, which is crucial for accurate forecasting. Their simplicity and lower computational demands make them accessible and widely applicable. In contrast, 2D models, which integrate both spatial and temporal dimensions, offer a more comprehensive analysis by incorporating geographical variations and multiple meteorological variables. Nonetheless, their complexity and higher data requirements, coupled with increased computational costs, limit their practical application. The preference for 1D techniques reflects their proven effectiveness and practicality in managing time-series data, while the complexity and data demands of 2D techniques contribute to their less frequent adoption in WPF.

3.2. RQ2: What Are the Current Performance Metrics for Validating Models?

Performance metrics can be classified into the following categories based on what aspect of model performance they measure:

• Error Metrics (RMSE, MAE, MSE, MAPE, PINAW and others): These metrics assess the magnitude of prediction errors and help quantify how far the predicted values are from the actual values.
• Correlation-based Metrics ($R^2$, R and others): The difference between this group and the previous one is that it focuses on the relationship or correlation between actual and predicted values rather than the error.
• Statistical Test and Model Comparison (DM, Theil’s U and others): These metrics and tests are used to compare different models and determine their relative performance.
• Coverage Metrics (PICP, CWC and others): These metrics assess how well the model’s prediction intervals capture the actual outcomes.
• Forecasting Accuracy Improvement Metrics (INAW, TIC and others): These metrics are used to assess improvements in forecasting accuracy and compare model performance.

Taking into account the results shown in

Table 11. Performance criteria used in research.

Abbrev.	Performance Criteria	Studies
RMSE	Root-Mean-Squared Error	99
MAE	Mean Absolute Error	96
MAPE	Mean Absolute Percentage Error	66
$R^2$	Coefficient of Determination	46
MSE	Mean Squared Error	29
PICP	Prediction Interval Coverage Probability	13
PINAW	Prediction Interval Normalized Average Width	11
DM	Diebold–Mariano test statistic	11
R	Pearson’s Correlation Coefficient	10
CWC	Coverage Width-based Criterion	10

, RMSE and MAE are highly valued for their simplicity and directness in measuring forecasting accuracy. In addition, RMSE and MAE are easy-to-interpret, widely accepted standards and exhibit versatility across various types of models and datasets; this makes them common choices for evaluating model performance.

MAPE and R² are also significant, as they assess relative error and goodness-of-fit. Nevertheless, R² is not a true error metric like RMSE or MAE, having a dependence on the mean; MAPE can also be problematic with extreme values and it exhibits asymmetry in errors.

Metrics like DM and CWC are less frequently used because they may be more specialized or require additional assumptions and computations. They are often used in specific contexts or for particular types of analyses, which limits their broader applicability.

Note that counts in Table 11 reflect occurrences rather than unique papers; studies that report multiple metrics contribute to each relevant category.

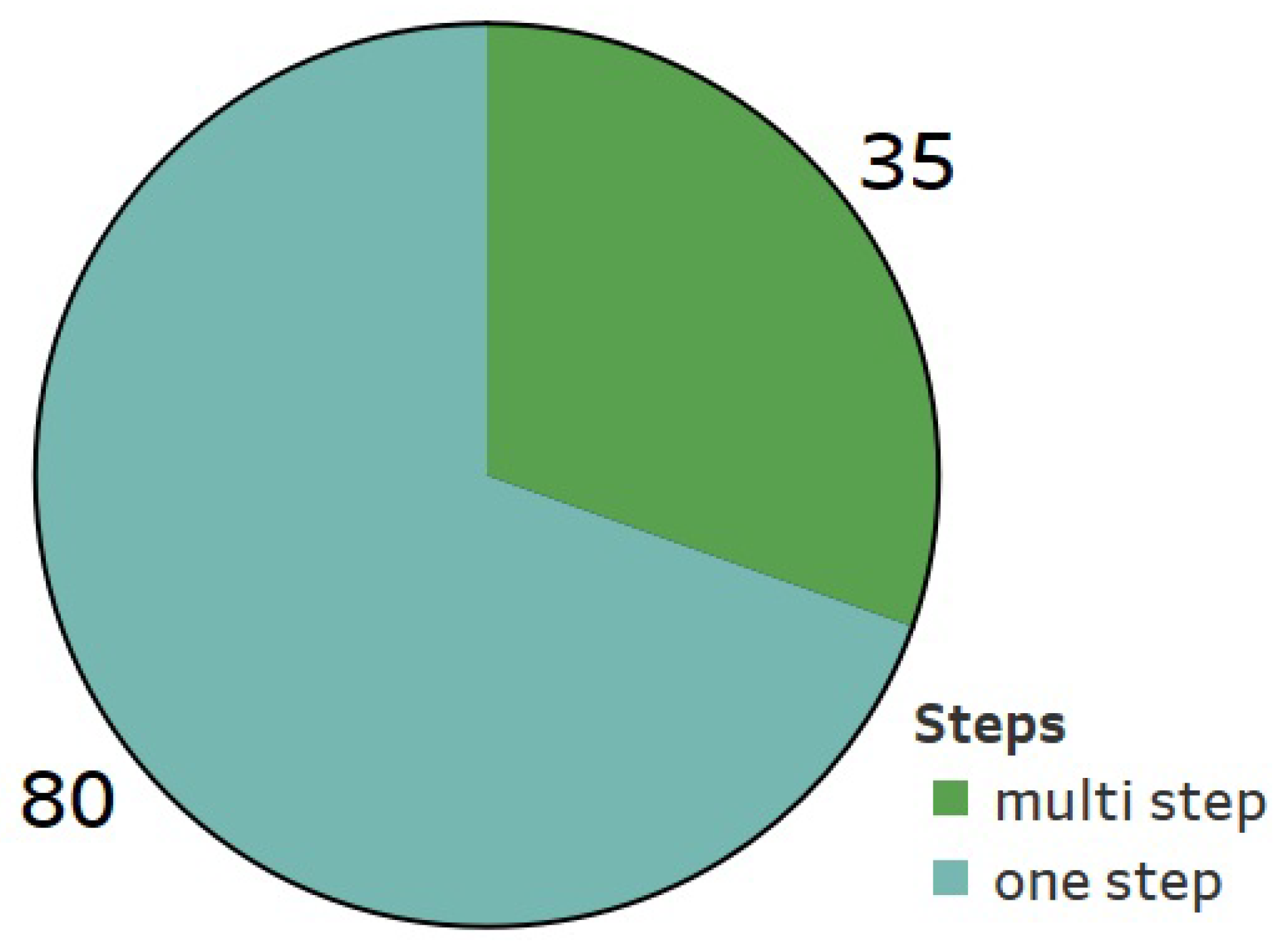
3.3. RQ3: What Is the Typical Forecasting Time Frame for Short-Term Horizon Forecasting Models?

In WPF research, according to Figure 5, there is a preference for one-step models likely due to their simplicity and efficiency, making them suitable for straightforward, high-resolution predictions. Multi-step models, though less common, are employed in scenarios requiring the capture of dynamics over several time steps, providing enhanced accuracy in more complex forecasting tasks.

Figure 6 shows short-term forecasting is predominantly favored, with 10-min intervals being the most common, used in 37 studies for high-resolution predictions. Other frequently used intervals include 1 h and 15 min, with less frequent use of longer intervals such as 2 to 24 h. This varied approach to forecasting horizons underscores the need for flexibility in WPF to address both immediate and slightly extended forecasting requirements, adapting to different operational and planning needs.

Additionally, it is important to emphasize that these steps are typically chosen based on dataset resolution, which is closely related to time steps. It is also important to note that resolution is often constrained by hardware performance or storage capacity for wind turbines or wind farms.

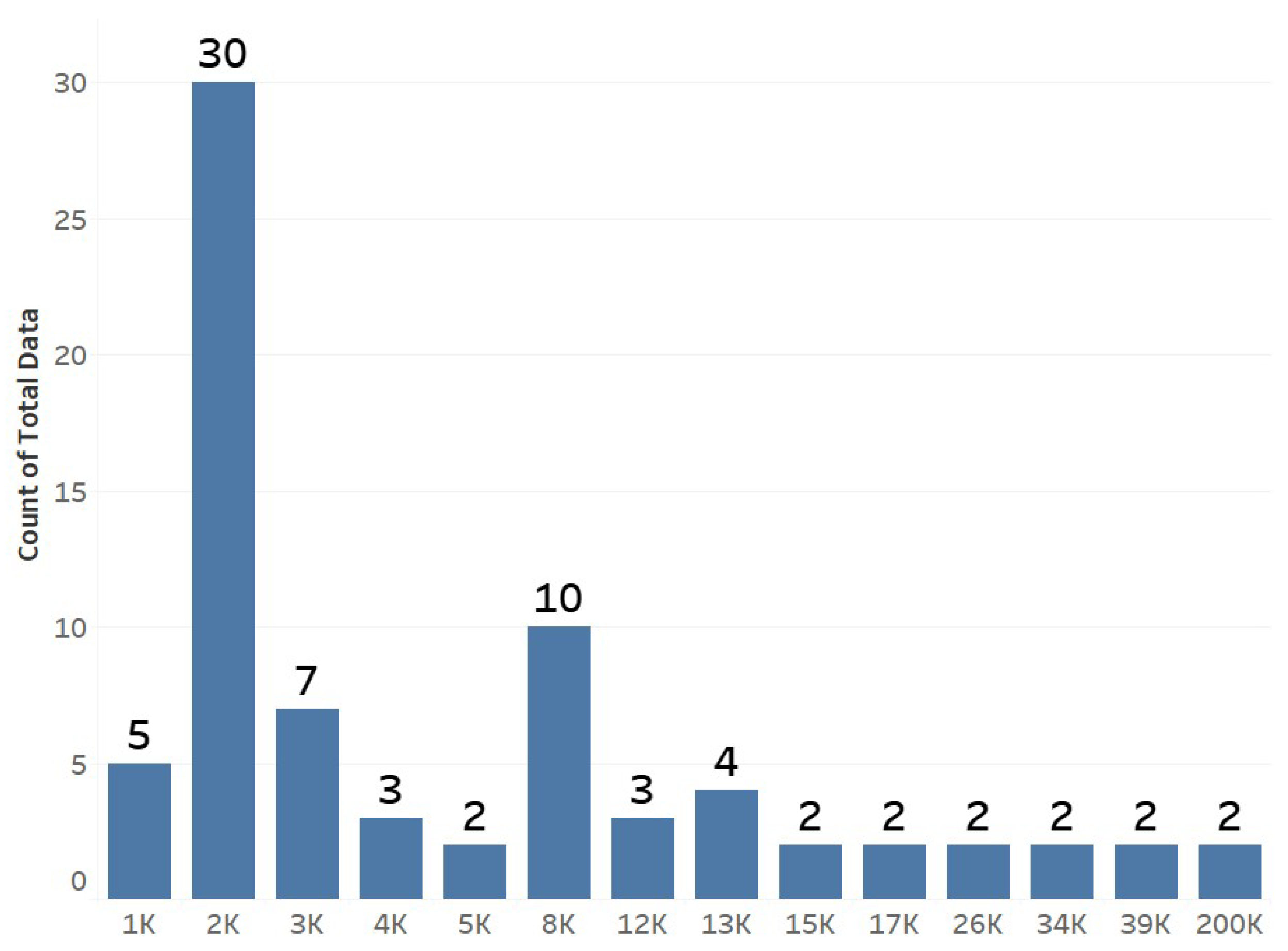
3.4. RQ4: What Are the Currently Accepted Datasets for Training Wind Power Forecasting Models Using Deep Neural Networks, and How Are These Datasets Distributed for Use?

WPF datasets originate from a range of countries, illustrating a global commitment to advancing WSP techniques.

Table 12. Datasets’ countries of origin.

Country	Studies
China	57
USA	21
Spain	8
India	7
France, Brazil	4
Canada	3
Greece, Scotland, Norway, Australia, Netherlands, Germany, Fiji, Sweden	2

shows that China stands out with 57 datasets, reflecting its significant focus on wind power research, while the USA contributes 21 datasets, showing considerable research efforts. India, Spain, and Brazil contribute 7, 8, and 4 datasets, respectively, indicating substantial regional interest. Additionally, France, Canada, Germany, Greece, Netherlands, Norway, Scotland, and Sweden each provide between 2 and 4 datasets, representing their involvement in the field. This broad international engagement and the availability of open datasets from Kaggle highlight a widespread and collaborative effort to improve WPF across various climates and operational settings.

As shown in Figure 7, datasets are categorized based on their accessibility. Private datasets, which are proprietary and often restricted to specific organizations or researchers, dominate, with a total of 74 datasets. In contrast, there are 20 public datasets, which are openly available to the broader research community. This distribution indicates that while there is substantial proprietary data held by various entities, the availability of public datasets remains crucial for collaborative research and the validation of forecasting models. Notably, there are five datasets available on Kaggle which are entirely free, making them accessible for further research and development.

In the reviewed studies, a diverse range of data sources was identified. Some studies utilize data from extensive wind farms, while others focus on a limited number of turbines. The sample sizes also vary, with only a subset of the available data being used. A discernible pattern is that, when assembling datasets, researchers typically prefer using data from a one-month period for each season (summer, autumn, winter, and spring), resulting in a total of four months of information. The volume of data varies depending on the resolution, which is linked to the forecasting horizon discussed in earlier sections, often set at 10 min. This influences the resolution of the dataset in this context.

The distribution of data sizes across the reviewed studies exhibits substantial variation, as illustrated in Figure 8. Among studies reporting specific data volumes, the majority cluster around modest sizes: 30 studies used approximately 2000 data points, while smaller groups employed 8000 (10 studies), 3000 (7 studies), and 1000 (5 studies) data points. Notably, two exceptional cases utilized significantly larger datasets of 200,000 points, followed by intermediate groups with up to 39,000 points. This wide dispersion in data scales raises concerns about potential reporting gaps or methodological inconsistencies, particularly given the frequent lack of detailed documentation regarding data acquisition and evaluation protocols. Such variability not only questions the reliability of comparative results but also highlights the critical need for standardized reporting frameworks to enable meaningful assessment of WPF model performance and scalability across studies.

Table 13. Proportions of datasets (training–testing–validation).

Dataset Division (%)	Studies
80–20%	23
70–30%	11
90–10%	10
80–10–10%	6
70–15–15%,	5
67–33%	5
60–20–20%	4
75–25%	4
70–20–10%	2
92–8%	2

presents the different training–validation–test splits commonly employed to evaluate forecasting models. The choice of partitioning strategy is critical, as it directly influences performance assessment. Some configurations allocate a larger proportion of data to testing or validation in order to achieve a more reliable evaluation of model robustness.

Overall, the review of the datasets used in the examined studies highlights a clear opportunity to strengthen future research by establishing more rigorous dataset selection protocols. Such improvement requires not only careful determination of appropriate sample sizes from the available population but also ensuring that sufficient data is dedicated to training. For effective sampling, the initial dataset should exhibit well-defined characteristics, including adequate resolution, variability, and population size. Moreover, applying statistical approaches similar to those used in financial forecasting may enhance the efficiency of WPF.

One promising direction involves segmenting data by season, a strategy adopted in several studies, to ensure that the sampled data reflects the overall population more accurately. To implement this effectively, further research should investigate how to incorporate wind speed variability—such as mean, minimum, and maximum values—when defining sampling protocols. Additionally, it would be beneficial to standardize the resolution time for training datasets, with a 10-min interval being a common choice among existing studies. Evaluating the most suitable data proportions for training and validation is also crucial, considering popular ratios such as 80–20%, 70–30%, and 90–10%. Moreover, assessing the adequacy of data volume for analysis is important, even though approximately 15,000 data points are frequently used in several studies. This evaluation could lead to specific recommendations regarding the use of models; for example, the feasibility of employing LSTM, BiLSTM, GRU, and their hybrid variants could be examined based on the available dataset size.

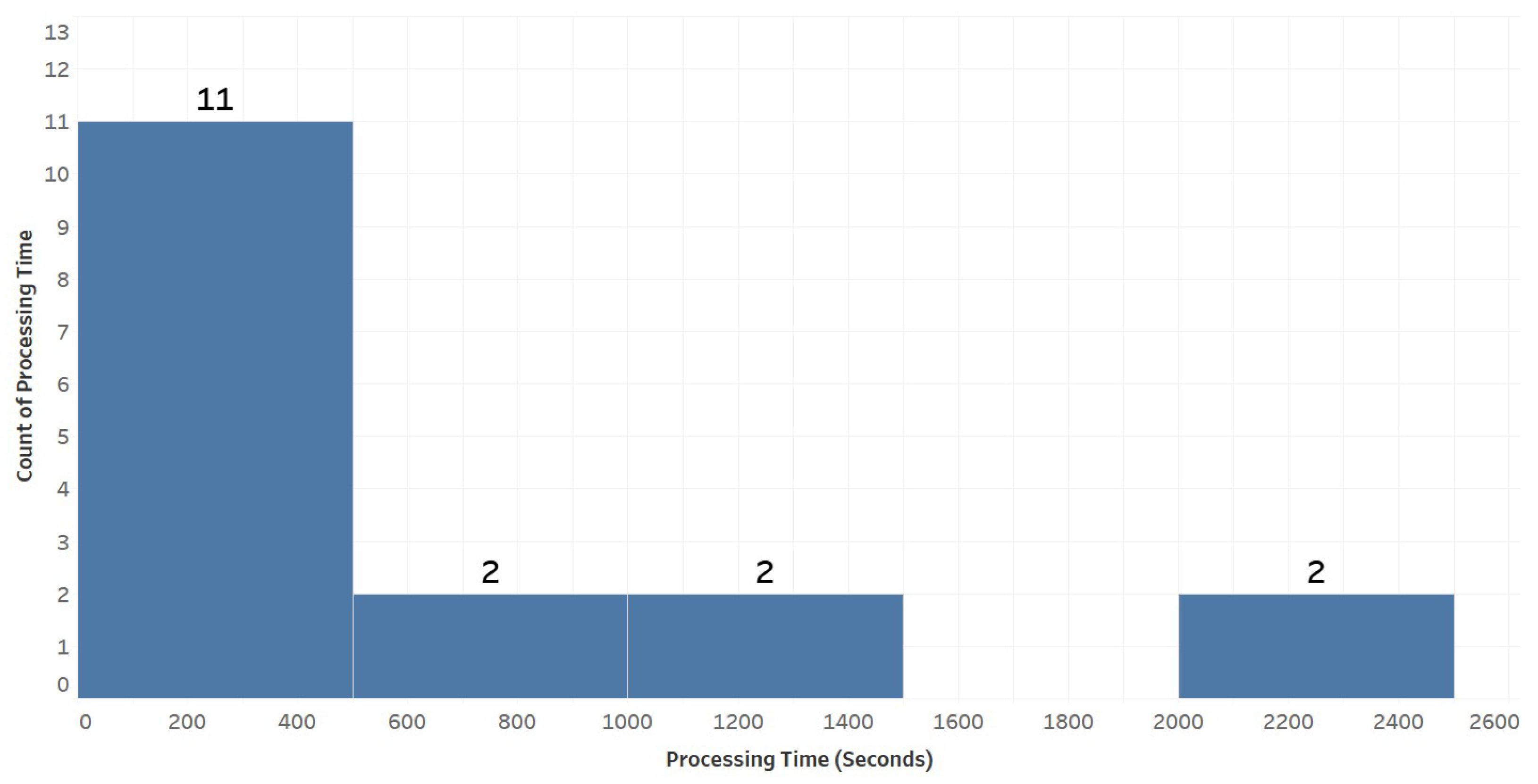
3.5. RQ5: What Are the Typical Processing Times for Current Wind Power Forecasting Models That Utilize Deep Neural Networks?

The processing times reported in the studies on WPF exhibit considerable variability, as illustrated in Figure 9. These variations highlight the diverse computational requirements of different forecasting models and their implementation. However, the limited number of studies providing detailed processing times underscores a critical gap. Addressing this gap is essential for future research to gain a clearer understanding of the performance of WPF models.

This quartile distribution demonstrates substantial variability in computational efficiency across different implementations, potentially reflecting differences in model complexity, hardware configurations, or optimization approaches. The presence of such wide-ranging processing times underscores the need for standardized benchmarking protocols to enable meaningful cross-study performance comparisons.

3.6. Additional Considerations

Due to the heterogeneity in methods and reported metrics, the study results were summarized narratively in structured tables (Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12) rather than pooled statistically.

A further limitation relates to the review process itself. Although multiple major databases (Scopus, Web of Science, IEEE Xplore, ScienceDirect) were searched, it is possible that some relevant studies were missed, particularly those published in non-indexed sources or in languages other than English. In addition, screening and data extraction were not performed independently by multiple reviewers at all stages, but disagreements were resolved by consensus with a third reviewer. Finally, no protocol was prospectively registered, which may limit the transparency and reproducibility of the process.

The findings of this review have implications for practice, policy, and research. From a practical perspective, operators and utilities can benefit from deep learning-based models, particularly for short-term forecasting, to improve scheduling and grid stability. From a policy perspective, greater efforts are needed to encourage the creation and sharing of standardized, open-access datasets and reporting guidelines. Future research should focus on addressing these gaps, as well as improving computational efficiency and exploring explainable artificial intelligence (XAI) methods to increase trust in forecasting models.

Although we did not carry out formal sensitivity analyses, the results of this review may vary depending on the datasets used, the forecasting models applied, and the performance metrics reported.

Nonetheless, because only peer-reviewed published articles were included, we cannot exclude the possibility of publication or selective reporting biases.

Since no protocol was prospectively registered, no amendments were applicable.

3.7. Shortages, Barriers, and Development Trends

3.7.1. Shortages

Comparability across studies remains limited by heterogeneous datasets and non-standard temporal splits; this is visible in the diversity of countries/sources and access types (private vs. public) and in the training–validation–test partitions (Table 12 and Table 13). Metric bundles are also mixed (Table 11), which complicates like-for-like evaluation. Reporting of computational efficiency is sparse: many papers do not disclose hardware, parameter counts, memory footprint, or latency, and reported times are limited and highly variable (Figure 9). Evidence for cross-site generalization is uneven (as discussed in RQ4 on data origins and sizes), and interpretability is only minimally addressed in the surveyed literature. Taken together, these shortages hinder reproducibility and fair cross-study comparison.

3.7.2. Barriers

Technology maturation is constrained by the dominance of private, site-specific datasets and the scarcity of standardized public datasets (Figure 7); the absence of shared benchmarking protocols with explicit horizons and temporal splits (discussed in RQ2); and incomplete efficiency reporting (hardware, model size, training/inference time; noted in Figure 9). Transparency about inputs and preprocessing pipelines is also irregular (Preprocessing/Feature Extraction section), raising integration costs and reducing portability across sites and hardware configurations.

3.7.3. Development Trends

Methodologically, practice is moving from RNN-centric baselines (LSTM/GRU/BiLSTM) toward richer hybrids that combine signal decomposition (VMD/SSA) with attention mechanisms, TCN modules, and early Transformer/GNN components (Table 7). While 1D time-series approaches still dominate (Figure 4), spatio-temporal formulations and probabilistic outputs are gradually increasing, supported by coverage metrics such as PICP and CWC. There is also a growing emphasis on efficiency for near-real-time deployment, alongside more systematic benchmarking practices. These trends are reflected across RQ1–RQ5 without extending beyond the surveyed corpus.

4. Conclusions and Gaps

The state of the art in WPF models based on DNNs is characterized by increasingly sophisticated architectures, advanced feature extraction methods, diverse optimization strategies, a broad set of performance metrics, and the use of global datasets. The field continues to advance, with a growing emphasis on improving forecasting accuracy, enhancing computational efficiency, and promoting the standardization of data practices. This body of work provides a solid foundation for understanding the current state of WPF models developed with deep neural networks.

4.1. Conclusions

• To summarize the findings from RQ1: In WPF research, the predominant architectures combine DNNs, feature extraction methods, and optimization algorithms designed to improve predictive accuracy. Among these, LSTM networks are the most widely applied because of their ability to capture long-range temporal dependencies. Hybrid approaches that integrate LSTM with convolutional neural networks (CNNs) and other models are gaining momentum, as they leverage both temporal and spatial features. For feature extraction, VMD—particularly in hybrid settings—is often preferred due to its robustness in signal decomposition, while ICEEMDAN and SSA stand out for their effectiveness in noise reduction and feature extraction. Optimization algorithms, especially hybrid strategies such as GWO and PSO, reflect a clear trend toward combining multiple techniques to enhance model performance. One-dimensional time-series methods remain dominant because of their simplicity and effectiveness, although 2D models provide richer analysis in certain contexts. Taken together, these methodological advances highlight the complexity of wind power data and the ongoing need for refined approaches to improve forecasting precision.
• For RQ2: The validation of WPF models relies on a broad set of performance metrics, spanning error-based measures, statistical tests, coverage indicators, goodness-of-fit, and accuracy-improvement indices. RMSE and MAE are the most common, with MAPE and R² complementing relative error and overall fit; comparative tests such as the DM test and interval-coverage measures such as PICP and CWC are also used. Benchmark models typically include LSTM, GRU, and BiLSTM, with ARIMA as a classical reference, while feature-extraction and optimization methods (for example VMD–PSO) enhance accuracy. Yet, in the absence of standard benchmarking protocols and consistent validation metrics, cross-study comparability remains limited. To address this, we advocate for blocked temporal splits with explicit horizon definitions and a minimal, consistent metric set (at least MAE, RMSE, and MAPE), reported together with the test period and sample size to improve reproducibility and comparisons.
• Regarding RQ3: Forecasting horizons in WPF studies are predominantly short term, with the 10-min interval being the most frequently adopted due to its relevance for high-resolution, near-term prediction. Other common horizons include 15 min and 1 h. One-step-ahead forecasting dominates because of its simplicity and efficiency in generating immediate predictions, whereas multi-step models are used when capturing longer-term dynamics is required. This indicates a clear preference for short-term accuracy using one-step approaches, while still acknowledging the role of multi-step forecasting in more complex scenarios. The strong emphasis on short-term horizons reflects the operational need for timely, frequent, and precise forecasting in wind power management.
• For RQ4: Accepted datasets for training WPF models using DNNs are globally distributed, led by China and the USA, followed by India, Spain, and Brazil. Private, site-specific datasets still dominate, whereas public resources (e.g., Kaggle) remain limited and heterogeneous. Typical coverage is one month per season at a 10 min resolution, but dataset sizes vary widely (many studies use fewer than 15,000 samples), and common training–validation splits (80–20, 70–30, 90–10) are not standardized across works. This scarcity of standardized public datasets and the reliance on private data hinder reproducibility, independent verification, and fair cross-study comparison, underscoring the need for consistent protocols (fixed temporal splits, clearly defined horizons, and a minimal set of evaluation metrics) to enhance reliability and comparability.
• Finally, for RQ5: The processing times for current WPF models using DNNs vary significantly. The most commonly reported times range from 0 to 288 s, though this range may reflect approximations or limited timing data. Other notable processing durations include approximately 576 s and 2016 s, each reported in a few studies. This variation underscores the diverse computational requirements of different models and implementations. The limited reporting of processing times highlights a gap in the research, pointing to the need for more detailed data to better assess the computational efficiency of DNN-based WPF models.

4.2. Gaps

Considering the evaluations of the research questions summarized in the previously outlined conclusions, a general research gap emerges concerning our primary research question: “What is the state of the art of current wind power forecasting models based on deep neural networks?”

• Significant progress has been observed with the use of BiLSTM-based models, largely due to advancements in computer processing speeds. This has made BiLSTM an increasingly attractive option for WSP, potentially surpassing the previously popular LSTM and GRU models. It is important to note that these models do not operate in isolation; their performance must be evaluated in conjunction with signal decomposition techniques. Among these techniques, VMD has proven to be superior to all existing variations of ICEEMDAN, and the enhanced processing power of modern computers supports VMD’s integration (similar to BiLSTM). Nonetheless, the benefits of combining VMD with BiLSTM will only be realized if they are paired with optimization algorithms. The review highlights a range of optimization algorithms, including several new versions of GWO. Each of these should be individually assessed for compatibility with the desired model.
• Furthermore, the most commonly used models, feature extraction techniques, and optimization algorithms are typically hybrid in nature, involving a combination of methods and/or the integration of new approaches to enhance performance. Although these methods are regarded as the most promising, the optimal hybrid combinations remain uncertain, leaving room for the discovery of more effective configurations.
• Additionally, considerations regarding datasets are crucial. It is important to establish a data extraction protocol that determines sample sizes based on seasonal variations and wind speed variability to obtain reliable results. The dataset should be classified according to its size, resolution, and characteristics. This classification can help match the dataset with suitable models; in our case, we will focus on short-term horizons models due to their relevance in energy demand markets.
• Moreover, reference models can be established to compare performance metrics based on the results obtained. A more rigorous approach to quantitative results may be necessary for comparing the proposed models with the procedures outlined above. A thorough analysis of processing times is also required. Although it is challenging to compare clock cycles (which might be the most accurate method), the continuous evolution of computer technology complicates fair comparisons of processing times in some instances.
• There is a reporting gap regarding computational efficiency and model complexity. Most studies do not disclose hardware specifications, training/inference times, latency per forecast window, or model-size indicators (e.g., parameter count, memory footprint). This lack of standardized reporting limits reproducibility and practical assessment for real-time deployment. Future work should pair accuracy metrics with these efficiency descriptors to enable fair benchmarking.
• In the surveyed literature, the interpretability of deep models is rarely reported, which limits operator trust, auditing, and practical adoption. We suggest complementing accuracy with concise interpretability artefacts such as variable and time-window importance (via feature attribution or attention summaries) and at least one local explanation per forecast window, together with uncertainty or calibration estimates and transparent documentation of inputs and preprocessing. Minimal, consistent interpretability reporting would improve transparency, help detect spurious correlations, and better support deployment in real-time settings.
• Future directions include integrating physical knowledge with deep learning (e.g., coupling NWP or physics-based components with DNNs or adding physics-inspired constraints), exploring transfer learning and domain adaptation to efficiently adapt models to new sites with limited data, and improving uncertainty quantification by producing calibrated probabilistic forecasts and reporting calibration diagnostics alongside accuracy.
• This review does not include physics-only forecasting studies, as the scope focuses on DNN-based approaches. Nevertheless, integrating physical knowledge with deep learning (e.g., physics-informed losses or NWP–DNN hybrids) is a promising direction and is highlighted for future work.
• Although this review prioritizes short-term horizons, we highlight the need to evaluate long-term forecasting and to develop models that explicitly handle non-stationary, nonlinear wind patterns; both are flagged as directions for future work.