Modeling Power Curve of Wind Turbine Using Support Vector Regression with Dynamic Analysis
Abstract
Nomenclature
| WT | Wind turbine |
| MWTP | Model of the wind turbine power |
| 5-ParLog | Five parameters logistic function |
| 6-ParLog | Six parameters logistic function |
| MTanh | Modified hyperbolic tangent |
| SVR | support vector regression |
| fitness function | |
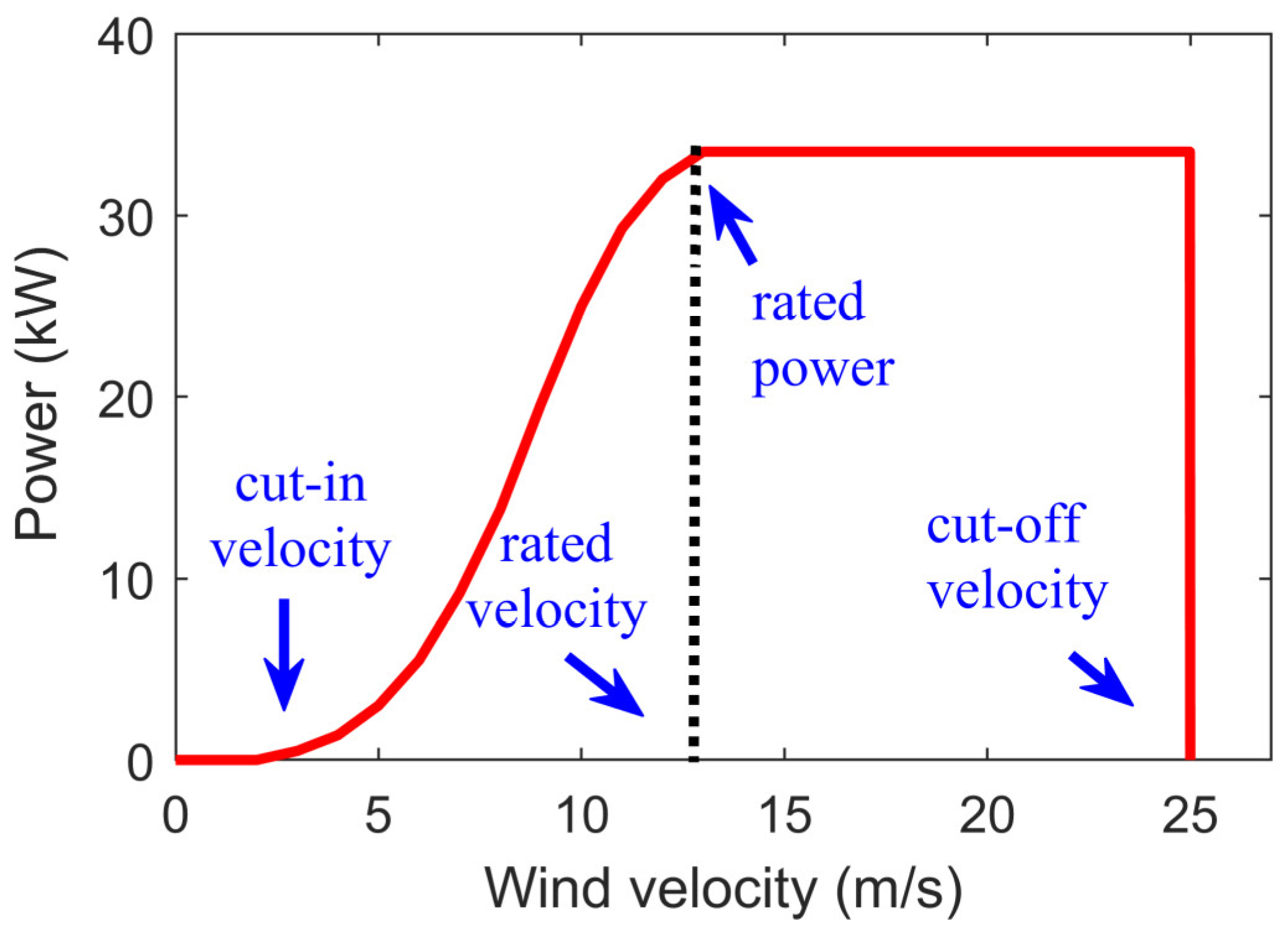
| cut-in velocity | |
| rated velocity | |
| cut-off velocity | |
| nominal power | |
| Five unknown parameters to be obtained | |
| Six unknown parameters to be found | |
| Unknown parameters to be defined | |
| RASE | Root of the average squared errors |
| Amount of measurements | |
| The measured and the estimated WT powers, respectively | |
| F | Force due to wind (N) |
| Air density (typically 1.225 kg/m3) | |
| A | Swept area of the turbine blades (m2) |
| CL | Lift coefficient, typically between 0.6 and 1.2 for WT blades |
| ν | Wind velocity (m) |
| FEM | Finite element method |
| HAWT | Horizontal-axis wind turbine |
| } | Force vector (N) at the corresponding degrees of freedom |
| [K] | Global element stiffness matrix |
| [M] | Global consistent mass matrix |
| Acceleration vectors at all degrees of freedom | |
| Displacement vectors at all degrees of freedom | |
| Vector of the motion amplitude | |
| Circular natural frequency | |
| Time (s) | |
| Phase angle | |
| Local to global transformation matrix | |
| m | Equivalent mass (kg) |
| Equivalent stiffness (N/m) | |
| N | Total number of elements |
| D | Rotor diameter (m) |
| H | Hub tallness (m) |
| EBBT | Euler–Bernoulli Beam Theory |
| Natural frequency (Hz) | |
| Eigenvalue for mode n (e.g., 1.875 for 1st mode) | |
| L | Effective length (tower + blade) (m) |
| Density (kg/m3) | |
| Cross-sectional area | |
| E | Young’s modulus (MPa) |
| I | Area moment of inertia |
| Centrifugal stiffness | |
| ω | Natural rotational speed (rad/s) |
| l | Blade length (m) |
| r | Rotor radius (m) |
| RBF | Radial basis function |
| CV | Cross-validation |
| ASOA | Atom search optimization algorithm |
| MBA | Mining blast algorithm |
| ISOA | Interior search optimization algorithm |
| LM | Levenberg–Marquardt |
1. Introduction
- 1.
- Engineering:
- 2.
- Energy:
- 3.
- Robotics and automation:
- Dynamic system modeling [42].
- 4.
- Manufacturing:
- Process monitoring [43].
- 5.
- Environmental sciences:
- Pollution level estimation [44].
- 6.
- Image processing:
- Image super-resolution [45].
- 7.
- Healthcare:
- 8.
- Financial forecasting:
- Stock price prediction [48].
- 9.
- Marketing and sales:
- Customer behavior prediction [49].
- Innovative application of the SVR to accurately identify the non-parametric MWTP.
- Analysis of two WTs using the non-parametric model.
- Comparison of the non-parametric MWTP based on SVR with the parametric MWTP based on evolutionary and non-evolutionary optimizers in accordance with the results of modeling a pair of WTs.
- Dynamic analysis of the natural frequencies of the WT is studied using two techniques, namely the FEM and the EEBT.
2. The Parametric MWTP
2.1. 5-ParLog
2.2. 6-ParLog
2.3. MTanh
3. The Non-Parametric MWTP
4. Expression of the Ffit
5. SVR
- The SVR can be sensitive to noisy data, particularly when the ε-insensitive zone is not optimally adjusted, possibly causing overfitting or underfitting in high-noise problems.
- Scalability is difficult with large datasets, as training the SVR includes solving a convex quadratic optimization problem, which typically scales between n2 and n3, where n is the number of training samples. Consequently, its computational and memory requirements increase rapidly with dataset size, restraining its direct applicability to large-scale cases without approximation approaches or kernel reduction methods.
6. Dynamic Analysis of the WT Blades
6.1. The Force Acting on the WT Blades
6.2. Natural Frequency of a Cantilever Beam
6.2.1. FEM
6.2.2. EBBT
7. Results and Discussions
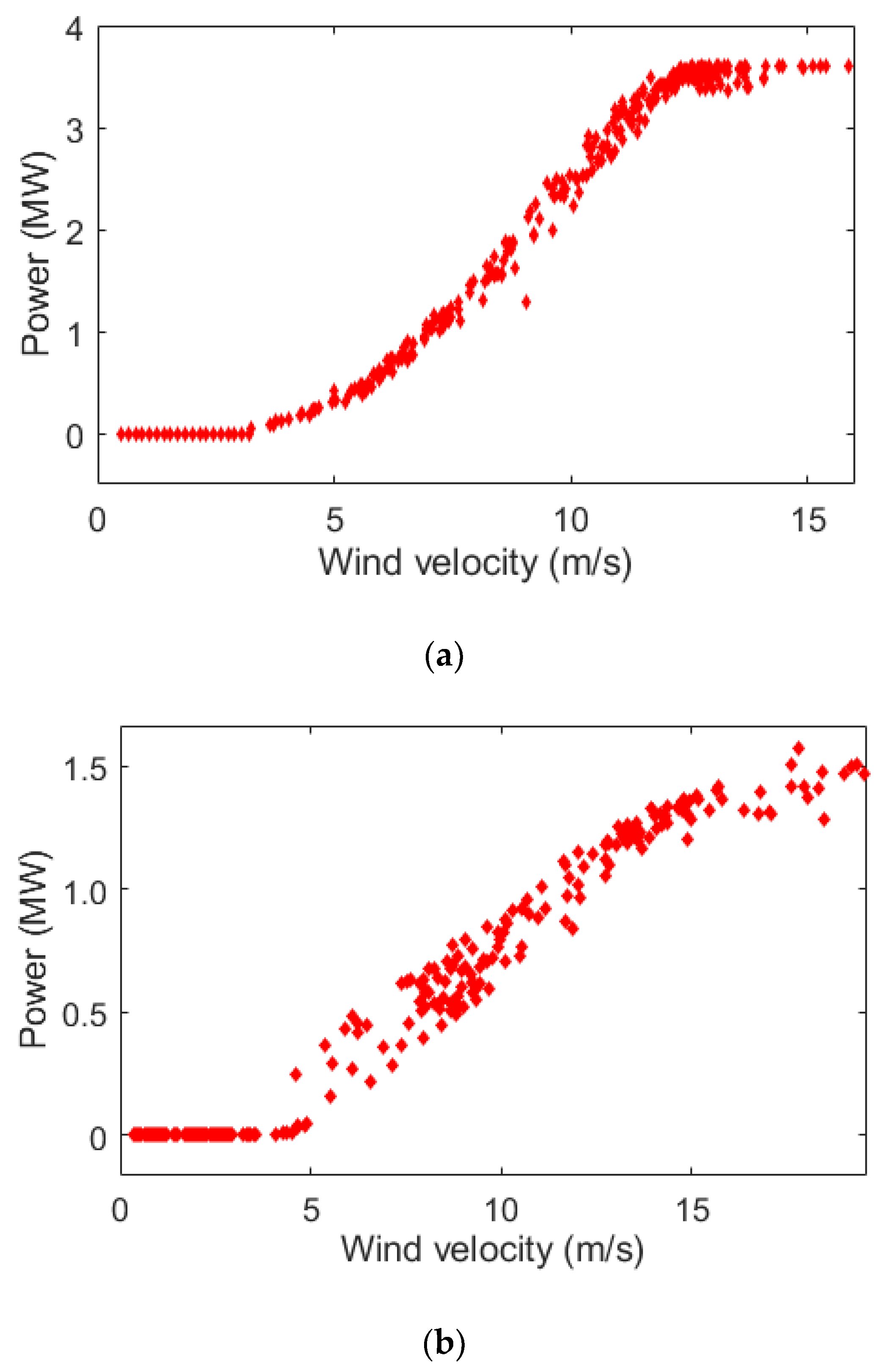
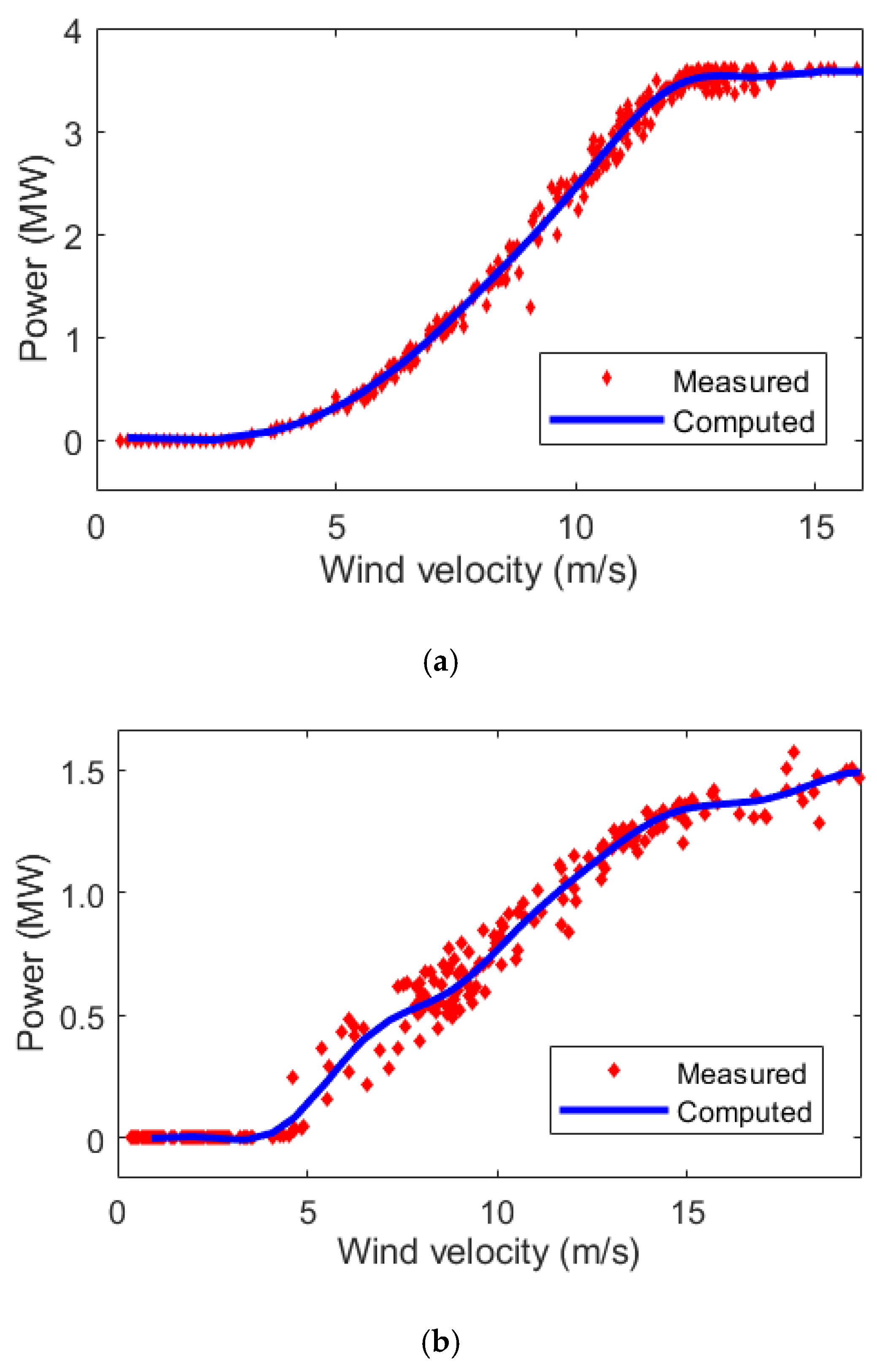
7.1. MWTP Using SVR
7.2. Dynamic Wind Force
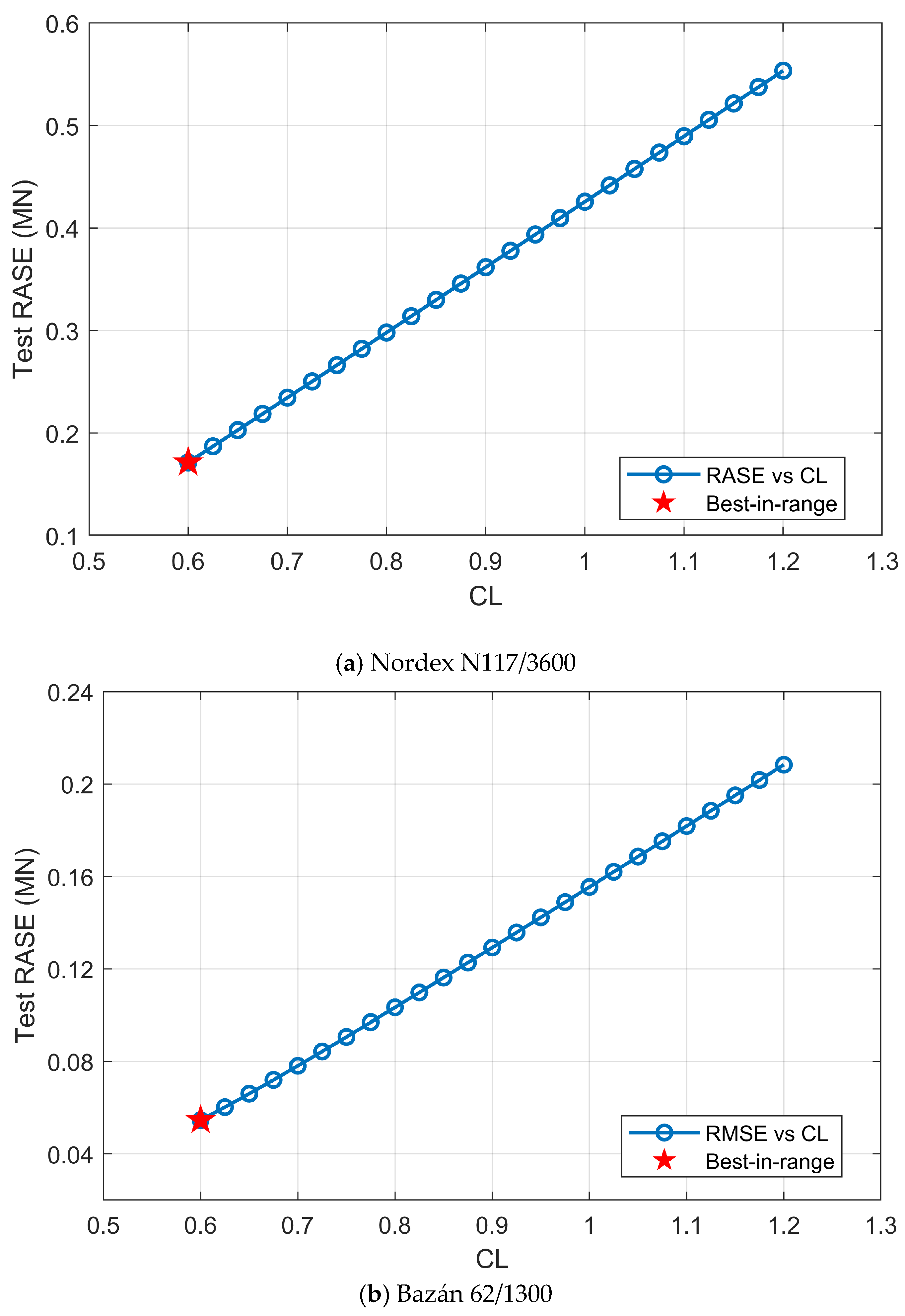
7.2.1. Parameter Sensitivity Analysis
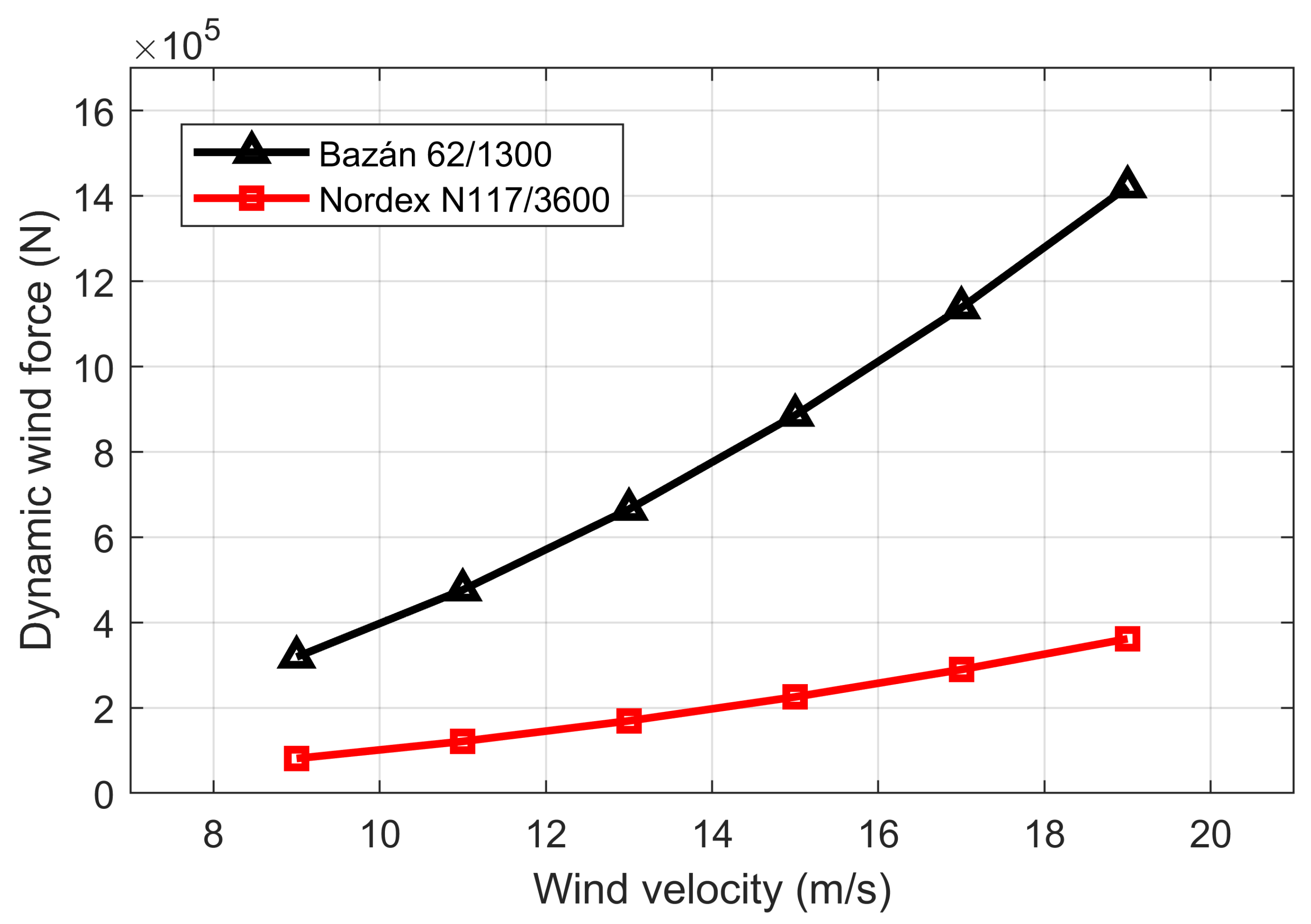
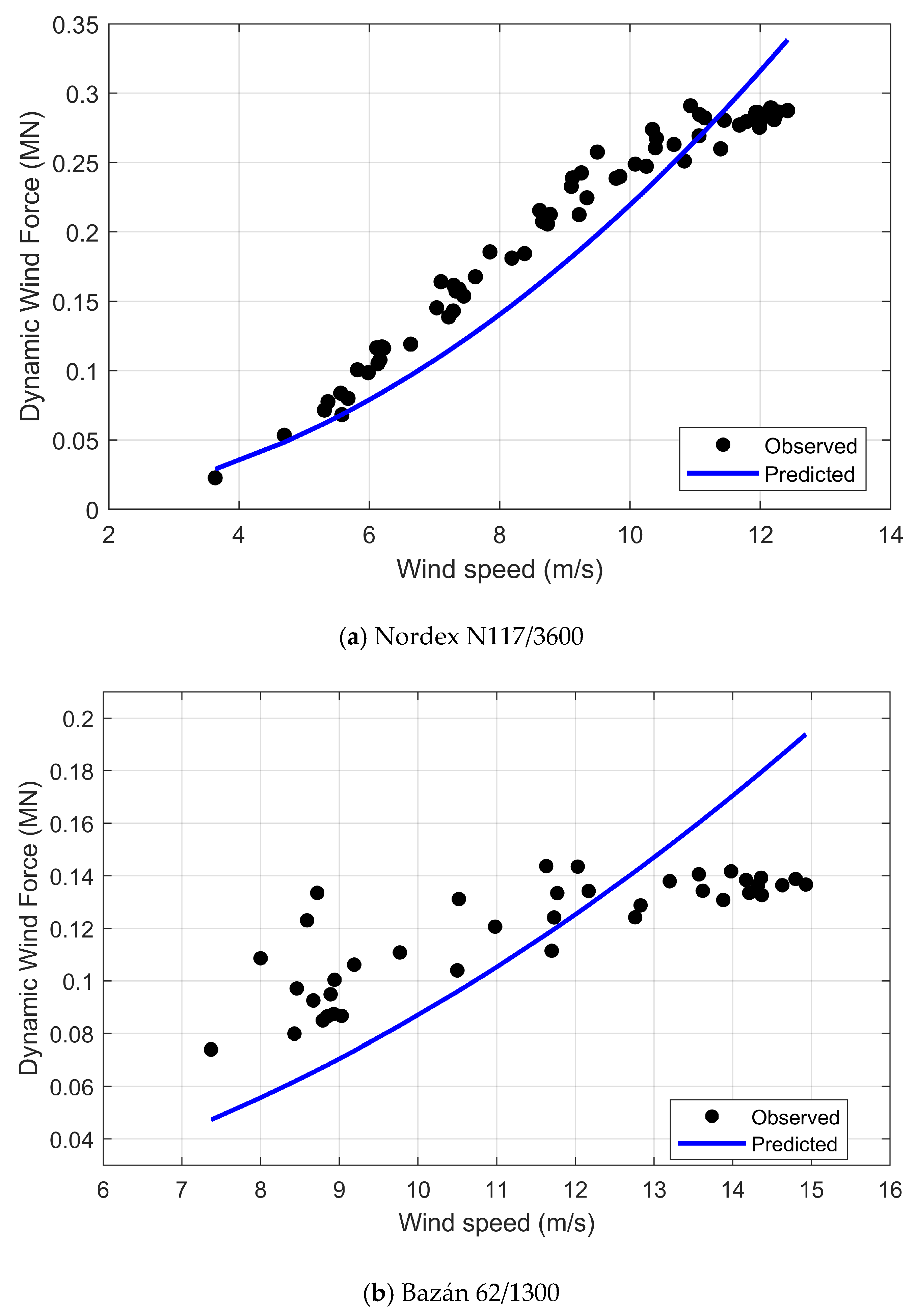
7.2.2. Analysis of Dynamic Wind Forces
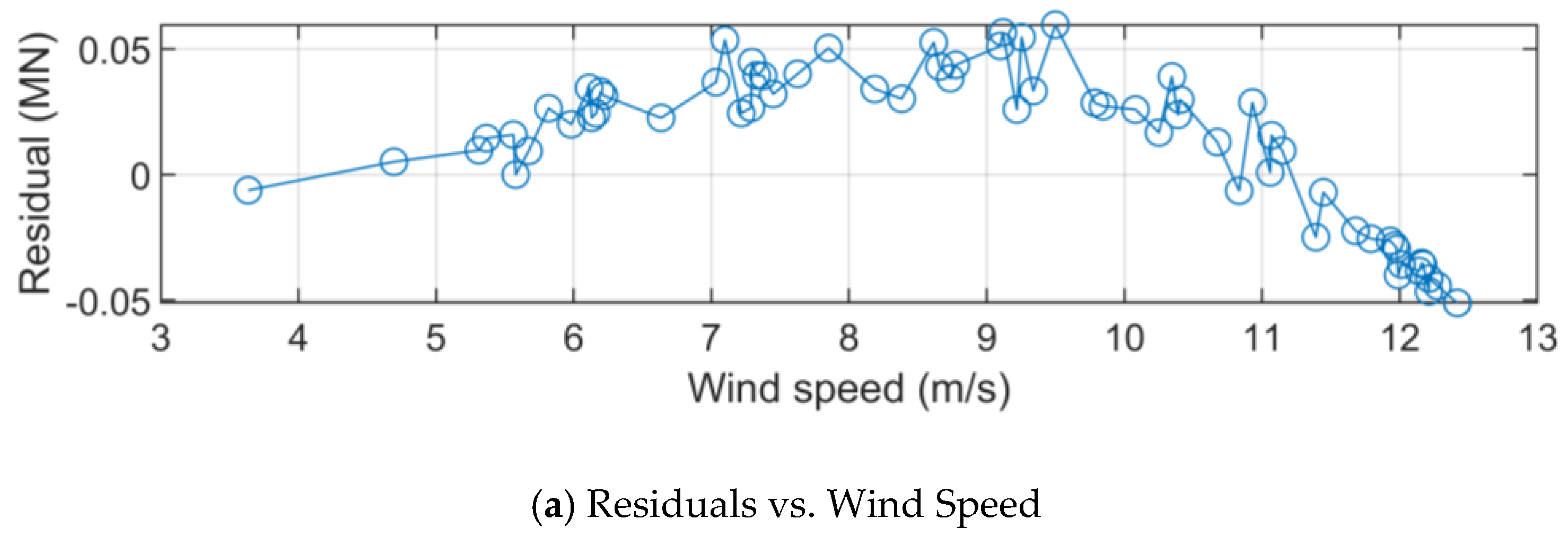
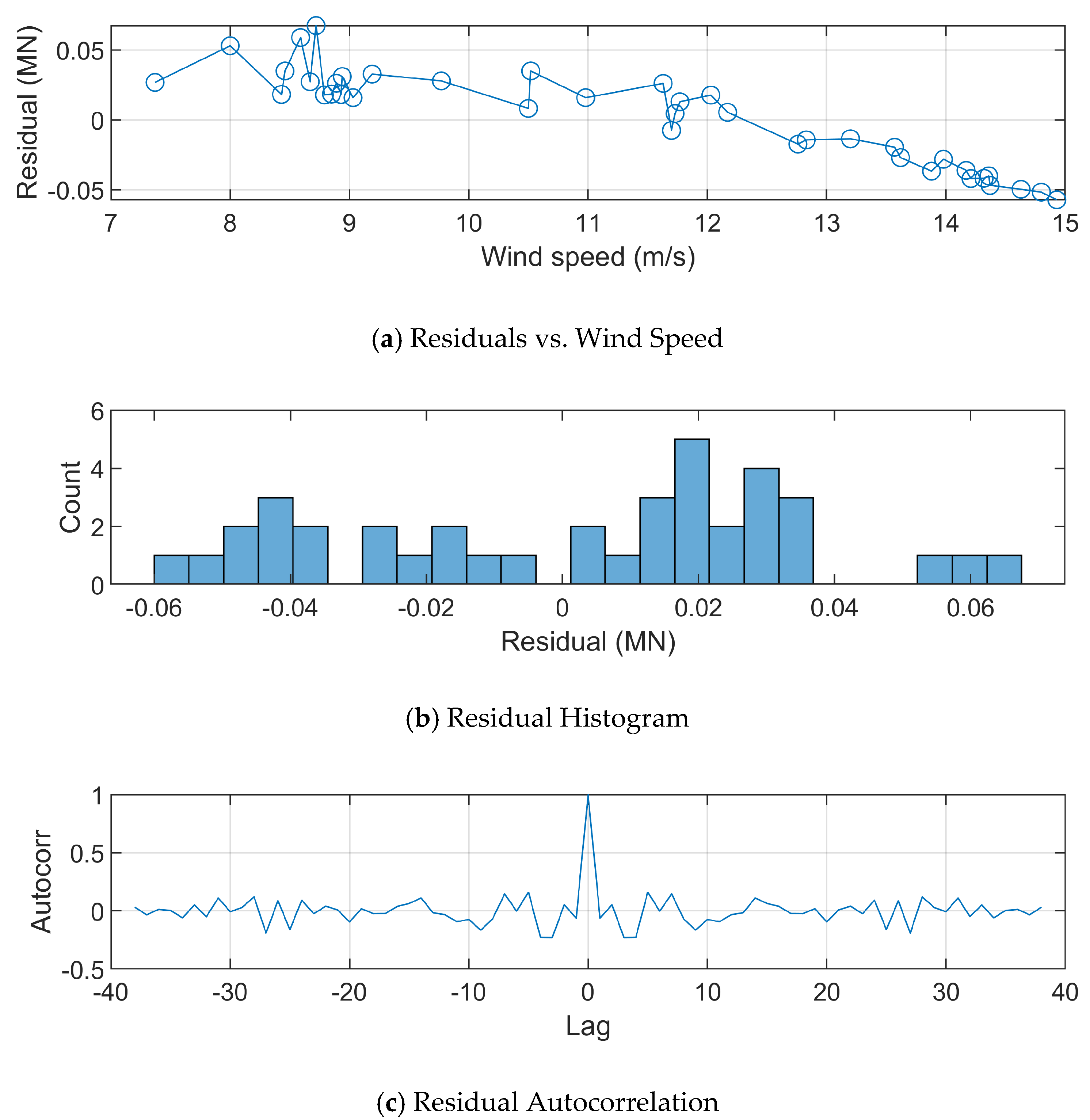
7.2.3. Residual Analysis
7.2.4. Independent Test Set Validation
7.3. Eigen Parameter Analysis
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kariman, H.; Hosseinzadeh, S.; Khiadani, M.; Nazarieh, M. 3D-CFD analysing of tidal Hunter turbine to enhance the power coefficient by changing the stroke angle of blades and incorporation of winglets. Ocean Eng. 2023, 287, 115713. [Google Scholar] [CrossRef]
- Aranizadeh, A.; Mirmozaffari, M.; Farahani, B.K. Maximizing Wind Turbine Power Generation Through Adaptive Fuzzy Logic Control for Optimal Efficiency and Performance. Wind 2025, 5, 4. [Google Scholar] [CrossRef]
- Dias, F.L.; Naik, A.J. A Novel Approach to Wavelet Neural Network-Based Wind Power Forecasting. Wind 2025, 5, 14. [Google Scholar] [CrossRef]
- Letzgus, S.; Müller, K.-R. An explainable AI framework for robust and transparent data-driven wind turbine power curve models. Energy AI 2023, 15, 100328. [Google Scholar] [CrossRef]
- Goudarzi, A.; Davidson, I.E.; Ahmadi, A.; Venayagamoorthy, G.K. Intelligent Analysis of Wind Turbine Power Curve Models. In Proceedings of the IEEE Symposium on Computational Intelligence Applications in Smart Grid (CIASG), Orlando, FL, USA, 9–12 December 2014; pp. 1–7. [Google Scholar]
- Lydia, M.; Selvakumar, A.I.; Kumar, S.S.; Kumar, G.E.P. Advanced Algorithms for Wind Turbine Power Curve Modeling. IEEE Trans. Sustain. Energy 2013, 4, 827–835. [Google Scholar] [CrossRef]
- Yesilbudak, M. Assessment of Power Curve Fitting Performance of Parametric Models for Wind Turbines. Int. J. Renew. Energy Res. 2025, 15, 22–29. [Google Scholar]
- Bao, Y.; Yang, Q.; Sun, Y. Iterative Modeling of Wind Turbine Power Curve Based on Least-Square B-Spline Approximation. Asian J. Control 2019, 21, 2004–2016. [Google Scholar] [CrossRef]
- Fu, Z.-Y.; Lin, G.-Q.; Tian, W.-D.; Pan, Z.-H.; Zhang, W.-C. Novel nonlinear wind power prediction based on improved iterative algorithm. Syst. Sci. Control. Eng. 2025, 13, 1. [Google Scholar] [CrossRef]
- Kusiak, A.; Zheng, H.; Song, Z. Models for Monitoring Wind Farm Power. Renew. Energy 2009, 34, 583–590. [Google Scholar] [CrossRef]
- Seo, S.; Oh, S.; Kwak, H. Wind Turbine Power Curve Modeling Using Maximum Likelihood Estimation Method. Renew. Energy 2019, 136, 1164–1169. [Google Scholar] [CrossRef]
- Goudarzi, A.; Swanson, A.G.; Kazemi, M.; Wang, K. Intelligent wind turbine power curve modelling using the third version of cultural algorithm (CA3). Int. J. Renew. Energy Res. 2017, 7, 1340–1351. [Google Scholar] [CrossRef]
- Yesilbudak, M.; Ozcan, A. Performance Comparison of Metaheuristic Optimization-Based Parametric Methods in Wind Turbine Power Curve Modeling. IEEE Access 2024, 12, 99372–99381. [Google Scholar] [CrossRef]
- Jin, R.; Wang, L.; Huang, C.; Jiang, S. Wind Turbine Generation Performance Monitoring with Jaya Algorithm. Int. J. Energy Res. 2019, 43, 1604–1611. [Google Scholar] [CrossRef]
- Marčiukaitis, M.; Žutautaitė, I.; Martišauskas, L.; Jokšas, B.; Gecevičius, G.; Sfetsos, A. Non-Linear Regression Model for Wind Turbine Power Curve. Renew. Energy 2017, 113, 732–741. [Google Scholar] [CrossRef]
- Tao, S.; Xu, Q.; Feijóo, A.; Kuenzel, S.; Bokde, N. Integrated Wind Farm Power Curve and Power Curve Distribution Function Considering the Wake Effect and Terrain Gradient. Energies 2019, 12, 2482. [Google Scholar] [CrossRef]
- Yesilbudak, M. A Novel Power Curve Modeling Framework for Wind Turbines. Adv. Electr. Comput. Eng. 2019, 19, 29–40. [Google Scholar] [CrossRef]
- Rose, J.; Hiskens, I.A. Estimating Wind Turbine Parameters and Quantifying Their Effects on Dynamic Behavior. In Proceedings of the IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7. [Google Scholar]
- Krishna, J.; Bhargava, V.; Donepudi, J. BEM Prediction of Wind Turbine Operation and Performance. Int. J. Renew. Energy Res. 2018, 8, 1962–1973. [Google Scholar]
- Agwa, A.M. Interior Search Optimization Algorithm for Modeling Power Curve of Wind Turbine. Int. J. Renew. Energy Res. 2020, 10, 1349–1358. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, X.; Zou, R.; Zhang, F.; Li, Y.; Hu, Q. A novel data-driven deep learning approach for wind turbine power curve modeling. Energy 2023, 270, 126908. [Google Scholar] [CrossRef]
- Caro, F.D.; Vaccaro, A.; Villacci, D. Adaptive Wind Generation Modeling by Fuzzy Clustering of Experimental Data. Electronics 2018, 7, 47. [Google Scholar] [CrossRef]
- Cao, Y.; Hu, Q.; Shi, H.; Zhang, Y. Prediction of Wind Power Generation Base on Neural Network in Consideration of the Fault Time. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 670–679. [Google Scholar] [CrossRef]
- Demirdelen, T.; Tekin, P.; Aksu, I.O.; Ekinci, F. The Prediction Model of Characteristics for Wind Turbines Based on Meteorological Properties Using Neural Network Swarm Intelligence. Sustainability 2019, 11, 4803. [Google Scholar] [CrossRef]
- Bai, L.; Crisostomi, E.; Raugi, M.; Tucci, M. Wind Turbine Power Curve Estimation Based on Earth Mover Distance and Artificial Neural Networks. IET Renew. Power Gener. 2019, 13, 2939–2946. [Google Scholar] [CrossRef]
- Mushtaq, K.; Waris, M.; Zou, R.; Shafique, U.; Khan, N.; Khan, M.; Jameel, M.; Khan, M.I. A Comprehensive Approach to Wind Turbine Power Curve Modeling: Addressing Outliers and Enhancing Accuracy. Energy 2024, 304, 131981. [Google Scholar] [CrossRef]
- Bilal, B.; Adjallah, K.; Sava, A.; Ouassaid, M. Wind turbine output power prediction and optimization based on a novel adaptive neuro-fuzzy inference system with the moving window. Energy 2023, 263, 126159. [Google Scholar] [CrossRef]
- Pandit, R.K.; Infield, D. Comparative Analysis of Gaussian Process Power Curve Models Based on Different Stationary Covariance Functions for The Purpose of Improving Model Accuracy. Renew. Energy 2019, 140, 190–202. [Google Scholar] [CrossRef]
- Mehrjoo, M.; Jozani, M.J.; Pawlak, M. Wind Turbine Power Curve Modeling for Reliable Power Prediction Using Monotonic Regression. Renew. Energy 2020, 147, 214–222. [Google Scholar] [CrossRef]
- He, C.; Peng, J.; Jiang, W.; Wang, C.; Li, J.; Tan, Z. A hybrid time series analysis-genetic algorithm-support vector machine model for enhanced landslide prediction. Int. J. Ind. Eng. Comput. 2025, 16, 785–798. [Google Scholar] [CrossRef]
- Xiao, J.; Liu, G.; Huang, M.; Yin, Z.; Gao, Z. A kernel-free L1 norm regularized ν-support vector machine model with application. Int. J. Ind. Eng. Comput. 2023, 14, 691–706. [Google Scholar] [CrossRef]
- Hosseini, M.S.; Karimi, A. Meta-Heuristic Enhanced SVR for Pile-Bearing Capacity Estimation. Int. J. Geotech. Eng. 2024, 15, 1234–1247. [Google Scholar]
- Wang, J.P.; Liu, Y. Novel Support Vector Regression Approach for Equipment Health Monitoring. Comput. Intell. Neurosci. 2021, 2021, 6675078. [Google Scholar]
- Li, X.; Wang, J.; Zhang, H. Combining SVR with genetic algorithms for equipment fault detection. J. Mach. Cond. Monit. 2021, 27, 357–367. [Google Scholar]
- Luo, J.; Hong, T.; Gao, Z.; Fang, S. A Robust Support Vector Regression Model for Electric Load Forecasting. Int. J. Forecast. 2023, 39, 1005–1020. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Liang, H.; Gorbani, B. Optimizing Electric Load Forecasting with Support Vector Regression/LSTM Optimized by Flexible Gorilla Troops Algorithm and Neural Networks A Case Study. Sci. Rep. 2024, 14, 22092. [Google Scholar] [CrossRef]
- Verma, R.; Tiwari, S. Improving Offshore Wind Farm Power Prediction with Enhanced SVR Models. J. Energy Eng. 2023, 149, 105–114. [Google Scholar]
- Chen, L.; Wang, X.; Zhang, Y. Support Vector Regression for Solar Power System Forecasting with Climatic Data. IEEE Trans. Sustain. Energy 2023, 14, 102–109. [Google Scholar]
- Lee, D.; Chang, K.; Oh, H. Application of SVR for Smart Renewable Energy System Forecasting. IEEE Access 2024, 11, 15050–15061. [Google Scholar]
- Gupta, A.; Mehta, P.; Sharma, K. Optimized SVR for Forecasting Renewable Energy Outputs Using Metaheuristics. Energy Rep. 2023, 8, 1021–1032. [Google Scholar]
- Chandrakala, K.; Rajan, P. A Hybrid Machine Learning Approach for Price Forecasting in Electricity Market with Smart Bidding Strategies and Wind Energy Influence. Int. Rev. Model. Simul. (IREMOS) 2022, 15, 414–424. [Google Scholar] [CrossRef]
- Park, T.J.; Lee, J.K.; Choi, H. Real-Time Dynamic System Modeling in Robotics Using SVR. IEEE Trans. Robot. 2023, 39, 254–266. [Google Scholar]
- Yeganeh, A.; Abbasi, S.A.; Shongwe, S.C.; Malela-Majika, J.-C.; Shadman, A.R. An Evolutionary SVR Model for Monitoring Poisson Profiles in Manufacturing. Soft Comput. 2023, 27, 6789–6799. [Google Scholar]
- Das, P.K.; Gupta, S.K. Evolutionary SVR Model for Poisson Profiles in Pollution Monitoring. Soft Comput. 2023, 27, 8954–8966. [Google Scholar]
- Zhang, H.; Xu, L.; Wei, P. Enhancing Image Resolution With SVR. IEEE Trans. Image Process. 2023, 32, 1456–1467. [Google Scholar]
- Singh, R.K.; Verma, P.; Tripathi, S. Advancements in SVR for Healthcare Applications: A Review. Information 2023, 15, 235–248. [Google Scholar]
- Shoko, C.; Sigauke, C. Short-Term Forecasting of COVID-19 Using Support Vector Regression: An Application Using Zimbabwean Data. Am. J. Infect. Control 2023, 51, 1095–1107. [Google Scholar] [CrossRef]
- Fang, Y. Stock Price Forecasting Based on Improved Support Vector Regression. In Proceedings of the 2020 7th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 18–20 December 2020; pp. 1351–1354. [Google Scholar]
- Lee, P.L.; Kim, J.H. Predicting Customer Behavior Using Support Vector Regression. Mark. Sci. 2023, 41, 123–134. [Google Scholar]
- Villanueva, D.; Feijóo, A.E. Reformulation of Parameters of The Logistic Function Applied to Power Curves of Wind Turbines. Electr. Power Syst. Res. 2016, 137, 51–58. [Google Scholar] [CrossRef]
- Villanueva, D.; Feijóo, A. Comparison of Logistic Functions for Modeling Wind Turbine Power Curves. Electr. Power Syst. Res. 2018, 155, 281–288. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Q.; Li, L.; Foley, A.M.; Srinivasan, D. Approaches to Wind Power Curve Modeling: A Review and Discussion. Renew. Sustain. Energy Rev. 2019, 116, 109422. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Wan, J.-H.; Bai, R.; Li, X.-Y.; Liu, S.-W. Natural Frequency Analysis of Monopile Supported Offshore Wind Turbines Using Unified Beam-Column Element Model. J. Mar. Sci. Eng. 2023, 11, 628. [Google Scholar] [CrossRef]
- Li, X.Y.; Wan, J.H.; Zhao, H.P.; Liu, S.W. Three-Dimensional analysis of nonlinear pile–soil interaction responses using 3D pile element model. Int. J. Geomech. 2021, 21, 04021129. [Google Scholar] [CrossRef]
- Tong, W. Wind Power Generation and Wind Turbine Design; WIT Press: Southampton, UK, 2010. [Google Scholar]
- Rao, S.S.; Yap, F.F. Mechanical Vibrations; Addison-Wesley: New York, NY, USA, 1995. [Google Scholar]


| Model | Nordex N117/3600 | Bazán 62/1300 |
|---|---|---|
| 3.6 | 1.3 | |
| 13 | 15 | |
| 3 | 3 | |
| 25 | 25 | |
| 76 | 50 | |
| 116.8 | 62 | |
| 50 | 50 | |
| 660 | 690 |
| Kernel Type | Tested Values of C | Tested Values of Kernel Bandwidth (γ) | Tested Values of ε | Best Parameters Found | Best RASE | |
|---|---|---|---|---|---|---|
| Nordex N117/3600 | Bazán 62/1300 | |||||
| RBF | 1, 10, 100, 1000, 10,000, 100,000 | 0.001, 0.01, 0.1, 1 | 0.001, 0.01, 0.1 | C = 100, γ = 0.1, ε = 0.01 | 0.089663 | 0.098871 |
| Linear | 1, 10, 100, 1000, 10,000, 100,000 | — | 0.001, 0.01, 0.1 | C = 100, ε = 0.01 | 0.300341 | 0.168406 |
| Polynomial | 1, 10, 100, 1000, 10,000, 100,000 | γ = 0.001, 0.01, 0.1, 1 degree = 2, 3, 4 | 0.001, 0.01, 0.1 | C = 100, γ = 0.1, degree = 3, ε = 0.01 | 0.160875 | 0.147320 |
| The Parametric MWTP | Model | |||
| 5-ParLog | 6-ParLog | MTanh | ||
| ASA [21] | 0.202482 | 0.164542 | 0.379188 | |
| MBA [21] | 0.127102 | 0.121236 | 0.193832 | |
| ISOA [21] | 0.099776 | 0.099275 | 0.129178 | |
| LM | 1.396756 | 0.122146 | 0.098229 | |
| The Non-Parametric MWTP | SVR | 0.089663 | ||
| The Parametric MWTP | Model | |||
| 5-ParLog | 6-ParLog | MTanh | ||
| ASA [21] | 0.177636 | 0.164542 | 0.379188 | |
| MBA [21] | 0.153891 | 0.121236 | 0.193832 | |
| ISOA [21] | 0.112980 | 0.099275 | 0.129178 | |
| LM | 1.590634 | 0.128906 | 0.104787 | |
| The Non-Parametric MWTP | SVR | 0.098871 | ||
| Parametric MWTP | Model | 5-ParLog | 6-ParLog | MTanh |
| ASA | 55.33 | 55.70 | 56.96 | |
| MBA | 68.27 | 62.77 | 67.81 | |
| ISOA | 69.04 | 63.71 | 61.49 | |
| LM | 0.02 | 0.05 | 0.11 | |
| Non-Parametric MWTP | SVR | 0.27 | ||
| Parametric MWTP | Model | 5-ParLog | 6-ParLog | MTanh |
| ASA | 48.99 | 46.50 | 50.99 | |
| MBA | 66.69 | 66.33 | 78.11 | |
| ISOA | 56.52 | 49.94 | 53.01 | |
| LM | 0.06 | 0.05 | 0.09 | |
| Non-Parametric MWTP | SVR | 0.23 | ||
| ν (m/s) | F (N) | |
|---|---|---|
| Nordex N117/3600 | Bazán 62/1300 | |
| 9 | 318,958.7 | 81,184.1 |
| 11 | 476,469.3 | 121,275 |
| 13 | 665,481.9 | 169,384.1 |
| 15 | 885,996.5 | 225,511.4 |
| 17 | 1,138,013.4 | 289,656.8 |
| 19 | 1,421,532.3 | 361,820.5 |
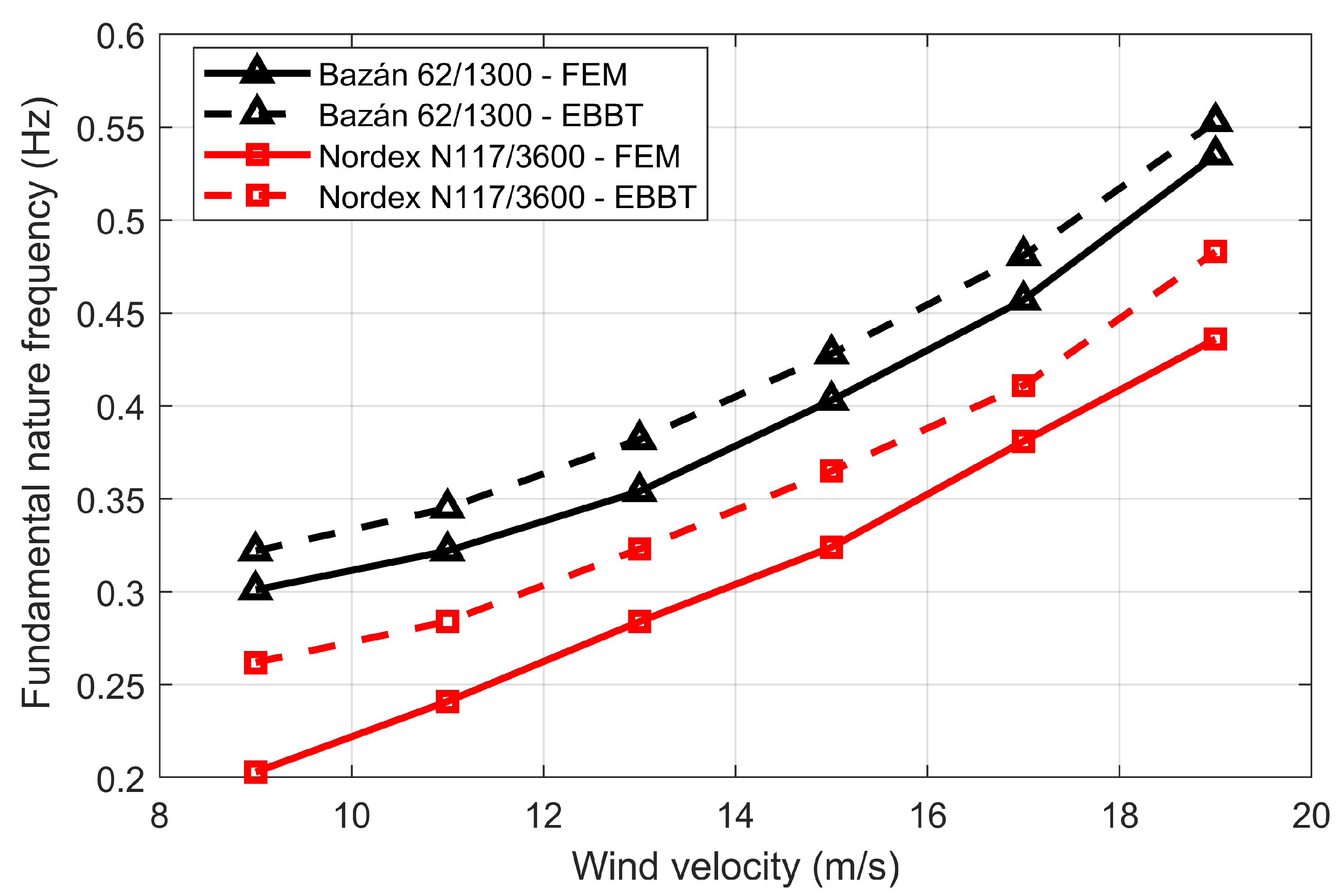
| ν (m/s) | Fundamental fn (Hz) | |||
|---|---|---|---|---|
| FEM | EBBT | |||
| Nordex N117/3600 | Bazán 62/1300 | Nordex N117/3600 | Bazán 62/1300 | |
| 9 | 0.203 | 0.301 | 0.262 | 0.322 |
| 11 | 0.241 | 0.322 | 0.284 | 0.345 |
| 13 | 0.284 | 0.354 | 0.323 | 0.382 |
| 15 | 0.324 | 0.403 | 0.365 | 0.428 |
| 17 | 0.381 | 0.457 | 0.411 | 0.481 |
| 19 | 0.436 | 0.535 | 0.483 | 0.553 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agwa, A.M.; Elamy, M.I. Modeling Power Curve of Wind Turbine Using Support Vector Regression with Dynamic Analysis. Wind 2025, 5, 20. https://doi.org/10.3390/wind5030020
Agwa AM, Elamy MI. Modeling Power Curve of Wind Turbine Using Support Vector Regression with Dynamic Analysis. Wind. 2025; 5(3):20. https://doi.org/10.3390/wind5030020
Chicago/Turabian StyleAgwa, Ahmed M., and Mamdouh I. Elamy. 2025. "Modeling Power Curve of Wind Turbine Using Support Vector Regression with Dynamic Analysis" Wind 5, no. 3: 20. https://doi.org/10.3390/wind5030020
APA StyleAgwa, A. M., & Elamy, M. I. (2025). Modeling Power Curve of Wind Turbine Using Support Vector Regression with Dynamic Analysis. Wind, 5(3), 20. https://doi.org/10.3390/wind5030020





