Flow Patterns Providing Maximum Speed-Up Ratio and Maximum Speed-Up Area of Pedestrian-Level Winds
Abstract
1. Introduction
2. Description of Numerical Simulation
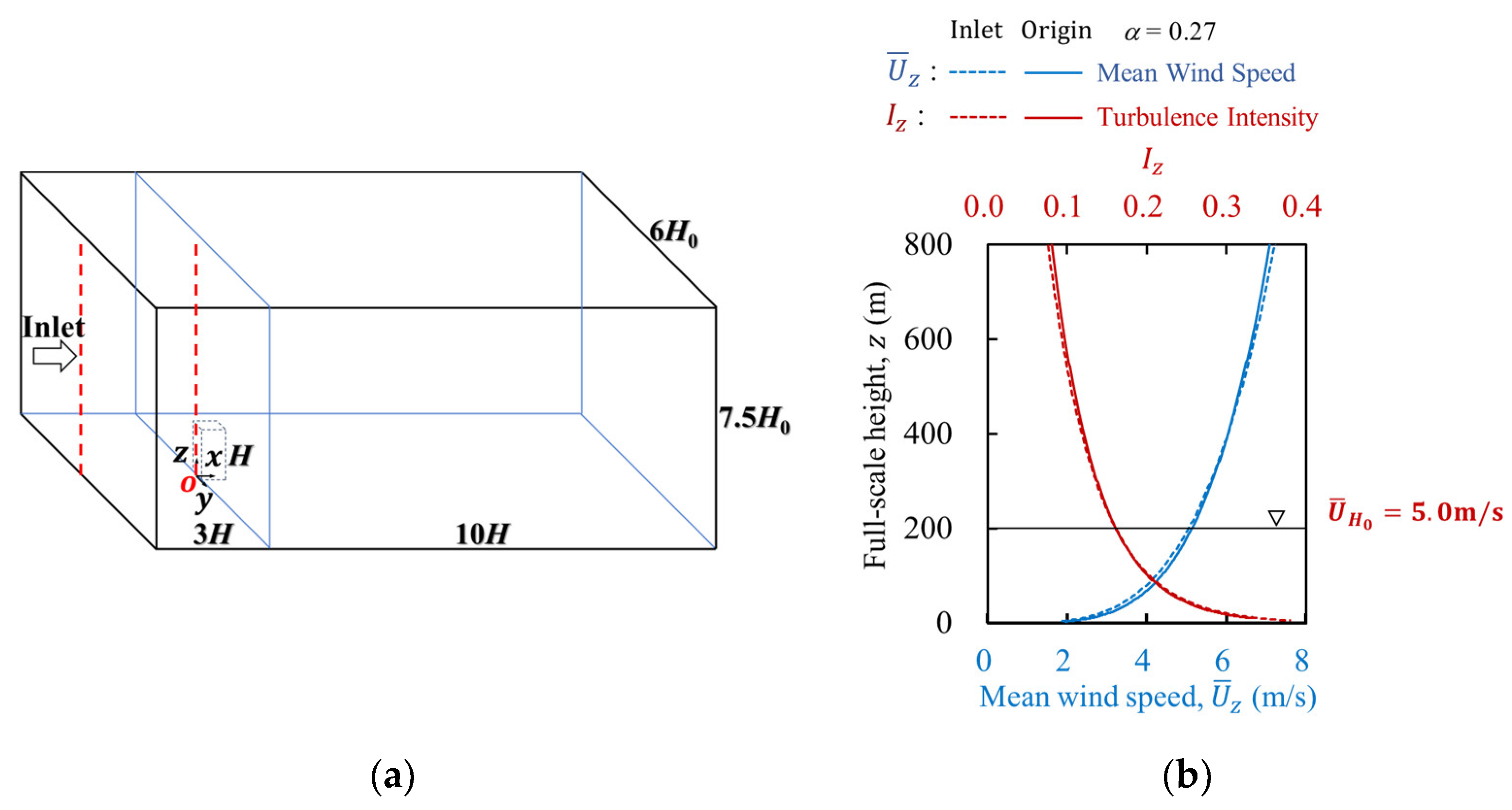
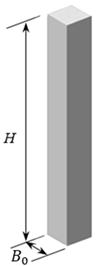
2.1. Model Configurations
2.2. Numerical Setting
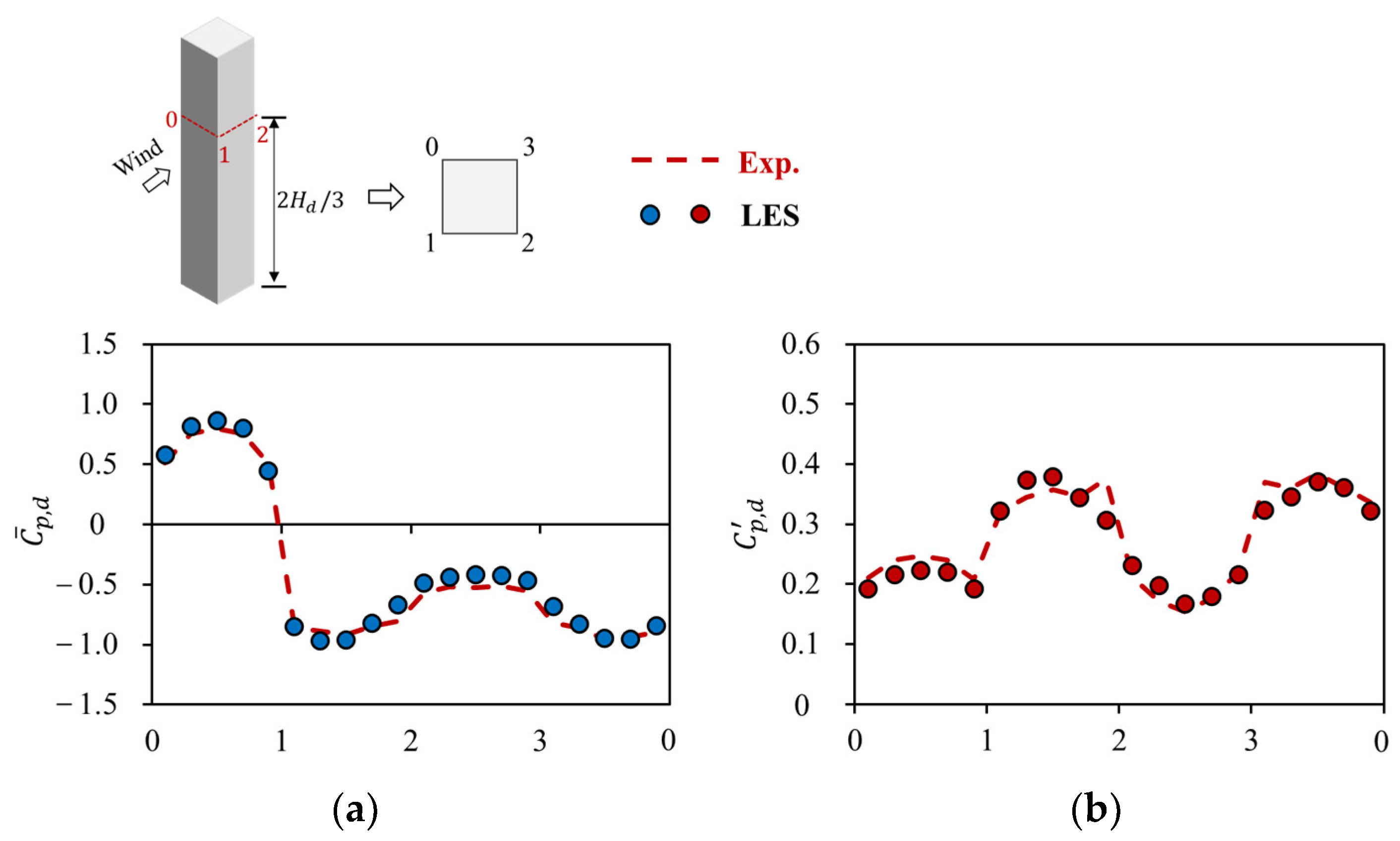
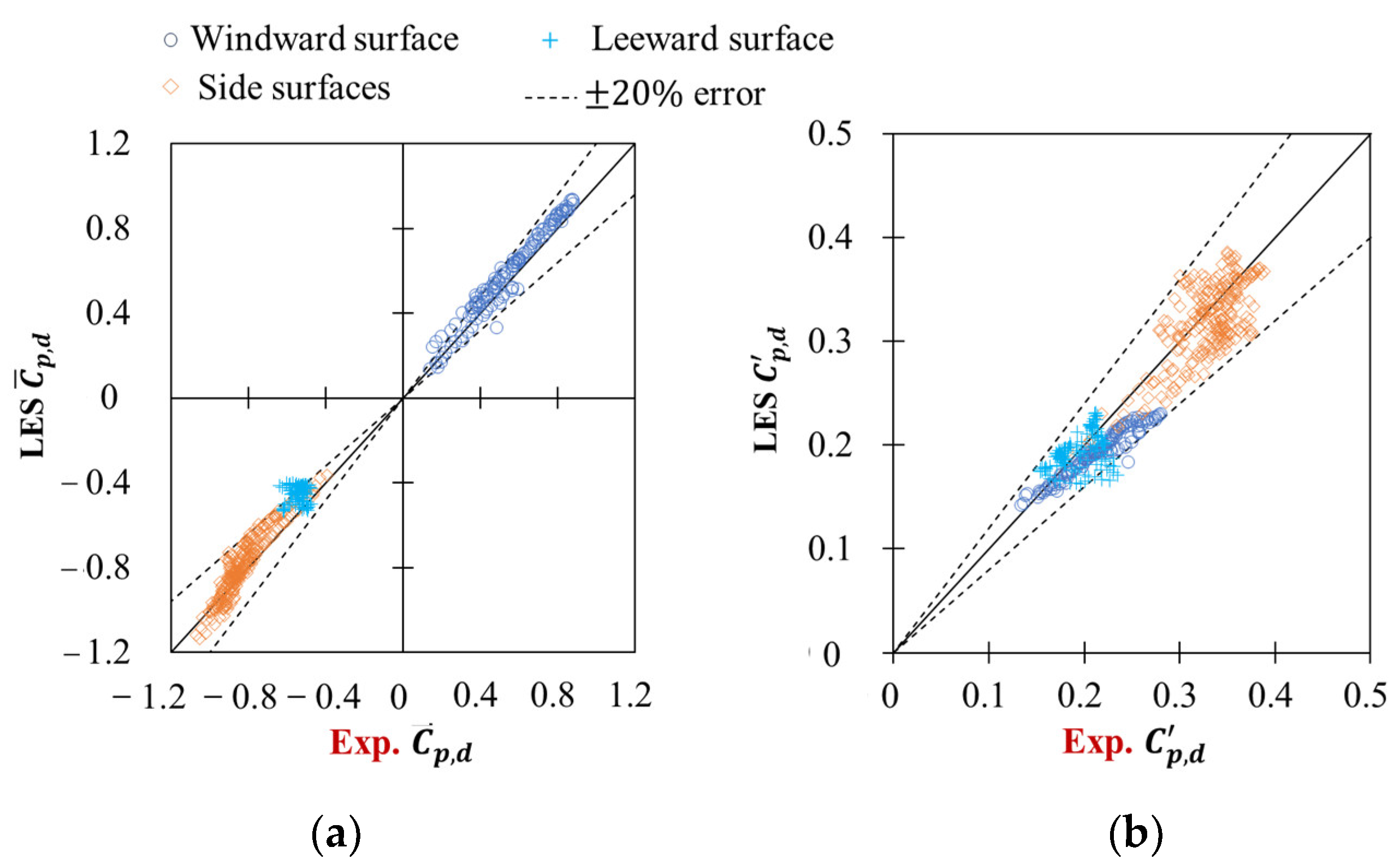
2.3. Validation of Surface Pressure from LES
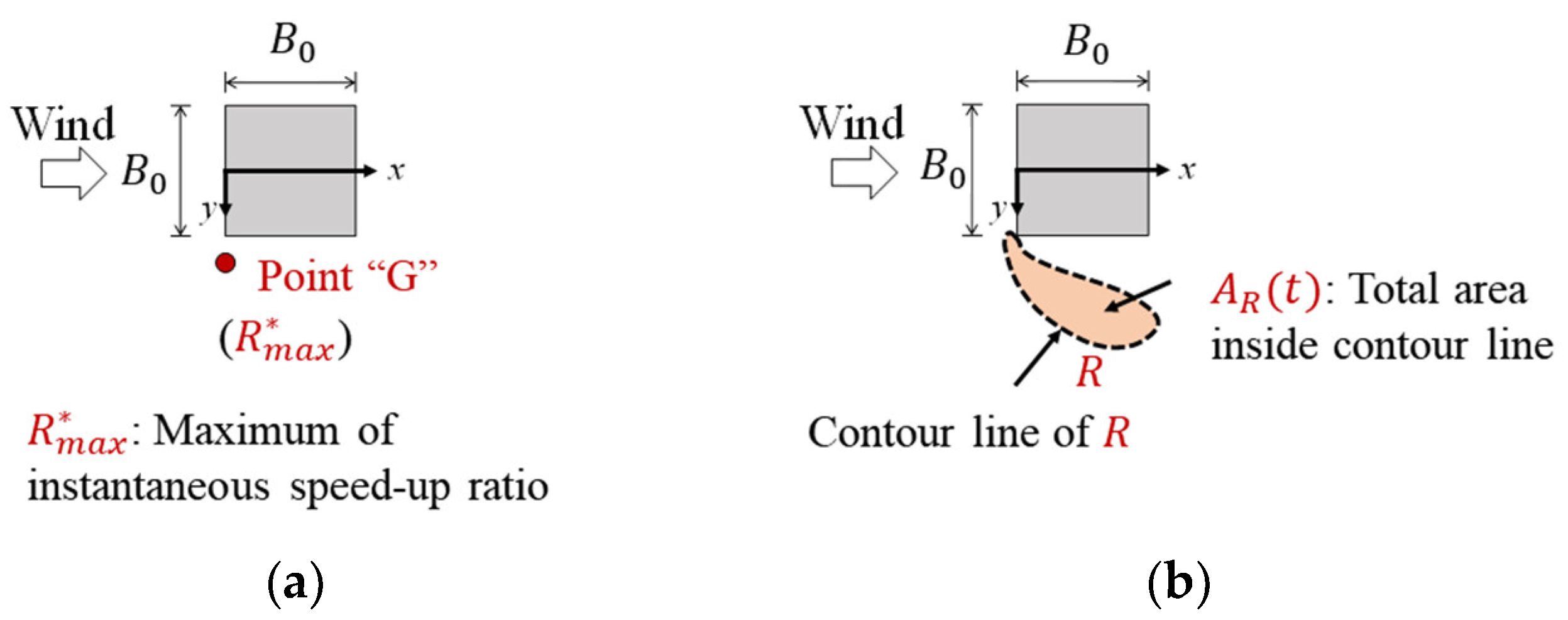
3. Definition of Instantaneous Strong Wind Events
4. Simulation Results and Analysis
4.1. Determination of Data Acquisition Period
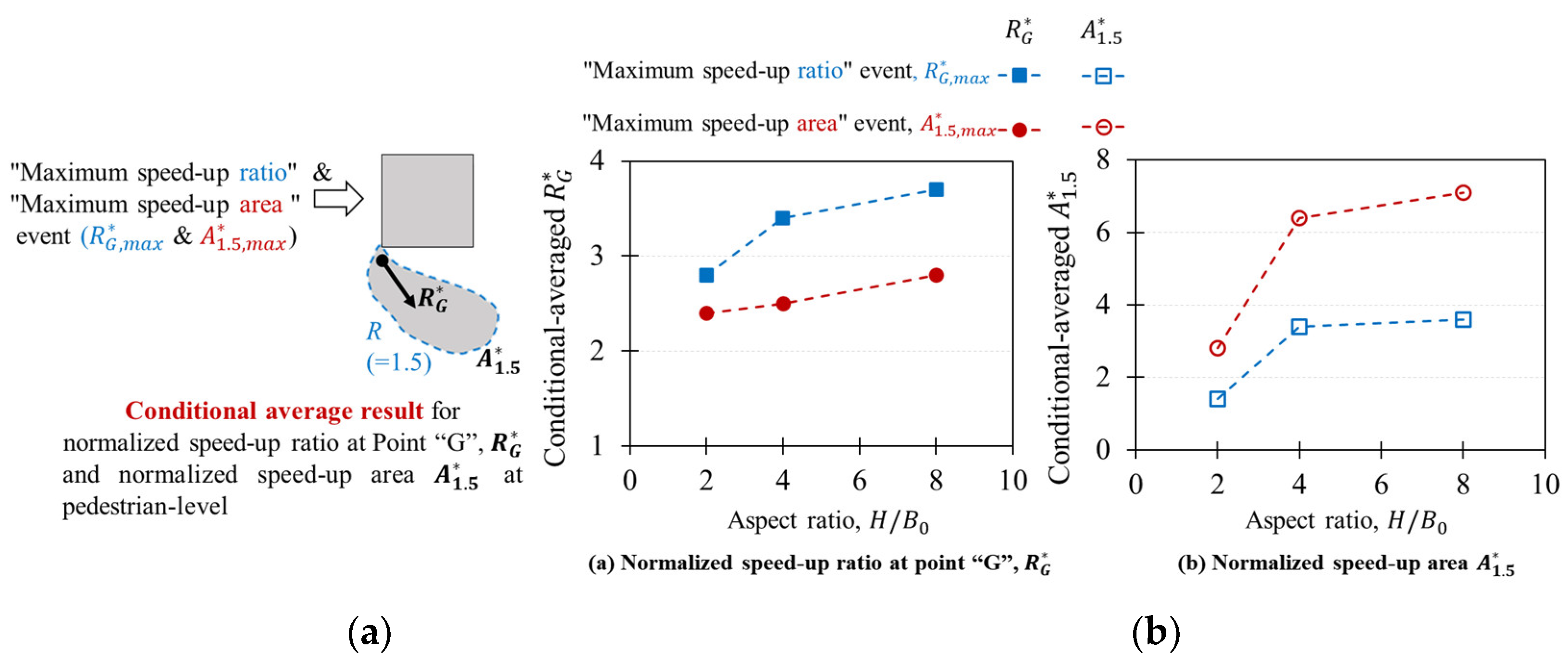
4.2. Conditional Average Results
5. Conclusions
- Two strong wind events do not occur simultaneously.
- Conditional average flow patterns around buildings for the two instantaneous strong wind events are different: the contribution of downwash tends to be larger for the strong wind event providing the “maximum speed-up area” of pedestrian-level wind, showing more three-dimensional flow characteristics.
- For building models with different heights, represented by , or different aspect ratios, represented by , a similar phenomenon as described above can also be seen. The difference is that the values of the speed-up ratio, , the positive pressure on the upper part of the windward surface, and its difference with the lower part of the windward surface as well as the negative pressure on the side, i.e., the pressure gradient, are larger for building models with higher heights represented by , or larger aspect ratios, represented by .
6. Limitations of the Present Study
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Data Acquisition Period for Conditional Average Analysis
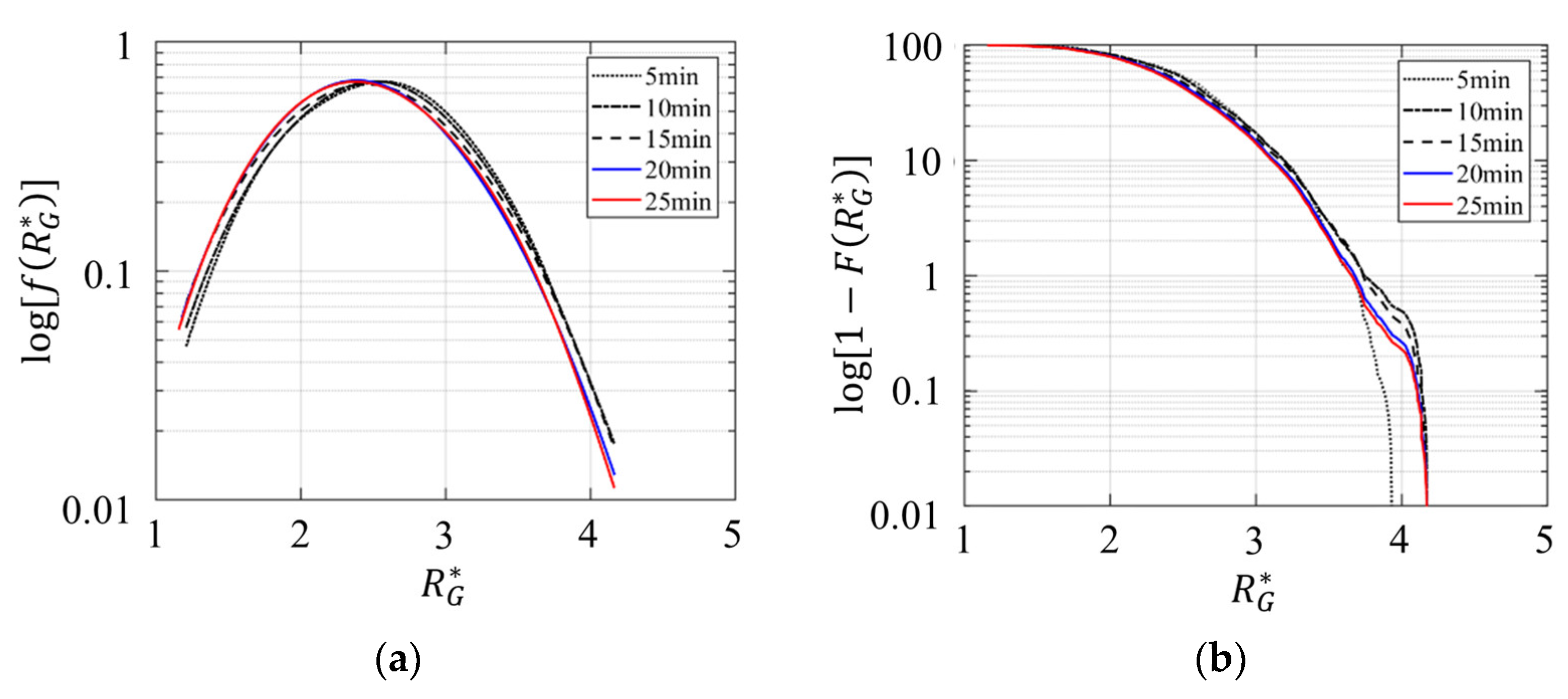
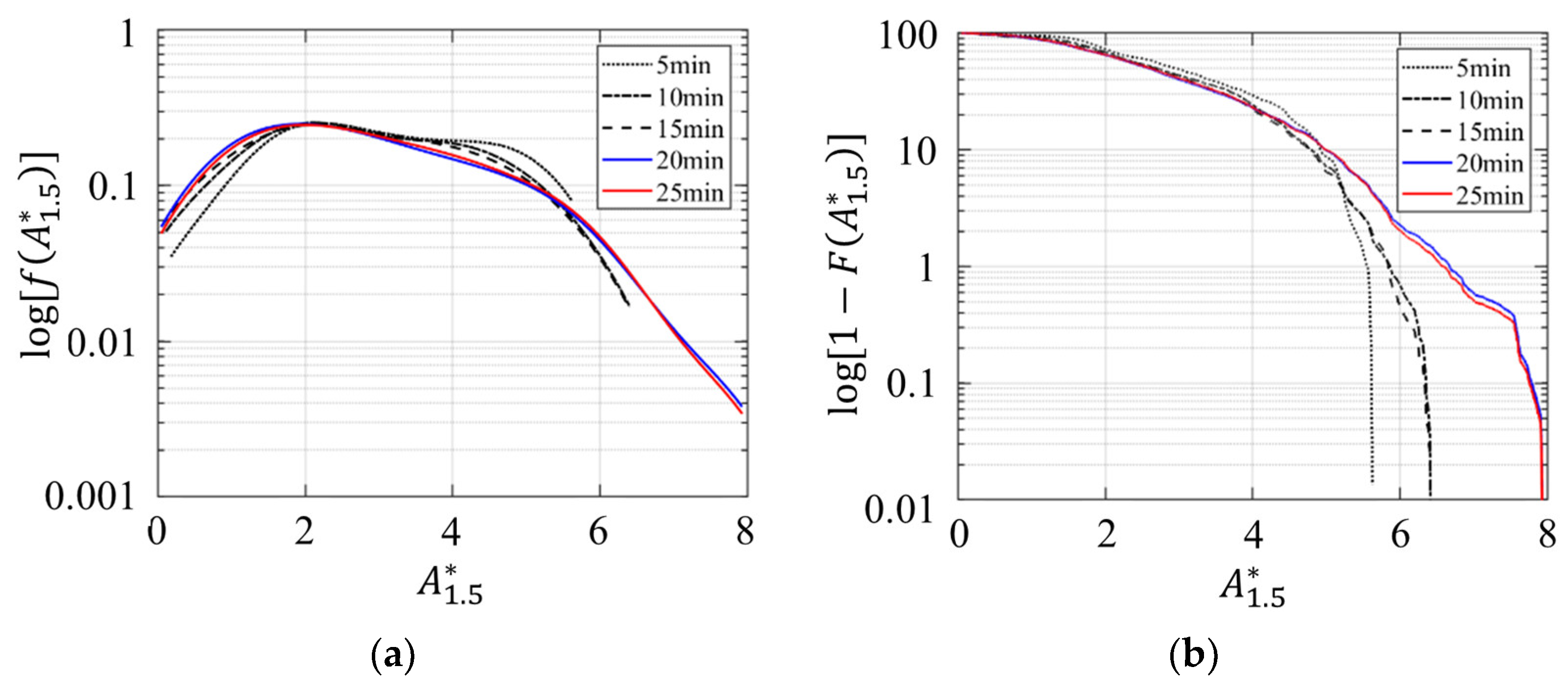
References
- Lawson, T.V.; Penwarden, A.D. The Effect of Wind on People in the Vicinity of Buildings. In Proceedings of the 4th International Conference on Wind Effects on Buildings and Structures; Cambridge University Press: Cambridge, UK, 1975; pp. 605–622. [Google Scholar]
- Wise, A.F.E. Effects Due to Groups of Buildings. Philosophical Transactions of the Royal Society of London. Ser. A Math. Phys. Sci. 1971, 269, 469–485. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Poulton, E.C.; Mumford, J.C. The Effects of Wind on People; New Criteria Based on Wind Tunnel Experiments. Build. Environ. 1976, 11, 15–28. [Google Scholar] [CrossRef]
- Murakami, S.; Deguchi, K. New Criteria for Wind Effects on Pedestrians. J. Wind Eng. Ind. Aerodyn. 1981, 7, 289–309. [Google Scholar] [CrossRef]
- Vita, G.; Shu, Z.; Jesson, M.; Quinn, A.; Hemida, H.; Sterling, M.; Baker, C. On the Assessment of Pedestrian Distress in Urban Winds. J. Wind Eng. Ind. Aerodyn. 2020, 203, 104200. [Google Scholar] [CrossRef]
- Blocken, B.; Moonen, P.; Stathopoulos, T.; Carmeliet, J. Numerical Study on the Existence of the Venturi Effect in Passages between Perpendicular Buildings. J. Eng. Mech. 2008, 134, 1021–1028. [Google Scholar] [CrossRef]
- Dutt, A.J. Wind Flow in an Urban Environment. Environ. Monit. Assess. 1991, 19, 495–506. [Google Scholar] [CrossRef] [PubMed]
- Gandemer, J. Discomfort Due to Wind near Buildings: Aerodynamic Concepts; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1978. [Google Scholar] [CrossRef]
- Tamura, Y.; Xu, X.D.; Yang, Q.S. Characteristics of Pedestrian-Level Mean Wind Speed around Square Buildings: Effects of Height, Width, Size and Approaching Flow Profile. J. Wind Eng. Ind. Aerodyn. 2019, 192, 74–87. [Google Scholar] [CrossRef]
- Yang, Q.; Xu, X.; Lin, Q.; Tamura, Y. Generic Models for Predicting Pedestrian-Level Wind around Isolated Square-Section High-Rise Buildings. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104842. [Google Scholar] [CrossRef]
- Cook, N.J. The Designer’s Guide to Wind Loading of Building Structures. I. Background, Damage Survey, Wind Data and Structural Classification; Building Research Establishment Report; Butterworths: London, UK, 1985; ISBN 978-0-408-00870-9. [Google Scholar]
- Blocken, B.; Carmeliet, J. Pedestrian Wind Environment around Buildings: Literature Review and Practical Examples. J. Therm. Envel. Build. Sci. 2004, 28, 107–159. [Google Scholar] [CrossRef]
- Beranek, W.J. Wind Environment around Single Buildings of Rectangular Shape. Heron 1984, 29, 1–31. [Google Scholar]
- Sexton, D. Building Aerodynamics; Building Research Station, Structural Department: Martinez, GA, USA, 1967. [Google Scholar]
- Franke, J.; Hellsten, A.; Schlunzen, K.H.; Carissimo, B. The COST 732 Best Practice Guideline for CFD Simulation of Flows in the Urban Environment: A Summary. IJEP 2011, 44, 419. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ Guidelines for Practical Applications of CFD to Pedestrian Wind Environment around Buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Lin, Q.; Ishida, Y.; Tanaka, H.; Mochida, A.; Yang, Q.; Tamura, Y. Large Eddy Simulations of Strong Wind Mechanisms at Pedestrian Level around Square-Section Buildings with Same Aspect Ratios and Different Sizes. Build. Environ. 2023, 243, 110680. [Google Scholar] [CrossRef]
- Okaze, T.; Mochida, A. Cholesky Decomposition–Based Generation of Artificial Inflow Turbulence Including Scalar Fluctuation. Comput. Fluids 2017, 159, 23–32. [Google Scholar] [CrossRef]
- TPU Aerodynamic Database. Available online: https://wind.arch.t-kougei.ac.jp/system/eng/contents/code/tpu (accessed on 16 February 2024).
- Ikegaya, N.; Ikeda, Y.; Hagishima, A.; Tanimoto, J. Evaluation of Rare Velocity at a Pedestrian Level Due to Turbulence in a Neutrally Stable Shear Flow over Simplified Urban Arrays. J. Wind Eng. Ind. Aerodyn. 2017, 171, 137–147. [Google Scholar] [CrossRef]
- Kawaminami, T.; Ikegaya, N.; Hagishima, A.; Tanimoto, J. Velocity and Scalar Concentrations with Low Occurrence Frequencies within Urban Canopy Regions in a Neutrally Stable Shear Flow over Simplified Urban Arrays. J. Wind Eng. Ind. Aerodyn. 2018, 182, 286–294. [Google Scholar] [CrossRef]
- Wang, W.; Okaze, T. Statistical Analysis of Low-Occurrence Strong Wind Speeds at the Pedestrian Level around a Simplified Building Based on the Weibull Distribution. Build. Environ. 2022, 209, 108644. [Google Scholar] [CrossRef]
- Du, Y.; Mak, C.M.; Kwok, K.; Tse, K.-T.; Lee, T.; Ai, Z.; Liu, J.; Niu, J. New Criteria for Assessing Low Wind Environment at Pedestrian Level in Hong Kong. Build. Environ. 2017, 123, 23–36. [Google Scholar] [CrossRef]
- Lawson, T.V. The Widn Content of the Built Environment. J. Wind Eng. Ind. Aerodyn. 1978, 3, 93–105. [Google Scholar] [CrossRef]
- Murakami, S.; Iwasa, Y.; Morikawa, Y. Study on Acceptable Criteria for Assessing Wind Environment at Ground Level Based on Residents’ Diaries. J. Wind Eng. Ind. Aerodyn. 1986, 24, 1–18. [Google Scholar] [CrossRef]




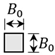
| Width, B (m) | (Constant) | ||
| Height, H (m) | 100 | 400 | |
| Aspect Ratio, | 2 | 4 | 8 |
 | 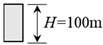 | 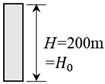 | 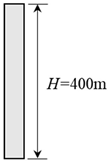 |
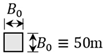 | 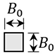 |  | |
| Code | OpenFOAM v8 |
|---|---|
| Computational domain | |
| SGS model | WALE model |
| Time scheme | Second-order backward |
| Time interval for time advancement | 1 × 10−4 s |
| Advection scheme | Second-order central difference (95%) + First-order upwind difference (5%) |
| Diffusion scheme | Second-order linear difference |
| Pressure solver | PISO |
| Inflow fluctuation | Artificial generation method [18] |
| Outlet boundary | Advective outflow condition |
| Upper and side boundaries | No-slip wall |
| Ground and building boundaries | Spalding’s law |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Q.; Konno, N.; Tanaka, H.; Yang, Q.; Tamura, Y. Flow Patterns Providing Maximum Speed-Up Ratio and Maximum Speed-Up Area of Pedestrian-Level Winds. Wind 2025, 5, 8. https://doi.org/10.3390/wind5010008
Lin Q, Konno N, Tanaka H, Yang Q, Tamura Y. Flow Patterns Providing Maximum Speed-Up Ratio and Maximum Speed-Up Area of Pedestrian-Level Winds. Wind. 2025; 5(1):8. https://doi.org/10.3390/wind5010008
Chicago/Turabian StyleLin, Qiang, Naoko Konno, Hideyuki Tanaka, Qingshan Yang, and Yukio Tamura. 2025. "Flow Patterns Providing Maximum Speed-Up Ratio and Maximum Speed-Up Area of Pedestrian-Level Winds" Wind 5, no. 1: 8. https://doi.org/10.3390/wind5010008
APA StyleLin, Q., Konno, N., Tanaka, H., Yang, Q., & Tamura, Y. (2025). Flow Patterns Providing Maximum Speed-Up Ratio and Maximum Speed-Up Area of Pedestrian-Level Winds. Wind, 5(1), 8. https://doi.org/10.3390/wind5010008








