The Financial Aspects behind Designing a Wind Turbine Generator
Abstract
1. Introduction
2. Materials and Methods
2.1. Designing the Generator Using Analytical Equations [44,45,46]
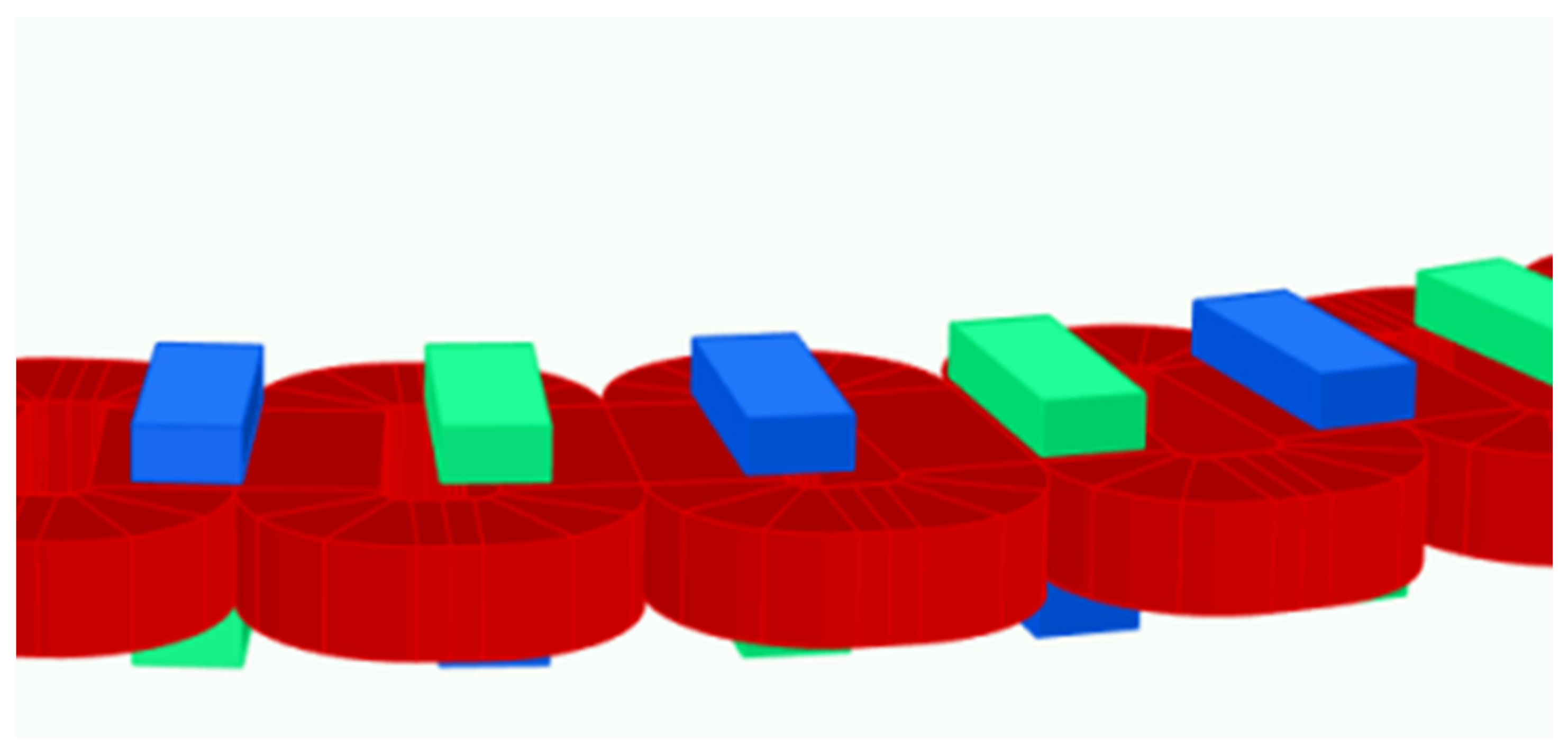
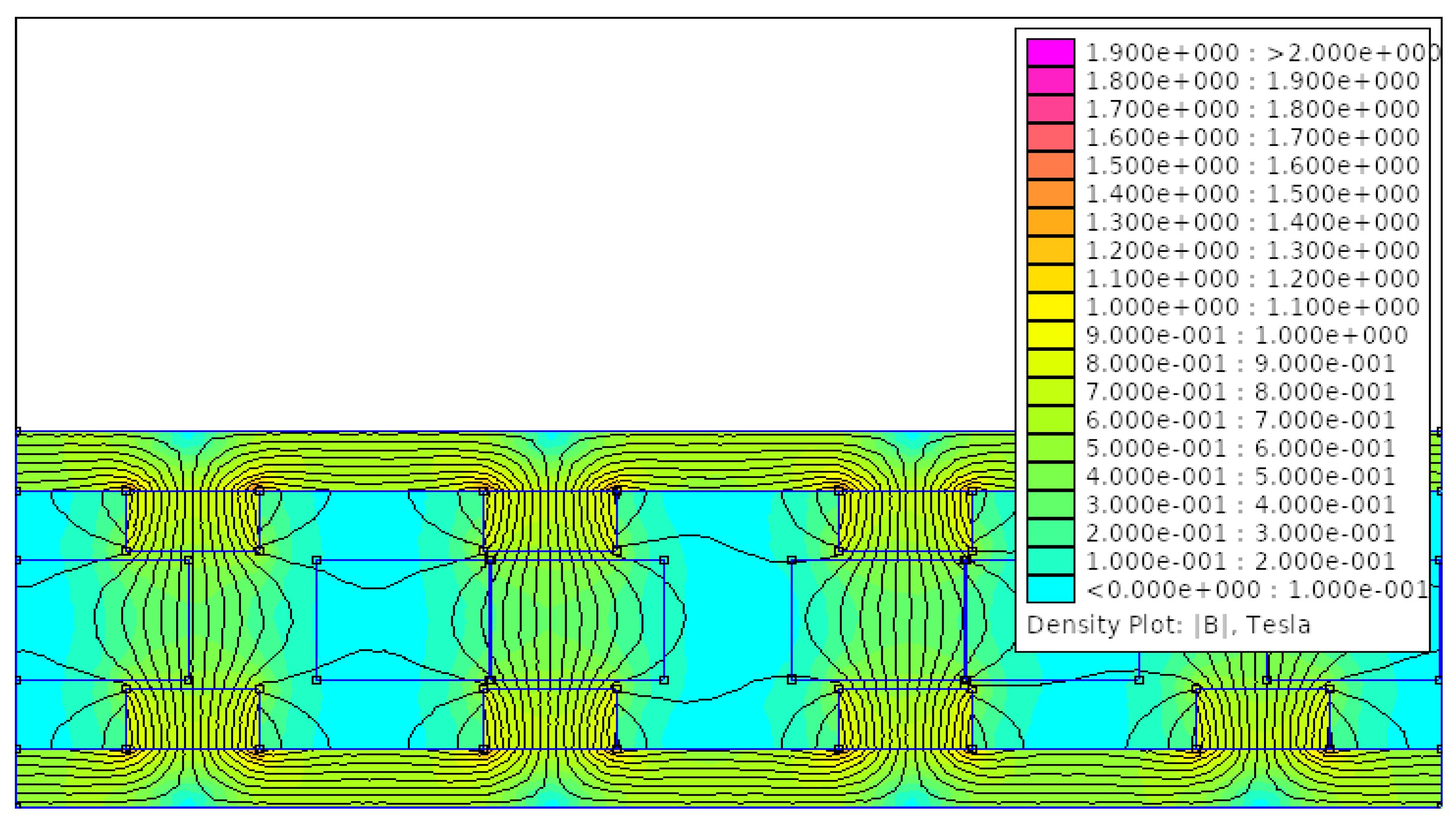
2.2. Designing the Generator Using OpenAFPM 2D-FEM
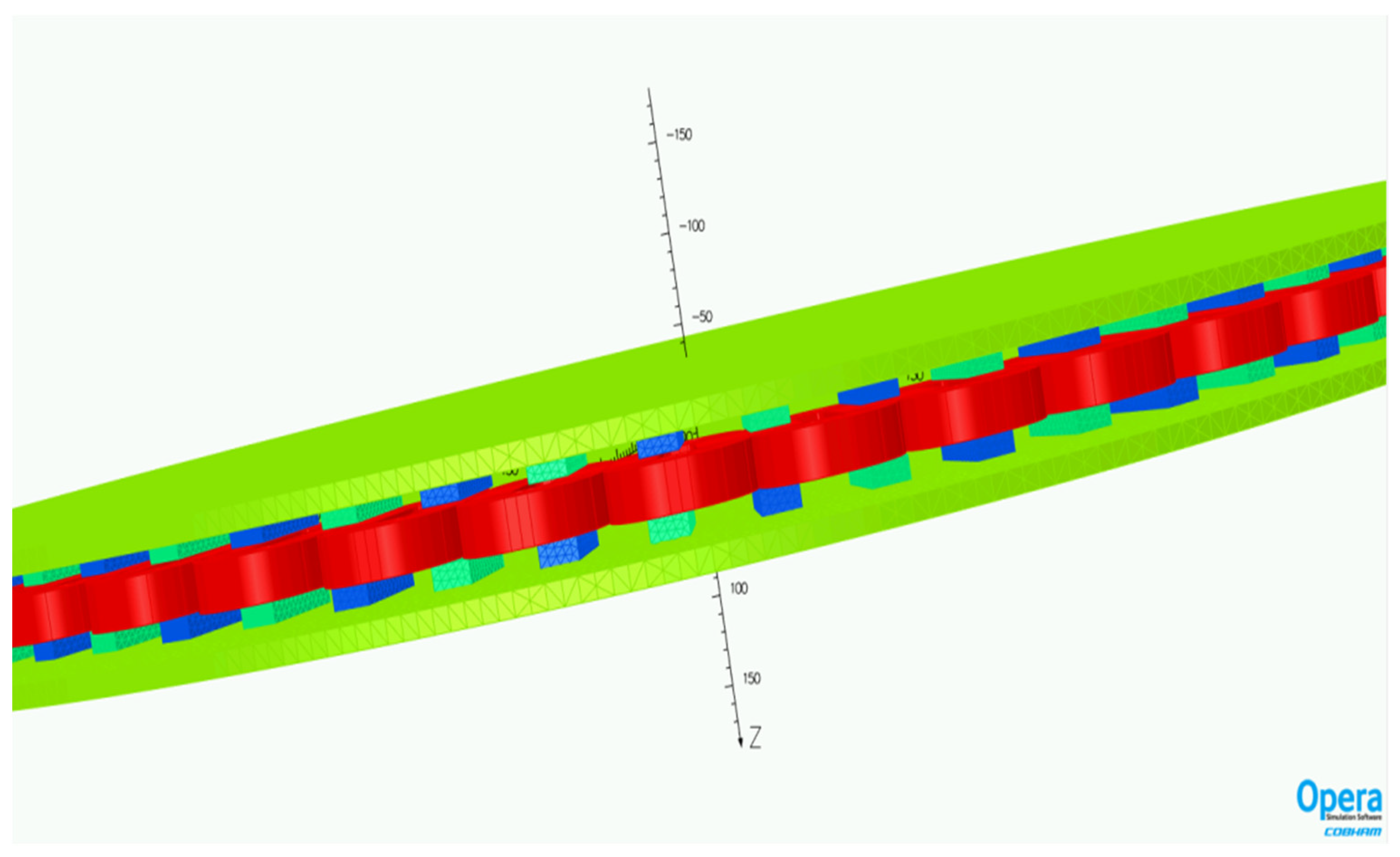
2.3. Designing the Generator Using 3D-FEM
2.4. The Mass Production versus Dispersed Construction Economics—Economic Evaluation and Feasibility of a Dispersed Produced Low Speed Small Generator
- the education/culture times economy,
- the nature law times norms/standards
- the use value times exchange value,
- conception result
- production result
- operation result
3. Results
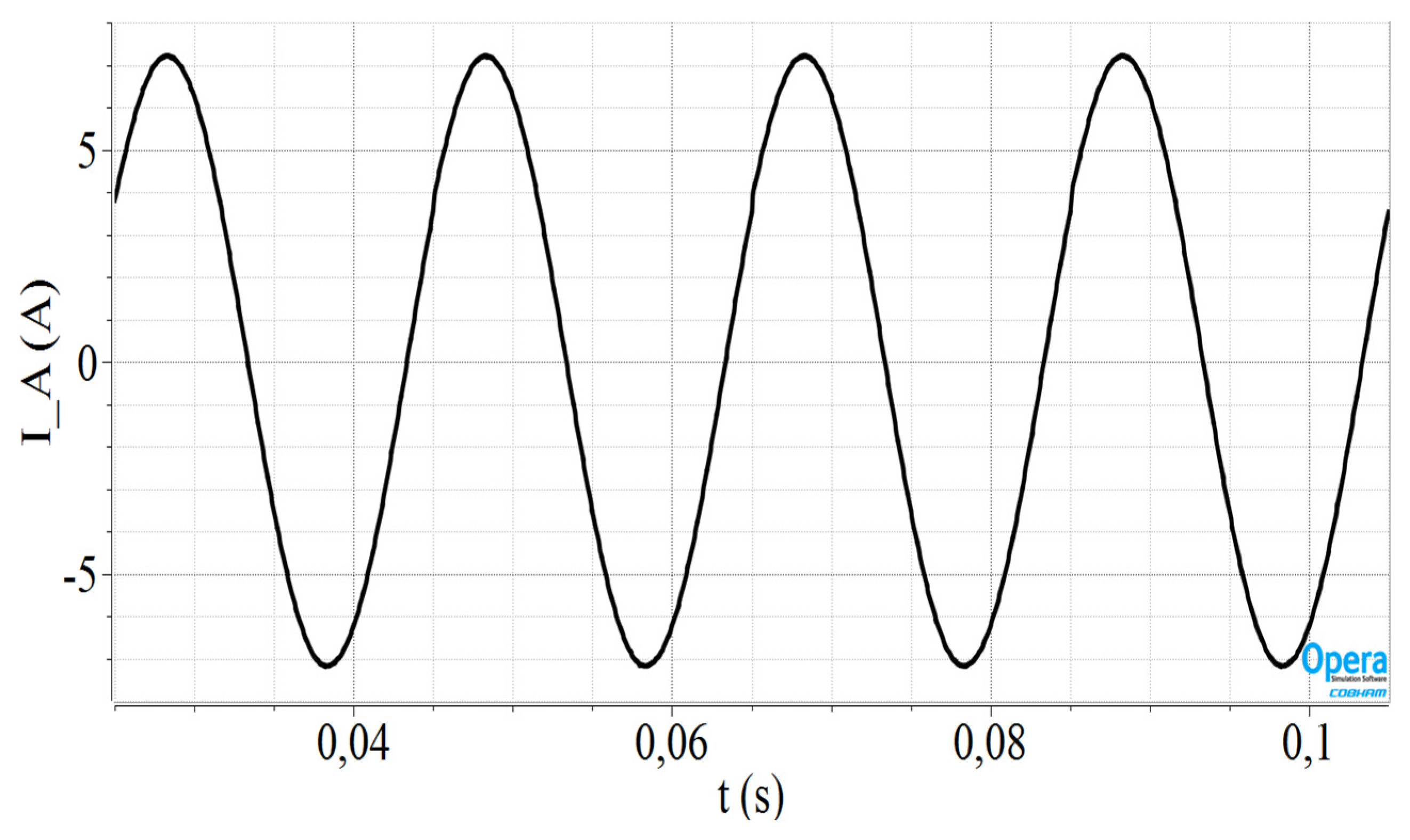
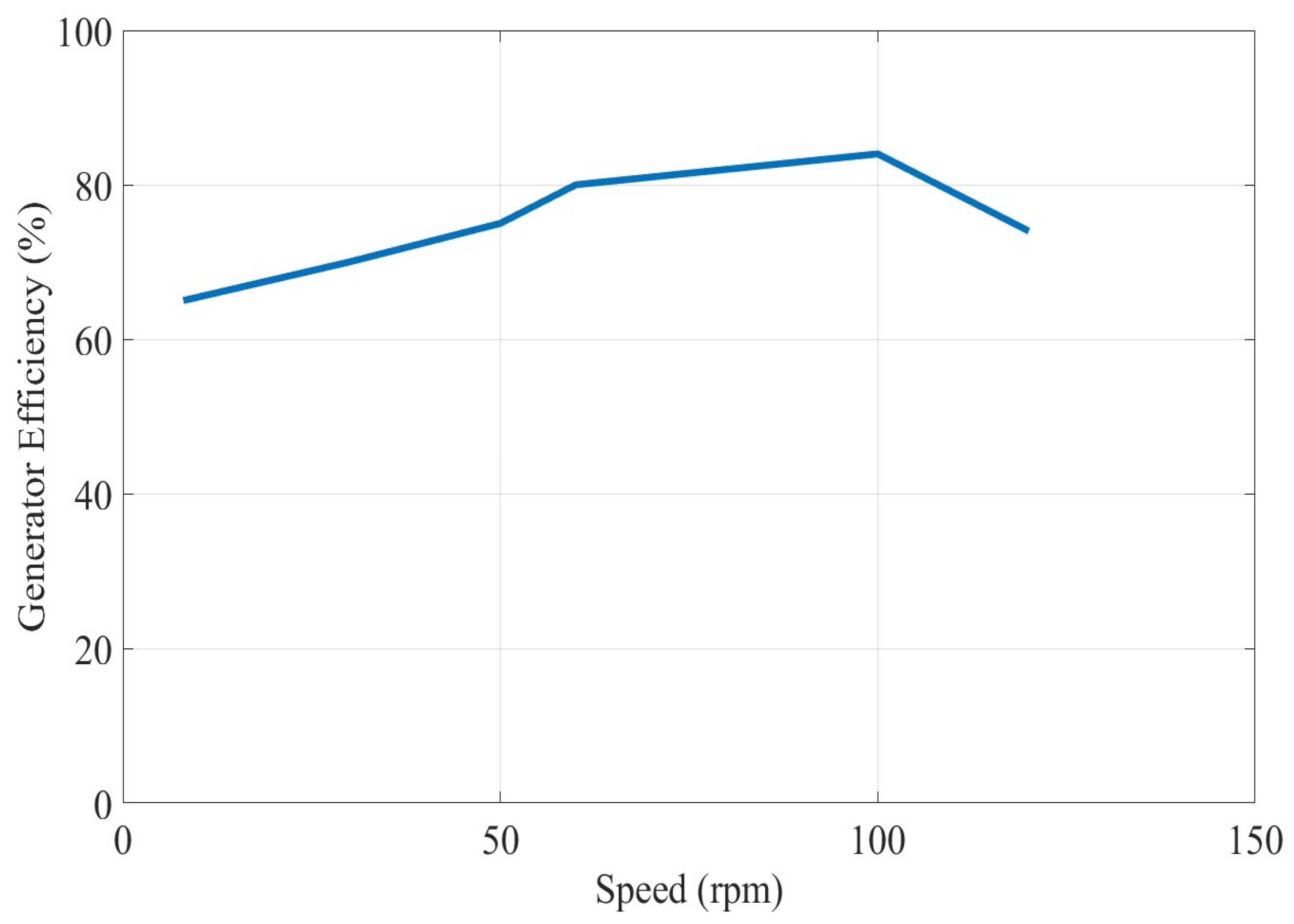
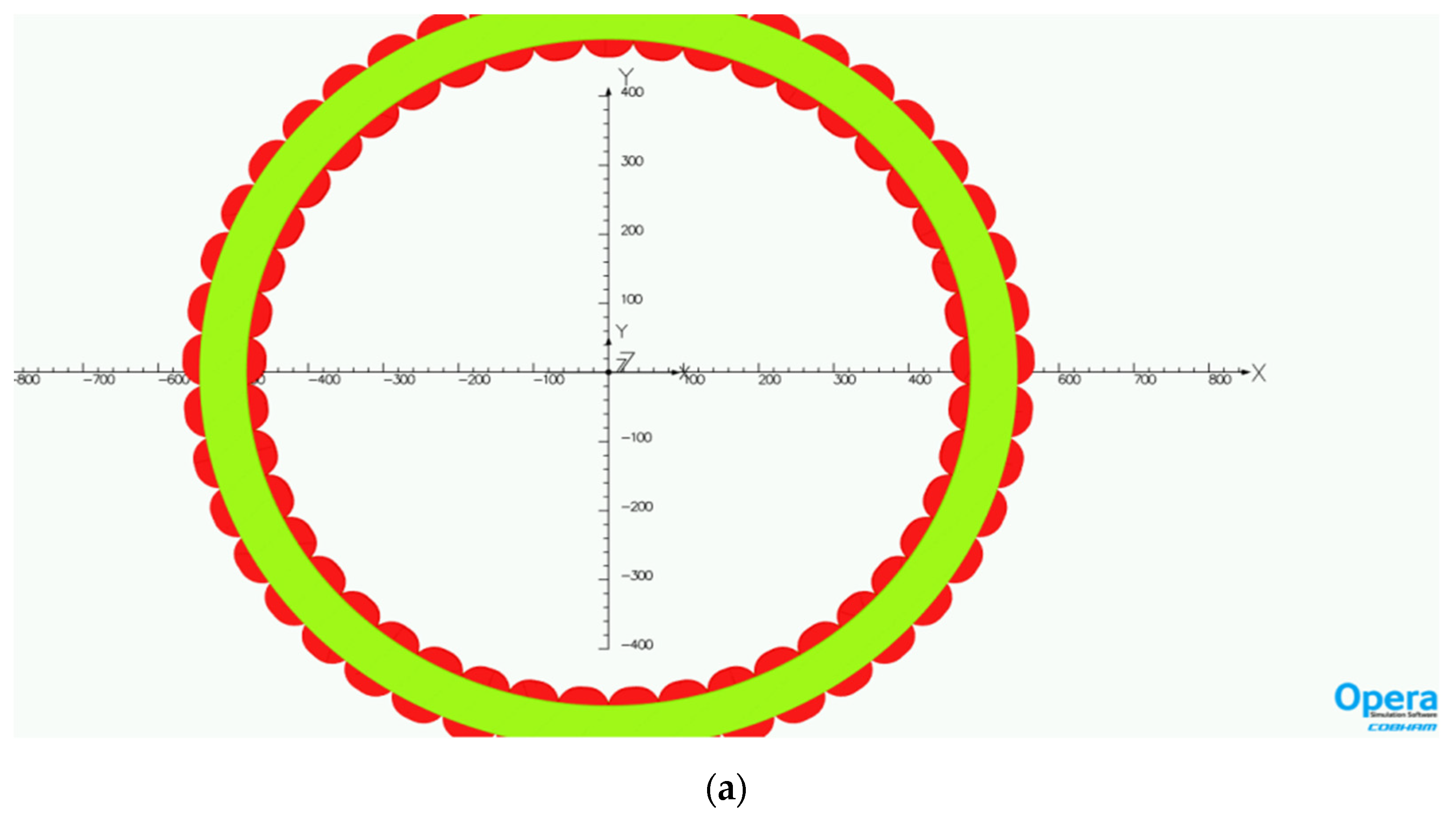
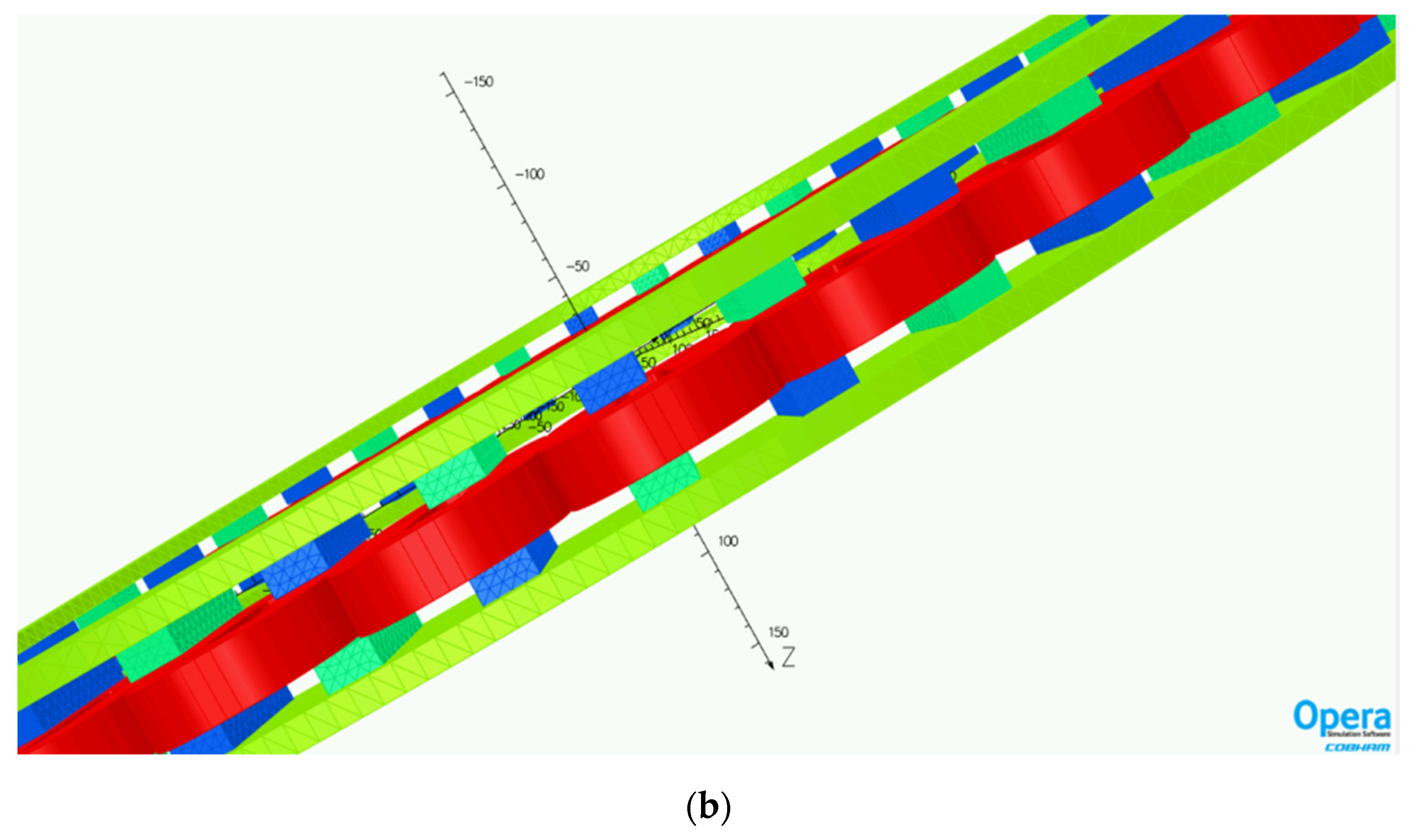
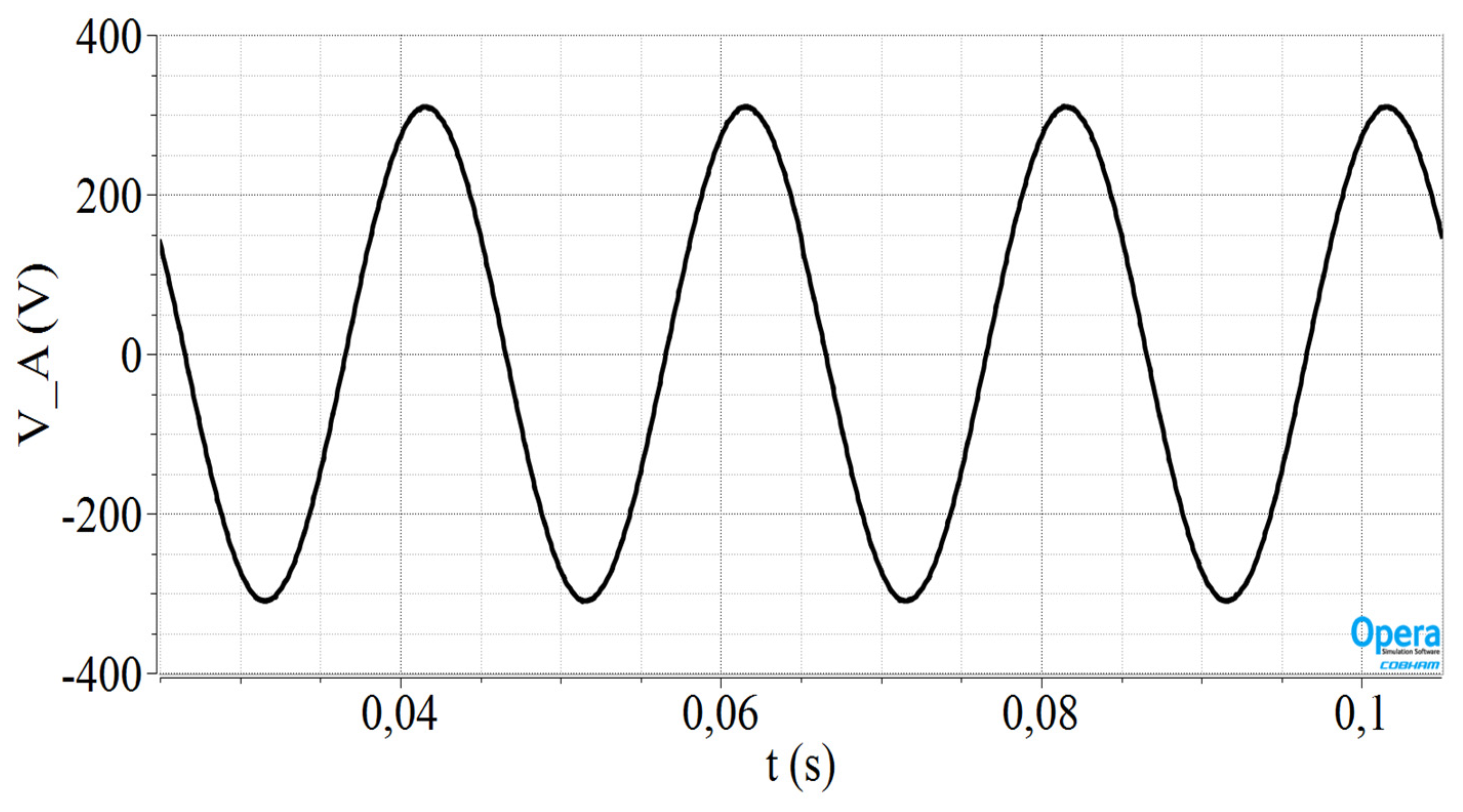
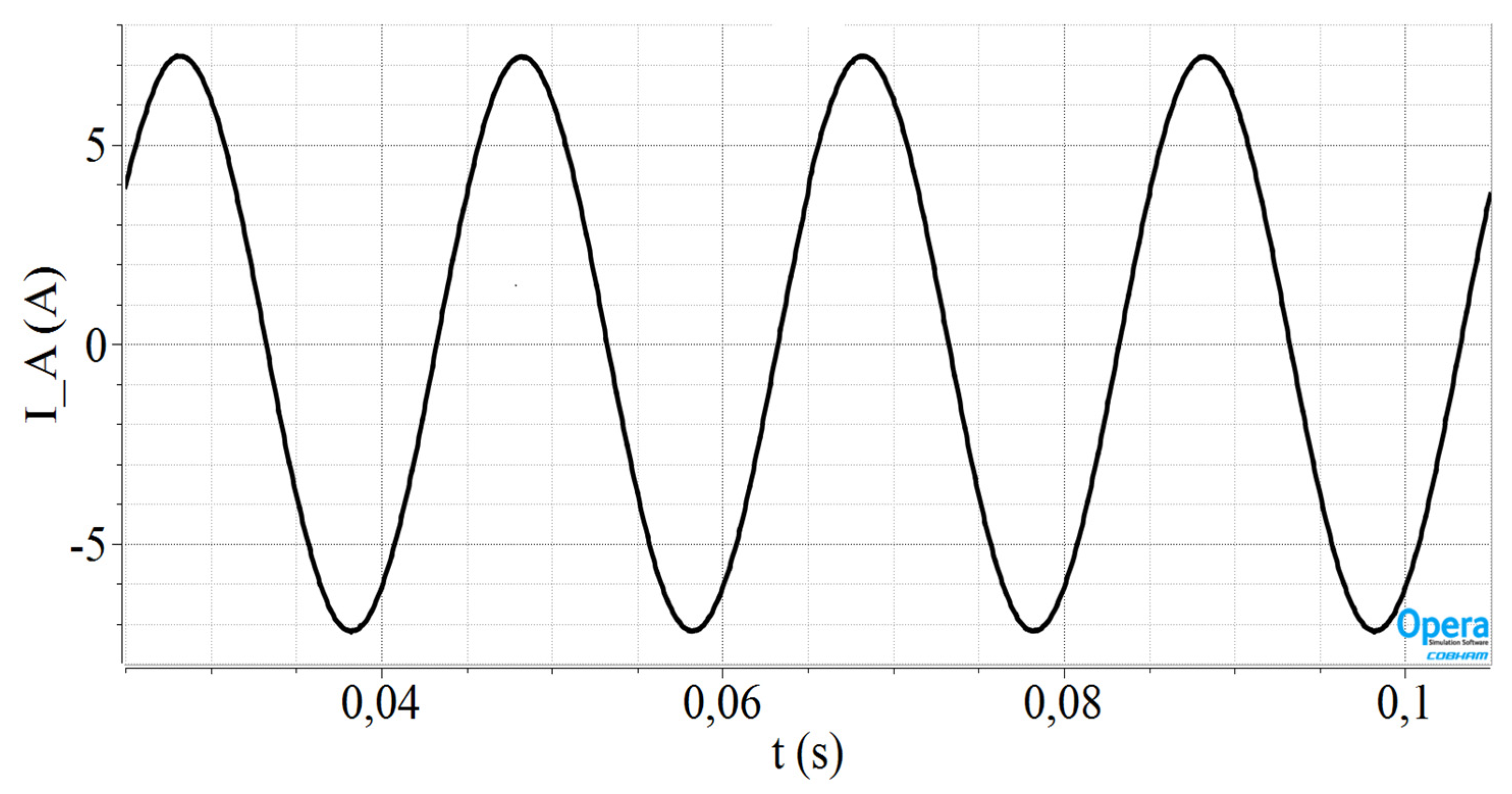
3.1. Simulation Results Using 3D-FEM
3.2. Economic Cost Estimation Results Using OpenAFPM 2D-FEM
4. Suggestion for Novel Generator Concept
5. Discussion
6. Hints for Further Results
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taran, N. Efficiency Optimi Ization of an Axial Flu Ux Permanent Magnet Synchrono Ous Generator for Low w Speed Wind. In Proceedings of the 2014 22nd Iranian Conference on Electrical Engineering, Tehran, Iran, 20–22 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 539–544. [Google Scholar]
- Kappatou, J.C.; Zalokostas, G.D.; Spyratos, D.A. 3-D FEM Analysis, Prototyping and Tests of an Axial Flux Permanent-Magnet Wind Generator. Energies 2017, 10, 1269. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, Y.J.; Lee, K.S.; Kim, S.J. Multiobjective Optimization Design of Small-Scale Wind Power Generator with Outer Rotor Based on Box-Behnken Design. IEEE Trans. Appl. Supercond. 2016, 26, 5202605. [Google Scholar] [CrossRef]
- Saruwatari, M.; Yun, K.; Iwakuma, M.; Tamura, K.; Hase, Y.; Sasamori, Y.; Izumi, T. Design Study of 15-MW Fully Superconducting Generators for Offshore Wind Turbine. IEEE Trans. Appl. Supercond. 2016, 26, 5206805. [Google Scholar] [CrossRef]
- Nakamura, K.; Ichinokura, O. Super-Multipolar Permanent Magnet Reluctance Generator Designed for Small-Scale Wind-Turbine Generation. IEEE Trans. Magn. 2012, 48, 3311–3314. [Google Scholar] [CrossRef]
- Imanuddin, N.; Furqani, J.; Rizqiawan, A. Effects of Radial Divided Magnet Shifting on Cogging Torque of Axial Flux Permanent Magnet Generator for Small Scale Wind Turbine. In Proceedings of the 2023 4th International Conference on High Voltage Engineering and Power Systems (ICHVEPS), Sanur-Denpasar, Indonesia, 6–10 August 2023; pp. 555–560. [Google Scholar] [CrossRef]
- Kappatou, J.C.; Zalokostas, G.D.; Spyratos, D.A. Design Optimization of Axial Flux Permanent Magnet (AFPM) Synchronous Machine Using 3D FEM Analysis. J. Electromagn. Anal. Appl. 2016, 8, 247–260. [Google Scholar] [CrossRef]
- Latoufis, K.; Troullaki, K.; Pazios, T.; Hatziargyriou, N. Design of Axial Flux Permanent Magnet Generators Using Various Magnetic Materials in Locally Manufactured Small Wind Turbines. In Proceedings of the 2016 22nd International Conference on Electrical Machines, ICEM 2016, Lausanne, Switzerland, 4–7 September 2016; pp. 1545–1551. [Google Scholar] [CrossRef]
- Taran, N.; Ardebili, M. A Novel Approach for Efficiency and Power Density Optimization of an Axial Flux Permanent Magnet Generator through Genetic Algorithm and Finite Element Analysis. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 709–714. [Google Scholar] [CrossRef]
- Zhao, X.; Niu, S.; Fu, W. Sensitivity Analysis and Design Optimization of a New Hybrid-Excited Dual-PM Generator with Relieving-DC-Saturation Structure for Stand-Alone Wind Power Generation. IEEE Trans. Magn. 2020, 56, 7504105. [Google Scholar] [CrossRef]
- Labuschagne, C.J.J.; Kamper, M.J. Design Optimisation and Comparison of Non-Overlap Winding PM Wind Generators for Active and Passive Battery Charging Systems. In Proceedings of the 23rd International Conference on Electrical Machines, ICEM Alexandroupoli, Greece, 3–6 September 2018; pp. 690–696. [Google Scholar] [CrossRef]
- Beik, O.; Al-Adsani, A.S. A Wind Turbine Generator Design and Optimization for DC Collector Grids. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 484–493. [Google Scholar] [CrossRef]
- Bhuiyan, N.A.; McDonald, A. Optimization and Comparison of Flux-Concentrating Nd-Fe-B Generator Considering Variable Power Factor and Wind Conditions for a 6MW Offshore Wind Turbine. In Proceedings of the 53rd International Universities Power Engineering Conference, UPEC 2018, Glasgow, UK, 4–7 September 2018; pp. 1–5. [Google Scholar] [CrossRef][Green Version]
- Karmaker, H.; Ho, M.; Kulkarni, D. Comparison between Different Design Topologies for Multi-Megawatt Direct Drive Wind Generators Using Improved Second Generation High Temperature Superconductors. IEEE Trans. Appl. Supercond. 2015, 25, 5201605. [Google Scholar] [CrossRef]
- Barmpatza, A.C.; Kappatou, J.C. Study of the Total Demagnetization Fault of an AFPM Wind Generator. IEEE Trans. Energy Convers. 2021, 36, 725–736. [Google Scholar] [CrossRef]
- Minaz, M.R.; Akcan, E. An Effective Method for Detection of Demagnetization Fault in Axial Flux Coreless PMSG with Texture-Based Analysis. IEEE Access 2021, 9, 17438–17449. [Google Scholar] [CrossRef]
- Chen, H.; Qu, R.; Li, J.; Li, D. Demagnetization Performance of a 7 MW Interior Permanent Magnet Wind Generator with Fractional-Slot Concentrated Windings. IEEE Trans. Magn. 2015, 51, 8205804. [Google Scholar] [CrossRef]
- Hsieh, M.F.; Yeh, Y.H. Rotor Eccentricity Effect on Cogging Torque of PM Generators for Small Wind Turbines. IEEE Trans. Magn. 2013, 49, 1897–1900. [Google Scholar] [CrossRef]
- Huang, Z.; Zhao, A.; Huang, X.; Zhu, B.; Jiang, Y.; Jin, Z. Short-Circuit Fault Simulations in an HTS Wind Generator with Different Mechanical Conditions. IEEE Trans. Appl. Supercond. 2018, 28, 5204606. [Google Scholar] [CrossRef]
- Lamprokostopoulos, A.; Mitronikas, E.; Barmpatza, A. Detection of Demagnetization Faults in Axial Flux Permanent-Magnet Synchronous Wind Generators. Energies 2022, 15, 3220. [Google Scholar] [CrossRef]
- Barmpatza, A.C.; Kappatou, J.C. Study of a Combined Demagnetization and Eccentricity Fault in an AFPM Synchronous Generator. Energies 2020, 13, 5609. [Google Scholar] [CrossRef]
- Wang, A.; Wang, C.; Wang, H. Performance and Demagnetization Analysis of the Permanent Magnet Generator with FSCW for Small Scale Wind Power Systems. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems, ICEMS 2014, Hangzhou, China, 22–25 October 2014; Volume 483, pp. 483–487. [Google Scholar] [CrossRef]
- Guo, Y.; Ding, Y.; Jin, P. Demagnetization Analysis of a V-Shape PM Salient Pole Wind Generator under Sudden Short-Circuits after Rated Load Condition. In Proceedings of the 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference, APPEEC, Nanjing, China, 20–23 September 2020. [Google Scholar] [CrossRef]
- Barmpatza, A.C. The Neutral Voltage Difference Signal as a Means of Investigating Eccentricity and Demagnetization Faults in an AFPM Synchronous Generator. Machines 2023, 11, 647. [Google Scholar] [CrossRef]
- Abd-Rabou, A.S.; Marei, M.I.; El-Sattar, A.A.; Basha, M.A. Multiobjective Design Optimization of Axial Flux Permanent Magnet Brushless DC Micromotor Using Response Surface Methodology and Multi-Verse Optimization Algorithm. In Proceedings of the 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology, Amman, Jordan, 9–11 April 2019; pp. 13–18. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Kahourzade, S.; Ping, H.W.; Gandomkar, A. Design Optimization and Analysis of AFPM Synchronous Motor Considering Electrical and Thermal Parameters. In Proceedings of the 1st International Future Energy Electronics Conference, IFEEC 2013, Tainan, Taiwan, 3–6 November 2013; pp. 562–567. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Z.; Liu, Y.; Geng, W.; Gao, H. Effect of Slot-Pole Combination on the Electromagnetic Performance of Ironless Stator AFPM Machine with Concentrated Windings. IEEE Trans. Energy Convers. 2020, 35, 1098–1109. [Google Scholar] [CrossRef]
- Hwang, C.C.; Li, P.L.; Chuang, F.C.; Liu, C.T.; Huang, K.H. Optimization for Reduction of Torque Ripple in an Axial Flux Permanent Magnet Machine. IEEE Trans. Magn. 2009, 45, 1760–1763. [Google Scholar] [CrossRef]
- Taran, N.; Rallabandi, V.; Ionel, D.M. WAVED: A Coreless Axial Flux PM Motor for Drive Systems with Constant Power Operation. In Proceedings of the ITEC 2019–2019 IEEE Transportation Electrification Conference and Expo, Detroit, MI, USA, 19–21 June 2019. [Google Scholar] [CrossRef]
- Yang, X.; Patterson, D.; Hudgins, J. Multi-Objective Design Optimization of a Single-Sided Axial Flux Permanent Magnet Machine. In Proceedings of the 2013 International Conference on Electrical Machines and Systems, ICEMS 2013, Busan, Republic of Korea, 26–29 October 2013; pp. 822–825. [Google Scholar] [CrossRef]
- Li, Q.; Wang, J.; Ge, S.; Jian, G.; Li, L.; Geng, W.; Zhang, Z. Analysis and Optimization of Winding Losses of Axial Flux Permanent Magnet Machine with Concentrated Winding Flat Wires. IEEE Trans. Transp. Electrif. 2023, 99, 1. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Geng, W. Design and Optimization of Halbach-Array PM Rotor for High-Speed Axial-Flux Permanent Magnet Machine with Ironless Stator. IEEE Trans. Ind. Electron. 2020, 67, 7269–7279. [Google Scholar] [CrossRef]
- Gao, B.; Cheng, Y.; Wang, Y.; Zhao, T.; Ding, L.; Cui, S.; Liu, X.; Shi, Y. Optimal Design of PCB Coreless Axial Flux Permanent Magnet Synchronous Motor With Arc Windings. IEEE Trans. Energy Convers. 2023, 41, 55–64. [Google Scholar] [CrossRef]
- Wang, C.; Han, J.; Zhang, Z.; Hua, Y.; Gao, H. Design and Optimization Analysis of Coreless Stator Axial-Flux Permanent Magnet In-Wheel Motor for Unmanned Ground Vehicle. IEEE Trans. Transp. Electrif. 2022, 8, 1053–1062. [Google Scholar] [CrossRef]
- Yu, F.; Chen, H.; Yan, W.; Pires, V.F.; Martins, J.F.A.; Rafajdus, P.; Musolino, A.; Sani, L.; Aguirre, M.P.; Saqib, M.A.; et al. Design and Multiobjective Optimization of a Double-Stator Axial Flux SRM with Full-Pitch Winding Configuration. IEEE Trans. Transp. Electrif. 2022, 8, 4348–4364. [Google Scholar] [CrossRef]
- Min, S.G. Analytical Design and Optimization of Axial Flux Permanent Magnet Machines with Slotless Structure. IEEE Trans. Transp. Electrif. 2022, 8, 1994–2004. [Google Scholar] [CrossRef]
- Yang, X.; Patterson, D.; Hudgins, J. Design Optimization of Single-Sided Axial Flux Permanent Magnet Machines by Differential Evolution. In Proceedings of the 2014 International Conference on Electrical Machines, ICEM 2014, Berlin, Germany, 2–5 September 2014; pp. 1090–1095. [Google Scholar] [CrossRef]
- Di Gerlando, A.; Foglia, G.M.; Iacchetti, M.F.; Perini, R. Sizing Comparison of Axial Flux PM Motors, for Automotive Application. In Proceedings of the 2014 International Conference on Electrical Machines, ICEM 2014, Berlin, Germany, 2–5 September 2014; pp. 1409–1414. [Google Scholar] [CrossRef]
- Taran, N.; Rallabandi, V.; Ionel, D.M.; Heins, G.; Patterson, D.; Zhou, P. Design Optimization of Electric Machines with 3D FEA and a New Hybrid DOE-DE Numerical Algorithm. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference, IEMDC 2019, San Diego, CA, USA, 12–15 May 2019; pp. 603–608. [Google Scholar] [CrossRef]
- Hoang, T.K.; Quéval, L.; Berriaud, C.; Vido, L. Design of a 20-MW Fully Superconducting Wind Turbine Generator to Minimize the Levelized Cost of Energy. IEEE Trans. Appl. Supercond. 2018, 28, 2–6. [Google Scholar] [CrossRef]
- Landi, G.; Musolino, A.; Sani, L.; Simonelli, C. Design Criteria for an Axial Flux Wind Generator with Halbach Array Permanent Magnets. In Proceedings of the 12th International Conference on Renewable Energy Research and Applications, ICRERA 2023, Oshawa, ON, Canada, 29 August–1 September 2023; pp. 213–218. [Google Scholar] [CrossRef]
- Sun, S.; Jiang, F.; Li, T.; Xu, B.; Yang, K. Design and Optimization of a Novel Axial-Radial Flux Permanent Magnet Machine. IEEE Trans. Appl. Supercond. 2020, 30, 5205106. [Google Scholar] [CrossRef]
- Liu, C.; Yang, F.; Zhang, W.; Wang, Y. Design Optimization of a Novel Axial-Radial Flux Permanent Magnet Claw Pole Machine with SMC Cores and Ferrite Magnets. CES Trans. Electr. Mach. Syst. 2023, 7, 358–365. [Google Scholar] [CrossRef]
- Kamper, M.J.; Wang, R.J.; Rossouw, F.G. Analysis and Performance of Axial Flux Permanent-Magnet Machine with Air-Cored Nonoverlapping Concentrated Stator Windings. IEEE Trans. Ind. Appl. 2008, 44, 1495–1504. [Google Scholar] [CrossRef]
- Rossouw, F.G. Analysis and Design of Axial Flux Permanent Magnet Wind Generator System for Direct Battery Charging Applications. Ph.D. Dissertation, University of Stellenbosch, Stellenbosch, South Africa, 2009; 140p. [Google Scholar]
- Eindhoven, T.U.; Version, D. Design and Development of a High-Speed Axial-Flux Permanent-Magnet Machine Design and Development of a High-Speed Axial-Flux Permanent-Magnet Machine. Electromechanics Power Electron. 2019, 1, 242. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Han, L.; Zhang, D.; Zhang, J.; Qiu, Q.; Dai, S.; Zhang, Z.; Xia, D.; Zhang, G.; et al. Design of a High Temperature Superconducting Generator for Wind Power Applications. IEEE Trans. Appl. Supercond. 2011, 21, 1155–1158. [Google Scholar] [CrossRef]
- Super Magnetic Shop. Available online: https://supermagneticshop.com/product/magnetic-block-50x20x10-neodymium/ (accessed on 10 September 2023).
- Giulii Capponi, F.; De Donato, G.; Caricchi, F. Recent Advances in Axial-Flux Permanent-Magnet Machine Technology. IEEE Trans. Ind. Appl. 2012, 48, 2190–2205. [Google Scholar] [CrossRef]
- Eurostat. Available online: https://ec.europa.eu/eurostat/en/web/products-eurostat-news/w/ddn-20230330-3 (accessed on 18 September 2023).


| Magnetic Material | Number of Generator Magnets on Each Rotor | Magnet Lenght | Magnet Width | Magnet Thickness | Airgap Lenght | Rotor Thicknesss |
|---|---|---|---|---|---|---|
| NdFeB N35 | 60 | 50 mm | 20 mm | 10 mm | 1.5 mm | 10 mm |
| Generator Outer Radius ro | Generator Inner Radius ri |
|---|---|
| 537 mm | 483 mm |
| Number of Turns per Coil | Number of Generator Stator Coils | Coil Leg Thickness tw | Coil Leg Width wc | Coil Leg Height la | Stator Thickness |
|---|---|---|---|---|---|
| 145 | 45 | 20 mm | 26.5 mm | 54 mm | 20 mm |
| Turbine Rotor Radius | Cut-In Wind Speed | Nominal Wind Speed | Cut-In Tip-Speed Ratio (TSR) | Nominal TSR | Air Density |
|---|---|---|---|---|---|
| 3 m | 2.5 m/s | 10 m/s | 1.0 | 3.15 | 1.2 kg/m3 |
| Copper Price | Iron Price | Resin Price | Plywood Price | Permanent Magnet Price [48] | Cost of Miscellaneous Parts (Bolts, Glues) | Labor Cost |
|---|---|---|---|---|---|---|
| 18 €/kg | 1.7 €/kg | 16 €/kg | 17.60 €/m2 | 3.87 €/magnet | 150 € | 14.5 € |
| Generator Stator Output Parameters | Values Derived from OpenAPFM |
|---|---|
| Average Length of Coil Turn | 202.16 mm |
| Phase Resistance | 4.78905 Ohm |
| EMF at the Nominal Wind Speed | 224.525 V |
| Generator Output Power | 3435.23 W |
| Losses | Values Derived from OpenAPFM |
|---|---|
| Copper Losses | 373.69 W |
| Eddy Current Losses | 4.90538 W |
| Rotational losses | 43.638 W |
| Masses | Values Calculated by OpenAPFM |
|---|---|
| Copper Mass | 20.8395 kg |
| Resin Mass | 14.7857 kg |
| Magnets Mass | 9 kg |
| Mass of Rotor Disks | 142.595 kg |
| Total Generator Mass | 187.22 kg |
| Mass of Bearing Hub | 14.2907 kg |
| Blade Rotor Mass | 51.6121 kg |
| Generator Part | Cost (EUR) |
|---|---|
| Cost of magnets | 464.40 |
| Cost of Copper | 375.111 |
| Cost of Resin | 236.571 |
| Cost of Iron | 242.411 |
| Cost of Moulds | 299.04 |
| Cost of Miscellaneous Parts (Bolts, Glues) | 150 |
| Total Generator Cost | 1767.53 |
| Generator Part | Cost (EUR) |
|---|---|
| Cost of magnets | 464.40 |
| Cost of Copper | 375.111 |
| Cost of Resin | 236.571 |
| Cost of Iron | 51.446 |
| Cost of Moulds | 299.04 |
| Cost of Miscellaneous Parts (Bolts, Glues) | 150 |
| Total Generator Cost | 1576.569 |
| Bulgaria | Greece | Italy | France | |
|---|---|---|---|---|
| Hourly Labor Cost | EUR 8.2 € | 14.5 € | 29.4 € | 40.8 € |
| Total Labor Cost | 328 € | 580 € | 1176 € | 1632 € |
| Total Generator Cost based in Materials | 1576.569 € | 1576.569 € | 1576.569 € | 1576.569 € |
| Total Generator Cost (Including Materials and Labor Cost) | 1904.569 € | 2156.569 € | 2752.569 € | 3208.569 € |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barmpatza, A.C.; Peltier, R.; Condaxakis, C.; Christakis, D. The Financial Aspects behind Designing a Wind Turbine Generator. Wind 2024, 4, 25-43. https://doi.org/10.3390/wind4010002
Barmpatza AC, Peltier R, Condaxakis C, Christakis D. The Financial Aspects behind Designing a Wind Turbine Generator. Wind. 2024; 4(1):25-43. https://doi.org/10.3390/wind4010002
Chicago/Turabian StyleBarmpatza, Alexandra C., Remi Peltier, Constantinos Condaxakis, and Dimitris Christakis. 2024. "The Financial Aspects behind Designing a Wind Turbine Generator" Wind 4, no. 1: 25-43. https://doi.org/10.3390/wind4010002
APA StyleBarmpatza, A. C., Peltier, R., Condaxakis, C., & Christakis, D. (2024). The Financial Aspects behind Designing a Wind Turbine Generator. Wind, 4(1), 25-43. https://doi.org/10.3390/wind4010002







