Influence of the Blunt Trailing-Edge Thickness on the Aerodynamic Characteristics of the Very Thick Airfoil
Abstract
:1. Introduction
2. Method
2.1. Experimental Setup
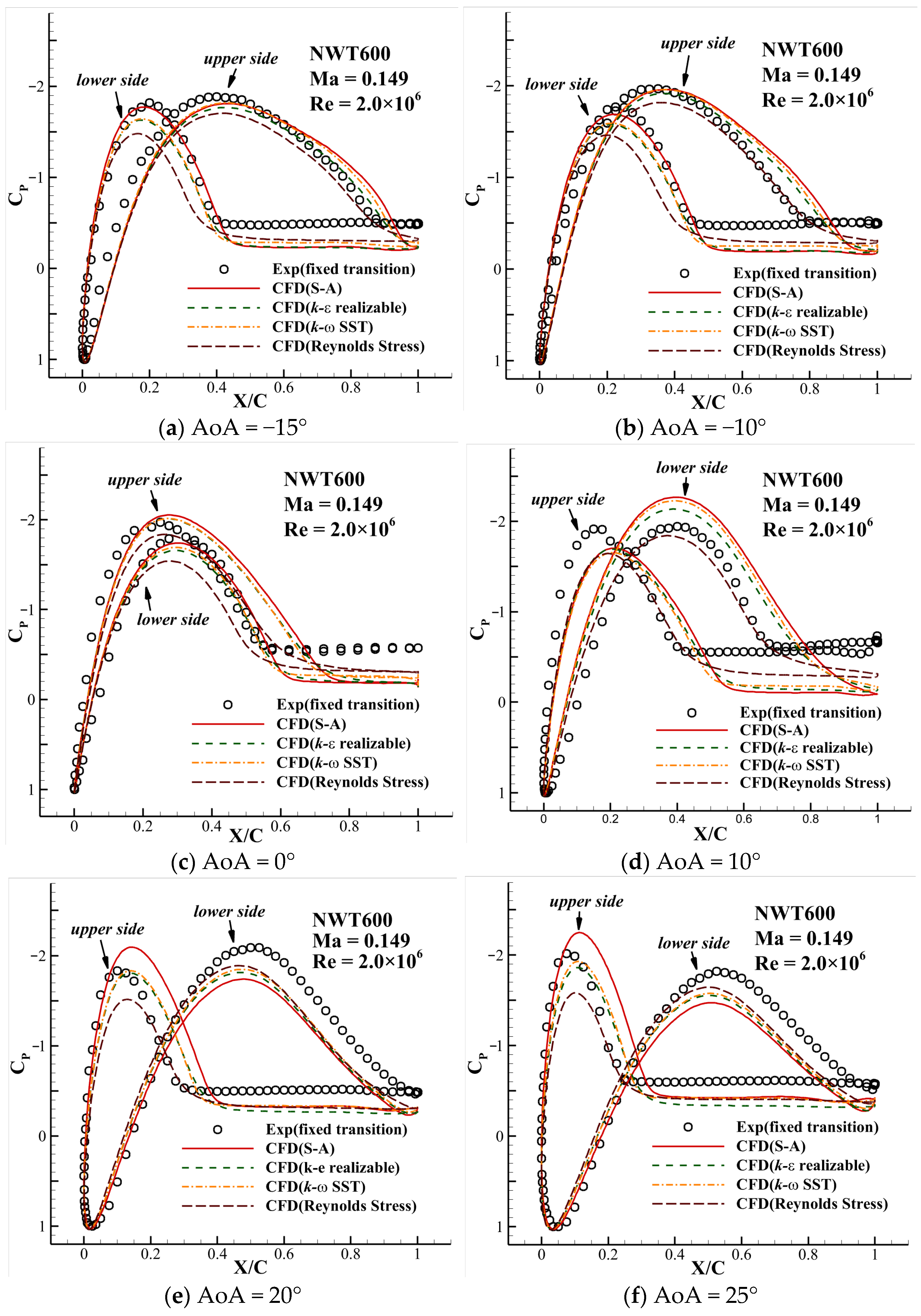
2.2. Numerical Method and Validation
3. Results and Discussion
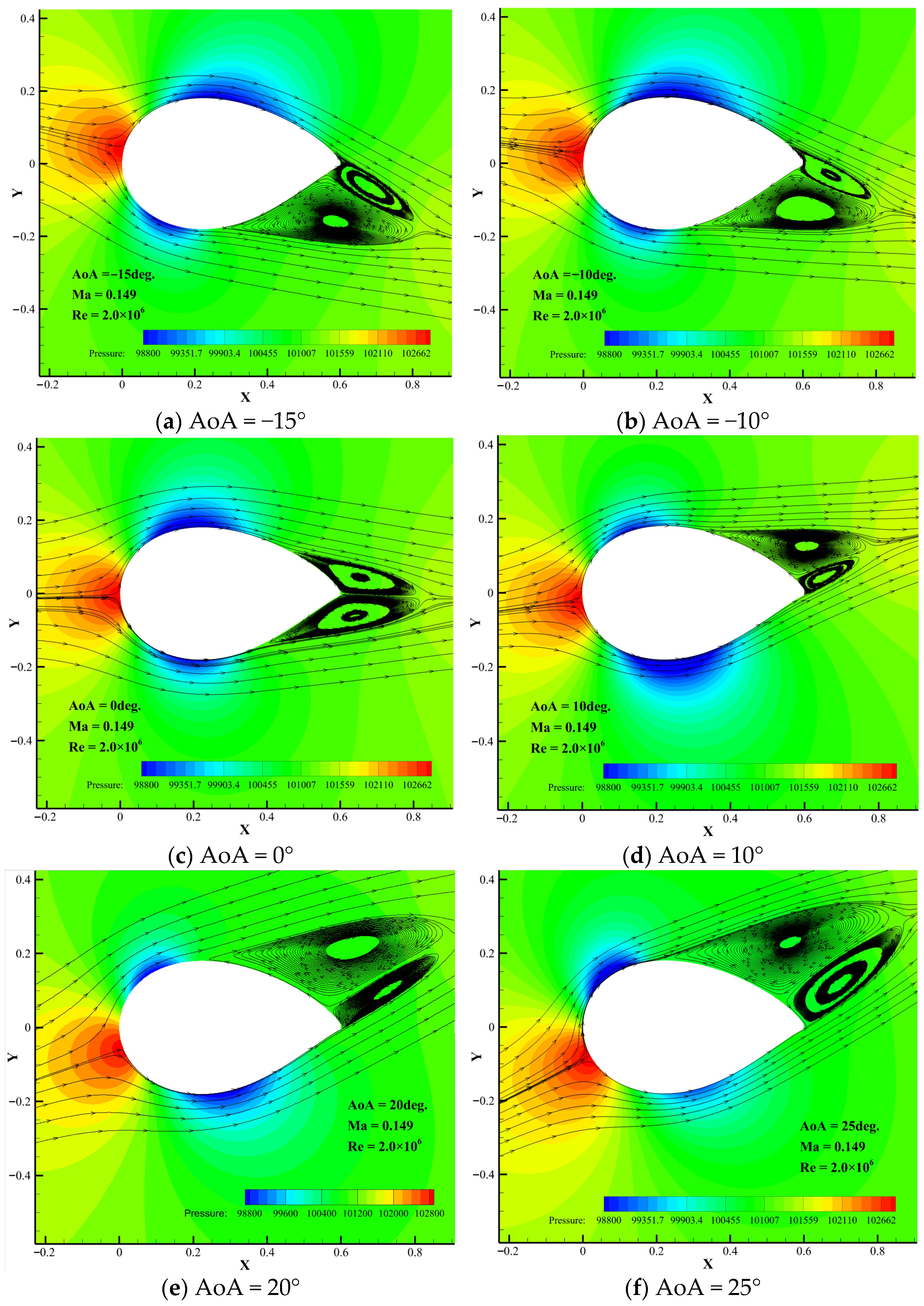
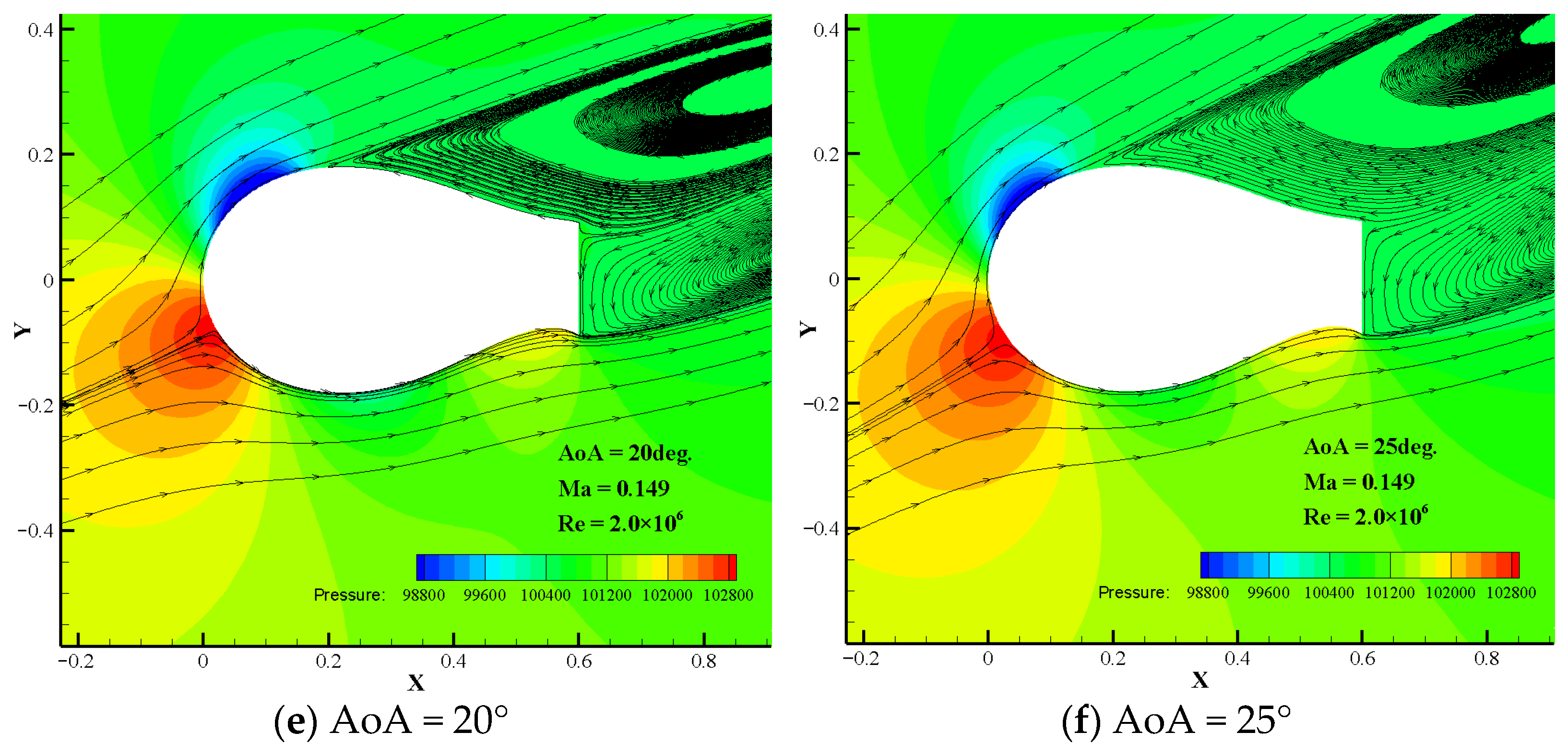
3.1. Analysis of Aerodynamic Characteristics of the NWT600 Airfoil
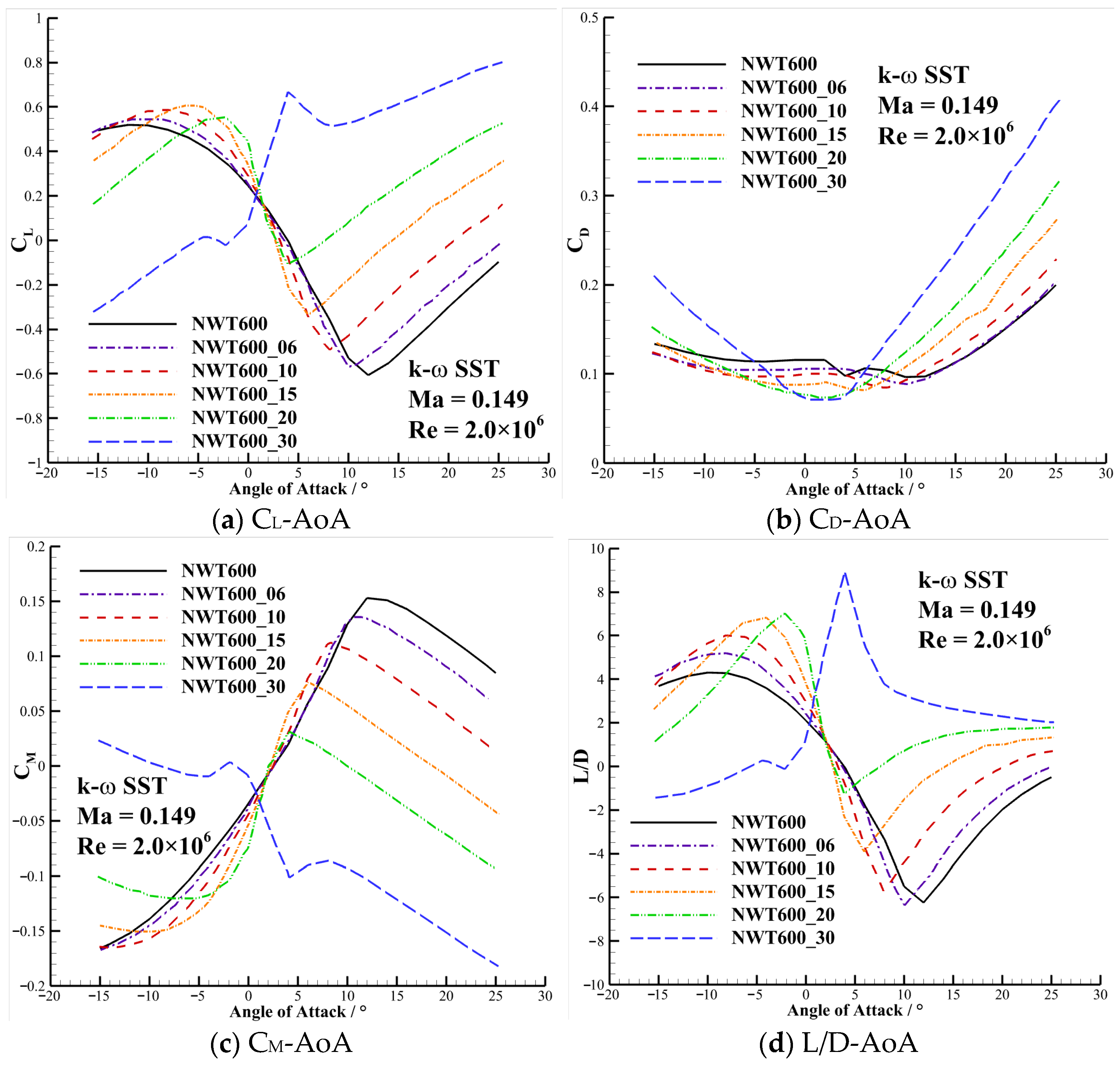
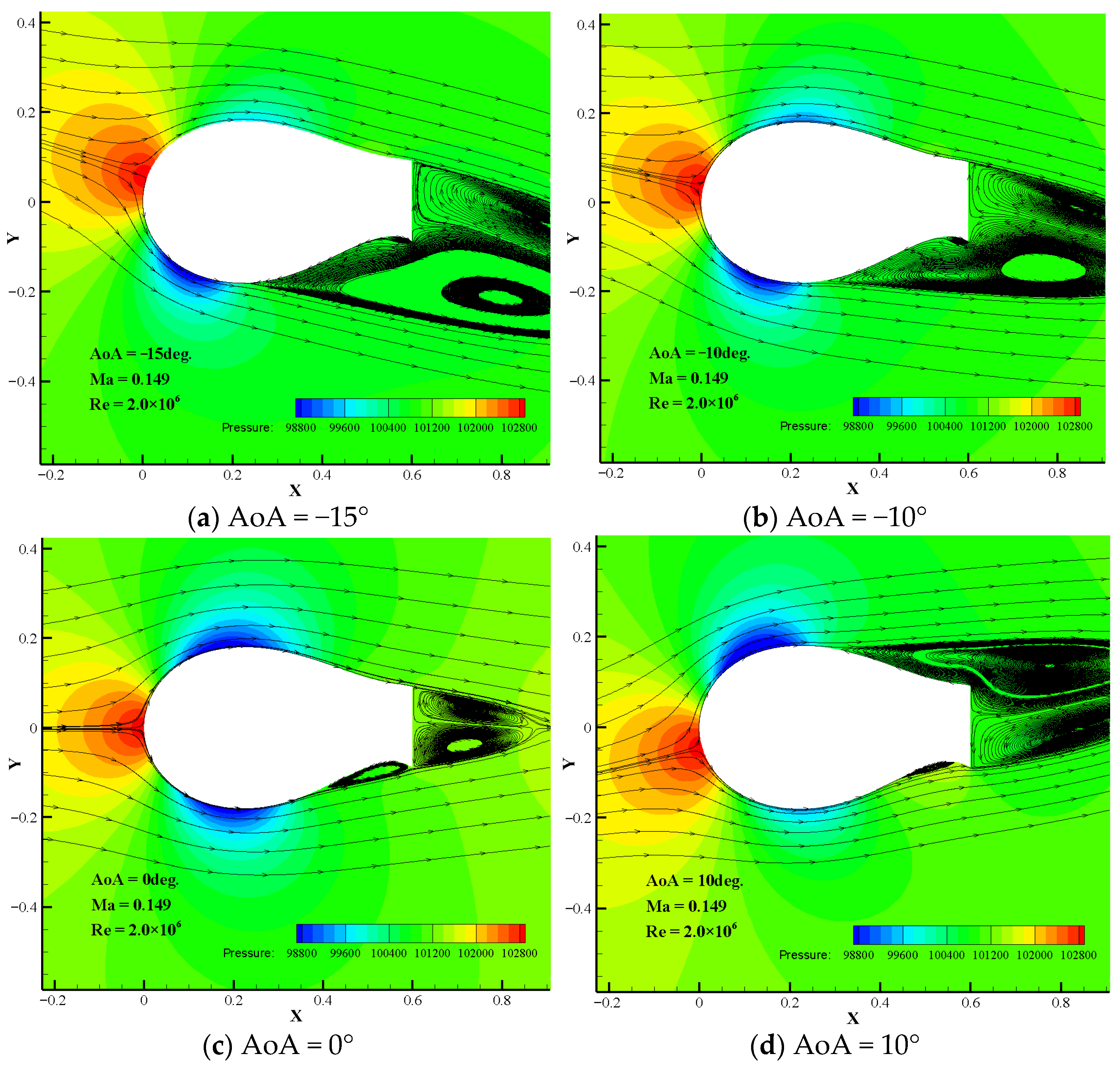
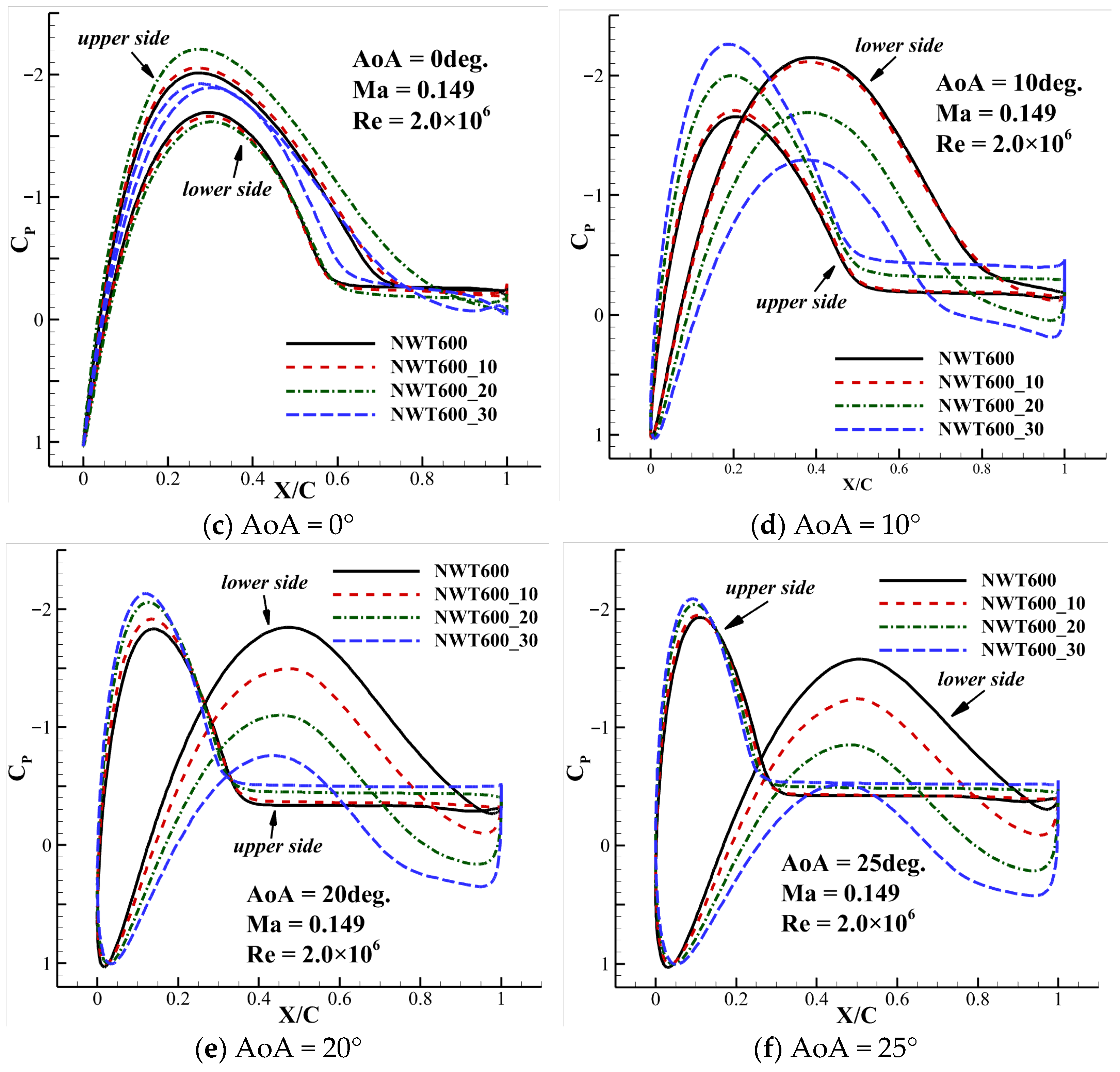
3.2. Influence of the BTE Thickness on the Aerodynamic Characteristics of the NWT600 Airfoil
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AoA | angle of attack [°] |
| CL | lift coefficient [-] |
| CLmax | maximum lift coefficient [-] |
| CD | drag coefficient [-] |
| CM | moment coefficient [-] |
| L/D | lift-to-drag ratio [-] |
| CP | pressure coefficient [-] |
| Ma | Mach number [-] |
| Re | Reynolds number [-] |
| c | chord length [m] |
| BTE | blunt trailing edge |
| RANS | Reynolds-averaged Navier–Stokes |
| S-A | Spalart–Allmaras model |
| RSM | Reynolds stress model |
References
- Yu, H.W.; Duan, J.H.; Du, W.; Xue, S.; Sun, J.H. China’s Energy Storage Industry: Develop Status, Existing Problems and Countermeasures. Renew. Sustain. Energy Rev. 2017, 71, 767–784. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.J.; Guo, H.; Zhang, X.J.; Guo, C.; Chen, H.S. A Hybrid Energy Storage System with Optimized Operating Strategy for Mitigating Wind Power Fluctuations. Renew. Energy 2018, 125, 121–132. [Google Scholar] [CrossRef]
- Grasso, F. Development of Thick Airfoils for Wind Turbines. J. Aircr. 2013, 50, 975–981. [Google Scholar] [CrossRef]
- Li, X.X.; Yang, K.; Bai, J.Y.; Xu, J.Z. A New Optimization Approach to Improve the Overall Performance of Thick Wind Turbine Airfoils. Energy 2016, 116, 202–213. [Google Scholar] [CrossRef]
- Griffith, D.T.; Richards, P.W. The SNL100-03 Blade: Design Studies with Flatback Airfoils for the Sandia 100-Meter Blade; SANDIA Report No. SAND2014-18129; Sandia National Laboratories: Albuquerque, NM, USA, 2014. [Google Scholar] [CrossRef]
- Cooperman, A.M.; Melennan, A.W.; Chow, R.; Baker, J.P.; Van Dam, C.P. Aerodynamic Performance of Thick Blunt Trailing Edge Airfoils. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar] [CrossRef]
- Van Dam, C.P.; Kahn, D.L.; Berg, D.E. Trailing Edge Modifications for Flatback Airfoils; SANDIA Report No. SAND2008-1781; Sandia National Laboratories: Albuquerque, NM, USA, 2008. [Google Scholar] [CrossRef]
- Tanner, M. A Method for Reducing the Base Drag of Wings with Blunt Trailing Edge. Aeronaut. Q. 1970, 23, 15–23. [Google Scholar] [CrossRef]
- Ramjee, V.; Tulapurkara, E.G.; Balabaskaran, V. Experimental and Theoretical Study of Wings with Blunt Trailing Edges. J. Aircr. 1986, 23, 349–352. [Google Scholar] [CrossRef]
- Sato, J. Experimental Research on Blunt Trailing-Edge Airfoil Sections at Low Reynolds Numbers. AIAA J. 1995, 33, 2001–2005. [Google Scholar] [CrossRef]
- Law, S.P.; Gregorek, G.M. Wind Tunnel Evaluation of a Truncated NACA 64-621 Airfoil for Wind Turbine Applications; NASA Report No. NASA CR-180803; NASA: Washington, DC, USA, 1987. [Google Scholar] [CrossRef]
- Fuglsang, P.; Antoniou, I.; Dahl, K.S. Wind Tunnel Tests of the FFA-W3-241, FFA-W3-301 and NACA 63-430 Airfoils; Risø National Laboratory: Roskilde, Denmark, 1998. [Google Scholar]
- Baker, J.P.; Mayda, E.A.; Van Dam, C.P. Experimental Analysis of Thick Blunt Trailing-Edge Wind Turbine Airfoils. J. Sol. Energy Eng. 2006, 128, 422–431. [Google Scholar] [CrossRef]
- Chao, D.D.; Van Dam, C.P. Computational Aerodynamic Analysis of a Blunt Trailing-edge Airfoil Modification to the NREL Phase VI rotor. Wind Energy 2010, 10, 529–550. [Google Scholar] [CrossRef]
- Lee, S.G.; Sang, J.P.; Lee, K.S.; Chung, C. Performance Prediction of NREL (National Renewable Energy Laboratory) Phase VI Blade Adopting Blunt Trailing Edge Airfoil. Energy 2012, 47, 47–61. [Google Scholar] [CrossRef]
- Papadakis, G.; Manolesos, M. The flow past a flatback airfoil with flow control devices: Benchmarking numerical simulations against wind tunnel data. Wind Energy Sci. 2020, 5, 911–927. [Google Scholar] [CrossRef]
- Manolesos, M. Papadakis, G, Investigation of the three-dimensional flow past a flatback wind turbine airfoil at high angles of attack. Phys. Fluids 2021, 33, 085106. [Google Scholar] [CrossRef]
- Bangga, G.; Seel, F.; Lutz, T.; Kvhn, T. Aerodynamic and Acoustic Simulations of Thick Flatback Airfoils Employing High Order DES Methods. Adv. Theory Simul. 2022, 2022, 2000129. [Google Scholar] [CrossRef]
- Fuchs, M.; Weihing, P.; Kuehn, T.; Herr, M.; Suryadi, A.; Mockett, C.; Knobbe-Eschen, H.; Kramer, F.; Knacke, T. Two computational studies of a flatback airfoil using non-zonal and embedded scale-resolving turbulence modelling approaches. In Proceedings of the 28th AIAA/CEAS Aeroacoustics 2022 Conference, Southampton, UK, 14–17 June 2022. [Google Scholar] [CrossRef]
- Wang, G.F.; Zhang, L.; Shen, W.Z. LES simulation and experimental validation of the unsteady aerodynamics of blunt wind turbine airfoils. Energy 2018, 158, 911–923. [Google Scholar] [CrossRef]
- Hoerner, S.F. Fluid-Dynamic Lift; Hoerner Fluid Dynamic: Bricktown, NJ, USA, 1985. [Google Scholar]
- Timmer, W.A.; Rooij, V.R. Summary of the Delft University Wind Turbine Dedicated Airfoils. J. Sol. Energy Eng. 2003, 125, 488–496. [Google Scholar] [CrossRef]
- Cene, A.; Grasso, F.; Manolesos, M. Aerodynamic and Aeroacoustic Measurements of the Flow Past a Very Thick Flatback Airfoil with Passive Flow Control Devices. In Proceedings of the AIAA SciTech 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Baldacchino, B.; Ferreira, C.; Tavernier, D.D.; Timmer, W.A.; Van Bussel, G.J.W. Experimental Parameter Study for Passive Vortex Generators on a 30% Thick Airfoil. Wind Energy 2018, 21, 745–765. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.X.; Yang, K.; Xue, D.Y. Effects of vortex generators on aerodynamic performance of thick wind turbine airfoils. J. Wind Eng. Ind. Aerodyn. 2016, 156, 84–92. [Google Scholar] [CrossRef]
- Metzinger, C.N.; Chow, R.; Baker, J.P.; Cooperman, A.M.; Van Dam, C.P. Experimental and Computational Investigation of Blunt Trailing-Edge Airfoils with Splitter Plates. AIAA J. 2018, 56, 3229–3239. [Google Scholar] [CrossRef]
- Manolesos, M.; Voutsinas, S.G. Experimental Study of Drag Reduction Devices on a Flatback Airfoil. AIAA J. 2016, 54, 3382–3396. [Google Scholar] [CrossRef]
- Xu, H.Y.; Qiao, C.L.; Yang, H.Q.; Ye, Z.Y. Active Circulation Control on the Blunt Trailing Edge Wind Turbine Airfoil. AIAA J. 2017, 56, 554–570. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.W.; Kolios, A. State of the art in the aeroelasticity of wind turbine blades: Aeroelastic modelling. Renew. Sustain. Energy Rev. 2016, 64, 195–210. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.X.; Yang, K. Experimental and computational aerodynamic investigations of very thick wind turbine airfoils. J. Renew. Sustain. Energy 2016, 8, 013306. [Google Scholar] [CrossRef]
- Li, X.X.; Yang, K.; Zhang, L.; Bai, J.Y. Experimental study of Reynolds number effects on performance of thick CAS wind turbine airfoils. J. Renew. Sustain. Energy 2017, 9, 063309. [Google Scholar] [CrossRef]
- White, E.B.; Kutz, D.; Freels, J.; Hidore, J.P. Leading-Edge Roughness Effects on 633-418 Airfoil Performance. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar] [CrossRef]
- Braslow, A.L.; Knox, E.C. Simplified Method for Determination of Critical Height of Distributed Roughness Particles for Boundary-Layer Transition at Mach Numbers from 0 to 5; National Advisory Committee for Aeronautics: Edwards, CA, USA, 1958. [Google Scholar]
- Wei, B.B.; Gao, Y.W.; Shi, Y.; Li, D.; Hao, L.S. Research on Sidewall interference Control in Airfoil Wind Tunnel Test Based on Vortex Generator. Adv. Aeronaut. Sci. Eng. 2021, 12, 38–51. (In Chinese) [Google Scholar] [CrossRef]
- Gao, L.Y.; Zhang, H.; Liu, Y.Q.; Han, S. Effects of Vortex Generators on a Blunt Trailing-Edge Airfoil for Wind Turbines. Renew. Energy 2015, 76, 303–311. [Google Scholar] [CrossRef]
- Standish, K.J.; Van Dam, C.P. Aerodynamic Analysis of Blunt Trailing Edge Airfoils. J. Sol. Energy Eng. 2003, 125, 479–487. [Google Scholar] [CrossRef]
- Xu, H.Y.; Qiao, C.L.; Yang, H.Q.; Ye, Z.Y. Delayed Detached Eddy Simulation of the Wind Turbine Airfoil S809 for Angles of Attack up to 90 Degrees. Energy 2017, 118, 1090–1109. [Google Scholar] [CrossRef]
- Launder, B.E.; Reece, G.J.; Rodi, W. Progress in the Development of a Reynolds-Stress Turbulence Closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Launder, B.E. Second-Moment Closure: Present… and Future? Int. J. Heat Fluid Flow 1989, 10, 282–300. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Yan, R.; Xu, P.; Wang, Q. Influence of the Modification of Asymmetric Trailing-edge Thickness on the Aerodynamic Performance of a Wind Turbine Airfoil. Renew. Energy 2020, 147, 1623–1631. [Google Scholar] [CrossRef]



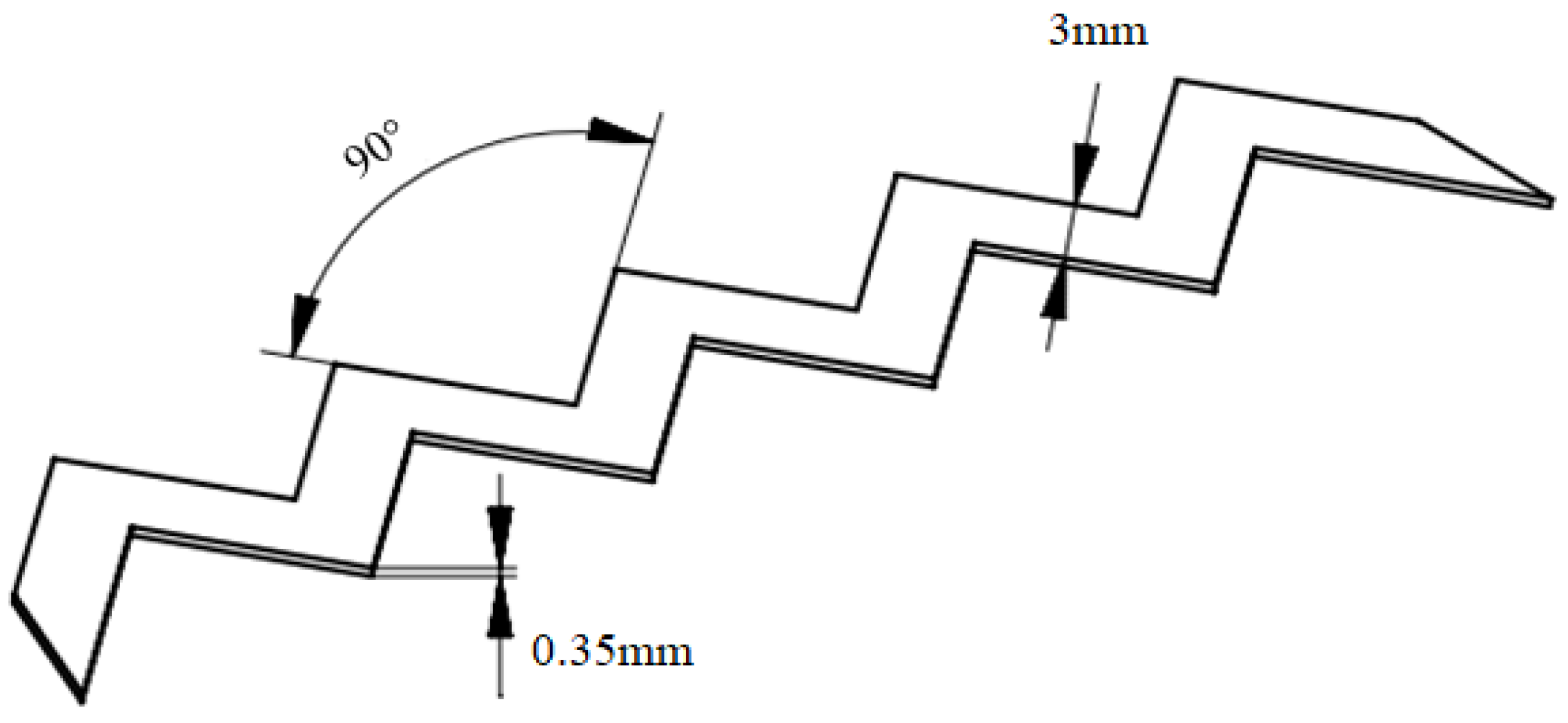

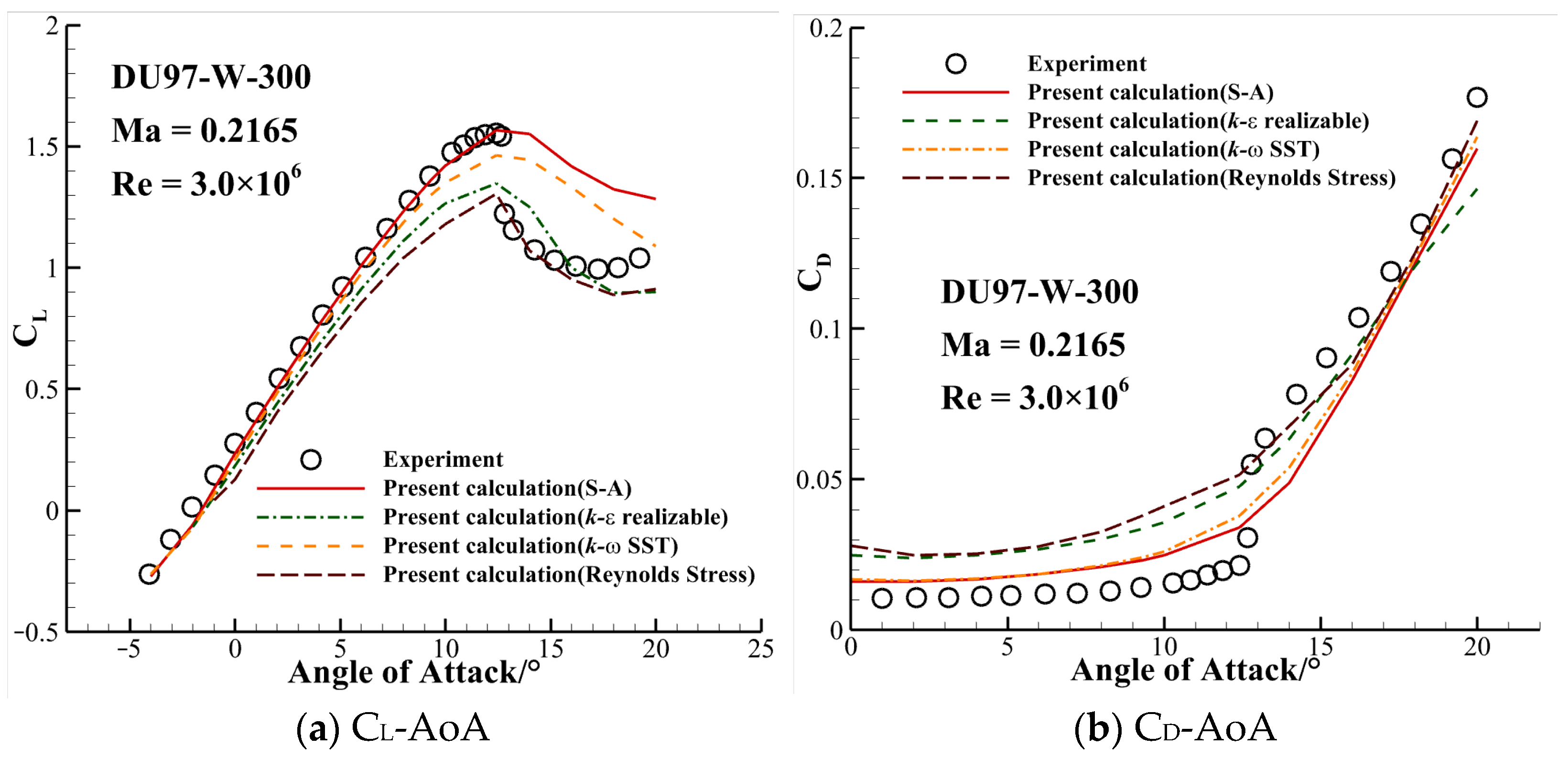
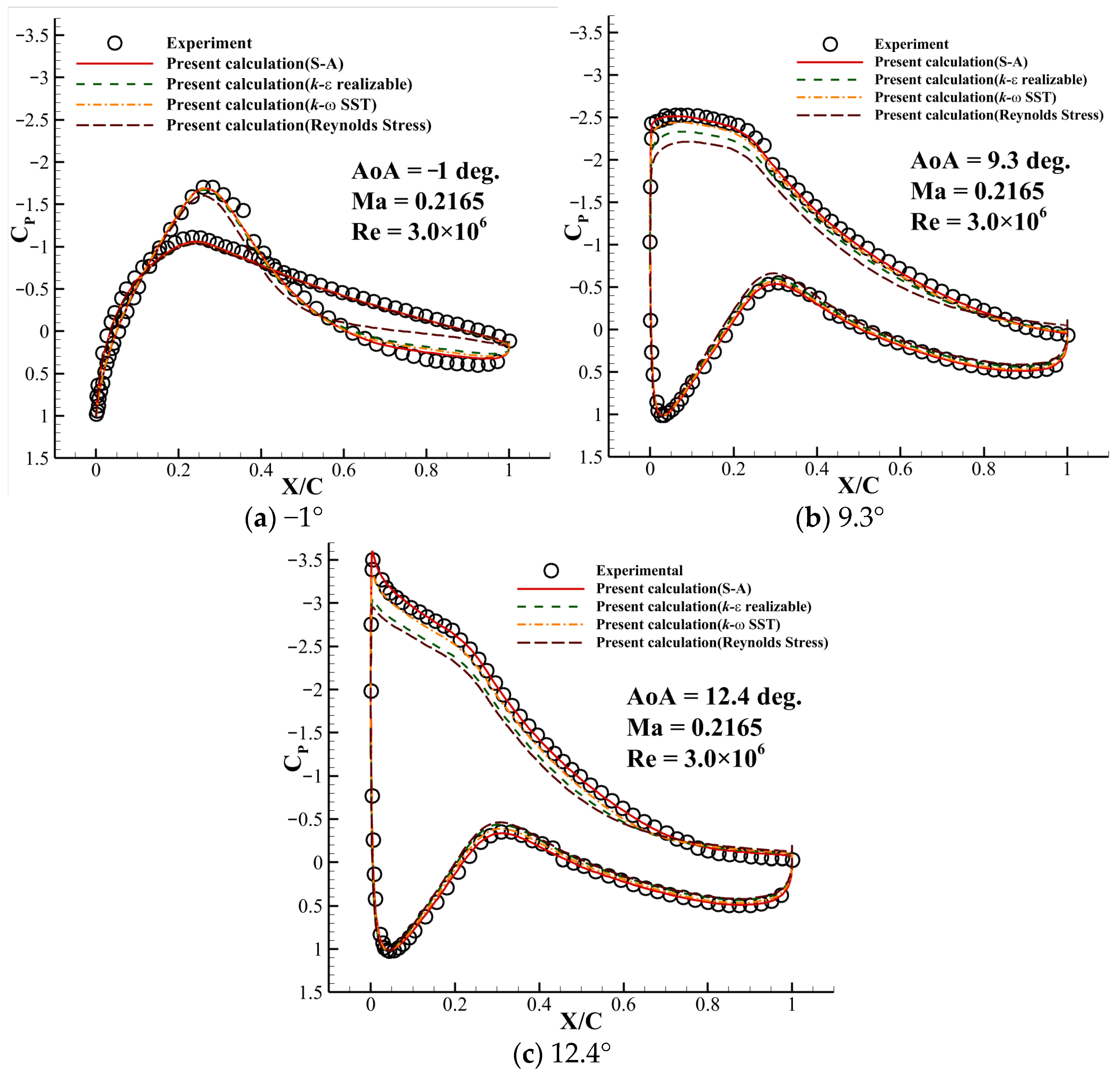

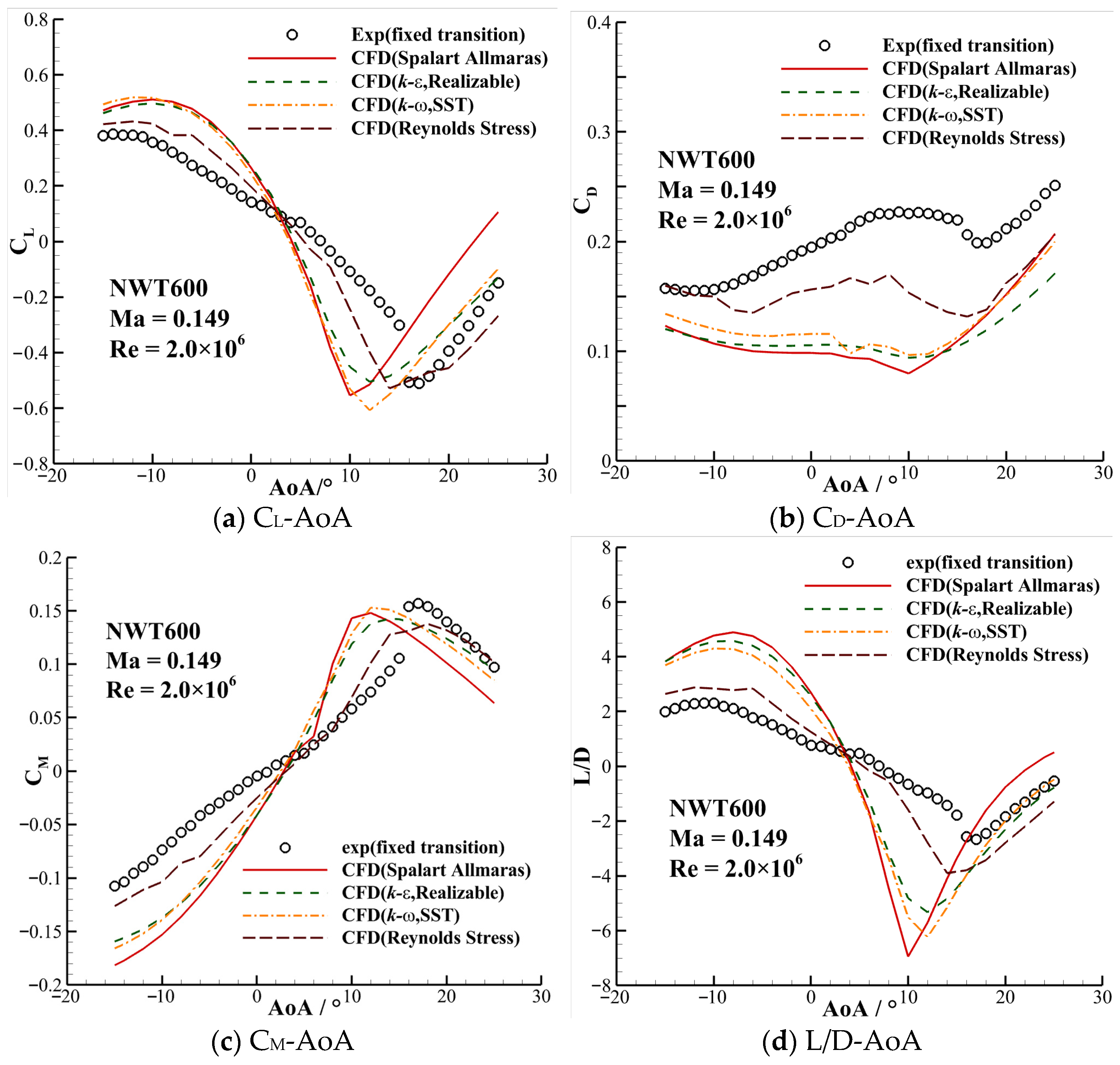


| Model | Run No. | Transition | Re | AoA Region | ΔAoA |
|---|---|---|---|---|---|
| NWT600 | 1 | Fixed | 2.0 ×106 | −15° to 25° | 1° |
| 2 | Fixed | 2.5 × 106 | −15° to 25° | 1° | |
| 3 | Fixed | 3.0 × 106 | −15° to 25° | 1° | |
| 4 | Free | 2.0 × 106 | −15° to 25° | 1° | |
| 5 | Free | 2.5 × 106 | −15° to 25° | 1° | |
| 6 | Free | 3.0 × 106 | −15° to 25° | 1° |
| Parameters | Grid A | Grid B | Grid C |
|---|---|---|---|
| Far-field radius/c | 50 | 50 | 50 |
| Wrap-around points | 240 | 400 | 480 |
| Normal layers | 120 | 200 | 240 |
| First layer height/m | 1.0 × 10−5 | 1.0 × 10−5 | 1.0 × 10−5 |
| Total cells number | 2.88 × 104 | 8.00 × 104 | 11.52 × 104 |
| Y plus | <1.00 | <1.00 | <1.00 |
| Grid A | Grid B | Grid C | CFD [35] | Experiment [22] | |
|---|---|---|---|---|---|
| Total number of cells | 2.88 × 104 | 8.00 × 104 | 11.52 × 104 | - | - |
| CL | 1.3941 | 1.3903 | 1.3819 | 1.3750 | 1.380 |
| CD | 0.0238 | 0.0234 | 0.0232 | 0.0206 | 0.014 |
| Airfoil | NWT600_06 | NWT600_10 | NWT600_15 | NWT600_20 | NWT600_30 |
|---|---|---|---|---|---|
| Relative thickness of the trailing edge | 6% | 10% | 15% | 20% | 30% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, Z.; Xu, H.-Y.; Deng, L.; Li, L.-X. Influence of the Blunt Trailing-Edge Thickness on the Aerodynamic Characteristics of the Very Thick Airfoil. Wind 2023, 3, 439-458. https://doi.org/10.3390/wind3040025
Pei Z, Xu H-Y, Deng L, Li L-X. Influence of the Blunt Trailing-Edge Thickness on the Aerodynamic Characteristics of the Very Thick Airfoil. Wind. 2023; 3(4):439-458. https://doi.org/10.3390/wind3040025
Chicago/Turabian StylePei, Zhen, He-Yong Xu, Lei Deng, and Ling-Xiao Li. 2023. "Influence of the Blunt Trailing-Edge Thickness on the Aerodynamic Characteristics of the Very Thick Airfoil" Wind 3, no. 4: 439-458. https://doi.org/10.3390/wind3040025
APA StylePei, Z., Xu, H.-Y., Deng, L., & Li, L.-X. (2023). Influence of the Blunt Trailing-Edge Thickness on the Aerodynamic Characteristics of the Very Thick Airfoil. Wind, 3(4), 439-458. https://doi.org/10.3390/wind3040025






