Simulative Investigation of the Risk of Smearing Damage for a WT Gearbox Roller Bearing during Rotor-Induced Excitations

Abstract

Wind turbine drivetrains can be subjected to highly dynamic loading conditions caused by grid faults, power converter faults and dynamic wind excitations. These loading conditions can cause additional wear and possibly damage their components. Some of the most critical components in the mechanical drivetrain are its bearings. High-speed shaft bearings are especially prone to failure. Smearing is one possible damage pattern for these bearings. Previous studies observed a highly increased smearing risk caused by generator-induced torque excitations. In contrast, this study focuses on rotor-induced torque excitations and investigates the resulting smearing risk. The goal is to ascertain the general damage potential stemming from rotor-induced excitations for high-speed shaft bearings regarding smearing. To this end, a detailed bearing model was integrated into a validated multibody simulation of a research nacelle which was operated on a test bench. A smearing criterion was used to evaluate the smearing risk. Multiple sinusoidal rotor-induced torque excitations were investigated. The resulting smearing risk is highly dependent on the excitation amplitude and frequency, with higher amplitudes resulting in a greater smearing risk. Regarding frequency, only excitations with frequencies close to the system’s first torsional eigenfrequency result in a significantly increased smearing risk. In general, the determined amplitudes and frequencies of rotor-induced torque excitations, necessary to cause a significant increase in smearing risk, are unlikely to occur in the field and therefore are of lesser importance to the high-speed shaft bearings than generator-induced torque excitations.

1. Introduction

Wind energy already produces a large share of the electricity consumed worldwide [1]. However, the energy yield and economic efficiency of wind turbines (WT) can be impaired by long downtimes. One common cause of downtime is damage to the turbine’s gearbox bearings [2,3,4]. The largest amount of bearing failure occurs at the high-speed shaft (HSS) bearings [2]. Bearing damage can occur due to various damage mechanisms. One possible pattern of bearing damage is smearing [5,6,7,8,9,10,11,12,13,14,15]. The drivetrain of the WT is exposed to dynamic torques due to the wind, fluctuating grid loads and failures in the power electronics [16,17]. Alternating bearing loads and the resulting rolling element slip favour the occurrence of smearing [6,7,10]. The occurrence of smearing is further favoured due to various influences such as load direction changes, low radial loads, rolling element tilting, high rolling element mass inertia or suboptimal lubrication [6,10,13,14,15,18,19]. Smearing is based on the damage mechanism of adhesive wear, in which the contact surfaces weld together for a short time. It occurs when two insufficiently lubricated surfaces slide over each other [6,7,8,10,11,14]. Smearing occurs mainly between the rolling element and the raceway. Smearing most commonly takes place upon entry of the rolling element into the loaded zone of the bearing [6,9,12]. Once smearing has taken place, it leads to circumferential smearing bands and thus to the spread of damage. Subsequently, smearing can lead to a complete failure of the bearing.

Alongside previous studies focusing on the smearing risk for the HSS bearings stemming from generator-induced torque excitations [20,21,22,23], this study investigates the smearing risk for HSS bearings caused by rotor-induced torque excitations. The determination of the necessary quantities in a real size WT is complex and time-consuming, even on a test bench. Therefore, the simulative investigation of the rotor torque excitations was carried out before beginning the experimental validation. The experimental validation will be accomplished in the course of the DynaGET project. The DynaGET project focusses on the improvement of WT gearbox design under the consideration of transient loads. The objective is to identify critical loading conditions regarding smearing damage for an HSS cylindrical roller bearing caused by rotor-induced excitations stemming from fluctuating wind conditions.

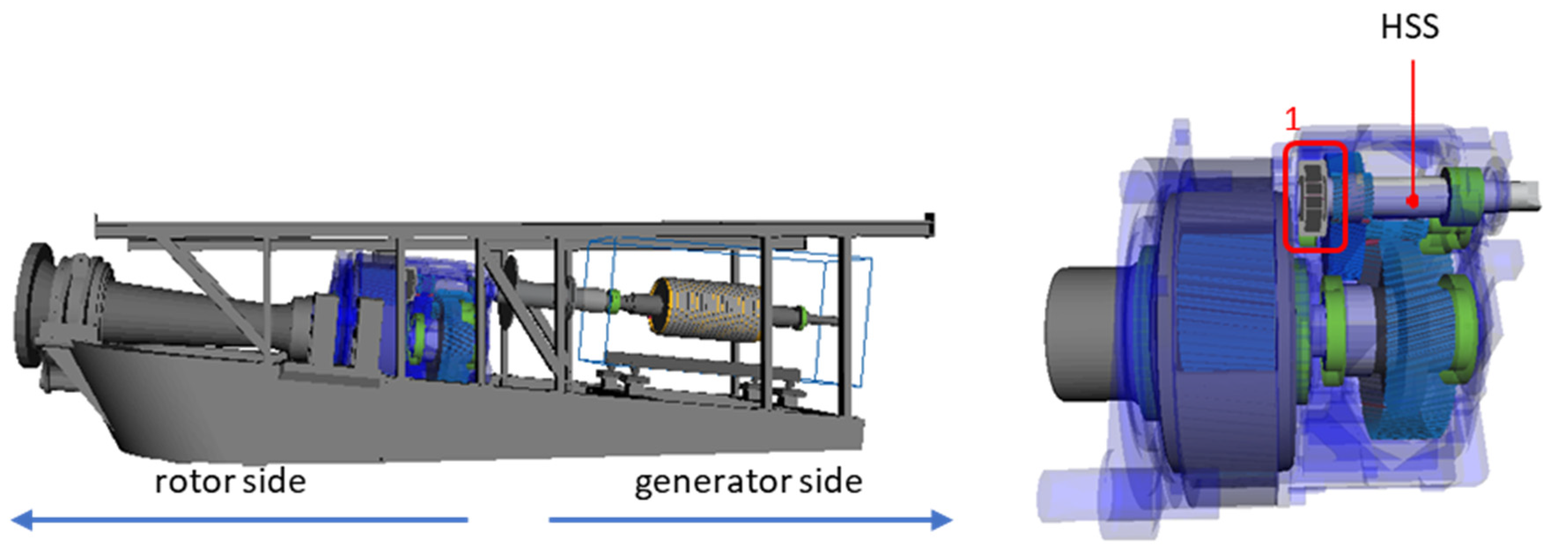
2. Approach

Figure 1 (left) shows the multibody simulation (MBS) model of the research nacelle and its gearbox (right) with an integrated detailed bearing model (see Figure 1, no. 1) [24]. The model and its parts are validated and can be used to calculate the load on the components of the electromechanical drivetrain [24]. The research nacelle has a rated power of $2.75\mathrm{MW}$. The rated speed of the generator is $1100\frac{\mathrm{U}}{\min }$.

The examined gearbox consists of one planetary stage and two helical gear stages. The gearbox ratio is 63. Bearings which are not in focus of the smearing analysis are modelled as spring-damper force elements. The stiffness of these bearing elements is based on the manufacturer’s data [25]. For the rotor-induced cylindrical bearing of the HSS, a detailed bearing model is implemented [26]. The bearing model’s kinematics, e.g., cage slippage, were verified using simulation and experimental results according to van Lier [7]. For the verification, the results of roller and cage slip were compared under various constant loading conditions. A good quantitative correlation for roller slip was achieved. For cage slip, a good quantitative correlation was achieved for loads greater than minimal load conditions defined by the SKF [27].

The exact causes of smearing are complex. Therefore, there are numerous approaches to describe the risk of smearing by means of energy parameters and specific thresholds. In this paper, the smearing criterion called friction power intensity, which was also used by van Lier and Evans [6,7], was utilized. The results from the MBS model were used as the input to calculate the criterion. The simulation results regarding the kinematics of the bearing will be validated in the course of the DynaGet project. Due to the outstanding validation of the bearing’s kinematics, in this paper, a relative comparison of the smearing criterion values during rotor-induced excitations to values during nominal operation was performed. The smearing criterion (see Equation (1)) is the product of maximum Hertzian contact pressure ${\mathrm{p}}_{\max }$, friction coefficient $\mathsf{\mu }$ and the difference in circumferential velocity of the contact partners $∆\mathrm{u}$ [6].

$$\left(\frac{\mathrm{P}}{\mathrm{A}}\right)=\mathsf{\mu }·{\mathrm{p}}_{\max }·∆\mathrm{u}$$

(1)

Thus, this criterion represents an expression for the ratio of frictional power $\mathrm{P}$ to the contact area $\mathrm{A}$. If not stated otherwise, the displayed smearing criterion values represent the mean value of the maxima of all rollers in the considered time interval.

In a dynamic wind environment, wind speed and therefore rotor torque are stochastically distributed. An increase in torque, especially during a 50-year extreme-operating-gust, to over 200% of the nominal value as well as a sudden drop of the torque close to zero are possible [28,29,30,31]. During wind gusts, the wind speed can change within a period of a few seconds. The field data of wind events is highly chaotic. To increase reproducibility and to identify specific critical loading conditions, the investigated rotor-induced excitations are standardized. The excitations are realized by a time-varying rotor torque. The excitations are simulated as sinusoidal oscillations with the nominal torque as the mean value for different oscillation amplitudes and frequencies (see Equation (2)). Non-torque loads are disregarded in this study.

$$\mathrm{torque}\left(\mathrm{t}\right)={\mathrm{torque}}_{\mathrm{t}=2\mathrm{s}}·\left(1+\mathrm{a}\sin \left(2\mathsf{\pi }\mathrm{ft}\right)\right)$$

(2)

The parameters a and f define amplitude factor and frequency, respectively. Both are constant during an excitation simulation. Each excitation starts at the 2 s mark under nominal conditions. Simulations were carried out for $\mathrm{f}$ between 0.5 Hz and 60 Hz with a parameter $\mathrm{a}$ between 0.1 and 2.0. In Figure 2, a rotor torque oscillation is shown. The oscillation has a frequency of 3 Hz and an amplitude corresponding to 40% of the nominal torque. The drivetrain is at nominal speed before excitation starts. After the excitation starts, the HSS rotational speed oscillates with the excitation frequency.

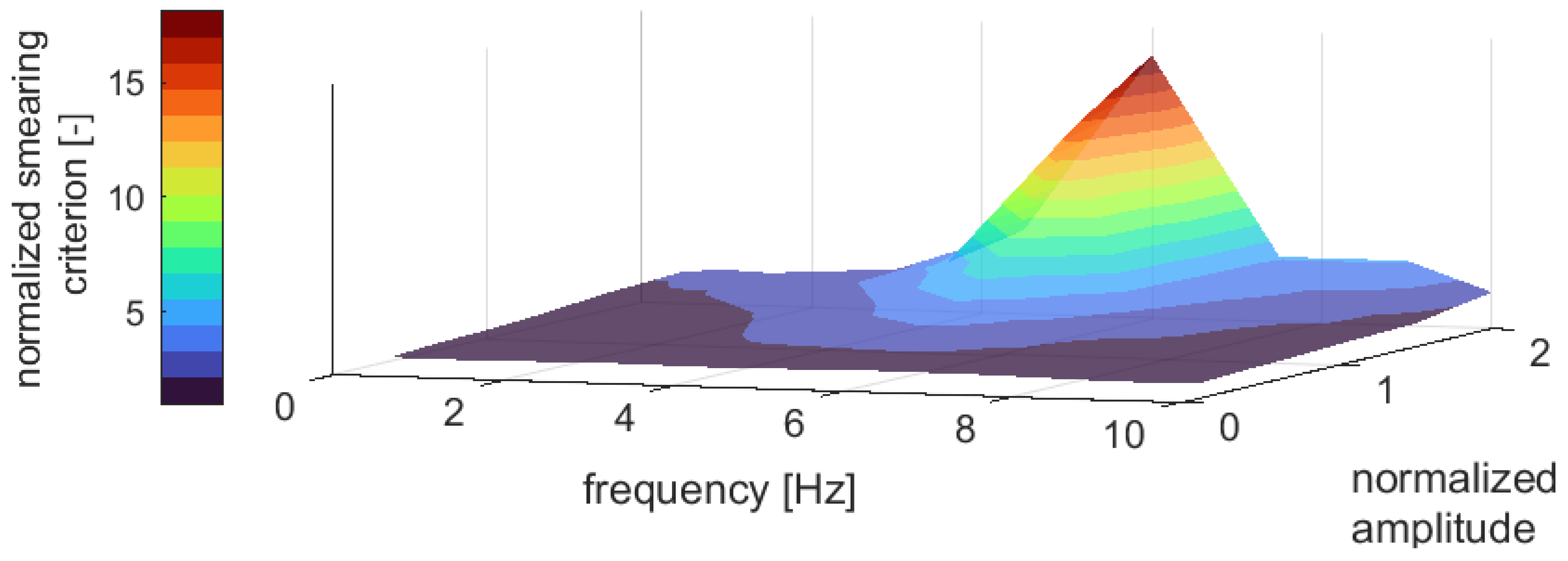
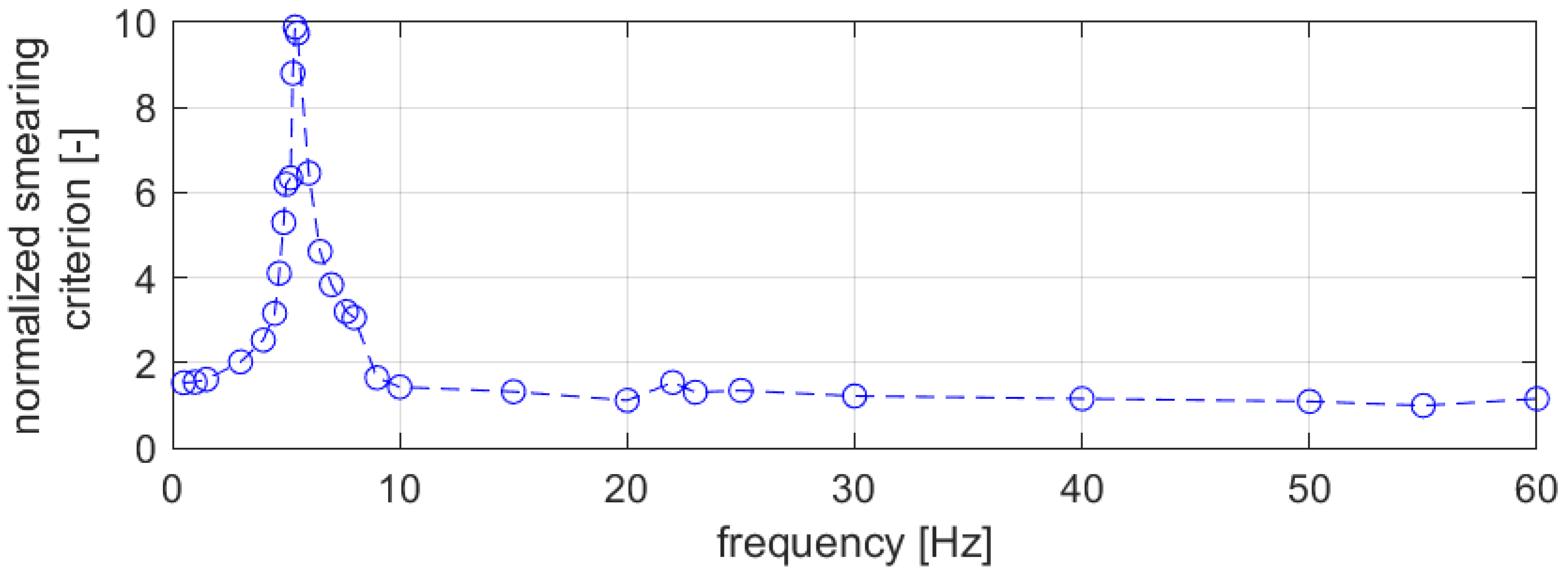
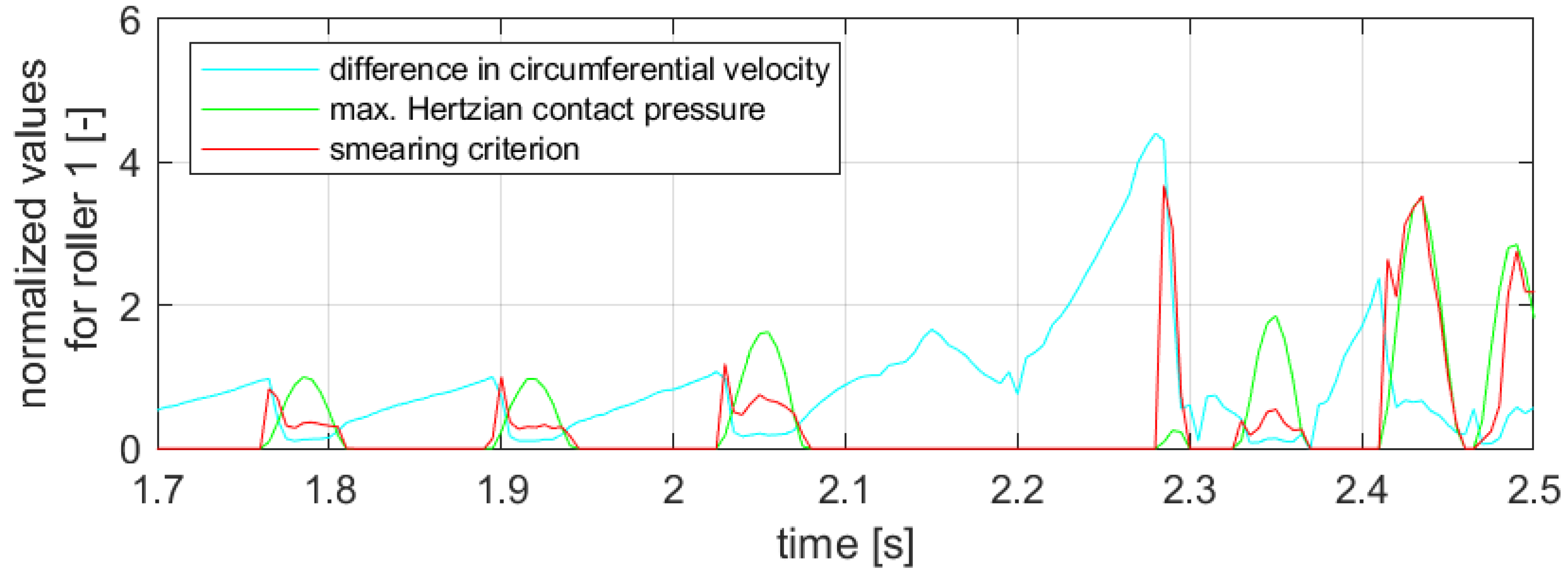
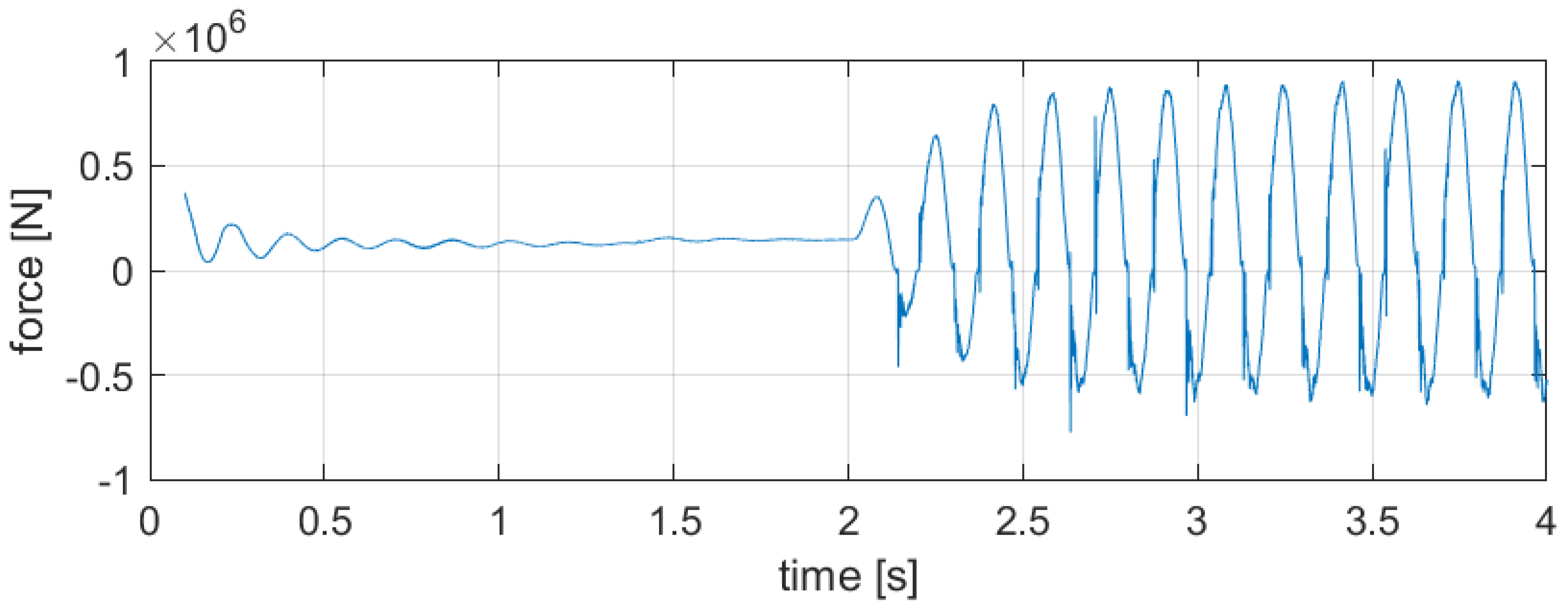
3. Results

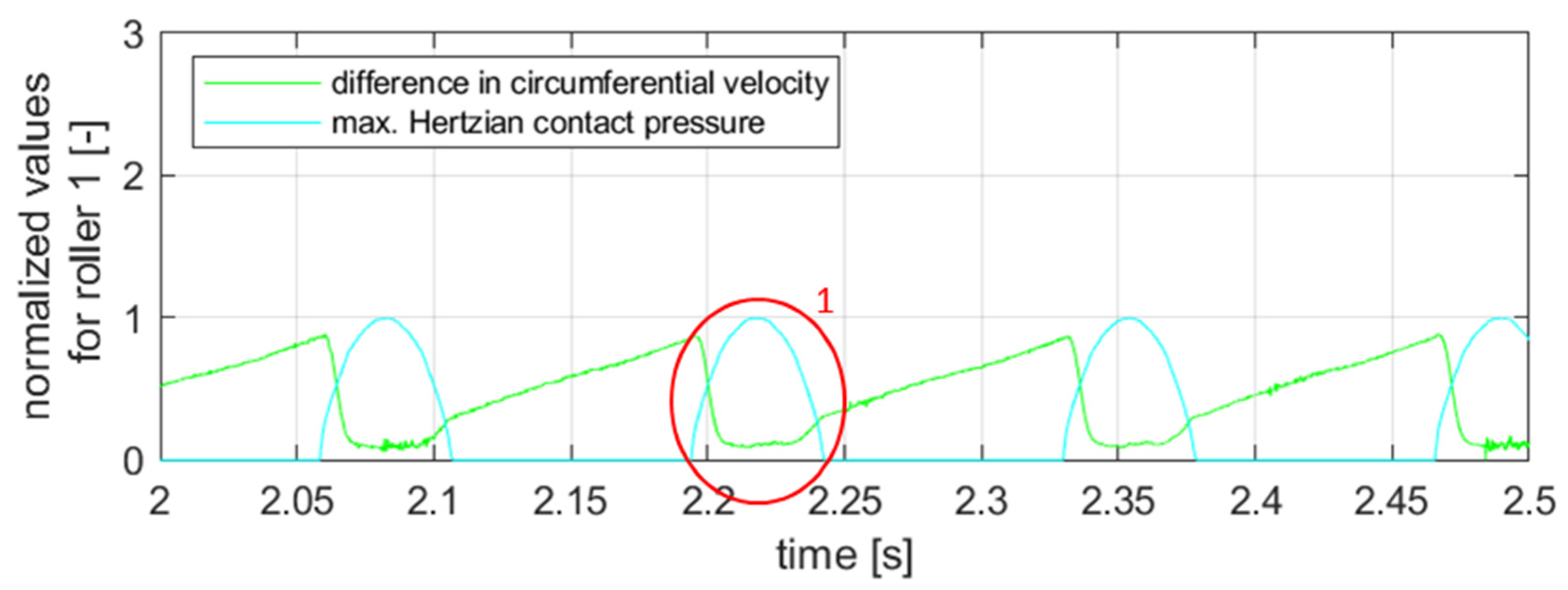
3.1. Nominal Conditions

Under nominal conditions, roller slip and contact pressure follow a regular pattern. Figure 3 shows the normalized Hertzian contact pressure and the normalized roller slip between roller and inner ring for the first roller. All normalized values in this work are normalized to their respective average maximum value under nominal conditions. The Hertzian contact pressure between the roller and the inner ring is equal to zero for most of the roller’s revolution around the inner ring. Upon entry into the load zone (see Figure 3, no. 1) the contact pressure increases and reaches its maximum when the roller is in the centre of the load zone. The roller slip, on the other hand, is minimal while the roller traverses the load zone. When the roller enters the load zone and begins to experience contact pressure, its circumferential velocity is accelerated. Therefore, roller slip decreases rapidly. Outside of the load zone, roller slip increases nearly linearly.

As well as the contact pressure and slip under nominal conditions, the course of the smearing criterion also follows a regular pattern. Figure 4 shows the normalized smearing criterion under nominal conditions. While the roller is outside of the load zone, the smearing criterion is equal to zero. Right before entry into the load zone, the roller possesses its lowest circumferential velocity. Upon entry, it experiences a rise in Hertzian contact pressure, resulting in the observed maximum smearing criterion. After the entry period the smearing criterion describes a plateau shape. The roller experiences high contact pressure under minimal slip conditions. The average maximum smearing criterion under nominal conditions was established to $1.70·{10}^7\frac{\mathrm{W}}{{\mathrm{m}}^2}$. The presented smearing criterion values in this study are normalized to this value.

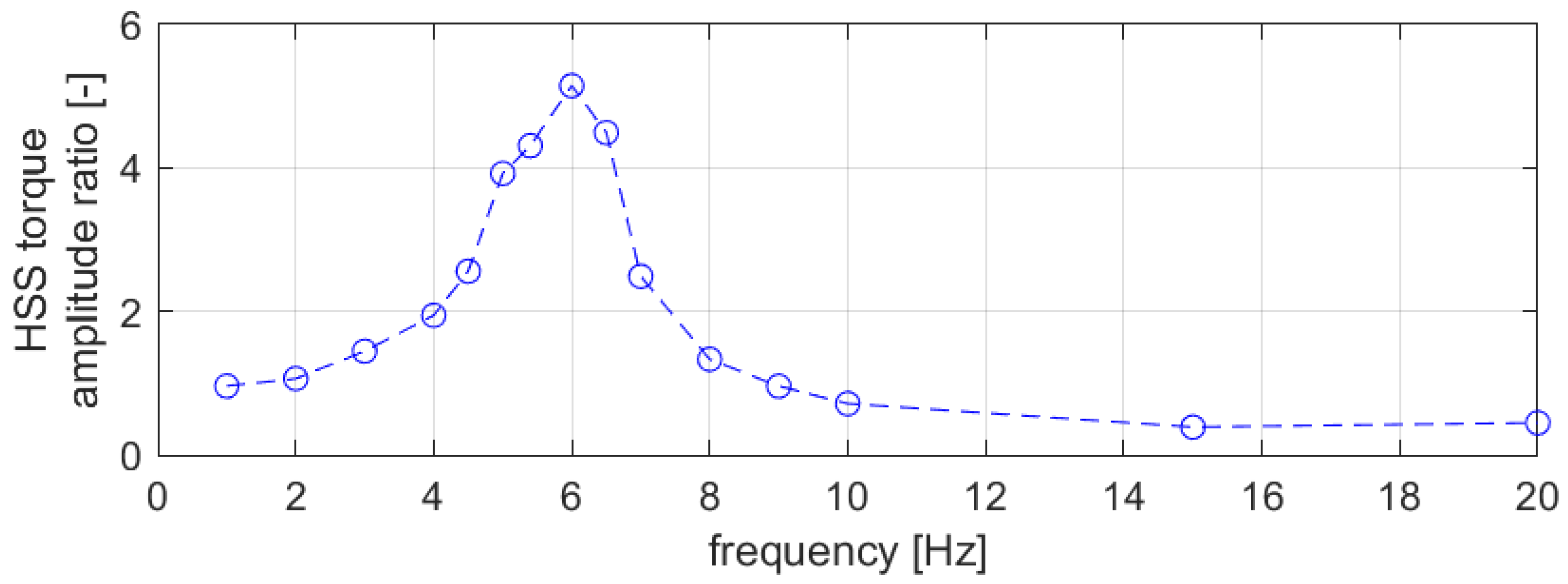
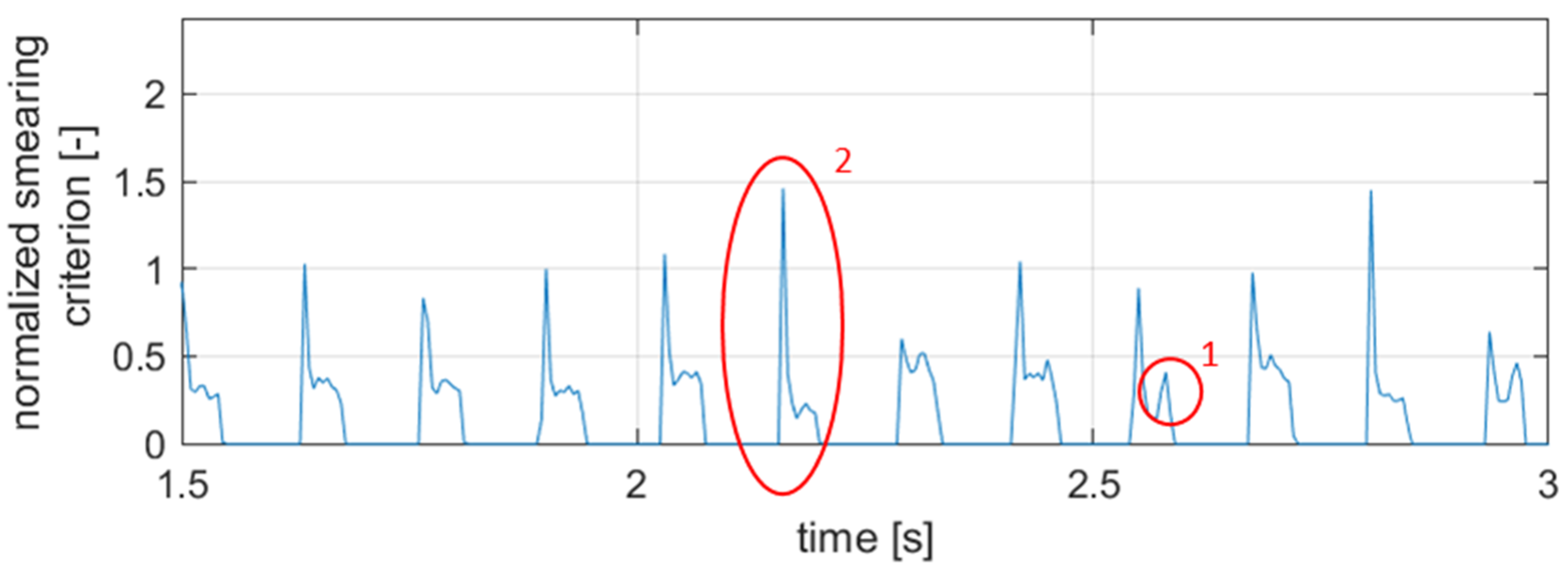
3.2. Sinusoidal Torque Excitations

Sinusoidal rotor-induced torque excitations also lead to a time-varying HSS torque. The research nacelle with test bench has torsional eigenfrequencies. Therefore, its drivetrain reacts differently to varying excitation frequencies, as some are amplified while others are dampened. The first three torsional eigenfrequencies of the research nacelle with the test bench are at 6.5 Hz, 23 Hz and 50 Hz. The first two eigenfrequencies are test bench-specific eigenfrequencies [24]. For excitations in the range of these eigenfrequencies, the stimulated amplitude of the HSS torque increases. The amplitude frequency response related to the HSS torque is shown in Figure 5. The torque on the HSS was examined with dynamic, rotor-induced excitation of different frequencies. The ratio of the HSS torque amplitude to the excitation amplitude is shown for the different frequencies. The maximum amplitude ratio occurs for a frequency of 6 Hz. The determined maximum roughly coincides with the first eigenfrequency. The deviation from the eigenfrequency is likely due to small changes in the MBS model, e.g., the integration of the detailed bearing model.

Rotor-induced dynamic torque excitations can have a profound effect on bearing load and slip behavior. Figure 6 depicts the normalized smearing criterion for the excitation seen in Figure 2. Under nominal conditions (before the 2 s mark), the smearing criterion follows the established regular pattern. After the excitation begins at the 2 s mark the course of the smearing criterion is altered. Its course loses its regularity and describes different shapes for each load zone. Second local maxima form at the end of individual load zones (e.g., Figure 6, no. 1) and single maxima exceed the nominal value while the height of the plateau is reduced (e.g. Figure 6, no. 2).

Figure 7 shows the resulting smearing criterion for excitations with ascending frequencies and amplitudes. The amplitudes are normalized to the nominal torque. In general, larger excitation amplitudes cause a higher smearing criterion. Thus, the smearing criterion of the excitations with a normalized amplitude of 2.0 is the highest in all frequency ranges. The maximum value is achieved at 6 Hz and is 18 times larger than the nominal smearing criterion. Smearing is therefore very likely for this load case. The average maximum smearing criterion achieved for all excitations during the considered time interval is always above the nominal value for constant loading. The smearing criterion also has a strong dependency on the excitation frequency. For each excitation amplitude the maximum is reached at 6 Hz. Comparable values are reached at 1 Hz and 10 Hz.

Above the excitation frequencies of 6 Hz, the smearing criterion drops off, regardless of the excitation amplitude. An increase in frequency significantly above the limits of Figure 7, results in a further decrease of the smearing criterion. Figure 8 depicts the normalized smearing criterion for a broader frequency spectrum for a normalized excitation amplitude of 1.0. After the maximum at 6 Hz, the smearing criterion returns to a value comparable to the lowest examined excitation frequencies. The course of the smearing criterion strongly resembles the amplitude frequency response of a system with a resonance frequency. For greater excitation frequencies, the smearing criterion decreases further to 1.16 times the nominal value at $\mathrm{f}=60\mathrm{Hz}$. The only exception are frequencies around 23 Hz, at which the smearing criterion increases slightly. This small increase is most likely due to the influence of the second torsional eigenfrequency of the MBS model. For the third torsional eigenfrequency at 55 Hz, no increase in the smearing criterion could be observed. The observed maximum at 6 Hz coincides with the amplitude frequency response (Figure 5). The excitation frequency has a very strong influence on the torque of the HSS and, therefore, also on the radial forces and the smearing criterion in the considered bearing.

The extreme increase in smearing criterion around 6 Hz is caused by an alteration in load and slip behavior in the HSS bearing. In Figure 9, the normalized Hertzian contact pressure and the normalized difference in circumferential velocity of the contact partners are depicted along with their resulting normalized smearing criterion for a singular roller. The excitation frequency is equal to 6 Hz with a normalized amplitude equal to 1.0. Before the excitation begins, all three curves demonstrate the regular pattern. Roller slip is minimal while traversing the load zone and at a maximum before re-entering. The smearing criterion follows the established shape and the contact pressure deviates from zero in regular intervals whenever the roller traverses the load zone. After the excitation begins, the Hertzian contact pressure curve is significantly altered. The time between leaving and re-entering the load zone is no longer constant. The considered roller does not experience any significant contact pressure between 2.08 s and 2.28 s, with regular time intervals between leaving and re-entry into the load zone being roughly 0.08 s. As a result, the difference in circumferential velocity drastically increases. Upon re-entering a comparatively weak load zone at ~2.28 s, the normalized smearing criterion reaches its maximum value for the considered time interval of 3.68. By contrast, the second highest peak in the smearing criterion at 2.44 s is reached during a comparatively low roller slip and a drastically increased Hertzian contact pressure.

The extreme loading conditions the roller experiences for the considered excitation are caused by load direction changes in the HSS bearing. Figure 10 shows the radial load component of the bearing load. The radial load oscillates with the frequency of the torque excitation. The acting maximum forces on a roller are therefore different each time it passes through the load zone. In addition, due to the change in direction of the load, the bearings’ load zone changes its position. If this occurs shortly after a roller traverses the load zone, the roller may pass through an additional load zone during the same revolution around the inner ring, resulting in a reduction of roller slip. Accordingly, if the direction change happens shortly before a roller would enter the load zone, the roller may complete a revolution without traversing a load zone at all, resulting in an increase of the roller slip. Under these conditions the smearing criterion also increases significantly. These changes in load direction only occur for sufficiently large excitation amplitudes and in a frequency range at around 6 Hz.

4. Conclusions

A simulative investigation of the effect of sinusoidal rotor-induced torque excitations on the smearing risk in a WT high-speed shaft bearing was carried out. Rotor-induced sinusoidal torque excitations result in an increase in the utilized smearing criterion and thus the smearing risk. An increase, relative to the nominal conditions, of the smearing criterion occurs for all excitation frequencies and amplitudes. As expected, higher excitation amplitudes result in a more drastic change in slip and load behavior for the considered bearing and thus result in a larger increase of the smearing risk than comparatively small amplitudes. The smearing criterion and therefore the smearing risk show a strong dependency on the excitation frequency. This is caused by the first torsional eigenfrequencies of the MBS model at 6 Hz. Torque excitations around 6 Hz experience amplification and thereby were able to induce load direction changes in the considered bearing. As a result, slip and load conditions are heavily altered, causing an extreme increase of the smearing risk. The nominal value is exceeded by more than 500% for excitations with 6 Hz and a normalized amplitude of 1.0 and by 320% with a normalized amplitude of 0.7. A further increase in the excitation frequency above 6 Hz does not lead to an increase of the smearing criterion.

Thus, specific excitations with a frequency around the first eigenfrequency of the MBS model and torque amplitudes at least 0.7 times the nominal torque can cause a significant increase of the smearing criterion and therefore the smearing risk. The observed eigenfrequency was specific for the research nacelle with test bench at the CWD. The original nacelle without test bench possesses eigenfrequencies at 2.5 Hz and 4.5 Hz [24]. Excitations of the necessary magnitude can occur in the field. Constant excitation of this magnitude with the system’s eigenfrequency, or the original nacelle’s eigenfrequencies, are near impossible. Wind speed changes, which would lead to the described critical torque excitation amplitudes with at least nominal torque with a frequency between 2.5 and 6 Hz, do not occur in the field with the required frequency regularity. Rotor-induced torque excitations are therefore of lower importance for the smearing risk in HSS bearings.