Multi-Terminal DC Grid with Wind Power Injection
Abstract
:1. Introduction
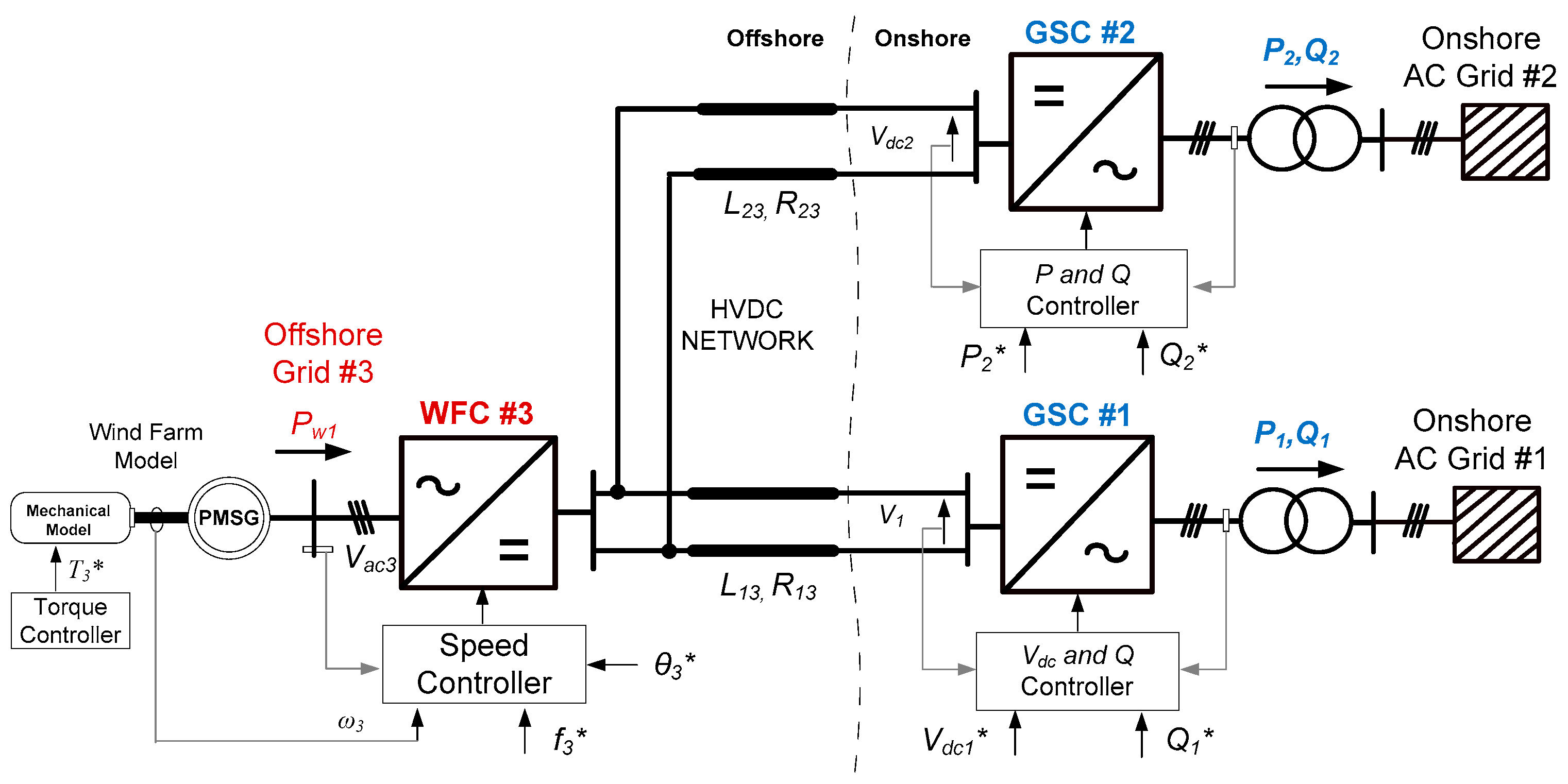
2. System Modeling Tools
- A wind farm with an AC-to-DC converter for frequency control and reactive power flow control;
- A grid-connected converter to control the DC link voltage and reactive power flow;
- A grid-connected converter to control the active power flow and reactive power flow;
- The models for points 2 and 3 above are similar up to the inner current control, with only the outer most control loops differing.
2.1. Wind Farm with AC-to-DC Converter for Frequency Control and Reactive Power Flow Control
2.1.1. PMSG, Transmission Line, and Converter Model
2.1.2. Rotor Dynamics Model
2.1.3. Reactive Power Dynamic Model
2.1.4. DC Link Voltage Dynamic Model
2.1.5. State-Space Model of the Wind Farm with AC-to-DC Converter for Frequency Control and Reactive Power Flow Control
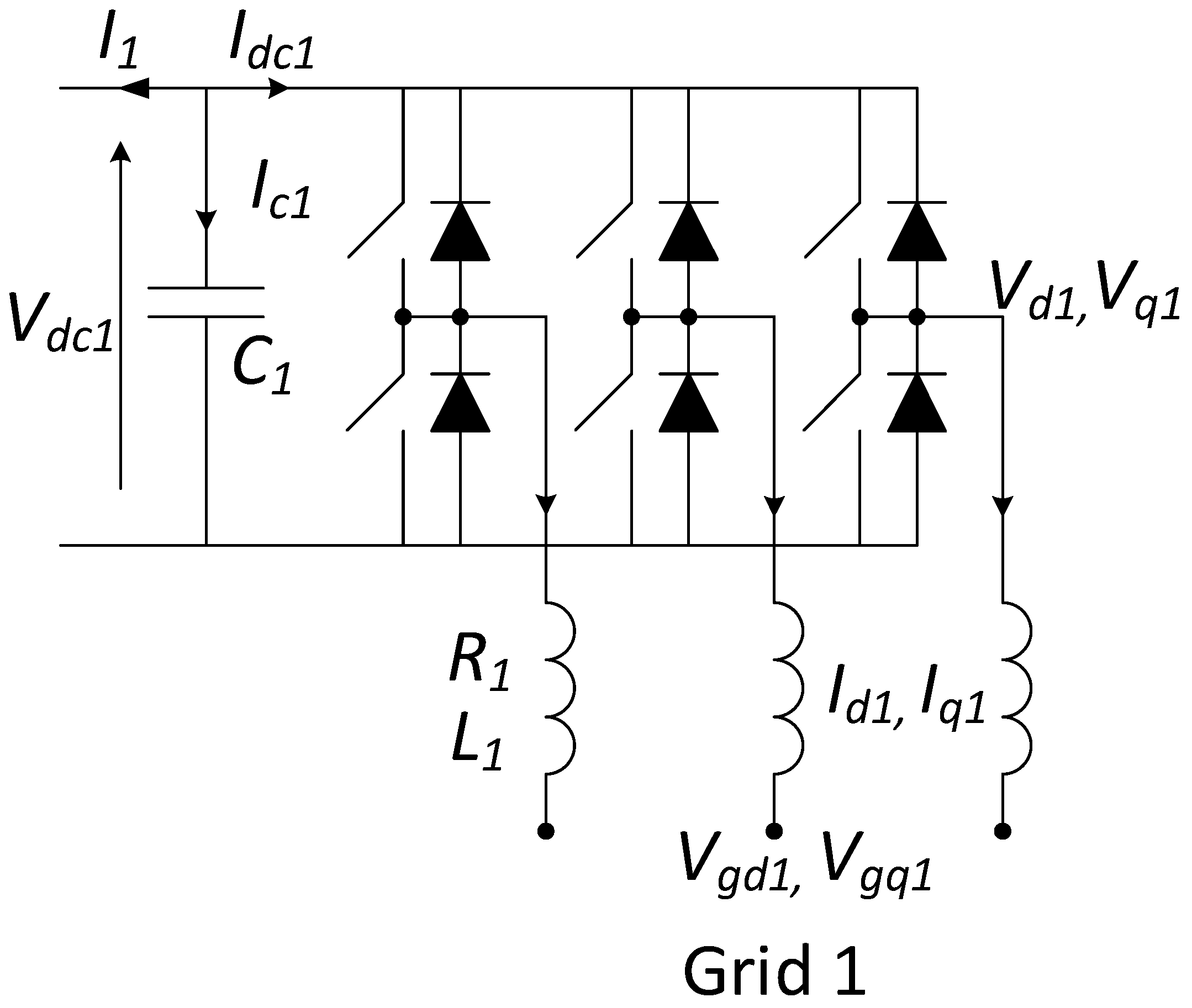
2.2. Grid-Connected Converter to Control the DC Link Voltage and Reactive Power Flow
2.2.1. Grid-Connected Transmission Line Model
2.2.2. Inner Current Controller Model
2.2.3. DC Link Voltage and Reactive Power Flow Controller Model
2.2.4. State-Space Model of the Grid-Connected Converter Used to Control the DC Link Voltage and Reactive Power Flow
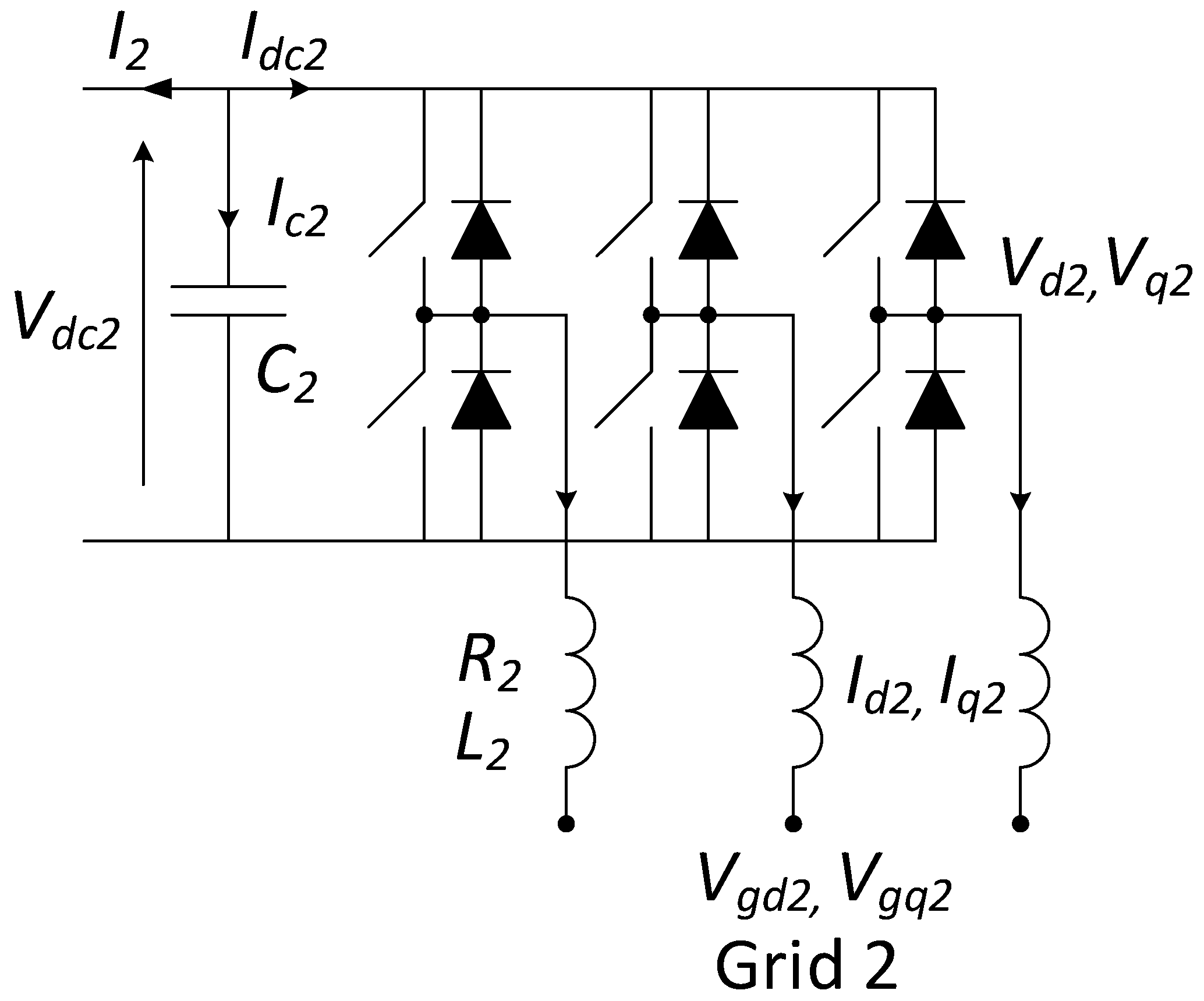
2.3. Grid-Connected Converter Used to Control the Active Power Flow and Reactive Power Flow
2.3.1. Active Power and Reactive Power Controller
2.3.2. Active Power Dynamic Model
2.3.3. State-Space Model of the Grid-Connected Converter to Control the Active Power Flow and Reactive Power Flow
3. Hardware-in-the-Loop Experimental Verification of Modeling Tools
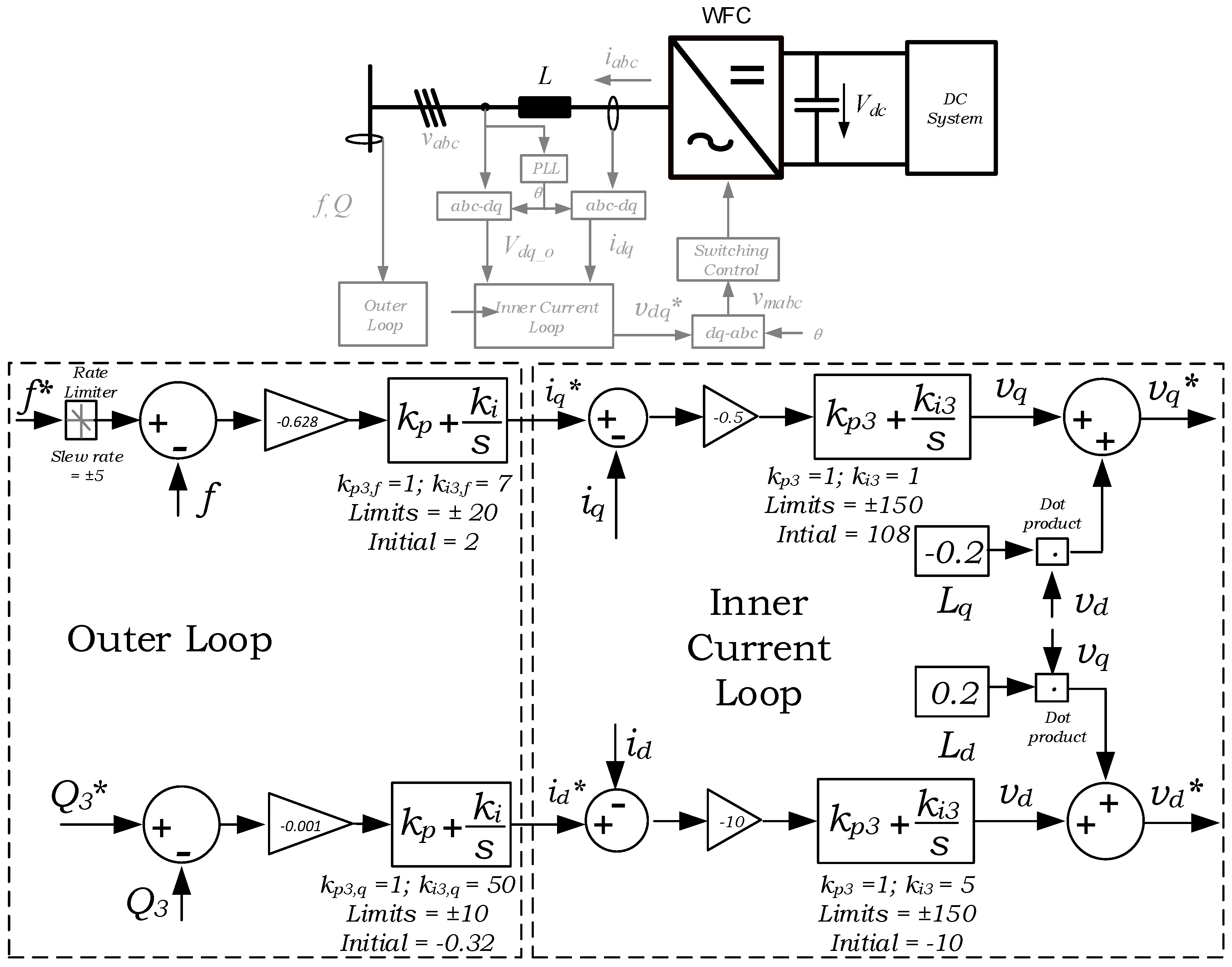
- WFC: Wind farm with AC-to-DC converter with frequency control and reactive power control;
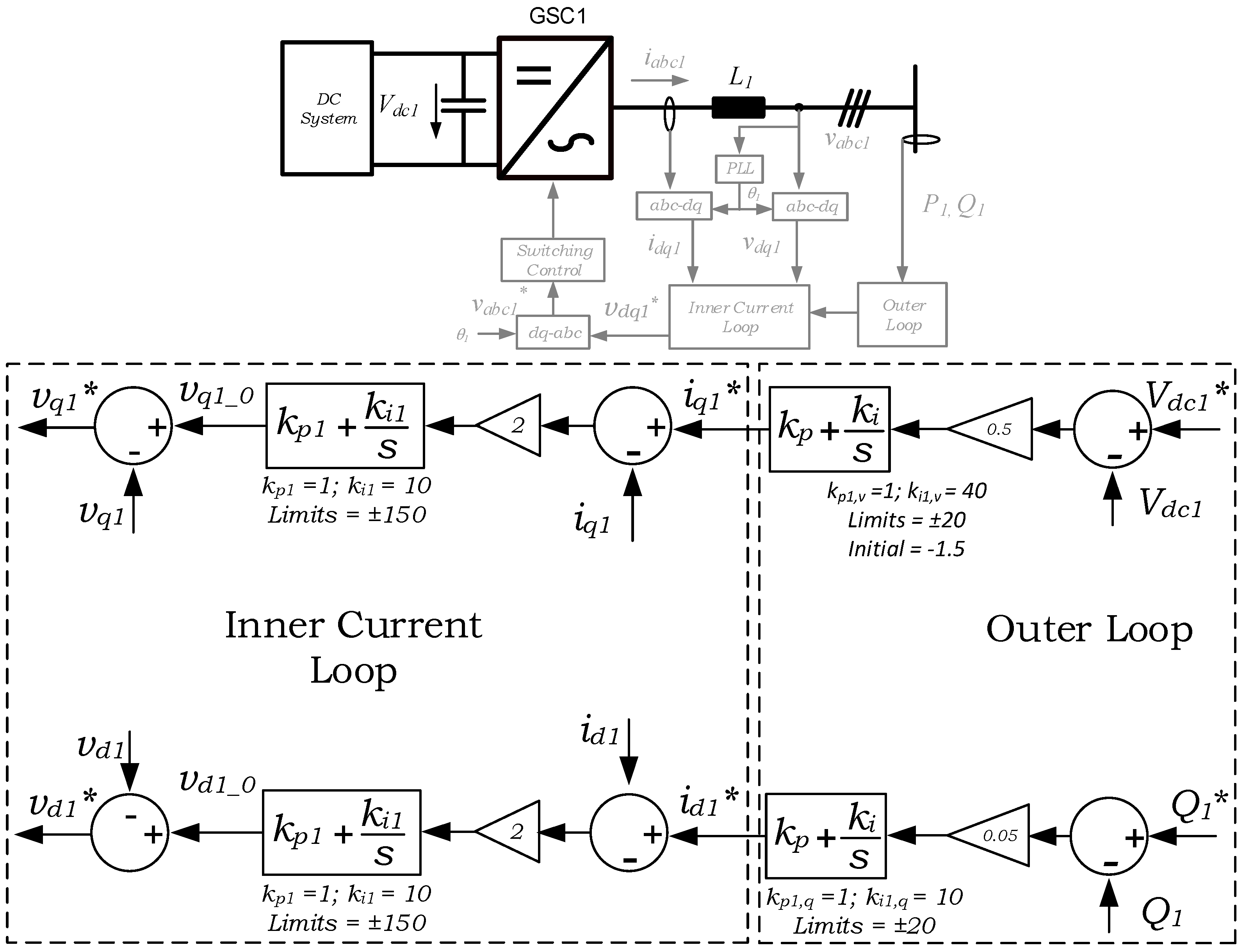
- GSC 1: Grid-connected converter used to control the DC link voltage and reactive power flow;
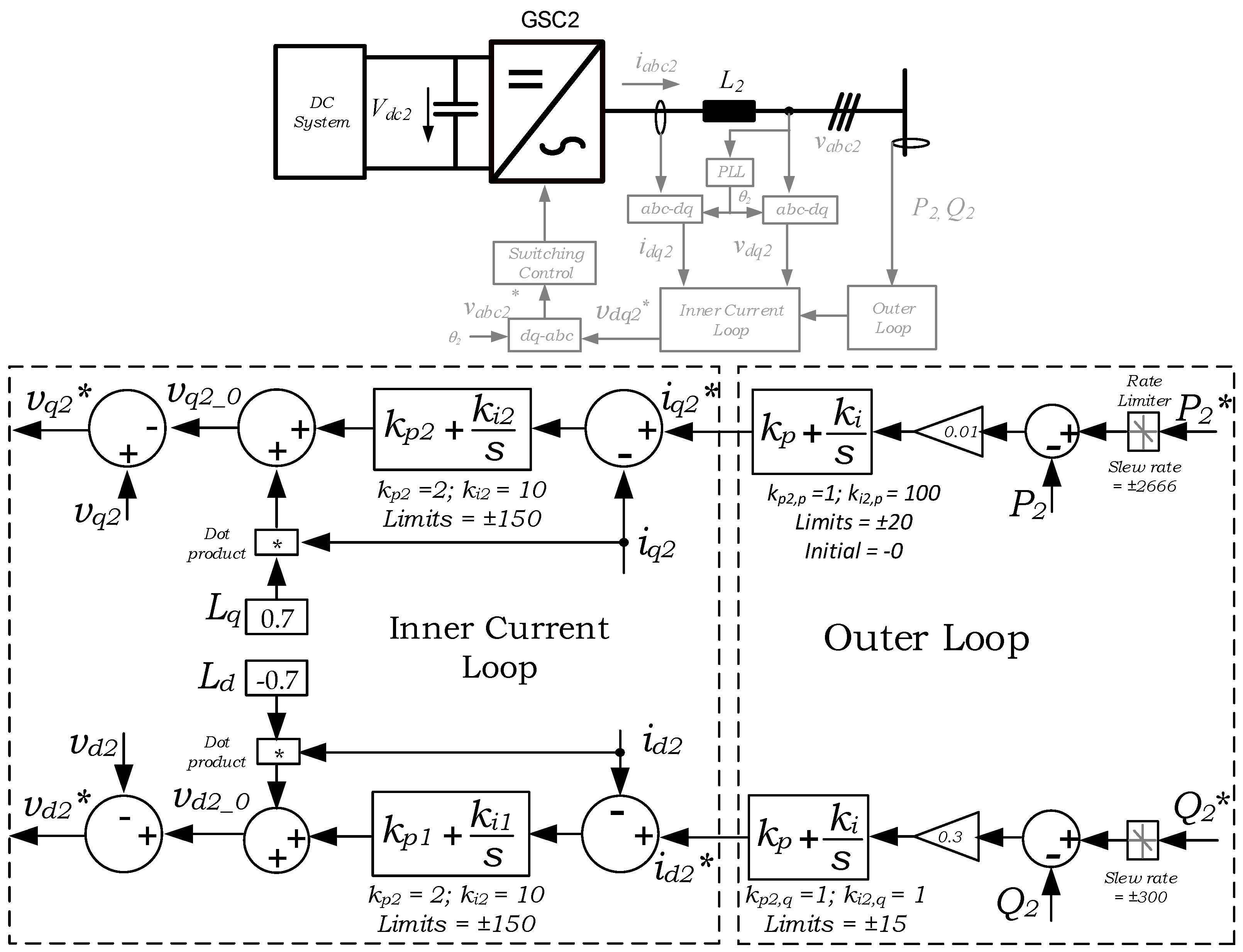
- GSC 2: Grid-connected converter used to control the active power flow and reactive power flow.
3.1. Hardware-in-the-Loop Experimental Setup
3.1.1. Main AC Grid Model in RTDS
3.1.2. Grid Simulator
3.1.3. Three-Terminal HVDC Test Rig
3.2. Controllers
3.2.1. DC Link Voltage and Reactive Power Controllers
3.2.2. Active and Reactive Power Controllers
3.2.3. Frequency Controller and Reactive Power Controller
4. Results and Discussion
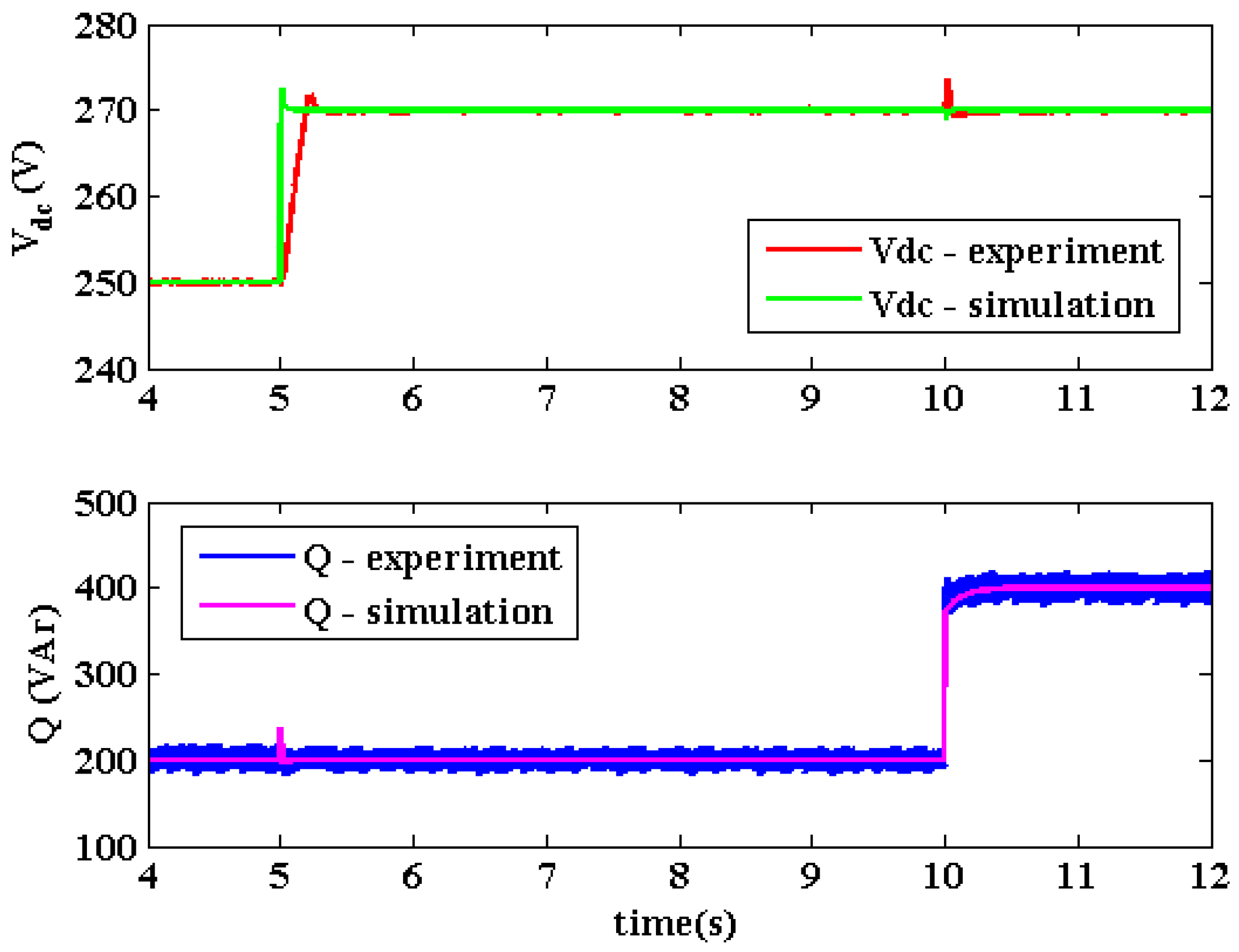
4.1. Verification 1: GSC1 Only
- Step change in DC voltage reference, Vdc1*, from 250 V to 270 V at t = 5 s;
- Step change in reactive power reference, Q1*, from 200 VAr to 400 VAr at t = 10 s.
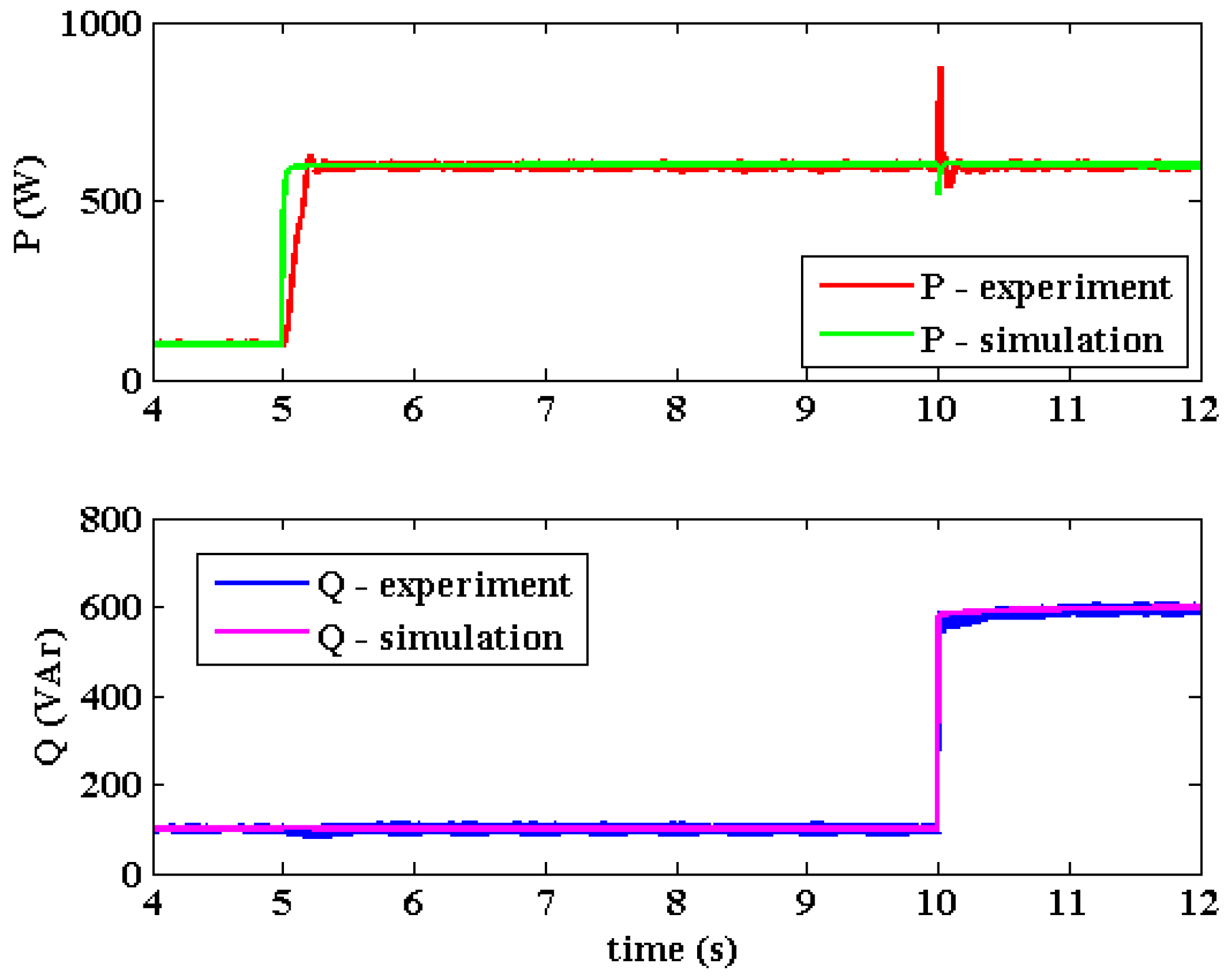
4.2. Verification 2: GSC1 Connected to GSC2
- Step change in active power reference, P2*, from 100 W to 600 W at t = 5 s;
- Step change in reactive power reference, Q2*, from 100 VAr to 600 VAr at t = 10 s.
4.3. Verification 3: GSC1 Connected to WFC
- Step change in frequency reference, f3*, from 75 Hz to 85 Hz at t = 5 s.
- Step change in torque reference, T3*, from 5.6 Nm to 10 Nm at t = 10 s.
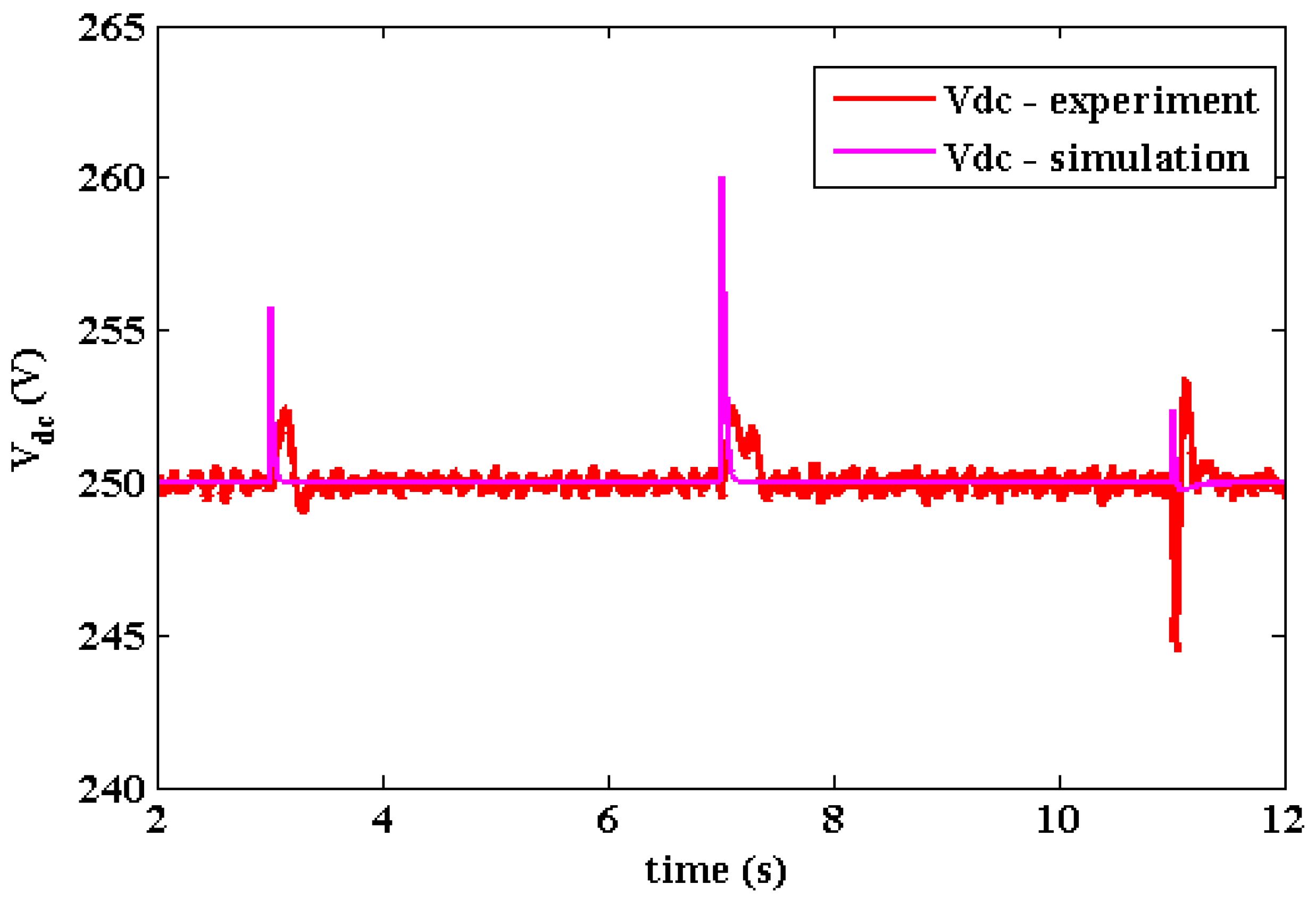
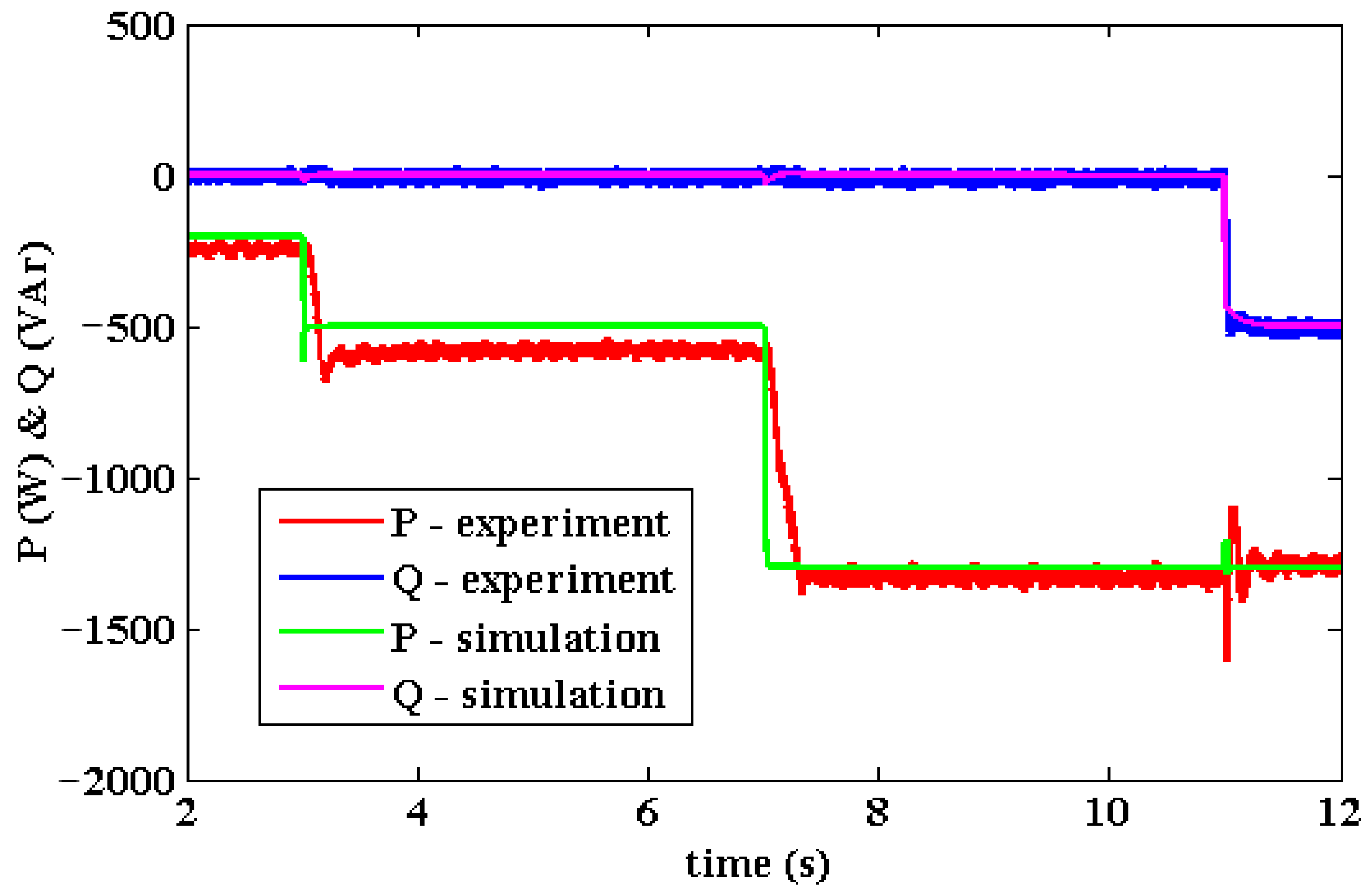
4.4. Verification 4: GSC1 Connected to GSC2 and WFC
- Step change in wind turbine torque reference, T3*, from 7 Nm to 12.8 Nm at t = 3 s;
- Step change in GSC2 active power reference, P2*, from 100 W to 900 W at t = 7 s;
- Step change in GSC2 reactive power reference, Q3*, from 0 VAr to −500 VAr at t = 11 s.
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ullah, N.; Sami, I.; Chowdhury, M.S.; Techato, K.; Alkhammash, H.I. Artificial Intelligence Integrated Fractional Order Control of Doubly Fed Induction Generator-Based Wind Energy System. IEEE Access 2021, 9, 5734–5748. [Google Scholar] [CrossRef]
- Almutairi, K.; Mostafaeipour, A.; Jahanshahi, E.; Jooyandeh, E.; Himri, Y.; Jahangiri, M.; Issakhov, A.; Chowdhury, S.; Hosseini Dehshiri, S.J.; Hosseini Dehshiri, S.S.; et al. Ranking Locations for Hydrogen Production Using Hybrid Wind-Solar: A Case Study. Sustainability 2021, 13, 4524. [Google Scholar] [CrossRef]
- Chowdhury, M.S.; Rahman, K.S.; Selvanathan, V.; Nuthammachot, N.; Suklueng, M.; Mostafaeipour, A.; Habib, A.; Akhtaruzzaman, M.; Amin, N.; Techato, K. Current trends and prospects of tidal energy technology. Environ. Dev. Sustain. 2021, 23, 8179–8194. [Google Scholar] [CrossRef] [PubMed]
- Stern, N. Stern Review: The Economics of Climate Change. 2006. Available online: http://mudancasclimaticas.cptec.inpe.br/~rmclima/pdfs/destaques/sternreview_report_complete.pdf (accessed on 20 October 2021).
- World Energy Council. World Energy Trilemma. In Time to Get Real—The Case for Sustainable Energy Investment; World Energy Council: London, UK, 2013. [Google Scholar]
- Ryndzionek, R.; Sienkiewicz, Ł. Evolution of the HVDC Link Connecting Offshore Wind Farms to Onshore Power Systems. Energies 2020, 13, 1914. [Google Scholar] [CrossRef] [Green Version]
- Pecoraro, G.; Pascucci, A.; Carlini, E.M.; Contu, M.; Cortese, M.; Gnudi, R.; Allella, F.; Bruno, G.; Michi, L. HVDC link between Italy and Montenegro: Impact of the commissioning on the real-time operation. In Proceedings of the 2019 AEIT International Annual Conference (AEIT), Florence, Italy, 18–20 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Iaria, A.; Rapizza, M.R.; Marzinotto, M. Control functions for a radially operated three-terminal VSC-HVDC system: The SA.CO.I. HVDC case. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018; pp. 1679–1684. [Google Scholar] [CrossRef]
- Giorgi, A.; Rendina, R.; Georgantzis, G.; Marchiori, C.; Pazienza, G.; Corsi, S.; Pincella, C.; Pozzi, M.; Danielsson, K.G.; Jonasson, H.; et al. The Italy-Greece HVDC Link. Cigré Session. 2002. Available online: https://library.e.abb.com/public/a759b260ee9d2d78c1256fda004aeab3/THE%20ITALY-GREECE%20HVDC%20LINK%20.pdf (accessed on 20 October 2021).
- Andersen, B.R. HVDC transmission-opportunities and challenges. In Proceedings of the 8th IEE International Conference on AC and DC Power Transmission (ACDC 2006), London, UK, 28–31 March 2006; pp. 24–29. [Google Scholar]
- Bahrman, M.P. HVDC transmission overview. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008; pp. 1–7. [Google Scholar]
- European Offshore Supergrid Proposal, Airtricity. Available online: airtricity_supergrid_V1.4.pdf (accessed on 12 October 2021).
- Veum, K. Roadmap to the Deployment of Offshore Wind Energy in the Central and Southern North Sea (2020–2030); ECN: Petten, The Netherlands, 2011. [Google Scholar]
- Durakovic, A. European TSOs Form Eurobar to Standardise Offshore Grids. 15 April 2021. Available online: https://www.offshorewind.biz/2021/04/15/european-tsos-form-eurobar-to-standardise-offshore-grids/ (accessed on 20 October 2021).
- Ye, Y.; Qiao, Y.; Xie, L.; Lu, Z. A Comprehensive Power Flow Approach for Multi-terminal VSC-HVDC System Considering Cross-regional Primary Frequency Responses. J. Mod. Power Syst. Clean Energy 2020, 8, 238–248. [Google Scholar] [CrossRef]
- Raza, A.; Dianguo, X.; Xunwen, S.; Weixing, L.; Williams, B.W. A Novel Multiterminal VSC-HVdc Transmission Topology for Offshore Wind Farms. IEEE Trans. Ind. Appl. 2017, 53, 1316–1325. [Google Scholar] [CrossRef]
- Torbaghan, S.S.; Gibescu, M.; Rawn, B.G.; Van der Meijden, M. A Market-Based Transmission Planning for HVDC Grid—Case Study of the North Sea. IEEE Trans. Power Syst. 2014, 30, 784–794. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, S.; Pinto, R.T.; Bauer, P.; Pierik, J. Optimal Power Flow Control of VSC-Based Multi-terminal DC Network for Offshore Wind Integration in the North Sea. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 260–268. [Google Scholar] [CrossRef]
- ABB. XLPE Submarine Cable Systems Attachment to XLPE Land Cable Systems—User’s Guide. Available online: https://new.abb.com/docs/default-source/ewea-doc/xlpe-submarine-cable-systems-2gm5007.pdf (accessed on 20 October 2021).
- Su, M.; Dong, H.; Chen, X.; Liu, K. Modeling and Analysis of VSC-MTDC Transmission Systems. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–25 May 2019; pp. 445–450. [Google Scholar] [CrossRef]
- Sayed, S.; Massoud, A. A Matlab/Simulink-Based Average-Value Model of Multi-Terminal HVDC Network. In Proceedings of the 2019 2nd International Conference on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 19–21 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zou, W.; Dong, H.; Chen, X.; Liu, K. Small Signal Modeling and Decoupling Control of VSC-MTDC. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 2786–2792. [Google Scholar] [CrossRef]
- De Decker, J. An offshore transmission grid for wind power integration: The European techno-economic study OffshoreGrid. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- Ugalde-Loo, C.E.; Liang, J.; Ekanayake, J.; Jenkins, N. State-Space Modelling of Variable-Speed Wind Turbines for Power System Studies. IEEE Trans. Ind. Appl. Soc. 2013, 49, 223–231. [Google Scholar] [CrossRef]
- Castro, L.M.; Acha, E. A Unified Modeling Approach of Multi-Terminal VSC-HVDC Links for Dynamic Simulations of Large-Scale Power Systems. IEEE Trans. Power Syst. 2016, 31, 5051–5060. [Google Scholar] [CrossRef]
- Pinares, G.; Tjernberg, L.B.; Tuan, L.A.; Breitholtz, C.; Edris, A.A. On the analysis of the dc dynamics of multi-terminal VSC-HVDC systems using small signal modelling. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Adam, G.P.; Ahmed, K.H.; Finney, S.J.; Williams, B.W. Generalized modeling of DC grid for stability studies. In Proceedings of the 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013; pp. 1168–1174. [Google Scholar] [CrossRef]
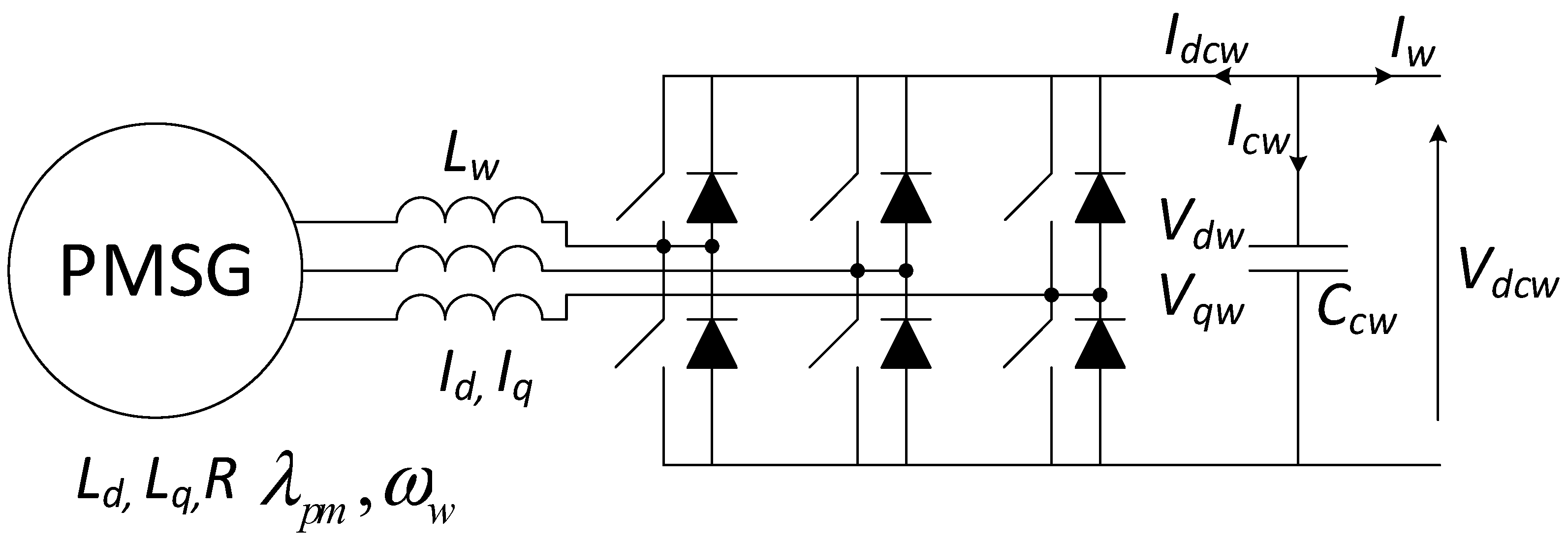


| Symbol | Definition |
|---|---|
| Vdw, Vqw | dq voltages of the AC side of the converter; |
| Vd, Vq | dq voltages of the generator output; |
| Id, Iq | dq currents on the AC side of the converter; |
| Ld, Lq | dq axis inductances of the PMSG; |
| R | winding resistance of the PMSG; |
| λpm | flux linkage of the PMSG; |
| ωw | electrical speed of the PMSG; |
| rotor speed of the PMSG; | |
| number of pole pairs of the PMSG; | |
| Lw | transmission line inductance; |
| τ | induced torque; |
| τm | mechanical torque given by the turbine; |
| DC voltage of the converter; | |
| reference DC voltage of the converter; | |
| d and q modulation indexes of the converter; |
| Symbol | Definition |
|---|---|
| Vd1, Vq1 | dq voltages of converter AC side; |
| Vgd1,Vgq1 | dq voltages of grid; 1 |
| Id1, Iq1 | dq currents of the AC side of the converter; |
| R1 | transmission line resistance; |
| L1 | transmission line inductance; |
| grid 1 frequency in rad/s; | |
| DC voltage of the converter; | |
| reference DC voltage of the converter; | |
| dq modulation indexes of the converter. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samaranayake, L.; Ugalde-Loo, C.E.; Adeuyi, O.D.; Licari, J.; Ekanayake, J.B. Multi-Terminal DC Grid with Wind Power Injection. Wind 2022, 2, 17-36. https://doi.org/10.3390/wind2010002
Samaranayake L, Ugalde-Loo CE, Adeuyi OD, Licari J, Ekanayake JB. Multi-Terminal DC Grid with Wind Power Injection. Wind. 2022; 2(1):17-36. https://doi.org/10.3390/wind2010002
Chicago/Turabian StyleSamaranayake, Lilantha, Carlos E. Ugalde-Loo, Oluwole D. Adeuyi, John Licari, and Janaka B. Ekanayake. 2022. "Multi-Terminal DC Grid with Wind Power Injection" Wind 2, no. 1: 17-36. https://doi.org/10.3390/wind2010002
APA StyleSamaranayake, L., Ugalde-Loo, C. E., Adeuyi, O. D., Licari, J., & Ekanayake, J. B. (2022). Multi-Terminal DC Grid with Wind Power Injection. Wind, 2(1), 17-36. https://doi.org/10.3390/wind2010002









