Nested Sampling for Detection and Localization of Sound Sources Using a Spherical Microphone Array †
Abstract
1. Introduction
2. Spherical Microphone Data and Models
2.1. Microphone Array Data
2.2. Prediction Models
3. Bayesian Calculations
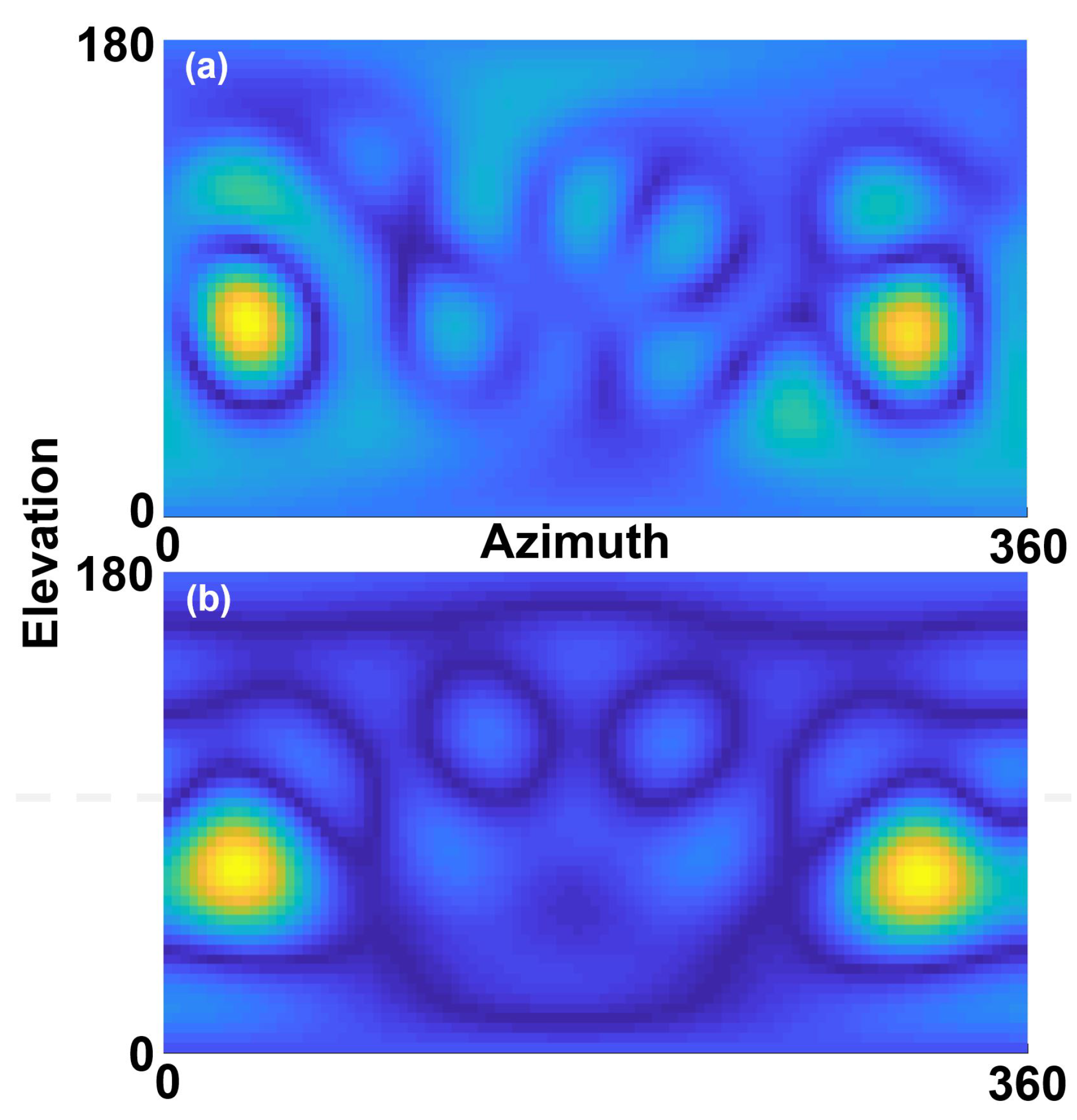
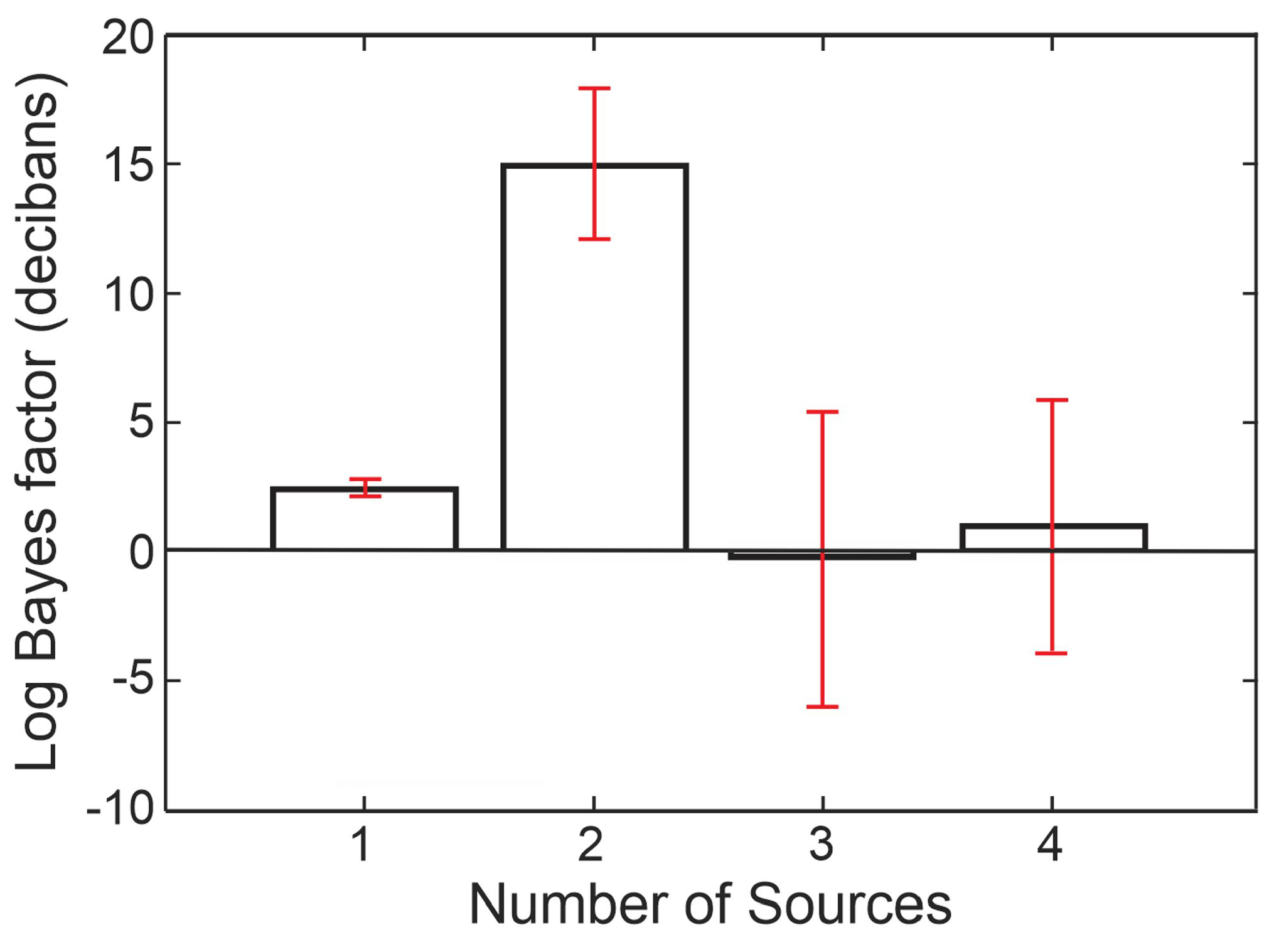
4. Sound Source Detection, Enumeration, and Localization
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DoA | Direction of arrival |
| NS | Nested sampling |
| MaxEnt | Principle of maximum entropy |
References
- Skilling, J. Nested sampling. In Proceedings of the Bayesian Inference and Maximum Entropy Methods in Science and Engineering, AIP Conference Proceedings, Garching, Germany, 25–30 July 2004; Volume 735, pp. 395–405. [Google Scholar]
- Jasa, T.; Xiang, N. Using nested sampling in the analysis of multi-rate sound energy decay in acoustically coupled rooms. AIP Conf. Proc. 2005, 803, 189–196. [Google Scholar]
- Jasa, T.; Xiang, N. Nested sampling applied in Bayesian room-acoustics decay analysis. J. Acoust. Soc. Am. 2012, 132, 3251–3262. [Google Scholar] [CrossRef] [PubMed]
- Botts, J.M.; Escolano, J.; Xiang, N. Design of IIR Filters With Bayesian Model Selection and Parameter Estimation. IEEE Trans. ASLP 2013, 21, 669–674. [Google Scholar] [CrossRef]
- Fackler, C.J.; Xiang, N.; Horoshenkov, K.V. Bayesian acoustic analysis of multilayer porous media. J. Acoust. Soc. Am. 2018, 144, 3582–3592. [Google Scholar] [CrossRef] [PubMed]
- Xiang, N.; Landschoot, C. Bayesian Inference for Acoustic Direction of Arrival Analysis Using Spherical Harmonics. J. Entropy 2019, 21, 579. [Google Scholar] [CrossRef] [PubMed]
- Skilling, J. Nested sampling for general Bayesian computation. Bayesian Anal. 2006, 1, 833–859. [Google Scholar] [CrossRef]
- Jeffreys, H. Theory of Probability; Oxford University Press: Oxford, NY, USA, 1961; Reprinted by Clarendon Press, Oxford, NY, USA, 2003. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, N.; Jasa, T. Nested Sampling for Detection and Localization of Sound Sources Using a Spherical Microphone Array. Phys. Sci. Forum 2023, 9, 26. https://doi.org/10.3390/psf2023009026
Xiang N, Jasa T. Nested Sampling for Detection and Localization of Sound Sources Using a Spherical Microphone Array. Physical Sciences Forum. 2023; 9(1):26. https://doi.org/10.3390/psf2023009026
Chicago/Turabian StyleXiang, Ning, and Tomislav Jasa. 2023. "Nested Sampling for Detection and Localization of Sound Sources Using a Spherical Microphone Array" Physical Sciences Forum 9, no. 1: 26. https://doi.org/10.3390/psf2023009026
APA StyleXiang, N., & Jasa, T. (2023). Nested Sampling for Detection and Localization of Sound Sources Using a Spherical Microphone Array. Physical Sciences Forum, 9(1), 26. https://doi.org/10.3390/psf2023009026





