Abstract
Analytical spherically symmetric static solution to the set of Einstein and Klein-Gordon equations in a synchronous reference frame is considered. In a synchronous reference frame, a static solution exists in the ultrarelativistic limit . Pressure p is negative when matter tends to contract. The solution pretends to describe a collapsed black hole. The balance at the boundary with dark matter ensures the static solution for a black hole. There is a spherical layer inside a black hole between two “gravitational” radii and , where the solution exists, but it is not unique. In a synchronous reference frame, and do not change signs. The non-uniqueness of solutions with boundary conditions at and makes it possible to find the gravitational field both inside and outside a black hole. The synchronous reference frame allows one to find the remaining mass of the condensate. In the model “”, total mass is three times that of what a distant observer sees. This gravitational mass defect is spent for bosons to be in the bound ground state, and for the balance between elasticity and density of the condensate.
1. Introduction
In Schwarzschild coordinates, when we consider a gravitational field created by spherically symmetric matter, it is customary to proceed from the metric [1]:
Exponential representation and fixes signs of the metric tensor components and the determinant . According to Einstein’s hypothesis [2], “always has a finite and negative value”. Setting in the metric (1), we fix the sign of the component g11. Thus, not caring about the presence or absence of a singularity, we exclude from consideration as non-physical. In this case, the coordinate system turns out to be incomplete [3,4,5]. A critical mass arises (for neutron stars, it is of the order of the Sun mass), so that for , regular static solutions to Einstein equations do not exist [6,7,8]. Shwartzshild’s solution [1]
is not regular in the center r = 0, though it describes a gravitational field in a vacuum far away from spherically symmetric matter, regardless of the mass, seen by a distant observer. For , metric (2) asymptotically coincides with the regular solution in Ref. [5] for .
It is believed that objects with a mass greater than the critical one are subject to unlimited compression [9]. The absence of static solutions in metric (1) for objects with a mass greater than the critical one contradicts the existence of the object with a mass seven orders of magnitude greater than the Sun mass [10] in the center of our Milky Way galaxy. “Unlimitedly collapsing objects” at the centers of galaxies are called black holes. Black holes in the centers of galaxies, like the galaxies themselves, exist as long as the universe exists. If we assume that the contraction is non-stop, then at the centers of galaxies we meet a singularity, contrary to Einstein’s hypothesis that “this is nowhere to be found” [2]. If we take into account that in the process of unlimited compression with increasing pressure chemical reactions transform neutrons into more “elementary particles”, then it can slow down and even stop compression. In order to find a regular static solution, describing the state of matter to which a collapse can lead (with no restriction on mass), we abandon the sign-fixing representation . It is sufficient to restrict ourselves by a weaker condition of regularity: all invariants of the metric tensor are finite. With mass in a static state, gravitational contraction is compensated by elasticity of fermions. With , elasticity of fermions cannot resist the gravitational contraction. For a degenerate relativistic Fermi gas, the critical mass [8]. The Planck mass g, mf is the fermion mass, and k is the gravitational constant. For neutron stars (neutron rest mass g) the critical mass g is of the order of the Sun mass.
The static state of boson matter is energetically more preferable than that of fermionic matter. Unlike fermions, all bosons in equilibrium at zero temperature are in the ground state. This ultra-quantum state of matter is called a Bose-Einstein condensate. In equilibrium, concentrations of particles, transforming one into another in chemical reactions, depend on temperature and pressure, and do not depend on reaction channels [11] (§101). If we proceed from the modern Standard Model of “elementary” particles [12], then, in the state of equilibrium, massive Z- and W-bosons, the scalar Higgs boson, as well as bosonic quasiparticles of paired fermions (the Cooper effect [13]), can be dominant. The wave function of a condensate of neutral bosons is the classical scalar field [14] (§30).
Lagrangian L of a complex scalar field : . With a large mass of the condensate, in the expansion of the potential
the main first term is the source of gravity, m is the rest mass of a boson. Leaving only the first term in the potential (3), we are dealing with an ideal gas of noninteracting bosons. The second and following terms are corrections that take into account non-gravitational interactions, including elasticity of a condensate. Only taking into account the two first terms in expansion (3) with λ = const, we deal with a phenomenological model. This model can be named “”.
Equilibrium of a gravitating scalar field has been considered in a number of papers in relation to black holes and hypothetical boson stars, see [15,16,17,18,19] and references therein. As in the case of fermions, with the restriction , equilibrium of a gravitating degenerate Bose gas only exists if the mass M of the condensate is less than the critical mass [20]. For Standard Model bosons (with the rest mass mb about 100 GeV/c2) the critical mass of the condensate is g. It is only about a million tons.
With no restriction , a static solution to the set of Einstein and Klein-Gordon equations with mass exists [21]. In Schwarzschild coordinates, there are two real gravitational radii in this solution. The metric component changes sign twice: at inside the condensate and at on its surface. Inside the spherical layer , the metric component , and the signature of metric tensor is (+, +, −, −).
It follows from Einstein’s Equation (100.6) in Ref. [22] that if the energy density on the condensate surface, then and . One can see from another Einstein’s Equation (100.4) in Ref. [22], that the pressure does not vanish on the surface of the condensate. Negative pressure means that gravitational forces are directed to compress the gas of bosons, and not to expand.
The sphere is the interface of a black hole and dark matter. The observed manifestations of dark matter, such as the rotation curves of galaxies, are adequately described by a longitudinal vector field [23]. A covariant divergence of a longitudinal vector field is a scalar. A Bose condensate wave function is also a scalar. Both satisfy the same Klein-Gordon equation, though the masses of their quanta are extremely different. Conditions of regular continuity of pressure at the interface between a black hole and dark matter made it possible to determine the dependence of the plateau velocity (of galaxy rotation curves) on the mass of a black hole. See formula (68) in Ref. [21].
If in the potential (3) only the first term of expansion is used (ideal Bose gas with no elasticity), then the wave function of the condensate logarithmically diverges at the center [21]. A regular at the center static solution to the set of Einstein and Klein-Gordon equations with mass exists in the model “”, provided that there is a balance of elasticity and density of the condensate [24]. In the Schwarzschild coordinates, a solution with boundary conditions of regularity exists at the center, but it is only unique in the interval . Solutions with boundary conditions on spheres and , where are not unique. This freedom makes it possible to find a solution with any mass , as well as to ensure the balance of a black hole with dark matter at the boundary.
In the Schwarzschild coordinates in the “” model, static states of a black hole are determined by two free parameters. One of them characterizes elasticity of the condensate. It uniquely defines the density of a condensate in the center, and the inner gravitational radius rg. Inside the sphere r < rg; the equation of state of the condensate is
while the energy density and metric component are independent of r. The second free parameter ensures the existence of a regular static solution with arbitrary mass M in the range Mcr < M < ∞ [25].
2. In Synchronous Coordinates
A reference frame with is called synchronous. It is shown in Ref. [22] (§97), that, on the one hand, it is possible to switch to a synchronous frame of reference in any space-time. On the other hand, it is argued that, generally speaking, “space-filling matter cannot be at rest with respect to a synchronous frame of reference”. An exception “may occur only in special cases”. This statement is based on the fact that, in a synchronous frame of reference in statics, the component of the Ricci tensor , and the expression on the right side of the Einstein equation “is positive with any distribution of matter”. Note that the pressure p is positive when matter tends to expand, and negative when matter tends to contract. From the point of view stated in Ref. [22] (§97), the state of a condensate, compressed to the ultra-relativistic limit (4) by its own gravitational field, should be considered as an “exception in a special case”.
It has been known since the time of Eddington [26] and Lemaître [27] that the gravitational radius rg, on which the component , is not a physical singularity in the Schwarzschild metric. In the problem 4 at the end of §100 in Ref. [22], the transformation of the Schwarzschild metric (2) to the conformal Euclidean form is given. The non-uniqueness of the solution to the system of Einstein and Klein-Gordon equations with boundary conditions exactly on the gravitational radii and , where [25], is a feature of the Schwarzschild metric. In the conformal Euclidean form, does not vanish.
In a synchronous frame of reference, a static spherically symmetric metric
contains two functions and , depending on one coordinate r. Unlike the Schwarzschild metric (1), the coordinate r is the true distance from the center. The length of the central circle at a distance r from the center is . Radii and play an important role in a synchronous reference system: solutions to Einstein and Klein-Gordon equations with boundary conditions on these radii are not unique. However, the component does not vanish now on the spheres and . Therefore, as it is customary for everyone, we here use exponential representations in the metric (5). Substitution
makes the metric (5) containing only one function :
Ricci tensor is diagonal:
Energy is the integral of motion in a time-independent gravitational field. The wave function of the boson condensate in the state with a certain energy E per particle satisfies the Klein-Gordon equation . The radial part obeys the equation
Unlike the Schwarzschild metric, in Equation (9), the coefficient at the highest derivative (unity) does not vanish anywhere.
Lagrangian of a scalar field does not depend on the derivatives of the metric tensor . The energy-momentum tensor of the condensate is easily derived using the formula : , , . In the synchronous reference system (8). Therefore, it is convenient to work with the Einstein equations in the form
It follows from Equations (8) and (10):
In (11), , and are constants. Therefore, the wave function of the condensate is also a constant:
Using relations (9), (11), and (12), the energy of a boson E in the bound ground state and the balance between elasticity and density of a condensate are determined:
—parameter characterizing the elasticity of a condensate in the model “”. Taking into account (13), the energy-momentum tensor of the condensate
corresponds to the ultra-relativistic equation of state for the matter compressed by its own gravitational field. Einstein Equation (10) with Ricci tensor (8) and energy-momentum tensor (14)
define the metric function . These equations are not independent. Excluding , and subtracting (16) from (15), we obtain:
Since (12), the energy density and pressure (14) are also constants. Therefore, Equation (18) is the derivative of Equation (17). Multiplied by , Equation (17) is reduced to
The partial derivative suffers a discontinuity at . According to the existence and uniqueness theorem (see [28] (§3)), is a solution of Equation (19). However, it is not unique: is also a solution to Equation (19). is the integration constant. The metric component (7) has two solutions: a constant independent of x, and an oscillating function . These solutions periodically coincide at .
In accordance with (6), for the general metric (5), the oscillating solution
contains an arbitrary function , is an integration constant. At (in a vacuum), solution (20) establishes the relation between and . One of these two functions is arbitrary.
In a simple case , a regular solution at the center is . It is unique only in the interval , is the internal “gravitational radius”. In the region , Equation (19), with the boundary condition , is satisfied by both solutions. Here, at is preferred, because there is no reason to choose the oscillating one.
In a synchronous reference frame, this is the same analytical solution as in Ref. [23] in Schwarzschild coordinates. It can be verified by putting in formula (20) and solving this equation with respect to . It will be obtained as in formula (41) in Ref. [23] (up to notation). Both in the Schwarzschild metric and in the synchronous metric, the inner gravitational radius is the boundary of the central region in which the solution is unique and independent of the mass of the entire condensate. In the region , the solution with the boundary condition is not unique. This ambiguity makes it possible to choose a solution corresponding to a given mass of a condensate. The difference lies in the fact that in the Schwarzschild coordinates at the branch points and , the metric component , but in the synchronous reference system (7) , and it does not vanish anywhere.
The total mass inside a sphere of radius r is obtained by integrating the energy density : Total mass is , and .
The energy E of one particle in the condensate (13) is less than the rest energy of the same particle in a vacuum. In the “” model, elastic collisions of particles occur without dissipation. This model shows that one third of the total energy is spent creating the bound state for bosons. The second third provides a balance of density and elasticity. Only one third of the original rest mass remains as the source of the gravitational field. If the boundary of the condensate , then the total mass of a black hole is three times greater than the Schwarzschild mass . This is the composition of a gravitational mass defect in the “” model.
3. Dark Matter
The sphere is the boundary separating a black hole and dark matter. Manifestations of dark matter are adequately described using a longitudinal vector field [28]. Lagrangian:
For ideal gas of gravitating quanta of dark matter, the potential at .
Dark matter energy-momentum tensor
Outside a black hole, the right side of Einstein equations (10), in accordance with (22), has the form
With the Ricci tensor (8) and tensor (23), the Einstein equations outside the black hole reduce to , . From equation we obtain . C is the integration constant. Eliminating from and , we get the equation . Multiplying by , we reduce this equation to the form , determining the metric component in the synchronous reference system:
The dark matter Lagrangian (21) is required to have a negative . Note that < 0 is also a condition of regularity at the center (formula (39) in Ref. [28]). Two integration constants and in (24) provide a smooth transition of the gravitational field through the boundary between a black hole and dark matter. In view of it is convenient to express in terms of the gravitational radii and :
Solution (25) for and is demonstrated in Figure 1. Since in the synchronous reference frame, there is no reason to call an event horizon.
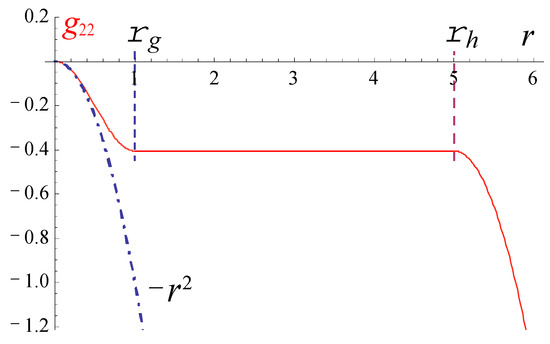
Figure 1.
Red line is (25). , .
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Schwarzschild, K. Uber das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie; Sitzungsberichte der Koniglich Preuischen Academie der Wissenschaften: Berlin, Germany, 1916; pp. 189–196. [Google Scholar]
- Einstein, A. Die Grundlage der allgemeinen Relativitatstheorie. Ann. Phys. 1916, 49, 769–822. [Google Scholar] [CrossRef]
- Kruskal, M.D. Maximal extension of Schwarzschild metric. Phys. Rev. 1960, 119, 1743–1745. [Google Scholar] [CrossRef]
- Szekers, G. On the singularities of a Riemannian manifold. Publ. Mat. Debrecen 1960, 7, 285–301. [Google Scholar] [CrossRef]
- Novikov, I.D. On the Evolution of a Semiclosed World. Ph.D. Thesis, Shternberg Astronomical Institute, Moscow, Russia, 1963. [Google Scholar]
- Chandrasekhar, S. The maximum mass of ideal white dwarfs. Astrophys. J. 1931, 74, 81. [Google Scholar] [CrossRef]
- Landau, L.D. On the theory of stars. Phys. Zs. Sowjet. 1932, 1, 285. [Google Scholar]
- Oppenheimer, J.R.; Volkoff, G. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Snyder, H. On continued gravitational contraction. Phys. Rev. 1939, 56, 455–459. [Google Scholar] [CrossRef]
- Gillessen, S.; Eisenhauer, F.; Trippe, S.; Alexander, T.; Genzel, R.; Martins, F.; Ott, T. Monitoring Stellar Orbits around the Massive Black Hole in the Galactic Center. Astrophys. J. 2009, 692, 1075. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Part 1; Science-fizmatlit: Moscow, Russia, 1995. (In Russian) [Google Scholar]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Standard_Model (accessed on 14 March 2023).
- Cooper, L.N. Bound Electron Pairs in a Degenerate Fermi Gas. Phys. Rev. 1956, 104, 1189–1190. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Part 2; Fizmatlit: Moscow, Russia, 2000. (In Russian) [Google Scholar]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. arXiv 2018, arXiv:1707.04966v1. [Google Scholar] [CrossRef] [PubMed]
- Colpi, M.; Shapiro, S.L.; Wasserman, I. Boson Stars: Gravitational Equilibria of Self-Interacting Scalar Fields. Phys. Rev. Lett. 1986, 57, 2485. [Google Scholar] [CrossRef]
- Friedberg, R.; Lee, T.D.; Pang, Y. Mini-soliton stars. Phys. Rev. D 1987, 35, 3640. [Google Scholar] [CrossRef]
- Kaup, D.J. Klein-Gordon Geon. Phys. Rev. 1968, 172, 1331. [Google Scholar] [CrossRef]
- Torres, D.F.; Capozziello, S.; Lambiase, G. Supermassive boson star at the galactic center? Phys. Rev. D 2000, 62, 104012. [Google Scholar] [CrossRef]
- Meierovich, B.E. On the equilibrium of the boze-einstein gravitating condensate. J. Exp. Theor. Phys. 2018, 154, 1000–1015. (In Russian) [Google Scholar]
- Meierovich, B.E. Static state of a black hole supported by dark matter. Universe 2019, 5, 198. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Field theory; Science: Moscow, Russia, 1973. (In Russian) [Google Scholar]
- Meierovich, B.E. Galaxy rotation curves driven by massive vector fields: Key to the theory of the dark sector. Phys. Rev. D Part. Fields Gravit. Cosmol. 2013, 87, 103510. [Google Scholar] [CrossRef]
- Meierovich, B.E. Guessing the Riddle of a Black Hole. Universe 2020, 6, 113. [Google Scholar] [CrossRef]
- Meierovich, B.E. Gravitational Radius in view of Existence and Uniqueness Theorem. J. Phys. Conf. Ser. 2021, 2081, 012026. [Google Scholar] [CrossRef]
- Eddington, A.S. A comparison of Whitehead’s and Einstein’s formulas. Nature 1924, 113, 192. [Google Scholar] [CrossRef]
- Lemaître, G. L’univers en expansion. Ann. Soc. Sci. Bruxelles 1933, A53, 51–85. [Google Scholar]
- Meierovich, B.E. Macroscopic Theory of Dark Sector. J. Gravity 2014, 2014, 568958. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).