Abstract
We investigated the Friedmann–Lemaitre–Robertson–Walker (FLRW) cosmological models within the framework of Rastall gravity incorporating particle creation. The modified field equations for Rastall gravity are derived, and exact solutions are obtained under various types of scale factors. The qualitative behaviour of our solutions depends on the Rastall coupling parameter . Following the literature, we have restricted the Rastall coupling parameter to the range at 68% CL from CMB+BAO data. Furthermore, we have discussed the distinct physical behaviour of the derived models in detail.
1. Introduction
Researchers have always been curious to understand the universe from the past to the future scientifically. Einstein presented the general theory of relativity and gained considerable attention due to its success in building cosmological models. Currently, modifications of Einstein’s gravity or extensions of Einstein’s general theory of gravity are being studied to solve some of the problems presented by Einstein’s general theory of relativity to study cosmology. The CDM model seems to be sufficient to describe the current scenario of the universe, although there are some unresolved issues. One of the critical ingredients of Einstein’s theory of relativity is the covariant conservation of energy–momentum. A number of modified theories of gravity have been proposed in the last few decades, such as gravity [1], gravity [2], gravity [3], gravity [4], gravity [5], gravity [6], gravity [7] and gravity [8]. In the present study, we are interested in Rastall’s gravity theory. Rastall’s gravity theory was developed in 1972. Modified theories of gravity may or may not satisfy the conservation law of energy–momentum [9]. Thus, one of the possible ways of extending general relativity is through relaxing the conservation law. In curved space time, the conservation law may or may not hold. In response to this, Rastall [9] proposed that the covariant divergence of the energy–momentum tensor might not be vanishing, but should be determined by the curvature of space–time through a coupling parameter, so that general relativity can be recovered at zero coupling. Recently, Moraes and Santos proposed [10] the Lagrangian formalism of Rastall gravity by a non-minimal coupling between geometry and matter fields. Shabani and Ziaie [11] developed the Lagrangian formulation for Rastall theory under the influence of perfect fluid matter content and a linear equation of state in the framework of gravity.
In this study, our primary focus is on the study of particle creation in Rastall gravity. Particle creation remains one of the most important unsolved problems in cosmology. Several cosmologists have discussed this phenomenon and its effects on the evolution of the universe. Furthermore, they developed a cosmological model to discuss the thermodynamical aspects of the universe by using the mechanism of particle creation. A detailed exploration of the thermodynamics of particle creation with the change of specific entropy has been discussed [12,13,14]. Hamil et al. [15] discussed the mechanism of particle creation in the absence of a time-like singularity in the emergent universe scenario. Lyth et al. [16] discussed the cosmological consequences of particle creation during the inflation era of the universe. Particle creation arises due to a change in the space–time metric at the end of the inflationary era during the early universe [17]. The nature and origin of quantum fields are due to the back-reaction of particle creation by deriving the effective action of a scalar field [18]. The time dependence of particle creation is due to a quantised, massless, minimally coupled scalar field in two-dimensional flat space–time with an accelerating mirror [19]. Recently, Bishi and Lepse [20] studied the influence of the deceleration parameter with the particle creation mechanism. Following the above-stated research work based on Rastall gravity and the particle creation mechanism, we were motivated to investigate the impact of particle creation in Rastall gravity by considering different types of scale factors .
2. Field Equations
The modified field equation of the Rastall gravity is expressed as [21]
It can be rewritten in the form
where k is the Rastall gravitational coupling constant and is the Rastall coupling parameter. Li et al. [22] constrained the Rastall coupling parameter (68% CL) with the help of 118 galaxy–galaxy strong gravitational lensing systems. Furthermore, using CMB + BAO data, Akarsu et al. [23] restricted to the range (68% CL) for . The Rastall coupling parameter measures the deviation from general relativity (, i.e., ). Let us consider the FLRW metric
where and represent the flat closed and open universes, respectively.
In the presence of the creation of matter, the energy momentum tensor is given by
where and p are the energy density and pressure, respectively, is the creation pressure, the fluid four-velocity vector, such that , and is the metric tensor. The trace of the energy momentum tensor is given as
Adiabatic particle production means the particles, as well as the entropy S (with entropy per particle ), remain constant when they are produced in space–time. The creation pressure in the case of conserved specific entropy (that is, entropy per particle ) is given by [24,25,26]
here, is the parametrization of the source function (see [27] and refs. therein). It determines whether particles are produced or annihilated. n refers to the particle number density, and is a constant. The positive, negative and zero values of the source function represent particle production, particle annihilation and no particle production, respectively. With the help of the parametrization of the source function , expression (6) leads to
3. Solution of the Modified Field Equations
3.1. Model I
Let us consider the scale factor of the form . The choice of this form of scale factor yields a time-dependent deceleration parameter. It is interesting to note that for , , and therefore the inflationary scenario of the universe can be observed for . The Hubble parameter and deceleration parameter q take the form
In this model, the universe evolves with and at the late times . We observe that when , we obtain . The physical quantities for this case are found as
3.2. Model II
Barrow [28] has studied the intermediate expansion law in cosmology for the first time. The intermediate form of the scale factor obtains an exponential function of the time as
where and are constant. Ample amounts of research work based on the intermediate scale factor in the isotropic and anisotropic metric backgrounds have been conducted using various gravity theories [29,30,31]. It will be interesting to study the intermediate form of the scale factor in the framework of Rastall gravity with particle creation. The Hubble parameter and deceleration parameter are given by
The physical quantities for this case are expressed as
4. Discussions
Figure 1 is the profile of the energy density against cosmic time t for different values of (). The energy density is a decreasing and positive-valued function of cosmic time t and when for flat, open and closed universes. The pressure shows negative to positive behaviour for different . The profile of the creation pressure shows a negative–positive–negative trend for different values and different universes (flat, open and closed; see Figure 2).
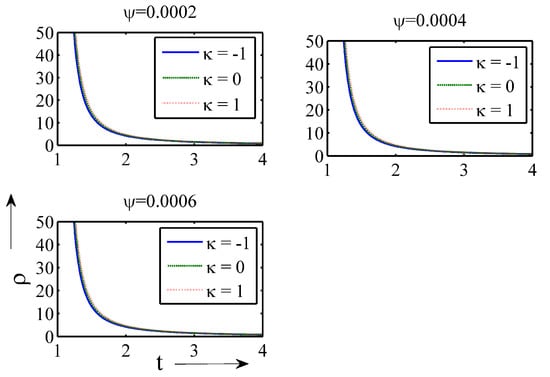
Figure 1.
Profile of energy density against time for Model−I for different .
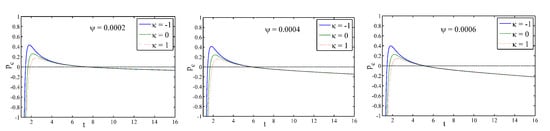
Figure 2.
Profile of particle creation for Model−I against time for different .
Figure 3 portrays the variations in the energy density with time t for different . Here, we observe that the energy density is a positive and decreasing function of cosmic time t with respect to different values of for all the universes (flat, open and closed). At the initial phase, the pressure takes positive values, and after that it takes negative values for different values of . In all the universes (flat, open and closed), the particle creation pressure is an increasing function of cosmic time and approaches zero with the evolution of time for different (see Figure 4).
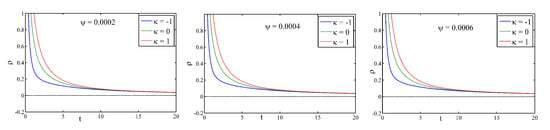
Figure 3.
Profile of energy density for Model−II against time for different .
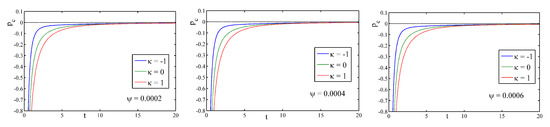
Figure 4.
Profile of particle creation pressure for Model−II against time for different .
5. Conclusions
In this manuscript, we examined particle creation in the context of Rastall gravity. Particle creation mechanisms in the considered modified gravity models permit us to understand particle production annihilation in the universe. Rastall gravity is a non-conservative theory and an extension of general relativity. The key element of this theory is that non-vacuum solutions are dependent on the Rastall coupling parameter and are significantly different from their corresponding solutions in general relativity. We derived and solved the Rastall gravity field equations under two different scale factors. The deceleration parameter q portrays negative behaviour for all the models, which indicates the universe’s accelerated expansion. Here, we can observe that all the models have positive energy density . Furthermore, we obtain the positive to negative and negative to positive behaviours of the pressure p. If the energy density is positive, the associated negative pressure will drive the accelerated expansion of the universe. This means that all the models indicate an accelerated expansion of the universe. Furthermore, for the particle creation pressure, its presence or absence is indicated by zero or negative particle creation pressure , respectively. As a result, particle creation occurs in all the models for different values of the Rastall coupling parameter (=), with .
Author Contributions
Conceptualization, B.K.B. and A.B.; methodology, B.K.B. and A.B.; software, P.V.L.; writing—original draft preparation, B.K.B. and P.V.L.; writing—review and editing, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
Binaya K. Bishi acknowledges the financial support provided by the National Research Foundation of South Africa (Grant Numbers: 118511) in the form of a postdoctoral fellowship, and also wishes to thank the University of Zululand, South Africa, for providing the necessary facilities.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
There are no new data associated with this article.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Capozziello, S.; Cardone, V.F.; Farajollahi, H.; Ravanpak, A. Cosmography in f(T) gravity. Phys. Rev. D 2011, 84, 043527. [Google Scholar] [CrossRef]
- Jimenez, J.B.; Heisenberg, L.; Koivisto, T.; Pekar, S. Cosmology in f(Q) geometry. Phys. Rev. D 2020, 101, 103507. [Google Scholar] [CrossRef]
- Najera, A.; Fajardo, A. Fitting f(Q, T) gravity models with a CDM limit using H(z) and Pantheon data. Phys. Dark Universe 2021, 34, 100889. [Google Scholar] [CrossRef]
- Cembranos, J.A. Dark matter from R2 gravity. Phys. Rev. Lett. 2009, 102, 141301. [Google Scholar] [CrossRef] [PubMed]
- De Felice, A.; Tsujikawa, S. Construction of Cosmologically viable f(G) gravity models. Phys. Lett. B 2009, 675, 1–8. [Google Scholar] [CrossRef]
- De Laurentis, M.; Paolella, M.; Capozziello, S. Cosmological inflation in f(R, G) gravity. Phys. Rev. D 2015, 91, 083531. [Google Scholar] [CrossRef]
- Akbar, M.; Cai, R.G. Friedmann equations of FRW universe in scalar–tensor gravity, f(R) gravity and first law of thermodynamics. Phys. Lett. B 2006, 635, 7–10. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.; Nojiri, S.I.; Odintsov, S.D. f(R, T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Rastall, P. Generalization of the Einstein theory. Phys. Rev. D 1972, 6, 3357. [Google Scholar] [CrossRef]
- De Moraes, W.A.G.; Santos, A.F. Lagrangian formalism for Rastall theory of gravity and Godel-type universe. Gen. Relativ. Gravit. 2019, 51, 1–17. [Google Scholar] [CrossRef]
- Shabani, H.; Ziaie, A.H. A connection between Rastall-type and f(R, T) gravities. EPL 2020, 129, 20004. [Google Scholar] [CrossRef]
- Prigogine, I.; Géhéniau, J.; Gunzig, E.; Nardone, P. Thermodynamics of cosmological matter creation. Proc. Natl. Acad. Sci. USA 1988, 85, 7428–7432. [Google Scholar] [CrossRef]
- Lima, J.A.S. Thermodynamics of decaying vacuum cosmologies. Phys. Rev. D 1996, 54, 2571. [Google Scholar] [CrossRef]
- Gunzig, E.; Maartens, R.; Nesteruk, A.V. Inflationary cosmology and thermodynamics. Class Quantum Gravity 1998, 15, 923. [Google Scholar] [CrossRef]
- Hamil, B.; Merad, M.; Birkandan, T. Particle creation in the context of the emergent universe. Rev. Mex. Física 2021, 67, 219–225. [Google Scholar] [CrossRef]
- Lyth, D.H.; Roberts, D.; Smith, M. Cosmological consequences of particle creation during inflation. Phys. Rev. D 1998, 57, 7120. [Google Scholar] [CrossRef]
- Ford, L.H. Gravitational particle creation and inflation. Phys. Rev. D 1987, 35, 2955. [Google Scholar] [CrossRef] [PubMed]
- Calzetta, E.; Hu, B.L. Dissipation of quantum fields from particle creation. Phys. Rev. D 1989, 40, 656. [Google Scholar] [CrossRef] [PubMed]
- Good, M.R.; Anderson, P.R.; Evans, C.R. Time dependence of particle creation from accelerating mirrors. Phys. Rev. D 2013, 88, 025023. [Google Scholar] [CrossRef]
- Bishi, B.K.; Lepse, P.V. Particle creation and quadratic deceleration parameter in Lyra geometry. New Astron. 2021, 85, 101563. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, B.P.; Ali, M.S.; Ghosh, S.G. Shadows of black hole surrounded by anisotropic fluid in Rastall theory. Phys. Dark Universe 2021, 34, 10088. [Google Scholar] [CrossRef]
- Li, R.; Wang, J.; Xu, Z.; Guo, X. Constraining the Rastall parameters in static space–times with galaxy-scale strong gravitational lensing. Mon. Not. R. Astron. Soc. 2019, 486, 2407–2411. [Google Scholar] [CrossRef]
- Akarsu, O.; Katırcı, N.; Kumar, S.; Nunes, R.C.; Öztürk, B.; Sharma, S. Rastall gravity extension of the standard ΛCDM model: Theoretical features and observational constraints. Eur. Phys. J. C 2020, 80, 1050. [Google Scholar] [CrossRef]
- Calvao, M.O.; Lima, J.A.S.; Waga, I. On the thermodynamics of matter creation in cosmology. Phys. Lett. A 1992, 162, 223–226. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Germano, A.S.M. On the equivalence of bulk viscosity and matter creation. Phys. Lett. A 1992, 170, 373–378. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Calvao, M.O.; Waga, I. Cosmology, Thermodynamics and Matter Creation, Frontier Physics, Essays in Honor of Jayme Timno; World Scientific: Singapore, 1990. [Google Scholar]
- Hulke, N.; Singh, G.P.; Bishi, B.K.; Singh, A. Variable Chaplygin gas cosmologies in f(R, T) gravity with particle creation. New Astron. 2020, 77, 101357. [Google Scholar] [CrossRef]
- Barrow, J.D.; Saich, P. The behaviour of intermediate inflationary universes. Phys. Lett. B 1990, 249, 406–410. [Google Scholar] [CrossRef]
- Rendall, A.D. Intermediate inflation and the slow-roll approximation. Class Quantum Gravity 2005, 22, 1655. [Google Scholar] [CrossRef]
- Khatua, P.B.; Debnath, U. Dynamics of logamediate and intermediate scenarios in the dark energy filled universe. Int. J. Theor. Phys. 2011, 50, 799–832. [Google Scholar] [CrossRef]
- Farajollahi, H.; Ravanpak, A. Tachyon field in intermediate inflation on the brane. Phys. Rev. D 2011, 84, 084017. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).