Abstract
Space-based gravitational-wave detectors, such as the Laser Interferometer Space Antenna, allow for the probing of the interior of white dwarfs in binaries through the imprints of tidal effects on the gravitational wave signal. In this study, we have computed the tidal deformability of white dwarfs in full general relativity, taking into account the crystallization of their core. The elasticity of the core is found to systematically reduce the tidal deformability, especially for low-mass stars. Moreover, it is shown that errors on the tidal deformability due to the use of the Newtonian theory can become important for massive white dwarfs. Finally, the orbital evolution of eccentric binaries is investigated. Measuring the precession rate of these systems could provide estimations of the individual masses. However, it is found that the neglect of crystallization could lead to very large errors.
1. Introduction
The recent detection of gravitational waves (GWs) from compact binary systems by the LIGO-Virgo collaboration has opened a brand new era in the field of astronomy [1]. The upcoming space-based detector “Laser Interferometer Space Antenna” (LISA) [2], which is expected to be operative within the next decade, will allow for the detection of GW signals in the range of 0.1 mHz to 1 Hz, mainly supposing to come from white dwarf (WD) binaries. According to population synthesis models, more than 10,000 WD binaries are expected to be detected over the four-year mission of LISA [3,4,5,6]. Among these systems, eccentric binaries are the targets of choice to study the internal constitution of WDs. Indeed, the precession of their periastron caused by tidal forces leads to a frequency splitting of the gravitational signal, which is proportional to the precession rate [7,8]. In turn, this precession rate, potentially measurable by LISA, depends on the tidal deformability parameter, and therefore on the internal structure of the WDs. Information on the tidal effects could also be obtained for WD binaries with circular orbits from the long-term monitoring of the GW signal [9,10,11,12].
Some of the WD binaries that will be observed by LISA will be aged a few billions of years, and could then be at least partially crystallized. Crystallization of the WD cores was predicted long ago [13,14,15] and had observational support from an asteroseismological study of BPM 37093 [16]. Very recently, new, strong observational evidence has been brought about by the analysis of the GAIA data [17]. The crystallization of the WD cores may have an impact on their tidal deformability, and should then be taken into account when analyzing the GW signal from old WD binaries. In spite of this, previous studies on the tidal deformations of WDs considered only purely perfect fluid stars in Newtonian theory [18,19].
In this paper, we compute the tidal deformability of a WD, taking into account the elasticity of the crystallized core in full general relativity. After briefly presenting the equation of state and the way to calculate tidal deformations in general relativity in Section 2, we present our numerical results in Section 3.
2. Structure and Deformability of White Dwarfs
2.1. Equation of State of White Dwarfs
The core of a WD with densities reaching ~106 g/cm3 is made of fully ionized atomic nuclei in a charge compensating gas of relativistic electrons. These nuclei typically consist of light elements such as carbon and oxygen, but also helium [20,21,22], neon, or magnesium [23]. In this work, we assume, for simplicity, that the core is pure. Moreover, we consider that the WD is sufficiently aged so that the core has cooled down and crystallized. The WD is then so cold that the thermal effects in the equation of state are neglected. The elastic properties of the crystallized core are described by a single elastic constant, the shear modulus, assuming that each element of matter at a given density consists of an isotropic polycrystalline solid [24,25,26]. Finally, the surrounding layers of hydrogen or helium composing the atmosphere are ignored, as they can only represent a maximum of ~1% of the total stellar mass to avoid a thermonuclear runaway.
2.2. Tidal Deformability including Elasticity
WDs in a close orbit are tidally deformed by mutual gravitational interactions. In the adiabatic approximation, the static external quadrupolar tidal field and the induced quadrupolar mass moment in the star are related, to first order, by [27]
where is the universal gravitational constant, is the stellar radius, and is the Love number (also called the apsidal motion constant) characterizing the tidal deformability of the star. The tidal parameter which is observable through the GW detections is thus proportional to the combination (for a given mass).
The background structure of the star is described by the famous Tolman–Oppenheimer–Volkoff (TOV) equations [28,29], which relate the pressure, mass–energy density, and gravitational mass inside the star, with the radial coordinate being the independent variable. Integrating these equations from the center up to the surface and using the equation of state gives the mass and the radius of the star.
To describe static tidal perturbations, one has to solve the perturbed Einstein field equations. For this purpose, one has to define a perturbed space–time metric,
with representing the metric of a spherically symmetric space–time, and representing the linear metric perturbation, which is chosen to be reduced in the Regge–Wheeler gauge [30]. To take into account the existence of elasticity in the core, one has to add the shear constraint contribution to the perfect fluid one , in the right-hand side of the perturbed Einstein equations [31,32]:
where is the speed of light. Using definition (2) in Equation (3) and using appropriate combinations of the different components leads to a system of six first-order ordinary differential equations. This system is to be solved from the stellar center by using the initial conditions from the Taylor expansions of the different functions up to the surface, where appropriate boundary conditions are imposed (see Ref. [33] for details). The matching of the interior solution with the exterior solution (in vacuum) at the stellar surface allows for the obtainment of the tidal Love number [27]. Note that elasticity has no effect on the stellar radius or on the mass, since it comes into play at the perturbed level only.
3. Results and Discussion
In this section, we present the numerical results obtained by solving the perturbation equations, characterizing the tidal deformations together with the TOV equations.
3.1. Effect of the Crystallization on the Deformability
In Figure 1, we show as a function of the stellar gravitational mass for a WD made of oxygen 16O or magnesium 24Mg, comparing entirely perfect fluid and entirely solid stars. We notice that the presence of a crystallized core systematically reduces the tidal deformability, especially for low-mass stars. Moreover, the presence of heavy elements in the crystallized core reduces the tidal deformability even more, as we can see from comparing the two plots in Figure 1: these reductions amount to 3.3% and 4.2% for 0.6 M⊙ oxygen or magnesium WDs, respectively. The deviations on the observable combination are the same as those on , since the radius is unaffected by the presence of elasticity.
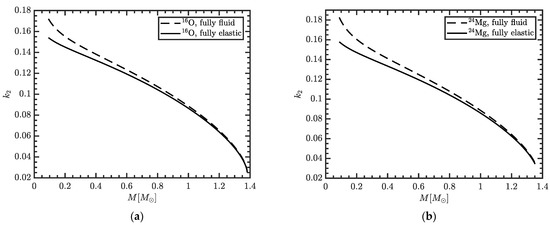
Figure 1.
Love number as a function of the gravitational mass for a fully fluid or a fully elastic WD made of oxygen (a), or magnesium (b).
3.2. Comparison with Newtonian Results
In Figure 2, we show the errors on the stellar radius and the Love number incurred by the use of the Newtonian theory instead of general relativity for purely fluid stars, as it has been commonly done in previous studies on WDs. We notice that the Newtonian theory systematically increases both the radius and the Love number. These deviations remain negligible for low-mass stars up to ~1 M⊙. However, for more massive WDs, the deviations become increasingly important, and reach ~10% both for and at the Chandrasekhar limit. A direct consequence of this is that the observable combination is even more affected: the errors on this parameter reach up to 100% close to the maximum mass. This enlightens the importance of considering general relativity, at least for massive WDs.
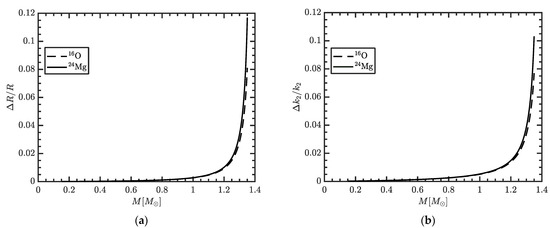
Figure 2.
Relative errors incurred by the use of Newtonian theory instead of general relativity on the stellar radius (a), and the Love number (b), as a function of the gravitational mass , for oxygen or magnesium WDs.
3.3. Eccentric Binaries
In this last part, we focus on eccentric binary WDs. The precession of the periastron leads to a frequency splitting of the GW signal proportional to the precession rate (the dotted notation denotes a time derivative), which is the sum of three contributions [7,8]:
with representing the contribution from general relativity, and representing the contributions from the tidal effects and the rotation of the two stars (with the index identifying each star), respectively. While the general relativity contribution depends only on the eccentricity and the total mass of the binary, the two others from the tidal effects and rotation also depend on the individual masses and the observable tidal deformability parameters of each star, and then on their internal constitution.
By solving the equations governing the orbital evolution of a binary system and using Equation (4), we have shown that there exists eccentric WDs with crystallized cores, close enough to merger for the tidal and rotational contributions to be measurable by LISA. Detailed results can be found in Ref. [33]. From such measurements, it will potentially be possible to infer the individual masses. However, we have found that neglecting the elasticity of the crystallized core could lead to dramatic errors: for a given value of , the relative error on the mass is about 10% for a 0.6 M⊙ oxygen WD, and can even reach ~80% for a very low-mass star of the same composition.
4. Conclusions
We have investigated the role of the crystallization of the core of binary WDs on their tidal deformability in the framework of full general relativity. Such old WDs could be potentially observed by the space-based GW detector LISA.
We have found that the elasticity of the solid core systematically reduces the tidal deformability, especially for low-mass stars. Moreover, the presence of heavy elements in the core increases this effect.
When comparing Newtonian results with our general relativistic ones for fluid stars, we have found that the deviations on the radius and the tidal deformability incurred by the use of the Newtonian theory remain negligible for low-mass stars, but become increasingly important close to the maximum mass.
Focusing on eccentric binaries, we have shown that the measure of the precession rate of the periastron of such systems with LISA could potentially provide information on the tidal deformability parameters or the individual masses. We have found that neglecting the elasticity of the crystallized WD core can lead to dramatic errors on the inferred masses.
Finally, in our study, we have considered cold WDs that have entirely crystallized. However, during the inspiral phase, the outermost layers of the star could melt due to tidal heating, especially close to merger. This issue could be investigated by running thermal evolution simulations of WD binaries.
Author Contributions
Methodology, L.P. and N.C.; software, L.P.; validation, L.P. and N.C.; writing—original draft preparation, L.P. and N.C.; supervision, N.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fonds de la Recherche Scientifique (Belgium). L.P. is a FRIA grantee of the Fonds de la Recherche Scientifique (Belgium).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank J.P. Pereira and F. Gittins for valuable discussions, and E. Gourgoulhon for his kind help regarding the use of SageMath.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bailes, M.; Berger, B.K.; Brady, P.R.; Branchesi, M.; Danzmann, K.; Evans, M.; Holley-Bockelmann, K.; Iyer, B.R.; Kajita, T.; Katsanevas, S.; et al. Gravitational-wave physics and astronomy in the 2020’s and 2030’s. Nat. Rev. Phys. 2021, 3, 344–366. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Andrews, J.; Sedda, M.A.; Askar, A.; Balasov, R.; Bartos, I.; Bavera, S.S.; Bellovary, J.; Berry, C.P.L.; Berti, E.; et al. Astrophysics with the Laser Interferometer Space Antenna. arXiv 2023, arXiv:2203.06016. [Google Scholar]
- Korol, V.; Rossi, E.M.; Groot, P.J.; Nelemans, G.; Toonen, S.; Brown, A.G.A. Prospects for detection of detached double white dwarf binaries with Gaia, LSST and LISA. MNRAS 2017, 470, 1894–1910. [Google Scholar] [CrossRef]
- Lamberts, A.; Blunt, S.; Littenberg, T.B.; Garrison-Kimmel, S.; Kupfer, T.; Sanderson, R.E. Predicting the LISA white dwarf binary population in the Milky Way with cosmological simulations. MNRAS 2019, 490, 5888–5903. [Google Scholar] [CrossRef]
- Li, Z.; Chen, X.; Chen, H.-L.; Li, J.; Yu, S.; Han, Z. Gravitational-wave radiation of double degenerates with extremely low-mass white dwarf companions. ApJ 2020, 893, 2–14. [Google Scholar] [CrossRef]
- Breivik, K.; Coughlin, S.; Zevin, M.; Rodriguez, C.L.; Kremer, K.; Ye, C.S.; Andrews, J.J.; Kurkowski, M.; Digman, M.C.; Larson, S.L.; et al. COSMIC variance in binary population synthesis. ApJ 2020, 898, 71–84. [Google Scholar] [CrossRef]
- Willems, B.; Vecchio, A.; Kalogera, V. Probing white dwarf interiors with LISA: Periastron precession in eccentric double white dwarfs. Phys. Rev. Lett. 2008, 100, 041102. [Google Scholar] [CrossRef]
- Valsecchi, F.; Farr, W.M.; Willems, B.; Deloye, C.J.; Kalogera, V. Tidally induced apsidal precession in double white dwarfs: A new mass measurement tool with LISA. ApJ 2012, 745, 137–144. [Google Scholar] [CrossRef]
- Benacquista, M.J. Tidal perturbations to the gravitational inspiral of J0651+2844. ApJ 2011, 740, L54–L57. [Google Scholar] [CrossRef]
- Shah, S.; Nelemans, G. Measuring tides and binary parameters from gravitational wave data and eclipsing timings of detached white dwarf binaries. ApJ 2014, 791, 76–84. [Google Scholar] [CrossRef]
- Piro, A.L. Inferring the presence of tides in detached white dwarf binaries. ApJ 2019, 885, L2–L6. [Google Scholar] [CrossRef]
- Wolz, A.; Yagi, K.; Anderson, N.; Taylor, A.J. Measuring individual masses of binary white dwarfs with space-based gravitational-wave interferometers. MNRAS 2021, 500, L52–L56. [Google Scholar] [CrossRef]
- Kirzhnits, D.A. Internal structure of super-dense stars. Sov. Phys. JETP 1960, 11, 365. [Google Scholar]
- Abrikosov, A.A. Contribution to the theory of highly compressed matter. Part II. Sov. Phys. JETP 1961, 12, 1254. [Google Scholar]
- Salpeter, E.E. Energy and pressure of a zero-temperature plasma. ApJ 1997, 134, 669–682. [Google Scholar] [CrossRef]
- Winget, D.E.; Kepler, S.O.; Kanaan, A.; Montgomery, M.H.; Giovannini, O. An empirical test of the theory of crystallization in stellar interiors. ApJ 1997, 487, L191–L194. [Google Scholar] [CrossRef]
- Tremblay, P.-E.; Fontaine, G.; Fusillo, N.P.G.; Dunlap, B.H.; Gänsicke, B.T.; Hollands, M.A.; Hermes, J.J.; Marsh, T.R.; Cukanovaite, E.; Cunningham, T. Core crystallization and pile-up in the cooling sequence of evolving white dwarfs. Nature 2019, 565, 202–205. [Google Scholar] [CrossRef]
- Boshkayev, K.; Quevedo, H. Non-validity of I–Love–Q relations for hot white dwarf stars. MNRAS 2018, 478, 1893–1899. [Google Scholar] [CrossRef]
- Taylor, A.J.; Yagi, K.; Arras, P.L. I–Love–Q relations for realistic white dwarfs. MNRAS 2020, 492, 978–992. [Google Scholar] [CrossRef]
- Nelemans, G.; Tauris, T.M. Formation of undermassive single white dwarfs and the influence of planets on late stellar evolution. A&A 1998, 335, L85–L88. [Google Scholar] [CrossRef]
- Liebert, J.; Bergeron, P.; Eisenstein, D.; Harris, H.C.; Kleinman, S.J.; Nitta, A.; Krzesinski, J. A helium white dwarf of extremely low mass. ApJ 2004, 606, L147–L149. [Google Scholar] [CrossRef]
- Benvenuto, O.G.; De Vito, M.A. The formation of helium white dwarfs in close binary systems—II. MNRAS 2005, 362, 891–905. [Google Scholar] [CrossRef]
- Nomoto, K. Evolution of 8-10 solar mass stars toward electron capture supernovae. I—Formation of electron-degenerate O + Ne + Mg cores. ApJ 1984, 277, 791–805. [Google Scholar] [CrossRef]
- Baiko, D.A. Shear modulus of neutron star crust. MNRAS 2011, 416, 22–31. [Google Scholar] [CrossRef]
- Chugunov, A.I. Neutron star crust in Voigt approximation: General symmetry of the stress–strain tensor and an universal estimate for the effective shear modulus. MNRAS 2021, 500, L17–L21. [Google Scholar] [CrossRef]
- Kobyakov, D.; Pethick, C.J. Elastic properties of polycrystalline dense matter. MNRAS 2015, 449, L110–L112. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love numbers of neutron stars. ApJ 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Regge, T.; Wheeler, J.A. Stability of a Schwarzschild singularity. Phys. Rev. 1957, 108, 1063–1069. [Google Scholar] [CrossRef]
- Penner, A.J.; Andersson, N.; Samuelsson, L.; Hawke, I.; Jones, D.I. Tidal deformations of neutron stars: The role of stratification and elasticity. Phys. Rev. D 2011, 84, 103006. [Google Scholar] [CrossRef]
- Gittins, F.; Andersson, N.; Pereira, J.P. Tidal deformations of neutron stars with elastic crusts. Phys. Rev. D 2020, 101, 103025. [Google Scholar] [CrossRef]
- Perot, L.; Chamel, N. Tidal deformability of crystallized white dwarfs in full general relativity. Phys. Rev. D 2022, 106, 023012. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).